Abstract
This paper focuses on the problem of the pth moment and almost sure exponential stability of impulsive neutral stochastic functional differential equations (INSFDEs). Based on the Lyapunov function and average dwell time (ADT), two sufficient criteria for the exponential stability of INSFDEs are derived, which manifest that the result obtained in this paper is more convenient to be used than those Razumikhin conditions in former literature. Finally, two numerical examples and simulations are given to verify the validity of our result.
Keywords:
impulse; exponential stability; neutral stochastic functional differential equations; average dwell time MSC:
60H10; 34F05; 34K45
1. Introduction
As is known to all, neutral stochastic functional differential equations already have attracted much consideration in engineering and science since they can be applied in many fields such as medical, economic, physics and so on [1,2,3,4,5,6,7]. The stability analysis is one of the most important topics in NSFDEs and has already been studied by some classical methods: for example, the Lyapunov–Krasovskii [8], the Lyapunov functional [9,10] and the Razumikhin-type theorem [11,12]. Furthermore, many NSFDEs are often influenced by some impulsive phenomenon which can stabilize or disturb the original system. In fact, when the continuous part of the system is unstable, the impulse can play a positive effect on stabilizing the unstable system [13]; on the contrary, when the continuous part of the system is stable, the impulse can also induce the instability to disturb the original system [14]. Thus, it is extremely necessary and meaningful to investigate the effect of impulse on stability.
The theory of INSFDEs has attracted many authors’ interest over the past few years, and a lot of literature has been published. For instance, without thinking the stochastic item, several criteria of the uniformly asymptotically stability have been studied in [15] by using the classical Razumikhin method. By making the use of contraction, mapping principle and generalized Gronwall–Bellmain inequality, the global exponential stability of a special delayed impulsive neutral differential equation has been studied in [16]. Under the condition of the Euler–Maruyama method, the framework of exponential stability of a special delayed impulsive neutral system has been studied in [17]. While in [18], a new sufficient criterion for the pth moment exponential stability has been investigated under the ADT condition. In addition, readers can refer [19,20,21,22,23,24,25,26,27,28,29,30] to learn more about the investigation of the stability analysis for stochastic functional differential equations.
However, as far as we know, only a few papers reported on the general pth moment and almost sure exponential stability for INSFDEs, for which sporadic results are expected. For example, in [18], the authors investigate the pth moment exponential stability of INSFDEs by using the ADT condition, but the paper only considers the systems with stable continuous stochastic dynamic and unstable discrete dynamics; the other situation, i.e., the system with an unstable continuous part of the stochastic dynamics and stable discrete dynamics, is not considered. In [19], the paper is concerned with the exponential stability of INSFDEs by using the classical Razumikhin technique, but sometimes, it is not easy for us to verify the Razumikhin conditions. The previous literature makes the theoretical results more conservative, which motivates us to close such a gap in this paper.
According to the above discussion, the further investigation about the stability analysis of INSFDEs is absolutely necessary. In this paper, by using Lyapunov function and ADT condition, a Lyapunov theorem is established to handle the pth moment and almost sure exponential of INSFDEs. The results proposed in this paper are suitable for stabilizing impulses or destabilizing impulses; on the other hand, under the ADT condition, the time sequence with eventually uniformly bounded impulse frequency, that is to say, neither nor are needed ( are positive constants), which is very different from the former literature. Moreover, a useful corollary is obtained by using impulsive condition and some inequality techniques. The remainder of the paper is organized as follows. Some definitions and assumptions are going to be firstly introduced in Section 2. The new conditions are proposed to guarantee the pth moment and almost sure exponential stability of INSFDEs in Section 3. In Section 4, we shall also provide two examples and simulations to verify the effectiveness of our result. Finally, we will give a conclusion to enhance the continuity of this paper in the last section.
2. Preliminaries
Let be a complete probability space with a filtration satisfying the usual conditions, i.e., it is increasing and right continuous while contains all -null sets. Let be an m-dimensional Brownian motion defined on the probability space. Let denote the set of positive integers, denote the set of positive real numbers, the n-dimensions real Euclidean space and the space of real matrices. For , denotes the Euclidean norm, and represents the mathematical expectation operator. If A is a vector or matrix, its transpose is denoted by .
Let , denote the family of all continuous -valued functions on exists and , where and denote the right-hand and left-hand limits of function at t. denotes the family of all -measurable -valued random processes such that . denotes the family of all measurable bounded -valued functions.
The INSFDE we considered in the paper is as follows
Here, the initial value , is the system state, . Moreover, and . . The fixed moments impulse times satisfy , as .
Assumption A1.
Assume that there is a constant such that for any
Remark 1.
Assumption 1 mainly gives a limitation to neutral term. In fact, the neutral term can be regarded as a perturbation for the stochastic functional differential equations (SFDEs), which can disturb the original system. So, the coefficient κ is chosen from in order to reduce the disturbance of neutral term.
Throughout the paper, we always assume that satisfied the needful condition for the global existence and uniqueness of solution for all , denoted by , which is continuous on the right-hand side and limited on the left-hand side. In addition, we assume that and , which implies that is a trivial solution. For convenience, we denote for and for . Let denotes the non-negative valued and continuous twice differential for x and once for t. For , we define the following operator for Equation (1).
Definition 1.
The trivial solution of (1) is said to be pth moment exponentially stable if there exist two positive constants such that
for any initial value.
Remark 2.
([1]). When , it is often said to be exponentially stable in mean square.
Definition 2.
The trivial solution of (1) is said to be almost surely exponentially stable if there exist such that
for any initial value.
Definition 3.
([31,32,33]). Let denote the impulsive sequence and represent the number of instant on the semiopen interval , if
For , then and are named ADT and elasticity number, respectively.
Lemma 1.
([5]). Suppose Assumption 1 holds. Then, for any and , we have
and
3. Main Results
In this part, by Lyapunov function and ADT condition, we will establish a framework to check both the pth moment and almost sure exponential stability. The criteria proposed in this section are more general than the previous result in [16].
3.1. pth Moment Exponential Stability
Theorem 1.
Let be positive numbers. Suppose that Assumption 1 holds and there exists a function such that
- (H1)
- , for any ;
- (H2)
- For any
- (H3)
- For ;
- (H4)
- and
Then, the trivial solution of (1) is pth moment exponentially stable, where and are positive constants defined in Definition 3.
Proof.
For , by applying the Dynkin’s [34] formula and condition (H2) we have
which implies
For , from condition (H3) and (4), we deduce that
Thus, for , by inequality (4), we obtain
Then, by inequality (5), we have
For , according to the inequality (4) and (6), we obtain
Similiar as the deduction of inequality (5), we obtain
For , by the same method, together with (4) and (7), we obtain
By induction, we obtain from
With the help of Lemma 1, it yields from (9) that
Based on the condition (H4), inequality and continuity, one can choose and a small enough constant such that
By the definition of M, we have
Next, we shall claim that
Suppose the above inequality (13) is not true; thus, there must exists such that
By inequality (10) and (14), we deduce that
There are two cases that need to be considered.
Case 1.. In this case, we obtain
where
Case 2.. In this case, we have
where
Therefore, based on the analysis of inequality (16) and (17) and the technique proposed in [21], we know that inequality (11) implies that , which is a contradiction. So (13) is proven, and the trivial solution of Equation (1) is pth moment exponentially stable. □
Remark 3.
Theorem 1 can be regarded as a complement of literature [2] in impulsive cases. In fact, this theorem tells us that the impulse can potentially destroy the stability of INSFDEs when and can also be beneficial to the stability when .
Remark 4.
The condition guarantees that the series is convergent, if , set , then can be redefined as .
Remark 5.
In Theorem 1, we define a Lyapunov function , and we should point out that the Lyapunov function can not only be affected by the impulse condition defined in Equation (1), but also be influenced by a neutral item when , which is the crucial different from the traditional impulsive systems.
3.2. Almost Sure Exponential Stability
Lemma 2.
([1]). Suppose that there is a positive constant such that
Let be a continuous function and define for all . Let and . Then
implies that
Remark 6.
Lemma 2 tells us that if is exponentially stable; then, we can deduce that is also exponentially stable.
Assumption A2.
Suppose the impulsive instants satisfy
Theorem 2.
Let , suppose that Assumption 2 holds and all the conditions of Theorem 1 are satisfied. If there exists positive constants such that for all ,
and
then for any
Proof.
For , we deduce that
By Assumption 1, we obtain
By inequality, combining (22), we obtain
According to the Burkholder–Davis–Gundy inequality, we have
where is a positive constant. By (22) and inequality, we obtain
By inequality (23), we have
and
where is the maximum integer not more than . Substituting (26), (27), (29), (30), and (31) into (25), we have for ,
where is a positive constant. Let and be arbitrary. Inequality (32) implies that
By the Borel–Cantelli lemma, one can choose a positive constant , then for almost all ,
Then, for and for almost all
However, is finite on . Thus, we conclude that for almost all , there exist a finite positive number H such that for any ,
Therefore, by Lemma 2
Then, let . the proof is completed. □
In the next part, we will extend the results we obtained to the impulsive neutral stochastic differential delay equations (INSDDEs).
Consider the following INSDDE
where , are Borel measurable functions with and for all . This is a special case of Equation (1) with , and for all . If ; for the special case, the operator L defined in (1) becomes
where and . The above result is applied to (38) and the following useful corollary is obtained.
Corollary 1.
Let , be positive numbers. Assume that there exists a constant such that
and there exists a function such that
- (H1)
- , for all ;
- (H2)
- for all and
- (H3)
- for all ;
- (H4)
- and , where will be defined in the following process; then, the trivial solution of Equation (38) is pth moment exponentially stable.
Proof.
For any , by inequality (40) and Lemma 1, we can obtain
and
If , in this case, for any , we have
If , in this case, for any , we obtain
For , we obtain
Let and . If , choose and ; If , choose and . Then, by condition (H4) and Theorem 1, we obtain that the trivial solution of Equation (38) is pth moment exponentially stable. Of course, if the equation satisfies the inequality (21)–(23), the trivial solution is also almost surely exponentially stable. □
4. Examples
In this section, we shall give two examples and simulations to show the effectiveness of the results obtained in this paper.
Example 1.
Consider the one-dimensional INSDDE
By applying Corollary 1, we shall show that the zero solution of Equation (44) is exponentially stable in mean square.
One can choose a simple Lyapunov function
then (H1) is satisfied with and
By calculating the operator , utilizing It’s formula and Corollary 1, we have
Thus, one can verify that (H2) is satisfied by choosing and .
For , we compute that
which implies that (H3) holds by letting and
The impulsive time sequence is given by with and , which illustrates that (H4) is satisfied.
According to Corollary 1, the trivial solution of (44) is exponentially stable in mean square. Set ; the simulation result is presented in Figure 1 and Figure 2. For linear INSDDE, the conditions of Theorem 2 are obviously satisfied, so the trivial is also almost surely exponentially stable.
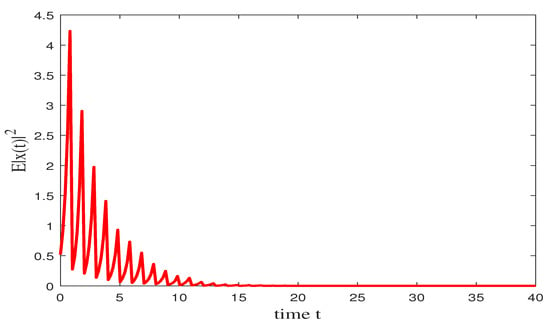
Figure 1.
State trajectories of (44) with impulsive control.
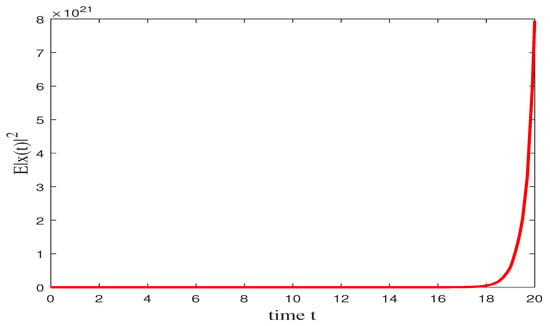
Figure 2.
State trajectories of (44) without impulsive control.
Remark 7.
In Example 1, the impulses play a positive effect on stabilizing the unstable dynamical system. Thus, we need to guarantee that the impulses must be frequent enough to ensure their amplitude is suitable for the growth rate of .
Remark 8.
It should be pointed out that and > 0 imply the operator cannot be controlled by nonpositive constants. In such a situation, those results in [16] cannot be applied because they need to keep the operator to be negative.
Example 2.
Consider the following INSDDE
where
and .
We conclude from Corollary 1 that the zero solution of Equation (46) is exponentially stable in mean square. Just as the former example, one can choose the following Lyapunov function
where condition (H2) implies and .
By calculating the operator , utilizing It formula and Corollary 1, we have
Thus, one can verify that (H2) is satisfied by choosing and
For , we compute that
then (H3) holds by letting and
The impulsive time sequence is given by [35] with and , which illustrates that (H4) is satisfied.
According to Corollary 1, the trivial solution of (46) is exponentially stable in mean square. Of course, the trivial solution of (46) is also almost surely exponentially stable, the simulation is presented in Figure 3 in which the initial value is .
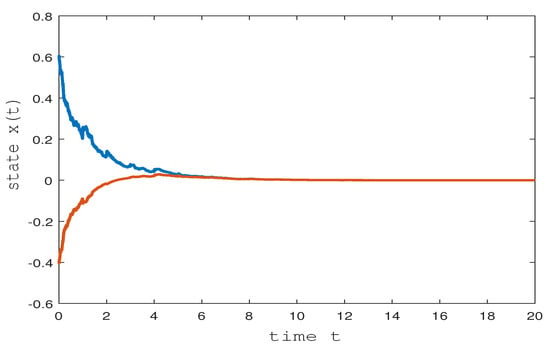
Figure 3.
State trajectories of (46) under destabilizing impulsive perturbation.
Remark 9.
We find that the results in [14,16] are invalid for this example because the impulse condition proposed in [14,16] is too restrictive to be applied. Meanwhile, the impulse condition mentioned in this paper can be satisfied easily.
5. Conclusions
With the help of the ADT condition, less constructive conditions for the pth moment and almost sure exponential stability have been derived for INSFDEs. The method proposed in this paper can be further used to investigate the time-varying systems, which will be studied in the near future.
Author Contributions
Y.L.: writing—original draft preparation, P.C. and Z.W.: writing—review and editing, P.C.: funding acquisition. All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Natural Science Foundation of China under Grant 11771001, the Key Natural Science Research Project of Universities in Anhui Province under Grant KJ2020A0121, and the Support Program for Outstanding Young Talents of Universities in Anhui Province under Grant gxyq2021204.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mao, X. Stochastic Differential Equation and Applications; Horwood Publishing Limited: Oxford, UK, 1997. [Google Scholar]
- Jankovic, S.; Randjelovic, J. Razumikhin-type exponential stability criteria of neutral stochastic functional differential equations. J. Math. Anal. 2009, 355, 811–820. [Google Scholar] [CrossRef]
- Mao, X. Exponential stability in mean square of neutral stochastic differential functional equations. Syst. Control Lett. 1995, 26, 245–251. [Google Scholar] [CrossRef]
- Mao, X. Asymptoic properties of neutral stochastic differential delay equation. Stochastics 2014, 68, 273–295. [Google Scholar]
- Karthikeyan, S.; Balachandran, K. Controllability of nonlinear stochastic neutral impulsive systems. Nonlinear Anal. Hybrid Syst. 2009, 3, 266–276. [Google Scholar] [CrossRef]
- Song, Y.; Sun, W.; Jiang, F. Mean-square exponential input-to-state stability for neutral stochastic neural networks with mixed delays. Neurocomputing 2016, 205, 195–203. [Google Scholar] [CrossRef]
- Chen, H.; Shi, P.; Lim, C. Cluster synchronization for neutral stochastic delay networks via intermittent adaptive control. IEEE Trans Neural Netw. Learn. Syst. 2019, 30, 3246–3259. [Google Scholar] [CrossRef]
- Luo, Q.; Mao, X.; Shen, Y. New criteria on exponential stability of neutral stochastic differential delay equations. Syst. Control Lett. 2006, 55, 826–834. [Google Scholar] [CrossRef]
- Chen, W.; Xu, S. Stabilization of hybrid neutral stochastic differential delay equations by delay feedback control. Syst. Control Lett. 2016, 115, 1–8. [Google Scholar] [CrossRef]
- Shen, M.; Fei, W. Stability of highly nonlinear neutral stochastic differential delay equations. Syst. Control Lett. 2018, 115, 1718–1723. [Google Scholar] [CrossRef]
- Huang, L.; Deng, F. Razumikhin-type theorems on stability of neutral stochastic functional differential equations. IEEE Trans. Autom. Control 2009, 53, 1718–1723. [Google Scholar] [CrossRef]
- Hu, W. A new stability criterion for neutral stochastic delay differential equations with Markovian switching. Math. Prob. Eng. 2018, 2018, 7814974. [Google Scholar] [CrossRef]
- Cheng, P.; Deng, F. Global exponential stability of impulsive stochastic functional differential systems. Stat. Probab. Lett. 2010, 80, 1854–1862. [Google Scholar] [CrossRef]
- Pan, L.; Cao, J. Exponential stability of impulsive stochastic functional differential equations. J. Math. Anal. Appl. 2011, 382, 672–685. [Google Scholar] [CrossRef]
- Li, X.; Deng, F. Razumikhin method for impulsive functional differential equations of neutral type. Chaos Solitons Fractals 2017, 101, 41–49. [Google Scholar] [CrossRef]
- Kaviya, R.; Muthukumar, P. Exponential stability of non-linear neutral stochastic delay differential system with generalized delay-dependent impulsive points. J. Frankl. Inst. 2021, 358, 5014–5038. [Google Scholar] [CrossRef]
- He, J.; Kong, F. Globally exponential stability of piecewise pseudo almost periodoc solutions for neutral differential equations with impulses and delays. Qual. Theory Dyn. Syst. 2022, 21, 1–7. [Google Scholar] [CrossRef]
- Fu, X.; Zhu, Q. Exponential stability of neutral stochastic delay differential equation with delay-dependent impulses. Appl. Math. Comput. 2020, 377, 125146. [Google Scholar] [CrossRef]
- Yu, G.; Yang, W.; Xu, L.; Chen, H.; Zhao, Y. pth moment and almost sure exponential stability of impulsive neutral stochastic functional differential equations with Markovian switching. Int. J. Syst. Sci. 2018, 49, 1441467. [Google Scholar] [CrossRef]
- Liu, J.; Xu, W. An averaging result for impulsive fractional neutral stochastic differential equations. Syst. Control Lett. 2021, 114, 106892. [Google Scholar] [CrossRef]
- Chen, H.; Shi, P. Exponential stability for neutral stochastic Markov systems with time-varying delay and its applications. IEEE Trans. Autom. Control 2016, 46, 6. [Google Scholar] [CrossRef]
- Chen, H.; Shi, P. Stability analysis for neutral stochastic delay systems with Markovian switching. Appl. Math. Lett. 2017, 110, 38–48. [Google Scholar] [CrossRef]
- Chen, H.; Shi, P. Stability analysis for stochastic neutral switched systems with time-varying delay. SIAM J. Control Optim. 2021, 59, 24–49. [Google Scholar] [CrossRef]
- Cai, T.; Cheng, P. Stability analysis of discrete-time stochastic delay systems with impulses. Mathematics 2021, 9, 418. [Google Scholar] [CrossRef]
- Liu, L.; Deng, F.; Qu, B. Fundamental properities of nonlinear stochastic differential equations. Mathematics 2022, 10, 2690. [Google Scholar] [CrossRef]
- Pankov, P.S.; Zheentaeva, Z.K.; Shirinov, T. Asymptotic reduction of solution space dimension for dynamical systems. TWMS J. Pure Appl. Math. 2021, 12, 243–253. [Google Scholar]
- Shokri, A.; Saadat, H. Trigonometrically fitted high-order predictor-corrector method with phase-lag of order infinity for the numerical solution of radial Schrödinger equation. J. Math. Chem. 2014, 52, 1870–1894. [Google Scholar] [CrossRef]
- Shokri, A.; Saadat, H. P-stability, TF and VSDPL technique in Obrechkoff methods for the numerical solution of the Schrodinger equation. Bull. Iran. Math. Soc. 2016, 42, 687–706. [Google Scholar]
- Qalarov, A.A.; Khaldjigitov, A.A. Mathematical and numerical modeling of the coupled dynamic thermoelastic problems for isotropic bodies. TWMS J. Pure Appl. Math. 2020, 11, 119–126. [Google Scholar]
- Li, B. Stability of stochastic functional differential equations with impulses by an average approach. Nonlinear Anal. Hybrid Syst. 2018, 29, 221–233. [Google Scholar] [CrossRef]
- Hespanha, P.; Liberzon, D.; Teel, A. Lyapunov conditions for input-to-state stability of impulsive systems. Automatica 2008, 44, 2735–2744. [Google Scholar] [CrossRef]
- Lu, J.; Ho, D.; Cao, J. A unified synchronization criterion for impulsive dynamical networks. Automatica 2010, 46, 1215–1221. [Google Scholar] [CrossRef]
- Peng, S.; Deng, F. New criteria on pth moment input-to-state stability of impulsive stochastic delayed differential systems. IEEE Trans. Autom. Control 2017, 7, 3573–3579. [Google Scholar] [CrossRef]
- Bernt, Ø. Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Lee, L.; Liu, Y.; Liang, J.; Cai, X. Finite time stability of nonlinear impulsive systems and its application in sampled-data systems. ISA Trans. 2015, 37, 172–178. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).