Coupling Chemotaxis and Growth Poromechanics for the Modelling of Feather Primordia Patterning
Abstract
1. Introduction
2. A Coupled Model of Linear Poroelasticity and Chemotaxis
3. Linear Stability Analysis and Dispersion Relation
3.1. Preliminaries
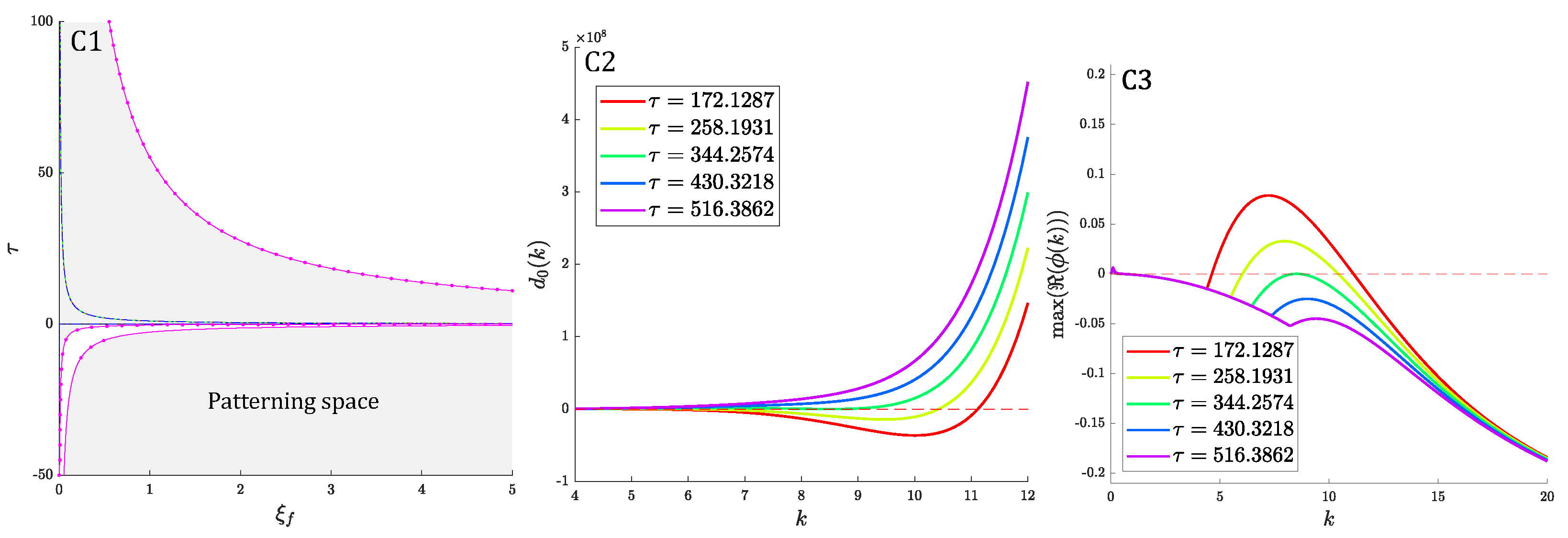
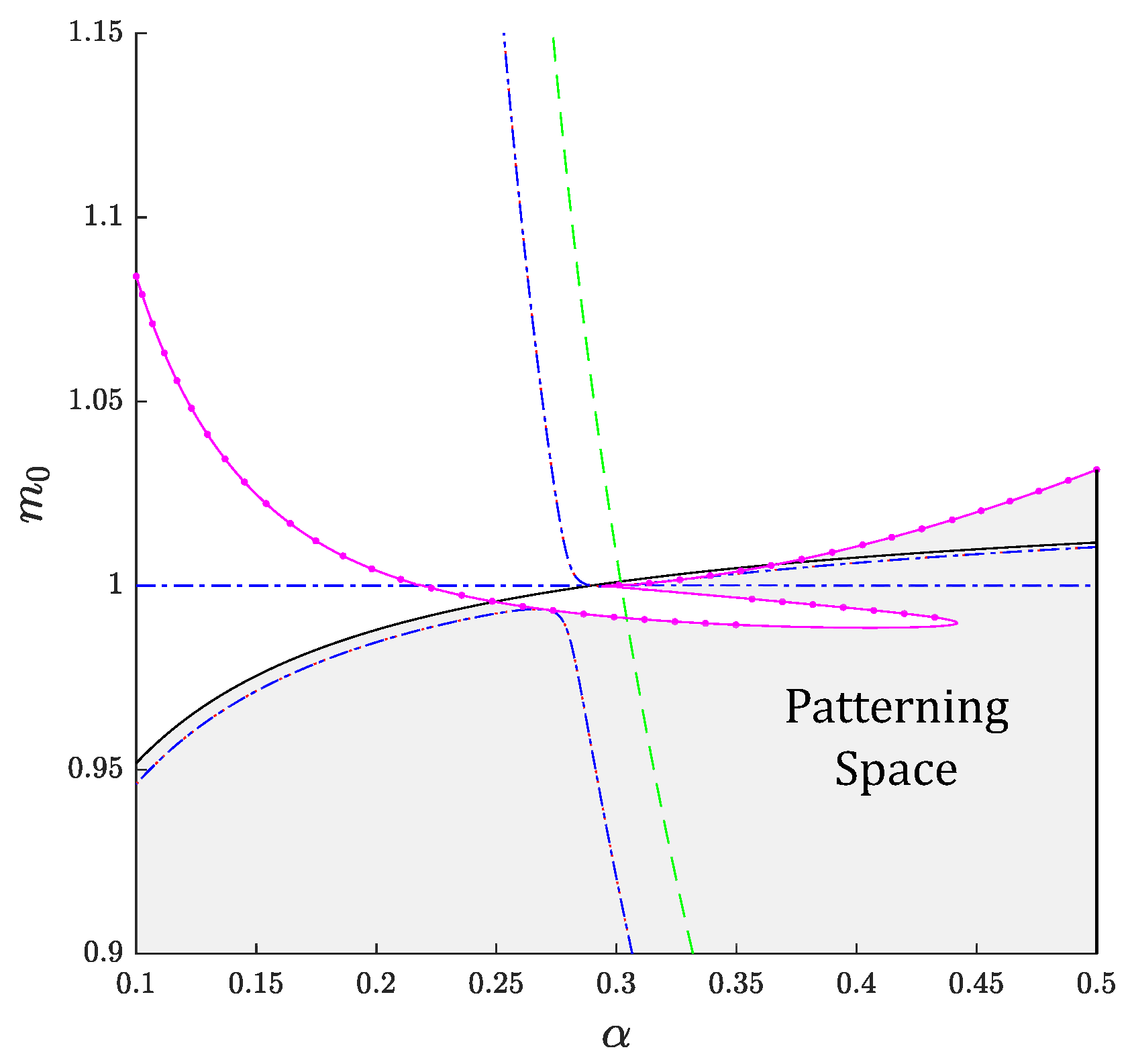
3.2. Spatially Homogeneous Distributions
3.3. Zero Chemotaxis
3.4. Uncoupled System
3.5. Zero Activation/Inactivation of Epithelium
3.6. General Case
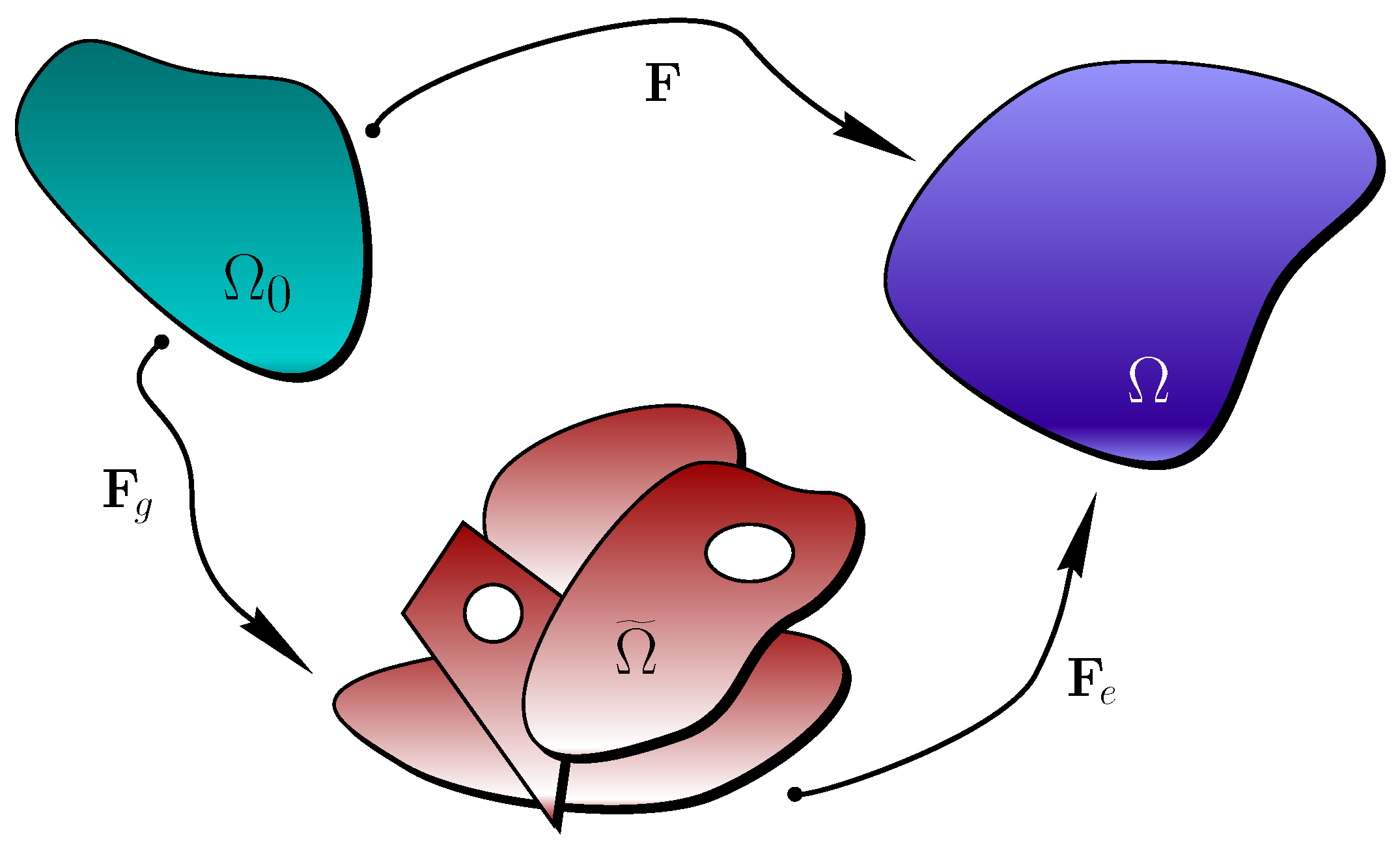
4. Extension to Finite-Strain Poroelasticity and Growth
5. Numerical Tests
5.1. Discretisation and Implementation
5.2. Mesh Independence Study
5.3. Efficient Preconditioners
- Chemotaxis. This problem considers four similar building block physics, consisting essentially of three parabolic problems and one algebraic constraint . We consider an additive block solver, meaning that we use a block-wise Jacobi preconditioner with only the diagonal block of each variable. At the block level, we consider the action of an AMG preconditioner for the parabolic problems and the action of a Jacobi preconditioner for the algebraic one.
- Poromechanics. The poromechanics block is more difficult, which is reflected in the complexity of the preconditioner under consideration. It is based on the block preconditioner proposed in [8] for large-strain poromechanics, where we use a lower Schur complement block factorisation with the fields and . For such a block we consider the action of an AMG preconditioner, whereas for the corresponding Schur complement block we consider instead a sparse representation given by an ad hoc extension of the fixed-stress splitting scheme proposed in [25]. For this, we add two stabilisation terms given bywhere we have denoted with the test function corresponding to each variable and have used the values . As this approach yields a sparse operator that approximates the Schur complement, we simply use the action of an AMG preconditioner based on it.
5.4. Suppressed Solid Motion vs. Periodic Boundary Traction
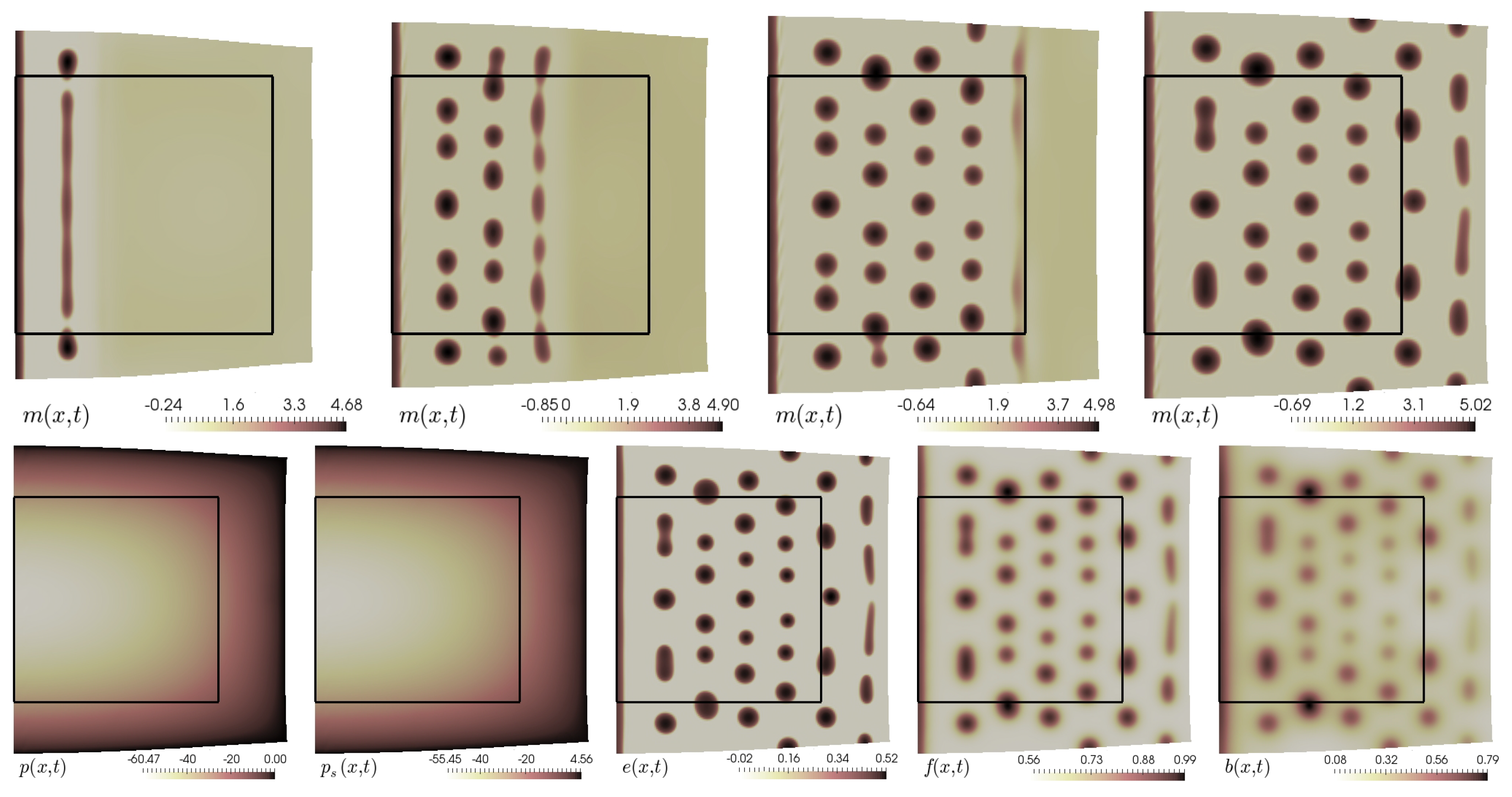
5.5. Finite Growth in 2D
5.6. Finite Growth in 3D
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Proposition 1
References
- Keller, E.F.; Segel, L.A. Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 1970, 26, 399–415. [Google Scholar] [CrossRef]
- Yang, X.; Dormann, D.; Münsterberg, A.E.; Weijer, C.J. Cell movement patterns during gastrulation in the chick are controlled by positive and negative chemotaxis mediated by FGF4 and FGF8. Dev. Cell 2002, 3, 425–437. [Google Scholar] [CrossRef]
- Lin, C.M.; Jiang, T.X.; Baker, R.E.; Maini, P.K.; Widelitz, R.B.; Chuong, C.M. Spots and stripes: Pleomorphic patterning of stem cells via p-ERK-dependent cell chemotaxis shown by feather morphogenesis and mathematical simulation. Dev. Biol. 2009, 334, 369–382. [Google Scholar] [CrossRef] [PubMed]
- Mou, C.; Pitel, F.; Gourichon, D.; Vignoles, F.; Tzika, A.; Tato, P.; Yu, L.; Burt, D.W.; Bed’Hom, B.; Tixier-Boichard, M.; et al. Cryptic patterning of avian skin confers a developmental facility for loss of neck feathering. PLoS Biol. 2011, 9, e1001028. [Google Scholar] [CrossRef] [PubMed]
- Painter, K.J.; Hunt, G.S.; Wells, K.L.; Johansson, J.A.; Headon, D.J. Towards an integrated experimental–theoretical approach for assessing the mechanistic basis of hair and feather morphogenesis. Interface Focus 2012, 2, 433–450. [Google Scholar] [CrossRef]
- Painter, K.J.; Ho, W.; Headon, D.J. A chemotaxis model of feather primordia pattern formation during avian development. J. Theor. Biol. 2018, 437, 225–238. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Barnafi, N.; Gómez-Vargas, B.; Lourenço, W.J.; Reis, R.F.; Rocha, B.M.; Lobosco, M.; Ruiz-Baier, R.; Santos, R.W.d. Finite element methods for large-strain poroelasticity/chemotaxis models simulating the formation of myocardial oedema. J. Sci. Comput. 2022, 92, e92. [Google Scholar] [CrossRef]
- Lourenço, W.d.J.; Reis, R.F.; Ruiz-Baier, R.; Rocha, B.M.; Santos, R.W.d.; Lobosco, M. A poroelastic approach for modelling myocardial oedema in acute myocarditis. Front. Physiol. 2022, 13, e888515. [Google Scholar] [CrossRef] [PubMed]
- Barnafi, N.; Gregorio, S.D.; Dedè, L.; Zunino, P.; Vergara, C.; Quarteroni, A. A multiscale poromechanics model integrating myocardial perfusion and systemic circulation. SIAM J. Appl. Math. 2021, 82, 1113–1660. [Google Scholar]
- Vuong, A.-T.; Yoshihara, L.; Wall, W.A. A general approach for modeling interacting flow through porous media under finite deformations. Comput. Methods Appl. Mech. Eng. 2015, 283, 1240–1259. [Google Scholar] [CrossRef]
- Berger, L.; Bordas, R.; Burrowes, K.; Grau, V.; Tavener, S.; Kay, D. A poroelastic model coupled to a fluid network with applications in lung modelling. Int. J. Numer. Methods Biomed. Eng. 2016, 32, e02731. [Google Scholar] [CrossRef] [PubMed]
- Vilaca, L.M.D.O.; Gómez-Vargas, B.; Kumar, S.; Ruiz-Baier, R.; Verma, N. Stability analysis for a new model of multi-species convection-diffusion-reaction in poroelastic tissue. Appl. Math. Model. 2020, 84, 425–446. [Google Scholar] [CrossRef]
- Moeendarbary, E.; Valon, L.; Fritzsche, M.; Harris, A.R.; Moulding, D.A.; Thrasher, A.J.; Stride, E.; Mahadevan, L.; Charras, G.T. The cytoplasm of living cells behaves as a poroelastic material. Nat. Mater. 2013, 12, e3517. [Google Scholar] [CrossRef] [PubMed]
- Collis, J.; Brown, D.L.; Hubbard, M.E.; O’Dea, R.D. Effective equations governing an active poroelastic medium. Proc. R. Soc. A 2017, 473, e20160755. [Google Scholar] [CrossRef] [PubMed]
- Penta, R.; Ambrosi, D.; Shipley, R.J. Effective governing equations for poroelastic growing media. Q. J. Mech. Appl. Math. 2014, 67, 69–91. [Google Scholar] [CrossRef]
- Jones, G.W.; Chapman, S.J. Modeling growth in biological materials. SIAM Rev. 2012, 54, 52–118. [Google Scholar] [CrossRef]
- Kuhl, E. Growing matter: A review of growth in living systems. J. Mech. Behav. Biomed. Mater. 2014, 29, 529–543. [Google Scholar] [CrossRef]
- Mascheroni, P.; Carfagna, M.; Grillo, A.; Boso, D.P.; Schrefler, B.A. An avascular tumor growth model based on porous media mechanics and evolving natural states. Math. Mech. Solids 2018, 23, 686–712. [Google Scholar] [CrossRef]
- Moreo, P.; Gaffney, E.A.; García-Aznar, J.M.; Doblaré, M. On the modelling of biological 795 patterns with mechanochemical models: Insights from analysis and computation. Bull. Math. Biol. 2010, 72, 400–431. [Google Scholar] [CrossRef]
- Murray, J.D.; Maini, P.K.; Tranquillo, R.T. Mechanochemical models for generating biological pattern and form in development. Phys. Rep. 1988, 171, 59–84. [Google Scholar] [CrossRef]
- Radszuweit, M.; Engel, H.; Bär, M. An active poroelastic model for mechanochemical patterns in protoplasmic droplets of physarum polycephalum. PLoS ONE 2014, 9, e99220. [Google Scholar] [CrossRef] [PubMed]
- Barnafi, N.; Zunino, P.; Dedè, L.; Quarteroni, A. Mathematical analysis and numerical approximation of a general linearized poro-hyperelastic model. Comput. Math. Appl. 2021, 91, 202–228. [Google Scholar] [CrossRef]
- Berger, L.; Bordas, R.; Kay, D.; Tavener, S. A stabilized finite element method for finite-strain three-field poroelasticity. Comput. Mech. 2017, 60, 51–68. [Google Scholar] [CrossRef] [PubMed]
- Borregales, M.; Radu, F.A.; Kumar, K.; Nordbotten, J.M. Robust iterative schemes for non-linear poromechanics. Computat. Geosci. 2018, 22, 1021–1038. [Google Scholar] [CrossRef]
- Costanzo, F.; Miller, S.T. An arbitrary Lagrangian-Eulerian finite element formulation for a poroelasticity problem stemming from mixture theory. Comput. Methods Appl. Mech. Eng. 2017, 323, 64–97. [Google Scholar] [CrossRef]
- Korsawe, J.; Starke, G.; Wang, W.; Kolditz, O. Finite element analysis of poro-elastic consolidation in porous media: Standard and mixed approaches. Comput. Methods Appl. Mech. Eng. 2006, 195, 1096–1115. [Google Scholar] [CrossRef]
- Verma, N.; Gómez-Vargas, B.; Vilaca, L.M.D.O.; Kumar, S.; Ruiz-Baier, R. Well-posedness and discrete analysis for advection-diffusion-reaction in poroelastic media. Appl. Anal. 2022, 101, 4914–4941. [Google Scholar] [CrossRef]
- Kadeethum, T.; Lee, S.; Ballarind, F.; Choo, J.; Nick, H.M. A locally conservative mixed finite element framework for coupled hydro-mechanical–chemical processes in heterogeneous porous media. Comput. Geosci. 2021, 152, e104774. [Google Scholar] [CrossRef]
- Armstrong, M.H.; Tepole, A.B.; Kuhl, E.; Simon, B.R.; Geest, J.P.V. A finite element model for mixed porohyperelasticity with transport, swelling, and growth. PLoS ONE 2016, 11, e0152806. [Google Scholar] [CrossRef]
- Jin, L.; Zoback, M.D. Fully dynamic spontaneous rupture due to quasi-static pore pressure and poroelastic effects: An implicit nonlinear computational model of fluid-induced seismic events. J. Geophys. Res. Solid Earth 2018, 123, 9430–9468. [Google Scholar] [CrossRef]
- Luo, P.; Rodrigo, C.; Gaspar, F.J.; Oosterlee, C.W. Multigrid method for nonlinear poroelasticity equations. Comput. Visual. Sci. 2015, 17, 255–265. [Google Scholar] [CrossRef]
- Showalter, R.E. Diffusion in poro-elastic media. J. Math. Anal. Appl. 2000, 251, 310–340. [Google Scholar] [CrossRef]
- Routh, E.J. A Treatise on the Stability of a Given State of Motion: Particularly Steady Motion; Macmillan and Company: London, UK, 1877. [Google Scholar]
- Lee, E.H. Elastic-plastic deformation at finite strains. J. Appl. Mech. 1969, 36, 1–6. [Google Scholar] [CrossRef]
- Rodriguez, E.K.; Hoger, A.; McCulloch, A.D. Stress-dependent finite growth in soft elastic tissues. J. Biomech. 1994, 27, 455–467. [Google Scholar] [CrossRef]
- Kida, N.; Morishita, Y. Continuum mechanical modeling of developing epithelial tissues with anisotropic surface growth. Finite Elem. Anal. Des. 2018, 144, 49–60. [Google Scholar] [CrossRef]
- Amar, M.B.; Goriely, A. Growth and instability in elastic tissues. J. Mech. Phys. Solids 2005, 53, 2284–2319. [Google Scholar] [CrossRef]
- Giverso, C.; Scianna, M.; Grillo, A. Growing avascular tumours as elastoplastic bodies by the theory of evolving natural configurations. Mech. Res. Commun. 2015, 68, 31–39. [Google Scholar] [CrossRef]
- Braess, D.; Ming, P. A finite element method for nearly incompressible elasticity problems. Math. Comp. 2005, 74, 25–52. [Google Scholar] [CrossRef]
- Alnæs, M.S.; Blechta, J.; Hake, J.; Johansson, A.; Kehlet, B.; Logg, A.; Richardson, C.; Ring, J.; Rognes, M.E.; Wells, G.N. The FEniCS project version 1.5. Arch. Numer. Softw. 2015, 3, 9–23. [Google Scholar]
- Rathgeber, F.; Ham, D.A.; Mitchell, L.; Lange, M.; Luporini, F.; McRae, A.T.T.; Bercea, G.T.; Markall, G.R.; Kelly, P.H.J. Firedrake: Automating the finite element method by composing abstractions. ACM T. Math. Softw. (TOMS) 2016, 43, 1–27. [Google Scholar] [CrossRef]
- Dembo, R.S.; Eisenstat, S.C.; Steihaug, T. Inexact Newton methods. SIAM J. Numer. Anal. 1982, 19, 400–408. [Google Scholar] [CrossRef]
- Dervaux, J.; Ciarletta, P.; Amar, M.B. Morphogenesis of thin hyperelastic plates: A constitutive theory of biological growth in the Föppl–von Kármaán limit. J. Mech. Phys. Solids 2009, 57, 458–471. [Google Scholar] [CrossRef]
- Vilaca, L.M.D.O.; Milinkovitch, M.C.; Ruiz-Baier, R. Numerical approximation of a 3D mechanochemical interface model for skin patterning. J. Comput. Phys. 2019, 384, 283–404. [Google Scholar]
- Bociu, L.; Guidoboni, G.; Sacco, R.; Webster, J.T. Analysis of nonlinear poro-elastic and poro-visco-elastic models. Arch. Ration. Mech. Anal. 2016, 222, 1445–1519. [Google Scholar] [CrossRef]
- Kaouri, K.; Méndez, P.E.; Ruiz-Baier, R. Mechanochemical models for calcium waves in embryonic epithelia. Vietnam J. Math. 2022, 50, 947–975. [Google Scholar] [CrossRef]






| DoF | r | r | r | r | r | r | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 64 | * | * | * | * | * | * | ||||||
| 176 | 1.77 | 1.16 | 1.88 | 0.70 | 0.67 | 0.63 | ||||||
| 568 | 1.19 | 0.97 | 1.36 | 0.57 | 0.53 | 0.56 | ||||||
| 2024 | 1.08 | 1.19 | 1.09 | 0.61 | 0.73 | 0.73 | ||||||
| 7624 | 1.02 | 1.11 | 1.02 | 0.76 | 0.96 | 0.96 | ||||||
| 29,576 | 0.98 | 0.94 | 1.01 | 0.82 | 1.00 | 0.99 | ||||||
| 116,488 | 0.98 | 0.92 | 1.00 | 0.95 | 1.00 | 1.00 |
| Mesh | Cardinality | Total DoFs | CPU Time | Error |
|---|---|---|---|---|
| I | 30 K | 110 K | 15% | 9% |
| II | 60 K | 218 K | 25% | 5% |
| III | 120 K | 430 K | 40% | 4% |
| DoFs | 1 CPU | 2 CPUs | 4 CPUs | 8 CPUs | 12 CPUs | 16 CPUs |
|---|---|---|---|---|---|---|
| 3528 | 0.57 (10) | 0.56 (10) | 0.68 (10) | 0.72 (10) | 0.77 (10) | 0.7 (10) |
| 20,172 | 1.01 (10) | 1.00 (9) | 1.01 (10) | 0.93 (10) | 1.25 (10) | 0.93 (10) |
| 59,536 | 2.35 (11) | 1.95 (9) | 1.46 (10) | 1.31 (9) | 1.03 (10) | 1.29 (10) |
| 131,220 | 5.43 (11) | 3.44 (10) | 2.48 (10) | 1.81 (10) | 1.63 (10) | 1.6 (10) |
| 244,824 | 10.72 (11) | 6.36 (11) | 4.35 (11) | 2.7 (10) | 2.59 (10) | 2.34 (10) |
| 409,948 | 19.03 (12) | 12.93 (12) | 7.09 (12) | 4.7 (12) | 3.72 (12) | 3.26 (12) |
| 636,192 | 31.57 (12) | 20.14 (12) | 11.27 (12) | 7.11 (12) | 5.38 (12) | 4.72 (12) |
| 933,156 | 49.81 (12) | 29.2 (12) | 16.24 (12) | 9.73 (12) | 7.55 (12) | 6.82 (12) |
| (a) Performance of chemotaxis solver. | ||||||
| DoFs | 1 CPU | 2 CPUs | 4 CPUs | 8 CPUs | 12 CPUs | 16 CPUs |
| 16,893 | 2.5 (8) | 1.8 (8) | 1.8 (8) | 2.05 (8) | 1.91 (8) | 2.17 (8) |
| 108,501 | 12.13 (12) | 7.27 (12) | 4.8 (12) | 3.11 (12) | 2.8 (12) | 2.89 (12) |
| 337,229 | 39.71 (13) | 22.62 (14) | 12.31 (14) | 7.57 (14) | 6.6 (14) | 5.72 (14) |
| 765,477 | 98.6 (14) | 52.06 (14) | 28.45 (14) | 16.5 (14) | 12.57 (14) | 10.79 (14) |
| 1,455,645 | 202.15 (14) | 102.76 (14) | 56.51 (14) | 32.32 (14) | 23.83 (14) | 19.58 (14) |
| 2,470,133 | 350.59 (14) | 192.52 (14) | 99.84 (14) | 55.04 (14) | 40.24 (14) | 33.75 (14) |
| 3,871,341 | 598.98 (15) | 324.14 (15) | 168.48 (15) | 89.02 (15) | 63.27 (15) | 54.29 (15) |
| 5,721,669 | 869.06 (15) | 462.3 (15) | 242.9 (15) | 130.09 (15) | 98.15 (15) | 78.02 (15) |
| (b) Performance of poromechanics solver. | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barnafi, N.A.; De Oliveira Vilaca, L.M.; Milinkovitch, M.C.; Ruiz-Baier, R. Coupling Chemotaxis and Growth Poromechanics for the Modelling of Feather Primordia Patterning. Mathematics 2022, 10, 4096. https://doi.org/10.3390/math10214096
Barnafi NA, De Oliveira Vilaca LM, Milinkovitch MC, Ruiz-Baier R. Coupling Chemotaxis and Growth Poromechanics for the Modelling of Feather Primordia Patterning. Mathematics. 2022; 10(21):4096. https://doi.org/10.3390/math10214096
Chicago/Turabian StyleBarnafi, Nicolás A., Luis Miguel De Oliveira Vilaca, Michel C. Milinkovitch, and Ricardo Ruiz-Baier. 2022. "Coupling Chemotaxis and Growth Poromechanics for the Modelling of Feather Primordia Patterning" Mathematics 10, no. 21: 4096. https://doi.org/10.3390/math10214096
APA StyleBarnafi, N. A., De Oliveira Vilaca, L. M., Milinkovitch, M. C., & Ruiz-Baier, R. (2022). Coupling Chemotaxis and Growth Poromechanics for the Modelling of Feather Primordia Patterning. Mathematics, 10(21), 4096. https://doi.org/10.3390/math10214096







