Robust Stabilization of Impulsive Boolean Control Networks with Function Perturbation

Abstract

This paper studies the robust stabilization of impulsive Boolean control networks (IBCNs) with function perturbation. A Boolean control network (BCN) with a state-dependent impulsive sequence is converted to an equivalent BCN by the semi-tensor product method. Based on the equivalence of stabilization between the IBCN and the corresponding BCN, several criteria are proposed for the robust stabilization of IBCNs. Furthermore, when the IBCN is not robustly stabilizable after the function perturbation, an algorithm is presented to modify the control or the impulse-triggered set. Finally, an example is given to verify the obtained results.

1. Introduction

With the flourishing development of system biology, the investigation of gene regulatory networks has attracted considerable attention [1]. As a convenient and potential mathematical model, the Boolean network was proposed by Kauffman in 1969 [2], which is a qualitative description of gene regulatory networks. In a Boolean network, the gene expression is modelled as a Boolean variable, that is, 1 (active) or 0 (inactive). When the external binary inputs and outputs are considered, the Boolean network is naturally extended to the Boolean control network (BCN) [3]. Recently, the study of Boolean networks and BCNs has been promoted by an effective tool named the semi-tensor product of matrices [4]. A lot of interesting results have been derived, such as synchronization [5], observability [6,7], stabilization [8,9] and so on [10]. In addition, the semi-tensor product method is extensively used in game theory [11], fuzzy control [12], shift register [13] and so on.

Actually, for many biological networks, including Boolean networks and BCNs, it is common to experience abrupt changes at some instants in its evolutionary process. This is often caused by sudden changes in the interconnections of subsystems or the external environment. Therefore, characterizing this phenomenon mathematically is indispensable. One advisable method is to regard the changes as impulsive effects [14,15]. BCN with impulsive effects was introduced by Li and Sun [16]. The set controllability of IBCNs was investigated in [17]. Furthermore, Tong et al. [18] discussed the stabilization of impulsive Boolean networks with stochastic disturbances. Besides the time-triggered impulses, the impulses can also be triggered by the state. The stability of the state-triggered random impulsive Boolean networks was studied in [19]. For other results of IBCNs, see [20,21].

Another common phenomenon in the study of Boolean networks and BCNs is the gene mutation, which can be depicted by the function perturbation [22]. Recently, many outstanding results have been presented for Boolean networks with function perturbation [23,24,25]. Among these results, robust stability and stabilization are of particular importance. Wu et al. [26] studied the robust stability of switched Boolean networks with function perturbation. Ren et al. [27] addressed the robust stability in the distribution of Boolean networks under the multi-bits stochastic function perturbations.

As a fundamental issue, the stabilization of IBCNs has attracted a lot of attention. Hu et al. [28] investigated the stabilization problem for BCNs with stochastic impulses. Lin et al. [29] proposed a necessary and sufficient condition to determine the event-triggered set stabilization of IBCNs. A criterion for the stabilization of IBCNs in the hybrid domain was presented in [30]. The robust set stabilization of IBCNs was fixed in [31]. It can be seen that the study of robust stabilization of IBCNs is still lacking. When both impulse and mutation occur in the gene regulatory networks, it is meaningful to study the influence of function perturbation on the stabilization of IBCNs.

In the paper, we investigate the robust stabilization of IBCNs with function perturbation, where the impulsive sequence is dependent on the states and the function perturbation occurs at a non-impulsive instant. Furthermore, the function perturbation considered in the paper is one-bit, that is, only a truth value of a certain logical function in the update flips. Since the objective of this paper is to investigate the robustness of a given state feedback stabilizer before and after the function perturbation, we assume that the considered system is stabilizable to the fixed point before the function perturbation occurs. We propose criteria for the robust stabilization of the IBCN under a given impulse-triggered set. Furthermore, we present an algorithm to modify the control or the impulse-triggered set when the IBCN is not robustly stabilizable to a fixed point. The novelty of this paper is below:

(i)

Fewer results are available on the robust stabilization of IBCNs subject to function perturbation. When the impulse is not considered, the impact of function perturbation on the robust stabilization of BCNs was addressed in [25,26]. Compared with them, the introduction of an impulse not only affects the upper bound of convergence time but also leaves room for modification to achieve the robust stabilization of IBCNs.

(ii)

Compared with the studies for the stabilization of IBCNs [28,29], the introduction of function perturbation not only characterizes the gene mutation better but also predicts the impact of gene mutations on the stabilization.

(iii)

Furthermore, compared with [31] which presented a necessary and sufficient condition for the robust stabilization of IBCNs with the disturbance inputs, we can modify the control or the impulse-triggered set to achieve the robust stabilization of IBCNs in this paper.

The rest of this paper is organized as follows. Section 2 gives some preliminaries for the conversion from IBCNs to BCNs under a given impulse-triggered set and reviews the concept of function perturbation. Section 3 investigates the robust stabilization of IBCNs with function perturbation based on the equivalent BCN. Section 4 illustrates the obtained results with an example. The conclusion is presented in Section 5.

2. Preliminaries

The notations of this paper are listed below. $\mathcal{D}$ represents the set $\{0,1\}$. Denote the s-th column of identity matrix $I_n$ by $Co{l}_s\left(I_n\right)={\delta }_n^s$. Then ${\mathsf{\Delta }}_n:=\{{\delta }_n^s:s=1,\dots ,n\}$. Furthermore, the $p\times q$ logical matrix is denoted by $F={\delta }_p[i_1\dots i_q]$. The set of $p\times q$ logical matrices is represented by ${\mathcal{L}}_{p\times q}$. Denote ${\mathsf{\Phi }}_n=diag\{{\delta }_n^1,\dots ,{\delta }_n^n\}$, which satisfies $z^2={\mathsf{\Phi }}_{n}z$, $\forall z\in {\mathsf{\Delta }}_n$. For any two matrices $C\in {\mathbb{R}}^{p\times q}$ and $E\in {\mathbb{R}}^{m\times n}$, the semi-tensor product of C and E is defined as $C⋉E=\left(C\otimes I_{\frac{\eta }{q}}\right)\left(E\otimes I_{\frac{\eta }{m}}\right)$, where $\eta$ is the least common multiple of q and m.

Denote two different forms of the same object by “∼”. Then we identify $1\sim {\delta }_2^1$ and $0\sim {\delta }_2^2$. Correspondingly, $\mathcal{D}\sim \mathsf{\Delta }$. Furthermore, we call ${\delta }_2^1$ and ${\delta }_2^2$ the vector form of logical variables 1 and 0, respectively.

Lemma 1

([4]). Denote a logical function by $f:{\mathcal{D}}^n\to \mathcal{D}$. There exists a unique matrix $F\in {\mathcal{L}}_{2\times 2^n}$ satisfying

$$f(a_1,\dots ,a_n)=F{⋉}_{i=1}^n{a}_i.$$

Here, F is named the structure matrix of f.

Given an impulse-triggered set $P\subseteq {\mathcal{D}}^n$. Consider the following IBCN with n states and m control inputs:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{a}_i(t+1)=f_i(A\left(t\right),U\left(t\right)),i=1,\dots ,n,t\in \mathbb{N}\backslash \mathsf{\Lambda },\hfill \\ a_i\left(t_k\right)=g_i\left(A(t_k-1)\right),i=1,\dots ,n,k\in {\mathbb{Z}}_{+},\hfill \end{array}\right.\end{array}$$

(1)

where $A\left(t\right)=(a_1\left(t\right),\dots ,a_n\left(t\right))\in {\mathcal{D}}^n$ and $U\left(t\right)=(u_1\left(t\right),\dots ,u_m\left(t\right))\in {\mathcal{D}}^m$ are states and control inputs, respectively. $f_i:{\mathcal{D}}^{n+m}\to \mathcal{D}$ and $g_i:{\mathcal{D}}^n\to \mathcal{D}$, $i=1,\dots ,n$ are logical functions. $\mathsf{\Lambda }:=\{t_k-1,k\in {\mathbb{Z}}_{+}\}$ is determined by the sequence of impulsive instant $\{t_k=t+1:A\left(t\right)\in P,k\in {\mathbb{Z}}_{+}\}$.

Definition 1.

Given an impulse-triggered set $P\subseteq {\mathcal{D}}^n$. $A_e=(a_1^e,\dots ,a_n^e)\in {\mathcal{D}}^n\backslash P$ is said to be a fixed point of system (1), if for $A\left(t\right)=A_e$, $t\in \mathbb{N}$, there exists a control $U\left(t\right)\in {\mathcal{D}}^m$ such that

$$\begin{array}{c}\hfill A(t+1;A\left(t\right),U\left(t\right))=A_e.\end{array}$$

(2)

Note that $A_e\notin P$. If $A\left(t^{\prime }\right)=A_e\in P$, $t^{\prime }\in \mathbb{N}$, then system (1) will update through the second equation in (1) after $t^{\prime }$. Thus, we do not discuss the case that the fixed point belongs to the given impulse-triggered set.

Definition 2.

Under the given impulse-triggered set $P\subseteq {\mathcal{D}}^n$ and the control sequence $U=\{U\left(t\right),t\in \mathbb{N}\backslash \mathsf{\Lambda }\}\subseteq {\mathcal{D}}^m$, system (1) is said to be stabilizable to $A_e\in {\mathcal{D}}^n\backslash P$, if there exists a positive integer T such that

$$\begin{array}{c}\hfill A(t;A_0,U)=A_e\end{array}$$

(3)

holds for any initial state $A_0\in {\mathcal{D}}^n$ and any integer $t\ge T$.

The type of control used in this paper is the state feedback control, which is expressed as

$$u_j\left(t\right)={\kappa }_j\left(A\left(t\right)\right),$$

(4)

where ${\kappa }_j:{\mathcal{D}}^n\to \mathcal{D}$, $j=1,\dots ,m$ are logical functions.

Let $a\left(t\right)={⋉}_{i=1}^n{a}_i\left(t\right)\in {\mathsf{\Delta }}_{2^n}$ and $u\left(t\right)={⋉}_{j=1}^m{u}_j\left(t\right)\in {\mathsf{\Delta }}_{2^m}$. With the help of Lemma 1, the algebraic state space representation of IBCN (1) is derived as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}a(t+1)=Fu\left(t\right)a\left(t\right),t\in \mathbb{N}\backslash \mathsf{\Lambda },\hfill \\ a\left(t_k\right)=Ga(t_k-1),k\in {\mathbb{Z}}_{+},\hfill \end{array}\right.\end{array}$$

(5)

where $F\in {\mathcal{L}}_{2^n\times 2^{m+n}}$ and $G\in {\mathcal{L}}_{2^n\times 2^n}$. Correspondingly, $A_e$ becomes $a_e={⋉}_{i=1}^n{a}_i^e$. $P\subseteq {\mathsf{\Delta }}_{2^n}$ and the sequence of impulsive instant is changed to

$$\{t_k=t+1:a\left(t\right)\in P,k\in {\mathbb{Z}}_{+}\}.$$

(6)

In a similar manner, the algebraic form of the state feedback control (4) is obtained as

$$u\left(t\right)=Ka\left(t\right),$$

(7)

where $K\in {\mathcal{L}}_{2^m\times 2^n}$.

In this paper, we discuss the one-bit function perturbation for system (1), occurring at a non-impulsive instant, that is, only a truth value of some function $f_i$, $i\in \{1,\dots ,n\}$ flips. Denote the function after the perturbation by $f_i^j$, $j\in \{1,\dots ,2^n\}$, which represents that the j-th row in the truth table of $f_i$ flips [22]. Moreover, the multi-bits function perturbation for system (1) means that several truth values of $f_i$ flip [27]. The investigation of one-bit function perturbation is basic and can be used to investigate the multi-bits function perturbation for the system (1).

We aim to investigate the influence of one-bit function perturbation on the stabilization of the system (1) and explore the criteria for the robust stabilization of the system (1). If the system (1) is not robustly stabilizable, we want to modify K or P such that system (1) is stabilizable after the function perturbation.

3. Main Results

At first, we convert system (5) to a BCN under the given impulse-triggered set $P\subseteq {\mathsf{\Delta }}_{2^n}$. Denote $F=[F_1\dots F_{2^m}]$, where $F_i\in {\mathcal{L}}_{2^n\times 2^n}$, $i\in \{1,\dots ,2^m\}$. Let $\tilde{F}=\left[FG\right]=[F_1\dots F_{2^m}G]\in {\mathcal{L}}_{2^n\times 2^n(2^m+1)}$. We construct a new state feedback control expressed as

$$\begin{array}{c}\hfill \tilde{u}\left(t\right)=\tilde{K}a\left(t\right)={\delta }_{2^m+1}[{\tilde{k}}_1\dots {\tilde{k}}_{2^n}]a\left(t\right),\end{array}$$

(8)

where $\tilde{K}\in {\mathcal{L}}_{(2^m+1)\times 2^n}$.

Denote the state feedback gain matrix in (7) by $K={\delta }_{2^m}[k_1\dots k_{2^n}]$. If $a\left(t\right)={\delta }_{2^n}^i\notin P$, then ${\tilde{k}}_i=k_i$, $i\in \{1,\dots ,2^n\}$. If $a\left(t\right)={\delta }_{2^n}^i\in P$, then ${\tilde{k}}_i=2^m+1$. Thereby, system (5) is converted to the BCN below:

$$\begin{array}{c}\hfill a(t+1)=\tilde{F}\tilde{u}\left(t\right)a\left(t\right),\end{array}$$

(9)

where $\tilde{u}\left(t\right)\in {\mathsf{\Delta }}_{2^m+1}$ relies on P and K.

The state feedback stabilization of BCNs was studied in [32]. Namely, system (9) is said to be stabilizable to $a_e\in {\mathsf{\Delta }}_{2^n}$, if there exists a positive integer $\varsigma$ such that

$$\begin{array}{c}\hfill a(t;a_0,\tilde{u})=a_e,t\ge \varsigma \end{array}$$

(10)

holds for any initial state $a_0\in {\mathsf{\Delta }}_{2^n}$ under the given state feedback control $\tilde{u}\left(t\right)=\tilde{K}a\left(t\right)$, $\tilde{K}\in {\mathcal{L}}_{(2^m+1)\times 2^n}$. The equivalence between system (5) and system (9) is shown in the proposition below.

Proposition 1.

Given $P\subseteq {\mathsf{\Delta }}_{2^n}$. System (5) is stabilizable to $a_e$ under the state feedback control (7), if and only if system (9) is stabilizable to $a_e$ under the state feedback control (8).

Next, we investigate the robust stabilization of the system (5) with function perturbation based on Proposition 1. Some necessary assumptions are given on the function perturbation below.

Assumption 1.

After the function perturbation, the s-th column of $F_{k^{*}}\in {\mathcal{L}}_{2^n\times 2^n}$ is changed from ${\delta }_{2^n}^{\alpha (k^{*},s)}$ to some ${\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}\in {\mathsf{\Delta }}_{2^n}$, where $\alpha (k^{*},s)\ne {\alpha }^{\prime }(k^{*},s)$ and $k^{*}$ is chosen from $\{1,\dots ,2^m\}$.

Obviously, Assumption 1 guarantees that the one-bit function perturbation occurs at a non-impulsive instant. In this context, the function perturbation is always fixed by Assumption 1. Because the objective of this paper is to investigate the robustness of a given state feedback stabilizer for system (5) before and after the function perturbation, we give the assumption below.

Assumption 2.

Before the function perturbation occurs, system (5) is stabilizable to $a_e={\delta }_{2^n}^{{\alpha }_e}\in {\mathsf{\Delta }}_{2^n}\backslash P$ under $P\in {\mathsf{\Delta }}_{2^n}$ and the state feedback control (7).

Definition 3.

Given $P\in {\mathsf{\Delta }}_{2^n}$ and the state feedback control $u\left(t\right)=Ka\left(t\right)$, $K\in {\mathcal{L}}_{2^m\times 2^n}$, which make system (5) stabilizable to $a_e\in {\mathsf{\Delta }}_{2^n}\backslash P$. System (5) is said to be robustly stabilizable to $a_e$ with respect to P and u, if it is still stabilizable to $a_e$ under P and u after the function perturbation.

Analogously, we define robust stabilization for system (9) as follows.

Definition 4.

Given a state feedback control $\tilde{u}\left(t\right)=\tilde{K}a\left(t\right)$, $\tilde{K}\in {\mathcal{L}}_{(2^m+1)\times 2^n}$, which makes system (9) stabilizable to $a_e\in {\mathsf{\Delta }}_{2^n}$. System (9) is said to be robustly stabilizable to $a_e$ with respect to $\tilde{u}$, if it is still stabilizable to $a_e$ under $\tilde{u}$ after the function perturbation.

Using (8) and (9), we obtain a closed-loop system:

$$\begin{array}{c}\hfill a(t+1)=\tilde{F}\tilde{u}\left(t\right)a\left(t\right)=\tilde{F}\tilde{K}{\mathsf{\Phi }}_{2^n}a\left(t\right).\end{array}$$

(11)

For convenience, let $G=F_{2^m+1}$ and then $\tilde{F}=[F_1\dots F_{2^m}{F}_{2^m+1}]$. The state transition matrix of a closed-loop system (11) is further expressed as

$$\tilde{F}\tilde{K}{\mathsf{\Phi }}_{2^n}=\left[Co{l}_1\left(F_{{\tilde{k}}_1}\right)\dots Co{l}_{2^n}\left(F_{{\tilde{k}}_{2^n}}\right)\right]\in {\mathcal{L}}_{2^n\times 2^n}.$$

(12)

Suppose that $\tilde{F}$ is changed to $\widetilde{F^{\prime }}=[F_1^{\prime }\dots F_{2^m}^{\prime }{F}_{2^m+1}^{\prime }]$ after the function perturbation. Denote $L=\tilde{F}\tilde{K}{\mathsf{\Phi }}_{2^n}$. Then L is correspondingly changed to

$$\begin{array}{c}\hfill L^{\prime }=\left[Co{l}_1\left(F_{{\tilde{k}}_1}^{\prime }\right)\dots Co{l}_{2^n}\left(F_{{\tilde{k}}_{2^n}}^{\prime }\right)\right]\in {\mathcal{L}}_{2^n\times 2^n}.\end{array}$$

(13)

From Assumption 1, if $k^{*}={\tilde{k}}_s$, then

$$Co{l}_s\left(F_{{\tilde{k}}_s}^{\prime }\right)={\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)},$$

and $Co{l}_j\left(L^{\prime }\right)=Co{l}_j\left(L\right)$, $j=\{1,\dots ,s-1,s+1,\dots ,2^n\}$. Otherwise, $L^{\prime }=L$. It is easy to see that under the control (8), the stabilization of system (9) is not affected by the function perturbation when $k^{*}\ne {\tilde{k}}_s$. As shown in [25], system (9) is robustly stabilizable to $a_e$ under the given state feedback control $\tilde{u}\left(t\right)=\tilde{K}a\left(t\right)$, if $k^{*}\ne {\tilde{k}}_s$.

Theorem 1.

Given an impulse-triggered set $P\subseteq {\mathsf{\Delta }}_{2^n}$ and a state feedback control (7) which make system (5) stabilizable to $a_e$. System (5) is robustly stabilizable to $a_e$ with respect to P and control (7), if one of the following items holds: (i)  ${\delta }_{2^n}^s\in P$; (ii) ${\delta }_{2^n}^s\notin P$ and $k^{*}\ne k_s$.

Proof of Theorem 1.

Under P and the state feedback control (7), we construct the corresponding system (9) with the control (8). System (9) is robustly stabilizable to $a_e$ when $k^{*}\ne {\tilde{k}}_s$. Combined with the construction of control (8) and Assumption A1, $k^{*}\ne {\tilde{k}}_s$ for system (9) implies the following two cases for system (5):

(i)

${\delta }_{2^n}^s\in P$.

(ii)

${\delta }_{2^n}^s\notin P$ and $k^{*}\ne k_s$.

Then according to Proposition 1, system (5) is robustly stabilizable to $a_e$ if one of the above two conditions holds.    □

Remark 1.

Compared with this [25], the upper bound of convergence time for the robust stabilization of IBCNs may be greater than $2^n$. Therefore, the introduction of impulse brings a fundamental difference in the robust stabilization with respect to the function perturbation.

Now, we discuss the case that ${\delta }_{2^n}^s\notin P$ and $k^{*}=k_s$, i.e., $k^{*}={\tilde{k}}_s$ holds for system (9). In this case, we preferentially consider system (9). Denote the minimum positive integer $\varsigma$ satisfying (10) by $\tau$. Construct the r-step reachable set with respect to $a_e$ below:

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_0\left(a_e\right)& =& \left\{a_e\right\},\hfill \\ \hfill {\mathsf{\Omega }}_r\left(a_e\right)& =& \{a:L^{r}a=a_e,L^{r-1}a\ne a_e\},r=1,\dots ,\tau .\hfill \end{array}$$

(14)

One can easily find that ${\mathsf{\Omega }}_{r_1}\cap {\mathsf{\Omega }}_{r_2}=\varnothing$, $\forall r_1\ne r_2$, where $r_1,r_2\in \{0,\dots ,\tau \}$. Moreover, ${\bigcup }_{r^{\prime }=0}^{\tau }{\mathsf{\Omega }}_{r^{\prime }}\left(a_e\right)={\mathsf{\Delta }}_{2^n}$. For convenience, the following assumption gives the sets to which ${\delta }_{2^n}^{\alpha (k^{*},s)}$ and ${\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}$ belong.

Assumption 3.

For system (9), ${\delta }_{2^n}^{\alpha (k^{*},s)}\in {\mathsf{\Omega }}_l\left(a_e\right)$ and ${\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}\in {\mathsf{\Omega }}_{l^{\prime }}\left(a_e\right)$, where $l\in \{1,\dots ,\tau \}$ and $l^{\prime }\in \{0,\dots ,\tau \}$.

Remark 2.

Assumption 3 implies ${\delta }_{2^n}^s\ne a_e$. In fact, if ${\delta }_{2^n}^s=a_e$, then from Assumption 1, we have ${\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}\ne {\delta }_{2^n}^{\alpha (k^{*},s)}=a_e$. In this case, system (9) is not robustly stabilizable to $a_e$ with respect to control (8).

Similar to (14), we construct the $\tilde{r}$-step reachable set with respect to ${\delta }_{2^n}^s$ below:

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_0\left({\delta }_{2^n}^s\right)& =& \left\{{\delta }_{2^n}^s\right\},\hfill \\ \hfill {\mathsf{\Omega }}_{\tilde{r}}\left({\delta }_{2^n}^s\right)& =& \{a:L^{\tilde{r}}a={\delta }_{2^n}^s,L^{\tilde{r}-1}a\ne {\delta }_{2^n}^s\},\tilde{r}=1,\dots ,\tau -l.\hfill \end{array}$$

(15)

Let $\mathsf{\Psi }\left({\delta }_{2^n}^s\right)={\bigcup }_{{\tilde{r}}^{\prime }=0}^{\tau -l}{\mathsf{\Omega }}_{{\tilde{r}}^{\prime }}\left({\delta }_{2^n}^s\right)$. There is no intersection between ${\mathsf{\Omega }}_{{\tilde{r}}_1}$ and ${\mathsf{\Omega }}_{{\tilde{r}}_2}$, $\forall {\tilde{r}}_1\ne {\tilde{r}}_2$, where ${\tilde{r}}_1,{\tilde{r}}_2\in \{0,\dots ,\tau \}$.

As shown in [25], system (9) is robustly stabilizable to $a_e$ under the given state feedback control $\tilde{u}\left(t\right)=\tilde{K}a\left(t\right)$, if $k^{*}={\tilde{k}}_s$ and $l^{\prime }\le l-1$. The case that $k^{*}={\tilde{k}}_s$ for system (9) is equivalent to that ${\delta }_{2^n}^s\notin P$ and $k^{*}=k_s$ for system (5). Then we obtain the result as follows, which is a sufficient condition for the robust stabilization of system (5) subject to the function perturbation.

Theorem 2.

Given an impulse-triggered set $P\subseteq {\mathsf{\Delta }}_{2^n}$ and a state feedback control (7) which make system (5) is stabilizable to $a_e$. System (5) is robustly stabilizable to $a_e$ with respect to P and control (7), if ${\delta }_{2^n}^s\notin P$, $k^{*}=k_s$ and $l^{\prime }\le l-1$.

Note that for system (9), if $k^{*}={\tilde{k}}_s$ and $l^{\prime }\le l-1$, the function perturbation shortens the convergence time from $a\left(0\right)\in \mathsf{\Psi }\left({\delta }_{2^n}^s\right)$ to $a_e$. The remaining issue is to verify the case $k^{*}={\tilde{k}}_s$ and $l^{\prime }>l-1$, which may prolong the convergence time from $a\left(0\right)\in \mathsf{\Psi }\left({\delta }_{2^n}^s\right)$ to $a_e$.

If $k^{*}={\tilde{k}}_s$ and $l^{\prime }>l-1$, it is shown in [25] that system (9) is robustly stabilizable to $a_e$ under the given state feedback control $\tilde{u}\left(t\right)=\tilde{K}a\left(t\right)$ if and only if ${\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}\notin \mathsf{\Psi }\left({\delta }_{2^n}^s\right)$.

Theorem 3.

Given an impulse-triggered set $P\subseteq {\mathsf{\Delta }}_{2^n}$ and a state feedback control (7) which make system (5) is stabilizable to $a_e$. If ${\delta }_{2^n}^s\notin P$, $k^{*}=k_s$ and $l^{\prime }>l-1$, system (5) is robustly stabilizable to $a_e$ with respect to P and control (7), if and only if ${\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}\notin \mathsf{\Psi }\left({\delta }_{2^n}^s\right)$.

Proof of Theorem 3.

Under P and the state feedback control (7), we construct the corresponding system (9) with the control (8) and $\mathsf{\Psi }\left({\delta }_{2^n}^s\right)$. Because system (9) is robustly stabilizable to $a_e$ under the control (8) if and only if ${\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}\notin \mathsf{\Psi }\left({\delta }_{2^n}^s\right)$, when $k^{*}={\tilde{k}}_s$ and $l^{\prime }>l-1$, the conclusion is immediately established based on Proposition 1.    □

When the condition mentioned in Theorem 3 does not hold, there exists a cycle (maybe a new fixed point) produced by the function perturbation. Without losing generality, we denote the cycle as

$$\begin{array}{ccc}\hfill W_{\theta }& =& \{{\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)},\left(L^{\prime }\right){\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)},\dots ,{\left(L^{\prime }\right)}^{\theta }{\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}={\delta }_{2^n}^s\},\hfill \end{array}$$

(16)

where the length of $W_{\theta }$ is $\theta +1$ and the integer $0\le \theta \le \tau -l$. Furthermore, there exists a cycle $W_{\theta }$ if and only if ${\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}\in {\mathsf{\Omega }}_{\theta }\left({\delta }_{2^n}^s\right)$. In this case, we consider modifying K or P to achieve the robust stabilization of system (5).

For system (9), from (16), if there exist an integer $0\le \mu \le \theta$ and a state feedback control ${\tilde{u}}^{\prime }={\delta }_{2^m+1}^{\upsilon }\in {\mathsf{\Delta }}_{2^m+1}$, such that

$$\begin{array}{c}\hfill {\tilde{F}}^{\prime }{\tilde{u}}^{\prime }{\delta }_{2^n}^{{\mu }^{\prime }}\notin \mathsf{\Psi }\left({\delta }_{2^n}^s\right),\end{array}$$

(17)

where ${\delta }_{2^n}^{{\mu }^{\prime }}={\left(L^{\prime }\right)}^{\mu }{\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}$, change $\tilde{K}$ to ${\tilde{K}}^{\prime }={\delta }_{2^m+1}[{\tilde{k}}_1^{\prime }\dots {\tilde{k}}_{2^n}^{\prime }]$ satisfying

$$\begin{array}{c}\hfill {\tilde{k}}_i^{\prime }=\left\{\begin{array}{c}\upsilon ,\mathrm{if}i={\mu }^{\prime },\hfill \\ {\tilde{k}}_i,\mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(18)

Next, we consider system (5) based on Proposition 1. If the value of $\upsilon$ mentioned in (18) is $2^m+1$, let $P^{\prime }=P\cup \left\{{\delta }_{2^n}^{{\mu }^{\prime }}\right\}$. If $\upsilon \ne 2^m+1$, change K to $K^{\prime }={\delta }_{2^m}[k_1^{\prime }\dots k_{2^n}^{\prime }]$ which satisfies

$$\begin{array}{c}\hfill k_i^{\prime }=\left\{\begin{array}{c}\upsilon ,\mathrm{if}i={\mu }^{\prime },\hfill \\ k_i,\mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(19)

Moreover, if $\upsilon \ne 2^m+1$ and ${\delta }_{2^n}^{{\mu }^{\prime }}\in P$, let $P^{\prime }=P\backslash \left\{{\delta }_{2^n}^{{\mu }^{\prime }}\right\}$. However, we may not find an integer $0\le \mu \le \theta$ and a state feedback control ${\tilde{u}}^{\prime }\in {\mathsf{\Delta }}_{2^m+1}$, such that (17) holds for system (9). Then from Theorem 1, let $P^{\prime }=P\cup \left\{{\delta }_{2^n}^s\right\}$ and $K=K^{\prime }$.

If system (5) is stabilizable to $a_e$ under $P^{\prime }$ and $K^{\prime }$ after the function perturbation, K or P is said to be modified. In what follows, we integrate the above procedures into an algorithm, which is shown in Algorithm 1. Through Algorithm 1, we can modify K or P. In addition, we analyze the complexity of the algorithm. The computational cost of calculating $\mathsf{\Psi }\left({\delta }_{2^n}^s\right)$ is $\mathcal{O}\left((\tau -l-1)2^{3n}\right)$. Since $0\le \theta \le \tau -l$, the computational cost of calculating $W_{\theta }$ is $\mathcal{O}\left((\tau -l)2^{2n}\right)$. The computational complexity of checking (17) is $\mathcal{O}\left((\tau -l)2^{3n+2m}\right)$. Then the computational complexity of Algorithm 1 is $\mathcal{O}\left((\tau -l)2^{3n+2m}\right)$.

Algorithm 1: Algorithm to modify K or P to achieve the robust stabilization of system (5)

Give an impulse-triggered set $P\subseteq {\mathsf{\Delta }}_{2^n}$ and a state feedback control (7) which make system (5) be stabilizable to $a_e$. Suppose that ${\delta }_{2^n}^s\notin P$, $k^{*}=k_s$, $l^{\prime }>l-1$ and ${\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}\in \mathsf{\Psi }\left({\delta }_{2^n}^s\right)$. (1) Convert system (5) into system (9) equivalently. Then calculate $\mathsf{\Psi }\left({\delta }_{2^n}^s\right)$ and $W_{\theta }$ defined by (15) and (16), respectively; (2) For any integer $\mu \in \{0,\dots ,\theta \}$, if there exists a state feedback control ${\tilde{u}}^{\prime }={\delta }_{2^m+1}^{\upsilon }$$\in {\mathsf{\Delta }}_{2^m+1}$ satisfying (17), let ${\delta }_{2^n}^{{\mu }^{\prime }}={\left(L^{\prime }\right)}^{\mu }{\delta }_{2^n}^{{\alpha }^{\prime }(k^{*},s)}$. Otherwise, repeat this step until all $\mu \in \{0,\dots ,\theta \}$    are checked; (3) When $\upsilon =2^m+1$, let $P=P\cup \left\{{\delta }_{2^n}^{{\mu }^{\prime }}\right\}$. When $\upsilon \ne 2^m+1$, denote $K^{\prime }={\delta }_{2^m}[k_1^{\prime }\dots k_{2^n}^{\prime }]$ where      $k_i^{\prime }=\upsilon$, if $i={\mu }^{\prime }$ and $k_i^{\prime }=k_i$, if $i\ne {\mu }^{\prime }$. Then let $K=K^{\prime }$. Particularly, if ${\delta }_{2^n}^{{\mu }^{\prime }}\in P$, let $P=P\backslash \left\{{\delta }_{2^n}^{{\mu }^{\prime }}\right\}$; (4) If K and P do not change, let $P=P\cup \left\{{\delta }_{2^n}^s\right\}$; (5) If K or P can be modified, output P and $K={\delta }_{2^m}[k_1^{\prime }\dots k_{2^n}^{\prime }]$. Otherwise, stop.

Remark 3.

Compared with [25], both K and P can be modified, which leaves more room to achieve the robust stabilization of system (5).

4. Illustrative Examples

Example 1.

Consider the IBCN, which is depicted as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}a(t+1)=Fu\left(t\right)a\left(t\right),t\in \mathbb{N}\backslash \mathsf{\Lambda },\hfill \\ a\left(t_k\right)=Ga(t_k-1),k\in {\mathbb{Z}}_{+},\hfill \end{array}\right.\end{array}$$

(20)

where $F=\left[F_1{F}_2\right]$, $F_1={\delta }_8\left[43178576\right]$, $F_2={\delta }_8\left[23486771\right]$ and $G={\delta }_8\left[54832156\right]$. Furthermore, given an impulse-triggered set $P=\{{\delta }_8^2,{\delta }_8^3,{\delta }_8^6\}$ and a state feedback control

$$\begin{array}{c}\hfill u\left(t\right)=Ka\left(t\right)={\delta }_2\left[12212112\right]a\left(t\right).\end{array}$$

(21)

The sequence of impulsive instant is denoted by $\{t_k=t+1:a\left(t\right)\in P,k\in {\mathbb{Z}}_{+}\}$. Let $a_e={\delta }_8^7$.

From Definition 1, $a_e$ is a fixed point of system (20). Let $\tilde{F}=\left[FG\right]$. In order to convert system (20) to system (9), we construct a state feedback control in the form of (8). Corresponding to (21), we have

$$\begin{array}{c}\hfill \tilde{u}\left(t\right)=\tilde{K}a\left(t\right)={\delta }_3\left[13312312\right]a\left(t\right).\end{array}$$

(22)

One can easily prove that system (9) is stabilizable to $a_e$ under the control (22). Then according to Proposition 1, system (20) is stabilizable to $a_e$ under the control (21).

Furthermore, for system (9), under the state feedback control (22), we obtain a closed-loop system as

$$a(t+1)=La\left(t\right),$$

where $L=\tilde{F}\tilde{K}{\mathsf{\Phi }}_8={\delta }_8\left[44876171\right]$. After a simple calculation, we derive the following r-step reachable set with respect to $a_e={\delta }_8^7$, $r=0,\dots ,4$:

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_0\left(a_e\right)& =& \left\{{\delta }_8^7\right\},\hfill \\ \hfill {\mathsf{\Omega }}_1\left(a_e\right)& =& \left\{{\delta }_8^4\right\},\hfill \\ \hfill {\mathsf{\Omega }}_2\left(a_e\right)& =& \{{\delta }_8^1,{\delta }_8^2\},\hfill \\ \hfill {\mathsf{\Omega }}_3\left(a_e\right)& =& \{{\delta }_8^6,{\delta }_8^8\},\hfill \\ \hfill {\mathsf{\Omega }}_4\left(a_e\right)& =& \{{\delta }_8^3,{\delta }_8^5\}.\hfill \end{array}$$

(23)

Then we consider the robust stabilization of system (20) subject to the following four kinds of function perturbation under the given set P and control (21):

(i)

Assume that the third column of $F_2$ is changed from ${\delta }_8^4$ to ${\delta }_8^1$ after the function perturbation. According to Theorem 1, because ${\delta }_8^3\in P$, system (20) is robustly stabilizable to $a_e={\delta }_8^7$ with respect to P and control (21).

(ii)

Assume that the eighth column of $F_1$ is changed from ${\delta }_8^6$ to ${\delta }_8^4$ after the function perturbation. Correspondingly, $s=8$, $k^{*}=1$, $\alpha (1,8)=6$ and ${\alpha }^{\prime }(1,8)=4$. According to Theorem 1, since ${\delta }_8^8\notin P$ and $k^{*}\ne k_8=2$, system (20) is robustly stabilizable to $a_e={\delta }_8^7$ with respect to P and control (21).

(iii)

Assume that the eighth column of $F_2$ is changed from ${\delta }_8^1$ to ${\delta }_8^4$ after the function perturbation. Correspondingly, $s=8$, $k^{*}=k_8=2$, $\alpha (2,8)=1$ and ${\alpha }^{\prime }(2,8)=4$. Then from (23), $l=2$ and $l^{\prime }=1$, that is, $l^{\prime }=l-1$. According to Theorem 2, system (20) is robustly stabilizable to $a_e={\delta }_8^7$ with respect to P and control (21) (see Figure 1).

(iv)

Assume that the eighth column of $F_2$ is changed from ${\delta }_8^1$ to ${\delta }_8^3$ after the function perturbation. Correspondingly, $s=8$, $k^{*}=k_8=2$, $\alpha (2,8)=1$ and ${\alpha }^{\prime }(2,8)=3$. Then $l=2$ and $l^{\prime }=4$, that is, $l^{\prime }>l-1$. Moreover, $\mathsf{\Psi }\left({\delta }_8^8\right)=\{{\delta }_8^3,{\delta }_8^8\}$. According to Theorem 3, system (20) is not robustly stabilizable to $a_e={\delta }_8^7$ with respect to P and control (21) (see Figure 2).

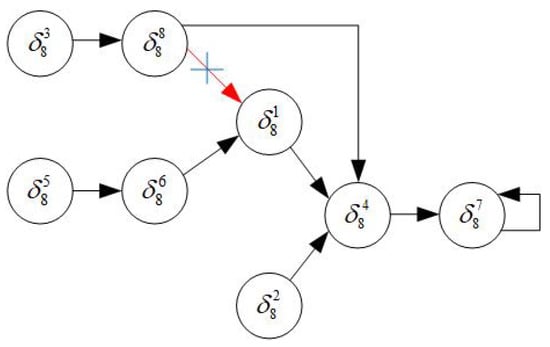
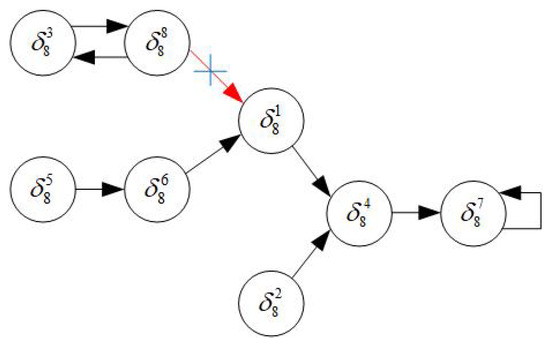
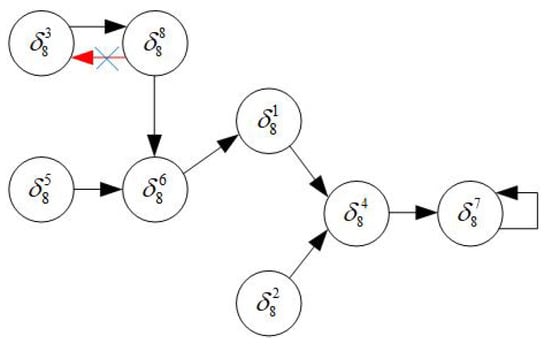
For case (iv), we modify K to make system (20) stabilizable to $a_e$ after the function perturbation. Since the eighth column of $F_2$ is changed from ${\delta }_8^1$ to ${\delta }_8^3$, we derive a cycle $W_1=\{{\delta }_8^3,{\delta }_8^8\}$. Then one can find a control ${\tilde{u}}^{\prime }={\delta }_3^1$ such that

$${\tilde{F}}^{\prime }{\tilde{u}}^{\prime }{\delta }_8^8={\delta }_8^6\notin \mathsf{\Psi }\left({\delta }_8^8\right).$$

Thus, we change the state feedback control (21) to

$$\begin{array}{c}\hfill u\left(t\right)=K^{\prime }a\left(t\right)={\delta }_2\left[12212111\right]a\left(t\right),\end{array}$$

(24)

under which system (20) is stabilizable to $a_e$ after the function perturbation (see Figure 3).

Example 2.

Consider the following reduced BCN model for the λ switch [33]:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{a}_1(t+1)=(\neg a_2\left(t\right))\wedge (\neg a_5\left(t\right)),\hfill \\ a_2(t+1)=(\neg a_5\left(t\right))\wedge (a_2\left(t\right)\vee a_3\left(t\right)),\hfill \\ a_3(t+1)=(\neg a_2\left(t\right))\wedge u\left(t\right)\wedge (a_1\left(t\right)\vee a_4\left(t\right)),t\in \mathbb{N},\hfill \\ a_4(t+1)=(\neg a_2\left(t\right))\wedge u\left(t\right)\wedge a_1\left(t\right),\hfill \\ a_5(t+1)=(\neg a_2\left(t\right))\wedge (\neg a_3\left(t\right)),\hfill \end{array}\right.\end{array}$$

(25)

where $a_1$, $a_2$, $a_3$, $a_4$, and $a_5$ represent the phage genes N, oI, cII, cIII, and cro, respectively. u represents the inputs. When the environmental conditions are favourable (not favourable), the value of u is 1 (0). Considering the impulsive phenomenon in the processes of gene expression of the bacterium, the impulsive Boolean network is described as [34]

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{a}_1(t+1)=(a_1\left(t\right)\vee a_3\left(t\right))\leftrightarrow a_5\left(t\right),\hfill \\ a_2(t+1)=(\neg a_1\left(t\right))\vee a_3\left(t\right),\hfill \\ a_3(t+1)=\neg a_4\left(t\right),t=t_k-1,k\in {\mathbb{Z}}_{+}.\hfill \\ a_4(t+1)=(a_1\left(t\right)\wedge a_2\left(t\right))\vee a_3\left(t\right),\hfill \\ a_5(t+1)=a_1\left(t\right)\leftrightarrow (a_3\left(t\right)\vee a_4\left(t\right)),\hfill \end{array}\right.\end{array}$$

(26)

Let $a\left(t\right)={⋉}_{i=1}^5{a}_i\left(t\right)$. Based on Lemma 1, we obtain the algebraic state space representation of this IBCN below:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}a(t+1)=Fu\left(t\right)a\left(t\right),t\in \mathbb{N}\backslash \mathsf{\Lambda },\hfill \\ a\left(t_k\right)=Ga(t_k-1),k\in {\mathbb{Z}}_{+},\hfill \end{array}\right.\end{array}$$

(27)

where $F=\left[F_1{F}_2\right]$,

$$\begin{array}{cc}\hfill F_1={\delta }_{32}[& 3224322432243224262262259259\hfill \\ \hfill & 322432243224322428432827113115],\hfill \\ \hfill F_2={\delta }_{32}[& 322432243224322432832831153115\hfill \\ \hfill & 322432243224322432832831153115],\hfill \end{array}$$

and

$$G={\delta }_{32}\left[5211171329102652111715311228622218248193622218248193\right].$$

Given an impulse-triggered set $P=\{{\delta }_{32}^1,{\delta }_{32}^9,{\delta }_{32}^{10},{\delta }_{32}^{17},{\delta }_{32}^{19},{\delta }_{32}^{21},{\delta }_{32}^{27},{\delta }_{32}^{30},{\delta }_{32}^{31}\}$, and a state feedback control

$$\begin{array}{c}\hfill u\left(t\right)=Ka\left(t\right)={\delta }_2\left[11122112111222121112212112111122\right]a\left(t\right).\end{array}$$

(28)

The sequence of impulsive instant is denoted by $\{t_k=t+1:a\left(t\right)\in P,k\in {\mathbb{Z}}_{+}\}$. Let $a_e={\delta }_{32}^{24}$.

From Definition 1, $a_e$ is a fixed point of system (27). Let $\tilde{F}=\left[FG\right]$. We construct a state feedback control in the form of (8). Corresponding to (28), we have

$$\begin{array}{c}\hfill \tilde{u}\left(t\right)=\tilde{K}a\left(t\right)={\delta }_3\left[31122112331222123132312112311332\right]a\left(t\right).\end{array}$$

(29)

According to Proposition 1, system (27) is stabilizable to $a_e$ under the control (28).

Furthermore, for system (9), under the state feedback control (29), we obtain a closed-loop system as

$$a(t+1)=La\left(t\right),$$

where

$$\begin{array}{cc}\hfill L=\tilde{F}\tilde{K}{\mathsf{\Phi }}_{32}={\delta }_{32}[& 52432243224322452126831152515\hfill \\ \hfill & 62422424243224288282781915].\hfill \end{array}$$

After a simple calculation, we derive the following r-step reachable sets with respect to $a_e$, $r=0,\dots ,7$:

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_0\left(a_e\right)& =& \left\{{\delta }_{32}^{24}\right\},\hfill \\ \hfill {\mathsf{\Omega }}_1\left(a_e\right)& =& \{{\delta }_{32}^2,{\delta }_{32}^4,{\delta }_{32}^6,{\delta }_{32}^8,{\delta }_{32}^{18},{\delta }_{32}^{20},{\delta }_{32}^{21},{\delta }_{32}^{22}\},\hfill \\ \hfill {\mathsf{\Omega }}_2\left(a_e\right)& =& \{{\delta }_{32}^{10},{\delta }_{32}^{12},{\delta }_{32}^{17},{\delta }_{32}^{19},{\delta }_{32}^{26},{\delta }_{32}^{27},{\delta }_{32}^{28},{\delta }_{32}^{30}\},\hfill \\ \hfill {\mathsf{\Omega }}_3\left(a_e\right)& =& \{{\delta }_{32}^{11},{\delta }_{32}^{25},{\delta }_{32}^{29},{\delta }_{32}^{31}\},\hfill \\ \hfill {\mathsf{\Omega }}_4\left(a_e\right)& =& \{{\delta }_{32}^{13},{\delta }_{32}^{15}\},\hfill \\ \hfill {\mathsf{\Omega }}_5\left(a_e\right)& =& \{{\delta }_{32}^{14},{\delta }_{32}^{16},{\delta }_{32}^{32}\},\hfill \\ \hfill {\mathsf{\Omega }}_6\left(a_e\right)& =& \{{\delta }_{32}^3,{\delta }_{32}^5,{\delta }_{32}^7,{\delta }_{32}^{23}\},\hfill \\ \hfill {\mathsf{\Omega }}_7\left(a_e\right)& =& \{{\delta }_{32}^1,{\delta }_{32}^9\}.\hfill \end{array}$$

(30)

Then we consider the robust stabilization of system (27) subject to the following two kinds of function perturbation under the given set P and control (28):

(i)

Assume that the first column of $F_1$ is changed from ${\delta }_{32}^{32}$ to ${\delta }_{32}^2$ after the function perturbation. According to Theorem 1, because ${\delta }_{32}^1\in P$, system (27) is robustly stabilizable to $a_e={\delta }_{32}^{24}$ with respect to P and control (28).

(ii)

Assume that the twenty third column of $F_2$ is changed from ${\delta }_{32}^{32}$ to ${\delta }_{32}^2$ after the function perturbation. Correspondingly, $s=23$, $k^{*}=k_{23}=2$, $\alpha (2,23)=32$ and ${\alpha }^{\prime }(2,23)=2$. Then from (30), $l=5$ and $l^{\prime }=1$, that is, $l^{\prime }<l-1$. According to Theorem 2, system (27) is robustly stabilizable to $a_e={\delta }_{32}^{24}$ with respect to P and control (28).

5. Conclusions

Considering the living phenomena, when both impulse and mutation occur in the gene regulatory networks, it is significant to study the impact of function perturbation on the stabilization of IBCNs. In this paper, we have investigated the robust stabilization of IBCNs with function perturbation. We have given some necessary convertions, under which we have presented several criteria for the robust stabilization of IBCNs. When the considered IBCN is not robustly stabilizable after the function perturbation, we have proposed an algorithm to modify the control or the impulse-triggered set, which leaves more room to achieve the robust stabilization of IBCNs.

Compared with [25,26,28,29,31], our results can not only predict the impact of gene mutations on the stabilization but also modify the control or the impulse-triggered set to achieve the robust stabilization.

Our results are applicable to IBCNs with a small number of nodes. With the help of MATLAB toolbox (Please refer to “STP Toolbox” in “http://lsc.amss.ac.cn/~dcheng/”), these matrix-based conditions of checking the robust stabilization of IBCNs and modifying the control or the impulse-triggered set are easily operated. Future work may devote to reducing the computational complexity. Moreover, we will further discuss the robust stabilization of IBCNs with function perturbation occurring at an impulsive instant in the future work.