Nonlocal Impulsive Fractional Integral Boundary Value Problem for (ρk,ϕk)-Hilfer Fractional Integro-Differential Equations
Abstract
1. Introduction
2. Preliminaries
2.1. The -Hilfer Fractional Calculus and Its Properties
- (i)
- .
- (ii)
- .
- (iii)
- .
2.2. The Linear -Hilfer Fractional Cauchy Problem
2.3. An Auxiliary Lemma
3. Existence Results
3.1. Uniqueness Result via Banach’s Fixed Point Theorem
- ()
- There exist constants , , so thatfor all and , , , .
- ()
- There exists a constant so that
3.2. Existence Result via O’Regan’s Fixed Point Theorem
- ()
- There exists such that for all , .
- ()
- There exist a continuous non-decreasing function and , , , such thatfor any .
- ()
- There exist a continuous non-decreasing function and , such thatfor any u, , satisfying where is defined by (23).
- ()
4. Stability Results
- (i)
- , , ,
- (ii)
- , ,
- (iii)
- .
- (i)
- , , ,
- (ii)
- , ,
- (iii)
- .
- (i)
- , , ,
- (ii)
- , ,
- (iii)
- .
4.1. Ulam–Hyers Stability Results
4.2. Ulam–Hyers–Rassias Stability Results
- ()
- There exists a non-decreasing function and there is , for each , such that the following inequality
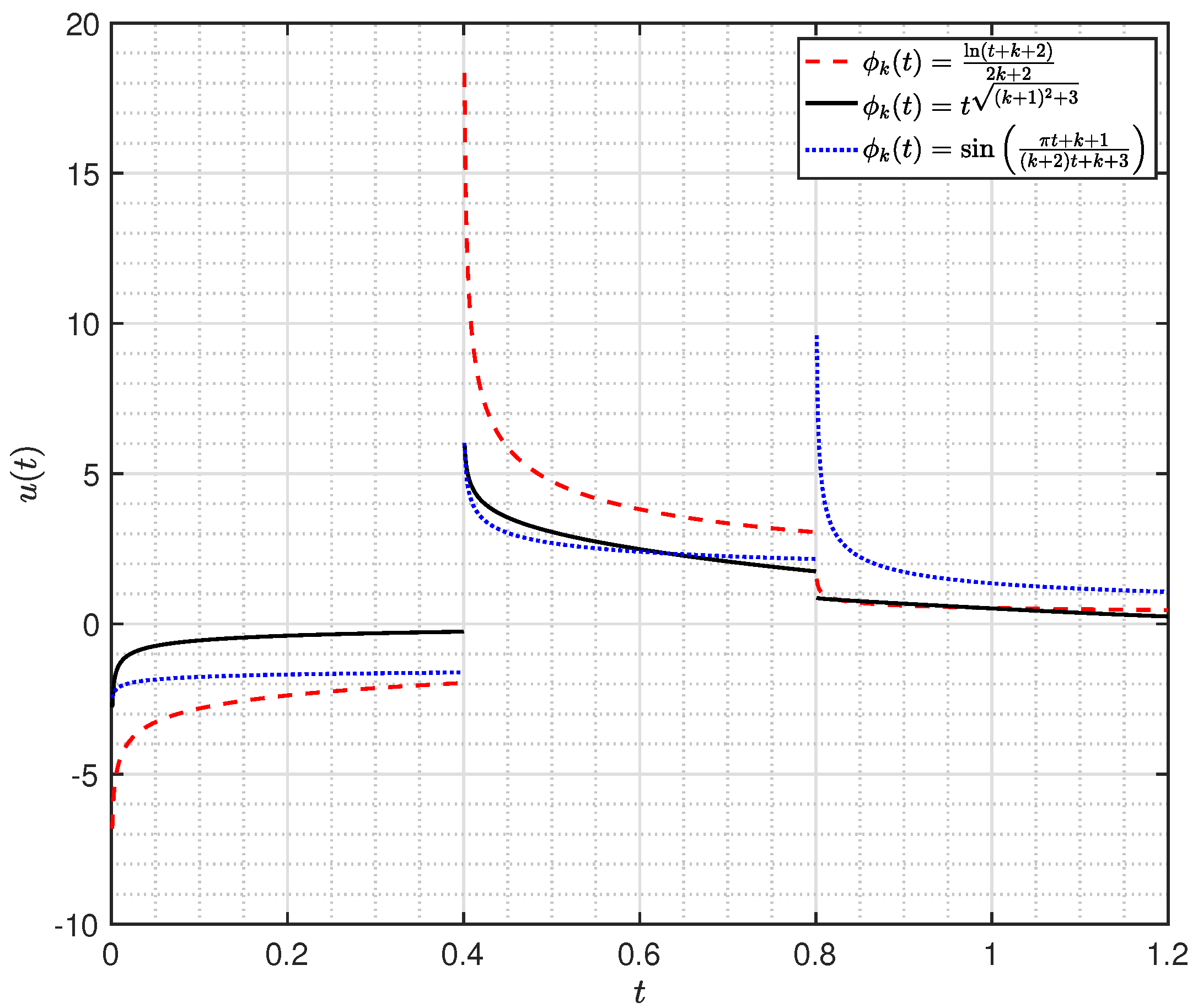
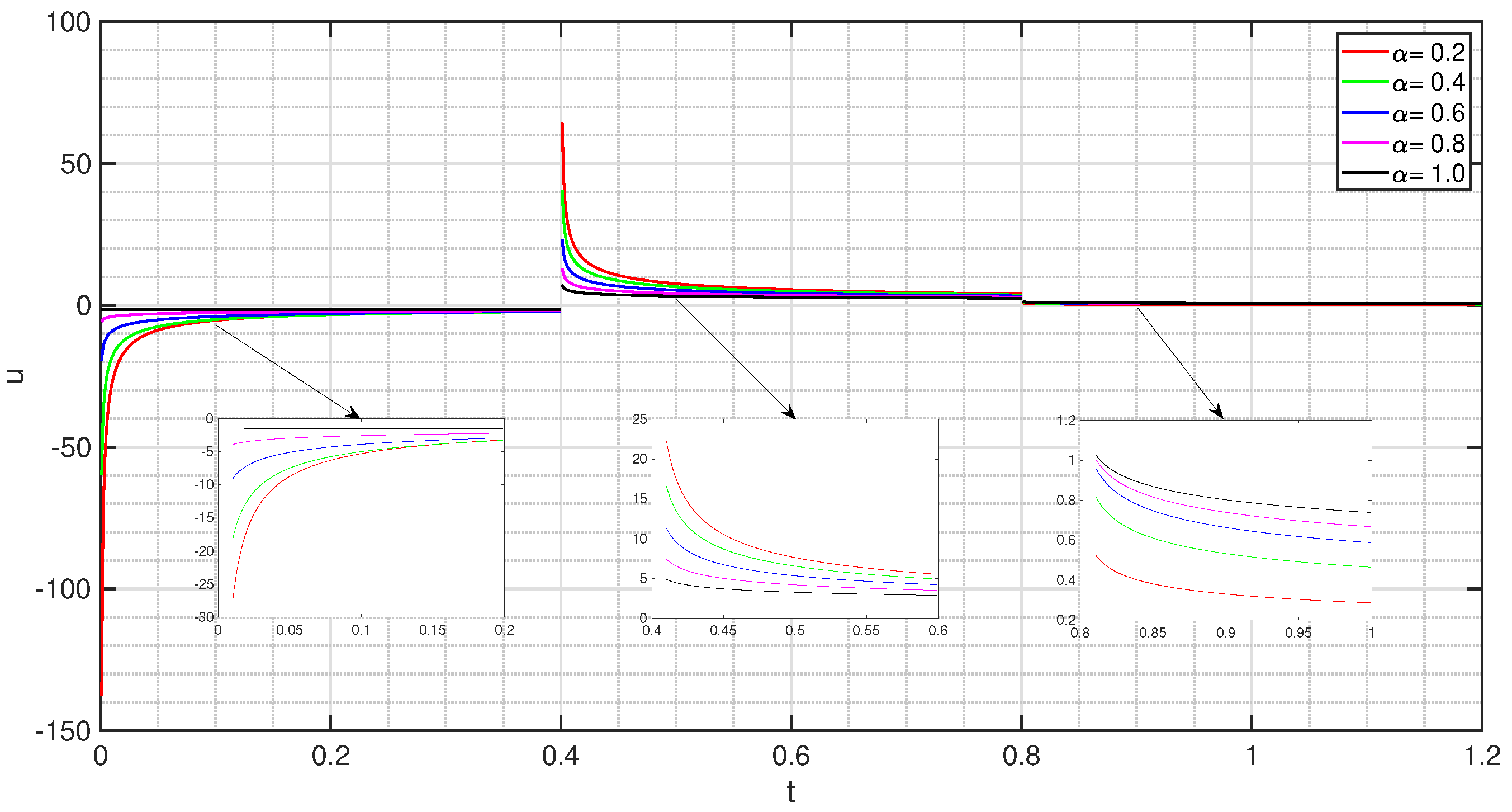
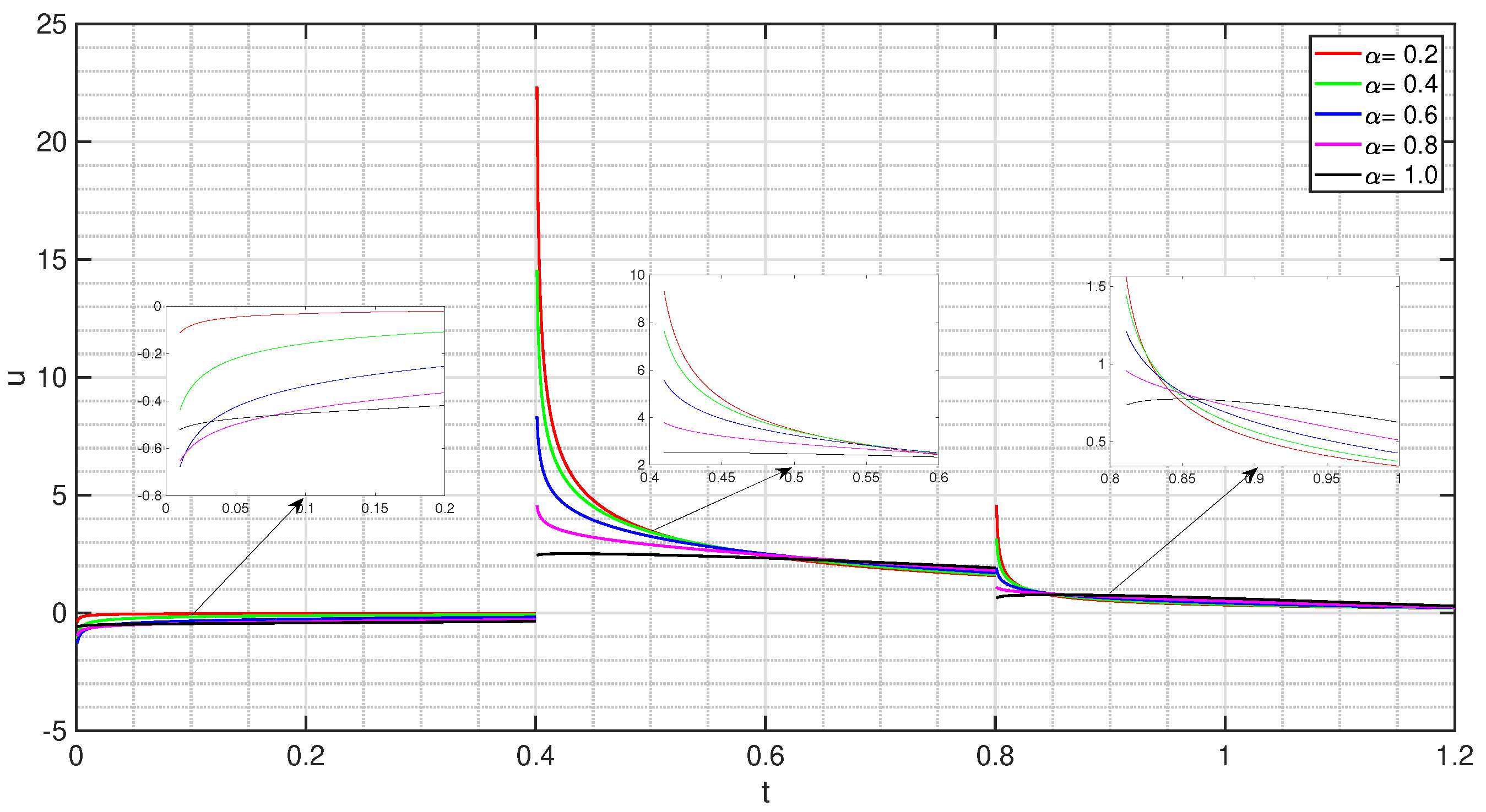
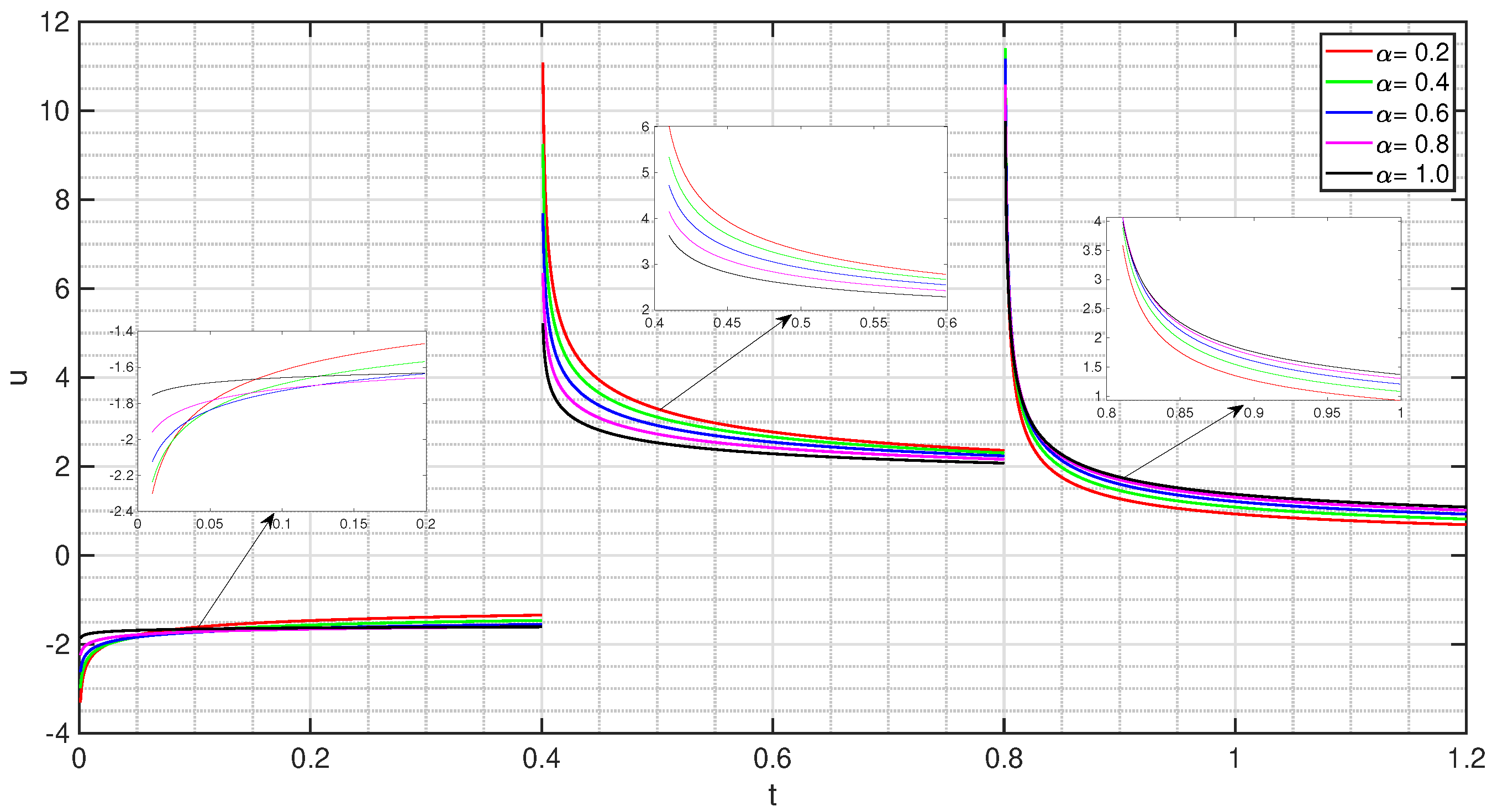
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Fractional calculus | |
| Riemann–Liouville | |
| Non-local multi-point | |
| Boundary value problem | |
| Fractional integral operator | |
| Fractional derivative operator | |
| Fractional differential equation | |
| Fractional integral boundary condition | |
| Fractional integro-differential equation |
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Fallahgoul, H.A.; Focardi, S.M.; Fabozzi, F.J. Fractional Calculus and Fractional Processes with Applications to Financial Economics; Theory and Application; Elsevier/Academic Press: London, UK, 2017. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Application of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer & HEP: Berlin, Germany, 2011. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers: Danbury, CT, USA, 2006. [Google Scholar]
- Thaiprayoon, C.; Kongson, J.; Sudsutad, W.; Alzabut, J.; Etemad, S.; Rezapour, S. Analysis of a nonlinear fractional system for Zika virus dynamics with sexual transmission route under generalized Caputo-type derivative. J. Appl. Math. Comput. 2022. [Google Scholar] [CrossRef]
- Kongson, J.; Thaiprayoon, C.; Neamvonk, A.; Alzabut, J.; Sudsutad, W. Investigation of fractal-fractional HIV infection by evaluating the drug therapy effect in the Atangana-Baleanu sense. Math. Biosci. Eng. 2022, 19, 10762–10808. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, A.N.; Ahmad, B. A fractional-order differential equation model of COVID-19 infection of epithelial cells. Chaos Solitons Fractals 2021, 147, 110952. [Google Scholar] [CrossRef] [PubMed]
- Pleumpreedaporn, S.; Pleumpreedaporn, C.; Kongson, J.; Thaiprayoon, C.; Alzabut, J.; Sudsutad, W. Dynamical Analysis of Nutrient-Phytoplankton-Zooplankton Model with Viral Disease in Phytoplankton Species under Atangana-Baleanu-Caputo Derivative. Mathematics 2022, 10, 1578. [Google Scholar] [CrossRef]
- Mainardi, F. Some basic problems in continuum and statistical mechanics. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: Berlin, Germany, 1997; pp. 291–348. [Google Scholar]
- Mukhtar, S.; Shah, R.; Noor, S. The numerical investigation of a fractional-order multi-dimensional Model of Navier-Stokes equation via novel techniques. Symmetry 2022, 14, 1102. [Google Scholar] [CrossRef]
- Kongson, J.; Sudsutad, W.; Thaiprayoon, C.; Alzabut, J.; Tearnbucha, C. On analysis of a nonlinear fractional system for social media addiction involving Atangana-Baleanu-Caputo derivative. Adv. Differ. Equ. 2021, 2021, 356. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of the Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations. In Lecture Notes in Mathematics; Springer: New York, NY, USA, 2010. [Google Scholar]
- Lakshmikantham, V.; Leela, S.; Devi, J.V. Theory of Fractional Dynamic Systems; Cambridge Scientific Publishers: Cambridge, UK, 2009. [Google Scholar]
- Zhou, Y. Basic Theory of Fractional Differential Equations; World Scientific: Singapore, 2014. [Google Scholar]
- Sousa, J.V.C.; de Oliveira, E.C. On the ψ-Hilfer fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 72–91. [Google Scholar] [CrossRef]
- Sousa, J.V.C.; de Oliveira, E.C. A Gronwall Inequality and the Cauchy-Type Problem by Means of ψ-Hilfer Operator. Differ. Equ. Appl. 2019, 11, 87–106. [Google Scholar]
- Almalahi, A.; Panchal, K. Existence Results of ψ-Hilfer Integro-Differential Equations with Fractional Order in Banach Space. Ann. Univ. Paedagog. Crac. Stud. Math. 2020, 19, 171–192. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; O’Regan, D. Ulam-Hyers-Mittag-Leffer Stability for ψ-Hilfer Fractional-Order Delay Differential Equations. Adv. Differ. Equ. 2019, 2019, 50. [Google Scholar] [CrossRef]
- Alzabut, J.; Adjabi, Y.; Sudsutad, W.; Rehman, M.-U. New Generalizations for Gronwall Type Inequalities Involving a ψ-Fractional Operator and Their Applications. AIMS Math. 2021, 6, 5053–5077. [Google Scholar] [CrossRef]
- Thaiprayoon, C.; Sudsutad, W.; Ntouyas, S.K. Mixed Nonlocal Boundary Value Problem for Implicit Fractional Integro-Differential Equations via ψ-Hilfer Fractional Derivative. Adv. Differ. Equ. 2021, 2021, 50. [Google Scholar] [CrossRef]
- Kucche, K.D.; Mali, A.D. On the nonlinear (k,ψ)-Hilfer fractional differential equations. Chaos Solitons Fractals 2021, 152, 111335. [Google Scholar] [CrossRef]
- Bainov, D.D.; Simeonov, P.S. Impulsive Differential Equations: Periodic Solutions and Applications; Longman Scientific and Technical Group Limited: New York, NY, USA, 1993. [Google Scholar]
- Benchohra, M.; Henderson, J.; Ntouyas, S.K. Impulsive Differential Equations and Inclusions; Hindawi Publishing Corporation: New York, NY, USA, 2006; Volume 2. [Google Scholar]
- Samoilenko, A.M.; Perestyuk, N.A. Impulsive Differential Equations; World Scientific: Singapore, 1995. [Google Scholar]
- Benchohra, M.; Slimani, B.A. Existence and Uniqueness of Solutions to Impulsive Fractional Differential Equations. Elect. J. Diff. Equ. 2009, 2009, 111. [Google Scholar]
- Benchohra, M.; Seba, D. Impulsive Fractional Differential Equations in Banach Spaces. Elect. J. Qual. Theory Differ. Equ. 2009, 8, 14. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, W.; Fečkan, M. Nonlinear Impulsive Problems for Fractional Differential Equations and Ulam Stability. Comput. Math. Appl. 2012, 64, 3389–3405. [Google Scholar] [CrossRef]
- Wang, J.R.; Lin, Z. On the Impulsive Fractional Anti-Periodic BVP Modelling with Constant Coefficients. J. Appl. Math. Comput. 2014, 46, 107–121. [Google Scholar] [CrossRef]
- Zuo, M.; Hao, X.; Liu, L.; Cui, Y. Existence Results for Impulsive Fractional Integro-Differential Equation of Mixed Type with Constant Coefficient and Antiperiodic Boundary Conditions. Bound. Value Probl. 2017, 2017, 161. [Google Scholar] [CrossRef]
- Kucche, K.D.; Kharade, J.P.; Sousa, J.V.C. On the Nonlinear Impulsive ψ-Hilfer Fractional Differential Equations. Math. Model. Anal. 2020, 25, 642–660. [Google Scholar] [CrossRef]
- Salim, A.; Benchohra, M.; Lazreg, J.E.; Henderson, J. On k-Generalized ψ-Hilfer Boundary Value Problems with Retardation and Anticipation. Adv. Theory Nonlinear Anal. Appl. 2022, 6, 173–190. [Google Scholar]
- Fečkan, M.; Zhou, Y.; Wang, J. On the Concept and Existence of Solution for Impulsive Fractional Differential Equations. Commun. Nonlinear Sci. Numer Simulat. 2012, 17, 3050–3060. [Google Scholar] [CrossRef]
- Guo, T.L.; Jiang, W. Impulsive Fractional Functional Differential Equations. Comput. Math. Appl. 2012, 64, 3414–3424. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Y.; Fečkan, M. On Recent Developments in the Theory of Boundary Value Problems for Impulsive Fractional Differential Equations. Comput. Math. Appl. 2012, 64, 3008–3020. [Google Scholar] [CrossRef][Green Version]
- Shah, K.; Ali, A.; Bushnaq, S. Hyers-Ulam Stability Analysis to Implicit Cauchy Problem of Fractional Differential Equations with Impulsive Conditions. Math. Meth. Appl. Sci. 2018, 41, 8329–8343. [Google Scholar] [CrossRef]
- Malti, A.I.N.; Benchohra, M.; Graef, J.R.; Lazreg, J.E. Impulsive Boundary Value Problems for Nonlinear Implicit Caputo- Exponential Type Fractional Differential Equations. Electron. J. Qual. Theory Differ. Equ. 2020, 78, 1–17. [Google Scholar] [CrossRef]
- Abbas, M.I. On the Initial Value Problems for the Caputo-Fabrizio Impulsive Fractional Differential Equations. Asian-Eur. J. Math. 2020, 14, 2150073. [Google Scholar] [CrossRef]
- Salim, A.; Benchohra, M.; Karapinar, E.; Lazreg, J.E. Existence and Ulam Stability for Impulsive Generalized Hilfer-Type Fractional Differential Equations. Adv. Differ. Equ. 2020, 2020, 601. [Google Scholar] [CrossRef]
- Salim, A.; Benchohra, M.; Lazreg, J.E.; Henderson, J. Nonlinear Implicit Generalized Hilfer-Type Fractional Differential Equations with Non-Instantaneous Impulses in Banach Spaces. Adv. Theory Nonlinear Anal. Appl. 2020, 4, 332–348. [Google Scholar] [CrossRef]
- Khaminsou, B.; Sudsutad, W.; Thaiprayoon, C.; Alzabut, J.; Pleumpreedaporn, S. Analysis of Impulsive Boundary Value Pantograph Problems via Caputo Proportional Fractional Derivative under Mittag-Leffler Functions. Fractal Fract. 2021, 5, 251. [Google Scholar] [CrossRef]
- Kharade, J.P.; Kucche, K.D. On the Impulsive Implicit ψ-Hilfer Fractional Differential Equations with Delay. Math. Meth. Appl. Sci. 2020, 43, 1938–1952. [Google Scholar] [CrossRef]
- Savrankumar, S.; Raja, R.; Alzabut, J. Delay-Dependent Passivity Analysis of Non-Deterministic Genetic Regulatory Networks with Leakage and Distributed Delays Against Impulsive Perturbations. Adv. Differ. Equ. 2021, 2021, 353. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Alzabut, J.; Cao, J.; Rajachakit, G.; Hunag, C. Mittag-Leffler Stability and Adaptive Impulsive Synchronization of Fractional Order Neural Networks in Quaternion Field. Math. Meth. Appl. Sci. 2020, 43, 6223–6253. [Google Scholar] [CrossRef]
- Afshari, H.; Marasi, H.R.; Alzabut, J. Applications of New Contraction Mappings on Existence and Uniqueness Results for Implicit Φ-Hilfer Fractional Pantograph Differential Equations. J. Inequa. Appl. 2021, 2021, 185. [Google Scholar] [CrossRef]
- Kwun, Y.C.; Farid, G.; Nazeer, W.; Ullah, S.; Kang, S.M. Generalized Riemann-Liouville k-fractional integrals associated with Ostrowski type inequalities and error bounds of Hadamard inequalities. IEEE Access 2018, 6, 64946–64953. [Google Scholar] [CrossRef]
- Diaz, R.; Pariguan, E. On hypergeometric functions and Pochhammer k-symbol. Divulg. Mat. 2007, 2, 179–192. [Google Scholar]
- Dorrego, G.A. An Alternative Definition for the k-Riemann-Liouville Fractional Derivative. Appl. Math. Sci. 2015, 9, 481–491. [Google Scholar] [CrossRef]
- Naz, S.; Naeem, M.N. On the Generalization of k-Fractional Hilfer-Katugampola Derivative with Cauchy Problem. Turk. J. Math. 2021, 45, 110–124. [Google Scholar] [CrossRef]
- Wang, J.R.; Fečkan, M.; Zhou, Y. Presentation of Solutions of Impulsive Fractional Langevin Equations and Existence Results. Eur. Phys. J. Spec. Top. 2013, 222, 1857–1874. [Google Scholar] [CrossRef]
- Almalahi, M.A.; Panchal, S.K. Some existence and stability results for ϕ-Hilfer fractional implicit diferential equation with periodic conditions. J. Math. Anal. Model. 2020, 1, 1–19. [Google Scholar] [CrossRef]
- Granas, A.; Dugundji, J. Fixed Point Theory; Springer: New York, NY, USA, 2003. [Google Scholar]
- O’Regan, D. Fixed-point theory for the sum of two operators. Appl. Math. Lett. 1996, 9, 1–8. [Google Scholar] [CrossRef]
| 0.2 | 2.892662425 | 1.3437981140 | 2.058239791 | 0.8286028011 |
| 0.4 | 3.213267392 | 0.8843819924 | 1.946083874 | 0.8450705102 |
| 0.6 | 3.328008050 | 0.6154263942 | 1.917611370 | 0.8499260482 |
| 0.8 | 3.199108790 | 0.4512723574 | 1.962021647 | 0.8435009608 |
| 1.0 | 2.903673651 | 0.3448765974 | 2.059944134 | 0.8272976029 |
| 0.2 | 0.979991112 | 4.377072500 | 3.467001554 | 0.6667371782 |
| 0.4 | 1.086173111 | 4.286940343 | 3.644959141 | 0.6463248146 |
| 0.6 | 1.192145946 | 4.039684022 | 3.713433921 | 0.6338233539 |
| 0.8 | 1.288330209 | 3.702297047 | 3.704677442 | 0.6253964583 |
| 1.0 | 1.366630096 | 3.320188403 | 3.641434555 | 0.6183465441 |
| 0.2 | 2.706972884 | 5.693274732 | 1.322584648 | 0.7888666540 |
| 0.4 | 3.075302870 | 3.950732086 | 1.271388814 | 0.8122697082 |
| 0.6 | 3.448104601 | 2.748016737 | 1.239777125 | 0.8313127993 |
| 0.8 | 3.800110763 | 1.924362576 | 1.227618946 | 0.8461678966 |
| 1.0 | 4.087413705 | 1.363408014 | 1.236212063 | 0.8565872889 |
| Case | |||||
|---|---|---|---|---|---|
| I | 3.350618629 | ||||
| II | 3 | 1.221677115 | |||
| III | 3.593850012 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaewsuwan, M.; Phuwapathanapun, R.; Sudsutad, W.; Alzabut, J.; Thaiprayoon, C.; Kongson, J. Nonlocal Impulsive Fractional Integral Boundary Value Problem for (ρk,ϕk)-Hilfer Fractional Integro-Differential Equations. Mathematics 2022, 10, 3874. https://doi.org/10.3390/math10203874
Kaewsuwan M, Phuwapathanapun R, Sudsutad W, Alzabut J, Thaiprayoon C, Kongson J. Nonlocal Impulsive Fractional Integral Boundary Value Problem for (ρk,ϕk)-Hilfer Fractional Integro-Differential Equations. Mathematics. 2022; 10(20):3874. https://doi.org/10.3390/math10203874
Chicago/Turabian StyleKaewsuwan, Marisa, Rachanee Phuwapathanapun, Weerawat Sudsutad, Jehad Alzabut, Chatthai Thaiprayoon, and Jutarat Kongson. 2022. "Nonlocal Impulsive Fractional Integral Boundary Value Problem for (ρk,ϕk)-Hilfer Fractional Integro-Differential Equations" Mathematics 10, no. 20: 3874. https://doi.org/10.3390/math10203874
APA StyleKaewsuwan, M., Phuwapathanapun, R., Sudsutad, W., Alzabut, J., Thaiprayoon, C., & Kongson, J. (2022). Nonlocal Impulsive Fractional Integral Boundary Value Problem for (ρk,ϕk)-Hilfer Fractional Integro-Differential Equations. Mathematics, 10(20), 3874. https://doi.org/10.3390/math10203874