Interactions of Logistic Distribution to Credit Valuation Adjustment: A Study on the Associated Expected Exposure and the Conditional Value at Risk
Abstract
1. Introduction
1.1. Credit Valuation Adjustment
1.2. Counterparty Credit Risk
1.3. CVA Value-at-Risk (VaR) and a Variant
1.4. Motivation
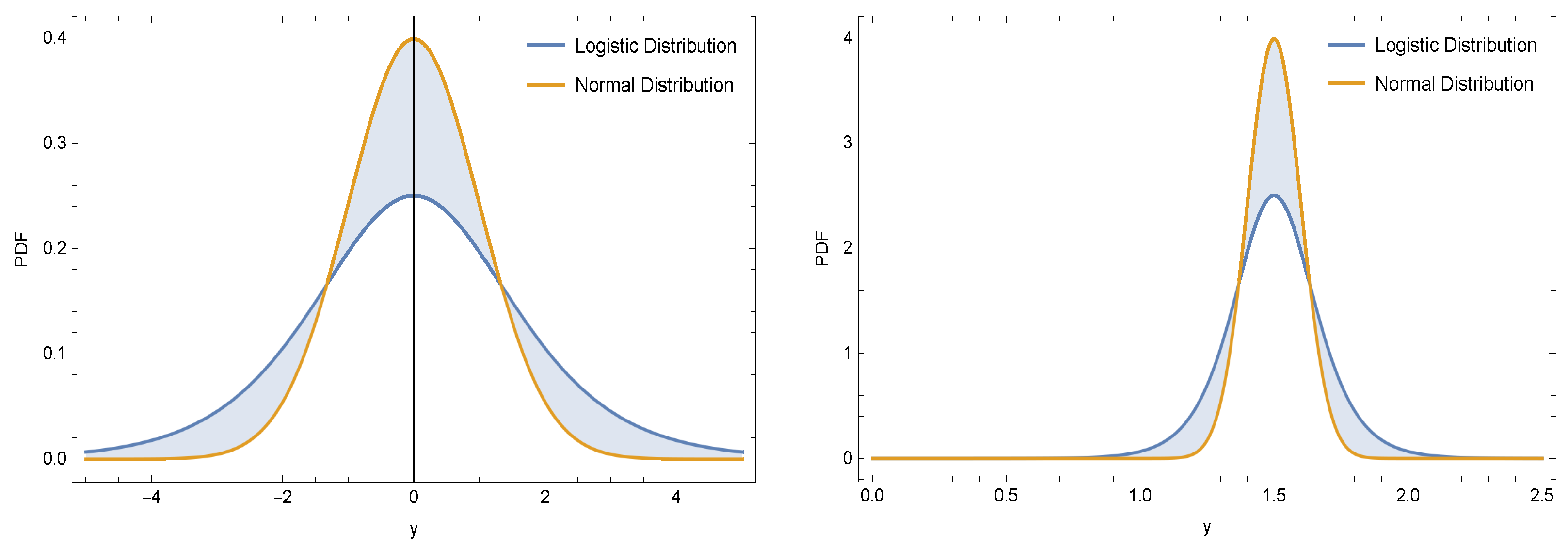
- As pointed out in [21], credit spread levels and changes provide signs of the characteristic fat-tailed behavior and, in both cases, recommend that both series are away from a distribution of the normal. This justifies why we chose the fatter tail logistic distribution in this work in contrast to the normal distribution.
- The logistic model has also recently been applied in the work [22] in another context and showed promising results.
- It is pointed out that, in Table 1 of [23], some empirical evidence for the use of a logistic distribution for modeling the distribution of a risk variable is provided.
- Note that experiencing all of the non-Gaussian distributions in modeling stock data [24] is not the major aim here since it is not feasible. As a matter of fact, our strategy is to adopt a fat-tailed distribution, namely, logistic distribution, that is good enough to accommodate the features of financial data with respect to computing the CVA VaR and CVA CVaR in higher dimensions.
1.5. Problems to Be Solved and Novelty
- Here, we first focused on IRS CVA and improved the existing EEs formulas given for IRS CVA using the logistic distribution. The existing relations are based on the normal distribution. In fact, here, the novelty is that we explored the model distribution for the exposure based on a proxy for the swap duration and the logistic distribution.
- Next, we employed the logistic distribution to propose a new formulation for CVA VaR. In fact, the existing CVA VaR formulation is based on the normal distribution and, here, we assumed that the CDS spread follows a logistic distribution and obtained a new formulation that is more consistent with real financial data having fatter tails.
- The final important factor that has been addressed in this piece of work is to assume that not only the credit spread but also the EPE follow logistic distributions having different parameters. This novelty of the work extends the computation of CVA VaR and CVaR in higher dimensions.
1.6. Organization
2. New EE Formulas
2.1. Logistic Distribution
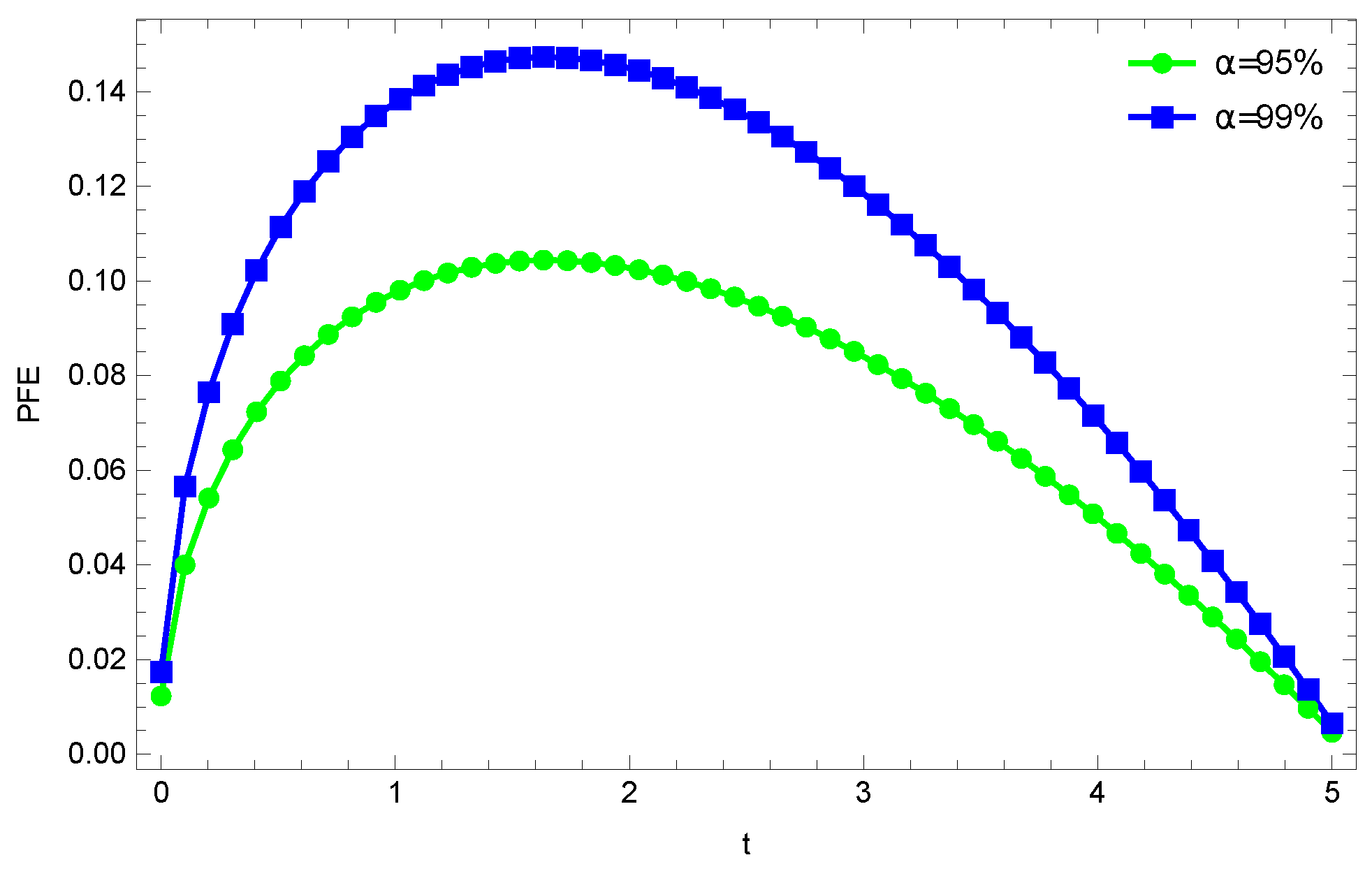
2.2. PFE
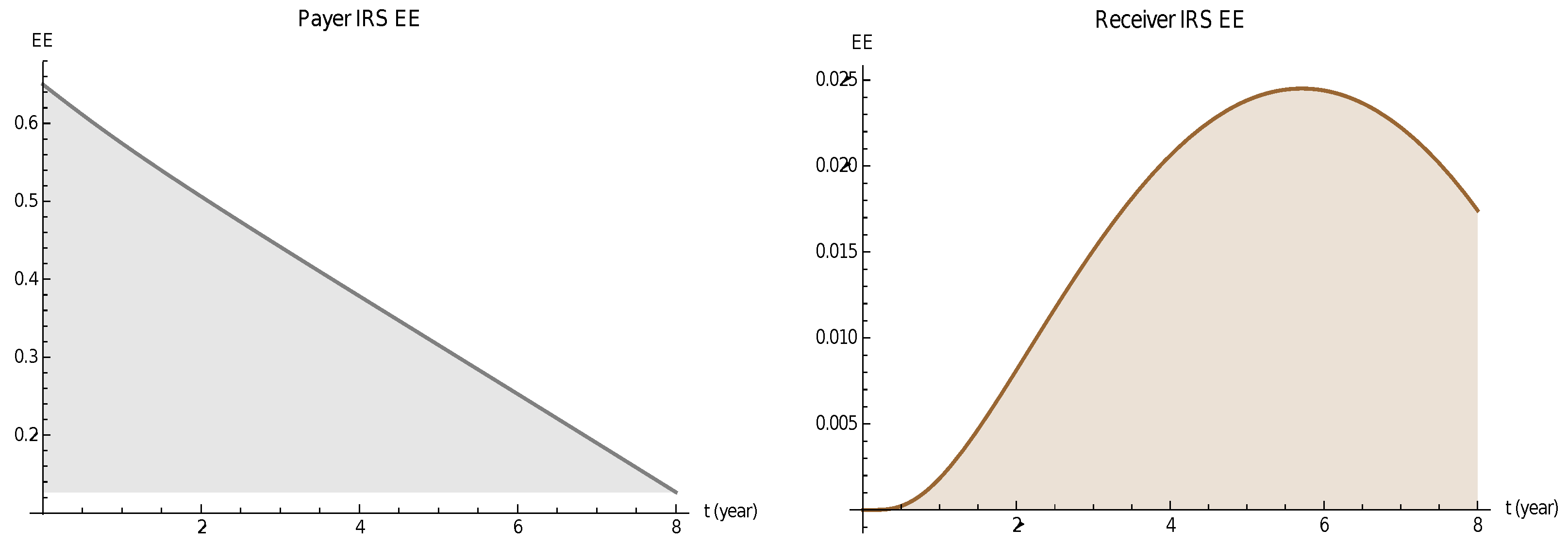
2.3. Derivation of New EE Relations
3. Novel Risk Measure Formulas for CVA
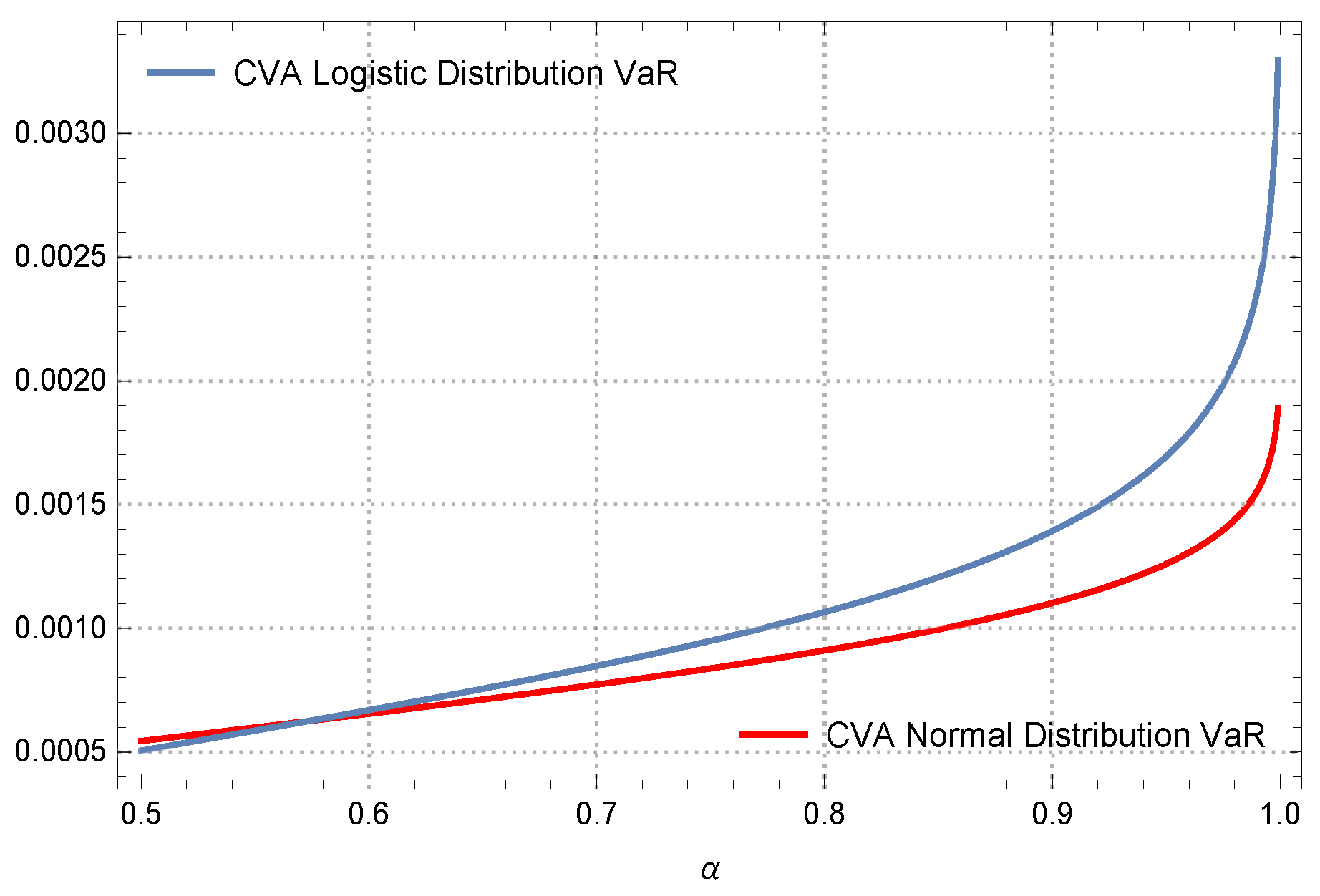
3.1. CVA VaR under the Logistic Distribution
3.2. Extension to Higher Dependency Based on the Logistic Distribution
4. Applications
4.1. EEs for the Payer and Receiver Swap
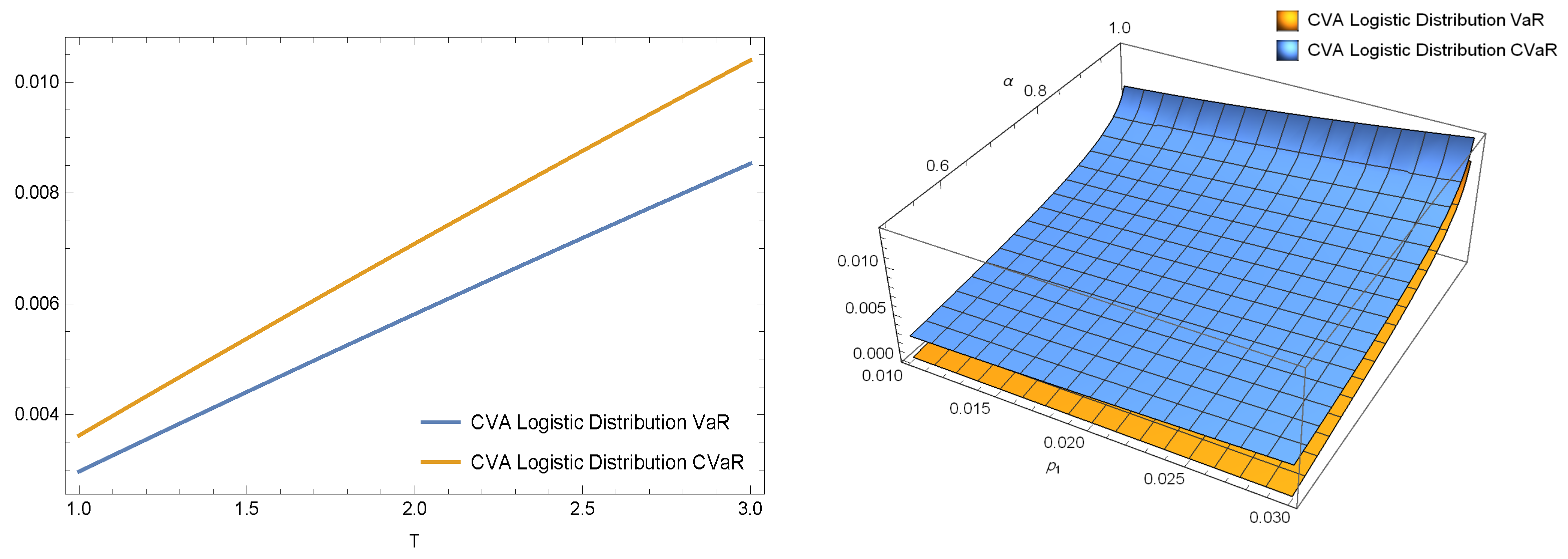
4.2. Results for 1D CVA VaR and Advantages over the Existing Solver
4.3. Results for 2D CVA VaR
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geurdes, J.F. On the mathematical form of CVA in Basel III. 2011, MPRA Paper No. 30955. Available online: https://mpra.ub.unimuenchen.de/30955/ (accessed on 26 August 2022).
- Hlivka, I. Credit Valuation Adjustment with Mathematica 10; Research Note; Quant Solutions Group: London, UK, 2014; pp. 1–2. [Google Scholar]
- Bade, B.; Rosch, D.; Scheule, H. Default and recovery risk dependencies in a simple credit risk model. Euro. Finan. Manag. 2011, 17, 120–144. [Google Scholar] [CrossRef]
- Pouliasis, P.; Kyriakou, I.; Papapostolou, N. On equity risk prediction and tail spillovers. Int. J. Fin. Econ. 2017, 22, 379–393. [Google Scholar] [CrossRef]
- Hlivka, I. VaR, CVaR and Their Time Series Applications; Research Note; Quant Solutions Group: London, UK, 2015; pp. 1–2. [Google Scholar]
- Thurner, S.; Doyne Farmer, J.; Geanakoplos, J. Leverage causes fat tails and clustered volatility. Quant. Finan. 2012, 12, 695–707. [Google Scholar] [CrossRef]
- Green, A. XVA: Credit, Funding and Capital Valuation Adjustments; Wiley Finance, John Wiley and Sons Inc.: Chichester, UK, 2015. [Google Scholar]
- Piterbarg, V. Cooking with collateral. Risk Mag. 2012, 2, 58–63. [Google Scholar]
- Kenyon, C.; Green, A. Landmarks in XVA: From Counterparty Risk to Funding Costs and Capital; Risk Publications: London, UK, 2016; p. 688. [Google Scholar]
- Skoglund, J.; Chen, W. Financial Risk Management, Applications in Market, Credit, Asset and Liability Management and Firmwide Risk; Wiley: Toronto, ON, Canada, 2015. [Google Scholar]
- Mohamadinejad, R.; Neisy, A.; Biazar, J. ADI method of credit spread option pricing based on jump-diffusion model. Iran. J. Numer. Anal. Optim. 2021, 11, 195–210. [Google Scholar]
- Itkin, A.; Soleymani, F. Four-factor model of quanto CDS with jumps-at-default and stochastic recovery. J. Comput. Sci. 2021, 54, 101434. [Google Scholar] [CrossRef]
- Soleymani, F.; Zhu, S. On a high-order Gaussian radial basis function generated Hermite finite difference method and its application. Calcolo 2021, 50, 58. [Google Scholar] [CrossRef]
- Soheili, A.R.; Soleymani, F. Iterative methods for nonlinear systems associated with finite difference approach in stochastic differential equations. Numer. Algorithms 2016, 71, 89–102. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Finance 1952, 7, 77–91. [Google Scholar]
- Lechner, L.A.; Ovaert, T.C. Value-at-risk: Techniques to account for leptokurtosis and asymmetric behavior in returns distributions. J. Risk Fin. 2010, 11, 464–480. [Google Scholar] [CrossRef]
- Artzner, P.; Delbaen, F.; Eber, J.-M.; Heath, D. Coherent measures of risk. Math. Finan. 1999, 9, 203–228. [Google Scholar] [CrossRef]
- Witzany, J. Credit Risk Management; Springer International Publishing AG: Cham, Switzerland, 2017. [Google Scholar]
- Sarykalin, S.; Serraino, G.; Uryasev, S. Value-at-risk vs. conditional value-at-risk in risk management and optimization. Tutorials Oper. Res. 2008, 270–294. [Google Scholar] [CrossRef]
- Mwaniki, I.J. Modeling heteroscedastic, skewed and leptokurtic returns in discrete time. J. Appl. Finan. Bank. 2019, 9, 1–14. [Google Scholar]
- Manzoni, K. Modeling credit spreads: An application to the sterling Eurobond market. Int. Rev. Finan. Anal. 2002, 11, 183–218. [Google Scholar] [CrossRef]
- Itkin, A.; Lipton, A.; Muravey, D. From the Black-Karasinski to the Verhulst model to accommodate the unconventional Fed’s policy. arXiv 2021, arXiv:2006.11976v2. [Google Scholar]
- Toma, A.; Dedu, S. Quantitative techniques for financial risk assessment: A comparative approach using different risk measures and estimation methods. Procedia Econ. Finan. 2014, 8, 712–719. [Google Scholar] [CrossRef]
- Kaweto, K.S.; Joseph, M.I.; Onyino, S.R. Modeling stock returns and trading volume in regime switching world. Finan. Math. Appl. 2021, 6, 1–14. [Google Scholar]
- Gregory, J. Counterparty Credit Risk, The New Challenge for Global Financial Markets; John Wiley & Sons Ltd.: West Sussex, UK, 2010. [Google Scholar]
- Yeh, H.-C. Multivariate semi-logistic distributions. J. Multi. Anal. 2010, 101, 893–908. [Google Scholar] [CrossRef]
- Akkizidis, I.; Kalyvas, L. Final Basel III Modelling: Implementation, Impact and Implications; Palgrave Macmillan: Cham, Switzerland, 2018. [Google Scholar]
- Hlivka, I. Explaining CVA Derivatives; Research Note; Quant Solutions Group: London, UK, 2015; pp. 1–13. [Google Scholar]
- Savalei, V. Logistic approximation to the normal: The KL rationale. Psychometrika 2006, 71, 763–767. [Google Scholar] [CrossRef]
- Arévalo, R.-V.; Cortés, J.-C.; Villanueva, R.-J. The Cox-Ingersoll-Ross Interest Rate Model Revisited: Some Motivations and Applications; Instituto Universitario de Matematica Multidisciplinar: Valencia, Spain, 2016; Chapter 13; pp. 165–176. [Google Scholar]
- Lipton, A.; Sepp, A. Credit value adjustment for credit default swaps via the structural default model. J. Credit Risk 2009, 5, 127–150. [Google Scholar] [CrossRef]
- Georgakopoulos, N.L. Illustrating Finance Policy with Mathematica; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]

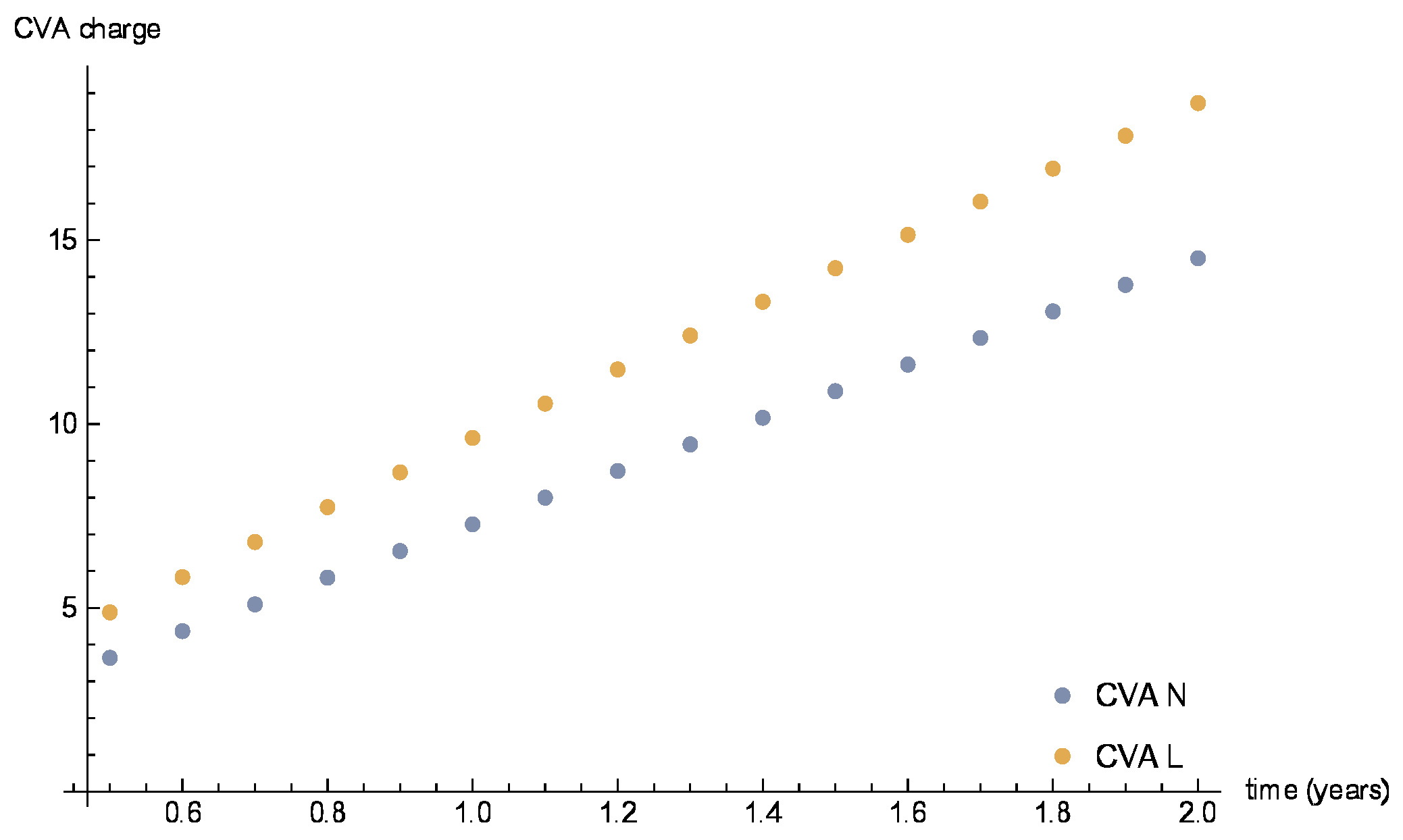
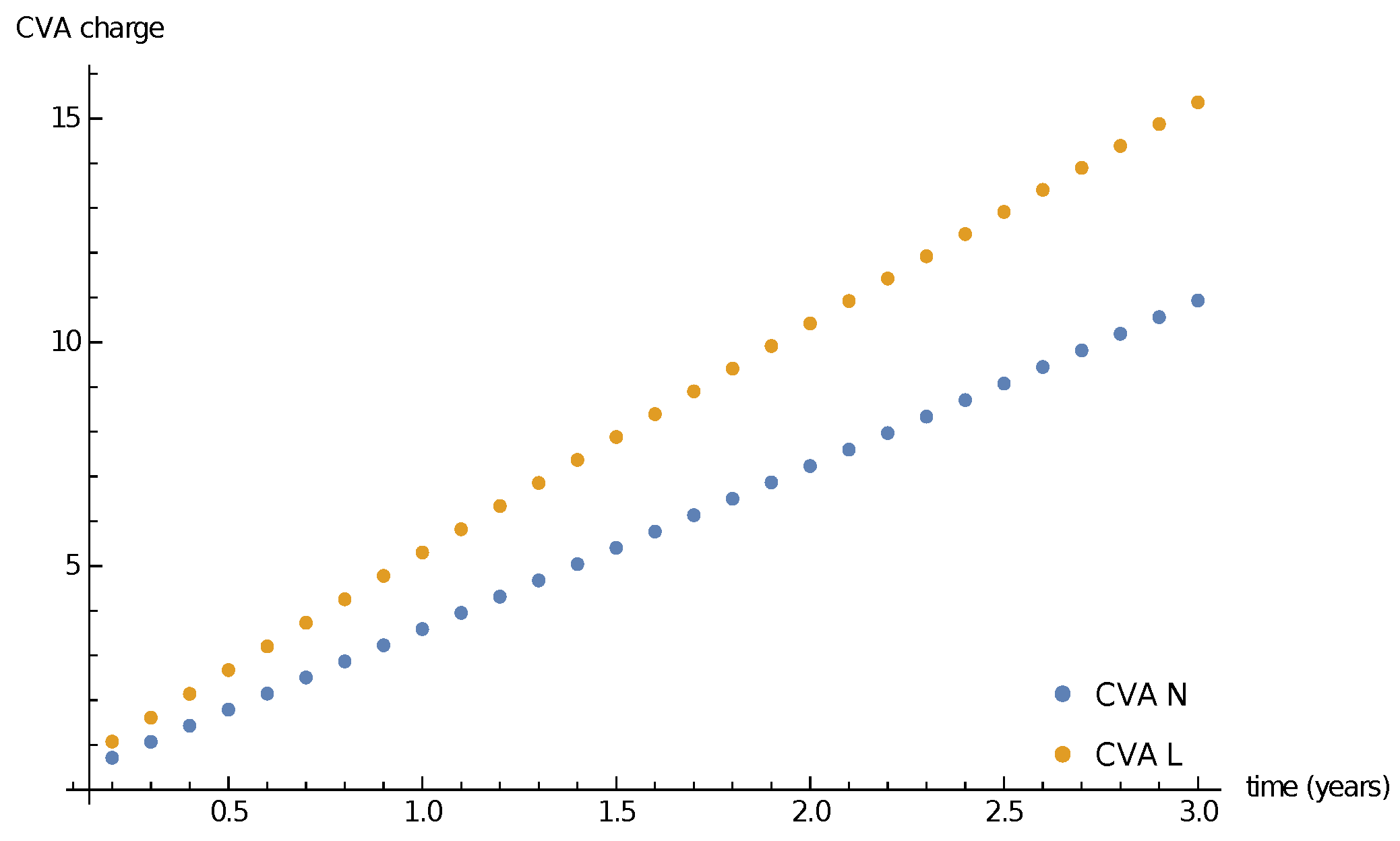
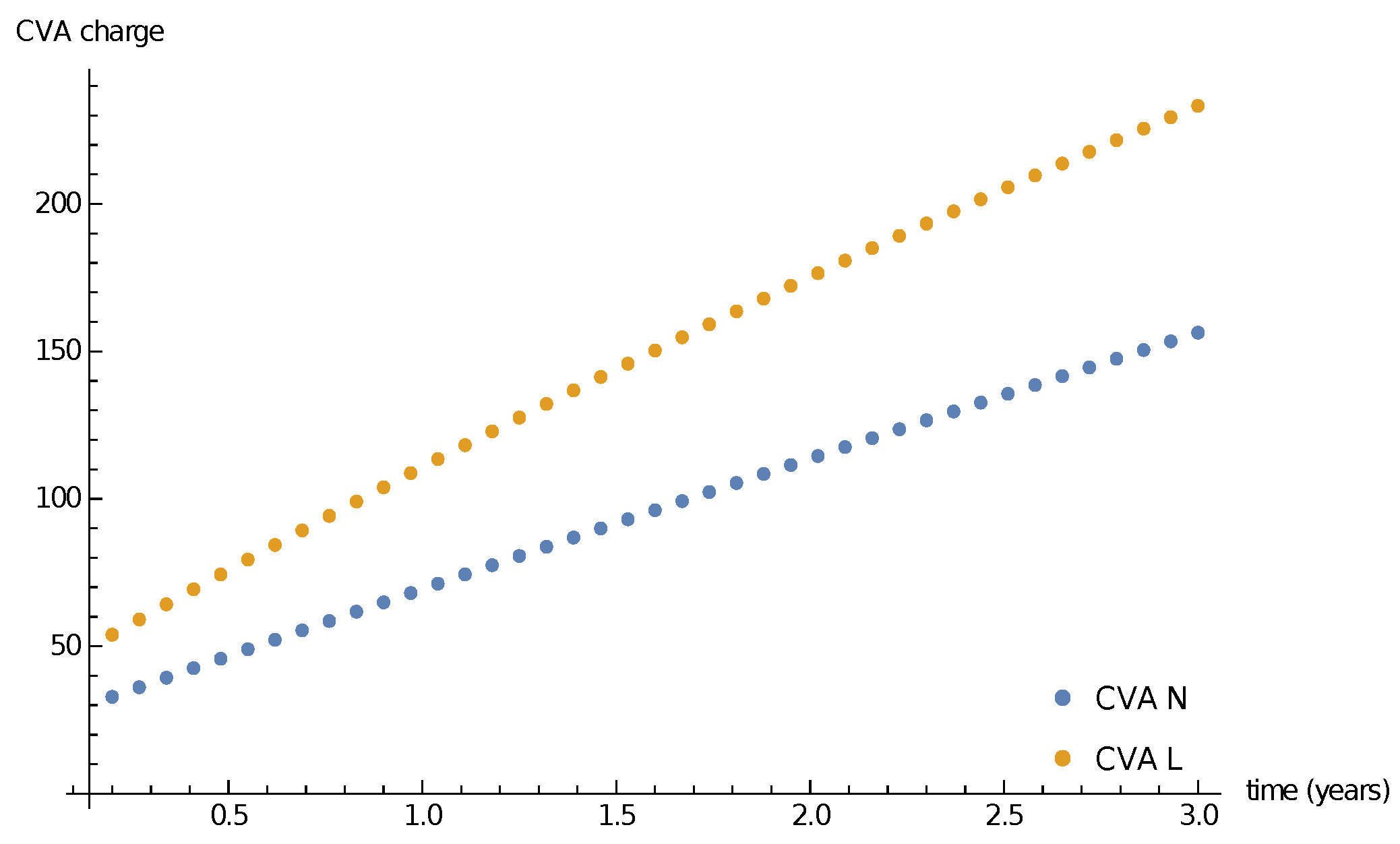
| Name | Mean | Variance | Median | Skewness | Kurtosis | q-Quantile |
|---|---|---|---|---|---|---|
| Normal | 0 | 3 | , | |||
| Logistic | 0 | , |
| T | 2.0 | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 3.0 |
| CVA charge | 3.44 | 3.60 | 3.77 | 3.93 | 4.09 | 4.25 | 4.41 | 4.57 | 4.73 | 4.89 | 5.05 |
| CVA N, | 6.05 | 6.35 | 6.66 | 6.96 | 7.27 | 7.57 | 7.88 | 8.187 | 8.49 | 8.79 | 9.10 |
| CVA L, | 7.26 | 7.60 | 7.95 | 8.29 | 8.63 | 8.97 | 9.31 | 9.6517 | 9.98 | 10.3211 | 10.65 |
| CVA N, | 7.32 | 7.69 | 8.06 | 8.43 | 8.80 | 9.17 | 9.54 | 9.90 | 10.27 | 10.64 | 11.01 |
| CVA L, | 9.49 | 9.94 | 10.39 | 10.84 | 11.29 | 11.73 | 12.18 | 12.62 | 13.05 | 13.49 | 13.93 |
| CVA N, | 8.37 | 8.80 | 9.22 | 9.64 | 10.06 | 10.48 | 10.90 | 11.33 | 11.75 | 12.17 | 12.60 |
| CVA L, | 11.55 | 12.10 | 12.65 | 13.19 | 13.74 | 14.28 | 14.82 | 15.35 | 15.88 | 16.42 | 16.95 |
| CVA N, | 10.35 | 10.87 | 11.39 | 11.91 | 12.43 | 12.95 | 13.47 | 13.99 | 14.52 | 15.04 | 15.56 |
| CVA L, | 16.09 | 16.86 | 17.63 | 18.39 | 19.14 | 19.90 | 20.65 | 21.39 | 22.14 | 22.88 | 23.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Shateyi, S.; He, J.; Cui, X. Interactions of Logistic Distribution to Credit Valuation Adjustment: A Study on the Associated Expected Exposure and the Conditional Value at Risk. Mathematics 2022, 10, 3828. https://doi.org/10.3390/math10203828
Song Y, Shateyi S, He J, Cui X. Interactions of Logistic Distribution to Credit Valuation Adjustment: A Study on the Associated Expected Exposure and the Conditional Value at Risk. Mathematics. 2022; 10(20):3828. https://doi.org/10.3390/math10203828
Chicago/Turabian StyleSong, Yanlai, Stanford Shateyi, Jianying He, and Xueqing Cui. 2022. "Interactions of Logistic Distribution to Credit Valuation Adjustment: A Study on the Associated Expected Exposure and the Conditional Value at Risk" Mathematics 10, no. 20: 3828. https://doi.org/10.3390/math10203828
APA StyleSong, Y., Shateyi, S., He, J., & Cui, X. (2022). Interactions of Logistic Distribution to Credit Valuation Adjustment: A Study on the Associated Expected Exposure and the Conditional Value at Risk. Mathematics, 10(20), 3828. https://doi.org/10.3390/math10203828






