Abstract
Every business owner wishes that all sales were made on a cash basis, but in a cutthroat market, it is not always feasible. To entice buyers to purchase their goods, dealers may need to offer sales with credit terms. Unfortunately, selling with deferred payment conditions introduces a completely new facet of business management. Additionally, the salvage amount or value is significant for determining depreciation and can have an impact on the company’s overall depreciable amount used in its depreciation schedule. This study looks at an inventory model with the best possible pricing and ordering policy for retailers. Research is derived from when inventory is subjected to a constant deterioration rate and associated with appropriate salvage value. A perishable payments strategy inventory model is created, with the demand as a function of the stock level as well as selling price. Manufacturers provide to the retailer a tolerable deferred payment scheme to repay against the purchase products. That the cycle length and order size will rise under tolerable deferred period is refuted. The study’s goal is to determine the optimal replenishment cycle length and selling price to optimize retailer’s net income. With reference to cycle length and selling price, we developed an algorithm with a numerical example to optimize the net profit. The results are mathematically proven, and data is provided to validate the aforementioned model. Numerical examples are used to validate the model, and sensitivity analysis was performed. Using mathematical tools, a 3D graph will be used to demonstrate the concavity of the objective function.
Keywords:
price-sensitive policy; stock-dependent demand; deteriorating inventory; salvage value; deferred payments MSC:
90-10
1. Introduction
People are concerned about trends when progress is hurried along, in addition to quality. Many inventory management systems assume that demand will remain steady during the whole planning horizon, although this is not the case in reality. Selling price, advertising, degree of deterioration, discount level, stock availability, etc. can all have an impact on demand. Despite being new, cutting-edge technology in today’s commercial activities, inventory modelling places a high priority on concerns of protection and consciousness. Salvage value is a modest measure used by businesses and organizations to lower the overall cost. Additionally, people are drawn to businesses with a lot of product availability since there are more options for payment methods and a higher rate of consumption as a result. Additionally, buyers prefer to purchase products that are related to the selling price, so the selling price of the product has a significant impact on the consumption rate. A higher asking price will result in less demand, and vice versa. Fruits, vegetables, milk, and other products like those lose their quality and originality over time after being stored in the company. Losses will result both physically and financially as a result of the products’ failure to meet the criterion. This can be defined as deterioration. One should not neglect the rate of deterioration if one wants to examine the system correctly. The corporation provides an all-units discount, or a reduction in the unit purchase cost based on various order size intervals, to offset the damage caused by degradation. This tactic boosts sales while also increasing popularity. Moreover, companies frequently employ the proverb “buy now, pay later” to entice customers. The trade credit policy, which permits a merchant to purchase goods without paying for them upon receipt of the items since the manufacturer has provided a credit time to repay the debts, in fact matches this statement precisely. Retailers, especially the smaller ones, are drawn to this policy because it gives them a chance to keep the products on the market for longer, make sales, and build interest. The manufacturer, meanwhile, experiences constant demand. The manufacturer may impose a higher interest rate if the merchant does not pay the bill in full within the credit duration. Since the retailer is required to pay the account at the appointed period, the manufacturer and retailer’s agreement is known as a full trade credit. In actuality, some suppliers may decide to use a partial trade credit in order to improve their cash flow and maintain business continuity. Simply said, the retailer makes a partial payment for the items when they are received, and the remaining balance is paid over the manufacturer’s designated credit period. This benefits smaller manufacturers and retailers who might not appreciate cash flow disturbances. As a result, a partial trade credit policy is preferable to a complete trade credit policy for both the producer and the store. A perishable inventory model is created with all of these scenarios in mind, with the demand as a function of selling price and stock level. The total profit function is maximized with regard to selling price and cycle time using an algorithm that is provided with an example. To depict the effects of various inventory characteristics on choice variables and the profit function, a sensitivity analysis is performed. In this paper, we have developed mathematical model which maximized the retailer’s profit while taking cycle length and selling price into account. Moreover, stock level- and selling price-dependent demand make the model more realistic. The aim of this paper is to maximize the retailer’s profit for deteriorating items.
The rest of the paper is set up as follows: Previous research on the subject is presented in Section 2. Basic notations, assumptions, decision variables, the mathematical model formulation, calculation of the optimal cycle time and solution method are described in Section 3. An algorithm to solve the inventory model is described in Section 4. A numerical example, some observations as well as managerial insights and sensitivity analysis are used to validate the problem in Section 5. Section 6 comprises the discussions of the proposed model. At last, the conclusion and future scope comprise Section 7.
2. Literature Review
To promote sales and lure new customers, the provider utilizes a promotional strategy known as “trade credit”. By “trade credit”, we mean that if the debtor did not pay within the permissible credit period, an interest would be imposed on the unsold items according to the agreed-upon terms and conditions. So, the interest is earned by the retailer on revenue from the sale of products and the payment deferred up to the moratorium period provided by manufacturer. These promotional tools result retailer’s cost reduction, minimize the amount of capital investment in goods and services during the time allocated for trade credit, but offer the deferred payment scheme which amplifies the default risk borne by the manufacturer. Dave and Goyal produced articles on when late payments are sustainable [1,2]. Aggarwal and Jaggi looked at the influence of units on the offered credit period [3]. Jamal et al. have developed a generalized inventory model to settle an account for degrading coefficients and shortages [4]. Hwang and Shinn have calculated optimal pricing and ordering procedures under the situation of trade credit for the retailer [5]. Liao et al. have calculated a model when demand depends on stock as well as the producer’s offered credit period [6]. Jamal et al. as well as Sarker et al. reflect interest gained on the sales price and advise that the vendor clear their account relatively sooner as the unit sales price grows analogously to the acquisition cost per unit [7,8]. Chang and Dye derived a model of inventory to allow for deterioration and partial backlog [9]. Chang et al. studied the effect of deterioration of units on a delayed payment scheme [10]. Teng demonstrated that it is profitable for a well-established buyer to place small-scale orders and avail benefits on the sanctioned trade credit [11]. For deteriorating goods, Chang et al. created an EOQ (economic order quantity) model where the length of the deferred payment is dependent to the consignment [12]. When product demand is deterministic, constant, and degrading, Teng et al. derived an ideal trading strategy (order and price) [13]. Huang et al. developed a derivative-free inventory model of limited storage and two tiers of trade credit [14]. Shah and Patel created a trading strategy from the retailer’s point of view for when demand links to stock [15]. In a supply chain system for a two-level trade credit policy which is dependent on the order quantity, Chung created straightforward solution processes [16]. An inventory model with quadratic demand and price-sensitive salvage value was developed by Rangavajhala and Mohan [17]. Chen et al. regarded retailers as having an EOQ (economic order quantity) as the manufacturer gives a conditionally acceptable payment delay linked to the order amount [18]. Using particle swarm optimization, Bhunia et al. developed two levels warehouse inventory model of degrading goods under allowable trade credit. [19]. Bardhan et al. investigated the effects of an inventory model based on investments in preservation technology and a replenishment plan for non-immediately deteriorating goods when demand depends on stock [20]. Sen and Saha developed an inventory model including deterioration, shortages, and time-dependent holding costs under a permissible payment delay [21]. The challenge of identifying the ideal order quantity to minimize the total cost function with variable holding costs and stock-dependent demand was investigated by Pervin et al. [22]. Tripathi and Tomar as well as Kumar created an inventory strategy in which the demand rate is controlled by time-sensitive holding costs with parabolic time links and salvage value [23,24]. For demand that is influenced by price, stock, and time, Chen et al. developed a pricing and replenishment method [25]. Lu et al. developed a multistage sustainable production–inventory model with carbon emission reductions and price-dependent demand under Stackelberg game [26]. Saren et al. derived an application of various price discount policies for deteriorated products and delays in payments in an advanced inventory model [27]. An economic order quantity model was developed by Tripathi and Tomar for commodities with declining demand that has a delay period and salvage value [28]. A price- and stock-related demand model with shortages and investment in preservation technology was created by Khanna and Jaggi [29]. Miah et al. investigated a discount technique-based inventory management for an electronic products supply chain [30]. Pando et al. developed an inventory model with stock-dependent demand rate and maximization of the return on investment [31]. Pando et al. investigated profitability index maximization in an inventory model with a price- and stock-dependent demand rate in a power form [32]. When demand is trapezoidal, Mondal et al. devised a deterministic economic order quantity model of depleting products [33].
The present paper creates a model from the perspective of a retailer when inventory units depreciate at a constant rate. A reasonable time for deferred payment is allowed by the manufacturer. The salvage value for damaged goods is considered. The volume of items on hand and the price at which they are sold affect demand. The decision variables for the retailer are the unit selling price, order quantity, as well as cycle length. To maximize net income for the retailer, first we calculate the maximum cycle length for the given price after this, obtaining the maximum selling cost. The analytic findings show that while using authorized trade credit, the order replenishment cycle time and order size both falls. Higher tolerable deferred payments permitted have the effect of decreasing the unit selling price while boosting net profit.
We looked into the research on perishable payment strategies, stock level- and selling cost-dependent demand functions, and learning theories for deteriorating goods that are covered in the literature review section. Table 1 displays the authors’ contribution breakdown. According to a review of the literature, numerous research papers have been published that discuss the acceptable credit period under various payment strategies, but there are none that discuss the trade credit period for stock level and selling price-sensitive demand with salvage value under the learning concept for deteriorating goods. A salvage value is a modest measure done by businesses and nonprofits to lower the overall cost and raise the overall profit. Due to the degrading nature of the product, the effect of salvage value on the model is also researched. In this concept, the salvage value is also taken into account. The goal of the current work is to create an inventory model that accounts for the learning effect for deteriorating goods and perishable credit term, and stock- level and selling price-dependent demand functions. Our input is displayed in Table 1’s bottom row with the designated keywords. With the current effort, we have attempted to close this research gap.

Table 1.
The model-related contributions of various researchers.
3. Assumptions, Notations, Decision Variables, Mathematical Model Formulation and Calculation of the Optimal Cycle Time
To develop the research, we use the below assumptions, notations, and decision variables. Mathematical formulation is also described in detail, with calculation of the optimal cycle time.
3.1. Assumptions
In order to develop the model, we use below assumptions:
- Considers only single product in the inventory system.
- There is no lead time and an endless replenishment rate.
- Shortages are not tolerated.
- The demand function is high in value as display stock raises at the display area (super mall or shop) also low according to the selling price of the goods. It is defined as , where a positive constant demand is large enough that , displayed goods, depends on the change in demand rate and constant mark-up .
- The retailer has a variety of options for how to use the sales revenue, including expansion, the creation of new products, the upgrading of gear and software, and others. For the sake of simplicity, let us imagine that retailers pay out the money for something other than paying down the debt. Sales revenue is generated and placed in an interest generating account while an account is not resolved. At the end of this period, the retailer starts paying interest on the goods in stock, pays for all sold goods, maintains the balance for future use and then starts paying for all units purchased. The retailer begins to build up profit in the meantime, which will be used for the other activities. Here, the manufacturer offers an N-days-deferred period to the retailer. The produced revenue is put into the retailer’s account during the deferred period. When the deferred period finishes, the retailer pays off for all sold units, keeping the rest for daily expenses as well as for spending on the unsold goods for which retailer starts paying the interest charges.
- () Assuming that the deterioration rate is constant, it begins as soon as the objects are added to the inventory. Additionally, damaged things cannot be repaired or replaced for the duration of the cycle.
- Salvage cost is connected to deteriorated components throughout the purchase period.
3.2. Notations
We make the following assumptions:
Unit holding cost
Unit purchase cost
Cost of Order per cycle
Deterioration rate,
Interest charged/ annum by the manufacturer
Interest earned/ annum by the retailer where
Inventory at time t, where
Net income per unit of time
3.3. Decision Variables
We make the following decision variables:
Unit selling price, where
Order size
Length of replenishment cycle
3.4. Mathematical Model Fomulation
This section develops an inventory model of perishable goods for stock-linked and selling price-dependent demand, with a constant rate of degradation in such situations. In light of the simultaneous effects of demand rate and degradation rate, the inventory level and order size K are decreasing when t = 0. At the end of the cycle time T, an inventory level drops to be zero i.e., . Additionally, salvage value is applied to the defective objects.
The rate of inventory depletion related to demand and rate of degradation, recognizing the following connection with a boundary condition when :
Therefore, the inventory system can be described as below.
Solve above the first-order differential Equation (1), the rate of inventory depletion as below,
The total order quantity is given by at the time t = 0,
Now, the retailer’s net income per unit time as below,
Retailer’s whole income from all sources (sales revenue + salvage value for imperfect goods) − ordering cost − holding cost − deteriorating cost + rate of interest earned—rate of interest charged.
The profit function’s parameters have all been computed numerically as follows with both the cases of trade credit.
- The total income, which is determined by the retailer’s demand rate throughout the course of the period, yields the overall revenue.
Sales revenue:
- 2.
- Ordering cost per cycle:
- 3.
- Holding charge:
- 4.
- Deterioration cost:
- 5.
- Salvage value:
The objective function is continuous according to selling cost (S), and cycle length (T).
For interest earned (I.E), two cases are calculated and interest charged (I.C) as per the length of replenishment cycle time as well as deferred period of N days. Both the cases are shown in following Figure 1.
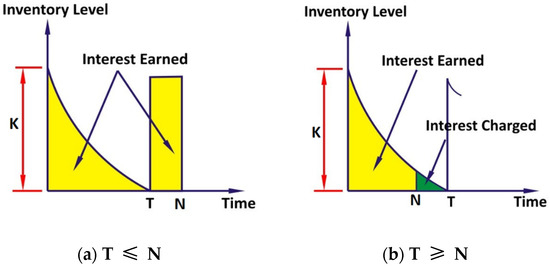
Figure 1.
Graphical representation according to deferred period and replenishment cycle time.
Case 1.
From the Figure 1a, retailer sells units and their account is credited by to pay to the manufacturer when the cycle is finished at the end of the N-days-deferred period.
Therefore, as shown in Figure 1a interest charged (I.C) is zero and interest earned (I.E) is calculated as below
So, we get the net profit per cycle is as below
Case 2. .
According to the assumption and Figure 1b, the retailer sells units during [0, N] and their account is credited by . This is smaller than the total purchase cost paid for K units so, manufacturer charged at the interest rate for the unsold units in stock during [N, T].
So, as shown in Figure 1b, the interest charge () is calculated as below
Products sold by the retailer, and their account receives the generated income during the deferred period [0, N], this incurs interest at the rate per annum.
Hence, as shown in Figure 1b interest earned is calculated as below
Therefore, we get the net profit per cycle is as below
Hence, the net profit is as below for both the cases
Hence, it is clear that, when deferred period is same as the length of replenishment cycle then .
So, is continuous function of the lengh of replenishment cycle, either in or but not in both intervals.
3.5. Calculation of the Optimal Cycle Time
We use the series expansion in the Equations (10) and (13) for a small value of stock-dependent parameter and deterioration rate. Therefore, approximated profits are as below
And
Hence, the approximation of overall income can be represented for both the cases as
A blocked shape solution is produced by the approximation for the cycle time as per the following section.
3.6. Solution Method
We maximize the retailer’s overall profit in this segment. The complex equations are solved using the Maple 12 software tool. The necessary condition for optimum net income will be . Obtained the cycle length T = T1 (suppose), then the second-order derivative is evaluated and after substituting the value of T = T1 in the second-order derivative, we obtain , so T = T1 is considered as maximum value of T, which is an optimal cycle length. As the concavity of net income is represented graphically in Figure 2 for both cases. Solving the with the help of mathematical tools to obtain retailer’s cycle length and net income.
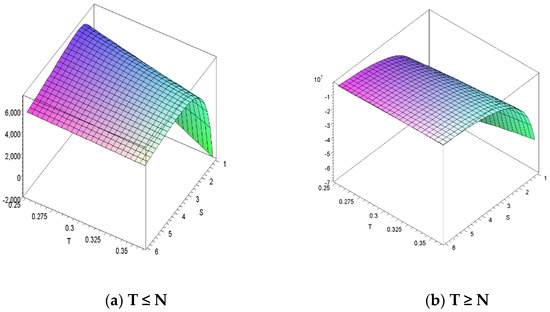
Figure 2.
Representation of net income per unit time (concave function of T).
As mentioned above, required calculations to find optimum cycle length (decision variable) and maximum profit are presented as below:
By differentiating the Equations (15) and (16) we get,
Therefore, for a fixed S become as concave function of T. It is shown in Figure 2a for the case I.
Hence, using the Equation (18) and with the help of solution method we get as follows
where
To ensure , we substitute the value of as per the Equation (22) in the inequality It gives us if and only if inequality
Hence, the optimum order size is for the case I as
Using the value of as per the Equation (22) in Equation (15), we get net income for the case I considered as a function of selling price S (decision variable) only.
Now for the case II apply the same procedure:
Therefore, from the Equation (21), for a fixed S become as concave function of T. It is shown in Figure 2b for the case II.
Hence, using the Equation (19) and with the help of solution method the value of is as
where,
Substituting the value of as per the Equation (26) in inequality gives
Hence, the optimal order size is as
Substitute the value of as per the Equation (26) in Equation (16) to reduce the profit function into function of selling price S (decision variable) only.
When β = 0, and , developed model reduces to the model of Teng et al. (2005). We have next theorem using (24) and (29).
Theorem 1.
For the small value of stock related parameter and degradation rate,
- 1.
- Ifthen optimal cycle time is
- 2.
- Ifthen optimal cycle time is
- 3.
- Ifthen optimal cycle time is N
Proof.
As a result of (24) and (29). Find by solving
In Section 4, we get approximated net profit function of only S.
The optimal value of selling price S is determined by simplifying as per the following computational algorithm. □
4. Computational Algorithm
We created the following solution algorithm to get the best answer for the approximate model based on the explanation in Section 3 (Teng et al. (2005). The following steps are recommended to settle most favorable scheme for retailer:
- Determine by solving the Equation (31).
- Calculate by taking . If there exist such that and satisfies both the first-order derivative according to the Equation (18) and the second-order derivative for concavity according to the Equation (20), then we determine by Equation (22) and by Equation (15). Otherwise, we set .
- Calculate by taking . If there exist such that and satisfies both the first-order derivative according to the Equation (19) and the second-order derivative for concavity according to the Equation (21), then we determine by Equation (26) and by Equation (16). Otherwise, we set .
- If then is an optimal net annual profit so stop. Otherwise, an optimal net annual profit is , and stop.
- Calculate related cycle time as well as net profit per cycle.
5. Numerical Investigation
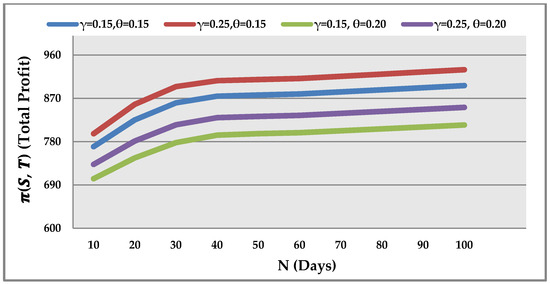
To validate the derived research, we use the parametric values in appropriated units are = . We calculate the amount of decision variables, as well as objective function for the different deferred period days (N), using the computational algorithm. The results are demonstrated in Table 2 and Table 3 when is equal to respectively. Moreover, the graphical representation based on Table 2 and Table 3 is shown in Figure 3. The below observations are made by using Table 2 and Table 3 and Figure 3.

Table 2.
Variations in net profit when = .

Table 3.
Variations in net profit when = .
5.1. Sensitivity Analysis
In order to perform a sensitivity analysis, parameters are changed by up to 10%, 10%, 20%, 20%. Table 4 illustrates the relationship between decision variables and the net income. Also, Figure 4 represents the variation in total profit due to the change in parameters.

Table 4.
Sensitivity analysis.
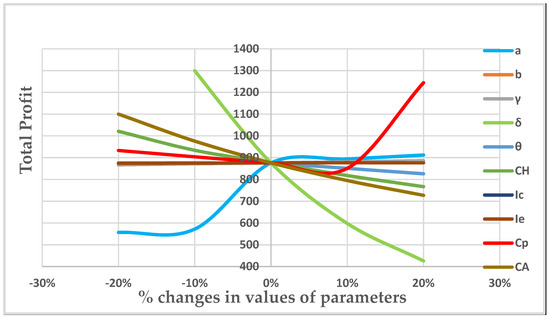
Figure 4.
Sensitive analysis for different parameters.
5.2. Observations and Managerial Insights
We obtained the computational outcomes for various values of N days using the algorithmic technique mentioned above. The following discussions are made according to Table 2 and Table 3 and Figure 3. Moreover, by examining the sensitivity analysis table (Table 4) and Figure 4, the following consequences were witnessed.
- For higher value of fix display parameter, salvage value and degradation component during the deferred payment period increases the net profit per cycle but decreases cycle length and optimal selling price.
- When (optimal), there is a decrease in optimum lot size and an increase in the deferred payment period N.
- If , then there were increases in optimum order quantity as higher value in the deferred payment period N.
- Higher value in display parameter and degradation component as well as lower in salvage value decrease the overall income per cycle and order size. This happens due to more degradation and less salvage value in inventory system. Moreover, higher value in stock-linked parameter raises selling price.
- The rise in order size is evident when the stock-dependent parameter is increased. With rising stock levels, the profit function rises. Therefore, increasing b is recommended.
- One of the main elements in the inventory model that has a direct impact on both the cycle time and the overall profit function is holding cost. Increased cycle times brought on by higher holding costs result in a decline in profit margin.
- It is not advisable to raise the interest rate because doing so will directly reduce the retailer’s profit when the selling price rises.
- A higher interest rate is advised since it will immediately optimize the retailer’s profit while lowering the selling price and cycle time.
- Increased rates of deterioration cause objects to lose their usefulness. The profit function will suffer as a result of the increased unit deterioration.
6. Discussions
In the developed inventory model, we have established from the retailer’s perspective an optimal trading scheme related to ordering and pricing policy for stock-linked demand. The manufacturer recommends a deferred period to the retailer to promote the sales and to attract new customers. The items considered in inventory systems degrade at a steady rate. In addition, the salvage value holds an important role in the calculation of depreciation and can affect the total depreciable amount used by the manufacturer in its depreciation schedule, which is considered for damaged goods in the calculation of the net profit. The observations suggests that salvage value is affected by cycle length (T) as well as selling price (S). Moreover, salvage value directly affects a retailer’s net income. The salvage value provided positive effects on the retailer’s total profit. Optimal cycle time is directly dependent on the value of order. The Taylor series expansion is used to obtain the explicit closed-form optimal solution after the necessary and sufficient conditions for the one and only optimal replenishment interval have been established. We next derive the first- and second-order derivatives to find an optimal pricing policy and construct an algorithm to validate the problem. We also prove Theorem 1m by taking a close look at the explicit criterion, which provides us with a simple method for figuring out the ideal replenishment interval which is shown in Figure 2. Then, the corresponding profit maximization problem is developed. We evaluated the analytic solutions to calculate the retailer’s optimal scheme. In case of credit period increases there is significant net profit and order quantity versus selling cost and cycle time fallout. Furthermore, trade credit had a favorable effect on the retailer overall profit. If we increase the deterioration rate the net profit will reduced while increase for higher salvage coefficient as shown in Figure 3. This model is not suitable if items have high deterioration rate and lower salvage value.
7. Conclusions
The main contributions of this paper as regards the previous research in the field is the development of an inventory model with the best possible pricing and ordering policy for retailers for a constant deteriorating item with the stock- and selling price-dependent demand. Results clearly shown credit period is directly related to net profit and inversely related to selling cost and cycle time. We have derived a method to find ideal replenishment interval for trade credit. Finally, total profit is optimized simultaneously for decision variables cycle length and selling price, which followed a graphical representation of convexity. This model gives win–win situation for both manufacturer and retailer. It helps managers which relate with the industries like FMCG, cosmetic etc. It is possible to expand the research to include time-linked holding costs, time-dependent deterioration rates, order-linked delay periods, inflation, unit cash discounts, tolerable shortages, etc. Using the parameters as fuzzy numbers is another development of this work. Some of the parameters in the proposed model that can be determined through pertinent surveys can be used to assist make the model more accurate.
Author Contributions
A.P. Conceptualization; writing—original draft preparation; investigation, methodology I.T.; writing—review and editing; conceptualization; investigation; A.D.O. writing—original draft preparation; data curation; software D.D.B.-N. and D.P.B.-N. writing—review and editing; methodology; Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Gheorghe Asachi Technical University of Iaşi—TUIASI, Romania, Scientific Research Funds, FCSU—2022.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This paper was financially supported by the Project “Network of excellence in applied research and innovation for doctoral and postdoctoral programs”/InoHubDoc, project co-funded by the European Social Fund financing agreement no. POCU/993/6/13/153437. This paper was also supported by “Gheorghe Asachi” Technical University from Iaşi (TUIASI), through the Project “Performance and excellence in postdoctoral research 2022”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dave, U. “Economic order quantity under conditions of permissible delay in payments” by Goyal. J. Oper. Res. Soc. 1985, 36, 10–69. [Google Scholar] [CrossRef]
- Goyal, S.K. Economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 1985, 36, 335–338. [Google Scholar] [CrossRef]
- Aggarwal, S.P.; Jaggi, C.K. Ordering policies of deteriorating items under permissible delay in payments. J. Oper. Res. Soc. 1995, 46, 658–662. [Google Scholar] [CrossRef]
- Jamal, A.M.M.; Sarker, B.R.; Wang, S. Ordering policies for deteriorating items with allowable shortage and permissible delay in payments. J. Oper. Res. Soc. 1997, 48, 826–833. [Google Scholar] [CrossRef]
- Hwang, H.; Shinn, S.W. Retailer’s pricing and lot sizing policy for exponentially permissible delay in payments. Comput. Oper. Res. 1997, 24, 539–547. [Google Scholar] [CrossRef]
- Liao, H.C.; Tsai, C.H.; Su, C.T. An inventory model with deteriorating items under inflation when a delayin payment is permissible. Int. J. Prod. Econ. 2000, 63, 207–214. [Google Scholar] [CrossRef]
- Jamal, A.M.M.; Sarker, B.R.; Wang, S. Optimal payment time for a retailer under permitted delay of payment by the wholesaler. Int. J. Prod. Econ. 2000, 66, 59–66. [Google Scholar] [CrossRef]
- Sarker, B.R.; Jamal, A.M.M.; Wang, S. Optimal payment time under permissible delay for products with deterioration. Prod. Plan. Control 2000, 11, 380–390. [Google Scholar] [CrossRef]
- Chang, H.J.; Dye, C.Y. An inventory model for deteriorating items with partial backlogging and permissible delay in payments. Int. J. Syst. Sci. 2001, 32, 345–352. [Google Scholar] [CrossRef]
- Chang, H.J.; Dye, C.Y.; Chung, B.R. An inventory model for deteriorating items under the condition of permissible delay in payments. Yugosl. J. Oper. Res. 2002, 12, 73–84. [Google Scholar] [CrossRef]
- Teng, J.T. On the economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 2002, 53, 915–918. [Google Scholar] [CrossRef]
- Chang, C.T.; Ouyang, L.Y.; Teng, J.T. An EOQ model for deteriorating items under manufacturer credits linked to ordering quantity. Appl. Math. Model. 2003, 27, 983–996. [Google Scholar] [CrossRef]
- Teng, J.T.; Chang, C.T.; Goyal, S.K. Optimal pricing and ordering policy under permissible delay in payments. Int. J. Prod. Econ. 2005, 97, 121–129. [Google Scholar] [CrossRef]
- Huang, Y.F. An inventory model under two-level of trade-credit and limited storage space derived without derivatives. Appl. Math. Model. 2006, 30, 418–436. [Google Scholar] [CrossRef]
- Shah, N.H.; Patel, A.R. Optimal pricing and ordering policy for stock-dependent demand under delay in payments. Aust. Soc. Oper. Res. Inc. 2009, 28, 2–9. [Google Scholar]
- Chung, K.J. The simplified solution procedures for the optimal replenishment decisions under two-level of trade-credit policy depending on the order quantity in a supply chain system. Exp. Syst. Appl. 2011, 38, 13482–13486. [Google Scholar] [CrossRef]
- Venkateswarlu, R.; Mohan, R. An inventory model for time varying deterioration and price dependent quadratic demand with salvage value. J. Comput. Appl. Math. 2013, 1, 21–27. [Google Scholar]
- Chen, S.C.; Cárdenas-Barrón, L.E.; Teng, J.T. Retailers economic order quantity when the supplier offers conditionally permissible delay in payments link to order quantity. Int. J. Prod. Econ. 2014, 155, 284–291. [Google Scholar] [CrossRef]
- Bhunia, A.K.; Shaikh, A.A.; Sahoo, S. A two-warehouse inventory model for deteriorating item under permissible delay in payment via particle swarm optimization. Int. J. Logist. Syst. Manag. 2016, 24, 45–69. [Google Scholar]
- Bardhan, S.; Pal, H.; Giri, B.C. Optimal replenishment-policy and preservation-technology investment for a non instantaneous deteriorating item with stock dependent demand. Oper. Res. 2017, 19, 347–368. [Google Scholar] [CrossRef]
- Pervin, M.; Roy, S.K.; Weber, G.W. A two echelon inventory model with stock-dependent demand and variable holding-cost for deteriorating items. Numer. Algebra Control Optim. 2017, 7, 21. [Google Scholar] [CrossRef]
- Sen, N.; Saha, S. An inventory model for deteriorating items with time dependent holding cost and shortages under permissible delay in payment. Int. J. Procure. Manag. 2018, 11, 518–531. [Google Scholar]
- Tripathi, R.P.; Tomar, S.S. Establishment of EOQ Model with Quadratic Time Sensitive Demand and Parabolic Time Linked Holding-cost with Salvage-value. Int. J. Oper. Res. 2018, 15, 135–144. [Google Scholar]
- Kumar, P. An inventory planning problem for time varying linear demand and parabolic holding-cost with salvage-value. Croat. Oper. Res. Rev. 2019, 10, 187–199. [Google Scholar] [CrossRef]
- Chen, L.; Chen, X.; Keblis, M.F.; Li, G. Optimal pricing and replenishment policy for deteriorating inventory under stock level dependent, time varying and price sensitive demand. Comput. Ind. Eng. 2019, 135, 1294–1299. [Google Scholar] [CrossRef]
- Lu, C.J.; Lee, T.S.; Gu, M.; Yang, C.T. A Multistage Sustainable Production–Inventory Model with Carbon Emission Reduction and Price-Dependent Demand under Stackelberg Game. Appl. Sci. 2020, 10, 4878. [Google Scholar] [CrossRef]
- Saren, S.; Sarkar, B.; Bachar, R.K. Application of Various Price-Discount Policy for Deteriorated Products and Delay-in-Payments in an Advanced Inventory Model. Inventions 2020, 5, 50. [Google Scholar] [CrossRef]
- Tripathi, R.P.; Tomar, S.S. Innovative study of economic order quantity model for quadratic time dependent demand under tolerable delay in payments with inconsistent holding cost and associated salvage-value. Int. J. Comput. Syst. Eng. 2020, 6, 52–62. [Google Scholar] [CrossRef]
- Khanna, A.; Jaggi, C.K. An inventory model under price and stock-dependent demand for controllable deterioration rate with shortages and preservation technology investment: Revisited. Opsearch 2021, 58, 181–202. [Google Scholar]
- Miah, M.S.; Islam, M.M.; Hasan, M.; Mashud, A.H.M.; Roy, D.; Sana, S.S. A Discount Technique-Based Inventory Management on Electronics Products Supply Chain. J. Risk Financ. Manag. 2021, 14, 398. [Google Scholar] [CrossRef]
- Pando, V.; San-José, L.A.; Sicilia, J. An Inventory Model with Stock-Dependent Demand Rate and Maximization of the Return on Investment. Mathematics 2021, 9, 844. [Google Scholar] [CrossRef]
- Pando, V.; San-José, L.A.; Sicilia, J.; Alcaide-López-de-Pablo, D. Profitability Index Maximization in an Inventory Model with a Price- and Stock-Dependent Demand Rate in a Power-Form. Mathematics 2021, 9, 1157. [Google Scholar] [CrossRef]
- Mondal, R.; Shaikh, A.A.; Bhunia, A.K.; Hezam, I.M.; Chakrabortty, R.K. Impact of trapezoidal demand and deteriorating preventing technology in an inventory model in interval uncertainty under backlogging situation. Mathematics 2022, 10, 78. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).