Optimal Neural Network Model for Short-Term Prediction of Confirmed Cases in the COVID-19 Pandemic
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
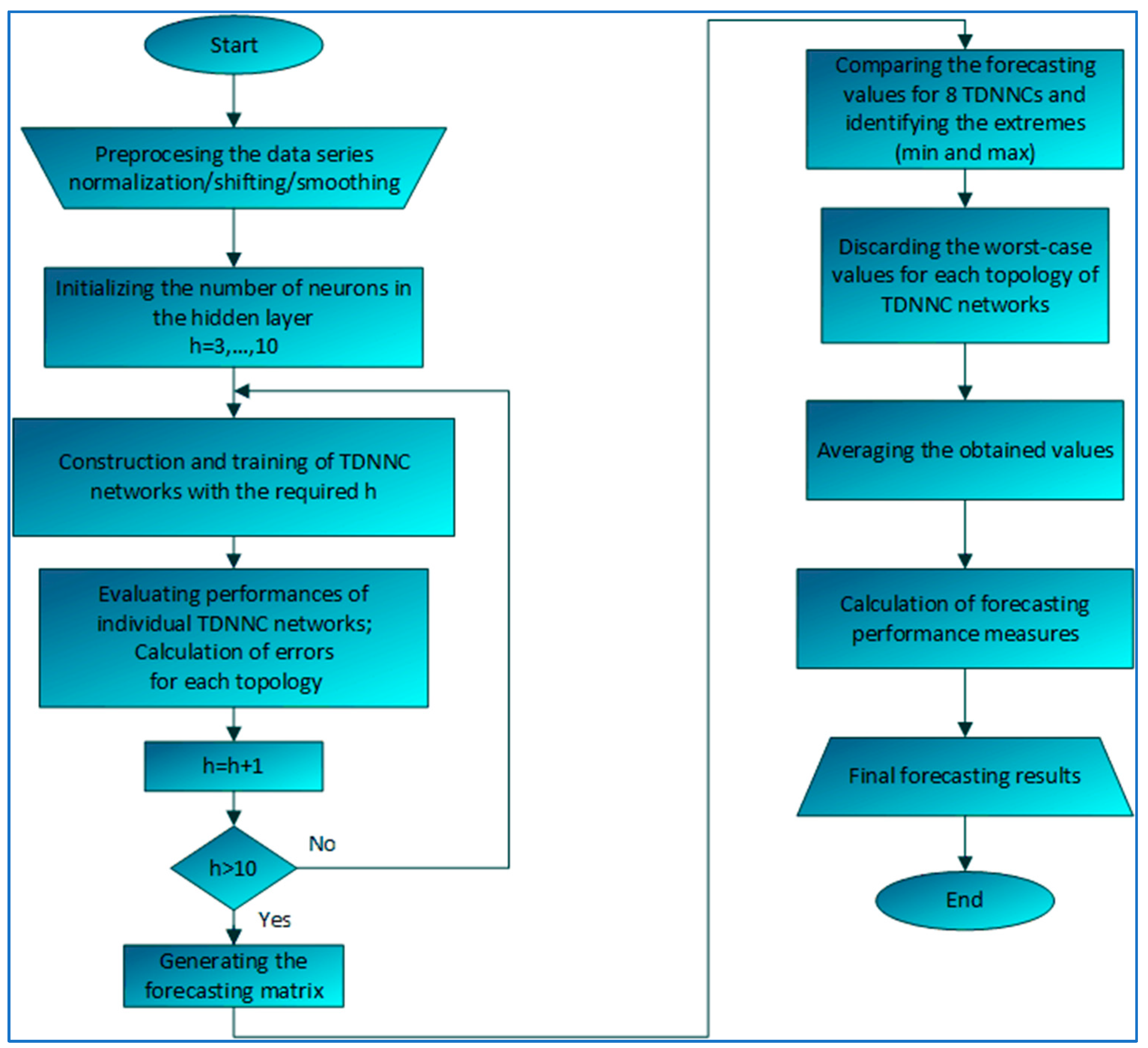
2.2. Forecasting Methodogy
2.3. Prediction Accuracy Measures
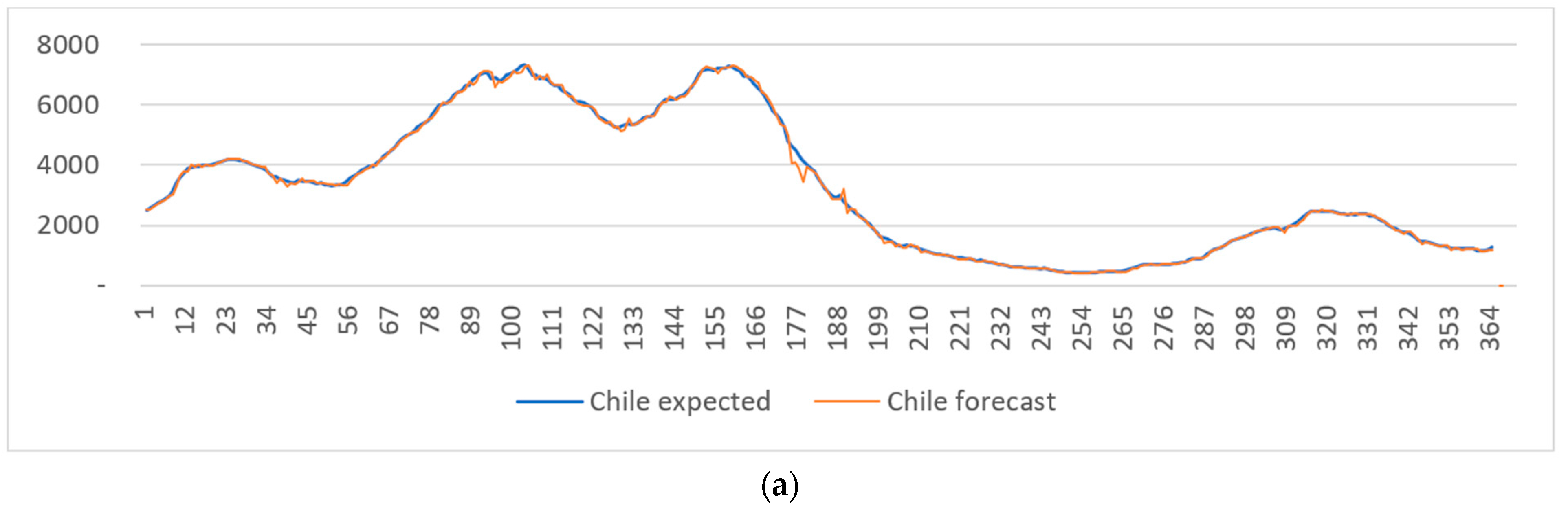
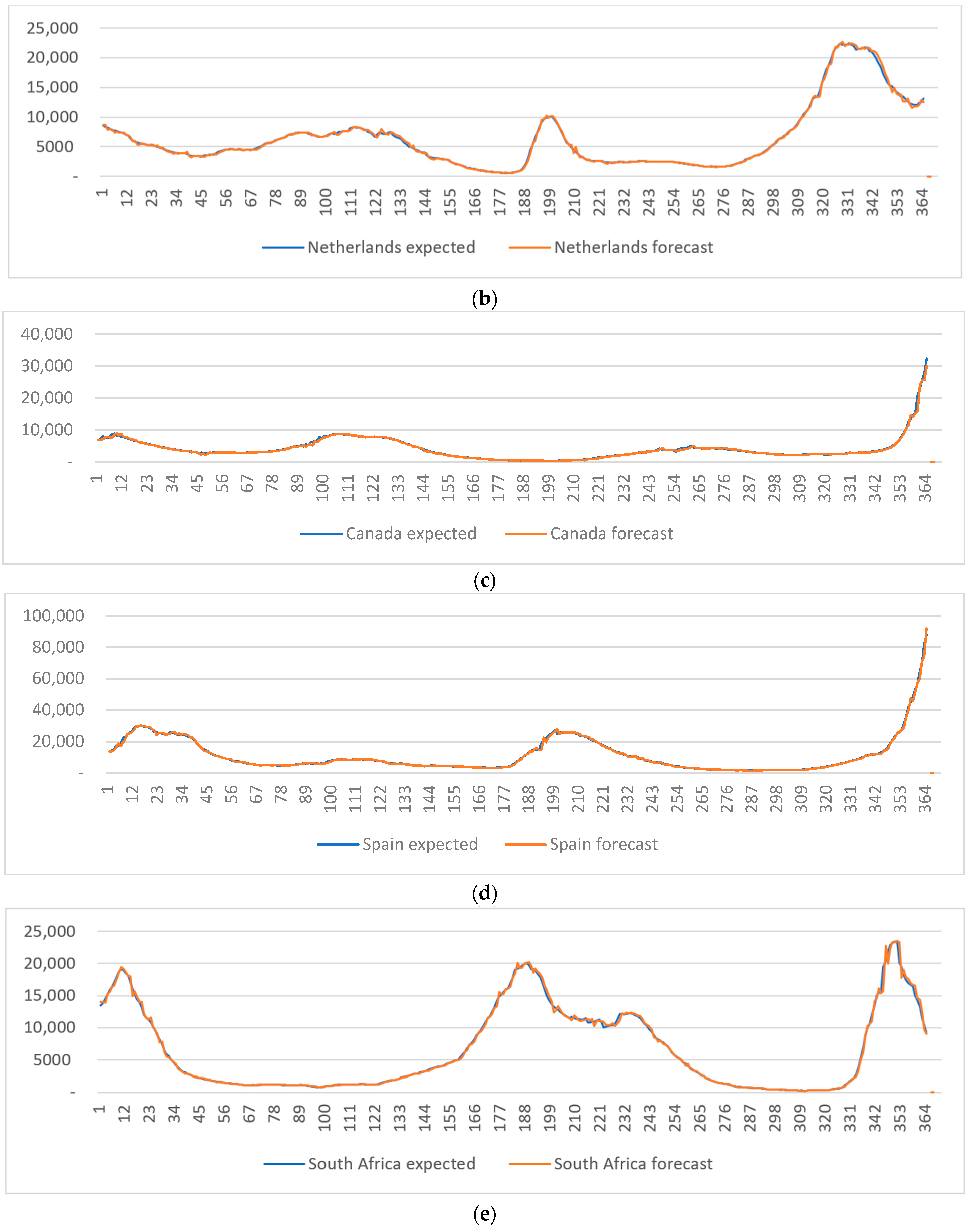
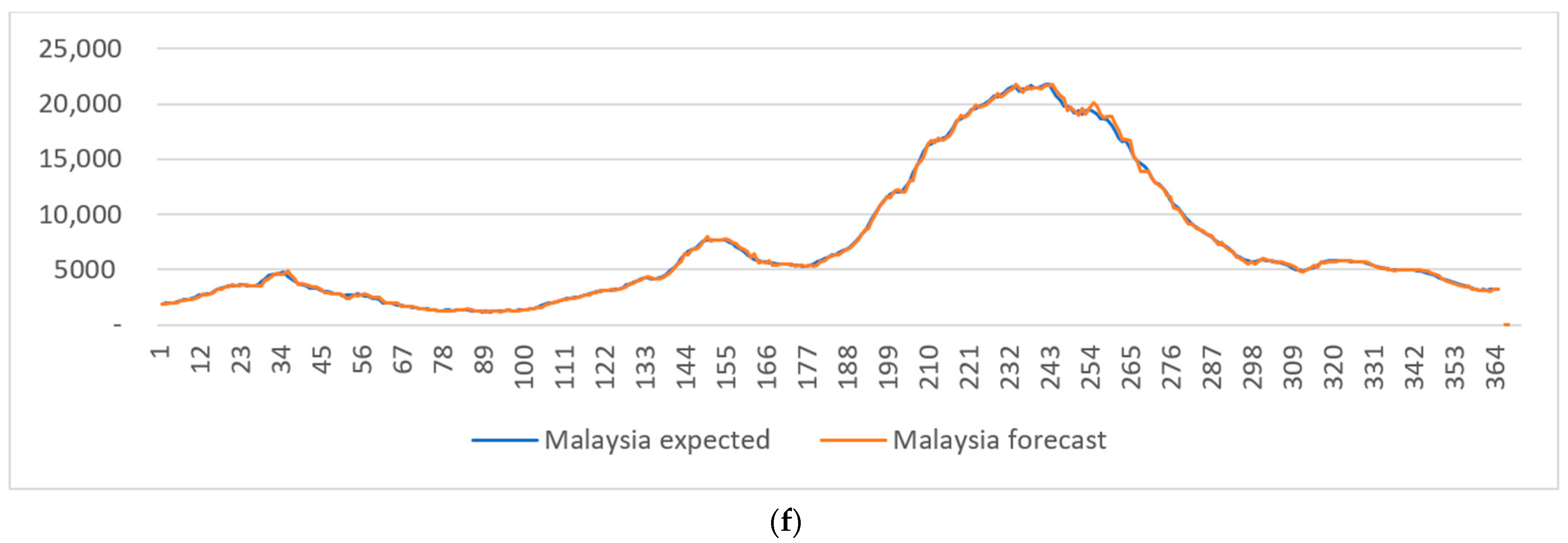
3. Results and Discussion
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, C.; Horby, P.W.; Hayden, F.G.; Gao, G.F. A novel corona virus outbreak of global health concern. Lancet 2020, 395, 470–473. [Google Scholar] [CrossRef] [Green Version]
- WHO Coronavirus (COVID-19) Dashboard. Available online: https://covid19.who.int/ (accessed on 15 September 2022).
- Nasserie, T.; Hittle, M.; Goodman, S.N. Assessment of the Frequency and Variety of Persistent Symptoms Among Patients with COVID-19 A Systematic Review. JAMA Netw. Open 2021, 4, e2111417. [Google Scholar] [CrossRef]
- Wang, P.; Lu, J.A.; Jin, Y.; Zhu, M.; Wang, L.; Chen, S. Statistical and network analysis of 1212 COVID-19 patients in Henan, China. Int. J. Infect. Dis. 2020, 95, 391–398. [Google Scholar]
- Gao, Y.D.; Ding, M.; Dong, X.; Zhang, J.J.; Kursat Azkur, A.; Azkur, D.; Gan, H.; Sun, Y.L.; Fu, W.; Li, W.; et al. Risk factors for severe and critically ill COVID-19 patients: A review. Allergy 2021, 76, 428–455. [Google Scholar] [CrossRef]
- Turk, M.A.; Landes, S.D.; Formica, M.K.; Goss, K.D. Intellectual and developmental disability and COVID-19 case-fatality trends: TriNetXanalysis. Disabil. Health J. 2020, 13, 100942. [Google Scholar] [CrossRef] [PubMed]
- Ceylan, Z. Short-term prediction of COVID-19 spread using grey rolling model optimized by particle swarm optimization. Appl. Soft Comput. 2021, 109, 107592. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Cravioto, D.A.; Diaz-Ramos, R.E.; Cantu-Ortiz, F.J.; Ceballos, H.G. Data Analysis and Forecasting of the COVID-19 Spread: A Comparison of Recurrent Neural Networks and Time Series Models. Cogn. Comput. 2021, 1–12. [Google Scholar] [CrossRef]
- Pavlyutin, M.; Samoyavcheva, M.; Kochkarov, R.; Pleshakova, E.; Korchagin, S.; Gataullin, T.; Nikitin, P.; Hidirova, M. COVID-19 Spread Forecasting, Mathematical Methods vs. Machine Learning, Moscow Case. Mathematics 2022, 10, 195. [Google Scholar] [CrossRef]
- Frausto-Solis, J.; Hernández-González, L.J.; González-Barbosa, J.J.; Sánchez-Hernández, J.P.; Román-Rangel, E. Convolutional Neural Network–Component Transformation (CNN–CT) for Confirmed COVID-19 Cases. Math. Comput. Appl. 2021, 26, 29. [Google Scholar] [CrossRef]
- Borghi, P.H.; Zakordonets, O.; Teixeira, J.P. A COVID-19 time series forecasting model based on MLP ANN. Procedia Comput. Sci. 2021, 181, 940–947. [Google Scholar] [CrossRef] [PubMed]
- Milić, M.; Milojković, J.; Marković, I.; Nikolić, P. Concurrent, Performance-Based Methodology for Increasing the Accuracy and Certainty of Short-Term Neural Prediction Systems. Comput. Intell. Neurosci. 2019, 2019, 9323482. [Google Scholar] [CrossRef]
- Shakhovska, N.; Melnykova, N.; Chopiyak, V.; Gregus, M. An ensemble method for medical insurance costs prediction task. Comput. Mater. Contin. 2022, 70, 3969–3984. [Google Scholar] [CrossRef]
- Tkachenko, R.; Izonin, I. Model and principles for the implementation of neural-like structures based of geometric data transformations. In International Conference on Computer Science, Engineering and Education Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 578–587. [Google Scholar]
- Tkavhenko, R.; Izonin, I.; Vitynskyi, P.; Lotoshunska, N.; Pavlyuk, O. Development of the Non-Iterative Supervised Learning Predictor Based on the Ito Decomposition and SGTM Neural-Like Structure for Managing Medical Insurance Costs. Data 2018, 3, 46. [Google Scholar] [CrossRef] [Green Version]
- Ahuja, S.; Shelke, N.A.; Singh, P.K. A deep learning framework using CNN and stacked Bi-GRU for COVID-19 predictions in India. Signal Image Video Process 2022, 16, 579–586. [Google Scholar] [CrossRef]
- Al-qaness, M.A.; Fan, H.; Ewees, A.A.; Yousri, D.; Elaziz, M.A. Improved ANFIS model for forecasting Wuhan City Air Quality and analysis COVID-19 lockdown impacts on air quality. Environ. Res. 2021, 194, 110607. [Google Scholar] [CrossRef]
- Polishchuk, E.A. The Analysis of the Selection Criteria of the Optimal Model of the Dynamics in the Case of Extrapolative Forecasting for Short Time Series. In Proceedings of the International Scientific Conference, Far East Con, Online, 17 March 2020; Atlantis Press: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Hernandez-Matamoros, A.; Fujita, H.; Hayashi, T.; Perez-Meana, H. Forecasting of COVID19 per regions using ARIMA models and polynomial functions. Appl. Soft Comput. 2020, 96, 106610. [Google Scholar] [CrossRef] [PubMed]
- Miyama, T.; Jung, S.M.; Hayashi, K.; Anzai, A.; Kinoshita, R.; Kobayashi, T.; Linton, N.M.; Suzuki, A.; Yang, Y.; Yuan, B.; et al. Phenomenological and mechanistic models for predicting early transmission data of COVID-19. Math. Biosci. Eng. 2022, 19, 2043–2055. [Google Scholar] [CrossRef]
- Friston, K.J.; Parr, T.; Zeidman, P.; Razi, A.; Flandin, G.; Daunizeau, J.; Hulme, O.J.; Billig, A.J.; Litvak, V.; Moran, R.J.; et al. Dynamic causal modelling of COVID-19. Welcome Open Res. 2020, 5, 04463. [Google Scholar]
- Tealab, A.; Hefny, H.; Badr, A. Forecasting of nonlinear time series using ANN. Future Comput. Inform. J. 2017, 2, 39–47. [Google Scholar]
- Maier, H.R.; Dandy, G.C. Neural Network Based Modelling of Environmental Variables: A Systematic Approach. Math. Comput. Model. 2001, 33, 669–682. [Google Scholar] [CrossRef]
- Lu, Y.; Mei, G.; Piccialli, F.A. Deep Learning Approach for Predicting Two-Dimensional Soil Consolidation Using Physics-Informed Neural Networks (PINN). Comput. Eng. Financ. Sci. 2022, 10, 05710. [Google Scholar] [CrossRef]
- Qin, Y.; Zhao, M.; Lin, Q.; Li, X.; Ji, J. Data-Driven Building Energy Consumption Prediction Model Based on VMD-SA-DBN. Mathematics 2022, 10, 3058. [Google Scholar] [CrossRef]
- He, L.; Kong, D.; Lei, Z. Research on Vibration Propagation Law and Dynamic Effect of Bench Blasting. Mathematics 2022, 10, 2951. [Google Scholar] [CrossRef]
- Bagnasco, A.; Siri, A.; Aleo, G.; Rocco, G.; Sasso, L. Applying artificial neural networks to predict communication risks in the emergency department. J. Adv. Nurs. 2015, 71, 2293–2304. [Google Scholar] [CrossRef]
- Shahid, N.; Rappon, T.; Berta, W. Applications of artificial neural networks in health care organizational decision-making: A scoping review. PLoS ONE 2019, 14, e0212356. [Google Scholar] [CrossRef]
- World Map. Available online: https://www.mapchart.net/world.html (accessed on 15 September 2022).
- Trepanowski, R.; Drazkowski, D. Cross-National Comparison of Religion as a Predictor of COVID-19 Vaccination Rates. J. Relig. Health 2022, 61, 2198–2211. [Google Scholar] [CrossRef]
- Tang, J.W.; Caniza, M.A.; Dinn, M.; Dwyer, D.E.; Heraud, J.M.; Jennings, L.C.; Kok, J.; Kwok, K.O.; Li, Y.; Loh, T.P.; et al. An exploration of the political, social, economic and cultural factors affecting how different global regions initially reacted to the COVID-19 pandemic. Interface Focus 2022, 12, 20210079. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, Z.; Wang, D.; Yang, M.; Li, Z.; Gong, X.; Wu, D.; Zhai, L.; Zhang, W.; Wang, Y. Prediction and analysis of COVID-19 daily new cases and cumulative cases: Times series forecasting and machine learning models. BMC Infect. Dis. 2022, 22, 495. [Google Scholar] [CrossRef]
- Abu-Abdoun, D.I.; Al-Shihabi, S. Weather Conditions and COVID-19 Cases: Insights from the GCC Countries. Intell. Syst. Appl. 2022, 15, 200093. [Google Scholar] [CrossRef]
- Allain-Dupré, D.; Chatry, I.; Michalun, V.; Moisio, A. OECD Policy Responses Coronavirus (COVID-19), The Territorial Impact of COVID-19: Managing the Crisis across Levels of Government; OECD: Paris, France, 2020.
- Available online: https://worldometer.info/coronavirus (accessed on 15 September 2022).
- Jones, J.S.; Goldring, J. Exploratory and Descriptive Statistics; SAGE Publications Ltd.: London, UK, 2022. [Google Scholar]
- Jha, G.K.; Sinha, K. Time-delay neural networks for time series prediction: An application to the monthly wholesale price of oilseeds in India. Neural Comput. Appl. 2014, 24, 563–571. [Google Scholar] [CrossRef]
- Milojković, J.; Milić, M.; Litovski, V. ANN model for one day ahead Covid-19 prediction. In Proceedings of the Conference IcETRAN, Novi Pazar, Serbia, 6–8 June 2022; pp. 296–300. [Google Scholar]
- Masters, T. Practical Neural Network Recipes in C++; Elsevier: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Yuehjen, E.S.; Lin, S.C. Using a Time Delay Neural Network Approach to Diagnose the Out-of-Control Signals for a Multivariate Normal Process with Variance Shifts. Mathematics 2019, 7, 959. [Google Scholar]
- Zhang, G.; Eddy Patuwo, B.; Hu, Y.M. Forecasting with artificial neural networks. Int. J. Forecast. 1998, 1, 35–62. [Google Scholar] [CrossRef]
- Milojković, J.; Litovski, V. Dynamic Short-Term Forecasting of Electricity Load Using Feed-Forward ANNs. Eng. Intell. Syst. Electr. Eng. Commun. 2009, 17(1), 39–48. [Google Scholar]
- Milojković, J.; Litovski, V. One step ahead prediction in electronics based on limited information. In Proceedings of the Conference ETRAN, Vrnjačka Banja, Serbia, 15–18 June 2019; p. EL1.7. [Google Scholar]
- Milojković, J.; Litovski, V. Short-Term Forecasting of Electricity Load Using Recurrent ANNs. In Proceedings of the Electronics, Banja Luka, Bosnia and Hercegovina, 14 June 2010; pp. 45–49. [Google Scholar]
- Meza, J.C. Steepest descent. In Wiley Interdisciplinary Reviews: Computational Statistics 2.6 2010; Willey: Hoboken, NJ, USA, 2010; pp. 719–722. [Google Scholar]
- Drummond, L.M.G.; Svaiter, B.F. A steepest descent method for vector optimization. J. Comput. Appl. Math. 2005, 175, 395–414. [Google Scholar] [CrossRef] [Green Version]
- Fletcher, R. A limited memory steepest descent method. Math. Program. 2012, 135, 413–436. [Google Scholar] [CrossRef]
- Narkhede, M.V.; Bartakke, P.P.; Sutaone, M.S. A review on weight initialization strategies for neural networks. Artif. Intell. Rev. 2022, 55, 291–322. [Google Scholar] [CrossRef]
- Yam, J.Y.F.; Chow, T.W.S. A weight initialization method for improving training speed in feedforward neural network. Neurocomputing 2000, 30, 219–232. [Google Scholar] [CrossRef]
- Denoeux, T.; Lengelle, R. Initializing backpropagation networks with prototypes. Neural Netw. 1993, 6, 351–363. [Google Scholar] [CrossRef]
- Raschka, S.; Mirjalili, V. Python Machine Learning; Packt Publishing: Birmingham, UK, 2019. [Google Scholar]
- Milić, M.; Milojković, J.; Jeremić, M. A deep learning approach for hydrological time-series prediction with ELM model. In Proceedings of the Small Systems Simulation Symposium, Niš, Serbia, 28 February–2 March 2022; Atlantis Press: Amsterdam, The Netherland, 2022; pp. 61–65. [Google Scholar]
- Das, A.K.; Mishra, D.; Das, K.; Mallick, P.K.; Kumar, S.; Zymbler, M.; El-Sayed, H. Prophesying the Short-Term Dynamics of the Crude Oil Future Price by Adopting the Survival of the Fittest Principle of Improved Grey Optimization and Extreme Learning Machine. Mathematics 2022, 10, 1121. [Google Scholar] [CrossRef]
- Nguyen, D.-T.; Ho, J.-R.; Tung, P.-C.; Lin, C.-K. Prediction of Kerf Width in Laser Cutting of Thin Non-Oriented Electrical Steel Sheets Using Convolutional Neural Network. Mathematics 2021, 9, 2261. [Google Scholar] [CrossRef]
- Díaz-Narváez, V.; San-Martín-Roldán, D.; Calzadilla-Núñez, A.; San-Martín-Roldán, P.; Parody-Muñoz, A.; Robledo-Veloso, G. Which curve provides the best explanation of the growth in confirmed COVID-19 cases in Chile? Rev. Lat.-Am. Enferm. 2020, 28, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Medeiros, M.C.; Street, A.; Valladao, D.; Vasconcelos, G.; Zilberman, E. Short-term COVID-19 forecast for latecomers. Int. J. Forecast. B 2022, 38, 467–488. [Google Scholar] [CrossRef] [PubMed]
- Bekker, R.; Broek, M.; Koole, G. Modeling COVID-19 hospital admissions and occupancy in the Netherlands. Eur. J. Oper. Res. 2023, 304, 207–218. [Google Scholar] [CrossRef]
- Ahterberg, M.A.; Prasse, B.; Ma, L.; Trajanovski, S.; Kitsak, M.; Mieghem, P.V. Comparing the accuracy of several network-based COVID-19 prediction algorithms. Int. J. Forecast. 2022, 38, 489–504. [Google Scholar] [CrossRef]
- Chimmula, V.K.R.; Zhang, L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 2020, 135, 109864. [Google Scholar] [CrossRef]
- Zhang, J.; Pathak, H.S.; Snowdon, A.; Greiner, R. Learning models for forecasting hospital resource utilization for COVID-19 patients in Canada. Sci. Rep. 2022, 12, 8751. [Google Scholar] [CrossRef]
- Ahmar, A.S.; del Val, E.B. SutteARIMA: Short-term forecasting method, a case: COVID-19 and stock market in Spain. Sci. Total Environ. 2020, 729, 138883. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. Forecasting of COVID-19 time series for countries in the world based on a hybrid approach combining the fractal dimension and fuzzy logic. Chaos Solitons Fractals 2020, 140, 110242. [Google Scholar] [CrossRef]
- Appadu, A.A.; Kelil, A.S.; Tijani, Y.O. Comparison of some forecasting methods for COVID-19. Alex. Eng. J. 2021, 60, 1565–1589. [Google Scholar] [CrossRef]
- Perc, M.; Gorišek Miksić, N.; Slavinec, M.; Stožer, A. Forecasting COVID-19. Front. Phys. 2020, 8, 00127. [Google Scholar] [CrossRef] [Green Version]
- Alsayed, A.; Sadir, H.; Kamil, R.; Sari, H. Prediction of Epidemic Peak and Infected Cases for COVID-19 Disease in Malaysia. Int. J. Environ. Res. Public Health 2020, 17, 4076. [Google Scholar] [CrossRef]
- Salim, N.; Chan, W.H.; Mansor, S.; Bazin, N.E.; Amaran, S.; Faudzi, A.A.; Zainal, A.; Huspi, S.H.; Hooi, E.K.; Shithil, S.M. COVID-19 epidemic in Malaysia: Impact of lockdown on infection dynamics. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Shetty, R.P.; Pai, P.S. Forecasting of COVID 19 cases in Karnataka state using artificial neural network (ANN). J. Inst. Eng. Ser. B 2021, 102, 1201–1211. [Google Scholar] [CrossRef]
- Wieczorek, M.; Siłka, J.; Woźniak, M. Neural network powered COVID-19 spread forecasting model. Chaos Solitons Fractals 2020, 140, 110203. [Google Scholar] [CrossRef] [PubMed]
- Namasudra, S.; Dhamodharavadhani, S.; Rathipriya, R. Nonlinear neural network based forecasting model for predicting COVID-19 cases. Neur. Proc. Lett. 2021, 1–21. [Google Scholar] [CrossRef]
- Alazab, M.; Awajan, A.; Mesleh, A.; Abraham, A.; Jatana, V.; Alhyari, S. COVID-19 prediction and detection using deep learning. Int. J. Comp. Inf. Syst. Ind. Manag. Appl. 2020, 12, 168–181. [Google Scholar]
- Rauf, H.T.; Lali, M.; Khan, M.A.; Kadry, S.; Alolaiyan, H.; Razaq, A.; Irfan, R. Time series forecasting of COVID-19 transmission in Asia Pacific countries using deep neural networks. Pers. Ubiquitous Comp. 2021, 1–8. [Google Scholar] [CrossRef]

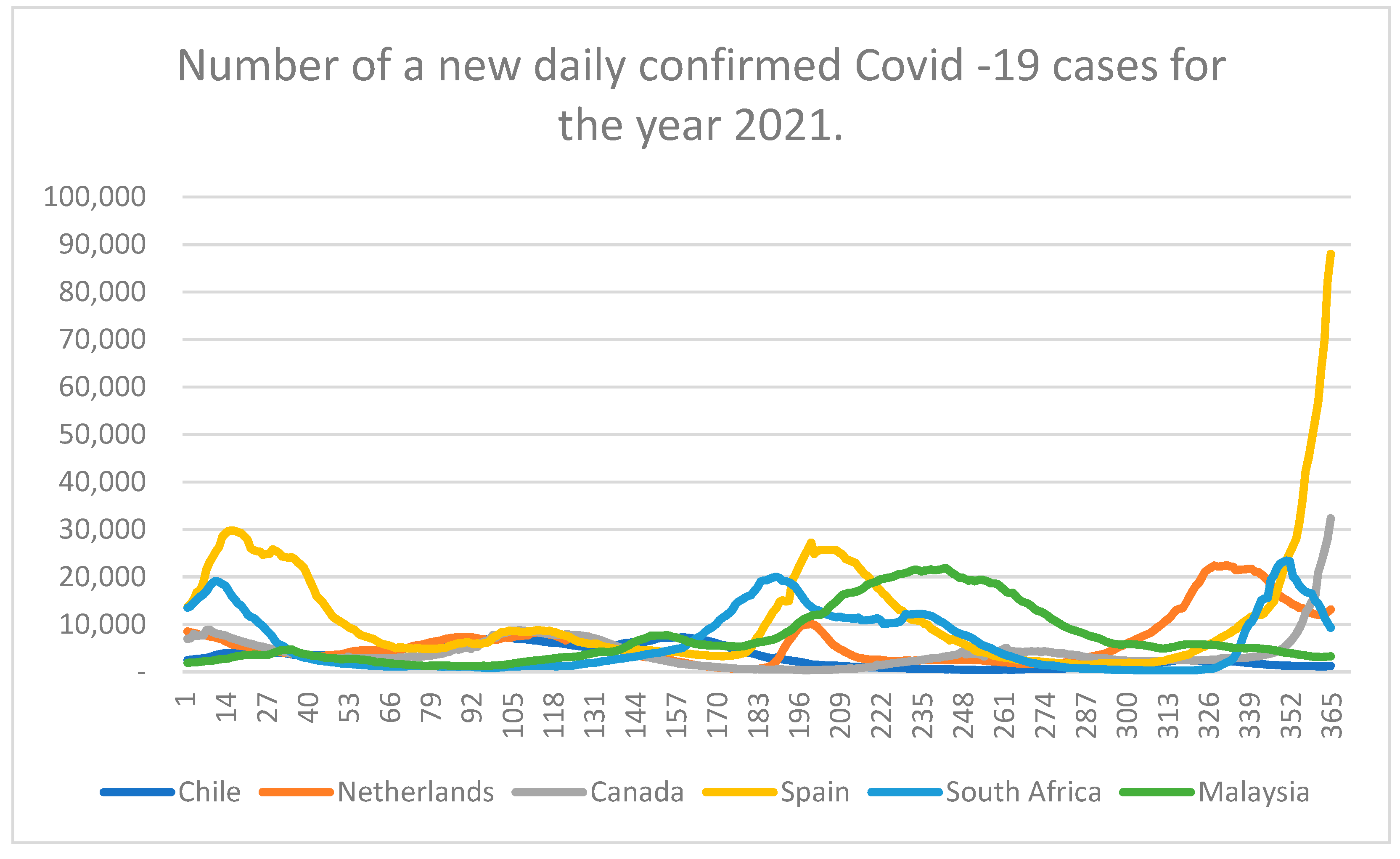


| Descriptive Statistics | Chile | Netherlands | Canada | Spain | South Africa | Malaysia |
|---|---|---|---|---|---|---|
| Number of scores | 365 | 365 | 365 | 365 | 365 | 365 |
| Mean | 3290.54 | 6348.32 | 4147.86 | 11,340.40 | 6575.88 | 7249.05 |
| Median | 2903 | 4758.5 | 3230 | 7020 | 3514 | 5343 |
| 25th Percentile | 1238.5 | 7493.75 | 2343.5 | 4192 | 1195.25 | 3086 |
| 75th Percentile | 5360.75 | 17,959.25 | 5079 | 15,095.5 | 11488 | 8636.2.5 |
| Interquartile Range | 4122.25 | 4969.25 | 2735.5 | 10,903.5 | 10,292.75 | 5550.25 |
| Minimum | 421 | 588 | 377 | 1464 | 259 | 1211 |
| Maximum | 7321 | 22,471 | 32370 | 88,040 | 23437 | 21,808 |
| Range | 6900 | 32,400 | 31993 | 86,576 | 23178 | 20,597 |
| Variance | 4,951,854.29 | 27,420,731.59 | 13,255,497.17 | 134,112,484.02 | 40,227,254.55 | 35,589,921.39 |
| Standard Deviation | 2225.28 | 5236.48 | 3640.81 | 11,580.69 | 6342.50 | 5965.73 |
| Skew | 0.38 | 1.61 | 3.53 | 2.75 | 0.79 | 1.22 |
| Kurtosis | −1.24 | 2.08 | 19.53 | 11.44 | −0.66 | 0.19 |
| Err. of the System | System vs. 3 h. n. TDNNC | System vs. 4 h. n. TDNNC | System vs. 5 h. n. TDNNC | System vs. 6 h. n. TDNNC | System vs. 7 h. n. TDNNC | System vs. 8 h. n. TDNNC | System vs. 9 h. n. TDNNC | System vs. 10 h. n. TDNNC | |
|---|---|---|---|---|---|---|---|---|---|
| Chile | 1.90 | 4.52% | 5.00% | 4.52% | 4.52% | 9.52% | 7.77% | 6.86% | 7.77% |
| Netherl. | 2.75 | 8.94% | 10.42% | 7.41% | 4.52% | 8.33% | 4.84% | 2.13% | 1.45% |
| Canada | 3.75 | 4.58% | 3.35% | 5.06% | 10.29% | 2.09% | 6.01% | 6.25% | 2.85% |
| Spain | 3.16 | 10.73% | 12.46% | 9.71% | 5.39% | 7.6% | 11.23% | 10.73% | 11.23% |
| S. Africa | 3.24 | 5.54% | 4.98% | 4.71% | 7.16% | 5.81% | 4.42% | 2.11% | 2.99% |
| Malaysia | 2.23 | 18.91% | 32.42% | 16.48% | 3.04% | 5.11% | 1.76% | 1.76% | 0.45% |
| Country | |||||||
|---|---|---|---|---|---|---|---|
| Accuracy Measure | Chile | Netherlands | Canada | Spain | S. Africa | Malaysia | |
| Optimal neural forecasting system | RMSE | 88.67 | 253.80 | 393.74 | 786.68 | 429.43 | 192.30 |
| MAPE [%] | 1.90 | 2.75 | 3.75 | 3.15 | 3.24 | 2.23 | |
| R2 | 0.9984 | 0.9977 | 0.9896 | 0.9955 | 0.9955 | 0.9990 | |
| Extreme Learning Machine | RMSE | 265.46 | 1110.15 | 3134.49 | 7380.34 | 2867.22 | 1283.14 |
| MAPE [%] | 4.66 | 7.8 | 22.94 | 16.68 | 10.77 | 5.69 | |
| R2 | 0.99 | 0.96 | 0.67 | 0.79 | 0.69 | 0.96 | |
| Country | Methodology | Performance Measure | Ref. | ||
|---|---|---|---|---|---|
| RMSE | Prediction Error [%] | MAPE [%] | |||
| Chile | Different exponential smoothing algorithms | 1.06–1.74 | - | 7.4 | [55] |
| Penalized LASSO regression model with an error correction mechanism | - | - | 0.32–5.22 | [56] | |
| Netherlands | Linear programing method | 5.76–16.15 | - | 5.9–8.2 | [57] |
| NIPA | - | - | 0.04 | [58] | |
| Logistic function | - | - | 0.07 | [58] | |
| Canada | LSTM | 34.83–51.46 | 6.6-7.33 | - | [59] |
| Multiple Temporal Convolutional network | - | 6–9.47 | [60] | ||
| Spain | Sutte ARIMA | - | - | 0.036 | [61] |
| Fuzzy Fractal Approach | - | 3.58139 | - | [62] | |
| S. Africa | Hybrid-Euler | - | 0.56-35.63 | - | [63,64] |
| Malaysia | ANFIS | 46.85 | - | 1.31 | [65] |
| ARIMA | - | - | 16.01 | [66] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milić, M.; Milojković, J.; Jeremić, M. Optimal Neural Network Model for Short-Term Prediction of Confirmed Cases in the COVID-19 Pandemic. Mathematics 2022, 10, 3804. https://doi.org/10.3390/math10203804
Milić M, Milojković J, Jeremić M. Optimal Neural Network Model for Short-Term Prediction of Confirmed Cases in the COVID-19 Pandemic. Mathematics. 2022; 10(20):3804. https://doi.org/10.3390/math10203804
Chicago/Turabian StyleMilić, Miljana, Jelena Milojković, and Miljan Jeremić. 2022. "Optimal Neural Network Model for Short-Term Prediction of Confirmed Cases in the COVID-19 Pandemic" Mathematics 10, no. 20: 3804. https://doi.org/10.3390/math10203804
APA StyleMilić, M., Milojković, J., & Jeremić, M. (2022). Optimal Neural Network Model for Short-Term Prediction of Confirmed Cases in the COVID-19 Pandemic. Mathematics, 10(20), 3804. https://doi.org/10.3390/math10203804






