1. Introduction
Over the last decade, deep neural networks (DNNs) have shown superior performance in various ML tasks. However, their deployment in real-world practical applications is constrained by their high latency, high memory requirements, and energy consumption. Compressing a heavy pre-trained model is a straightforward approach to overcoming these constraints. One of the most effective approaches is a low-rank matrix/tensor approximation of the kernel weights in neural network (NN) layers by exploiting the fact that they lie in a low-rank linear space [
1].
Despite the efficiency of low-rank tensor decomposition methods, their application to NN compression requires a great effort to find optimal ranks that balance a trade-off between model performance and resource consumption. Tensor rank determination problems are, in general, NP-hard [
2]. The problem is complicated because influence of layers to accuracy of the compressed NNs is different and they should be processed individually. An improper decomposition rank for one layer can even lead to a degradation of the model, which can make it inapplicable.
This paper proposes a new method, the Proxy-based Automatic tensor Rank Selection method (PARS), for automatic rank selection given the model complexity level. More specifically, PARS considers the whole NN when choosing the suitable rank configuration for each layer. It models the problem as a constrained discrete optimization of a black-box function and solves it using Bayesian optimization. We also investigate the effect of low-rank weight decomposition on the compressed model feature distribution. This paper proposes an efficient proxy metric that highly correlates with the post-fine-tuning model metric.
To demonstrate the efficiency and applicability of the proposed method,
PARS was tested with various tensor decomposition methods (
CPD-EPC [
3],
TKD-2 decomposition [
4], and
Spatial-SVD [
5]), several DNN architectures (
AlexNet [
6],
VGG-16 [
7],
ResNet-18, and
ResNet-56 [
8]), and two datasets (the
CIFAR-10 [
9] and
ILSVRC-2012 [
10] datasets). For
ResNet-18,
PARS in combination with the recently proposed
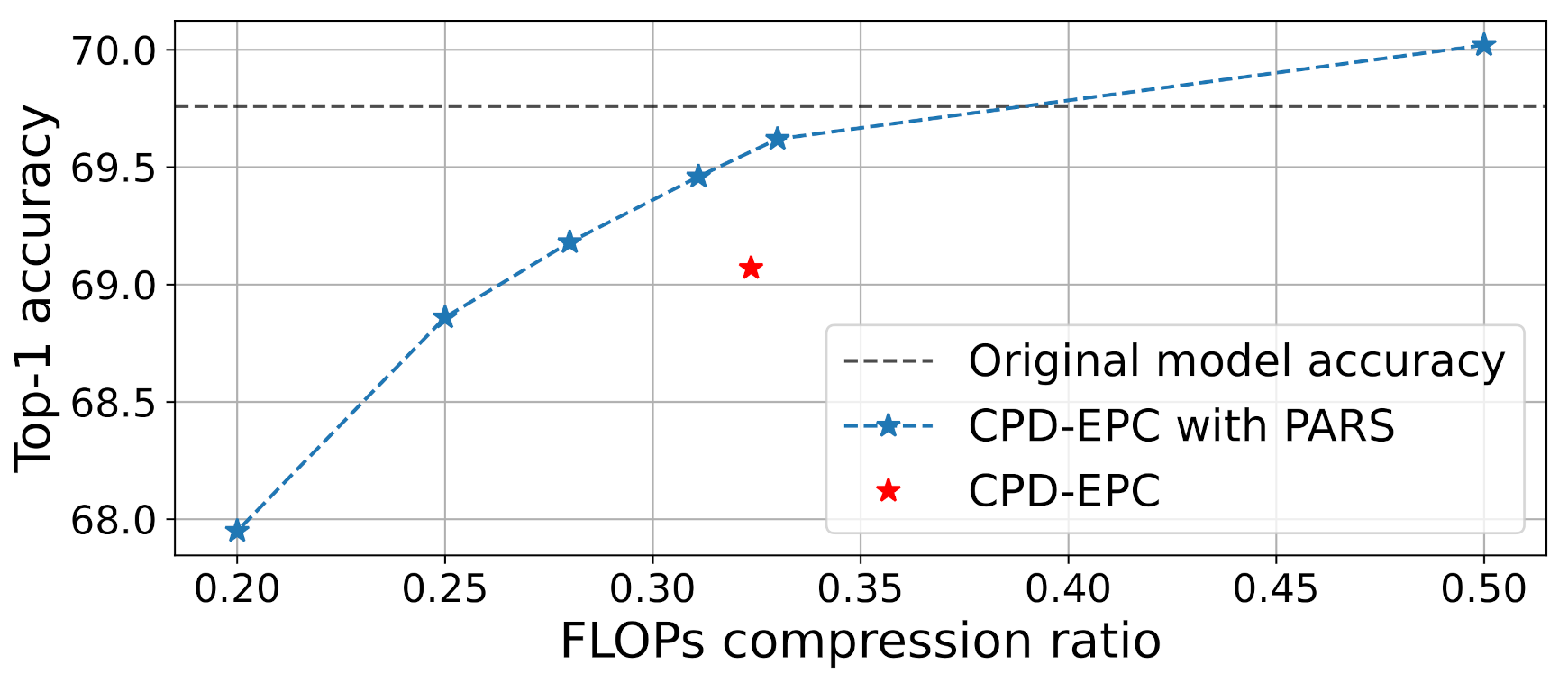
CPD-EPC decomposition showed a state-of-the-art accuracy–compression ratio trade-off, outperforming the results reported in the original paper [
3] (
Figure 1).
The contributions of this paper are summarized as follows:
A novel universal automatic rank selection algorithm (PARS) that selects the best sets of ranks for DNN compression with a given model compression ratio and can work with different matrix/tensor decompositions;
A novel proxy metric for an efficient automatic rank search that improves the predictability of post-compression DNN performance and increases the quality of the rank search procedure;
Investigation of the effect of layer decomposition on the NN feature distribution. This paper discovers that the decomposition of weight tensors adversely influences the feature distribution inside a neural network and impairs the predictability of post-compression DNN performance.
The rest of the paper is organized as follows.
Section 2 presents an overview of neural network compression and decomposition rank selection methods.
Section 3 provides additional clarifications on how decomposition-based neural network compression is performed.
Section 4 describes
PARS and the proposed proxy metric.
Section 5 analyzes the effect of low-rank weight decomposition on the compressed network feature distribution and justifies the selection of a proxy metric.
Section 6 evaluates the performance of
PARS in combination with different matrix/tensor decompositions.
Section 7 summarizes and interprets the key findings of the paper.
Section 8 concludes the paper.
2. Related Works
2.1. Neural Network Compression and Acceleration
Extensive research has been conducted on neural network compression and acceleration. Such methods modify neural networks by reducing the redundancy in their weights. The scope of neural network compression approaches can be divided into four subgroups: pruning (structured/unstructured), low-rank approximation of weights, quantization, and knowledge distillation. Weight sparsification or unstructured pruning compresses neural networks by removing individual weights with low importance [
11]. As a result, the number of parameters in the network can be significantly reduced [
12]. Structural pruning [
13] is an extension of the pruning approach that removes entire structural elements of the network (e.g., filters, channels). This approach allows for simultaneous speedup and compression of NNs without specialized software. A low-rank approximation-based method exploits the fact that neural networks are over-parameterized and that their weights lie in a low-rank linear space [
1]. Therefore, it is possible to approximate NN layer weights with a compact low-rank matrix or tensor decomposition, such as canonical polyadic decomposition (CPD) [
14,
15], Spatial-SVD [
5,
16,
17], or Tucker decomposition [
18,
19]. As a result, the initial layers can be replaced with lightweight layers in a factorized format, thereby making the model faster and smaller (we refer the reader to
Section 3 for a more detailed explanation). Quantization reduces redundancy in the weights’ and activations’ representations by approximating them with numbers with a lower precision [
20]. This approach allows one to reduce the model’s latency and memory footprint. The knowledge distillation approach leverages knowledge from cumbersome pre-trained teacher models to facilitate the training of a small student model [
21]. The knowledge can be outputs [
21], intermediate features [
22,
23], or relationships between features [
24,
25]. This approach reduces the performance gap between compact/fast and large/slow models.
2.2. Rank Selection or Tensor Decomposition Model Selection
This paper focuses on low-rank approximation-based NN compression methods. Matrix and tensor decompositions are parameterized by the decomposition rank, which defines the trade-off between the approximation error and number of parameters [
26]. DNN compression requires a choice of the decomposition rank for each compressed layer in a neural network, the number of which usually exceeds dozens [
5]. Poor rank selection may lead to significant DNN performance degradation (in the case of too small a number of ranks) or an insufficient DNN compression level (in the case of too high a number of ranks).
Rank search methods for NN compression usually use heuristic approaches to find the best decomposition rank for each model layer. The authors of [
18] used the global analytic solution of variational Bayesian matrix factorization (VBMF) [
27] to determine the ranks for TKD-2 for convolutional layers and the ranks for SVD for fully connected ones. An iterative-search-based approach was adopted in [
3,
16,
17] to obtain the suitable rank of CPD. The authors of [
16] used a greedy layer-wise strategy to determine the ranks of all layers satisfying the specific target complexity. This strategy assumed that the accuracy- network energy relation is linear and can be estimated as the leading principal component analysis (PCA). The authors defined an objective function to maximize the accumulated energy with time complexity constraint. In [
3], the authors applied a simple binary search to find the lowest possible rank for each layer that did not exceed a pre-selected accuracy drop threshold. The authors of [
17] proposed a model-wise rank search that selected ranks for all layers simultaneously, and it showed a better performance compared to that of the layer-wise search used in [
16]. A non-iterative approach that utilized energy-based and measurement-based PCA approaches was proposed in [
5]. Unlike other authors, the authors of [
5,
17] conducted a model-wise rank search, which was more optimal than a layer-wise search.
The literature shows that existing rank search methods have three major drawbacks. Firstly, there is a lack of a general rank search algorithm for a general tensor decomposition. Secondly, the authors of a recent paper [
28] found out that the pre-fine-tuning accuracy, which is used in most methods to accelerate the iteration of the rank search procedure, is a flawed proxy metric. Moreover, it does not correlate with the post-fine-tuning accuracy of the model. Thirdly, existing methods do not allow the explicit control of the compression ratio. Each model and each tensor decomposition method may have its own unique accuracy–compression ratio trade-off curve [
28]. For practical applications, NN compression should be able to control the model size during the compression process. This paper aims to develop a rank selection method that alleviates the above drawbacks.
3. Low-Rank Approximation of Neural Network Weight
Most weights in NNs are matrices (e.g., fully connected layers) and tensors (e.g., convolutional layers). Denil et al. [
1] showed that parameters in NNs are extremely redundant and lie in a low-rank space. This observation gave rise to many methods for compressing NNs by using low-rank approximations of weights. These methods replace weights in the layer with their low-rank approximations that are obtained by minimizing
, where
is a low-rank model (for more details, refer to [
26]). As a result, the initial linear operation is replaced by a sequence of linear operations defined by a low-rank decomposition
, where
X and
Y are the input and output of the layer, * is a linear operation performed by the layer (e.g., matrix multiplication in the case of fully connected layers or convolution in the case of a convolutional layer).
In the case of a convolutional layer, the original layer is replaced by the sequence of convolutions, as shown in
Figure 2. The structure of the factorized convolutions depends on the decomposition model.
CPD-3 [
3] replaces the initial layer with three layers (
Figure 2b): a
convolution that projects
input channels to
R channels, a
convolution with
R groups that perform spatial convolution, and a
convolution that projects
R input channels to
channels. The parameter and computation reduction rate is shown in Formula (
1). CPD-EPC is CPD-3 with a sensitivity minimization constraint. For more details, see
Appendix C.
Spatial-SVD [
5] replaces the initial layer with two layers (
Figure 2c): a
convolution layer that performs convolution in the vertical direction projects
input channels to
R channels and a
convolution that performs convolution in the horizontal direction projects
R input channels to
channels. The parameter and computation reduction rate is
TKD-2 [
18] replaces the initial layer with layers (
Figure 2d): a
convolution that projects
input channels to
channels, a
ordinary convolution that performs spatial convolution and projects
input channels to
output channels, and a
convolution that projects
input channels to
channels. The parameter and computation reduction rate is
4. Method
Consider a DNN of L layers. The goal is to find a rank set that maximizes the post-fine-tuning performance of the model for a given compression ratio , e.g., accuracy in the case of a classification problem. The rank search procedure is defined as the following optimization problem:
Problem 1 (Optimal Rank Search).
where
and
define the complexity, FLOPs, and number of parameters of the compressed and original models. In practice, applying a fine-tuning procedure in order to evaluate each set of ranks requires a significant amount of computational resources and is highly time-consuming.
4.1. Proxy Metric
Using the target metric of the compressed model after fine-tuning is impractical, since fine-tuning usually takes 10–20 epochs. Replacing expensive target metrics with an easy-to-compute proxy metric may resolve this issue and significantly reduce the optimization time. In the case of the classification task, a straightforward approach is to use the accuracy of the model after compression [
29]. However, the authors of [
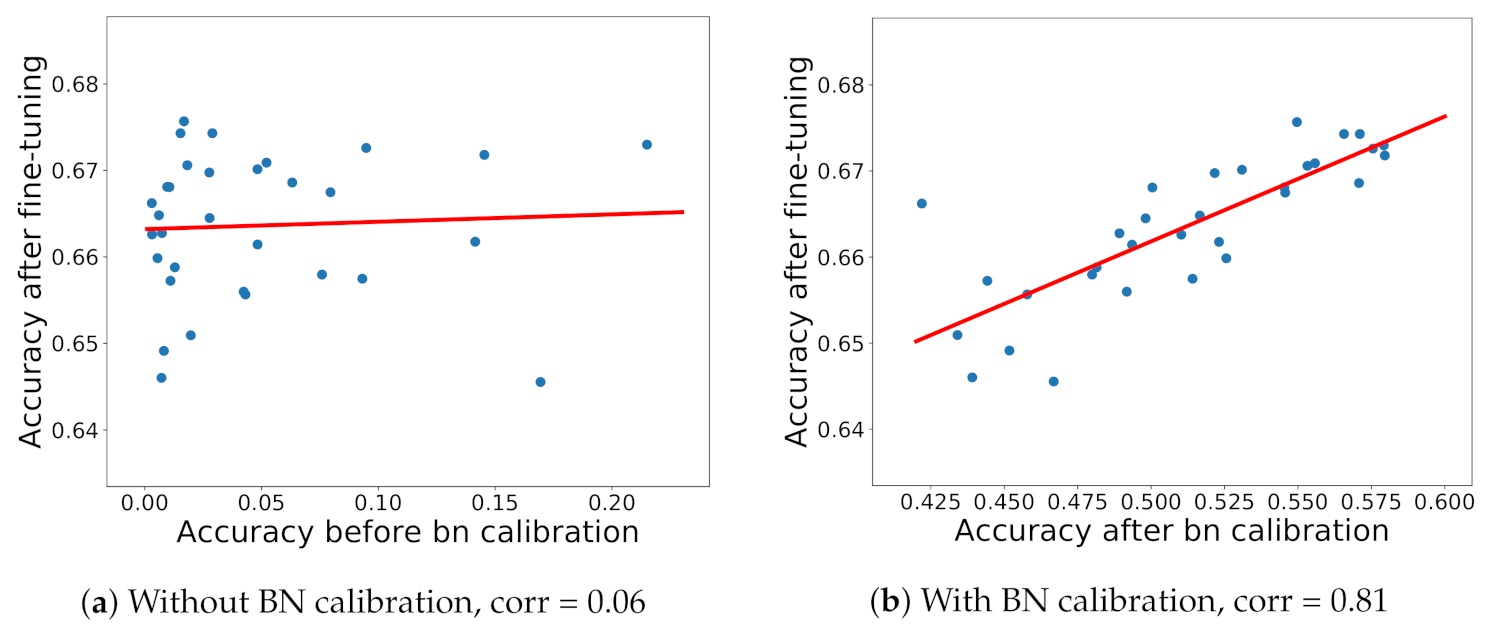
28] showed that for decomposition-based compression, this metric was not coherent with the accuracy of the model after fine-tuning. In this work, this important observation is confirmed in
Figure 3a. To this end, a novel proxy metric for the optimization problem is proposed. It was found that calibrating the BatchNorm (BN) statistics in the decomposed model significantly increased the correlation between the model accuracies before and after fine-tuning (see
Figure 3b). Thus, the accuracy of the calibrated model
was used as a proxy metric for the accuracy of the model after fine-tuning
to accelerate the optimization process, since it was much cheaper in terms of time and computation.
Section 5 explains how the calibration of the BN statistics affected the accuracy of the model.
4.2. Search Space
The search space of our algorithm was defined by all possible combinations of rank values in layers to be compressed. These combinations represent a vector space
, which can be defined by the Cartesian product:
where
is a decomposition rank of the
l-th layer,
, and
is the rank of the layer when the compression ratio is equal to 1. This vector space grows exponentially with the number of layers in the NN and may have a huge number of elements in the case of NNs with a great depth.
To facilitate the rank search process, additional constraints are introduced into Problem 1:
where
,
, and
define the current, maximum, and minimum complexity of layer
l, respectively. In addition, the model complexity constraint can be rewritten as:
By combining them together, these constraints limit the search space.
4.2.1. Single-Rank Case
In special cases in which the layer decomposition is defined by a single rank, e.g., CPD or SVD, the layer complexity is linear with respect to the rank value
. Thus, constraints (
6) and (
7) can be transformed into the following linear constraint:
where
,
, and
is the complexity of the uncompressed layers in the decomposed model, e.g., fully connected layers or
convolutions in the shortcut connections of residual blocks.
4.2.2. Multi-Rank Case
In cases in which several rank values determine the layer decomposition (e.g., Tucker decomposition, block-term tensor decomposition, tensor train, tensor ring), the expression for the layer complexity can take a more complex form. To avoid complications, one can search not in the space of ranks, but in the space of layer complexities. In this case, PARS finds the best complexity for a given layer, and the next auxiliary function finds a set of ranks for layer l that has an optimal approximation error for the given compression ratio .
4.3. Search Algorithm
Taking into account the proposed proxy metric
and adding constraint (
6) and relaxation (
7) to Problem 1, the optimization problem can be reformulated as follows:
Problem 2 (Optimal Rank Search using the Proxy Metric).
The function may not have an explicit form, and the problem is formulated as a discrete black-box optimization problem.In addition, compression of the model with the given ranks is still very time-consuming, since tensor approximation methods are computationally expensive and typically require up to several hours per layer.
The complexity of the problem described above means that a black-box optimization method is needed to find a reasonably good set of ranks in a relatively small number of iterations. To this end, a Bayesian optimization procedure [
30] is used to solve the constrained optimization (Problem 2) and to find the best set of ranks. It builds a surrogate function for the objective and iteratively samples an appropriate point based on the acquisition function defined from this surrogate.
Algorithm 1 and
Figure 4 describe the proposed rank search procedure in the single-rank case. In order to provide initial information about the objective function to our surrogate,
K quasi-random points are firstly sampled in the search space with a Sobol sequence [
31] and then evaluated. After the initial evaluation of the points, the Bayesian optimization procedure is conducted by using
Gaussian processes (GPs) as a surrogate model and the
expected improvement (EI) as the acquisition function:
where
is the best observed outcome. A
Matern 5/2 kernel is used for the kernel function. For more details, see
Appendix A.
| Algorithm 1 PARS |
Input: training set, validation set, pretrained neural network, , init budget K, search budget N Space exploration stage: , Initialize with Sobol seq. Bayesian optimization stage: for n = (1, …, N) do update GP prior find new candidate evaluate candidate end for Return: |
5. Feature Distribution Analysis
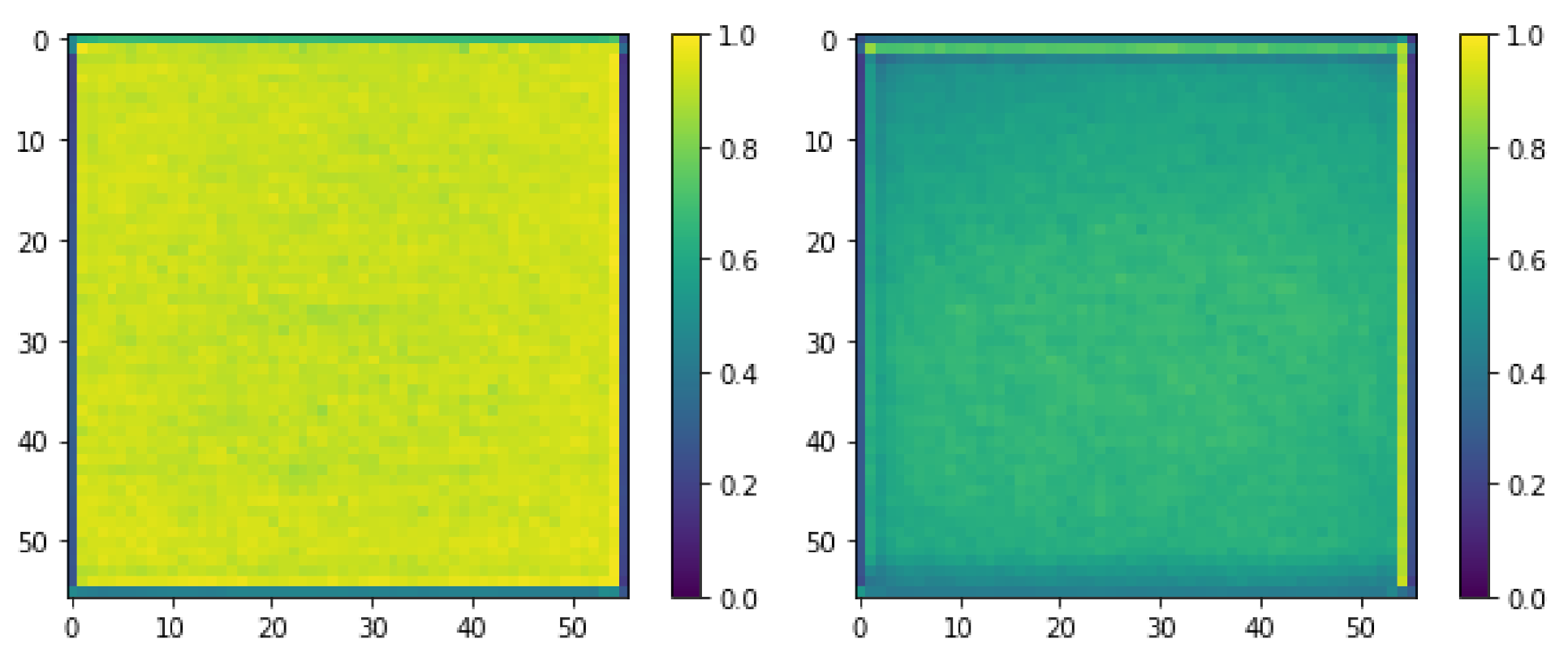
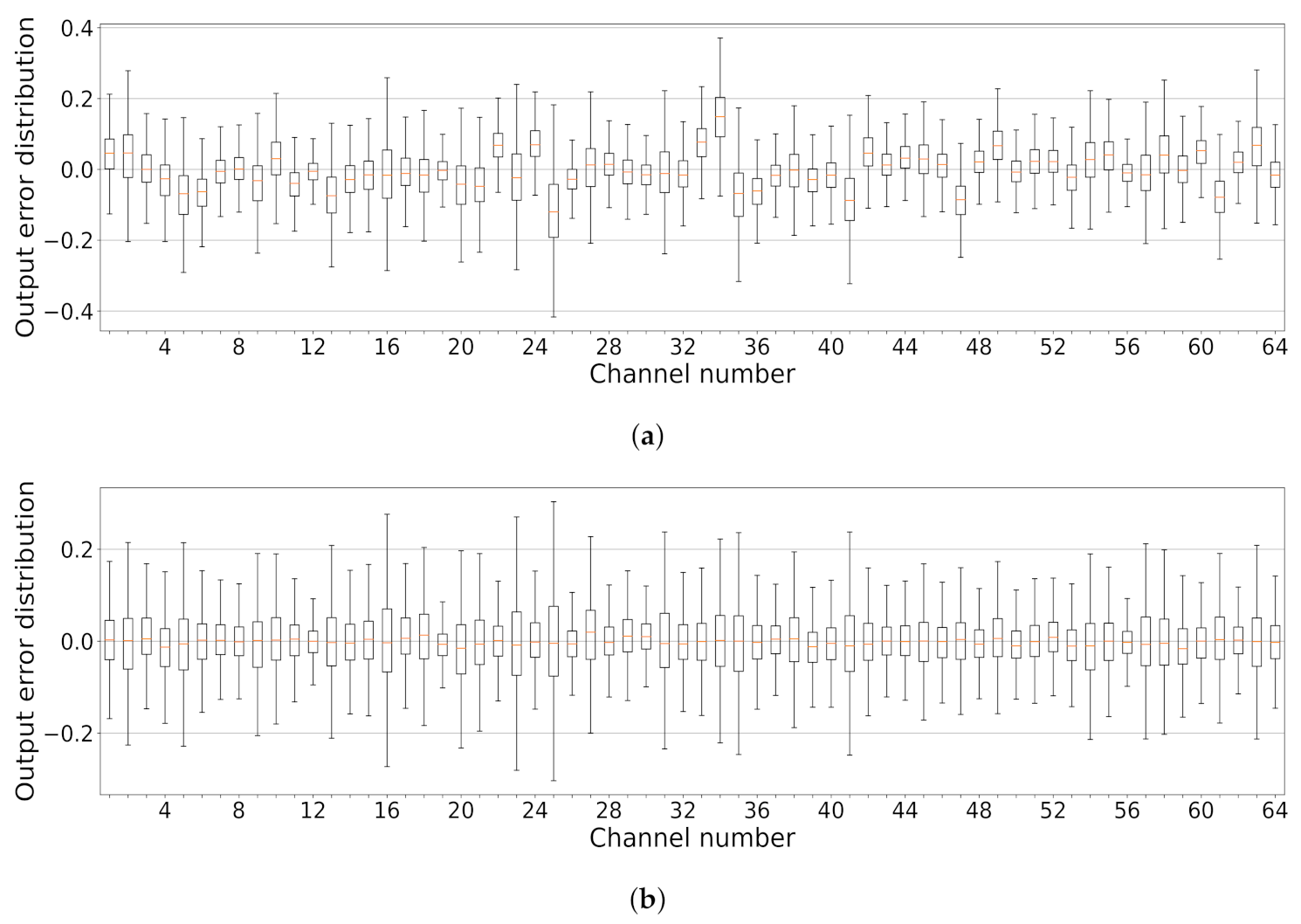
NN compression based on low-rank tensor decomposition replaces the original layer with a sequence of new lightweight layers with factor matrices or tensors as weights. This approach assumes that ; the outputs of these layers are also close , and their outcome error is relatively small.
However, in practice, when the decomposition rank is relatively small,
is not negligible. As observed in
Figure 5a, the distribution of the output features of the decomposed layer is significantly affected. The errors have different distributions in all channels with non-zero means. The problem is amplified when multiple layers are simultaneously decomposed. Shifts in the output distributions of the decomposed layers are aggregated, and the compressed model’s performance becomes unpredictable.
This problem can be partially resolved by calibrating the statistics of the BN layers after the decomposed layers. The BN layer produces the following operation along each channel of input features:
where
and
are trainable parameters, i.e., the scaling and shifting factors, and
is a constant. During training,
and
are calculated with a moving mean and variance:
where
m is the momentum coefficient, subscript
t denotes the number of training iterations, and
and
are unbiased estimations of the features’ mean and variance in the training batch. The BN layer uses statistics in the training regime, as shown in the formula above. During the testing time, the parameters and accumulated statistics are frozen, and the model uses aggregated statistics,
and
, where
is the total number of iterations passed.
The decomposition of the convolutional layer affects the feature distribution. As a result,
and
are no longer the valid mean and variance of the input distribution of the BN layer input. This problem demands calibration of the BN statistics. For this purpose, the BN layers are switched to a training mode and updated for several iterations (in our experiments, 100–200 iterations were sufficient) without updating the training parameters of the model. After the calibration of the BN statistics, the new aggregated statistics,
and
, represent more accurate feature distributions. This procedure corrects the feature distribution in the decomposed model and provides the difference between the output features of the compressed and original models in order to be zero-mean (
Figure 5b). Moreover, it partially recovers the model degradation and makes the behavior of the model more predictable (
Figure 3b), making the accuracy of the decomposed and calibrated model a good proxy metric for the prediction of the post-fine-tuning model behavior.
Single- and Multi-Layer Decomposition
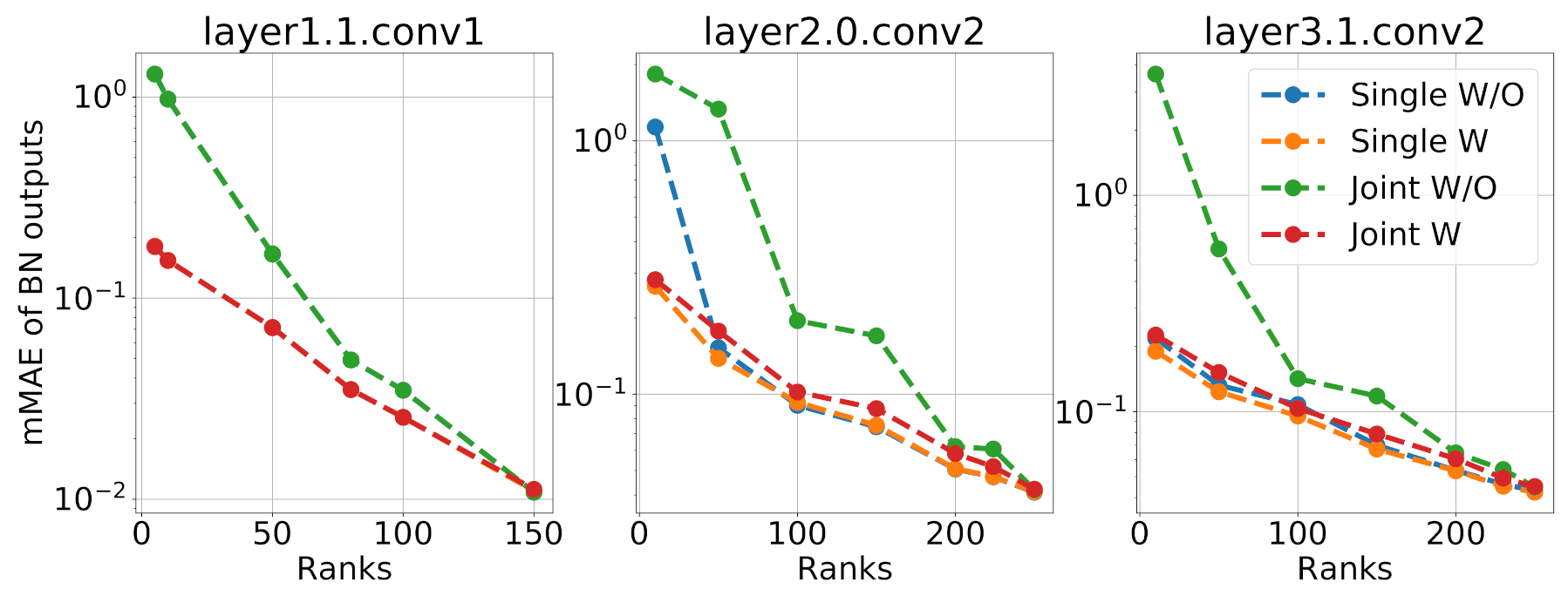
The positive effect of BN calibration can be seen more clearly in the case of simultaneous multi-layer decomposition. For this purpose, three layers of ResNet-18 are chosen for demonstration: layer1.1.conv1, layer2.0.conv2, and layer3.1.conv2. Their kernel weights are decomposed using CPD-EPC with different CP ranks. Next, the outputs of BN layers after original and decomposed layers are collected in two settings: Single, where the compressed model has only one decomposed layer, and Joint, where three layers are simultaneously decomposed.
The output of the BN layer is a 3-way array with modes: channels, width, and height. For the spatial dimension, width, and height, the
-norm of differences between outputs of original and decomposed layers is close to some constant level (see an example in
Figure A1 in
Appendix B). Thus, the values of the
-norm can be averaged over the spatial dimensions without substantial loss of information, resulting in a mean absolute error (MAE). Further, to compare the shifts in outputs of the decomposed layers for different CP ranks, the maximum of the MAE over the channels (mMAE) is taken (results for the mean of the MAE over the channels are presented in
Figure A2a in
Appendix B).
The results shown in
Figure 6 indicate that the mMAE before calibration is higher than after the calibration for both settings. In addition, for the
Joint setting, the mMAE for subsequent decomposed layers is higher than that for the
Single setting for both cases, before and after BN calibration. However, this difference decreases while the CP rank increases. Thus, the shift in the feature distribution is most notable when the decomposition rank is relatively low.
The experiments in
Appendix B for the cosine distance instead of the
-norm (see
Figure A2b,c) and for the bias (difference in the means of the outputs, see
Figure A2d,e) show similar behaviors.
6. Experimental Results
In this section, we present an experimental evaluation of the proposed method. Firstly, we analyze the effect of each component in
PARS—the rank search and proxy metric. Secondly, we compare our method with state-of-the-art NN compression methods by compressing
ResNet-18 [
8] and
VGG-16 [
7] after training on the
ILSVRC-2012 [
10] dataset. Thirdly, we compare our results with those of other representative rank search methods in compressing
ResNet-56 by
Spatial-SVD on the
CIFAR-10 dataset. Lastly, we evaluate our rank search method in a multi-rank tensor decomposition scenario by compressing
AlexNet [
6] after training on the
ILSVRC-2012 [
10] dataset.
Implementation Details: The experiments were conducted with the efficient NN framework Pytorch [
32] on a GPU server with one NVIDIA A-100 GPU, AMD EPYC 7452 32-Core CPU, and 80 GB RAM. We used a pre-trained
ILSVRC-2012 model shipped with
Torchvision:
ResNet-18 had top1 and top5 accuracies of 69.76 and 89.08,
VGG-16 with
BN had top1 and top5 accuracies of 73.36 and 91.52, and
AlexNet had top1 and top5 accuracies 56.52 and 79.07; for
CIFAR-10, the pre-trained
ResNet-56 model has had a top1 accuracy of
. The compressed models were fine-tuned with an SGD optimizer and the StepLR learning rate schedule; the details of the fine-tuning are provided in
Table 1.
Selection of the PARS hyperparameters:
and define the maximum and minimum compression ratios of the DNN’s layers during the rank search procedure. We used the following heuristic setting: and , where is the target compression ratio. This allowed us to avoid evaluating unreasonably low or high compression ratios, and it reduced the search space.
defines the acceptable deviation from the target compression level of the model. We set . If , then the output compressed models will have compression ratios in the range: .
K and N denote the number of space exploration steps and the number of Bayesian optimization steps. We set and , where is the total number of evaluations, which depends on the depth of the DNN; the higher the number of layers in the model, the more evaluation iterations it requires. We set for AlexNet, VGG-16, and ResNet-18 and for ResNet-56.
To avoid over-fitting to a validation set during the rank search process, we used two subsets of the training set to calibrate the BN statistics and evaluate the compressed model; these subsets consisted of 25,600 and 48,000 randomly sampled images, respectively.
6.1. Algorithm Analysis
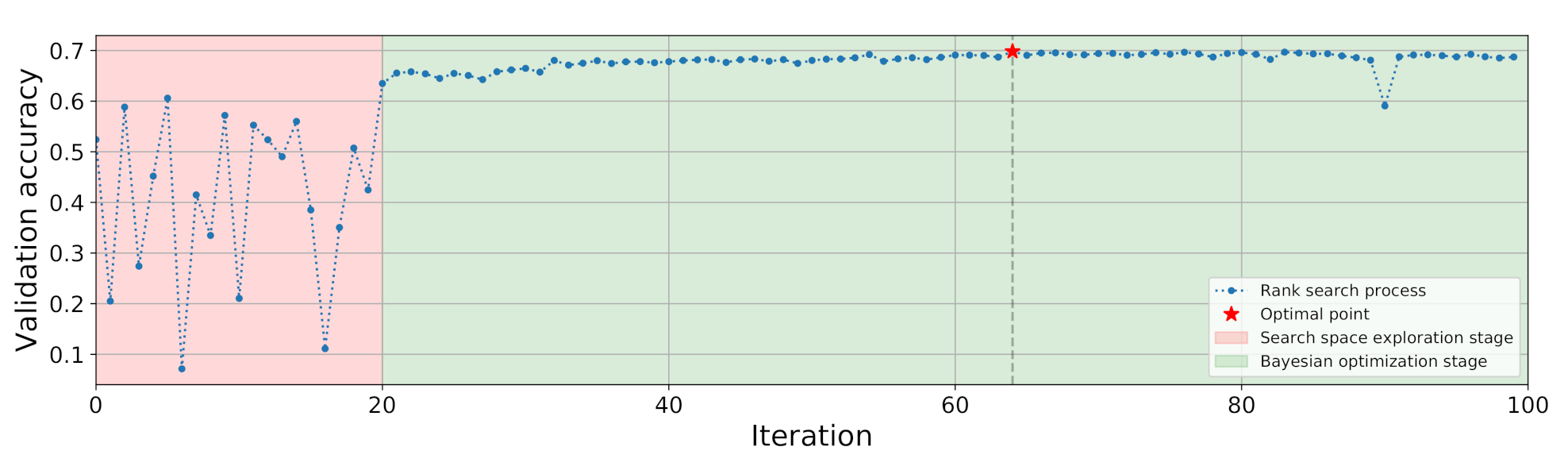
6.1.1. Rank Search Process
Figure 7 shows the convergence behavior of the rank search process for
ResNet-18 with a compression ratio of 3.5. After the random search stage in the first 20 iterations, the validation accuracy of our model significantly increased. This result indicates that we obtained better ranks than those obtained by using random sampling. During the Bayesian optimization process, the compressed model accuracy gradually increased with the number of iterations despite the metric drop at iteration 90. This drop meant that at iteration 90, the GP’s surrogate function put the maximum EI value at a worse point than its predecessors. This behavior is normal for the Bayesian search process, as each iteration of the search process updates and improves the accuracy of the surrogate function. Note that we evaluated our model on a part of the training set, so the validation accuracy values were higher than those on the test set. The maximal validation accuracy was achieved at iteration 64, which was then taken as a final prediction for this experiment. However, after this, the model found many other points with validation accuracies that were very close to the optimal one.
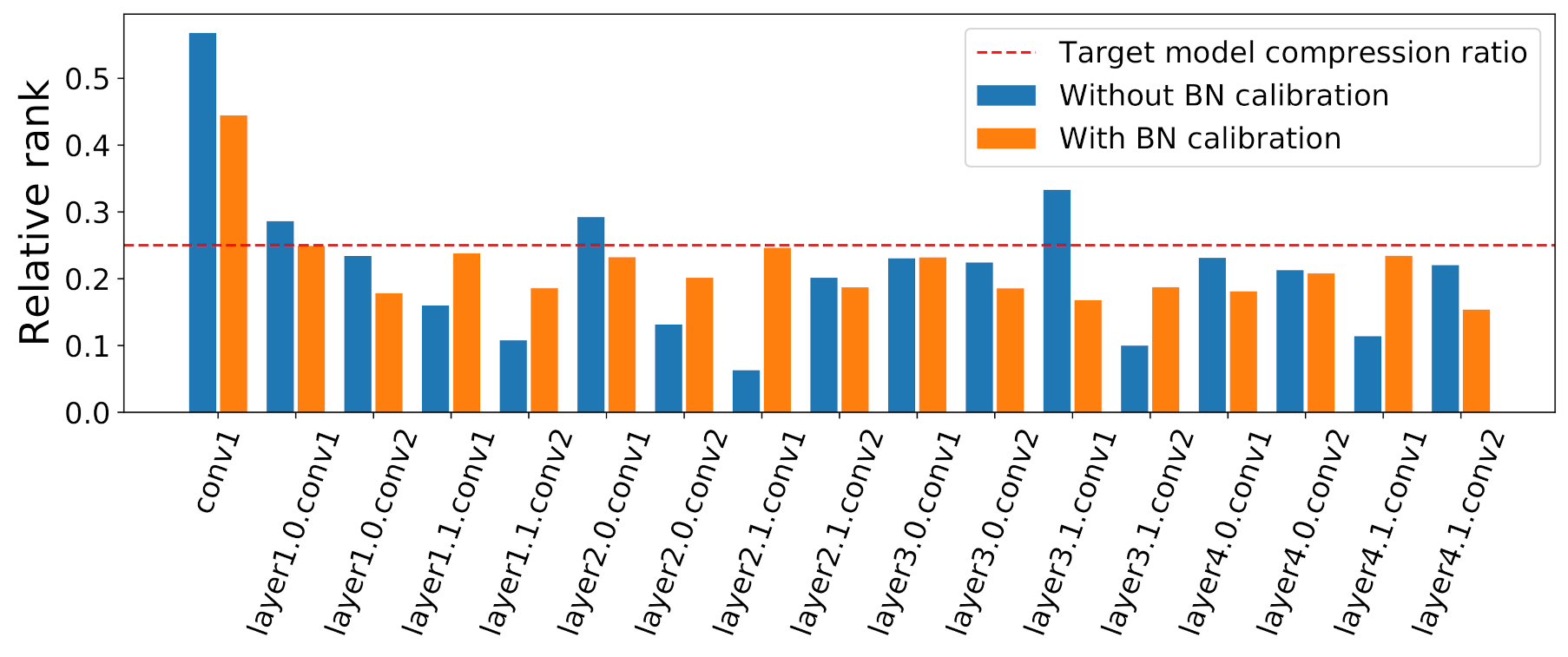
6.1.2. Rank Analysis
Figure 8 shows the relative ranks found by
PARS for different layers of
ResNet-18 with different compression ratios. The relative rank is denoted by the ratio
, where
is a decomposition rank found for layer
l and
is the rank for layer
l when the compression ratio is 1. Overall,
PARS found comparable levels of relative ranks for different compression ratios, except for the first and the last layers.
Conv1 had higher relative ranks. This observation could be explained by the fact that this was the first layer in the network, and it did not have any residual connections; thus, the overcompression in this layer could not be compensated by the other layers.
Layer4.1.conv2 had a notably lower relative rank compared to those of the other layers. The last layer before the average pooling operation squeezed all spatial information in the feature map. This fact might explain the relatively low importance of this layer. Moreover, this might also be connected to a
weight banding phenomenon [
33]. Note that our rank search algorithm did not have explicit information about the network structure and its weights; despite this, PARS found patterns that could later be explained by external knowledge.
6.1.3. Proxy Metric Evaluation
To evaluate the effectiveness of the proposed proxy metric, we applied
PARS for
CPD-EPC for
compression of
ResNet-18 on the
ILSVRC-2012 dataset with and without calibration of the BN statistics. After compression, both models were fine-tuned with the same schedule.
Table 2 shows that using BN calibration led to a noticeably smaller accuracy drop for the same compression ratio.
Figure 9 shows that using proxy metrics without the calibration of the BN statistics resulted in a poor balance of computational cost between layers. For example, layers
layer2.1.conv1 and
layer3.1.conv2 seemed to be overcompressed, whereas the adjacent layers had 2–3 times lower compression ratios. In contrast, using BN calibration resulted in a better compression ratio balance between layers. We also refer the reader to
Appendix E for batch size effect evaluation.
6.2. Model Compression Results
We compared our results from compression of
ResNet-18 and
VGG-16 on the
ILSVRC-2012 dataset with those of other recently proposed methods (See
Table 3 and
Spatial-SVD results in
Appendix D). Our method was compared with other methods for decomposition-based neural network compression (
LR Type), as well as with channel-pruning DNN compression methods (
CP Type). Our model-wise rank search algorithm showed considerably better results when in combination with
CPD-EPC than those of the layer-wise binary search reported in the original paper [
3]. Moreover, to the best of our knowledge, our method provides new state-of-the-art results for the accuracy–compression ratio trade-off for
ResNet-18 and
VGG-16 compression on the
ILSVRC-2012 dataset.
6.3. Comparison with Other Rank Selection Methods
We compared
PARS with a representative group of rank search methods,
ENC [
5]. For this purpose, we compressed
ResNet-56 when pre-trained on the
CIFAR-10 dataset by using the
Spatial-SVD decomposition method (
Figure 2c); the pre-trained model had a
top-1 accuracy.
Table 4 shows that
PARS resulted in a smaller accuracy drop than that of the family of
ENC [
5] methods and that a uniform rank reduction was applied with the same compression ratio, but it required more evaluation iterations
. It should be mentioned that
ENC rank search methods are designed specifically for the
Spatial-SVD layer compression method. In contrast,
PARS is a universal method that works with an arbitrary weight decomposition type.
6.4. Multi-Rank Compression
To evaluate our rank search method in a multi-rank decomposition scenario, we compressed
AlexNet [
6] with
TKD-2, which had two rank parameters per layer. As a function
, we used a simple heuristic that kept the ratio
equivalent to
. We compressed all convolutional and fully connected layers of the network except for the first convolutional layer, whereas the fully connected layers were compressed using truncated SVD.
The results were compared to those of [
18], who applied
TKD-2 and used VBMF [
27] for rank selection (
Table 5). Compared to VBMF, PARS found ranks that resulted in a smaller accuracy drop with a slightly higher compression ratio.
6.5. Search Time
We provided a search time for the
Spatial-SVD compression of
ResNet-56 when pre-trained on the
CIFAR-10 dataset from
Section 6.3. The rank search procedure consisted of 40 initialization iterations with the Sobol sequence [
31] and 160 iterations of Bayesian optimization. Model decomposition, BN calibration, and accuracy evaluation were performed during the candidate evaluation at each iteration.
Table 6 shows the details of the search time. Note that model decomposition time heavily depended on the type of decomposition used.
7. Discussion
This paper demonstrates that the rank search algorithm for decomposition-based neural network compression can be efficiently solved by using constrained black-box optimization, and a method called PARS is proposed. PARS eliminates the problems that its predecessors had: suboptimal layer-wise rank search, dependence on the decomposition algorithm, a flawed target proxy metric, and the absence of a compression ratio control.
We observed that layer factorization resulted in a shift in the distribution of the layer outcomes (
Figure 5a), which affected the predictability of the neural network performance after fine-tuning (
Figure 3a). This issue was resolved by calibrating the statistics in the BatchNorm (BN) layer (
Figure 3b). The proposed proxy metric showed a considerable improvement in the rank search method (
Table 5,
Figure 9).
A similar effect of BN calibration was observed in the models compressed by using channel pruning [
44]. Despite the similarities in the use of BN calibration, our method had a different motivation.
Figure 3 shows that matrix/tensor weight decomposition affected the feature distribution after the compressed layer. Most importantly, the difference between the original and factorized layer outputs was not zero-mean. These feature distribution shifts affected the performance of the compressed model. The calibration of the BN statistics aligned the compressed model’s feature distribution and made the difference of the feature distribution from that of the original model zero-centered. This effect could also be achieved through bias correction. EagleEye [
44] applied BN calibration (adaptive BN) to models compressed by using channel pruning. We cannot speak about feature distribution differences in channel pruning, since the compressed layer has fewer channels in the output feature map.
In
PARS, we formulated the rank search procedure as a constrained optimization problem and solved it with Bayesian search (
Figure 7). The optimization constraint defines the compression ratio of the model and, therefore, allows control over the model’s whole performance–compression ratio curve (
Figure 1). The experimental results show that
PARS may significantly improve the performance of well-known tensor-based neural network compression methods (
Table 3 and
Table 5).
Generally, PARS selects a compression ratio for each model layer. This allows PARS to work with each type of weight decomposition model. Moreover, one can combine it with other neural network compression methods, such as structured or unstructured pruning.
Despite the results shown here, PARS has several areas for further improvement. Firstly, the proposed algorithm works with only one type of decomposition at a time. Thus, the selection of a layer decomposition scheme is required. Secondly, the current compression constraints should have analytical formulas (such as FLOPs/MACs or the number of parameters). Working with non-analytical constraints (such as inference time on a particular device) might be more beneficial in practical scenarios.
8. Conclusions
This paper proposes PARS, a novel rank search algorithm that can automatically find ranks for decomposition-based neural network compression. PARS models the task as a constrained black-box optimization problem and solves it through Bayesian optimization. This study discovered that a low-rank weight decomposition of DNN weights adversely affects its feature distribution and makes its post-fine-tuning performance unpredictable. Based on this finding, we propose the calibration of the statistics in BatchNorm after compression. This approach stabilizes the feature distribution and results in a novel proxy metric for the rank search algorithm. As a result, PARS improves the performance of existing decomposition-based rank selection by providing a more efficient set of ranks for the selected compression ratio.
Author Contributions
Conceptualization, K.S.; methodology, K.S.; software, K.S. and D.E.; validation, K.S. and D.E.; formal analysis, K.S. and A.-H.P.; investigation, K.S. and D.E.; resources, A.-H.P. and A.C.; writing—original draft preparation, K.S.; writing—review and editing, K.S., D.E., A.-H.P., and A.C.; visualization, K.S. and D.E.; supervision, A.-H.P. and A.C.; project administration, K.S.; funding acquisition, A.-H.P. and A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partly supported by Ministry of Science and Higher Education grant No. 075-10-2021-068, and the joint projects: Artificial Intelligence for Life between Skoltech and the University of Sharjah.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable. All of the data used in this study were downloaded from a public online database.
Acknowledgments
The authors acknowledge the use of the computational resources of the Skoltech CDISE supercomputer Zhores [
45], which allowed them to obtain the results presented in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BN | BatchNorm layer |
| CPD | Canonical Polyadic Decomposition |
| CPD-EPC | Canonical Polyadic Decomposition with Error-Preserving Correction |
| DNN | Deep Neural Network |
| EI | Expected Improvement |
| GP | Gaussian Process |
| FLOPs | Number of Floating Point Opertions |
| MACs | Number of Multiply–Add Operations |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| NN | Neural Network |
| PCA | Principal Component Analysis |
| SGD | Stochastic Gradient Descent |
| SVD | Singular Value Decomposition |
| TKD | Tucker Decomposition |
| VBMF | Variational Bayesian Matrix Factorization |
Appendix A. Bayesian Optimization
Consider the problem of finding the minimum of an unknown real-valued function , where is a compact space, . With a limited budget N of the evaluations of the target function f, the algorithm should select the best query points at each iteration that minimize optimization gap or regret.
Appendix A.1. Gaussian Process
Given a dataset at step
t of points
and its respective outcomes
, the prediction of the Gaussian process at a new query point
with a kernel or covariance function
and with hyperparameters
is a normal distribution, such as
, where:
where
is the corresponding cross-correlation vector of the query point
with respect to the dataset
:
and
is the Gram or kernel matrix:
where
is a noise or nugget term that represents stochastic functions or surrogate mismodeling.
Appendix A.2. Acquisition Function
Ordinary regret functions that are used to select the next point at each iteration assume knowledge of the optimum
. Thus, they cannot be used in practice. Instead, the Bayesian optimization literature uses acquisition functions, such as the expected improvement (EI) criterion [
30], as a proxy of the optimality gap criterion. EI is defined as the expectation of the improvement function—in our case,
, where
is the best outcome until the current iteration. Taking the expectation over the predictive distribution, we can compute the expected improvement as:
where
and
are the corresponding Gaussian probability density function (PDF) and cumulative density function (CDF), where
. In this case,
and
are the prediction parameters computed with Equation (
A1). At each iteration
n, we select the next query at the point that maximizes the corresponding expected improvement:
Appendix A.3. Kernel
As a kernel function, we use the
Matern 5/2 kernel:
where
d is the distance between the vectors and
h is the kernel width.
Appendix A.4. Initialization
To provide initial information about the objective function to our surrogate, we first sample
K quasi-random points in the search space with a Sobol sequence [
31], and then evaluate these points.
Appendix B. MAE, Cosine Distance, and Bias Analysis
The outcomes of the BN layer can be 3D arrays with channel, width, and height dimensions. For the spatial dimension, width, and height, the cosine distance between the outputs of the original and decomposed layers is close to some constant level (see
Figure A1). Thus, we can average over the spatial dimensions to allow less complicated visualization.
From the experiment (see
Figure A2), it can be noted that the mean and maximum of the MAE/cosine distance/bias before calibration are higher than after calibration for both settings (except for big ranks for bias). In addition, for the
Joint setting, the mean and maximum of the MAE/cosine distance/bias for the subsequent decomposed layers are higher than for the
Single setting both before and after BN calibration. However, this difference decreases while the CP rank increases.
Figure A1.
Cosine distance for the output of the original and decomposed layer1.1.bn1. The fourth channel of the output tensor before (left) and after (right) BN calibration. Values inside the channel do not vary much, except for their bounds.
Figure A1.
Cosine distance for the output of the original and decomposed layer1.1.bn1. The fourth channel of the output tensor before (left) and after (right) BN calibration. Values inside the channel do not vary much, except for their bounds.
Figure A2.
The mean and maximum are taken over channels for the MAE/cosine distance/bias between outputs of BN layers subsequent to the original and decomposed layers. Bias is the difference between outputs’ means. In the Single setting, the compressed model has only one decomposed layer, while in the Joint setting, three layers are simultaneously decomposed. W/O corresponds to the case without calibration of the BN statistics, while W corresponds to the case with calibration of the BN statistics. The X-axis shows the CP rank. Note: for the first decomposed layer, layer1.1.conv1 (left subfigure), the results of the Single and Joint settings coincide. (a) Mean of the MAE. (b) Mean of the cosine distance. (c) Maximum of the cosine distance. (d) Mean of the bias. (e) Maximum of the bias.
Figure A2.
The mean and maximum are taken over channels for the MAE/cosine distance/bias between outputs of BN layers subsequent to the original and decomposed layers. Bias is the difference between outputs’ means. In the Single setting, the compressed model has only one decomposed layer, while in the Joint setting, three layers are simultaneously decomposed. W/O corresponds to the case without calibration of the BN statistics, while W corresponds to the case with calibration of the BN statistics. The X-axis shows the CP rank. Note: for the first decomposed layer, layer1.1.conv1 (left subfigure), the results of the Single and Joint settings coincide. (a) Mean of the MAE. (b) Mean of the cosine distance. (c) Maximum of the cosine distance. (d) Mean of the bias. (e) Maximum of the bias.
Appendix C. CPD-EPC and TKD
Appendix C.1. CPD
The canonical polyadic decomposition (CPD) of the order-three tensor
of the size
can be represented by the sum of
R rank-one tensors:
where
,
, and
are factor matrices of size
,
, and
, respectively (see an illustration of the model in
Figure A3). The tensor
is given in the Kruskal format with
parameters. Shorthand notation:
.
Figure A3.
Decomposition of a third-order tensor into (left) canonical polyadic tensor decomposition (CPD) with three-factor matrices and (right) Tucker two-tensor decomposition (TKD).
Figure A3.
Decomposition of a third-order tensor into (left) canonical polyadic tensor decomposition (CPD) with three-factor matrices and (right) Tucker two-tensor decomposition (TKD).
Appendix C.2. CPD-EPC
CPD-EPC expands the CPD with a correction method that minimizes the sensitivity of the decomposition and preserves the approximation error, i.e.,
The bound
can be the approximation error of the decomposition with diverging components. CPD sensitivity is defined as follows:
where
,
, and
have random i.i.d. elements from
Appendix C.3. TKD
The Tucker tensor decomposition (TKD) [
4] is an alternative tensor decomposition method. TKD provides more flexible interaction between the factor matrices through a core tensor, which is often dense in practice (
Figure A3). The TKD-2 decomposition of an order-three tensor
of the size
can be represented as follows:
where
and
are factor matrices of sizes
and
, respectively, and
is a core tensor of size
. The tensor
is given in the Tucker format with
parameters.
Appendix D. Evaluation of PARS in Combination with Spatial-SVD
We compress VGG-16 with BN layers with a ×4 compression ratio constraint. The original model has top1 and top5 accuracies of 73.36% and 91.52%, respectively.
Table A1 illustrates the results of the experiment. Our rank search method finds ranks that result in a relatively low drop in the model accuracy.
Table A1.
Comparison of different automatic rank search methods. The original model is VGG-16 pre-trained on the ILSVRC-12 dataset. All methods use Spatial-SVD for model compression.
Table A1.
Comparison of different automatic rank search methods. The original model is VGG-16 pre-trained on the ILSVRC-12 dataset. All methods use Spatial-SVD for model compression.
| Search Algorithm | ↓ FLOPs | Top-1 | Top-5 |
|---|
| Spatial-SVD PARS (Ours) | 4 | 73.09 (−0.27) | 91.41 (−0.11) |
Appendix E. Effect of Batch Size
To evaluate the effect of the batch size on the BN calibration process, we performed BatchNorm calibration with different batch sizes and measured the calibrated model accuracy on the validation set (calibration was performed for 200 iterations).
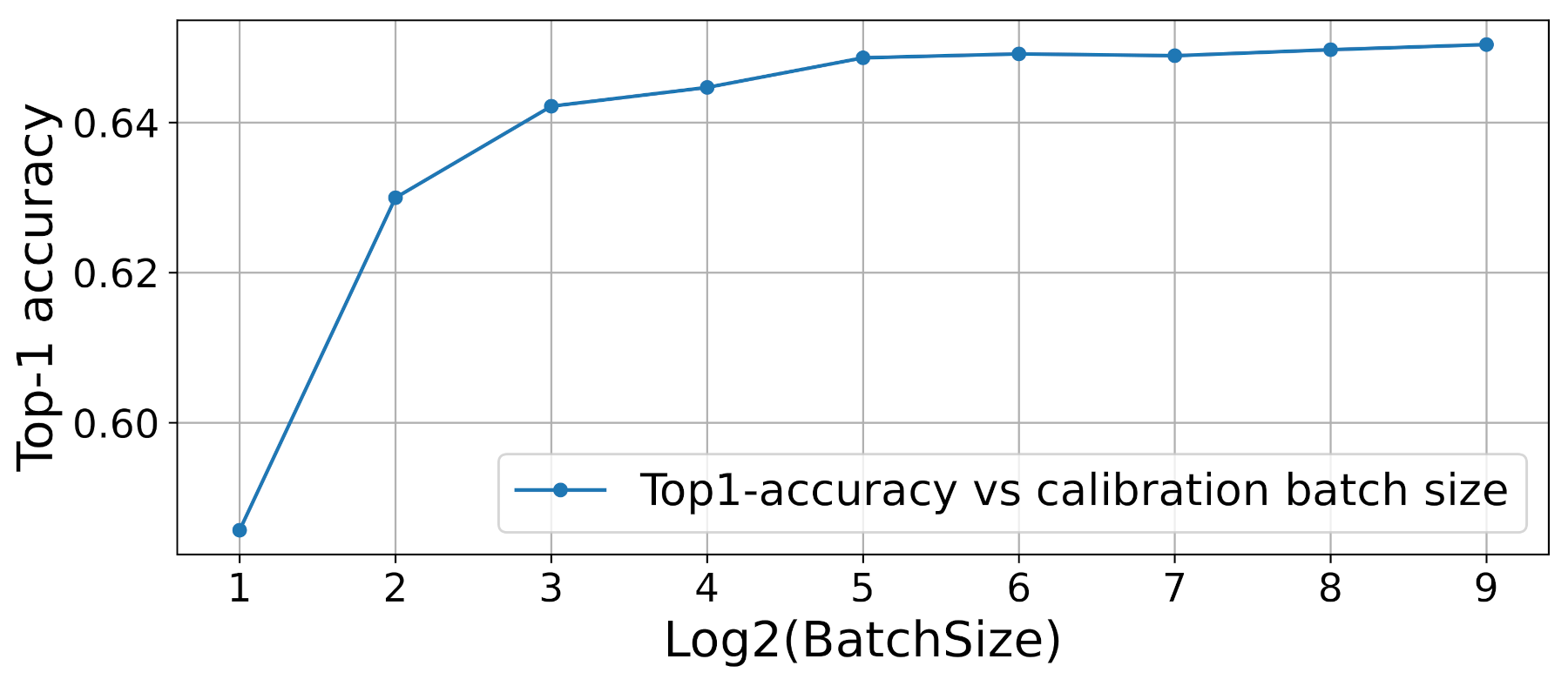
Figure A4 shows that small sizes of the calibration batch (e.g.,
) led to under-calibration of the model. A small calibration batch size cannot fully capture full dataset statistics (mean and variance). However, batch sizes starting from 32 allowed for the more efficient calibration of the model.
Figure A4.
Top-1 accuracy of the post-calibration model vs. the calibration batch size (Log2(BatchSize)).
Figure A4.
Top-1 accuracy of the post-calibration model vs. the calibration batch size (Log2(BatchSize)).
References
- Denil, M.; Shakibi, B.; Dinh, L.; Ranzato, M.A.; de Freitas, N. Predicting Parameters in Deep Learning. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; Burges, C.J.C., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2013; Volume 26. [Google Scholar]
- Hillar, C.J.; Lim, L.H. Most Tensor Problems are NP-hard. J. ACM (JACM) 2013, 60, 45. [Google Scholar] [CrossRef]
- Phan, A.H.; Sobolev, K.; Sozykin, K.; Ermilov, D.; Gusak, J.; Tichavský, P.; Glukhov, V.; Oseledets, I.; Cichocki, A. Stable Low-Rank Tensor Decomposition for Compression of Convolutional Neural Network. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 522–539. [Google Scholar]
- Tucker, L.R. Implications of factor analysis of three-way matrices for measurement of change. Probl. Meas. Chang. 1963, 15, 122–137. [Google Scholar]
- Kim, H.; Khan, M.U.K.; Kyung, C.-M. Efficient Neural Network Compression. In Proceedings of the The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; Volume 25. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Krizhevsky, A.; Nair, V.; Hinton, G. CIFAR-10 (Canadian Institute for Advanced Research). Available online: cs.toronto.edu/kriz/cifar.html (accessed on 20 March 2019).
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the CVPR09, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both Weights and Connections for Efficient Neural Network. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2015; pp. 1135–1143. Available online: https://arxiv.org/abs/1506.02626 (accessed on 30 January 2020).
- Frankle, J.; Carbin, M. The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. In Proceedings of the ICLR, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Molchanov, P.; Mallya, A.; Tyree, S.; Frosio, I.; Kautz, J. Importance Estimation for Neural Network Pruning. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Denton, E.L.; Zaremba, W.; Bruna, J.; LeCun, Y.; Fergus, R. Exploiting Linear Structure within Convolutional Networks for Efficient Evaluation. In Advances in Neural Information Processing Systems 27; Curran Associates, Inc.: Red Hook, NY, USA, 2014; pp. 1269–1277. [Google Scholar]
- Lebedev, V.; Ganin, Y.; Rakhuba, M.; Oseledets, I.; Lempitsky, V. Speeding-up Convolutional Neural Networks using Fine-tuned CP-Decomposition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Zhang, X.; Zou, J.; He, K.; Sun, J. Accelerating Very Deep Convolutional Networks for Classification and Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1943–1955. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Kyung, C. Automatic Rank Selection for High-Speed Convolutional Neural Network. arXiv 2018, arXiv:1806.10821. [Google Scholar]
- Kim, Y.; Park, E.; Yoo, S.; Choi, T.; Yang, L.; Shin, D. Compression of Deep Convolutional Neural Networks for Fast and Low Power Mobile Applications. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Gusak, J.; Kholyavchenko, M.; Ponomarev, E.; Markeeva, L.; Blagoveschensky, P.; Cichocki, A.; Oseledets, I. Automated Multi-Stage Compression of Neural Networks. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Korea, 27–28 October 2019; pp. 2501–2508. [Google Scholar]
- Nagel, M.; Baalen, M.v.; Blankevoort, T.; Welling, M. Data-Free Quantization Through Weight Equalization and Bias Correction. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. In Proceedings of the NIPS Deep Learning and Representation Learning Workshop, Montreal, QC, Canada, 7–12 December 2015; Available online: arxiv.org/abs/1503.02531 (accessed on 9 March 2019).
- Romero, A.; Kahou, S.E.; Montréal, P.; Bengio, Y.; Montréal, U.D.; Romero, A.; Ballas, N.; Kahou, S.E.; Chassang, A.; Gatta, C.; et al. Fitnets: Hints for thin deep nets. In Proceedings of the in International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer. In Proceedings of the ICLR, Toulon, France, 24–26 April 2017. [Google Scholar]
- Park, W.; Kim, D.; Lu, Y.; Cho, M. Relational Knowledge Distillation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3967–3976. [Google Scholar]
- Lee, S.H.; Kim, D.H.; Song, B.C. Self-supervised Knowledge Distillation Using Singular Value Decomposition. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 9–14 September 2018. [Google Scholar]
- Cichocki, A.; Lee, N.; Oseledets, I.; Phan, A.H.; Zhao, Q.; Mandic, D.P. Tensor Tetworks for Dimensionality Reduction and Large-Scale Optimization: Part 1 Low-Rank Tensor Decompositions. Found. Trends Mach. Learn. 2016, 9, 249–429. [Google Scholar] [CrossRef]
- Nakajima, S.; Sugiyama, M.; Babacan, S.D.; Tomioka, R. Global Analytic Solution of Fully-Observed Variational Bayesian Matrix Factorization. J. Mach. Learn. Res. 2013, 14, 1–37. [Google Scholar]
- Kuzmin, A.; Nagel, M.; Pitre, S.; Pendyam, S.; Blankevoort, T.; Welling, M. Taxonomy and Evaluation of Structured Compression of Convolutional Neural Networks. arXiv 2019, arXiv:1912.09802. [Google Scholar]
- He, Y.; Lin, J.; Liu, Z.; Wang, H.; Li, L.J.; Han, S. AMC: AutoML for Model Compression and Acceleration on Mobile Devices. In Proceedings of the Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Mockus, J.; Tiesis, V.; Zilinskas, A. The Application of Bayesian Methods for Seeking the Extremum. Towards Glob. Optim. 1978, 2, 2. [Google Scholar]
- Sobol’, I. On the Distribution of Points in a Cube and the Approximate Evaluation of Integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Petrov, M.; Voss, C.; Schubert, L.; Cammarata, N.; Goh, G.; Olah, C. Weight Banding. Distill 2021. [Google Scholar] [CrossRef]
- He, Y.; Zhang, X.; Sun, J. Channel Pruning for Accelerating Very Deep Neural Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1398–1406. [Google Scholar] [CrossRef]
- Peng, B.; Tan, W.; Li, Z.; Zhang, S.; Xie, D.; Pu, S. Extreme Network Compression via Filter Group Approximation. In Proceedings of the Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Zhuang, Z.; Tan, M.; Zhuang, B.; Liu, J.; Guo, Y.; Wu, Q.; Huang, J.; Zhu, J. Discrimination-Aware Channel Pruning for Deep Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 883–894. [Google Scholar]
- Hua, W.; Zhou, Y.; De Sa, C.M.; Zhang, Z.; Suh, G.E. Channel Gating Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Wallach, H., Larochelle, H., Beygelzimer, A., D’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Gao, X.; Zhao, Y.; Dudziak, L.; Mullins, R.; Xu, C.Z. Dynamic Channel Pruning: Feature Boosting and Suppression. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Tang, Y.; Wang, Y.; Xu, Y.; Deng, Y.; Xu, C.; Tao, D.; Xu, C. Manifold regularized dynamic network pruning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 5018–5028. [Google Scholar]
- Chang, J.; Lu, Y.; Xue, P.; Xu, Y.; Wei, Z. Global balanced iterative pruning for efficient convolutional neural networks. Neural Comput. Appl. 2022, 1–20. [Google Scholar] [CrossRef]
- Yin, M.; Sui, Y.; Liao, S.; Yuan, B. Towards Efficient Tensor Decomposition-Based DNN Model Compression with Optimization Framework. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 10674–10683. [Google Scholar]
- Yin, M.; Sui, Y.; Yang, W.; Zang, X.; Gong, Y.; Yuan, B. HODEC: Towards Efficient High-Order DEcomposed Convolutional Neural Networks. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 12299–12308.
- Yin, M.; Phan, H.; Zang, X.; Liao, S.; Yuan, B. BATUDE: Budget-Aware Neural Network Compression Based on Tucker Decomposition. In Proceedings of the Thirty-Sixth AAAI Conference on Artificial Intelligence (AAAI-22), Virtual, 22 February–1 March 2022; Volume 36, pp. 8874–8882. [Google Scholar] [CrossRef]
- Li, B.; Wu, B.; Su, J.; Wang, G. Eagleeye: Fast Sub-Net Evaluation for Efficient Neural Network Pruning. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 639–654. [Google Scholar]
- Zacharov, I.; Arslanov, R.; Gunin, M.; Stefonishin, D.; Bykov, A.; Pavlov, S.; Panarin, O.; Maliutin, A.; Rykovanov, S.; Fedorov, M. Zhores—Petaflops supercomputer for data-driven modeling, machine learning and artificial intelligence installed in Skolkovo Institute of Science and Technology. Open Eng. 2019, 9, 512–520. [Google Scholar] [CrossRef]
Figure 1.
Top-1 accuracy vs. FLOP compression ratio on the ILSVRC-2012 dataset for the compressed ResNet-18.
Figure 1.
Top-1 accuracy vs. FLOP compression ratio on the ILSVRC-2012 dataset for the compressed ResNet-18.
Figure 2.
Visualization of different convolutional layers. and denote numbers of channels in the input and output, respectively, D denotes the size of the convolutional layer, and R, , and denote the decomposition ranks. (a) Original convolutional layer. (b) CPD-3 layer. (c) Spatial-SVD layer. (d) TKD-2 layer.
Figure 2.
Visualization of different convolutional layers. and denote numbers of channels in the input and output, respectively, D denotes the size of the convolutional layer, and R, , and denote the decomposition ranks. (a) Original convolutional layer. (b) CPD-3 layer. (c) Spatial-SVD layer. (d) TKD-2 layer.
Figure 3.
Accuracy after vs. before fine-tuning without (a) and with BN calibration (b). The plot is based on 38 different networks compressed using CPD-EPC (with different rank sets and a fixed 3× FLOP compression ratio) and fine-tuned Resnet-18 with the ILSVRC-2012 dataset. The accuracy of the compressed model after the calibration of the BN statistics was strongly correlated with the post-fine-tuning model accuracy.
Figure 3.
Accuracy after vs. before fine-tuning without (a) and with BN calibration (b). The plot is based on 38 different networks compressed using CPD-EPC (with different rank sets and a fixed 3× FLOP compression ratio) and fine-tuned Resnet-18 with the ILSVRC-2012 dataset. The accuracy of the compressed model after the calibration of the BN statistics was strongly correlated with the post-fine-tuning model accuracy.
Figure 4.
Flowchart for the proposed rank search procedure in the single-rank case (Algorithm 1).
Figure 4.
Flowchart for the proposed rank search procedure in the single-rank case (Algorithm 1).
Figure 5.
Channel-wise boxplots of the differences between the layer1.1.bn1 layer outputs of ResNet-18 on the ILSVRC-2012 dataset with the original and decomposed layer1.1.conv1 layers. (a) Without the calibration of the BN statistics, the error distribution in each channel has a different mean and variance, which might negatively affect the network performance. (b) Calibration of the BN statistics allows the alignment of channel-wise error distributions and makes them zero-mean, which partially recovers model performance after decomposition.
Figure 5.
Channel-wise boxplots of the differences between the layer1.1.bn1 layer outputs of ResNet-18 on the ILSVRC-2012 dataset with the original and decomposed layer1.1.conv1 layers. (a) Without the calibration of the BN statistics, the error distribution in each channel has a different mean and variance, which might negatively affect the network performance. (b) Calibration of the BN statistics allows the alignment of channel-wise error distributions and makes them zero-mean, which partially recovers model performance after decomposition.
Figure 6.
Maximum of the MAE over the channels (mMAE) between outputs of the BN layers subsequent to the original and decomposed layers. In the Single setting, the compressed model has only one decomposed layer, while in the Joint setting, three layers are simultaneously decomposed. W/O corresponds to the case without calibration of the BN statistics, while W corresponds to the case with calibration of the BN statistics. The x-axis shows the CP rank. Note: for the first decomposed layer layer1.1.conv1(left subfigure), the results of the Single and Joint settings coincide.
Figure 6.
Maximum of the MAE over the channels (mMAE) between outputs of the BN layers subsequent to the original and decomposed layers. In the Single setting, the compressed model has only one decomposed layer, while in the Joint setting, three layers are simultaneously decomposed. W/O corresponds to the case without calibration of the BN statistics, while W corresponds to the case with calibration of the BN statistics. The x-axis shows the CP rank. Note: for the first decomposed layer layer1.1.conv1(left subfigure), the results of the Single and Joint settings coincide.
Figure 7.
Visualization of the convergence of the calibrated accuracy in our rank search procedure for the 3.5 FLOP compression ratio of ResNet-18.
Figure 7.
Visualization of the convergence of the calibrated accuracy in our rank search procedure for the 3.5 FLOP compression ratio of ResNet-18.
Figure 8.
Visualization of related ranks found by the PARS algorithm for different FLOP compression ratios.
Figure 8.
Visualization of related ranks found by the PARS algorithm for different FLOP compression ratios.
Figure 9.
Visualization of related ranks found by the PARS algorithm for the search with and without the calibration of the BN statistics.
Figure 9.
Visualization of related ranks found by the PARS algorithm for the search with and without the calibration of the BN statistics.
Table 1.
Details of the fine-tuning of the hyperparameters.
Table 1.
Details of the fine-tuning of the hyperparameters.
| Model | Batch Size | Initial lr | Epochs | lr Decay | Step Size | Weight Decay |
|---|
| AlexNet | 256 | | 16 | 0.5 | 2 | 0 |
| VGG-16 | 25 | 0.1 | 10 | |
| ResNet-18 | 25 | 0.1 | 10 | |
| ResNet-56 | 51 | 0.1 | 20 | |
Table 2.
Comparison of the performance of PARS with and without the calibration of the BN statistics. The ↓ FLOPs column denotes the compression of the computations; the top-1 and top-5 columns denote the top-1 and top-5 accuracy losses—the higher, the better.
Table 2.
Comparison of the performance of PARS with and without the calibration of the BN statistics. The ↓ FLOPs column denotes the compression of the computations; the top-1 and top-5 columns denote the top-1 and top-5 accuracy losses—the higher, the better.
| BN Calibration | ↓ FLOPs | Top-1, % | Top-5, % |
|---|
| ✗ | 4 | −1.64 | −0.78 |
| ✓ | −0.90 | −0.44 |
Table 3.
Comparison of different model compression methods on the ILSVRC-12 validation dataset. The ↓ FLOPs column denotes the compression of the computations; the top-1 and top-5 columns denote the differences in top-1 and top-5 accuracy from the original model—the higher, the better.
Table 3.
Comparison of different model compression methods on the ILSVRC-12 validation dataset. The ↓ FLOPs column denotes the compression of the computations; the top-1 and top-5 columns denote the differences in top-1 and top-5 accuracy from the original model—the higher, the better.
| Model | Method | Type | ↓ FLOPs | Top-1, % | Top-5, % |
|---|
| VGG-16 | TKD+VBMF [18] | LR | 4.93 | - | −0.50 |
| Asym. [16] | LR | 5.00 | - | −1.00 |
| CP-3C [34] | LR | 5.00 | - | −0.30 |
| ENC-Inf [5] | LR | 5.00 | - | +0.00 |
| CPD-EPC [3] | LR | 5.26 | −0.92 | −0.34 |
| GFA [35] | LR | 5.36 | −1.06 | −0.27 |
| CPD-EPC+PARS (Ours) | LR | 5.49 | +0.33 | +0.11 |
| ResNet-18 | DACP [36] | CP | 1.89 | −2.29 | −1.38 |
| Channel Gating NN [37] | CP | 1.93 | −0.40 | - |
| FBS [38] | CP | 1.98 | −2.54 | −1.46 |
| CPD-EPC+PARS (Ours) | LR | 2.00 | +0.26 | +0.40 |
| ManiDP [39] | CP | 2.04 | 0.88 | 0.32 |
| GBIP [40] | CP | 2.07 | 0.82 | 0.63 |
| MUSCO [19] | LR | 2.42 | −0.47 | −0.30 |
| TT [41] | LR | 2.47 | - | +0.00 |
| CPD-EPC+PARS (Ours) | LR | 3.03 | −0.14 | +0.03 |
| CPD-EPC [3] | LR | 3.09 | −0.69 | −0.15 |
| HODEC [42] | LR | 3.13 | −0.61 | −0.09 |
| BATUDE [43] | LR | 3.22 | - | −0.04 |
| CPD-EPC+PARS (Ours) | LR | 3.22 | −0.30 | −0.04 |
| TT [41] | LR | 4.62 | - | −1.61 |
| CPD-EPC+PARS (Ours) | LR | 4.99 | −1.81 | −0.83 |
Table 4.
Comparison of different rank search methods for the Spatial-SVD compression of ResNet-56 on the CIFAR-10 dataset.
Table 4.
Comparison of different rank search methods for the Spatial-SVD compression of ResNet-56 on the CIFAR-10 dataset.
| Method | ↓ FLOPs | Top-1, %, w/o f-t | Top-1, %, w f-t | |
|---|
| Uniform [5] | 2 | −12.7 | −0.2 | 20 |
| ENC-Inf [5] | −2.9 | −0.1 | 20 |
| ENC-Model [5] | −3.5 | −0.1 | 20 |
| ENC-MAP [5] | −3.3 | −0.1 | 20 |
| PARS (Ours) | −2.1 | −0.1 | 200 |
Table 5.
Evaluation of PARS in the multi-rank case of AlexNet on the ILSVRC-2012 dataset.
Table 5.
Evaluation of PARS in the multi-rank case of AlexNet on the ILSVRC-2012 dataset.
| Rank Search | ↓ FLOPs | TOP-1, % | Top-5, % |
|---|
| VBMF | 2.67 | - | −1.70 |
| PARS (Ours) | 2.76 | −0.94 | −0.37 |
Table 6.
Search time summary for the Spatial-SVD compression of ResNet-56 on the CIFAR-10 dataset.
Table 6.
Search time summary for the Spatial-SVD compression of ResNet-56 on the CIFAR-10 dataset.
| Operation | Time Spent |
|---|
| Search | 35 min |
| Model decomposition | 28 min |
| BN calibration | 9 min |
| Accuracy evaluation | 4 min |
| Total | 1 h 16 min |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).