Effects of Random Environmental Perturbation on the Dynamics of a Nutrient–Phytoplankton–Zooplankton Model with Nutrient Recycling

Abstract

A stochastic nutrient–phytoplankton–zooplankton model with instantaneous nutrient recycling is proposed and analyzed in this paper. When the nutrient uptake function and the grazing function are linear and the ingested phytoplankton is completely absorbed by the zooplankton, we establish two stochastic thresholds ${\mathcal{R}}_0^S$ and ${\mathcal{R}}_1^S$, which completely determine the persistence and extinction of the plankton. That is, if ${\mathcal{R}}_0^S<1$, both the phytoplankton and the zooplankton eventually are eliminated; if ${\mathcal{R}}_0^S>1$ and ${\mathcal{R}}_1^S<1$, the phytoplankton is persistent in mean but the zooplankton is extinct; while for ${\mathcal{R}}_1^S>1$, the entire system is persistent in mean. Furthermore, sufficient criteria for the existence of ergodic stationary distribution of the model are obtained and the persistent levels of the plankton are estimated. Numeric simulations are carried out to illustrate the theoretical results and to conclude our study. Our results suggest that environmental noise may cause the local bloom of phytoplankton, which surprisingly can be used to explain the formation of algal blooms to some extent. Moreover, we find that the nonlinear nutrient uptake function and grazing function may take credit for the periodic succession of blooms regardless of whether they are in the absence or presence of the environmental noises.

1. Introduction

Trophic interactions in marine ecosystems, which describe the relationship between nutrients and plankton, may impact the marine ecosystems by several ways, such as changing the spatiotemporal distribution of marine lives, altering the chemistry of their environment and shaping the ecosystem diversity [1,2,3]. A well-known example is harmful algal blooms, which are caused by the explosive proliferation of certain algae under specific environmental conditions. Therefore, trophic interactions play an important role in marine ecosystems, yet the empirical study on this is limited, largely because of the complexity of these interactions and of the difficulty and high cost in measuring planktonic biomass [4,5]. Since the pioneering work by Riley et al. [6], mathematical models have proven to be effective and powerful tools for studying the interaction between nutrient and plankton [7,8,9,10,11]. For example, Wroblewski et al. [12] established a food chain model of two trophic levels to investigate the plankton densities in different ocean layer; Edwards and Brindley [4] developed and investigated a simple plankton population model, illustrating the interaction of nutrient, phytoplankton and zooplankton in the oceanic mixed layer; Zhang and Wang [13] constructed a nutrient–phytoplankton–zooplankton model in an aquatic environment and studied its global dynamics.

It has shown that mathematical modeling provides a useful tool and a cheaper way to gain deep insights into the physical and biological interactions. Now, we consider a open system, which has three interacting components consisting of phytoplankton $\left(P\right)$, herbivorous zooplankton $\left(Z\right)$ and dissolved limiting nutrient $\left(N\right)$. Further suppose that the plankton are modeled by their nitrogen or phosphorous, and the nutrient is primarily responsible for limiting phytoplankton reproduction. Then a plankton–nutrient interaction model is given by the following equations

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill \frac{dN}{dt}=& D(N^0-N)-aPu\left(N\right)+(1-\delta )cZw\left(P\right)+{\mu }_{3}P+{\mu }_{4}Z,\hfill \\ \hfill \frac{dP}{dt}=& aPu\left(N\right)-cZw\left(P\right)-({\mu }_1+D_1)P,\hfill \\ \hfill \frac{dZ}{dt}=& \delta cZw\left(P\right)-({\mu }_2+D_2)Z.\hfill \end{array}\hfill \end{array}\right.$$

(1)

where function $u\left(N\right)$ describes the nutrient uptake rate of the phytoplankton; $w\left(P\right)$ represents the response function describing herbivore grazing. All parameters are assumed to be non-negative and have the biological meaning listed in Table 1. Clearly, we have $0<\delta \le 1$ and ${\mu }_3\le {\mu }_1$ and ${\mu }_4\le {\mu }_2$, under which Ruan [14,15] established sufficient conditions for the stability of non-negative equilibria and the persistence; the author also showed that the coexistence of zooplankton and phytoplankton may arise when incorporating a periodic washout rate into the system. Taking $u\left(N\right),w\left(P\right)$ as the linear forms and supposing that phytoplankton removed through zooplankton predation is all assimilated by zooplankton; that is, $u\left(N\right)=N,w\left(P\right)=P$ and $\delta =1$, model (1) becomes

$$\left\{\begin{array}{c}\frac{dN}{dt}=D(N^0-N)-aPN+{\mu }_{3}P+{\mu }_{4}Z,\hfill \\ \frac{dP}{dt}=aPN-cPZ-({\mu }_1+D_1)P,\hfill \\ \frac{dZ}{dt}=cPZ-({\mu }_2+D_2)Z,\hfill \end{array}\right.$$

(2)

which was studied by Refs. [16,17], where authors analyzed the stability of the feasible equilibria and pointed out that the dynamics of (2) is primarily dominated by

$${\mathcal{R}}_0=\frac{a{N}^0}{{\mu }_1+D_1}\mathrm{and}{\mathcal{R}}_1=\frac{cD(a{N}^0-{\mu }_1-D_1)}{a({\mu }_2+D_2)({\mu }_1+D_1-{\mu }_3)}.$$

Table 1. Biological explanation of parameters in model (1).

Parameter	Description
a	Maximal nutrient uptake rate of phytoplankton
c	Maximal zooplankton ingestion rate
$N^0$	Input concentration of nutrient
D	Washout rate of nutrient
$D_1$	Washout rate of phytoplankton
$D_2$	Washout rate of zooplankton
${\mu }_1$	Death rate of phytoplankton
${\mu }_2$	Death rate of zooplankton
$\delta$	Fraction of zooplankton nutrient conversion
${\mu }_3$	Nutrient recycling rate from the dead phytoplankton
${\mu }_4$	Nutrient recycling rate from the dead zooplankton

More precisely, the threshold ${\mathcal{R}}_0$ controls the persistence of the phytoplankton; the threshold ${\mathcal{R}}_1$ governs the existence of the positive interior equilibrium.

Models (1) and (2) were formulated based on the assumption that the biological parameters are all constants. Campillo et al. [18], however, pointed out that the impact of changing environment cannot be ignored when the homogeneity condition is not met. Until now, some stochastic models describing the interaction between fluctuating environment and population have been proposed by researchers [19,20,21]. Particularly, by analyzing a stochastic phytoplankton–zooplankton system, Sarkar and Chattopadhayay [22] found that noise intensity plays a key role in the termination of planktonic blooms. Imhof and Walcher [23] constructed a stochastic single substrate chemostat model and showed that the environmental noise may cause the extinction of microorganisms. Xu and Yuan [24] also proposed a stochastic chemostat model, but with competition and for multiple species. Zhao et al. [25] concluded that allelopathy can reduce the peak of harmful algal blooms.

The goal of the paper is to formulate a stochastic nutrient–phytoplankton–zooplankton model for understanding the effects of environmental fluctuations on the dynamics of plankton. Although there have been some results on stochastic plankton models, for example, stochastic nutrient–phytoplankton models [21,23,24] and stochastic phytoplankton–zooplankton models [20,22,26,27], these papers are mainly concerned with stochastic models with two trophic levels while the present paper focuses on three trophic levels. In general, it is difficult to obtain the dynamic properties of high-dimensional stochastic models because there is no unified method to construct Lyapunov functions. So, the innovation of our paper is obvious. The rest of the paper is organized as follows. In Section 2, we formulate the model and present our main results, including the survival analysis and the existence of ergodic stationary distribution. In Section 3, after giving some preliminaries and technical lemmas, we provide the strict mathematical proofs of the main results. Some numerical simulations are carried out to verify the theoretical results and further illustrate the effects of noise in Section 4. Finally, we conclude our study with a summary in Section 5.

2. Model Formulation and Main Results

2.1. Formulation of the Stochastic Model

In this section, we develop the stochastic version of model (1) using the approach due to Imhof and Walcher [23,24]. To this end, for a fixed time increment $\Delta t\equiv j>0$, we define process $X^{\left(j\right)}\left(t\right)={(N^{\left(j\right)}\left(t\right),P^{\left(j\right)}\left(t\right),Z^{\left(j\right)}\left(t\right))}^T\mathrm{for}t=0,j,2j,\cdots$ with initial value $X^{\left(j\right)}\left(0\right)={(N\left(0\right),P\left(0\right),Z\left(0\right))}^T\in {\mathbb{R}}_{+}^3$. Let ${\left\{R_i^{\left(j\right)}\left(h\right)\right\}}_{h=0}^{\infty }$ be a sequence of normally distributed random variables satisfying

$$E[R_i^{\left(j\right)}\left(h\right)]=0,E{[R_i^{\left(j\right)}\left(h\right)]}^2={\sigma }_i^{2}j,E{[R_i^{\left(j\right)}\left(h\right)]}^4=\circ \left(j\right)$$

for $i=1,2,3$ and $h=0,1,2,\cdots ,$ where ${\sigma }_i^2$ reflects the densities of stochastic effects. The variables $R_1^{\left(j\right)}\left(h\right)$ and $R_i^{\left(j\right)}\left(h\right)$, $i=2,3$ are supposed to capture the effects of random influences on the nutrient concentration and plankton concentration during time interval $[hj,(h+1\left)j\right)$, respectively. We also further $X^{\left(j\right)}$ grows within that time interval according to model (1) subject to the random effect ${(N^{\left(j\right)}\left(hj\right)R_1^{\left(j\right)}\left(h\right),P^{\left(j\right)}\left(hj\right)R_2^{\left(j\right)}\left(h\right),Z^{\left(j\right)}\left(hj\right)R_3^{\left(j\right)}\left(h\right))}^T$ as in Refs. [28,29], resulting the discrete model

$$\begin{array}{cc}\hfill N^{\left(j\right)}\left((h+1)j\right)=& N^{\left(j\right)}\left(hj\right)+N^{\left(j\right)}\left(hj\right)R_1^{\left(j\right)}\left(h\right)+[D(N^0-N^{\left(j\right)}\left(hj\right))-a{P}^{\left(j\right)}\left(hj\right)u(N^{\left(j\right)}\left(hj\right))\hfill \\ & +(1-\delta )c{Z}^{\left(j\right)}\left(hj\right)w(P^{\left(j\right)}\left(hj\right))+{\mu }_3{P}^{\left(j\right)}\left(hj\right)+{\mu }_4{Z}^{\left(j\right)}\left(hj\right)]j,\hfill \\ \hfill P^{\left(j\right)}\left((h+1)j\right)=& P^{\left(j\right)}\left(hj\right)+P^{\left(j\right)}\left(hj\right)R_2^{\left(j\right)}\left(h\right)\hfill \\ & +\left[a{P}^{\left(j\right)}\left(hj\right)u(N^{\left(j\right)}\left(hj\right))-c{Z}^{\left(j\right)}\left(hj\right)w(P^{\left(j\right)}\left(hj\right))-({\mu }_1+D_1)P^{\left(j\right)}\left(hj\right)\right]j,\hfill \\ \hfill Z^{\left(j\right)}\left((h+1)j\right)=& Z^{\left(j\right)}\left(hj\right)+Z^{\left(j\right)}\left(hj\right)R_3^{\left(j\right)}\left(h\right)\hfill \\ & +\left[\delta c{Z}^{\left(j\right)}\left(hj\right)w(P^{\left(j\right)}\left(hj\right))-({\mu }_2+D_2)Z^{\left(j\right)}\left(hj\right)\right]j.\hfill \end{array}$$

Then, according to Theorem 7.1 and Lemma 8.2 in [30], we can conclude that as $j\to 0$,

$$X^{\left(j\right)}\left(t\right)\to X\left(t\right)=(N\left(t\right),P\left(t\right),Z\left(t\right))\mathrm{weakly}.$$

Here, $X\left(t\right)$ is the solution of the following system of stochastic differential equations

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill dN=& [D(N^0-N)-aPu\left(N\right)+(1-\delta )cZw\left(P\right)\hfill \\ \hfill & +{\mu }_{3}P+{\mu }_{4}Z]dt+{\sigma }_{1}Nd{B}_1\left(t\right),\hfill \\ \hfill dP=& [aPu\left(N\right)-cZw\left(P\right)-({\mu }_1+D_1)P]dt+{\sigma }_{2}Pd{B}_2\left(t\right),\hfill \\ \hfill dZ=& [\delta cZw\left(P\right)-({\mu }_2+D_2)Z]dt+{\sigma }_{3}Zd{B}_3\left(t\right),\hfill \end{array}\hfill \end{array}\right.$$

(3)

with initial value $X\left(0\right)=(N\left(0\right),P\left(0\right),Z\left(0\right))\in {\mathbb{R}}_{+}^3$ and the standard independent Brownian motion $B_i\left(t\right),i=1,2,3$ is defined on a complete probability space $({\mathbb{R}}_{+}^3,\mathfrak{B}\left({\mathbb{R}}_{+}^3\right),{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P})$, provided its unique solution exists. The well-posedness of stochastic model (3) is discussed in Lemma 2, which implies that the above approach to introduce stochasticity into deterministic model (1) is mathematically and biologically reasonable. Due to the existence of stochastic effects, it is much more difficult to study the threshold dynamics of general stochastic food chains model (3). Then we first consider a special case that the nutrient uptake function and the grazing function are linear and all phytoplankton removed through zooplankton predation is assimilated by zooplankton. Then model (3) becomes

$$\left\{\begin{array}{c}dN=[D(N^0-N)-aPN+{\mu }_{3}P+{\mu }_{4}Z]dt+{\sigma }_{1}Nd{B}_1\left(t\right),\hfill \\ dP=[aPN-cPZ-({\mu }_1+D_1)P]dt+{\sigma }_{2}Pd{B}_2\left(t\right),\hfill \\ dZ=[cPZ-({\mu }_2+D_2)Z]dt+{\sigma }_{3}Zd{B}_3\left(t\right),\hfill \end{array}\right.$$

(4)

which happens to be the stochastic version of (2). A natural question is how the environmental noises effect the threshold dynamics of model (4), namely whether stochastic model (4) has a similar threshold dynamics to its deterministic counterpart (2). More precisely, in this study, we aim to explore:

(a)

Does stochastic model (4) still have thresholds, which completely determine the persistence and extinction of plankton?

(b)

How does stochastic perturbation affect the dynamics of model (4)?

For the general case, in order to explore the interaction between randomness and plankton, we numerically investigate the effects of nonlinear nutrient uptake functions and the fraction of zooplankton nutrient conversion on the asymptotic dynamics of model (3).

2.2. Main Results

For the simplicity of discussion, we define the stochastic versions of ${\mathcal{R}}_0$ and ${\mathcal{R}}_1$ as follows

$${\mathcal{R}}_0^S=\frac{a{N}^0}{{\mu }_1+D_1}-\frac{{\sigma }_2^2}{2({\mu }_1+D_1)},$$

$${\mathcal{R}}_1^S=\frac{cD(a{N}^0-{\mu }_1-D_1-\frac{1}{2}{\sigma }_2^2)}{a({\mu }_2+D_2)({\mu }_1+D_1-{\mu }_3)}-\frac{{\sigma }_3^2}{2({\mu }_2+D_2)}.$$

Please notice that without the perturbation, namely ${\sigma }_i=0$, $i=1,2,3$, the stochastic thresholds ${\mathcal{R}}_j^S$ becomes the deterministic versions ${\mathcal{R}}_j$, $j=0,1$.

We are now presenting our main results of the paper, but the proofs will be given in Section 3.

Theorem 1.

Assume $X\left(t\right)=\left(N\right(t),P(t),Z(t\left)\right)$ is the solution of the stochastic model (4) with initial value $X_0\in {\mathbb{R}}_{+}^3$. Then, the following conclusions hold.

(a) 

If ${\mathcal{R}}_0^S<1$, then both phytoplankton and zooplankton go extinct, namely

$$\underset{t\to \infty }{lim}P\left(t\right)=0and\underset{t\to \infty }{lim}Z\left(t\right)=0$$

almost surely (a.s.). Moreover,

$$\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}N\left(s\right)ds=N^{0}a.s.$$

(5)

(b) 

If ${\mathcal{R}}_0^S>1$ and ${\mathcal{R}}_1^S<1$, then the population of phytoplankton is stable in mean and the zooplankton goes extinct. Mathematically, it means $\underset{t\to \infty }{lim}Z\left(t\right)=0$ a.s. and

$$\begin{array}{cc}\hfill & \underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}N\left(s\right)ds=\frac{{\mu }_1+D_1}{a}+\frac{{\sigma }_2^2}{2a}={\tilde{N}}_{1}a.s.,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds=\frac{D({\mu }_1+D_1)({\mathcal{R}}_0^S-1)}{a({\mu }_1+D_1-{\mu }_3)}={\tilde{P}}_{1}a.s.\hfill \end{array}$$

(7)

(c) 

If ${\mathcal{R}}_1^S>1$, then both phytoplankton and zooplankton are persistent in mean, namely

$$\underset{t\to \infty }{lim\; inf}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds>\zeta >0and\underset{t\to \infty }{lim\; inf}\frac{1}{t}{\int }_0^{t}Z\left(s\right)ds>\zeta >0$$

(8)

almost surely for some constant $\zeta >0$.

Theorem 1 gives the sufficient and necessary criteria for the persistence of plankton, but it does not provide information about the level of persistence of the plankton. The following theorem will address this.

Theorem 2.

Let $X\left(t\right)=\left(N\right(t),P(t),Z(t\left)\right)$ be the solution of model (4) with any given initial value $X_0\in {\mathbb{R}}_{+}^3$. If ${\mathcal{R}}_1^S>1$ and $min\{D,{\mu }_1+D_1-{\mu }_3,{\mu }_2+D_2-{\mu }_4\}>\frac{1}{2}max\left\{{\sigma }_1^2,{\sigma }_2^2,{\sigma }_3^2\right\}$, model (4) admits a unique stationary distribution $\pi (·)$ and it has the ergodic property. Furthermore, the solution $X\left(t\right)$ of model (4) has the following property:

$$\begin{array}{cc}\hfill & \mathbb{P}\left\{\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}N\left(s\right)ds={\int }_{{\mathbb{R}}_{+}^3}{x}_1\pi (d{x}_1,d{x}_2,d{x}_3)=\tilde{N}*\right\}=1,\hfill \\ \hfill & \mathbb{P}\left\{\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds={\int }_{{\mathbb{R}}_{+}^3}{x}_2\pi (d{x}_1,d{x}_2,d{x}_3)=\tilde{P}*\right\}=1,\hfill \\ \hfill & \mathbb{P}\left\{\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}Z\left(s\right)ds={\int }_{{\mathbb{R}}_{+}^3}{x}_3\pi (d{x}_1,d{x}_2,d{x}_3)=\tilde{Z}*\right\}=1,\hfill \end{array}$$

(9)

where

$$\begin{array}{cc}\hfill & \tilde{N}*=\frac{{\mu }_1+D_1+c\tilde{Z}*}{a}+\frac{{\sigma }_2^2}{2a},\hfill \\ \hfill & \tilde{P}*=\frac{{\mu }_2+D_2}{c}+\frac{{\sigma }_3^2}{2c},\hfill \\ \hfill & \tilde{Z}*=\frac{a({\mu }_2+D_2)({\mu }_1+D_1-{\mu }_3)({\mathcal{R}}_1^S-1)}{ac({\mu }_2+D_2-{\mu }_4)+c^{2}D}.\hfill \end{array}$$

(10)

Remark 1.

Similar to the proof of Theorem 2 in Section 3.2, we can further obtain that under ${\mathcal{R}}_0^S<1$, model (4) has a unique ergodic plankton-free stationary distribution ${\nu }_1(·)$ satisfying

$$\mathbb{P}\left\{\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}N\left(s\right)ds={\int }_{{\mathbb{R}}_{+}}{x}_1{\nu }_1\left(d{x}_1\right)=N^0\right\}=1.$$

In addition, under ${\mathcal{R}}_0^S>1$ and ${\mathcal{R}}_1^S<1$, model (4) also has a unique ergodic zooplankton-free stationary distribution ${\nu }_2(·)$ satisfying

$$\begin{array}{cc}\hfill & \mathbb{P}\left\{\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}N\left(s\right)ds={\int }_{{\mathbb{R}}_{+}^2}{x}_1{\nu }_2(d{x}_1,d{x}_2)={\tilde{N}}_1\right\}=1,\hfill \\ \hfill & \mathbb{P}\left\{\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds={\int }_{{\mathbb{R}}_{+}^2}{x}_2{\nu }_2(d{x}_1,d{x}_2)={\tilde{P}}_1\right\}=1.\hfill \end{array}$$

Remark 2.

When the parameters in model (4) are replaced by some quantities that may change over time according to a discrete Markov chain or periodically, model (4) becomes a switching system or a non-autonomous system, which is also studied in our other related papers. It is worth noting that the research given in present paper is more thorough. Especially, the dynamics of model (4) is completely determined by the two stochastic thresholds, ${\mathcal{R}}_0^S$ and ${\mathcal{R}}_1^S$. In addition, the persistent levels of plankton are also estimated explicitly.

3. Proofs of Our Main Results

3.1. Preliminaries

In this section, we provide some auxiliary definitions and results concerning the asymptotic properties, which are needed when proving the main results. To be biological meaningful, we restrict our discussion on model (4) in region

$${\mathbb{R}}_{+}^3=\{(N,P,Z)\in {\mathbb{R}}^3:N>0,P>0,Z>0\},$$

over which define the Borel $\sigma$-algebra $\mathfrak{B}\left({\mathbb{R}}_{+}^3\right)$ and $({\mathbb{R}}_{+}^3,\mathfrak{B}\left({\mathbb{R}}_{+}^3\right),{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathbb{P})$ a complete probability space with a filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ satisfying the usual conditions. Then, in state space $({\mathbb{R}}_{+}^3,\mathfrak{B}\left({\mathbb{R}}_{+}^3\right),\mathbb{P})$, consider the Markov process $X\left(t\right)$ described by

$$dX\left(t\right)=F\left(X\left(t\right)\right)dt+G\left(X\left(t\right)\right)dB\left(t\right),X\left(0\right)=X_0,$$

(11)

where $B\left(t\right)$ is a standard 3-dimensional Brownian motion, functions $F(·):{\mathbb{R}}_{+}^3\to {\mathbb{R}}^3$ and $G(·):{\mathbb{R}}_{+}^3\to {\overline{\mathbb{R}}}_{+}^{3\times 3}$ satisfy the local Lipschitz condition. Then, the diffusion matrix of $X\left(t\right)$ is

$$A\left(X\right)=G\left(X\right)G^T\left(X\right)=\left(a_{ij}\left(X\right)\right).$$

Introduce a differential operator

$$\mathcal{L}=\sum _{i=1}^3{F}_i\left(X\right)\frac{\partial }{\partial X_i}+\frac{1}{2}\sum _{i,j=1}^3{a}_{ij}\left(X\right)\frac{{\partial }^2}{\partial X_i\partial X_j}.$$

It is easy to see that $\mathcal{L}$ is uniformly elliptical in ${\mathbb{R}}_{+}^3$. That is, there exists $M>0$ such that

$$\sum _{i,j=1}^3{a}_{ij}\left(X\right){\psi }_i{\psi }_j\ge M{\left|\psi \right|}^2$$

for any $X\in {\mathbb{R}}_{+}^3$ and $\psi \in {\mathbb{R}}^3$, where the norm is defined as $\left|X\right|=\sqrt{X_1^2+X_2^2+X_3^2}.$

Then, one has the following lemma established by Khasminskii [31].

Lemma 1

([31]). Assume there exists a bounded open set $U\subset {\mathbb{R}}_{+}^3$ with a smooth boundary Γ, satisfying the following conditions:

(a1) 

$\mathcal{F}$ is uniformly elliptical in the domain and some neighborhood thereof, where $\mathcal{F}u=F\left(X\right)u_x+\frac{1}{2}tr\left(A\left(X\right)u_{xx}\right)$.

(a2) 

There exists a non-negative $C^2$-function $V\left(X\right)$ and a positive constant C such that $\mathcal{L}V\left(X\right)\le -C$, for any $X\in {\mathbb{R}}_{+}^3\setminus U$. Here, $\mathcal{L}$ is the generator of X.

Then the Markov process $X\left(t\right)$ has a unique stationary distribution $\pi (·)$, and for any integrable function $f(·)$ with respect to the measure π we have

$$\mathbb{P}\left\{\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}f\left(X\left(s\right)\right)ds={\int }_{{\mathbb{R}}_{+}^3}f\left(x\right)\pi \left(dx\right)\right\}=1.$$

Furthermore, we can prove some basic properties of model (4) that are useful in discussing our main results. What we need to point out here is that for model (3), the following Lemmas 2–4 also hold.

Lemma 2.

Given initial valve $X\left(0\right)=X_0\in {\mathbb{R}}_{+}^3$, model (4) admits a unique positive solution $X\left(t\right)=\left(N\right(t),P(t),Z(t\left)\right)$ for $t\ge 0$; furthermore, the solution will remain in ${\mathbb{R}}_{+}^3$ with probability one.

Proof. 

The proof is similar to that of Theorem 3.1 in [32] and hence is omitted. □

Using the non-negative semimartingale convergence theorem, Theorem 3.9 in [33], it is easy to prove that the following conclusions are valid.

Lemma 3.

The solution $X\left(t\right)$=$\left(N\right(t),P(t),Z(t\left)\right)$ established in Lemma 2 satisfies

$$\begin{array}{cc}\hfill & \underset{t\to \infty }{lim\; sup}[N\left(t\right)+P\left(t\right)+Z\left(t\right)]<\infty ,and\hfill \\ \hfill & \underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^t{\sigma }_i{X}_i\left(s\right)d{B}_i\left(s\right)=0,i=1,2,3,a.s.\hfill \end{array}$$

Ecologically, the extinction of prey will lead to the extinction of predators, so the following conclusion is obvious.

Lemma 4.

For model (4), if $\underset{t\to \infty }{lim}P\left(t\right)=0$ a.s., then $\underset{t\to \infty }{lim}Z\left(t\right)=0$ a.s.

Lemma 5.

For any initial value $X\left(0\right)=X_0\in {\mathbb{R}}_{+}^3$, model (4) is stochastically ultimately bounded and permanent.

Proof. 

Define $V\left(t\right)=R\left(t\right)+\frac{1}{R\left(t\right)},V_1\left(t\right)=e^{H_{1}t}V\left(t\right),$ where $H_1=min\{D,{\mu }_1+D_1-{\mu }_3,{\mu }_2+D_2-{\mu }_4\}$, and

$$R\left(t\right)=N\left(t\right)+P\left(t\right)+Z\left(t\right).$$

(12)

Using the fact that $\mathbb{E}{\int }_0^{t}d{V}_1\left(s\right)=\mathbb{E}{\int }_0^t\mathcal{L}{V}_1\left(s\right)ds,$ we get

$$\mathbb{E}\left(V_1\left(t\right)\right)=\mathbb{E}\left(V\left(0\right)\right)+\mathbb{E}\left[{\int }_0^t{e}^{H_{1}s}(H_{1}V\left(s\right)+\mathcal{L}V\left(s\right))ds\right].$$

Note that

$$\begin{array}{cc}\hfill \mathcal{L}V\left(X\right)=& D{N}^0-DN-({\mu }_1+D_1-{\mu }_3)P-({\mu }_2+D_2-{\mu }_4)Z\hfill \\ & -\frac{D{N}^0-DN-({\mu }_1+D_1-{\mu }_3)P-({\mu }_2+D_2-{\mu }_4)Z}{R^2}+\frac{{\sigma }_1^2{N}^2+{\sigma }_2^2{P}^2+{\sigma }_3^2{Z}^2}{R^3}\hfill \\ \hfill \le & D{N}^0-H_{1}R-\frac{D{N}^0-H_{2}R}{R^2}+\frac{{\sigma }_1^2{N}^2+{\sigma }_2^2{P}^2+{\sigma }_3^2{Z}^2}{R^3}\hfill \\ \hfill =& D{N}^0-H_1(R+\frac{1}{R})+\frac{H_1+H_2}{R}-\frac{D{N}^0}{R^2}+\frac{{\sigma }_1^2{N}^2+{\sigma }_2^2{P}^2+{\sigma }_3^2{Z}^2}{R^3}\hfill \\ \hfill \le & D{N}^0-H_1(R+\frac{1}{R})+\frac{H_1+H_2+{\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2}{R}-\frac{D{N}^0}{R^2}\hfill \\ \hfill \le & K_1-H_{1}V\left(X\right),\hfill \end{array}$$

where

$$K_1=\frac{4{\left(D{N}^0\right)}^2+{(H_1+H_2+{\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2)}^2}{4D{N}^0},$$

$$H_2=max\{D,{\mu }_1+D_1-{\mu }_3,{\mu }_2+D_2-{\mu }_4\}.$$

Then

$$\mathbb{E}\left(V_1\left(t\right)\right)\le \mathbb{E}\left(V\left(0\right)\right)+K_1\mathbb{E}\left({\int }_0^t{e}^{H_{1}s}ds\right)=\mathbb{E}\left(V\left(0\right)\right)+\frac{K_1}{H_1}(e^{H_{1}t}-1),$$

which implies

$$\mathbb{E}\left(V\left(t\right)\right)\le e^{-H_{1}t}\mathbb{E}\left(V\left(0\right)\right)+\frac{K_1}{H_1}(1-e^{-H_{1}t})\le \mathbb{E}\left(V\left(0\right)\right)+\frac{K_1}{H_1}:=K_2.$$

Choose $\rho$ sufficiently large such that $0<\frac{K_2}{\rho }<1$. By virtue of Chebyshev inequality,

$$\mathbb{P}\left\{R+\frac{1}{R}>\rho \right\}\le \frac{\mathbb{E}(R+\frac{1}{R})}{\rho }\le \frac{K_2}{\rho }:=ϵ.$$

It follows that

$$\mathbb{P}\left\{\frac{1}{\rho }\le R\le \rho \right\}\ge \mathbb{P}\left\{R+\frac{1}{R}\le \rho \right\}\ge 1-ϵ.$$

Using the fundamental inequalities $R^2\le 3{\left|X\right|}^2\le 3R^2$, then

$$\mathbb{P}\left\{\frac{1}{\sqrt{3}\rho }\le \frac{R}{\sqrt{3}}\le \left|X\right|\le R\le \rho \right\}\ge 1-ϵ.$$

That is,

$$\underset{t\to \infty }{lim\; sup}\mathbb{P}\left\{\right|X|>\rho \}<ϵ,$$

and

$$\underset{t\to \infty }{lim\; inf}\mathbb{P}\left\{\right|X|\le \rho \}\ge 1-ϵ,\underset{t\to \infty }{lim\; inf}\mathbb{P}\left\{\right|X|\ge \chi \}\ge 1-ϵ,$$

where $\chi =\frac{1}{\sqrt{3}\rho }$. According to the definitions of stochastically ultimate boundedness and stochastic permanence (see [19]), the desired results can be obtained easily. This completes the proof. □

In what follows, we prove the main results, namely Theorems 1 and 2.

3.2. Proof of Theorem 1

Proof. 

Applying the Itô’s formula to (4) and then integrating both sides from 0 to t yields

$$\begin{array}{cc}\hfill & \frac{1}{t}ln\frac{P\left(t\right)}{P\left(0\right)}=-\left({\mu }_1+D_1+\frac{1}{2}{\sigma }_2^2\right)+\frac{a}{t}{\int }_0^{t}N\left(s\right)ds-\frac{c}{t}{\int }_0^{t}Z\left(s\right)ds+\frac{{\sigma }_2{B}_2\left(t\right)}{t},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & \frac{1}{t}ln\frac{Z\left(t\right)}{Z\left(0\right)}=-\left({\mu }_2+D_2+\frac{1}{2}{\sigma }_3^2\right)+\frac{c}{t}{\int }_0^{t}P\left(s\right)ds+\frac{{\sigma }_3{B}_3\left(t\right)}{t}.\hfill \end{array}$$

(14)

Then, we have

$$\begin{array}{c}\hfill D{N}^0-\frac{D}{t}{\int }_0^{t}N\left(s\right)ds-\frac{{\mu }_1+D_1-{\mu }_3}{t}{\int }_0^{t}P\left(s\right)ds-\frac{{\mu }_2+D_2-{\mu }_4}{t}{\int }_0^{t}Z\left(s\right)ds=\frac{{\phi }_1\left(t\right)}{t},\end{array}$$

(15)

where ${\phi }_1\left(t\right)=R\left(t\right)-R\left(0\right)-{\displaystyle \sum _{i=1}^3}{\int }_0^t{\sigma }_i{X}_{i}d{B}_i\left(t\right)$, and $R\left(t\right)$ is defined by (12). According to Lemma 3,

$$\underset{t\to \infty }{lim}\frac{{\phi }_1\left(t\right)}{t}=0\mathrm{a}.\mathrm{s}.$$

(16)

Next, we prove the three conclusions of Theorem 1 one by one.

Let us first prove $\left(a\right)$. Substituting (15) into (13) leads to that

$$\begin{array}{cc}\hfill \frac{1}{t}ln\frac{P\left(t\right)}{P\left(0\right)}=& a{N}^0-{\mu }_1-D_1-\frac{1}{2}{\sigma }_2^2-\frac{a({\mu }_1+D_1-{\mu }_3)}{D}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds\hfill \\ \hfill & -\left(c+\frac{a({\mu }_2+D_2-{\mu }_4)}{D}\right)\frac{1}{t}{\int }_0^{t}Z\left(s\right)ds+\frac{{\phi }_2\left(t\right)}{t},\hfill \end{array}$$

(17)

where ${\phi }_2\left(t\right)={\sigma }_2{B}_2\left(t\right)-\frac{a}{D}{\phi }_1\left(t\right).$ Noticing that $\underset{t\to \infty }{lim}\frac{B_2\left(t\right)}{t}=0$ and (16), we obtain

$$\underset{t\to \infty }{lim}\frac{{\phi }_2\left(t\right)}{t}=0\mathrm{a}.\mathrm{s}.$$

(18)

which, together with (17), yields

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim\; sup}\frac{1}{t}ln\frac{P\left(t\right)}{P\left(0\right)}\le & a{N}^0-{\mu }_1-D_1-\frac{1}{2}{\sigma }_2^2\hfill \\ \hfill =& ({\mu }_1+D_1)\left({\mathcal{R}}_0^S-1\right)\mathrm{a}.\mathrm{s}.\hfill \end{array}$$

That is, $\underset{t\to \infty }{lim}P\left(t\right)=0\mathrm{a}.\mathrm{s}.$ if ${\mathcal{R}}_0^S<1$. It then follows from Lemma 4 that $\underset{t\to \infty }{lim}Z\left(t\right)=0\mathrm{a}.\mathrm{s}.$ Furthermore, according to (15), it is easy to see that

$$\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}N\left(s\right)ds=N^0\mathrm{a}.\mathrm{s}.$$

(19)

This completes the proof of $\left(a\right)$.

Now we prove $\left(b\right)$. From (17),

$$\begin{array}{c}\hfill \frac{1}{t}ln\frac{P\left(t\right)}{P\left(0\right)}\le a{N}^0-{\mu }_1-D_1-\frac{1}{2}{\sigma }_2^2-\frac{a({\mu }_1+D_1-{\mu }_3)}{D}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds+\frac{{\phi }_2\left(t\right)}{t}.\end{array}$$

(20)

It then follows from ${\mathcal{R}}_0^S>1$ and Lemma 4 in [34] that

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim\; sup}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds\le & \frac{D\left(a{N}^0-{\mu }_1-D_1-\frac{1}{2}{\sigma }_2^2\right)}{a({\mu }_1+D_1-{\mu }_3)}\hfill \\ \hfill =& \frac{D({\mu }_1+D_1)({\mathcal{R}}_0^S-1)}{a({\mu }_1+D_1-{\mu }_3)}\mathrm{a}.\mathrm{s}.\hfill \end{array}$$

(21)

By (21) and (14), one can see that

$$\underset{t\to \infty }{lim\; sup}\frac{1}{t}ln\frac{Z\left(t\right)}{Z\left(0\right)}=-\left({\mu }_2+D_2+\frac{1}{2}{\sigma }_3^2\right)+c\underset{t\to \infty }{lim\; sup}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds,$$

(22)

which implies that

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim\; sup}\frac{1}{t}ln\frac{Z\left(t\right)}{Z\left(0\right)}\le & -\left({\mu }_2+D_2+\frac{1}{2}{\sigma }_3^2\right)+\frac{cD({\mu }_1+D_1)({\mathcal{R}}_0^S-1)}{a({\mu }_1+D_1-{\mu }_3)}\hfill \\ \hfill =& ({\mu }_2+D_2)({\mathcal{R}}_1^S-1)\mathrm{a}.\mathrm{s}.\hfill \end{array}$$

Clearly, if ${\mathcal{R}}_1^S<1$, then $\underset{t\to \infty }{lim}Z\left(t\right)=0\mathrm{a}.\mathrm{s}.$ That is to say, for arbitrary $0<ϵ<1$, there exist a set ${\mathsf{\Omega }}_{ϵ}$ with $\mathbb{P}\left({\mathsf{\Omega }}_{ϵ}\right)\ge 1-ϵ$ and a constant $T=T\left(ϵ\right)$ such that

$$\left(c+\frac{a({\mu }_2+D_2-{\mu }_4)}{D}\right)\frac{1}{t}{\int }_0^{t}Z\left(s\right)ds<ϵ$$

for $\omega \in {\mathsf{\Omega }}_{ϵ}$ and $t>T$. When this inequality is used in (17), we obtain

$$\begin{array}{cc}\hfill \frac{1}{t}ln\frac{P\left(t\right)}{P\left(0\right)}\ge & a{N}^0-{\mu }_1-D_1-\frac{1}{2}{\sigma }_2^2-ϵ-\frac{a({\mu }_1+D_1-{\mu }_3)}{D}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds+\frac{{\phi }_2\left(t\right)}{t}.\hfill \end{array}$$

This, together with Lemma 4 in [34] and the arbitrariness of $ϵ$, implies

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim\; inf}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds\ge \frac{D({\mu }_1+D_1)({\mathcal{R}}_0^S-1)}{a({\mu }_1+D_1-{\mu }_3)}\mathrm{a}.\mathrm{s}.\end{array}$$

(23)

So we have

$$\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds=\frac{D({\mu }_1+D_1)({\mathcal{R}}_0^S-1)}{a({\mu }_1+D_1-{\mu }_3)}\mathrm{a}.\mathrm{s}.$$

Using (15) again,

$$D{N}^0-D\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}N\left(s\right)ds-({\mu }_1+D_1-{\mu }_3)\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds=0.$$

That is,

$$\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}N\left(s\right)ds=\frac{{\mu }_1+D_1}{a}+\frac{{\sigma }_2^2}{2a}\mathrm{a}.\mathrm{s}.$$

(24)

This completes the proof of $\left(b\right)$.

We are now to prove $\left(c\right)$. From Lemma 3, the left of Equation (22) is non-positive, which implies

$$-\left({\mu }_2+D_2+\frac{1}{2}{\sigma }_3^2\right)+c\underset{t\to \infty }{lim\; sup}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds\le 0.$$

Thus,

$$\underset{t\to \infty }{lim\; sup}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds\le \frac{{\mu }_2+D_2}{c}+\frac{{\sigma }_3^2}{2c}\mathrm{a}.\mathrm{s}.$$

(25)

Taking upper limit on both sides of (17) and using (25) yields

$$\begin{array}{cc}\hfill \underset{t\to \infty }{lim\; sup}\frac{1}{t}ln\frac{P\left(t\right)}{P\left(0\right)}\ge & a{N}^0-{\mu }_1-D_1-\frac{1}{2}{\sigma }_2^2-\frac{a({\mu }_1+D_1-{\mu }_3)}{D}\underset{t\to \infty }{lim\; inf}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds\hfill \\ \hfill & -\left(c+\frac{a({\mu }_2+D_2-{\mu }_4)}{D}\right)\underset{t\to \infty }{lim\; inf}\frac{1}{t}{\int }_0^{t}Z\left(s\right)ds\hfill \\ \hfill \ge & \frac{a({\mu }_2+D_2)({\mu }_1+D_1-{\mu }_3)}{cD}({\mathcal{R}}_1^S-1)\hfill \\ \hfill & -\left(c+\frac{a({\mu }_2+D_2-{\mu }_4)}{D}\right)\underset{t\to \infty }{lim\; inf}\frac{1}{t}{\int }_0^{t}Z\left(s\right)ds.\hfill \end{array}$$

(26)

Applying Lemma 3 again leads to

$$\underset{t\to \infty }{lim\; inf}\frac{1}{t}{\int }_0^{t}Z\left(s\right)ds\ge \frac{a({\mu }_2+D_2)({\mu }_1+D_1-{\mu }_3)({\mathcal{R}}_1^S-1)}{ac({\mu }_2+D_2-{\mu }_4)+c^{2}D}\mathrm{a}.\mathrm{s},$$

which implies $\underset{t\to \infty }{lim\; inf}\frac{1}{t}{\int }_0^{t}Z\left(s\right)ds>0\mathrm{a}.\mathrm{s}.$ if ${\mathcal{R}}_1^S>1$. In addition, the persistence in mean of phytoplankton can be obtained easily by using Lemma 4. This completes the proof of $\left(c\right)$. □

3.3. Proof of Theorem 2

Due to the complexity of the proof of Theorem 2, we will split the proof into two steps.

3.3.1. Step 1: Existence of the Unique Ergodic Stationary Distribution

To complete the proof of ergodicity, we need to verify the conditions $\left(a1\right)$ and $\left(a2\right)$ in Lemma 1.

First, let us verify condition $\left(a2\right)$. That is, we need to construct a $C^2$-continuous function $V:{\mathbb{R}}_{+}^3\to {\mathbb{R}}_{+}$ and a bounded closed $U_{ϵ}$ such that $\mathcal{L}V\le -1$ for $(N,P,Z)\in {\mathbb{R}}_{+}^3\setminus U_{ϵ}$. For convenience, denote $m_1=\frac{{\mu }_1+D_1-{\mu }_3}{c},m_2=\frac{{\mu }_2+D_2-{\mu }_4+\frac{cD}{a}}{{\mu }_2+D_2}$, $\hat{D}=min\{D,{\mu }_1+D_1-{\mu }_3,{\mu }_2+D_2-{\mu }_4\}$, $\check{\sigma }=max\{{\sigma }_1^2,{\sigma }_2^2,{\sigma }_3^2\}$, and choose a constant $\theta >0$ such that $\eta =\widehat{D}-\frac{1}{2}\check{\sigma }(\theta +1)>0.$ Then define a $C^2$-function $\tilde{V}$: ${\mathbb{R}}_{+}^3\to \mathbb{R}$ as follows

$$\begin{array}{cc}\hfill \tilde{V}(N,P,Z)=& M\left[-N-P-Z-\frac{D}{a}lnP-m_{1}lnZ+m_{2}Z\right]-lnN+\frac{1}{\theta +2}{(N+P+Z)}^{\theta +2}\hfill \\ \hfill \equiv & M{V}_1+V_2+V_3,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill M=& \frac{2}{m_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)}max\{2,\mathsf{{\rm Y}}\},\hfill \\ \hfill \mathsf{{\rm Y}}=& \underset{(N,P,Z)\in {\mathbb{R}}_{+}^3}{sup}\left\{-\frac{1}{2}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})+m_{2}c(P^2+Z^2)+aP+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2\right\},\hfill \end{array}$$

and $\mathsf{\Psi }$ is defined as in (27). Then, it is easy to check that $\tilde{V}(N,P,Z)$ is continuous and

$$\underset{k\to \infty ,(N,P,Z)\in {\mathbb{R}}_{+}^3\setminus U_k}{lim\; inf}\tilde{V}(N,P,Z)=+\infty ,$$

where $U_k=(\frac{1}{k},k)\times (\frac{1}{k},k)\times (\frac{1}{k},k).$ Hence $\tilde{V}(N,P,Z)$ has a global minimum point $(\overline{N},\overline{P},\overline{Z})$ in the interior of ${\mathbb{R}}_{+}^3$. We finally define the non-negative and $C^2$-continuous function $V:{\mathbb{R}}_{+}^3\to {\mathbb{R}}_{+}$ by

$$V(N,P,Z)=\tilde{V}(N,P,Z)-\tilde{V}(\overline{N},\overline{P},\overline{Z}).$$

Note that from Itô’s formula, we have

$$\begin{array}{cc}\hfill \mathcal{L}{V}_1=& -[D{N}^0-DN-({\mu }_1+D_1-{\mu }_3)P-({\mu }_2+D_2-{\mu }_4)Z]\hfill \\ & -\frac{D}{a}\left[aN-cZ-{\mu }_1-D_1-\frac{1}{2}{\sigma }_2^2\right]\hfill \\ & -m_1\left[cP-{\mu }_2-D_2-\frac{1}{2}{\sigma }_3^2\right]+m_2[cPZ-({\mu }_2+D_2)Z]\hfill \\ \hfill =& -m_1({\mu }_2+D_2)\left[\frac{D(a{N}^0-{\mu }_1-D_1-\frac{1}{2}{\sigma }_2^2)}{a{m}_1({\mu }_2+D_2)}-\frac{{\sigma }_3^2}{2({\mu }_2+D_2)}-1\right]+m_{2}cPZ\hfill \\ \hfill =& -m_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)+m_{2}cPZ,\hfill \\ \hfill \mathcal{L}{V}_2=& -\frac{D{N}^0}{N}+aP-{\mu }_3\frac{P}{N}-{\mu }_4\frac{Z}{N}+D+\frac{1}{2}{\sigma }_1^2\hfill \\ \hfill \le & -\frac{D{N}^0}{N}+aP+D+\frac{1}{2}{\sigma }_1^2,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \mathcal{L}{V}_3=& {(N+P+Z)}^{\theta +1}[D{N}^0-DN-({\mu }_1+D_1-{\mu }_3)P-({\mu }_2+D_2-{\mu }_4)Z]\hfill \\ & +\frac{1}{2}(\theta +1){(N+P+Z)}^{\theta }({\sigma }_1^2{N}^2+{\sigma }_2^2{P}^2+{\sigma }_3^2{Z}^2)\hfill \\ \hfill \le & {(N+P+Z)}^{\theta +1}[D{N}^0-\hat{D}(N+P+Z)]+\frac{1}{2}\check{\sigma }(\theta +1){(N+P+Z)}^{\theta +2}\hfill \\ \hfill =& D{N}^0{(N+P+Z)}^{\theta +1}-\left[\hat{D}-\frac{1}{2}\check{\sigma }(\theta +1)\right]{(N+P+Z)}^{\theta +2}\hfill \\ \hfill \le & \mathsf{\Psi }-\frac{1}{2}\eta {(N+P+Z)}^{\theta +2}\hfill \\ \hfill \le & \mathsf{\Psi }-\frac{1}{2}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2}),\hfill \end{array}$$

where

$$\mathsf{\Psi }=\underset{(N,P,Z)\in {\mathbb{R}}_{+}^3}{sup}\left\{D{N}^0{(N+P+Z)}^{\theta +1}-\frac{1}{2}\eta {(N+P+Z)}^{\theta +2}\right\}<\infty .$$

(27)

Based on the above inequalities, we then obtain

$$\begin{array}{cc}\hfill \mathcal{L}V=& M\mathcal{L}{V}_1+\mathcal{L}{V}_2+\mathcal{L}{V}_3\hfill \\ \hfill \le & -M{m}_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)+M{m}_{2}cPZ-\frac{D{N}^0}{N}+aP\hfill \\ & -\frac{1}{2}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2.\hfill \end{array}$$

Now we further define a bounded closed set

$$U_{ϵ}=\left\{(N,P,Z)\in {\mathbb{R}}_{+}^3:ϵ\le N\le \frac{1}{ϵ},ϵ\le P\le \frac{1}{ϵ},ϵ\le Z\le \frac{1}{ϵ}\right\},$$

where $0<ϵ\ll 1$ and satisfies

$$-\frac{D{N}^0}{ϵ}+{\mathsf{\Phi }}_1\le -1,$$

(28)

$$-\frac{1}{4}\frac{\eta }{{ϵ}^{\theta +2}}+{\mathsf{\Phi }}_2\le -1,$$

(29)

$$0<ϵ<\frac{m_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)}{4m_{2}c},$$

(30)

$$0<ϵ<\frac{1}{M}.$$

(31)

Here, ${\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2$ are constants given by (32) and (33).

Next, we will prove $\mathcal{L}V\le -1$ on ${\mathbb{R}}_{+}^3\setminus U_{ϵ}$. For the sake of convenience, we divide ${\mathbb{R}}_{+}^3\setminus U_{ϵ}$ into ${\mathbb{R}}_{+}^3\setminus U_{ϵ}\equiv {\bigcup }_{i=1}^6{U}_{ϵ}^i$ where

$$\begin{array}{ccc}& & U_{ϵ}^1=\{(N,P,Z)\in {\mathbb{R}}_{+}^3:0<N<ϵ\},U_{ϵ}^2=\{(N,P,Z)\in {\mathbb{R}}_{+}^3:0<P<ϵ\},\hfill \\ & & U_{ϵ}^3=\{(N,P,Z)\in {\mathbb{R}}_{+}^3:0<Z<ϵ\},U_{ϵ}^4=\left\{(N,P,Z)\in {\mathbb{R}}_{+}^3:N>\frac{1}{ϵ}\right\},\hfill \\ & & U_{ϵ}^5=\left\{(N,P,Z)\in {\mathbb{R}}_{+}^3:P>\frac{1}{ϵ}\right\},U_{ϵ}^6=\left\{(N,P,Z)\in {\mathbb{R}}_{+}^3:Z>\frac{1}{ϵ}\right\}.\hfill \end{array}$$

If we show $\mathcal{L}V\le -1$ in each $U_{ϵ}^i,i=1,\cdots ,6$, then the conclusion on ${\mathbb{R}}_{+}^3\setminus U_{ϵ}$ is true. For this reason, we discuss it in six cases.

Case 1: $(N,P,Z)\in U_{ϵ}^1$. Define

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_1=\underset{(N,P,Z)\in {\mathbb{R}}_{+}^3}{sup}\left\{-\frac{1}{2}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})+M{m}_{2}cPZ+aP+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2\right\}.\end{array}$$

(32)

Then, when $(N,P,Z)\in U_{ϵ}^1$, we have

$$\begin{array}{cc}\hfill \mathcal{L}V\le & M{m}_{2}cPZ-\frac{D{N}^0}{N}+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2+aP-\frac{1}{2}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})\hfill \\ \hfill \le & -\frac{D{N}^0}{N}+{\mathsf{\Phi }}_1\le -\frac{D{N}^0}{ϵ}+{\mathsf{\Phi }}_1,\hfill \end{array}$$

which and (28) implying $\mathcal{L}V\le -1$ for all $(N,P,Z)\in U_{ϵ}^1$.

Case 2: $(N,P,Z)\in U_{ϵ}^2$. If $(N,P,Z)\in U_{ϵ}^2$, then $PZ\le ϵZ\le ϵ(1+Z^2)$ and

$$\begin{array}{cc}\hfill \mathcal{L}V\le & -M{m}_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)+M{m}_{2}cϵ(1+Z^2)+aP\hfill \\ \hfill & -\frac{1}{2}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2\hfill \\ \hfill =& -\frac{1}{4}M{m}_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)-M\left[\frac{1}{4}{m}_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)-m_{2}cϵ\right]\hfill \\ \hfill & -m_{2}c(1-Mϵ)Z^2-\frac{1}{2}M{m}_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)\hfill \\ \hfill & -\frac{1}{2}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})+m_{2}c{Z}^2+aP+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2.\hfill \end{array}$$

By the definition of M and Equations (30) and (31), we can show that for all $(N,P,Z)\in U_{ϵ}^2$,

$$\mathcal{L}V\le -\frac{1}{4}M{m}_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)\le -1.$$

Case 3: $(N,P,Z)\in U_{ϵ}^3$. In this case, we first have $PZ\le ϵP\le ϵ(1+P^2)$ and then

$$\begin{array}{cc}\hfill \mathcal{L}V\le & -M{m}_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)+M{m}_{2}cϵ(1+P^2)+aP\hfill \\ & -\frac{1}{2}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2\hfill \\ \hfill =& -\frac{1}{4}M{m}_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)-M\left[\frac{1}{4}{m}_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)-m_{2}cϵ\right]\hfill \\ & -m_{2}c(1-Mϵ)P^2-\frac{1}{2}M{m}_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)\hfill \\ & -\frac{1}{2}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})+m_{2}c{P}^2+aP+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2.\hfill \end{array}$$

Using M, (30) and (31) again, we obtain that for all $(N,P,Z)\in U_{ϵ}^3$,

$$\mathcal{L}V\le -\frac{1}{4}M{m}_1({\mu }_2+D_2)({\mathcal{R}}_1^S-1)\le -1.$$

Case 4: $(N,P,Z)\in U_{ϵ}^4$. If $(N,P,Z)\in U_{ϵ}^4$, then

$$\begin{array}{cc}\hfill \mathcal{L}V\le & -\frac{1}{4}\eta N^{\theta +2}-\frac{1}{4}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})+M{m}_{2}cPZ+aP+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2\hfill \\ \hfill \le & -\frac{1}{4}\eta N^{\theta +2}+{\mathsf{\Phi }}_2\le -\frac{1}{4}\frac{\eta }{{ϵ}^{\theta +2}}+{\mathsf{\Phi }}_2,\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_2=\underset{(N,P,Z)\in {\mathbb{R}}_{+}^3}{sup}\left\{-\frac{1}{4}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})+M{m}_{2}cPZ+aP+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2\right\}.\end{array}$$

(33)

In view of (29), we can conclude that $\mathcal{L}V\le -1$ for all $(N,P,Z)\in U_{ϵ}^4$.

Case 5: $(N,P,Z)\in U_{ϵ}^5$. If $(N,P,Z)\in U_{ϵ}^5$, then

$$\begin{array}{cc}\hfill \mathcal{L}V\le & -\frac{1}{4}\eta P^{\theta +2}-\frac{1}{4}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})+M{m}_{2}cPZ+aP+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2\hfill \\ \hfill \le & -\frac{1}{4}\eta P^{\theta +2}+{\mathsf{\Phi }}_2\le -\frac{1}{4}\frac{\eta }{{ϵ}^{\theta +2}}+{\mathsf{\Phi }}_2.\hfill \end{array}$$

Again, Inequality (29) implies $\mathcal{L}V\le -1$ for all $(N,P,Z)\in U_{ϵ}^5$.

Case 6: $(N,P,Z)\in U_{ϵ}^6$. Using (29), we have

$$\begin{array}{cc}\hfill \mathcal{L}V\le & -\frac{1}{4}\eta Z^{\theta +2}-\frac{1}{4}\eta (N^{\theta +2}+P^{\theta +2}+Z^{\theta +2})+M{m}_{2}cPZ+aP+\mathsf{\Psi }+D+\frac{1}{2}{\sigma }_1^2\hfill \\ \hfill \le & -\frac{1}{4}\eta Z^{\theta +2}+{\mathsf{\Phi }}_2\le -\frac{1}{4}\frac{\eta }{{ϵ}^{\theta +2}}+{\mathsf{\Phi }}_2\le -1\hfill \end{array}$$

for all $(N,P,Z)\in U_{ϵ}^6$.

In short, we have $\mathcal{L}V\le -1,\mathrm{for}\mathrm{all}(N,P,Z)\in {\mathbb{R}}_{+}^3\setminus U_{ϵ},$ implying that condition $\left(a2\right)$ in Lemma 1 holds with $C=1.$

On the other hand, we can find $\overline{M}=\underset{(N,P,Z)\in U_{ϵ}}{min}\{{\sigma }_1^2{N}^2,{\sigma }_2^2{P}^2,{\sigma }_3^2{Z}^2\}$ such that

$$\sum _{i,j=1}^3{a}_{ij}\left(X\right){\xi }_i{\xi }_j={\sigma }_1^2{N}^2{\xi }_1^2+{\sigma }_2^2{P}^2{\xi }_2^2+{\sigma }_3^2{Z}^2{\xi }_3^2\ge \overline{M}{\parallel \xi \parallel }^2$$

for all $X\in U_{ϵ},\xi =({\xi }_1,{\xi }_2,{\xi }_3)\in {\mathbb{R}}^3$, which implies that condition $\left(a1\right)$ in Lemma 1 also holds. Thanks to Lemma 1, model (4) has a unique stationary distribution $\pi (·)$ and it is ergodic.

3.3.2. Step 2: Estimation of the Convergence Rates

In the following, we establish the convergence rates of $N\left(t\right),P\left(t\right)$ and $Z\left(t\right)$. According to the ergodic property established in Step 1, for any $K>0$, we obtain

$$\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^t[X_i\left(s\right)\wedge K]ds={\int }_{{\mathbb{R}}_{+}^3}[x_i\wedge K]\pi (d{x}_1,d{x}_2,d{x}_3,)\mathrm{a}.\mathrm{s}.$$

Moreover, Lemma 5 implies that $E\left[X_i\left(t\right)\right]<K_0,$ where $K_0$ is a given positive constant. This, together with the dominated convergence theorem, implies

$$E\left[\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^t[X_i\left(s\right)\wedge K]ds\right]=\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}E[X_i\left(s\right)\wedge K]ds\le K_0.$$

Then,

$${\int }_{{\mathbb{R}}_{+}^3}[x_i\wedge K]\pi (d{x}_1,d{x}_2,d{x}_3)\le K_0,$$

which implies

$${\int }_{{\mathbb{R}}_{+}^3}{x}_i\pi (d{x}_1,d{x}_2,d{x}_3)\le K_0$$

by letting $K\to \infty$. Thus, function $f\left(X\right)=X$ is integrable with respect to $\pi (·)$. Then, by the ergodic property

$$\begin{array}{c}\hfill \mathbb{P}\left\{\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^t{X}_i\left(s\right)ds={\int }_{{\mathbb{R}}_{+}^3}{x}_i\pi (d{x}_1,d{x}_2,d{x}_3)\right\}=1,i=1,2,3.\end{array}$$

(34)

Next, we show that ${\kappa }_1:=\underset{t\to \infty }{lim}\frac{lnP\left(t\right)}{t}=0$ by proof of contradiction. In fact, if ${\kappa }_1>0$, there exists a $T_1>0$ such that $lnP\left(t\right)>\frac{{\kappa }_1}{2}t$ for $t>T_1$, which implies

$$\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds\to \infty .$$

This contradicts (34).

If ${\kappa }_1<0$, there exists a $T_2>0$ such that $lnP\left(t\right)<\frac{{\kappa }_{1}t}{2}$ for $t>T_2$. It thus derives

$$\underset{t\to \infty }{lim}\frac{1}{t}{\int }_0^{t}P\left(s\right)ds<0,$$

which contradicts with (34) again. Consequently, $\underset{t\to \infty }{lim}\frac{lnP\left(t\right)}{t}=0.$ Similarly, $\underset{t\to \infty }{lim}\frac{lnZ\left(t\right)}{t}=0$. This, together with (13), (14), (15) and (34), yields

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill D{\int }_{{\mathbb{R}}_{+}^3}{x}_1\pi (d{x}_1,d{x}_2,d{x}_3)& +({\mu }_1+D_1-{\mu }_3){\int }_{{\mathbb{R}}_{+}^3}{x}_2\pi (d{x}_1,d{x}_2,d{x}_3)\hfill \\ & +({\mu }_2+D_2-{\mu }_4){\int }_{{\mathbb{R}}_{+}^3}{x}_3\pi (d{x}_1,d{x}_2,d{x}_3)=D{N}^0,\hfill \\ \hfill a{\int }_{{\mathbb{R}}_{+}^3}{x}_1\pi (d{x}_1,d{x}_2,d{x}_3)& -c{\int }_{{\mathbb{R}}_{+}^3}{x}_3\pi (d{x}_1,d{x}_2,d{x}_3)={\mu }_1+D_1+\frac{1}{2}{\sigma }_2^2,\hfill \\ \hfill c{\int }_{{\mathbb{R}}_{+}^3}{x}_2\pi (d{x}_1,d{x}_2,d{x}_3)& ={\mu }_2+D_2+\frac{1}{2}{\sigma }_3^2.\hfill \end{array}\hfill \end{array}\right.$$

(35)

Obviously, (35) has a unique positive solution $(\tilde{N}*,\tilde{P}*,\tilde{Z}*)$ if ${\mathcal{R}}_1^S>1$, where

$$\left\{\begin{array}{c}\tilde{N}*=\frac{{\mu }_1+D_1+c\tilde{Z}*}{a}+\frac{{\sigma }_2^2}{2a},\hfill \\ \tilde{P}*=\frac{{\mu }_2+D_2}{c}+\frac{{\sigma }_3^2}{2c},\hfill \\ \tilde{Z}*=\frac{a({\mu }_2+D_2)({\mu }_1+D_1-{\mu }_3)({\mathcal{R}}_1^S-1)}{ac({\mu }_2+D_2-{\mu }_4)+c^{2}D}.\hfill \end{array}\right.$$

(36)

This completes the proof of Theorem 2.

4. Numerical Simulation

In this section, some numerical simulations are carried out to verify the obtained theoretical results and further explain the effects of noise and nonlinear uptake and grazing functions on the population persistence.

4.1. The Influence of the White Noise on the Dynamics of Model (4)

Denote the equilibrium points of the deterministic model (2) by $(N_1,P_1,0)$ and $(N*,P*,Z*)$. Then, we can verify that

$${\mathcal{R}}_0^S\to {\mathcal{R}}_0,{\mathcal{R}}_1^S\to {\mathcal{R}}_1$$

and

$$({\tilde{N}}_1,{\tilde{P}}_1,0)\to (N_1,P_1,0),(\tilde{N}*,\tilde{P}*,\tilde{Z}*)\to (N*,P*,Z*)$$

when ${\sigma }_i\to 0$, $i=1,2,3$. That is to say, stochastic model (4) preserves the properties of the solutions of its corresponding deterministic model (2) when the intensities of noise are relatively small. Please see Figure 1, where we numerically demonstrate this observation by different parameter settings. Figure 1a shows the solution of (4) without effects of environmental noise, namely ${\sigma }_i=0$. When parameters are set such that ${\mathcal{R}}_1=1.22>1$, the positive equilibrium $E*$ is asymptotically stable. When increasing noise intensities from zero, but keeping them relatively small such that ${\mathcal{R}}_1^S>1$, the solution is still stable, see Figure 1b,e,f. In this scenario, we can ignore the effect of noise, and use deterministic model to characterize the interaction between nutrient and plankton.

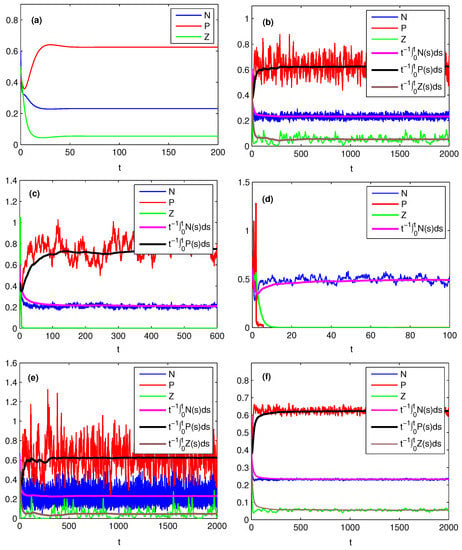
Figure 1. Effects of noise on the dynamics of model (4) for $a=1.7$, $c=0.8$, $D=0.7$, $D_1=0.25$, $D_2=0.2$, ${\mu }_1=0.1$, ${\mu }_2=0.3$, ${\mu }_3=0.08$, ${\mu }_4=0.15$, $N^0=0.5$. (a) ${\sigma }_1={\sigma }_2={\sigma }_3=0$, then ${\mathcal{R}}_1=1.22>1$, and $E*=(0.2316,0.6250,0.0547)$ which is asymptotically stable; (b) ${\sigma }_1=0.08$, ${\sigma }_3=0.03$, then ${\mathcal{R}}_1^S=1.2161>1$, i.e., the entire system is persistent; (c) ${\sigma }_1=0.08$, ${\sigma }_2=0.05$, ${\sigma }_3=0.6$, then ${\mathcal{R}}_0^S=2.425>1$ and ${\mathcal{R}}_1^S=0.857<1$, i.e., the phytoplankton is stable in mean and the zooplankton goes extinct; (d) ${\sigma }_1=0.08$, ${\sigma }_2=1.02$, ${\sigma }_3=0.03$, then ${\mathcal{R}}_0^S=0.9423<1$, i.e., both phytoplankton and zooplankton go extinct; (e) ${\sigma }_1=0.5$, ${\sigma }_2=0.05$, ${\sigma }_3=0.03$, then ${\mathcal{R}}_1^S=1.2161>1$; (f) ${\sigma }_1={\sigma }_2={\sigma }_3=0.001$, then ${\mathcal{R}}_1^S=1.2198>1$.

To obtain deep insights of the effects of noise on population dynamics, we take a closer look at the definitions of ${\mathcal{R}}_i^S,$ from which one can see ${\mathcal{R}}_i^S<{\mathcal{R}}_i$, $i=0,1$, implying the possibility that ${\mathcal{R}}_i^S<1<{\mathcal{R}}_i$ due to the continuity of ${\mathcal{R}}_i^S$ in ${\sigma }_j$, $j=1,2,3$. Then, biologically, ${\mathcal{R}}_0^S<1<{\mathcal{R}}_0$ implies that when the phytoplankton is persistent in deterministic model (2), it may be extinct with probability one in stochastic model (4) due to the effect of environmental noise; when ${\mathcal{R}}_1^S<{\mathcal{R}}_1$, we have the similar conclusion for population of zooplankton. The simulation results are reported in Figure 1a,c,d. Biologically, this means that the survival of plankton may change significantly when the stochastic perturbations are large. In this scenario, we can not ignore the effect of noise, and should use stochastic model instead of the deterministic model to describe the dynamics of plankton.

In previous studies, such as [23,34,35,36], researchers show that the environmental noise may increase extinction risk of a species. Different to that, in our present study for the nutrient–plankton food chain model, we find according to Theorem 1 that the environmental noise experienced by nutrient does not have any effect on the persistence of nutrient and plankton regardless of its intensity; however, if environmental noise experienced by phytoplankton is too large, i.e., ${\sigma }_2^2>{\eta }_1$, then both phytoplankton and zooplankton are extinct; if environmental noise experienced by phytoplankton is not too large while environmental noise experienced by zooplankton is very large, i.e., ${\sigma }_2^2<{\eta }_1$, ${\sigma }_3^2>{\eta }_2$, then phytoplankton is persistent and zooplankton will tend to extinction; If phytoplankton and zooplankton do not experience too large noise, i.e., ${\sigma }_2^2<{\eta }_1$, ${\sigma }_3^2<{\eta }_2$, then both phytoplankton and zooplankton will persist. Here

$${\eta }_1=2(a{N}^0-{\mu }_1-D_1),{\eta }_2=2\left[\frac{cD({\mathcal{R}}_0^S-1)({\mu }_1+D_1)}{a({\mu }_1+D_1-{\mu }_3)}-({\mu }_2+D_2)\right].$$

The above discussions show that the survival of phytoplankton only depends on the effect of environmental noise on itself, the survival of zooplankton depends on the effects of environmental noise on itself and phytoplankton, and nutrient is always persistent regardless of the intensity of the noise. Now let us give some numerical simulations, shown in Figure 1 for different ${\sigma }_1$, ${\sigma }_2$ and ${\sigma }_3$ to illustrate these conclusions. Comparing Figure 1b with Figure 1c, we know that with the increasing of ${\sigma }_3$, zooplankton goes extinct, however, nutrient and phytoplankton are still persistent. Similarly, comparing Figure 1b with Figure 1d one can see that with the increasing of ${\sigma }_2$, both phytoplankton and zooplankton go extinct; however, nutrient is persistent. Meanwhile, comparing Figure 1b with Figure 1e we can find easily that with the increasing of ${\sigma }_1$, the persistence of nutrient and plankton remains the same, namely, they are still persistent.

From Theorem 2, it is easy to see that the persistent level of nutrient or zooplankton depends on the effects of environmental noise on both phytoplankton and zooplankton, while the persistent level of phytoplankton only depends on the effect of environmental noise on zooplankton. Assuming ${\mathcal{R}}_1^S>1$ and noting that the expression of $\tilde{P}*$ in Theorem 2, phytoplankton will persist better when increasing ${\sigma }_3$. This is because zooplankton feeds on phytoplankton, and with the increasing of ${\sigma }_3$, zooplankton tends to become extinct, so phytoplankton can grow vigorously. For the effects of ${\sigma }_2$ and ${\sigma }_3$ on nutrient and zooplankton, we can analyze similarly. Next let us give some numerical simulations with different ${\sigma }_1$, ${\sigma }_2$ and ${\sigma }_3$ to verify these findings, see Figure 2. Comparing Figure 2a with Figure 2b, we see easily that the persistent levels of nutrient and plankton do not change with the increasing of ${\sigma }_1$. Comparing Figure 2a with Figure 2c, one can see that with the increasing of ${\sigma }_2$, the persistent level of nutrient increases, while the persistent level of zooplankton decreases. More interestingly, the persistent level of phytoplankton does not change. Comparing Figure 2a with Figure 2d we can obtain that with the increasing of ${\sigma }_3$, the persistent levels of nutrient and zooplankton decrease, while the persistent level of phytoplankton increases.

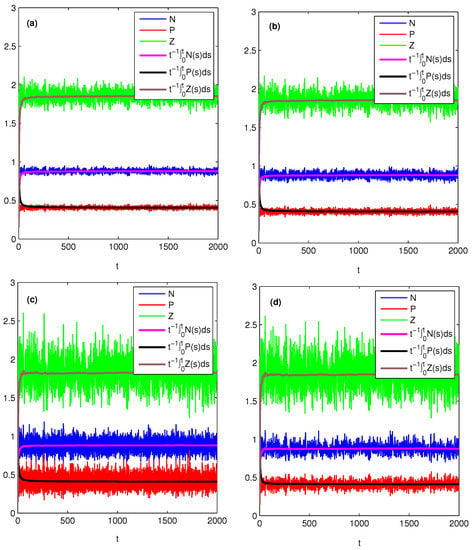
Figure 2. Effects of noise on the population persistent level. Here, $a=4$, $c=1.6$, $D=1$, $D_1=0.25,D_2=0.25,{\mu }_1=0.3,{\mu }_2=0.4,{\mu }_3=0.08,{\mu }_4=0.15,N^0=2$. Then ${\mathcal{R}}_1=9.7545>1$, and $E*=(0.8804,0.4063,1.8573)$ which is asymptotically stable. (a) ${\sigma }_1=0.02,{\sigma }_2=0.01$, ${\sigma }_3=0.03$, then $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}N\left(s\right)ds=0.8804$, $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}P\left(s\right)ds=0.4065$, $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}Z\left(s\right)ds=1.8571$; (b) ${\sigma }_1=0.05,{\sigma }_2=0.01,{\sigma }_3=0.03$, then $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}N\left(s\right)ds=0.8804$, $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}P\left(s\right)ds=0.4065$, $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}Z\left(s\right)ds=1.8571$; (c) ${\sigma }_1=0.02,{\sigma }_2=0.25,{\sigma }_3=0.03$, then $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}N\left(s\right)ds=0.8847$, $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}P\left(s\right)ds=0.4065$, $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}Z\left(s\right)ds=1.8485$; (d) ${\sigma }_1=0.02,{\sigma }_2=0.01,{\sigma }_3=0.1$, then $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}N\left(s\right)ds=0.8798$, $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}P\left(s\right)ds=0.4094$, $\underset{t\to \infty }{lim}{t}^{-1}{\int }_0^{t}Z\left(s\right)ds=1.8556$.

4.2. Role of Nonlinear Nutrient Uptake Rate and Functional Response for Herbivore Grazing

In this subsection, we numerically investigate how the nonlinear nutrient uptake rate and functional response for herbivore grazing affect the long-term dynamics of stochastic model (3). For certainty in numerical simulation, we assume as in [15] that

$$u\left(N\right)=\frac{N}{k+N},w\left(P\right)=1-e^{-\lambda P},$$

then stochastic model (3) becomes the following form:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill dN=& [D(N^0-N)-\frac{aNP}{k+N}+(1-\delta )cZ(1-e^{-\lambda P})\hfill \\ \hfill & +{\mu }_{3}P+{\mu }_{4}Z]dt+{\sigma }_{1}Nd{B}_1\left(t\right)\hfill \\ \hfill dP=& \left[\frac{aNP}{k+N}-cZw\left(P\right)-({\mu }_1+D_1)P\right]dt+{\sigma }_{2}Pd{B}_2\left(t\right),\hfill \\ \hfill dZ=& [\delta cZ(1-e^{-\lambda P})-({\mu }_2+D_2)Z]dt+{\sigma }_{3}Zd{B}_3\left(t\right).\hfill \end{array}\hfill \end{array}\right.$$

(37)

Ruan [15] proved that under $\frac{{\mu }_1+D_1}{a}<\frac{N^0}{k+N^0}$ and ${\mu }_2+D_2<\delta c$, the corresponding deterministic system of (37) persists if and only if

$$1-exp\left[-\frac{\lambda D(N^0-\frac{\alpha }{1-\alpha }k)}{{\mu }_1+D_1-{\mu }_3}\right]>\frac{{\mu }_2+D_2}{\delta c},$$

(38)

where $\alpha =\frac{{\mu }_1+D_1}{a}$.

Now we select several parameters as in Figure 3 satisfying condition (38), which ensures system (37) without stochastic perturbations is persistent. Figure 4 shows that the effects of different k, $\lambda$ and $\delta$ on the dynamics of model (37) under stochastic perturbations. From Figure 3 and Figure 4, it is not difficult to find that stochastic system (37) under small perturbations preserves the properties of the solutions of its corresponding deterministic system, which has been illustrated in Section 4.1. Comparing Figure 4a with Figure 4b, we further observed that increasing the half saturation constant k of the nutrient uptake function can significantly decrease the peak and period of the algae outbreak. These conclusions are contrary if we increase $\lambda$, see Figure 4b,c. Finally, comparing Figure 4c with Figure 4d, it is easy to see that increasing the fraction of zooplankton nutrient conversion may increase the frequency of algae blooms. All these numerical observations show that nutrient uptake functions and zooplankton nutrient conversion rate play an important role in the periodic oscillatory succession of bloom and greatly affect the interactions between nutrients and plankton.

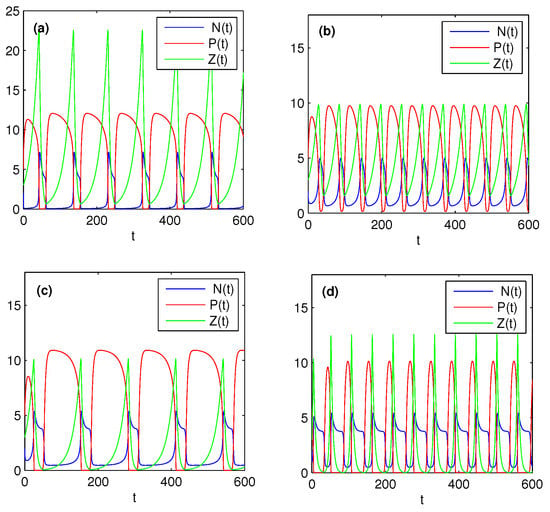
Figure 3. Effects of nonlinear uptake and grazing functions on the population persistence in deterministic environment. Here, we take $a=2$, $c=0.5$, ${\mu }_1=0.1$, ${\mu }_2=0.2$, ${\mu }_3=0.1$, ${\mu }_4=0.2$, $D=1$, $D_1=0.3$, $D_2=0$, $N^0=3.75$. (a) $k=0.2,\lambda =0.5,\delta =0.5$; (b) $k=1.8,\lambda =0.5,\delta =0.5$; (c) $k=1.8,\lambda =1,\delta =0.5$; (d) $k=1.8,\lambda =1,\delta =1$.

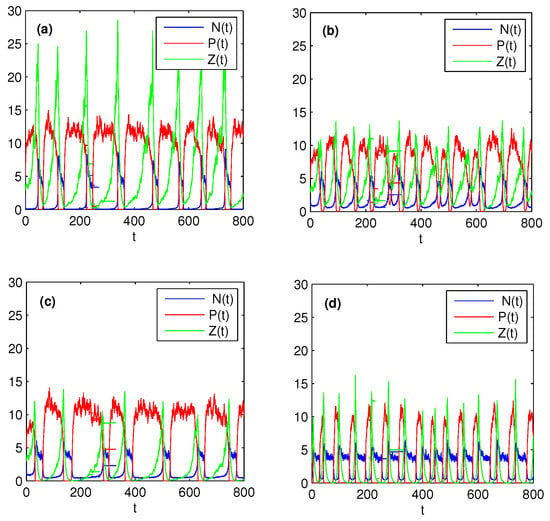
Figure 4. Effects of nonlinear uptake and grazing functions on the population persistence in stochastic environment. Here, ${\sigma }_1=0.1$, ${\sigma }_2=0.05$, ${\sigma }_3=0.08$. (a) $k=0.2,\lambda =0.5,\delta =0.5$; (b) $k=1.8$, $\lambda =0.5$, $\delta =0.5$; (c) $k=1.8,\lambda =1,\delta =0.5$; (d) $k=1.8,\lambda =1,\delta =1$. All the other parameters are the same as Figure 3.

5. Conclusions

Environmental noise is ubiquitous in nature and prominently affects population dynamics [37]. This may be especially true for plankton populations due to the unpredictability of weather, temperature and many other physical factors embedded in aquatic ecosystems (see [20,22,23]). To better understand the interactions between nutrients and food webs, in this paper, we proposed and studied a stochastic food chain model with instantaneous nutrient recycling. Under assumption that the functional response functions are linear, we observed that there are two thresholds between persistence in mean and extinction of plankton. The thresholds not only provide sufficient criteria for the existence of a unique ergodic stationary distribution, but also the explicit estimations of the mean abundance of plankton.

Comparing with the previous study, which shows that the deterministic model (2) has two thresholds ${\mathcal{R}}_0$ and ${\mathcal{R}}_1$, completely determining the dynamic behaviors of the model, we also found two thresholds ${\mathcal{R}}_0^S$ and ${\mathcal{R}}_1^S$ for the stochastic counterpart (4). They play the similar roles to that of ${\mathcal{R}}_0$ and ${\mathcal{R}}_1$, in determining the persistence and extinction of species. More precisely,

(a)

Neither the phytoplankton or the zooplankton can survive eventually if ${\mathcal{R}}_0^S<1$;

(b)

The phytoplankton is persistent in mean while the zooplankton goes extinct if ${\mathcal{R}}_0^S>1$ and ${\mathcal{R}}_1^S<1$;

(c)

The entire system is persistent in mean if ${\mathcal{R}}_1^S>1$.

These results are illustrated in Figure 1. In addition, we have also established sufficient criteria for the existence of plankton-coexistence stationary distribution (see Figure 5a), zooplankton-free stationary distribution (see Figure 5b) and plankton-free stationary distribution (see Figure 5c). Biologically, ${\mathcal{R}}_0^S$ and ${\mathcal{R}}_1^S$ may be treated as the basic reproduction numbers for the phytoplankton and zooplankton in stochastic sense, respectively. In what follows, we give more relevant biological explanations of them. From the definition,

$${\mathcal{R}}_0^S=\frac{a{N}^0}{{\mu }_1+D_1}-\frac{{\sigma }_2^2}{2({\mu }_1+D_1)},$$

we see that the second term is due to the effect of the environmental noise. Therefore, ${\mathcal{R}}_0^S$ can be interpreted as the ratio of the maximal nutrient uptake rate of phytoplankton to its loss rate under the influence of noise, which measures the ability of the nutrient environment to support a phytoplankton population. That

$${\mathcal{R}}_1^S=\frac{cD(a{N}^0-{\mu }_1-D_1-\frac{1}{2}{\sigma }_2^2)}{a({\mu }_2+D_2)({\mu }_1+D_1-{\mu }_3)}-\frac{{\sigma }_3^2}{2({\mu }_2+D_2)}=\frac{c{\tilde{P}}_1}{{\mu }_2+D_2}-\frac{{\sigma }_3^2}{2({\mu }_2+D_2)}$$

may be viewed as the ratio of the maximal ingestion rate of zooplankton to its loss rate under the influence of noise when the persistent level of phytoplankton biomass is stabilized at the ${\tilde{P}}_1$ level.

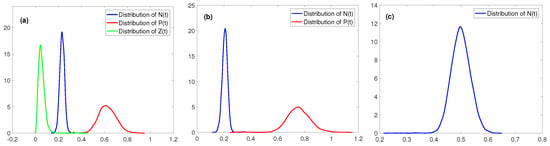
Figure 5. The distributions of $N\left(t\right)$, $P\left(t\right)$ and $Z\left(t\right)$, where all parameters in (a–c) are the same with these in Figure 1b–d, respectively.

In short, we can draw a conclusion that noise only affects the level of nutrient but does not change its asymptotic behavior. However, for plankton, environmental noise not only can affect its biomass levels, but also their destiny of survival. This may give some insightful understanding on how environmental noise affects the dynamics of nutrient–plankton. More importantly, an interesting phenomenon that we have observed is the mean abundance of phytoplankton under small stochastic perturbations exceeds the coexisting steady-state value, but the mean abundance of zooplankton is just the opposite, see Figure 2. In fact, these results are also obtained by (10). This is an important biological finding that implies that moderate noise may cause the bloom of phytoplankton, which partly explains the formation of algal blooms. Moreover, numerical observations show that uptake functions and zooplankton nutrient conversion rate play a key role in the periodic oscillatory succession of bloom and greatly affect the interactions between nutrients and plankton; therefore, the obtained results provide a possible predictive management theoretically.

This paper is concerned with the threshold dynamics and stationary distribution of a stochastic nutrient–plankton food chain model with instantaneous nutrient recycling. The obtained results enrich the research of dynamics in nutrient–plankton model, which can help us better understand the interaction between them in a stochastic sense. In addition, some interesting questions deserve further investigation, such as whether there are still two basic reproduction numbers for the stochastic nutrient–plankton food chain model with general nutrient uptake functions? We leave these for future investigations.