Another Case of Degenerated Discrete Chenciner Dynamic System and Economics

Abstract

The non-degenerate Chenciner bifurcation of a discrete dynamical system is studied using a transformation of parameters which must be regular at the origin of the parameters (the condition CH.1 of the well-known treatise of Kuznetsov). The article studies a complementary case, where the transformation is no longer regular at the origin, representing a degeneration. Four different bifurcation diagrams appear in that degenerated case, compared to only two in the non-degenerated one. Degeneracy may cause volatility in economics systems modeled by discrete Chenciner dynamical systems.

1. Introduction

Continuous and discrete-time dynamical systems can be used for modeling many applications in the surrounding world [1,2,3]. Discrete dynamical systems may appear in “practical applications when a phenomenon cannot be observed continuously in time” [4], but in certain moments of time [5]. Additionally, they can be obtained from dynamic systems with continuous time by discretizing time, that is, if we only take certain values for time [6] or as return maps that are return applications defined by the intersections of the system flows with certain “surfaces transversal to the flows” [4].

From a computational point of view, the use of dynamical systems with discrete time is more efficient in modeling because it can capture complex behaviors that cannot be easily captured otherwise [7,8,9]. Among the most “important topics in the qualitative theory” [10] of continuous and discrete dynamic systems is the analysis of bifurcations (see [11]).

One of the topics of interest in discrete dynamical systems is represented by the Chenciner bifurcation. Using the notations of the fundamental book of Kuznetsov, [12], page 405, a discrete Chenciner bifurcation happens when $r\left(0\right)=1$, $Re\left(b_1\left(0\right)\right)=0$ and $L_2\left(0\right)\ne 0.$

A parametric transformation $({\alpha }_1,{\alpha }_2)\to ({\beta }_1,{\beta }_2)$ is needed in the regular case where the functions

$${\beta }_1\left(\alpha \right)=\sum _{i+j=1}^p{a}_{ij}{\alpha }_1^i{\alpha }_2^j+O\left(\right|{\alpha }^{p+1}\left|\right)$$

$${\beta }_2\left(\alpha \right)=\sum _{i+j=1}^q{b}_{ij}{\alpha }_1^i{\alpha }_2^j+O\left(\right|{\alpha }^{q+1}\left|\right),p,q\ge 1,$$

$$a_{10}=\frac{\partial {\beta }_1}{\partial {\alpha }_1}{|}_{\alpha =0};a_{01}=\frac{\partial {\beta }_1}{\partial {\alpha }_2}{|}_{\alpha =0};b_{10}=\frac{\partial {\beta }_2}{\partial {\alpha }_1}{{|}_{\alpha =0};b_{01}=\frac{\partial {\beta }_2}{\partial {\alpha }_2}|}_{\alpha =0}$$

(1)

and so on, see [12], page 405. That transformation must be regular at the origin in order to have a non-degenerated Chenciner bifurcation.

The non-degenerate Chenciner bifurcation was firstly studied in the papers [6,13,14]. More recently this bifurcation appears in many papers from different areas of research, in “biology, physics, economy, informatics” [15] as well as multidisciplinary and applied sciences [12,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. For example, in [31], the Chenciner bifurcation was observed when a potential mechanism from bifurcation analyses was used for studying the occurrence of modulated oscillations in synchronous machine nonlinear dynamics, being reported for the first time in power engineering for this bifurcation. Other authors have analyzed the normal forms to provide the parameter conditions for the Chenciner bifurcation [32] or the conditions to obtain a Chenciner bifurcation in macroeconomics [33].

Rational expectations are the foundation of modern finance. However, in principle, the efficient market hypothesis cannot help accurately predict future prices. There is ample empirical evidence that developments in financial time series, in the form of “stylized facts”, cannot be explained by fundamentals alone, and markets appear to have specific internal dynamics. Among the so-called “stylized facts” is volatility clustering. It appears that if changes in asset prices are unpredictable, the magnitude of those changes is predictable; Thus, “large changes tend to be followed by large changes” [19] (either increasing or decreasing), while“ small changes tend to be followed by small changes” [19]. That is why it is found that asset price fluctuations present “episodes of high volatility” [19] (with large price changes), which alternate irregularly with “episodes of low volatility” [19] (with small price changes).

In economics, in a series of empirical studies, the used model is useful only for a statistical description of the data [34]. However, these models cannot explain the clustering of volatility that is recorded in many financial time series. Typically, such models assume that volatility clustering is generated by factors external to the analyzed system.

Some structural explanations of volatility clustering are provided by “multi-agent systems” [19], where financial markets have been approached as “complex evolutionary systems” [19]. In such systems, two large categories of traders have been identified: fundamentalists (who state that prices are oriented toward the value of their fundamental rational expectations, generated by future dividends) and technical analysts (who, starting from the past prices, and based on some established models, try to project them in the future). Such systems show an irregular transition between low volatility situations (during which prices tend toward the fundamental price and then the market is dominated by fundamentalists) and high volatility situations (during which “prices move away from the fundamental price” [19] and then the market is dominated by technical analysts) [19]. In these conditions, the grouping of volatility can have endogenous explanations, that is, it could be caused and even amplified by the process of the heterogeneity of trading, but also by the interaction between agents, as well as by the phenomenon of adaptive learning.

The evolutionary model proposed by A. Gaunersdorfer, C.H. Hommes and F.O.O. Wagener presents the “coexistence of a stable state and a stable limit cycle” [19]. When such a system is subject to dynamic noise, there is an irregular switching between fundamental equilibrium fluctuations close to rational expectations (in which “the market is dominated by fundamentalists) and large-amplitude price fluctuations” [19] (in which the market is dominated by technical analysts). “The coexistence of a stable equilibrium state and a stable limit cycle ” [19] is explained mathematically by means of the discrete Chenciner bifurcation. This is not caused by a particular specification of the model, but “is a generic feature for nonlinear systems with two or more parameters” [19].

The discrete degenerated Chenciner bifurcation is produced when the above mentioned regularity of the $\beta$ transformation is not fulfilled. That results in a much more difficult scenario. A first type of such a degenerated Chenciner discrete dynamical was solved in [4]. Two other types of possible degeneration were studied in [10,15]. Each of those cases has a quite different method of solving. In the present article, we study another case of a possible degeneration. So, why bother with such particular cases, each having a specific kind of approach? An Edmund Hillary type of answer would be, “because they exist”, and also one may see the complexity of nature’s singularities reflected by mathematics.

In [4], the bifurcation diagrams were discovered in a general case, where the functions ${\beta }_1\left(\alpha \right)$ and ${\beta }_2\left(\alpha \right)$ both have linear terms different from zero that satisfy the degeneracy condition $a_{10}{b}_{01}-a_{01}{b}_{10}=0,$ or $a_{10}=a_{01}=0,$ see (1). In that case, 32 bifurcation diagrams were obtained. A parallel approach to that of [4] is studied in [35] by using another regular transformation of parameters, where the product $a_{10}{a}_{01}{b}_{10}{b}_{01}\ne 0.$ In the article [15], the functions ${\beta }_1\left(\alpha \right)$ and ${\beta }_2\left(\alpha \right)$ have $a_{10}=0;a_{01}=0;b_{10}=0;b_{01}=0$, obtaining four bifurcation diagrams. Ref. [10] studied the case when $a_{20}=a_{11}=a_{02}=0$ and $b_{10}\ne 0,b_{01}\ne 0$ or $a_{20}=a_{11}=a_{02}=0$ and $b_{10}=0,b_{01}=0$, obtaining 18 different bifurcation diagrams. The stability of the fixed point O for $\left|\alpha \right|$ that is sufficiently small and, respectively, “the existence of closed invariant curves in the” [4] truncated normal form in all the cases was treated before [10,15,35].

A possible application of the degenerated Chenciner bifurcation was presented in [15], but one could analyze in all previous mentioned Chenciner papers what happens when degeneration occurs. For example, the volatility of the economics systems based on discrete Chenciner bifurcation may be interpreted as a variant of input data implying the degeneration of the bifurcation. One possible cause of that may be the presence of a noise, rendering a sequence of different degenerated and non-degenerated variants of the initial system in case the coefficients $a_{ij}$ have small values.

The purpose of this article is to investigate the behavior of the dynamical system when ${\beta }_1\left(\alpha \right)$ or ${\beta }_2\left(\alpha \right)$ has a zero linear part $a_{10}=a_{01}=0$ or $b_{10}=b_{01}=0$, see (1), and the second function has at least a term of order one different from zero. This aspect has not been analyzed before. As it is not possible to choose new coordinates ${\beta }_1,{\beta }_2$, the idea is to use only the initial parameters $({\alpha }_1,{\alpha }_2)$. This leads to the modifications of the structure of the sets of points $B_{1,2}$ and C, thus obtaining concurrent lines at the origin, similar to the situation analyzed in other articles [10,15], but different from the cases studied in [4,35]. We want to specify how many bifurcation diagrams are obtained, many or few. The first case studied, when ${\Delta }_1>0$, is the most important and complex of the two and requires different methods of approach (the second is when ${\Delta }_1<0$).

The starting hypothesis in this study is that in the case of a degeneracy, a larger number of bifurcation diagrams is needed than in a non-degeneracy setting. The objective of this article is to verify the mentioned hypothesis in a degeneracy case that does not involve resonance.

The work is structured in six sections; after the Introduction (Section 1 and Appendix A and Appendix B), Section 2 presents the analysis of degenerate Chenciner bifurcation that “means the existence and stability of equilibrium points and invariant closed curves” [4] for this form of degeneracy, known as non-transversality, i.e., the “transformation of parameters is not regular at $(0,0)$” [35]. In Section 3, it is described the existence of bifurcations curves and their dynamics in the parametric plane $({\alpha }_1,{\alpha }_2)$ in Theorem 1. Section 4 shows the bifurcation diagrams for this type of degeneracy of Chenciner bifurcation when the smooth function ${\beta }_1\left(\alpha \right)$ is of order two. These bifurcation diagrams are different from the bifurcation diagrams from the non-degenerate framework. In Section 5, several numerical simulations using Matlab check the theoretical results from the previous section. Section 6 indicates the relevant discussions and conclusions of the paper.

2. Materials and Methods

Since Chenciner bifurcation happens for the discrete dynamical system, we consider

$$x_{n+1}=f\left(x_n,\alpha \right)$$

(2)

where $x_n\in {\mathbb{R}}^2,$$n\in \mathbb{N},$$\alpha =\left({\alpha }_1,{\alpha }_2\right)\in {\mathbb{R}}^2$ and f is a smooth function of class $C^r$ with $r\ge 2.$ In order to avoid indices, the Equation (2) is sometimes written in the form

$$x⟼f\left(x,\alpha \right)$$

(3)

or $\tilde{x}=f\left(x,\alpha \right).$

A bifurcation as in (A4) which satisfies $r\left(0\right)=1$ and $Re\left(b_1\left(0\right)\right)=0$ but $L_2\left(0\right)\ne 0$ is known as “the Chenciner bifurcation (or generalized Neimark–Sacker bifurcation)” [4]. It follows from ${\beta }_1\left(0\right)=0$ that

$$L_2\left(0\right)=\frac{1}{2}\left(I{m}^2\left(b_1\left(0\right)\right)+2Re\left(b_2\left(0\right)\right)\right).$$

When the transformation of parameters

$$\left({\alpha }_1,{\alpha }_2\right)⟼\left({\beta }_1\left(\alpha \right),{\beta }_2\left(\alpha \right)\right)$$

(4)

is regular at $\left(0,0\right),$ then the dynamics system of (A4) can be put in a simpler form. “This is the non-degenerated Chenciner bifurcation” [15] as it is studied in [12]. However, “the degenerate case when the change of parameters is not regular at $(0,0)$ is not any” [15] longer considered there. The purpose of the present article is to study an aspect of the degenerate Chenciner bifurcation. Since it is not possible to choose new coordinates ${\beta }_1,{\beta }_2,$ the idea is to work only using the initial parameters $({\alpha }_1,{\alpha }_2)$.

3. Bifurcation Curves

Analysis of degenerated Chenciner bifurcation is performed in Appendix B and [4]. Since the smooth functions ${\beta }_{1,2}\left(\alpha \right)$ can be written as ${\beta }_1\left(\alpha \right)=a_{10}{\alpha }_1+a_{01}{\alpha }_2+{\sum }_{i+j\ge 2}{a}_{ij}{\alpha }_1^i{\alpha }_2^j$ and ${\beta }_2\left(\alpha \right)=b_{10}{\alpha }_1+b_{01}{\alpha }_2+{\sum }_{i+j\ge 2}{b}_{ij}{\alpha }_1^i{\alpha }_2^j,$ the transformation (4) is not regular at $\left(0,0\right)$ and, thus, “the Chenciner bifurcation is degenerate” [4], if and only if ${\left.\frac{\partial {\beta }_1}{\partial {\alpha }_1}\frac{\partial {\beta }_2}{\partial {\alpha }_2}{|}_{\alpha =0}-\frac{\partial {\beta }_1}{\partial {\alpha }_2}\frac{\partial {\beta }_2}{\partial {\alpha }_1}\right|}_{\alpha =0}=0,$ that is,

$$a_{10}{b}_{01}-a_{01}{b}_{10}=0.$$

(5)

Remark 1.

In [4], we studied “the case when (5) is satisfied with non-zero terms” [15], that is $a_{10}{b}_{01}{a}_{01}{b}_{10}\ne 0.$ In this work, we assume “that the linear part of ${\beta }_1\left(\alpha \right)$ nullifies, while ${\beta }_2\left(\alpha \right)$ has at least one linear term” [15]. Thus, “the degeneracy condition (5) remains valid while the functions ${\beta }_{1,2}\left(\alpha \right)$ become

$${\beta }_1\left(\alpha \right)=a{\alpha }_2^2+b{\alpha }_1{\alpha }_2+c{\alpha }_1^2+\sum _{i+j=3}^{p_1}{a}_{ij}{\alpha }_1^i{\alpha }_2^j+O\left({\left|\alpha \right|}^{p_1+1}\right)$$

(6)

and

$${\beta }_2\left(\alpha \right)=p{\alpha }_1+q{\alpha }_2+\sum _{i+j=2}^{q_1}{b}_{ij}{\alpha }_1^i{\alpha }_2^j+O\left({\left|\alpha \right|}^{q_1+1}\right)$$

(7)

for some $p_1\ge 3$ and $q_1\ge 2,$ where $abcq\ne 0$” [15]. We denote by $a=a_{02},$$b=a_{11}$ and $c=a_{20},$ respectively, $p=b_{10}$ and $q=b_{01}.$

Denote also by $B_{1,2}$ and C the following sets of points in ${\mathbb{R}}^2$

$$B_{1,2}=\left\{\left({\alpha }_1,{\alpha }_2\right)\in {\mathbb{R}}^2,{\beta }_{1,2}\left(\alpha \right)=0,\left|\alpha \right|<\epsilon \right\}$$

(8)

and

$$C=\left\{\left({\alpha }_1,{\alpha }_2\right)\in {\mathbb{R}}^2,\Delta \left(\alpha \right)=0,\left|\alpha \right|<\epsilon \right\}$$

(9)

for some $\epsilon >0$ that is sufficiently small. The expression $\Delta \left(\alpha \right)={\beta }_2^2\left(\alpha \right)-4{\beta }_1\left(\alpha \right)L_2\left(\alpha \right)$ becomes

$$\Delta \left(\alpha \right)=h{\alpha }_2^2\left(1+O\left(\left|\alpha \right|\right)\right)+k{\alpha }_1{\alpha }_2\left(1+O\left(\left|\alpha \right|\right)\right)+l{\alpha }_1^2\left(1+O\left(\left|\alpha \right|\right)\right)$$

(10)

where $h=q^2-4a{L}_0,$$k=2pq-4b{L}_0$ and $l=p^2-4c{L}_0.$ Assume $hkl\ne 0.$ When $p=0$ and $h\ne 0,$ this condition is satisfied in general since $bc{L}_0\ne 0.$ Notice that

$${\Delta }_2=k^2-4hl=16L_0^2\left(b^2-4ac\right)+16L_0\left(a{p}^2-bpq+c{q}^2\right).$$

(11)

In the following, we prove a theorem that was only stated in [15]. The structure of the set of points $B_{1,2}$ and C represents the main result in order to obtain the bifurcation diagrams; see also Remark 2. Recalling that $a=a_{02},b=a_{11},c=a_{20},p=b_{10},q=b_{01},h=q^2-4a{L}_0,k=2pq-4b{L}_0$, $l=p^2-4c{L}_0$ and ${\Delta }_1=b^2-4ac,{\Delta }_2=k^2-4hl$, the following theorem is stated:

Theorem 1.

1. 

The set $B_2$ is a smooth curve of the form

$${\alpha }_2=d_1{\alpha }_1+d_2{\alpha }_1^2+O\left({\alpha }_1^3\right),$$

(12)

$d_1=-\frac{p}{q},$$d_2=-\frac{1}{q}\left(b_{02}+d_1^2{b}_{20}+d_1{b}_{11}\right),$ tangent to the line $p{\alpha }_1+q{\alpha }_2=0.$

2. 

If ${\Delta }_1=b^2-4ac>0,$ the set $B_1$ is a reunion of two smooth curves of the form

$${\alpha }_2=e_{1,2}{\alpha }_1\left(1+O\left({\alpha }_1\right)\right),$$

(13)

where $e_1=\frac{-b-\sqrt{{\Delta }_1}}{2a}$and $e_2=\frac{-b+\sqrt{{\Delta }_1}}{2a}.$ If ${\Delta }_1<0,$ then $sign\left({\beta }_1\left(\alpha \right)\right)=sign\left(a\right)$ for $\left|\alpha \right|<\epsilon .$

3. 

If ${\Delta }_2=k^2-4hl>0,$ the set C is a reunion of two smooth curves of the form

$${\alpha }_2=m_{1,2}{\alpha }_1\left(1+O\left({\alpha }_1\right)\right),$$

(14)

where $m_1=\frac{-k-\sqrt{{\Delta }_2}}{2h}$and $m_2=\frac{-k+\sqrt{{\Delta }_2}}{2h}.$ If ${\Delta }_2<0,$ then $sign\left({\beta }_1\left(\alpha \right)\right)=sign\left(h\right)$ for $\left|\alpha \right|<\epsilon .$

Proof. 

1. Consider the function ${\beta }_2:V_0\subset {\mathbb{R}}^2\to \mathbb{R}$ given by (7), where $V_0=\left\{\alpha \in {\mathbb{R}}^2,\left|\alpha \right|<\epsilon \right\}$ for $\epsilon >0$ sufficiently small. Then ${\beta }_2\left(0,0\right)=0$ and $\frac{\partial {\beta }_2}{\partial {\alpha }_2}\left(0,0\right)=q\ne 0.$ Thus, from the implicit function theorem (IFT) applied to ${\beta }_2,$ there exists a unique curve ${\alpha }_2={\alpha }_2\left({\alpha }_1\right),$ which satisfies ${\beta }_2\left({\alpha }_1,{\alpha }_2\left({\alpha }_1\right)\right)=0$ for $\left|{\alpha }_1\right|$ that is small enough and can be written in the form (12). Notice that $d_1$ can be $0.$

2. One further writes ${\beta }_1\left(\alpha \right)$ in the form

${\beta }_1\left(\alpha \right)=a{\alpha }_2^2\left(1+O\left(\left|\alpha \right|\right)\right)+b{\alpha }_1{\alpha }_2\left(1+O\left(\left|\alpha \right|\right)\right)+c{\alpha }_1^2\left(1+O\left(\left|\alpha \right|\right)\right).$ Then ${\beta }_1\left(\alpha \right)=0$ becomes

$$a{\alpha }_2^2+b{\alpha }_1{\alpha }_2\left(1+O\left(\left|\alpha \right|\right)\right)+c{\alpha }_1^2\left(1+O\left(\left|\alpha \right|\right)\right)=0.$$

(15)

Solving for ${\alpha }_2$ in (15), one obtains ${\alpha }_2=e_{1,2}{\alpha }_1\left(1+O\left(\left|\alpha \right|\right)\right),$ where ${\Delta }_1=b^2-4ac$ and $e_{1,2}=\frac{-b\pm \sqrt{{\Delta }_1}}{2a},$ when ${\Delta }_1>0.$ Denote further by

$$F\left({\alpha }_1,{\alpha }_2\right)={\alpha }_2-e_{1,2}{\alpha }_1\left(1+O\left(\left|\alpha \right|\right)\right),$$

where $F:V_0\subset {\mathbb{R}}^2\to \mathbb{R}.$ Since $F\left(0,0\right)=0$ and $\frac{\partial F}{\partial {\alpha }_2}\left(0,0\right)=1\ne 0,$ the IFT yields the conclusion. When ${\Delta }_1<0,$ it does not exist $\alpha \ne 0$ with $\left|\alpha \right|<\epsilon$ such that ${\beta }_1\left(\alpha \right)=0.$ Thus, ${\beta }_1\left(\alpha \right)$ keeps a constant sign on $V_0,$ which is given, for example, by ${\beta }_1\left({\alpha }_2,0\right)=a{\alpha }_2^2\left(1+O\left(\left|\alpha \right|\right)\right).$ This yields the conclusion. For 3, one proceeds similarly to 2. □

Theorem 1 was only stated in [15], but the proof is also given here because it is used in the present article. In this theorem, the structure of the sets of points $B_{1,2}$ and C is established, i.e., what kind of curves appear in the three situations from points 1,2 and 3; Theorem 1 provides the necessary theoretical basis for drawing bifurcation diagrams.

4. Bifurcation Diagrams

Assume ${\beta }_{1,2}\left(\alpha \right)$ and $\Delta \left(\alpha \right)$ have nonzero coefficients in their lowest terms, that is, $abcq\ne 0$ and $hkl\ne 0.$ Thus, “the three bifurcation curves are well-defined when $\left|\alpha \right|$ is sufficiently small ” [4]. $B_2$ is a unique curve, while each of $B_1$ and “C is a reunion of two curves” [15].

Remark 2.

Figure A1 presents generic phase portraits “corresponding to different regions of the bifurcation diagrams, including the phase portraits on the bifurcation curves defined by $\Delta \left(\alpha \right)=0,$” [4] respectively, ${\beta }_1\left(\alpha \right)=0.$ We summarize in Table A1 the correspondence between $\Delta ,$${\beta }_{1,2},$$L_0$ and “the generic phase portraits, respectively, different regions from bifurcation diagrams. When ${\beta }_{1,2}\left(\alpha \right)=0$, then $\alpha =0$” [4].

The sign of a 2-nd degree polynomial of two real variables is discussed below.

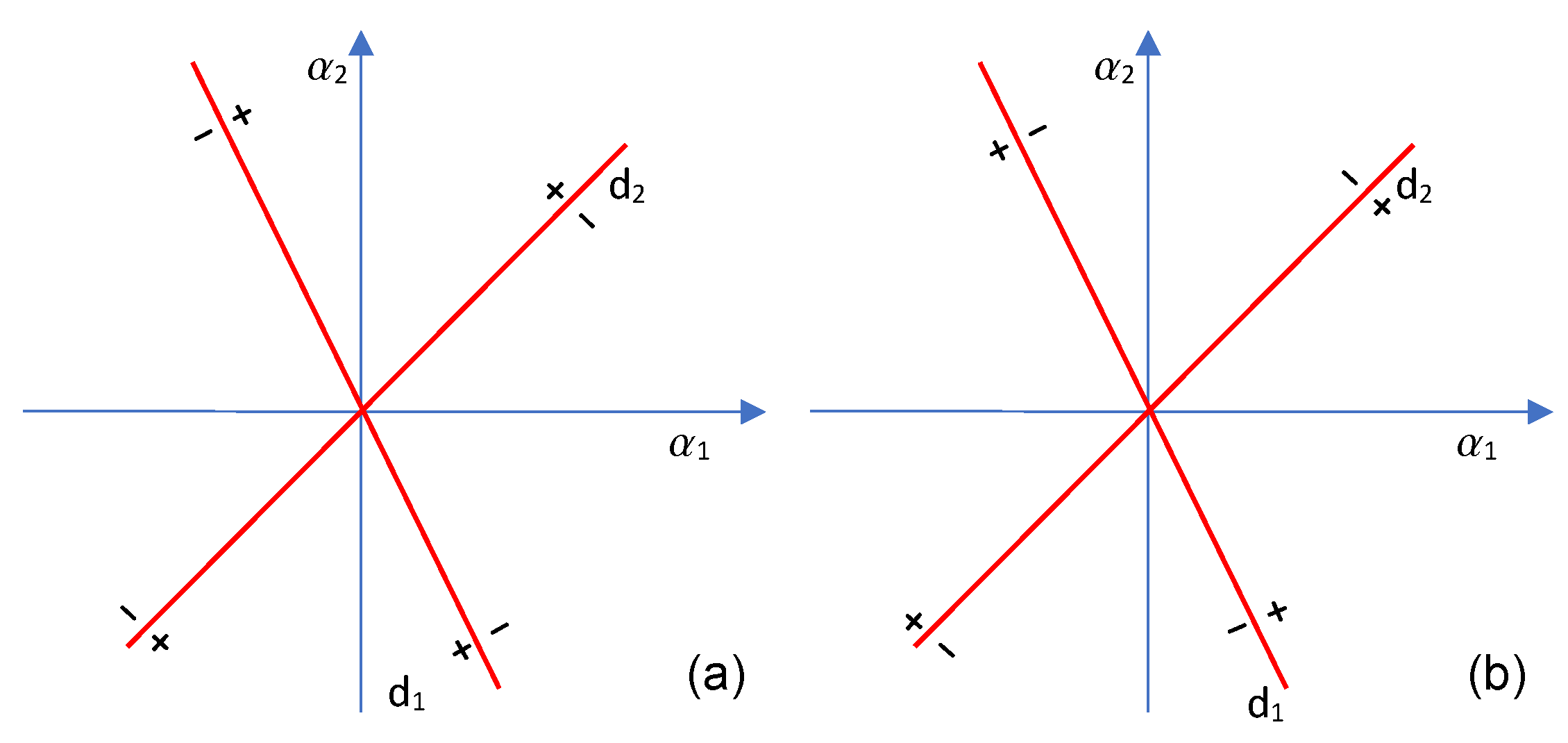
Let us consider a polynomial

$$\Delta ({\alpha }_1,{\alpha }_2)=a{\alpha }_2^2+b{\alpha }_1{\alpha }_2+c{\alpha }_1^2,a,b,c\in {\mathbb{R}}_{\ast }.$$

Considering its associated one-variable-polynomial $\delta \left(m\right)=a{m}^2+bm+c,$ the signs of $\Delta ({\alpha }_1,{\alpha }_2)$ and $\delta \left(m\right)$ are the same, for all the pairs $({\alpha }_1,{\alpha }_2)$, which are solutions of the equation, ${\alpha }_2=m{\alpha }_1.$

We use the convention that

$$m_1=\left\{\begin{array}{cc}\frac{-b-\sqrt{{\Delta }_1}}{2a},\hfill & \mathrm{if}a>0\hfill \\ \frac{-b+\sqrt{{\Delta }_1}}{2a},\hfill & \mathrm{if}a<0\hfill \end{array}\right.$$

and the corresponding formula for $m_2.$

The sign of $\Delta ({\alpha }_1,{\alpha }_2)$ is shown in Figure 1a for $a>0,$ and in Figure 1b for $a<0,$ where $\left(d_i\right):{\alpha }_2=m_i{\alpha }_1,$ for $i=1,2.$

Figure 1. The sign of $\Delta ({\alpha }_1,{\alpha }_2)$ when (a) $a>0;$ (b) $a<0$.

4.1. Bifurcation Diagrams When the First Discriminant Is Strictly Positive

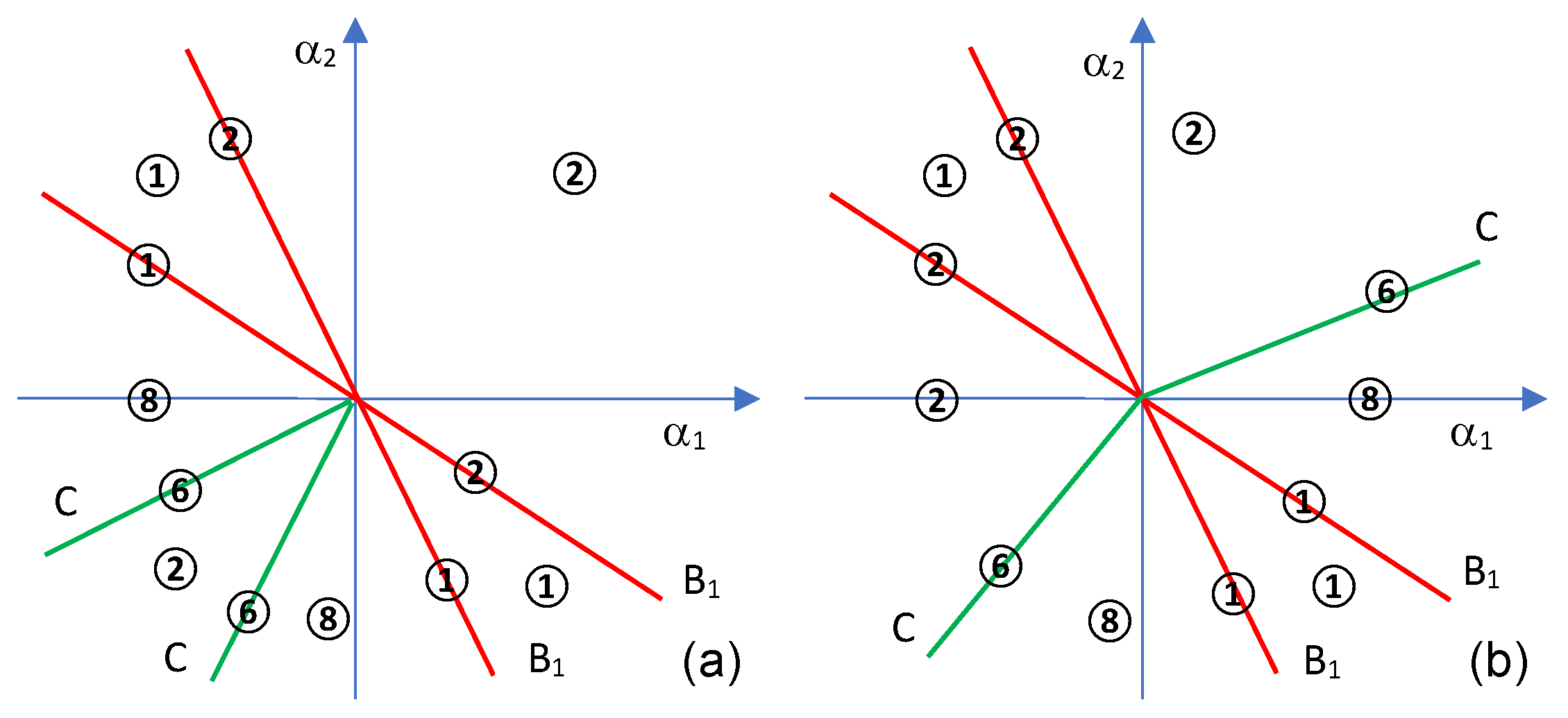
Bifurcation diagrams for ${\Delta }_1>0$ are given in this subsection.

Firstly, we suppose that ${\Delta }_2>0,$ and we consider the polynomials of ${\mathbb{R}}_{\ast }\left[T\right]:$ ${\beta }_1\left(T\right)=a{T}^2+bT+c,\delta \left(T\right)=h{T}^2+kT+l,$ having the distinct real roots $e_1,e_2$, respectively, $m_1,m_2.$

There will be considered the following cases of root ordering:

I

 :$e_1<e_2<m_1<m_2,$

II

   :$e_1<m_1<e_2<m_2,$

III

  :$e_1<m_1<m_2<e_2,$

IV

  :$m_1<e_1<e_2<m_2,$

V

 :$m_1<e_1<m_2<e_2.$

There is only one more case, $m_1<m_2<e_1<e_2,$ which will not be taken into account, since it is a rotated case of I.

That ordering will be applied to the associated polynomials of ${\beta }_1({\alpha }_1,{\alpha }_2),\Delta ({\alpha }_1,{\alpha }_2),$ that is ${\beta }_1\left(T\right),\delta \left(T\right)$; see Section 4.

Theorem 2.

The polynomials ${\beta }_1\left(T\right)$ and $\delta \left(T\right)$ have the following properties:

1. 

$\delta \left(e_1\right)+\delta \left(e_2\right)>0$

2. 

${\beta }_1\left(m_1\right)·{\beta }_1\left(m_2\right)\ge 0$

Proof. 

1. $\delta \left(e_1\right)+\delta \left(e_2\right)=h{e}_1^2+k{e}_1+l+h{e}_2^2+k{e}_2+l$ by Viete relations

$\delta \left(e_1\right)+\delta \left(e_2\right)=\frac{1}{a^2}(b^{2}h-2ach-abk+2a^{2}l),$ and by using the relations (11), $\delta \left(e_1\right)+\delta \left(e_2\right)=\frac{1}{a^2{q}^2}[2a^2{\left(\frac{p}{q}\right)}^2-2ab\frac{p}{q}+b^2-2ac],$ which is positive since the polynomial $P\left(T\right)=2a^2{T}^2-2abT+b^2-2ac>0,(\forall )T\in \mathbb{R}.$

Indeed, the reduced discriminant of P is ${\Delta }^{{}^{\prime }}=-a^2{\Delta }_1<0.$

2. ${\beta }_1\left(m_1\right)·{\beta }_1\left(m_2\right)=a^2{m}_1^2{m}_2^2+ab{m}_1{m}_2(m_1+m_2)+ac(m_1^2+m_2^2)+b^2{m}_1{m}_2+bc(m_1+m_2)+c^2$ by using Viete relations ${\beta }_1\left(m_1\right)·{\beta }_1\left(m_2\right)=\frac{1}{h^2}(a^2{l}^2-abkl+ac{k}^2-2achl+b^{2}hl-bchk+c^2{h}^2).$

Using (11), one concludes that

${\beta }_1\left(m_1\right){\beta }_1\left(m_2\right)=\frac{1}{h^2{q}^4}\left[a^2{\left(\frac{p}{q}\right)}^4-2ab{\left(\frac{p}{q}\right)}^3+(2ac+b^2){\left(\frac{p}{q}\right)}^2-2bc\frac{p}{q}+c^2\right]=$

$=\frac{a^2}{q^4{h}^2}{\left(\frac{p}{q}-\frac{b+\sqrt{{\Delta }_1}}{2a}\right)}^2·{\left(\frac{p}{q}-\frac{b-\sqrt{{\Delta }_1}}{2a}\right)}^2.$□

Corollary 1.

The cases II and V do not fulfill condition (2) of Theorem 2, and therefore they are eliminated.

Considering the possible sub-cases of I, III, and IV, depending on the signs of $a,h$, one remarks that the numbers of sub-cases is halved by condition (1) of Theorem 2.

The left sub-cases are graphically represented in Figure 2, Figure 3 and Figure 4.

Figure 2. Graphical representation of ${\Delta }_{1,2}.$ Case I ($e_1<e_2<m_1<m_2$) when (a) $a>0,h>0$; (b) $a<0,h>0$.

Figure 3. Graphical representation of ${\Delta }_{1,2}.$ Case III ( $e_1<m_1<m_2<e_2$): (a) $a>0,h>0$; (b) $a<0,h>0$.

Figure 4. Graphical representation of ${\Delta }_{1,2}.$ Case IV ( $m_1<e_1<e_2<m_2$): (a) $a<0,h<0$; (b) $a>0,h<0$.

Theoretically, for any of the previous sub-cases, one must consider two possibilities, depending on the sign of the $L_0$. However, the following theorem assigns a determined sign for any case.

Theorem 3.

The sign of $\beta \left(m_1\right)+\beta \left(m_2\right)$ equals that one of $L_0.$

Proof. 

We calculate $\beta \left(m_1\right)+\beta \left(m_2\right)=a(m_1^2+m_2^2)+b(m_1+m_2)+2c=$

$=\frac{1}{h^2}(a{k}^2-ahl-bhk+2c{h}^2).$

By using the relation (11): $\beta \left(m_1\right)+\beta \left(m_2\right)=\frac{1}{4h{L}_0}(2h^2{p}^2-2hl{q}^2-2hkpq+k^2{q}^2).$

Hence, the sign of $\beta \left(m_1\right)+\beta \left(m_2\right)$ is that of the expression in T:

$L_0(2h^2{T}^2-2hkT+k^2-2hl).$

The reduced discriminant of the last parenthesis is ${\Delta }^{{}^{\prime }}=-4h^2{\Delta }_2<0.$ Therefore,

$sign(\beta \left(m_1\right)+\beta \left(m_2\right))=sign\left(L_0\right).$□

Corollary 2.

By the previous theorem, one may specify the sign of $L_0$ in the following cases:

1. 

I a, III b, IV b have $L_0>0,$

2. 

I b, III a, IV a have $L_0<0.$

We may further reduce the sub-cases by the following theorems:

Theorem 4.

Denoting $M=a{p}^2-bpq+c{q}^2,$$N=h{p}^2-kpq+l{q}^2,$ it results that $N=-4L_{0}M.$

Proof. 

$N=h{p}^2-kpq+l{q}^2$ equals, by (11), $(q^2-4a{L}_0)p^2-(2pq-4b{L}_0)pq+(p^2-4c{L}_0)q^2=-4L_{0}M.$ □

Corollary 3.

In cases I a, III b, and IV b, M and N have different signs, and for the rest of the sub-cases, they have the same sign.

Theorem 5.

The sum $M+N$ has no definite sign.

Proof. 

$M+N=(a+h)p^2-(b+k)pq+(c+l)q^2,$ and by (11), $M+N=(1-4L_0)(a{p}^2-bpq+c{q}^2).$ $L_0$ is fixed, so $1-4L_0$ has a fixed sign. The second parenthesis has no fixed sign for all $p,q\in \mathbb{R},$ since ${\Delta }_1>0.$ □

Corollary 4.

If $M,N$ have the same sign, then $M+N$ has a definite sign for all $p,q\in \mathbb{R}.$ If $M,N$ do not have the same sign, then $M+N$ do not have a definite sign for all $p,q\in \mathbb{R}.$ Hence, by Theorem 5 and Corollary 3, we may eliminate the cases I b, III a, and IV a. The remaining cases are I a, III b, and IV b.

By Corollary 4, the cases for the graphical representation of the lines $B_1,B_2,C$ are as follows:

 I a1

 :$a>0,h>0,L_0>0,M<0,N>0.$

 I a2

 :$a>0,h>0,L_0>0,M>0,N<0.$

III b1

:$a<0,h>0,L_0>0,M<0,N>0.$

III b2

:$a<0,h>0,L_0>0,M>0,N<0.$

IV b1

:$a>0,h<0,L_0>0,M>0,N<0.$

IV b2

:$a>0,h<o,L_0>0,M<0,N>0.$

The bifurcation diagrams of cases I a1, III b1, and IV b2 are the same, represented in Figure 5a, and the bifurcation diagrams of cases I a2, III b2, and IV b1 are the same represented in Figure 5b.

Figure 5. Bifurcation diagrams when ${\Delta }_1>0$ and (a) when case I $\mathrm{a}1$, III $\mathrm{b}1$, or IV $\mathrm{b}2$ holds; (b) when case I $\mathrm{a}2$, III $\mathrm{b}2$ or IV $\mathrm{b}1$ holds. The numbers represent the corresponding phase portraits.

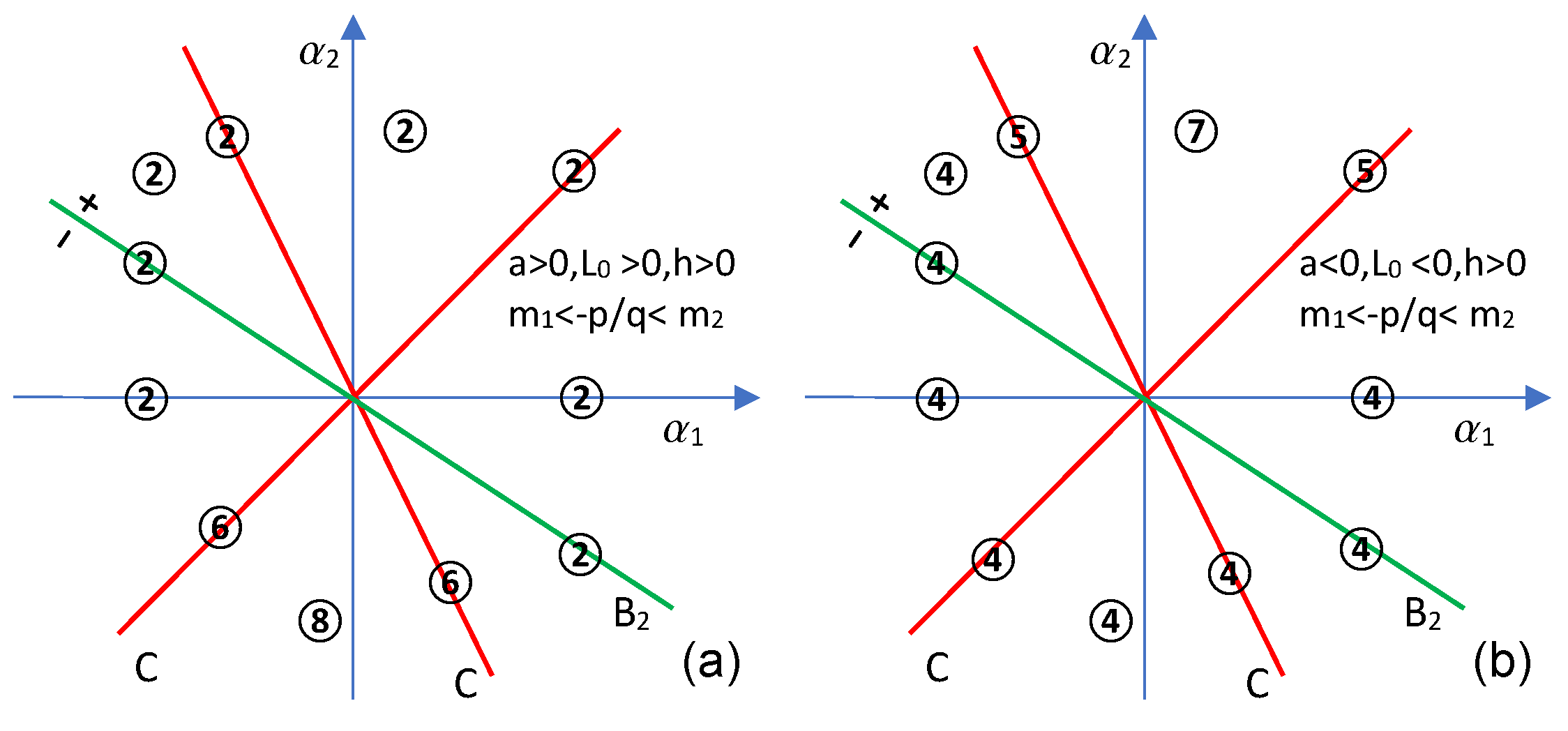
Remark 3.

The case ${\Delta }_1>0,{\Delta }_2<0$ is solved by Theorem 1, Section 3 since if ${\Delta }_2<0,$ then $sign{\beta }_1\left(\alpha \right)=sign\left(h\right)$ for all $\left|\alpha \right|<\epsilon .$ That is, the single straight line which remains is $B_1,$ and this case is trivial.

4.2. Bifurcation Diagrams When the First Discriminant Is Strictly Negative

Bifurcation diagrams for ${\Delta }_1<0$ are given in this subsection.

Remark 4.

If ${\Delta }_1<0$ and $a{L}_0<0$ then $\Delta \left(\alpha \right)>0.$ We will show that the single bifurcation curve is ${\beta }_2\left(\alpha \right)=0$ in this case.

We observe that $h=q^2-4a{L}_0$ and by $a{L}_0<0$ we have that $h>0.$ Taking into account Theorem 1, (3), we have that $sign\left({\beta }_1\left(\alpha \right)\right)=sign\left(a\right)$ and $sign(\Delta (\alpha \left)\right)=sign\left(h\right).$

There are more two trivial bifurcation diagrams which are not taken into account due to their triviality:

Remark 5.

(a) 

If ${\Delta }_1<0,a>0$ and $L_0<0$ then the bifurcation diagrams contain only region 3.

(b) 

If ${\Delta }_1<0,a<0$ and $L_0>0$, then the bifurcation diagrams contain only region 1.

Proof of Remark 4.

Using $a{L}_0<0$ results in $h=q^2-4a{L}_0>0.$ Taking into account that ${\Delta }_1<0$, we obtain ${\Delta }_{1}h<0.$ Because

$${\Delta }_3=b^2{q}^2-4a{L}_0{\Delta }_1-4ac{q}^2=q^2(b^2-4ac)-4a{L}_0{\Delta }_1={\Delta }_1(q^2-4a{L}_0)={\Delta }_{1}h$$

it follows that ${\Delta }_3<0.$ However,

$${\Delta }_2=k^2-4hl=16L_0^2(b^2-4ac)+16L_0(a{p}^2-bpq+c{q}^2)=$$

$$=16L_0[l_0(b^2-4ac)+a{p}^2-bpq+c{q}^2]=16L_0[L_0{\Delta }_1+a{p}^2-bpq+c{q}^2]=$$

$$=16L_0(a{p}^2-bpq+c{q}^2+L_0{\Delta }_1)$$

and by $a{L}_0<0,$ we have that ${\Delta }_2<0.$

Using Theorem 1, (3) and that ${\Delta }_2<0,h>0$, we have $sign(\Delta (\alpha \left)\right)=sign\left(h\right)>0.$ □

Case 4.2.1 When ${\Delta }_1<0$, $a{L}_0>0$ and $h>0.$

We see that ${\Delta }_3={\Delta }_{1}h<0$, and from $a{L}_0>0$, it follows that ${\Delta }_2>0$. Thus, the equation $\Delta \left(\alpha \right)=0$ has two real distinct roots, $m_{1,2}=\frac{-k\pm \sqrt{{\Delta }_2}}{2h}.$ We notice that $m_1<m_2.$

We consider the expression $P=(m_1+\frac{p}{q})(m_2+\frac{p}{q}).$

By calculus, we obtain $P=\frac{1}{h}\left(\frac{p^2}{q^2}h-k\frac{p}{q}+l\right).$ We replace further in the previous expression h by $q^2-4a{L}_0,$k by $2pq-4b{L}_0$, and l by $p^2-4c{L}_0$, and we have $P=-\frac{4L_0}{h{q}^2}\left(a{p}^2-pqb+c{q}^2\right).$

Now using that $a{L}_0>0,h>0$ and ${\Delta }_1<0$, we will find that $P<0.$ In this situation we have only the following two systems:

$$\left\{\begin{array}{cc}{m}_1+\frac{p}{q}>0\hfill & \\ m_2+\frac{p}{q}<0\hfill \end{array}\right.\mathrm{or}\left\{\begin{array}{cc}{m}_1+\frac{p}{q}<0\hfill & \\ m_2+\frac{p}{q}>0\hfill & .\hfill \end{array}\right.$$

By solving these systems, we find only the solution $m_1<-\frac{p}{q}<m_2$ because $m_1<m_2.$

In the previous case, two sub-cases arise:

Remark 6.

(a) 

If $a>0,L_0>0$ and $-\frac{p}{q}\in (m_1,m_2)$, then the following bifurcation diagram appears in Figure 6a:

Figure 6. Bifurcation diagrams corresponding to the case: (a) $a>0,L_0>0$, $-\frac{p}{q}\in (m_1,m_2)$; (b) $a<0,L_0<0$, $-\frac{p}{q}\in (m_1,m_2)$.

(b) 

If $a<0,L_0<0$ and $-\frac{p}{q}\in (m_1,m_2)$, then the following bifurcation diagram appears in Figure 6b:

Case 4.2.2 If ${\Delta }_1<0,a{L}_0>0,$ and $h<0$, then ${\Delta }_3>0$ and the equation ${\Delta }_2=0$ has two real and distinct roots:

$$p_{1,2}=\frac{bq\pm \sqrt{{\Delta }_3}}{2a}=\frac{bq\pm \sqrt{h{\Delta }_1}}{2a}.$$

Taking into account that $h<0,a{L}_0>0$ and ${\Delta }_1<0$. We obtain this time that $P>0.$ Now we compute also the sum, S, thus

$S=m_1+m_2+2\frac{p}{q}=-\frac{k}{h}+\frac{2p}{q}=\frac{4L_0(bq-2ap)}{qh}.$

From here, two cases arise.

When

$$\left\{\begin{array}{cc}P>0\hfill & \\ S>0\hfill \end{array}\right.or\left\{\begin{array}{cc}P>0\hfill & \\ S<0.\hfill \end{array}\right.$$

first sub-case, $\left\{\begin{array}{cc}P>0\hfill & \\ S>0\hfill \end{array}\right.,$ is equivalent to

$L_0\left(b-2a\frac{p}{q}\right)<0,$ and in this point we also have two possibilities:

(a) $\left\{\begin{array}{cc}{L}_0>0\hfill & \\ b-2a\frac{p}{q}<0\hfill \end{array}\right.$ or (b) $\left\{\begin{array}{cc}{L}_0<0\hfill & \\ b-2a\frac{p}{q}>0.\hfill \end{array}\right.$

In case (a), from $L_0>0$ we obtain $a>0$ and then $\frac{b}{2a}<\frac{p}{q}.$

In case (b), from $L_0<0$ we have $a<0$ and further $\frac{b}{2a}<\frac{p}{q}.$

This means that

$$\left\{\begin{array}{cc}{m}_1+\frac{p}{q}>0\hfill & \\ m_2+\frac{p}{q}>0\hfill \end{array}\right.$$

and using that $m_2<m_1$, we obtain $-\frac{p}{q}<m_2<m_1.$

Now, the second sub-case becomes $L_0\left(b-2a\frac{p}{q}\right)>0,$ and in this point, we also have two possibilities:

(a) $\left\{\begin{array}{cc}{L}_0>0\hfill & \\ b-2a\frac{p}{q}>0\hfill \end{array}\right.$ or (b) $\left\{\begin{array}{cc}{L}_0<0\hfill & \\ b-2a\frac{p}{q}<0.\hfill \end{array}\right.$

In case (a), from $L_0>0$ we obtain $a>0$ and then $\frac{b}{2a}>\frac{p}{q}.$

In case (b), from $L_0<0$ we have $a<0$ and further $\frac{b}{2a}>\frac{p}{q}.$

Therefore, now we have instead, $\left\{\begin{array}{cc}{m}_1+\frac{p}{q}<0\hfill & \\ m_2+\frac{p}{q}<0\hfill \end{array}\right.$ and using that $m_2<m_1$, we obtain $-\frac{p}{q}>m_1>m_2.$

Here, it does not appear to be the case that $m_2<-\frac{p}{q}<m_1.$

Case 4.2.2 I If $p\in (p_1,p_2)$, then ${\Delta }_2<0$ and from here, using that $h<0$, we obtain $\Delta \left(\alpha \right)<0.$

There are other two more trivial bifurcation diagrams which were not taken into account due to their triviality.

Remark 7.

(a) 

If $a>0,L_0>0$ and $p\in (p_1,p_2)$ then the bifurcation diagram contain only the region 2 in the whole plane of coordinates, ${\alpha }_{1}O{\alpha }_2.$

Using that $sign\left(\beta \right(\alpha \left)\right)=sign\left(a\right)=+$, $sign(\Delta (\alpha \left)\right)=-$, $L_0>0$ and taking into account that $\beta \left(\alpha \right)$ can have any sign, we see in Table A1 that for this configuration of signs will appear only the region 2.

(b) 

If $a<0,L_0<0,p\in (p_1,p_2)$ then the bifurcation diagram will contain only region 4 in the whole plane of coordinate ${\alpha }_{1}O{\alpha }_2.$

By the same reason, using that $sign\left({\beta }_1\left(\alpha \right)\right)=sign\left(a\right)=-,sign(\Delta \left(\alpha \right))=-,L_0<0$ and taking into account that $\beta \left(\alpha \right)$ can have any sign, we see in Table A1 that for this configuration of signs, it will appear only in region 4.

4.2.2 II If $p\in (-\infty ,p_1)\cup (p_2,\infty )$, then ${\Delta }_2>0.$ However, $h<0$ and therefore $\Delta \left(\alpha \right)$ has two distinct real roots $m_1$ and $m_2.$

$$sign(\Delta \left(\alpha \right))=\left\{\begin{array}{cc}+,\hfill & m\in (m_1,m_2);\hfill \\ -,\hfill & m\in (-\infty ,m_1)\cup (m_2,\infty ).\hfill \end{array}\right.$$

Because $-\frac{p}{q}$ is not between $m_2$ and $m_1$, we see that $sign(\Delta (\alpha \left)\right)=-.$

Remark 8.

In this case, the bifurcation diagrams are as in the case 4.2.1, Figure 6a,b, and only the conditions are different, not the dispersion of the regions.

5. Numerical Simulations

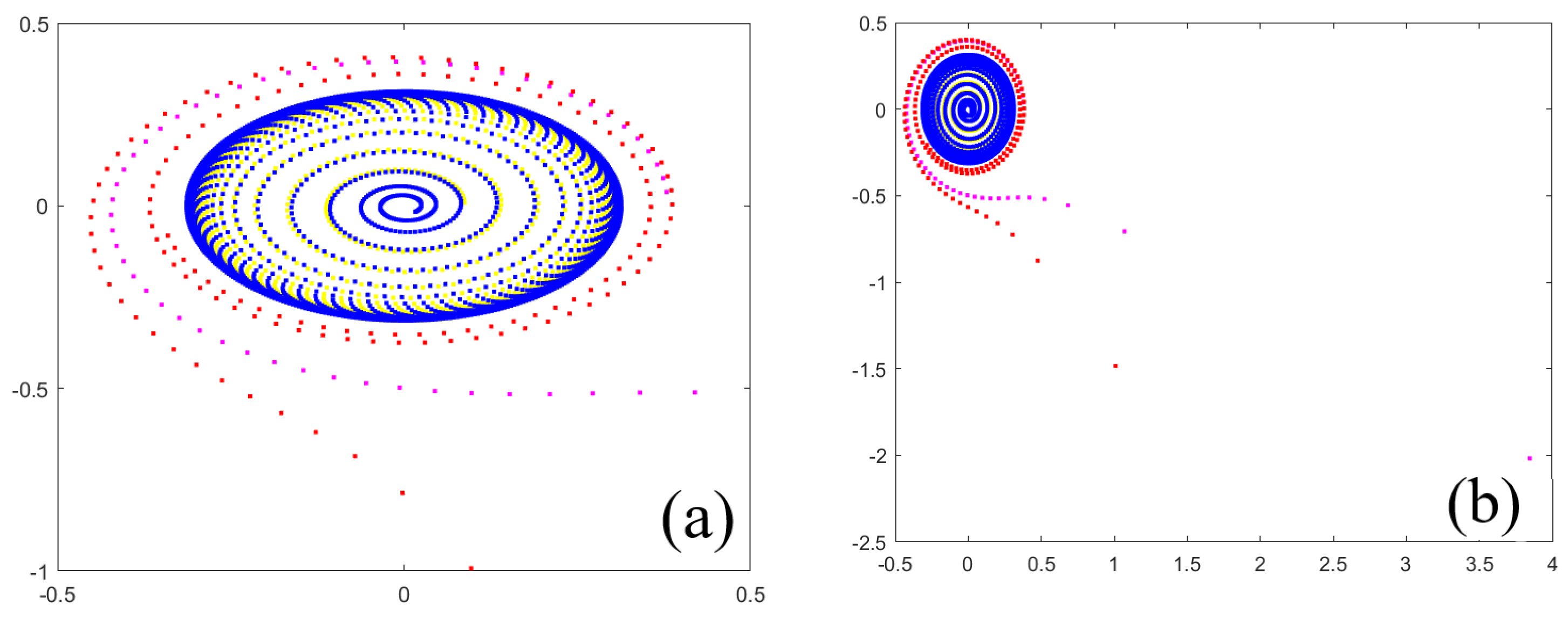
In order to numerically illustrate “the existence of closed invariant curves” [4] in some of the studied cases, the Matlab software was used. In the particular case when the two-dimensional map is given in polar coordinates by

$${\rho }_{n+1}={\rho }_n+{\beta }_1\left(\alpha \right){\rho }_n+{\beta }_2\left(\alpha \right){\rho }_n^3-{\rho }_n^{5}and{\phi }_{n+1}={\phi }_n+{\theta }_0,$$

$\left|\alpha \right|$ being sufficiently small and $L_0=-1,{\theta }_0=0.2,$ we choose

$${\beta }_1\left(\alpha \right)={\alpha }_1^2-{\alpha }_1{\alpha }_2+{\alpha }_2^2,{\beta }_2\left(\alpha \right)=-{\alpha }_1-3{\alpha }_2,{\alpha }_1=0.1,{\alpha }_2=-0.1.$$

Figure 7a,b shows the phase portraits 3 and 1 obtained when the conditions of Remark 5a,b are satisfied, respectively. In Figure 7a, the magenta orbit starting from $({\rho }_1,{\phi }_1)=(0.7,0)$ approximates the invariant closed curve (invariant circle) from Theorem 1 [4], being obtained for $N=400$ steps starting from the outside of the circle. The blue orbit starts from $({\rho }_2,{\phi }_2)=(0.06,0)$ and it is also obtained for $N=400$, which approximates the invariant circle starting from the inside and staying inside the circle. The red orbit starts in $({\rho }_3,{\phi }_3)=(0.4,0)$, approximates the invariant circle from the inside, and is obtained for $N=400$ steps. The green orbit starts from $({\rho }_4,{\phi }_4)=(0.59,0)$, from the outside of the invariant circle and approximates it. This is how the phase 3 portrait appears here, the conditions in Remark 5a, Case 4.2 being satisfied (${\Delta }_1=-3<0,a=1>0,L_0=-1<0$). For the invariant circle, the radius is ${\rho }_n=\sqrt{y_2}=0.547$; in our case, having ${\beta }_1\left(\alpha \right)=0.03,{\beta }_2\left(\alpha \right)=0,2>0,\Delta \left(\alpha \right)>0,L_0=-1$, we are also in the conditions of Theorem 1 (2) (b) [4]. We consider the particular case where the two-dimensional map is given in polar coordinates by

$${\rho }_{n+1}={\rho }_n+{\beta }_1\left(\alpha \right){\rho }_n+{\beta }_2\left(\alpha \right){\rho }_n^3+{\rho }_n^{5}and{\phi }_{n+1}={\phi }_n+{\theta }_0,$$

$\left|\alpha \right|$ being sufficiently small, ${\theta }_0=0.1,{\alpha }_1=0.1,{\alpha }_2=-0.1,$

$${\beta }_1\left(\alpha \right)=-{\alpha }_1^2-{\alpha }_1{\alpha }_2-{\alpha }_2^2,{\beta }_2\left(\alpha \right)=-{\alpha }_1-3{\alpha }_2,L_0=1,.$$

It is observed that $L_0>0,a=-1<0,{\Delta }_1<0$, so the conditions in Remark 5b are satisfied, and then the bifurcation diagram contains only phase portrait 1 (corresponding to region 1). We choose 3 orbits starting from the points $({\rho }_1,{\phi }_1)=(0.2035223739,0),({\rho }_2,{\phi }_2)=(0.181,0)$ and $({\rho }_3,{\phi }_3)=(0.187,0)$ of the colors magenta, red and blue, respectively, and which have $N=850$, $N=4000$ and $N=4000$ steps, respectively; see Figure 7b. The magenta orbit moves away from the invariant circle and may escape to infinity, while the red orbit tends toward the origin $(0,0)$, and the blue orbit likewise tends toward the origin. In addition, the radius of the invariant circle will be ${\rho }_n=\sqrt{y_1}=0.2035$ (the conditions of Theorem 1 (2), (a) being satisfied) ($L_0>0,{\beta }_1\left(\alpha \right)=-0.01<0,{\beta }_2\left(\alpha \right)=0.2>0$).

Figure 7. Numerical simulation for the map (A7) and (A8) with: (a) ${\beta }_1\left(\alpha \right)={\alpha }_1^2-{\alpha }_1{\alpha }_2+{\alpha }_2^2,{\beta }_2\left(\alpha \right)=-{\alpha }_1-3{\alpha }_2$ and $L_0=-1$, ${\alpha }_1=0.1,{\alpha }_2=-0.1$; (b) ${\beta }_1\left(\alpha \right)=-{\alpha }_1^2-{\alpha }_1{\alpha }_2-{\alpha }_2^2,{\beta }_2\left(\alpha \right)=-{\alpha }_1-3{\alpha }_2$ and $L_0=1$, ${\alpha }_1=0.1,{\alpha }_2=-0.1$.

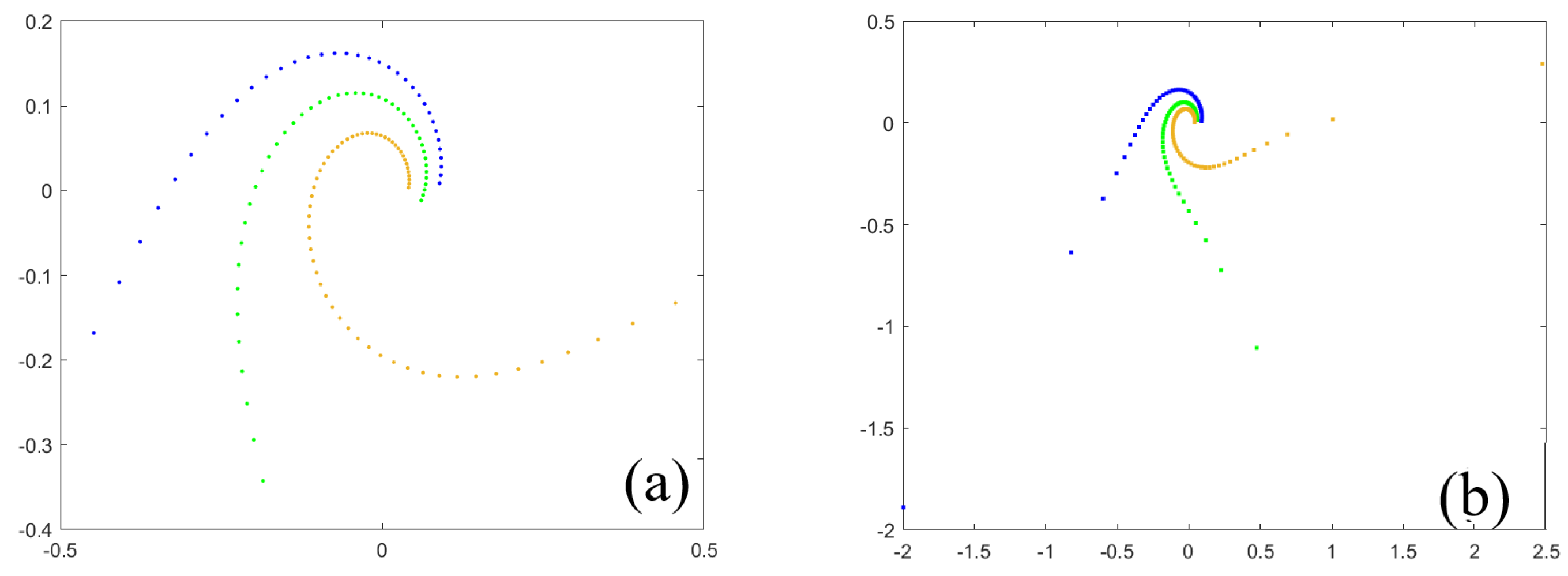
For Figure 6a, we wanted to check on a particular case where the appearance of regions 2, 6, and 8 corresponds to phase portraits 2, 6, and 8. We consider the map given in polar coordinates by

$${\rho }_{n+1}={\rho }_n+{\beta }_1\left(\alpha \right){\rho }_n+{\beta }_2\left(\alpha \right){\rho }_n^3+{\rho }_n^{5}and{\phi }_{n+1}={\phi }_n+{\theta }_0,$$

$\left|\alpha \right|$ being small enough $L_0=1,{\theta }_0=0.1$. We took ${\beta }_1\left(\alpha \right)={\alpha }_1^2+{\alpha }_1{\alpha }_2+{\alpha }_2^2,{\beta }_2\left(\alpha \right)={\alpha }_1+3{\alpha }_2$, ${\alpha }_1=0.1,{\alpha }_2=-0.1$ and we notice that the conditions are checked ($a>0$, $L_0>0$, $h>0$, $-p/q\in (m_1,m_2)$, $m_1=-1$, $m_2=0.6$ and $\frac{{\alpha }_1}{{\alpha }_2}=m_1$) to be on one of the straight lines that form the curve (C) in Figure 6a, the point $({\alpha }_1,{\alpha }_2)$ being in quadrant IV, so it is region 6. For the orbits of blue, red, magenta and yellow colors from Figure 8a, starting at points $({\rho }_1,{\phi }_1)=(0.023,0)$, $({\rho }_2,{\phi }_2)=(0.35,0)$, $({\rho }_3,{\phi }_3)=(0.38,0)$ and $({\rho }_4,{\phi }_4)=(0.078,0)$, respectively, we consider $N=4000$, $N=141$, $N=54$ and $N=4000$ steps, respectively. It can be seen that the blue orbit approximates the invariant circle, the red orbit tends to infinity (if we increase the number of steps to $N=142$ and $N=58$ for the red and magenta curves, we obtain Figure 8b), the magenta orbit, like the red one, tends at infinity moving away from the invariant circle, and the yellow orbit, like the blue one, approximates (tends to) the invariant circle. This proves that we have phase portrait 6, so region 6 (as in the figure) is in accordance with the theoretical results. More than that, ${\rho }_n=\sqrt{y_1}=0.3162$, is the radius of the invariant circle, and because $\Delta \left(\alpha \right)=0$, the equation $y^2-0.2y+0.01=0$ has a double root.

Figure 8. Numerical simulation for the map (A7) and (A8) with (a) ${\beta }_1\left(\alpha \right)={\alpha }_1^2+{\alpha }_1{\alpha }_2+{\alpha }_2^2,{\beta }_2\left(\alpha \right)={\alpha }_1+3{\alpha }_2$ and $L_0=1$, ${\alpha }_1=0.1,{\alpha }_2=-0.1$; (b) like (a), but the step number is increased, and $N=142$ and $N=58$ for red orbit and magenta orbit, respectively.

However, with ${\alpha }_1=0.1$ and ${\alpha }_2=0.1$, the point $({\alpha }_1,{\alpha }_2)$ is in quadrant I, $\frac{{\alpha }_1}{{\alpha }_2}$ will be different from $m_1$ and $m_2$, and in Figure 6a, region 2 will appear. For the orbits of blue, green and brown colors starting from points $({\rho }_1,{\phi }_1)=(0.087,0)$, $({\rho }_2,{\phi }_2)=(0.06,0)$ and $({\rho }_3,{\phi }_3)=(0.04,0)$, respectively, the numbers of steps are considered $N=35$, $N=45$ and $N=60$, respectively. The 3 orbits tend to infinity corresponding to phase 2 portrait (region 2); see Figure 9a. If we take $N=39$, $N=50$ and $N=64$ instead of the previous 3 values, we obtain Figure 9b, and it is observed that the last values increase a lot. Then, choosing ${\alpha }_1=-0.01,{\alpha }_2=-0.5$, the pair $({\alpha }_1,{\alpha }_2)$ is in quadrant III, and $\frac{{\alpha }_1}{{\alpha }_2}$ will be different from $m_1$ and $m_2$.

Figure 9. Numerical simulation for the map (A7) and (A8) with: (a) ${\beta }_1\left(\alpha \right)={\alpha }_1^2+{\alpha }_1{\alpha }_2+{\alpha }_2^2,{\beta }_2\left(\alpha \right)={\alpha }_1+3{\alpha }_2$ and $L_0=1$, ${\alpha }_1=0.1,{\alpha }_2=0.1$; (b) like to (a) but the step number is increased to $N=39$, $N=50$ and $N=64$, respectively, for blue orbit, green orbit and brown orbit.

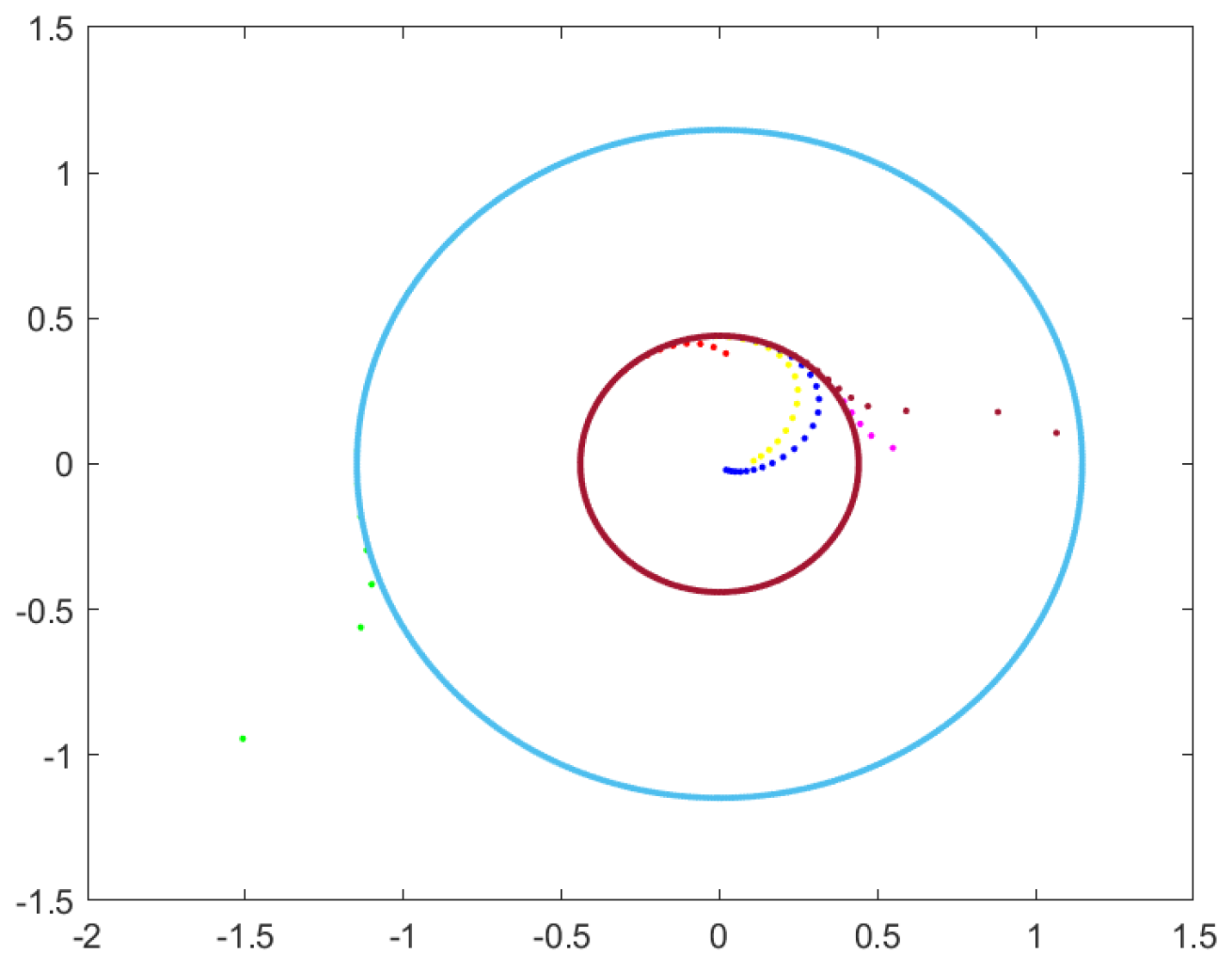
The six orbits start in Figure 10 from din $({\rho }_1,{\phi }_1)=(0.087,0)$, $({\rho }_2,{\phi }_2)=(0.78,0)$, $({\rho }_3,{\phi }_3)=(0.35,0)$, $({\rho }_4,{\phi }_4)=(1.14724966464545445,0)$, $({\rho }_5,{\phi }_5)=(0.023,0)$ and $({\rho }_6,{\phi }_6)=(1.127,0)$ having the colors yellow, magenta, red, green, blue and cherry, respectively, with steps $N=400$, $N=54$, $N=141$, $N=15$, $N=400$ and $N=400$, respectively. The cyan-colored orbit is the outer invariant circle. The cherry and magenta orbits approximate the inner invariant circle from the outside, and the blue, yellow and red orbits approximate the inner invariant circle from the inside. The green orbit moves away from the outer invariant circle tending to infinity, thus observing that the orbits move away from the outer circle and tend toward the inner invariant circle. We thus have the portrait of phase 8, region 8. The radii of the two invariant circles are known from Theorem 1 [4].

Figure 10. Numerical simulation for the map (A7) and (A8) with ${\beta }_1\left(\alpha \right)={\alpha }_1^2+{\alpha }_1{\alpha }_2+{\alpha }_2^2,{\beta }_2\left(\alpha \right)={\alpha }_1+3{\alpha }_2$ and $L_0=1$, ${\alpha }_1=-0.01,{\alpha }_2=-0.5$.

6. Discussions and Conclusions

6.1. Discussions

In this study, the truncated normal form of the Chenciner bifurcation was analyzed in a degeneracy case, where the degeneracy condition is given by $a_{10}{b}_{01}-a_{01}{b}_{10}=0$ and $a_{10}=a_{01}=0$ or $b_{10}=b_{01}=0$, as an answer to the problem open in [4,35].

In this article, all eight regions corresponding to the eight phase portraits (see Figure A1) appear in the bifurcation diagrams, unlike [15] or [10], where all of these are not present. In [15], only regions 1–4 appear in the bifurcation diagrams. If in a previous study [15] only two alternating regions appeared, in this article, more alternating regions (4 and 3 regions, respectively) appear in the bifurcation diagrams. This situation indicates a more complex structure of bifurcation diagrams. By modifying the structure of the sets of points $B_{1,2}$ and C, concurrent lines at the origin are obtained in the bifurcation diagrams, as in some recent studies [10,15], and different from other previous works [4,35]. When ${\Delta }_1>0$ (Section 4.1) the analysis of the six cases obtained leads to the first two diagrams in Figure 5a,b. When ${\Delta }_1<0$ (Section 4.2) Figure 6 presents the last two nontrivial bifurcation diagrams. However, in this last case, there are additionally four trivial situations when the bifurcation diagrams contain only one region in the whole plane (see Remarks 5a,b and 7a,b) and therefore do not require the creation of an additional representation.

The obtained theoretical results could be verified by means of the Matlab program, which allowed the realization of several representative simulations.

The Chenciner bifurcation in this case acts similar to an “organizing center” of dynamic behavior, generating “global dynamic phenomena such as the creation or disappearance of stable limit cycles” [19]. Near a Chenciner bifurcation point, “there is an open region in the parameter space where a stable equilibrium state and a stable limit cycle coexist” [19].

6.2. Conclusions

The advantage of using Chenciner degenerate bifurcation for modeling economics volatility versus chaotic behavior is that the transition to chaos amplifies itself and requires several iterations, but the volatility may be transitory. The case studied in this article has the advantage that it leads to the reduction of the large number of bifurcation diagrams that appeared in [4,10]. Thus, the hypothesis that was made is confirmed: if the degeneracy is not so large, we have a small number of bifurcation diagrams. The limitations of the present procedure is that it is applicable to degenerated cases, which seldom represent cases that have importance in special situations. Moreover, the more restrictive method leading to a new parameter change as in [35] is not necessary for this study. The results obtained for “the truncated normal form give an approximate description of the complicated bifurcation structure, near a generic Chenciner bifurcation” [4]. As in the case of the Neumark–Sacker bifurcation and in the case of the degenerate Chenciner bifurcations, it is observed that the normal form thus obtained captures “only the appearance of a closed invariant curve but does not describe the structure of the orbit on this curve” [12]. The article completes the studies started in another reference material on the degenerate Chenciner bifurcation [4] and not addressed in other cases of degeneracy [10,15]. In the mentioned articles, the functions ${\beta }_1$ and ${\beta }_2$ do not contain any terms of the first degree [15], one of the two functions does not contain terms of the first or second degree, and the other may or may not contain terms of the first degree [10].

A number of four different bifurcation diagrams were obtained instead of “two as in the non-degenerate Chenciner case” [15]. The first two bifurcation diagrams were obtained in Case 4.1 when ${\Delta }_1>0$, and the last two bifurcation diagrams were generated in Case 4.2 when ${\Delta }_1<0$. Several subcases that appeared (discussed) in Case 4.1 could be removed.

So, the conclusion is that eight different bifurcation diagrams were recorded, four of them being trivial.

In the case studied now, the linear part of ${\beta }_1$ cancels, and ${\beta }_2$ has at least one linear term. Compared to the mentioned articles [4,10], much fewer bifurcation diagrams appear. Thus, eight bifurcations diagrams result (if we also consider the four trivial ones from Remark 5 and Remark 7), and only four non-trivial ones are recorded, which are different from those previously highlighted [15].

The obtained results “can be used in bifurcation theory” [15] as a field of dynamic systems, but could also be exploited in other fields of activity, where the evolution of some processes and phenomena is in the form of discrete dynamic systems (economy, biology, ecology, medicine and computers).