An Improved Optimization Algorithm for Aeronautical Maintenance and Repair Task Scheduling Problem
Abstract
1. Introduction
- i.
- Slack of distributed constraints. Commercial airlines must manage a complex network of routes and the complex coupling between distributed workshops and routes, whereas the majority of military aeronautical maintenance tasks are concentrated in ship-based hanging bays on large sea platforms;
- ii.
- Differences in the maintenance cycles, civil aeronautical maintenance optimization models, and methods applied to solve problems in fleet decision optimization. A commercial fleet is highly stable and has longer maintenance cycle intervals than a military naval aircraft fleet. The carrier-based aircraft fleet aeronautical maintenance tasks investigated in this study involve military tasks with urgent task requirements [10];
- iii.
- Differences in maintenance goals. The literature on civil aeronautical maintenance mainly focuses on profitability, and the optimizations mainly consider economic benefits [11], such as balancing the maintenance cost of the fleet with the amount of hangar resources [12] or the labor costs of maintenance personnel [13]. By contrast, military aviation maintenance tasks are optimized to avoid delaying military response and to ensure appropriate conduct in both combat and training tasks. In other words, the goal is to positively impact operational effectiveness and subsequent warfare.
- i.
- Mission maintenance aspects: Han et al. [15] simulated mission maintenance for deck crews, with the number of aircraft ranging from five to nine. However, they considered only a single maintenance mode and not multimode/hybrid situations, such as preventative maintenance and failure repairs, and realistic constraints, such as maintenance coverage, parallel maintenance capacity, and maintenance workstation space. Thus, the simulation differs substantially from an actual task;
- ii.
- Optimization/scheduling of fleet maintenance tasks: Most studies on optimizing fleet maintenance tasks have focused on minimizing the maintenance completion time [16]. However, Raju et al. [17] defined a military aircraft availability index for fleet wave sortie availability; the index comprised the ratio of the number of aircraft in mission-capable states to the total number of aircraft in the fleet at a given time point. The military maintenance and operational characteristics of naval aircraft were used for closer integration by the index;
- iii.
- Optimization/Scheduling of resources: The main considerations in terms of resources have involved personnel and personnel scheduling strategies [18], resource constraints for maintenance personnel [19], and maintenance personnel time balancing [20]. No studies have been conducted to integrate limited maintenance resources, such as maintenance equipment, workshops, and space, in the models.
2. Problem Statement
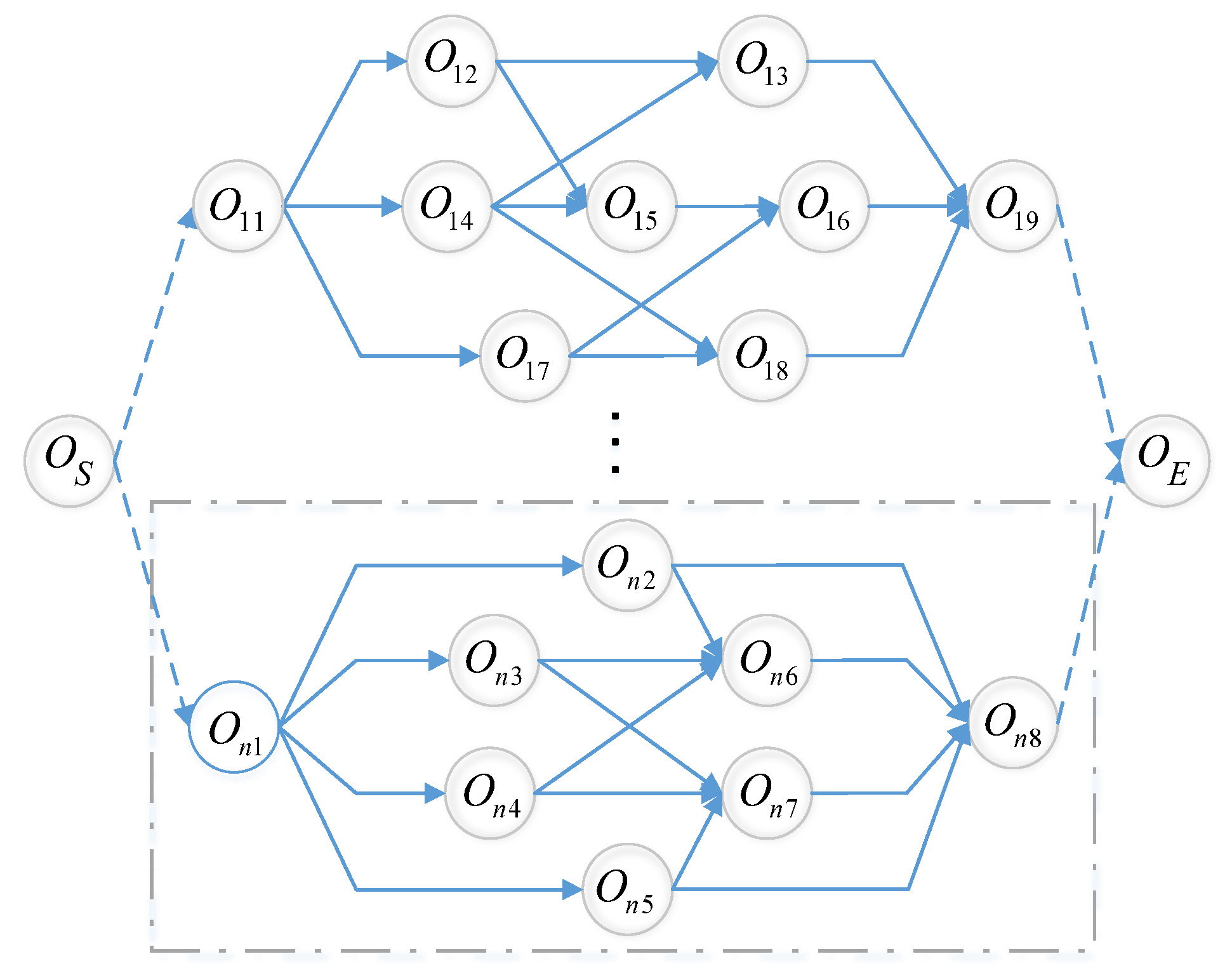
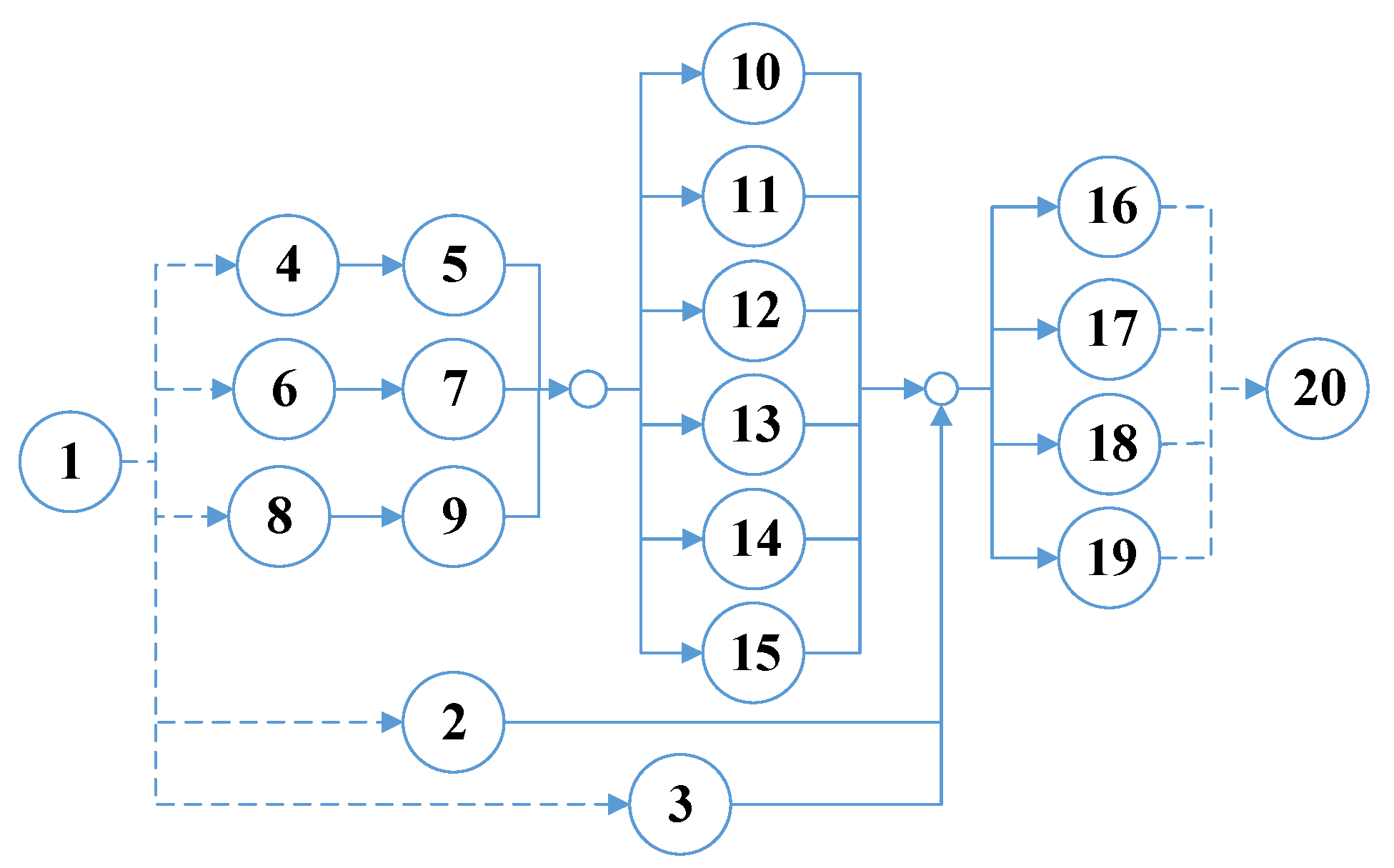
2.1. Maintenance Process
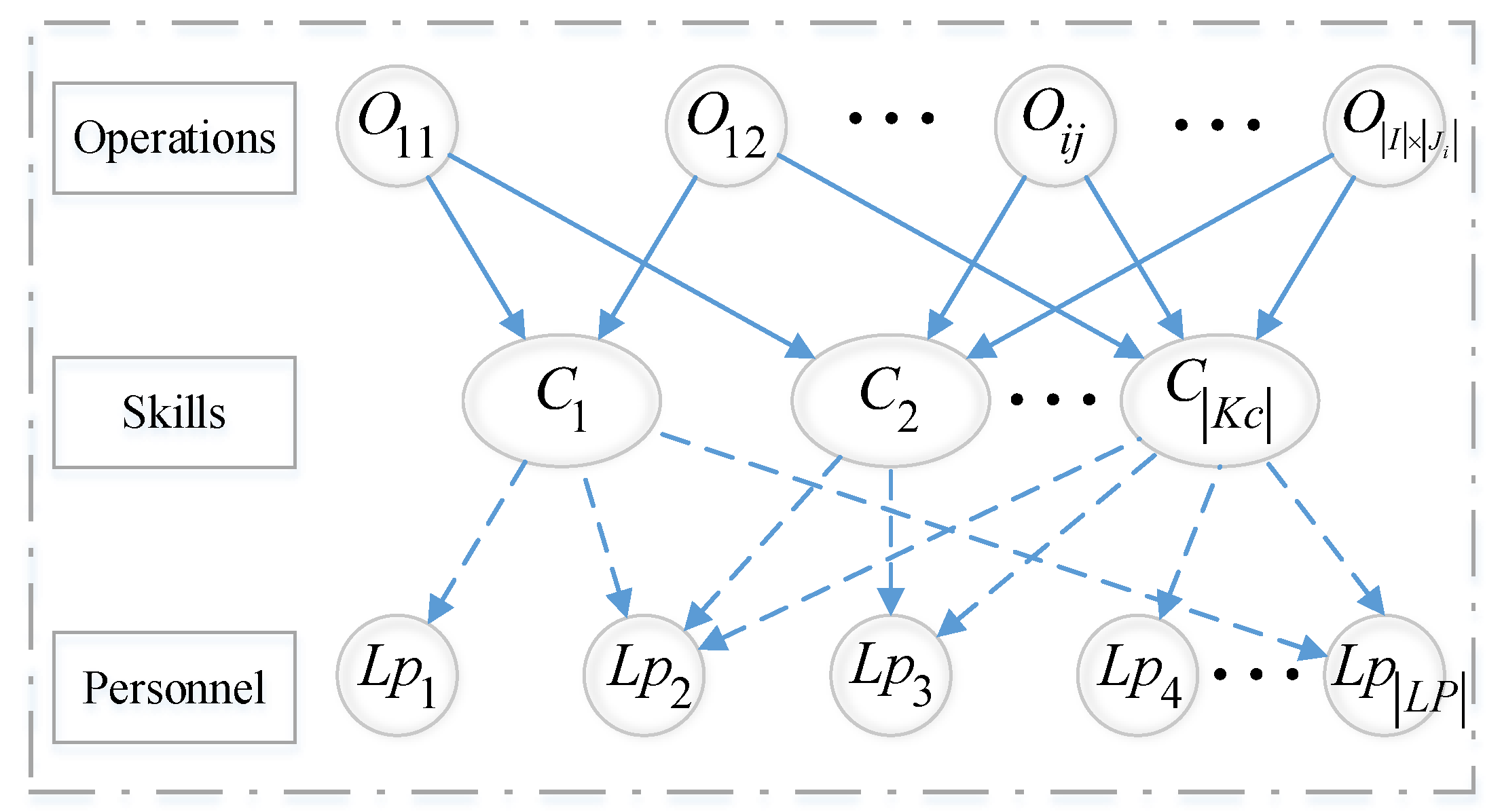
2.2. Maintenance Personnel and Skills
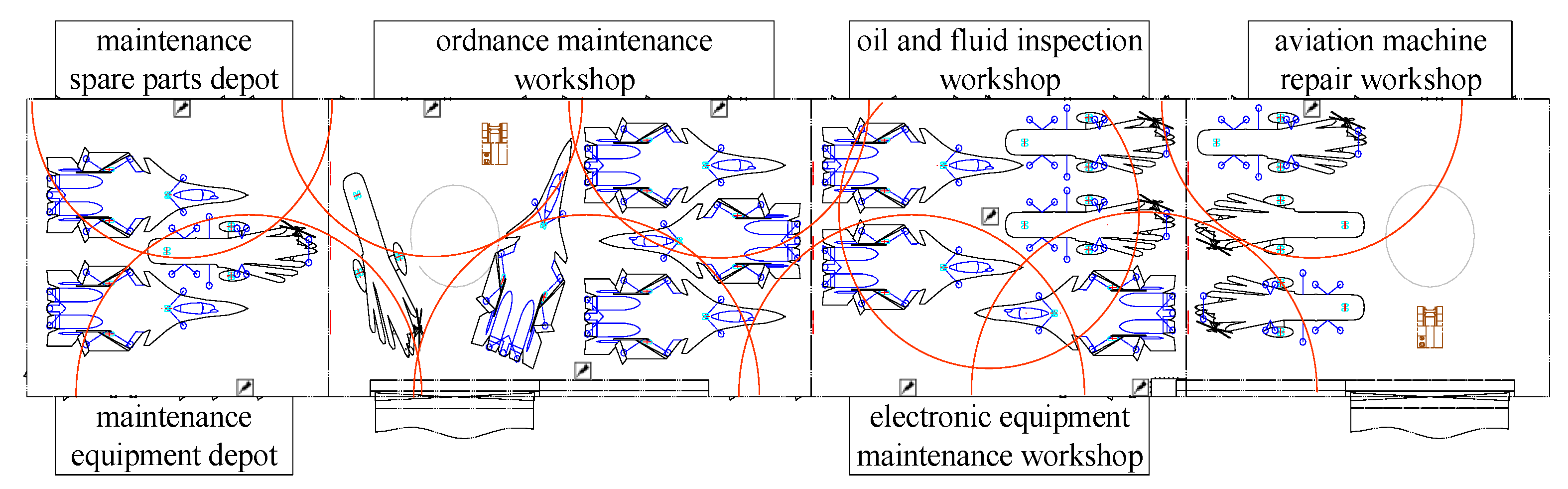
2.3. Maintenance Equipment, Workshop, and Workspace
3. Mathematical Model for Aeronautical Maintenance and Repair Task Scheduling Problem (AMRSP)
3.1. Problem Assumptions
- i.
- The MR tasks are known with certainty and do not consider the interference of dynamic factors.
- ii.
- The MR process cannot be preempted or interrupted once started.
- iii.
- The maintenance skills are adapted to each aircraft’s MR task mode.
- iv.
- The transit time in the hangar bay is ignored.
- v.
- An adequate reserve of fixed-resource station resources is available.
3.2. Constraints
3.3. Objective Function
- (1)
- Maximizing fleet-wave availability (WA)
- (2)
- Minimizing the personnel load variance (PLV) results in
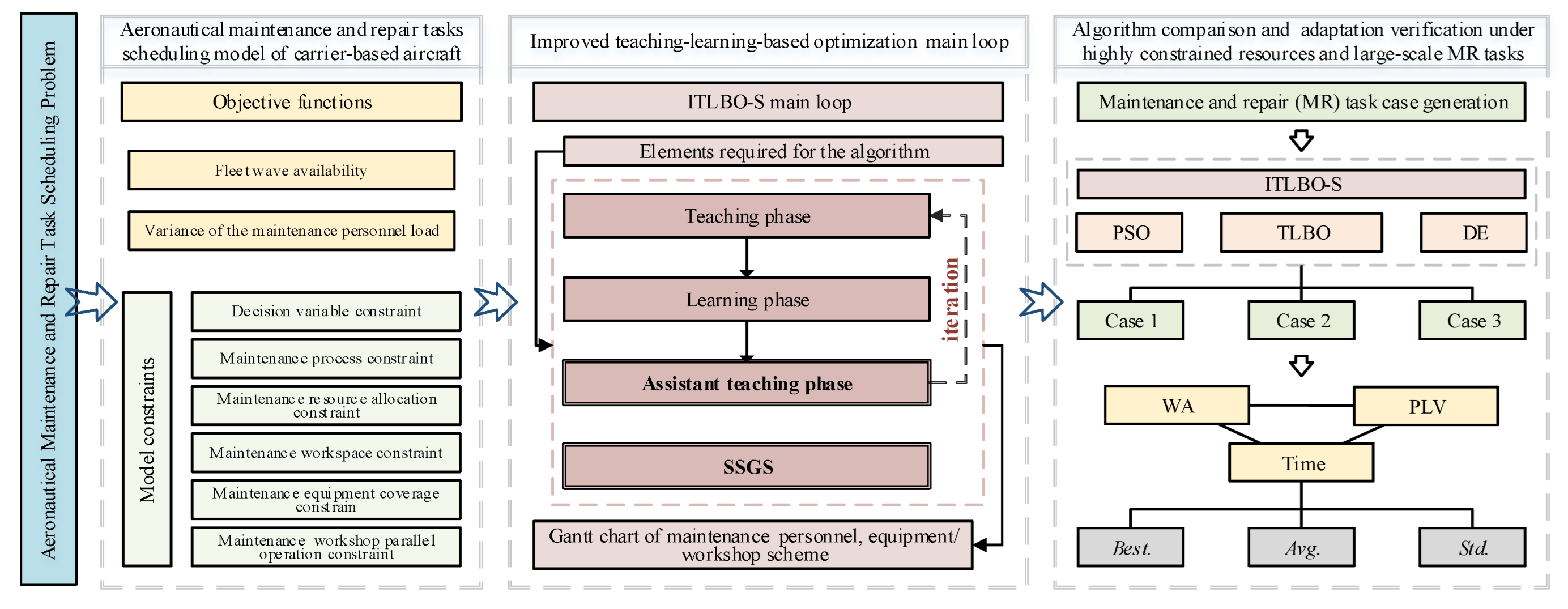
4. Algorithm for AMRSP
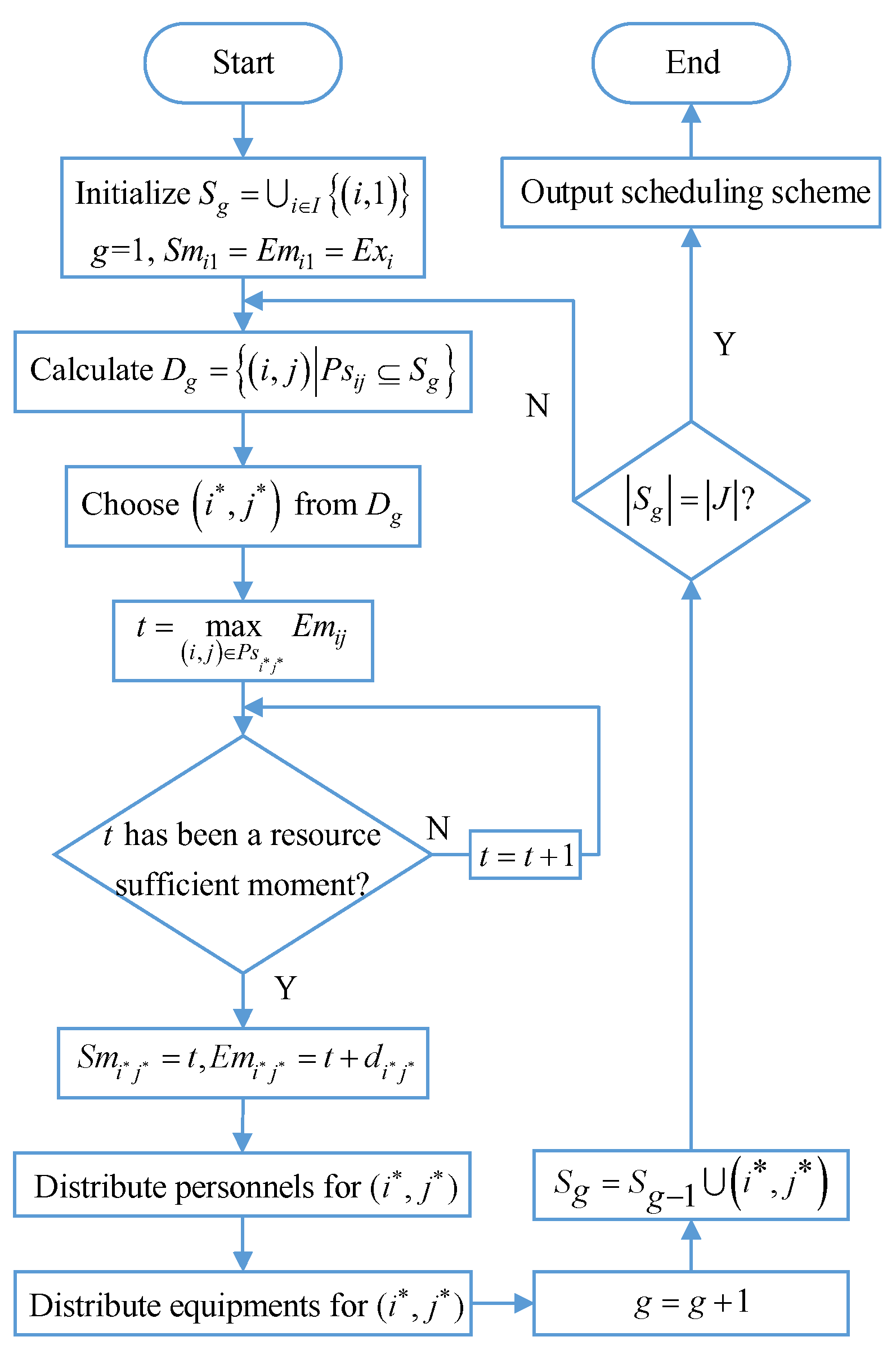
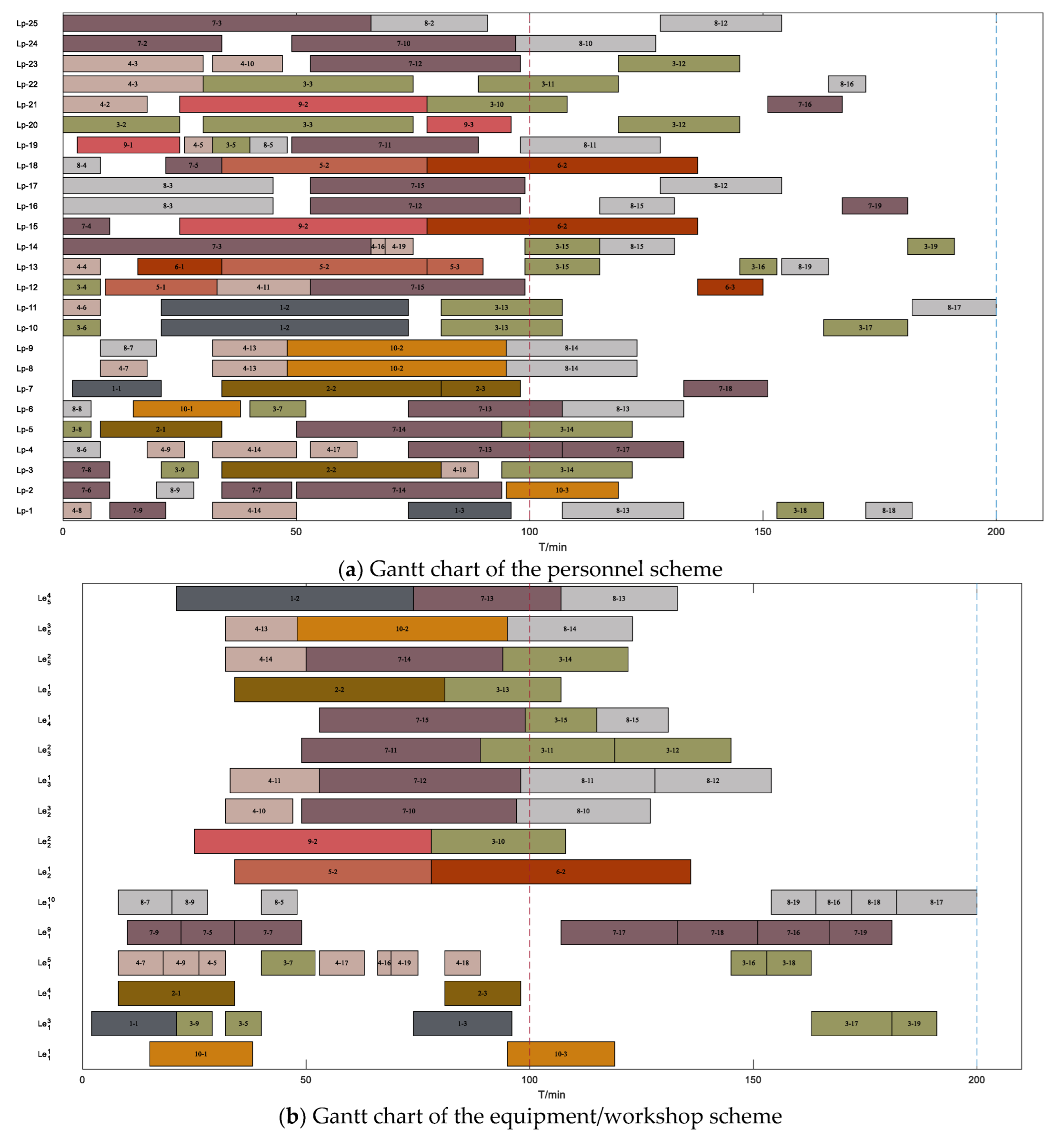
4.1. Encoding and Serial Scheduling Generation Scheme (SSGS)
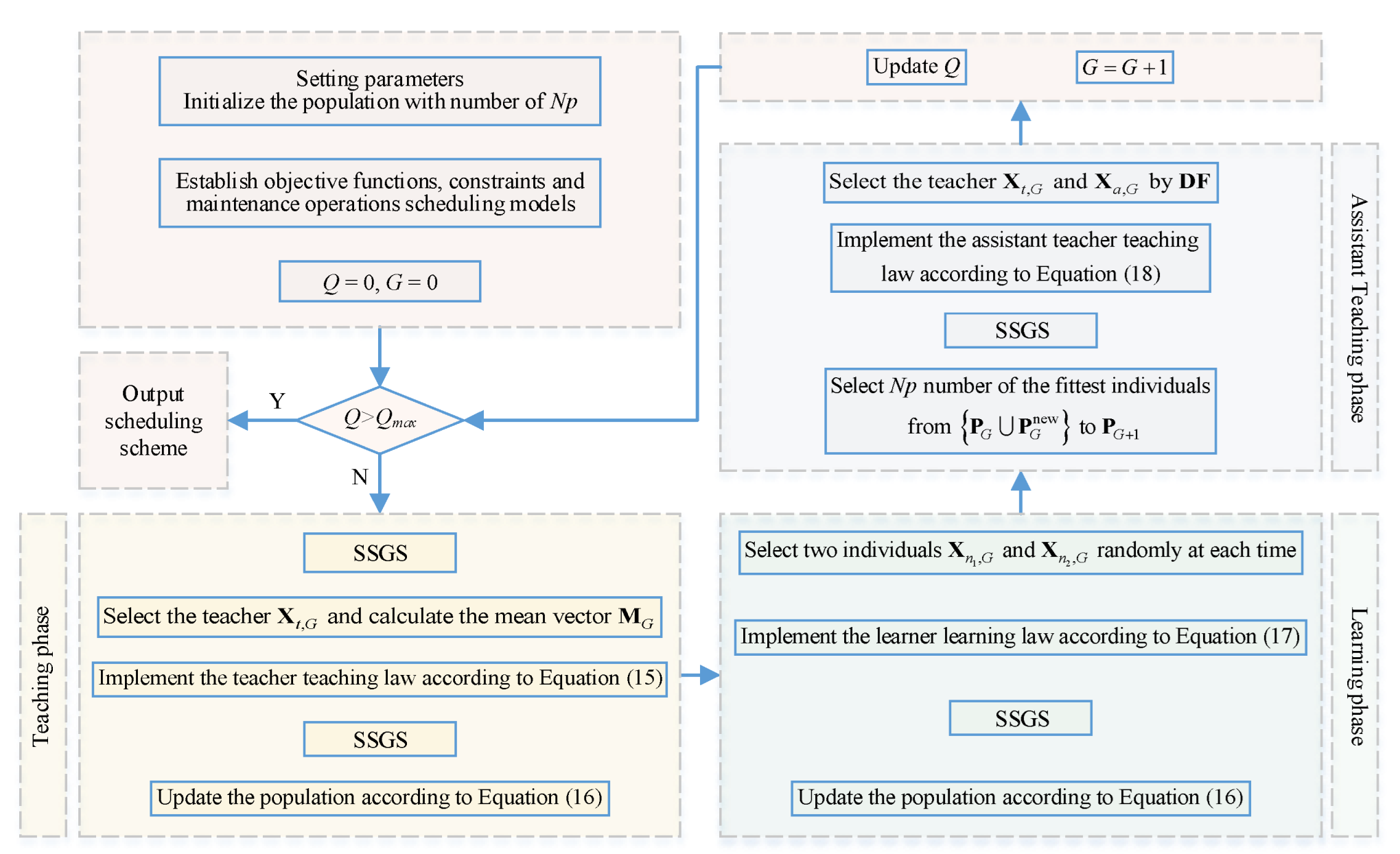
4.2. Improved Teaching-Learning-Based Optimization (ITLBO) Main Loop
4.2.1. Teaching Phase
4.2.2. Learning Phase
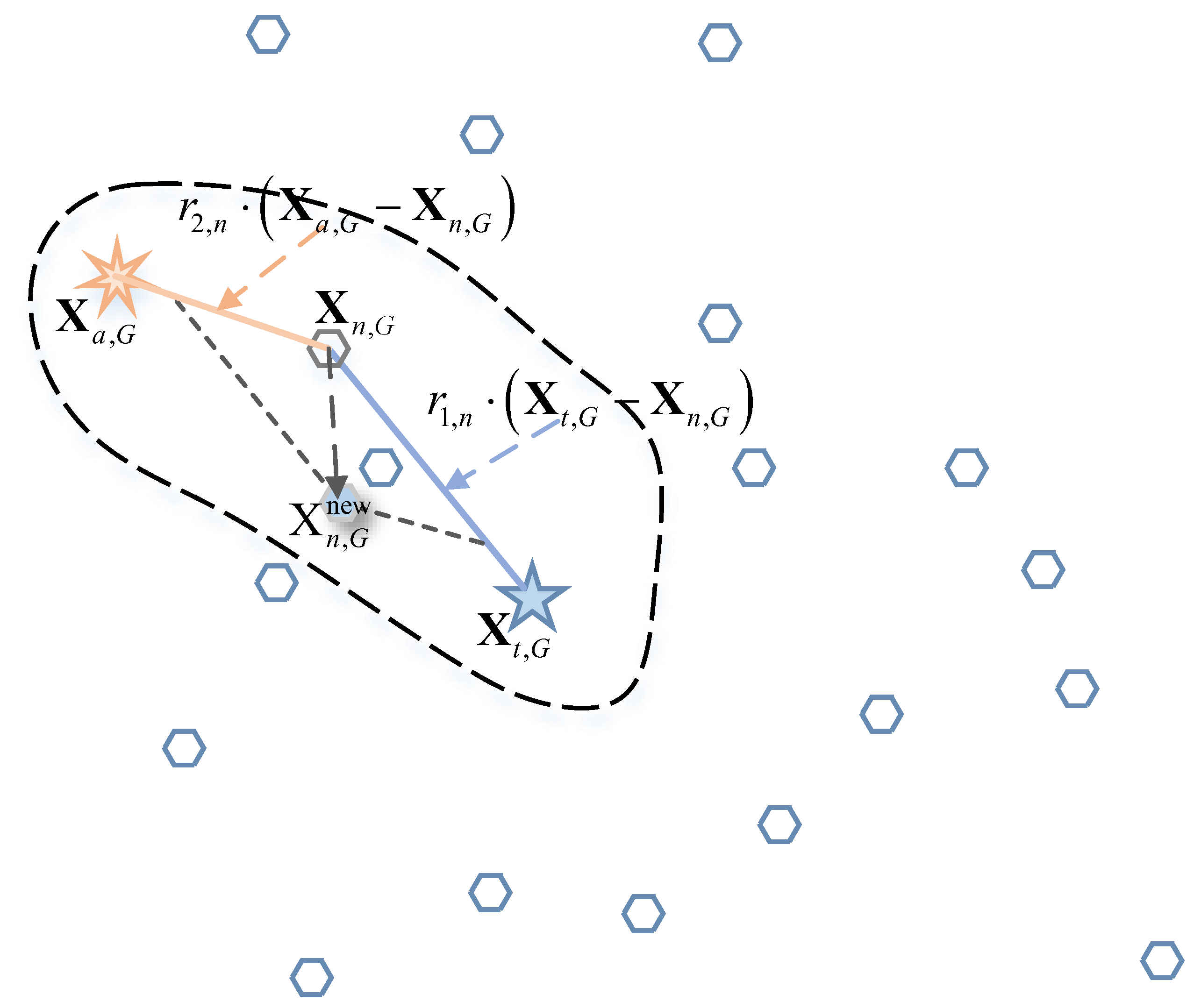
4.2.3. Assistant Teaching Phase
- (1)
- Fitness-distance ranking ratio
- (2)
- Assistant Teacher Teaching
4.3. Complexity Analysis
5. Simulation Case Analysis
5.1. Maintenance and Repair (MR) Task Case Generation
5.2. Simulation Comparison Analysis
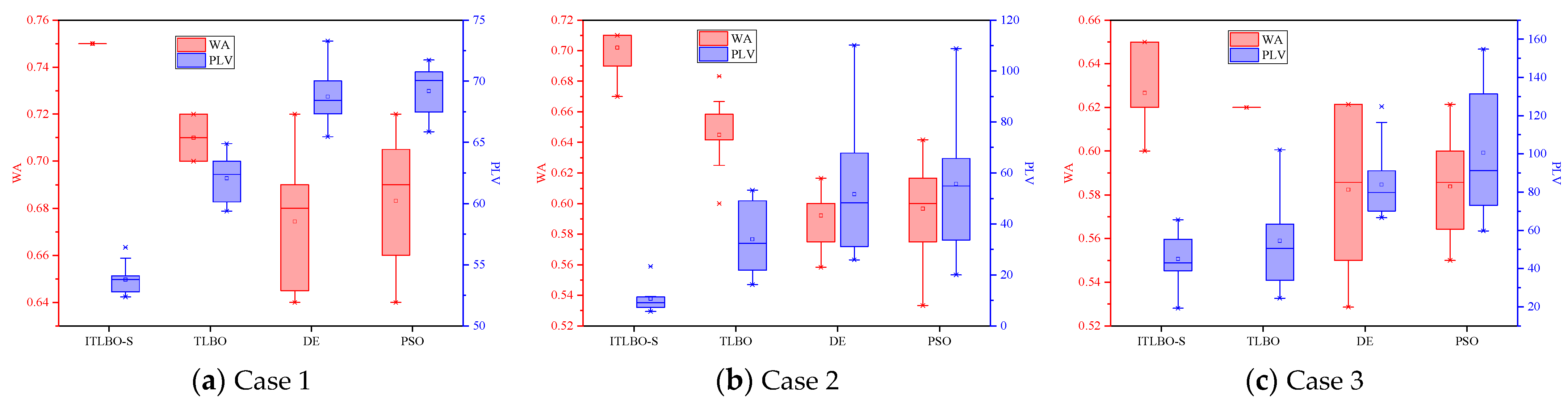
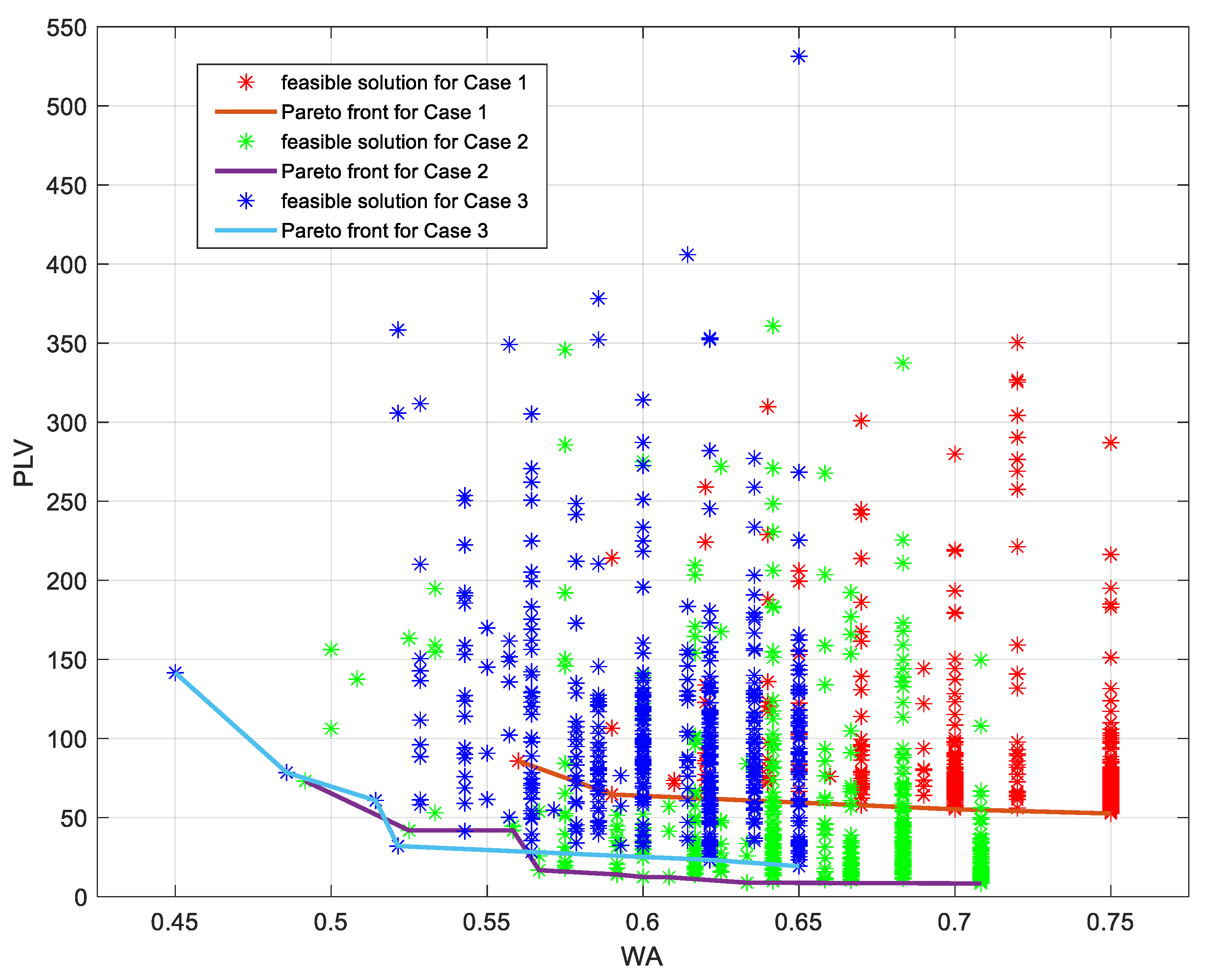
5.2.1. Algorithm Comparison
5.2.2. Adaptation Verification of Algorithms
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shafiee, M.; Chukova, S. Maintenance Models in Warranty: A Literature Review. Eur. J. Oper. Res. 2013, 229, 561–572. [Google Scholar] [CrossRef]
- Johnston, J.S. A Feasibility Study of a Persistent Monitoring System for the Flight Deck of US Navy Aircraft Carriers. Doctoral Dissertation, Air Force Air University, Maxwell, AL, USA, 2009. [Google Scholar]
- Uzun, B. A Multimodal Ouija Board for Aircraft Carrier Deck Operations. Doctoral Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 2016. [Google Scholar]
- Ryan, J.; Cummings, M.; Roy, N.; Banerjee, A.; Schulte, A. Designing an Interactive Local and Global Decision Support System for Aircraft Carrier Deck Scheduling. In Infotech@ Aerospace 2011; AIAA: Reston, VA, USA, 2011; p. 1516. [Google Scholar]
- Ryan, J.C.; Banerjee, A.G.; Cummings, M.L.; Roy, N. Comparing the Performance of Expert User Heuristics and an Integer Linear Program in Aircraft Carrier Deck Operations. IEEE Trans. Cybern. 2013, 44, 761–773. [Google Scholar] [CrossRef]
- Tsarouhas, P.; Makrygianni, M. A Framework for Maintenance and Combat Readiness Management of a Jet Fighter Aircraft. Int. J. Syst. Assur. Eng. Manag. 2017, 8, 1895–1909. [Google Scholar] [CrossRef]
- Liang, Z.; Feng, Y.; Zhang, X.; Wu, T.; Chaovalitwongse, W.A. Robust Weekly Aircraft Maintenance Routing Problem and the Extension to the Tail Assignment Problem. Transp. Res. Part B Methodol. 2015, 78, 238–259. [Google Scholar] [CrossRef]
- Deng, Q.; Santos, B.F.; Curran, R. A Practical Dynamic Programming Based Methodology for Aircraft Maintenance Check Scheduling Optimization. Eur. J. Oper. Res. 2020, 281, 256–273. [Google Scholar] [CrossRef]
- Kowalski, M.; Izdebski, M.; Żak, J.; Gołda, P.; Manerowski, J. Planning and Management of Aircraft Maintenance Using a Genetic Algorithm. Eksploat. Niezawodn. 2021, 23, 143–153. [Google Scholar] [CrossRef]
- Witteman, M.; Deng, Q.; Santos, B.F. A Bin Packing Approach to Solve the Aircraft Maintenance Task Allocation Problem. Eur. J. Oper. Res. 2021, 294, 365–376. [Google Scholar] [CrossRef]
- Eltoukhy, A.E.E.; Chan, F.T.S.; Chung, S.H.; Niu, B. A Model with a Solution Algorithm for the Operational Aircraft Maintenance Routing Problem. Comput. Ind. Eng. 2018, 120, 346–359. [Google Scholar] [CrossRef]
- Lin, L.; Wang, F.; Luo, B. An Optimization Algorithm Inspired by Propagation of Yeast for Fleet Maintenance Decision Making Problem Involving Fatigue Structures. Appl. Soft Comput. 2019, 85, 105755. [Google Scholar] [CrossRef]
- de Bruecker, P.; van den Bergh, J.; Beliën, J.; Demeulemeester, E. A Model Enhancement Heuristic for Building Robust Aircraft Maintenance Personnel Rosters with Stochastic Constraints. Eur. J. Oper. Res. 2015, 246, 661–673. [Google Scholar] [CrossRef]
- Verhoeff, M.; Verhagen, W.J.C.; Curran, R. Maximizing Operational Readiness in Military Aviation by Optimizing Flight and Maintenance Planning. Transp. Res. Procedia 2015, 10, 941–950. [Google Scholar] [CrossRef]
- Han, Q.T.; Cao, W.J.; Zhang, Y. Research on Maintenance Resources Distribution Based on Queuing Theory. Trans. Tech. Publ. 2013, 239, 1428–1431. [Google Scholar] [CrossRef]
- Zhaodong, H.; Wenbing, C.; Yiyong, X.; Rui, L. Optimizing Human Resources Allocation on Aircraft Maintenance with Predefined Sequence. In Proceedings of the 2010 International Conference on Logistics Systems and Intelligent Management (ICLSIM), Harbin, China, 9–10 January 2010; Volume 2, pp. 1018–1022. [Google Scholar]
- Raju, V.R.S.; Gandhi, O.P.; Deshmukh, S.G. Maintenance, Repair, and Overhaul Performance Indicators for Military Aircraft. Def. Sci. J. 2012, 62, 83–89. [Google Scholar] [CrossRef]
- Feng, Q.; Li, S.; Sun, B. A Multi-Agent Based Intelligent Configuration Method for Aircraft Fleet Maintenance Personnel. Chin. J. Aeronaut. 2014, 27, 280–290. [Google Scholar] [CrossRef]
- Safaei, N.; Banjevic, D.; Jardine, A.K.S. Workforce-Constrained Maintenance Scheduling for Military Aircraft Fleet: A Case Study. Ann. Oper. Res. 2011, 186, 295–316. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Su, X.; Cui, R.; Wan, B. A Baseline-Reactive Scheduling Method for Carrier-Based Aircraft Maintenance Tasks. Complex Intell. Syst. 2022. [Google Scholar] [CrossRef]
- Mollahassani-Pour, M.; Abdollahi, A.; Rashidinejad, M. Application of a Novel Cost Reduction Index to Preventive Maintenance Scheduling. Int. J. Electr. Power Energy Syst. 2014, 56, 235–240. [Google Scholar] [CrossRef]
- Lin, J.; Zhu, L.; Gao, K. A Genetic Programming Hyper-Heuristic Approach for the Multi-Skill Resource Constrained Project Scheduling Problem. Expert Syst. Appl. 2020, 140, 112915. [Google Scholar] [CrossRef]
- Cui, R.; Dong, X.; Lin, Y. Models for Aircraft Maintenance Routing Problem with Consideration of Remaining Time and Robustness. Comput. Ind. Eng. 2019, 137, 106045. [Google Scholar] [CrossRef]
- Moukrim, A.; Quilliot, A.; Toussaint, H. An Effective Branch-and-Price Algorithm for the Preemptive Resource Constrained Project Scheduling Problem Based on Minimal Interval Order Enumeration. Eur. J. Oper. Res. 2015, 244, 360–368. [Google Scholar] [CrossRef]
- Chakrabortty, R.K.; Sarker, R.; Essam, D. Resource Constrained Project Scheduling: A Branch and Cut Approach. In Proceedings of the 45th International Conference on Computers and Industrial Engineering, Metz, France, 28–30 October 2015. [Google Scholar]
- Kiefer, A.; Schilde, M.; Doerner, K.F. Scheduling of Maintenance Work of a Large-Scale Tramway Network. Eur. J. Oper. Res. 2018, 270, 1158–1170. [Google Scholar] [CrossRef]
- Ðumić, M.; Jakobović, D. Using Priority Rules for Resource-Constrained Project Scheduling Problem in Static Environment. Comput. Ind. Eng. 2022, 169, 108239. [Google Scholar] [CrossRef]
- Pellerin, R.; Perrier, N.; Berthaut, F. A Survey of Hybrid Metaheuristics for the Resource-Constrained Project Scheduling Problem. Eur. J. Oper. Res. 2020, 280, 395–416. [Google Scholar] [CrossRef]
- Feng, Q.; Bi, W.; Chen, Y.; Ren, Y.; Yang, D. Cooperative Game Approach Based on Agent Learning for Fleet Maintenance Oriented to Mission Reliability. Comput. Ind. Eng. 2017, 112, 221–230. [Google Scholar] [CrossRef]
- Peschiera, F.; Dell, R.; Royset, J.; Haït, A.; Dupin, N.; Battaïa, O. A Novel Solution Approach with ML-Based Pseudo-Cuts for the Flight and Maintenance Planning Problem. OR Spectrum 2021, 43, 635–664. [Google Scholar] [CrossRef]
- Blum, C.; Puchinger, J.; Raidl, G.R.; Roli, A. Hybrid Metaheuristics in Combinatorial Optimization: A Survey. Appl. Soft Comput. 2011, 11, 4135–4151. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–Learning-Based Optimization: A Novel Method for Constrained Mechanical Design Optimization Problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Shao, W.; Pi, D.; Shao, Z. An Extended Teaching-Learning Based Optimization Algorithm for Solving No-Wait Flow Shop Scheduling Problem. Appl. Soft Comput. 2017, 61, 193–210. [Google Scholar] [CrossRef]
- Buddala, R.; Mahapatra, S.S. Two-Stage Teaching-Learning-Based Optimization Method for Flexible Job-Shop Scheduling under Machine Breakdown. Int. J. Adv. Manuf. Technol. 2019, 100, 1419–1432. [Google Scholar] [CrossRef]
- Ji, X.; Ye, H.; Zhou, J.; Yin, Y.; Shen, X. An Improved Teaching-Learning-Based Optimization Algorithm and Its Application to a Combinatorial Optimization Problem in Foundry Industry. Appl. Soft Comput. 2017, 57, 504–516. [Google Scholar] [CrossRef]
- Joshi, D.; Mittal, M.L.; Sharma, M.K.; Kumar, M. An Effective Teaching-Learning-Based Optimization Algorithm for the Multi-Skill Resource-Constrained Project Scheduling Problem. J. Model. Manag. 2019, 14, 1064–1087. [Google Scholar] [CrossRef]
- Joshi, D.; Mittal, M.L.; Kumar, M. A Teaching–Learning-Based Optimization Algorithm for the Resource-Constrained Project Scheduling Problem. In Harmony Search and Nature Inspired Optimization Algorithms; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1101–1109. [Google Scholar]
- Deng, Q.; Santos, B.F.; Verhagen, W.J.C. A Novel Decision Support System for Optimizing Aircraft Maintenance Check Schedule and Task Allocation. Decis. Support Syst. 2021, 146, 113545. [Google Scholar] [CrossRef]
- Kolisch, R. Serial and Parallel Resource-Constrained Project Scheduling Methods Revisited: Theory and Computation. Eur. J. Oper. Res. 1996, 90, 320–333. [Google Scholar] [CrossRef]
- Hartmann, S.; Kolisch, R. Experimental Evaluation of State-of-the-Art Heuristics for the Resource-Constrained Project Scheduling Problem. Eur. J. Oper. Res. 2000, 127, 394–407. [Google Scholar] [CrossRef]
- Fu, Y.; Zhou, M.; Guo, X.; Qi, L. Scheduling Dual-Objective Stochastic Hybrid Flow Shop With Deteriorating Jobs via Bi-Population Evolutionary Algorithm. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 5037–5048. [Google Scholar] [CrossRef]
- Zou, F.; Chen, D.; Xu, Q. A Survey of Teaching–Learning-Based Optimization. Neurocomputing 2019, 335, 366–383. [Google Scholar] [CrossRef]
- Neri, F.; Tirronen, V. Recent Advances in Differential Evolution: A Survey and Experimental Analysis. Artif. Intell. Rev. 2010, 33, 61–106. [Google Scholar] [CrossRef]
- Xu, Y.; Peng, Y.; Su, X.; Yang, Z.; Ding, C.; Yang, X. Improving Teaching-Learning-Based-Optimization Algorithm by a Distance-Fitness Learning Strategy. Knowl. Based Syst. 2022, 257, 108271. [Google Scholar] [CrossRef]
- Cui, R.; Han, W.; Su, X.; Liang, H.; Li, Z. A Dual Population Multi-Operator Genetic Algorithm for Flight Deck Operations Scheduling Problem. J. Syst. Eng. Electron. 2021, 32, 331–346. [Google Scholar]
- Deng, Q.; Santos, B.F. Lookahead Approximate Dynamic Programming for Stochastic Aircraft Maintenance Check Scheduling Optimization. Eur. J. Oper. Res. 2022, 299, 814–833. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]



| Notations | Descriptions |
|---|---|
| . | |
| carrier-based aircraft. | |
| . | |
| . | |
| . | |
| . | |
| carrier-based aircraft. | |
| . | |
| carrier-based aircraft. | |
| . | |
| A sufficiently large real number. | |
| The set of maintenance personnel. | |
| The set of maintenance equipment/workshops. | |
| . | |
| . | |
| . | |
| skill category, whereas 0 indicates otherwise. | |
| maintenance equipment/workshop category, whereas 0 indicates otherwise. | |
| maintenance workspace, whereas 0 indicates otherwise. | |
| , whereas 0 indicates otherwise. | |
| workspace category. | |
| category. | |
| . | |
| . | |
| skill category, whereas 0 indicates otherwise. | |
| maintenance equipment/workshop category, whereas 0 indicates otherwise. | |
| , whereas 0 indicates otherwise. | |
| , whereas 0 indicates otherwise. |
| P. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MR Tasks | Carrier-based aircraft no.; Ex (min) MR tasks modes | |||||||||||||
| Case 1 | A; 2 2 | B; 8 3 | C; 0 5 | D; 0 4 | E; 9 1 | F; 16 1 | G; 0 6 | H; 0 5 | I; 3 1 | J; 15 2 | - | - | - | - |
| Case 2 | A; 2 2 | B; 8 3 | C; 0 5 | D; 0 4 | E; 9 1 | F; 16 1 | G; 0 6 | H; 0 5 | I; 3 1 | J; 15 2 | K; 21 5 | L; 22 3 | - | - |
| Case 3 | A; 2 2 | B; 8 3 | C; 0 5 | D; 0 4 | E; 9 1 | F; 16 1 | G; 0 6 | H; 0 5 | I; 3 1 | J; 15 2 | K; 21 3 | L; 22 4 | M; 27 4 | N; 29 4 |
| P. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ke1 | [3] | [4] | [3,5] | [5] | [9] | [10] | [9] | [10] | [6] | [1] | [3] | [7] | [2] | [8] |
| Ke2–5 | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] |
| MR Task Modes | Operation No. | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
| Operation Duration (min) | |||||||||||||||||||||
| Mechanical failure | 0 | 0 | 0 | 0 | 24 | 0 | 0 | 0 | 0 | 44 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | |
| Avionics system failure | 0 | 0 | 0 | 0 | 19 | 0 | 0 | 0 | 0 | 53 | 0 | 0 | 0 | 0 | 0 | 22 | 0 | 0 | 0 | 0 | |
| Special equipment failure | 0 | 0 | 0 | 0 | 26 | 0 | 0 | 0 | 0 | 47 | 0 | 0 | 0 | 0 | 0 | 17 | 0 | 0 | 0 | 0 | |
| Maintenance after 25 flight hours | 0 | 18 | 30 | 8 | 6 | 8 | 10 | 6 | 8 | 15 | 20 | 0 | 16 | 18 | 0 | 3 | 10 | 8 | 6 | 0 | |
| Maintenance after 50 flight hours | 0 | 25 | 45 | 8 | 8 | 8 | 12 | 6 | 8 | 30 | 30 | 26 | 26 | 28 | 16 | 8 | 18 | 10 | 10 | 0 | |
| Maintenance after 100 flight hours | 0 | 34 | 66 | 10 | 12 | 10 | 15 | 10 | 12 | 48 | 40 | 45 | 33 | 44 | 46 | 16 | 26 | 18 | 14 | 0 | |
| Required resource type | Kc | - | 4 | 4 | 3 | 1,2,3,4 | 2 | 2 | 1 | 1 | 1,2,4 | 4 | 4 | 2 | 1 | 3 | 1,2,4 | 2 | 1 | 3 | - |
| Ke | - | - | - | - | 1 | - | 1 | - | 1 | 2,5 | 3 | 3 | 5 | 5 | 4 | 1 | 1 | 1 | 1 | - | |
| Ks | - | - | - | - | 1 | - | 1 | - | 1 | - | - | - | - | - | - | 1 | 1 | 1 | 1 | - | |
| Cases | Objective Functions | Evaluating Indicators | Algorithms | |||
|---|---|---|---|---|---|---|
| ITLBO-S | TLBO | DE | PSO | |||
| Case 1 | WA | Best. | 0.750 | 0.720 | 0.720 | 0.720 |
| Avg. | 0.750 | 0.709 | 0.714 | 0.713 | ||
| Std. | 0 | 0.010 | 0.008 | 0.009 | ||
| PLV | Best. | 52.382 | 59.380 | 66.107 | 65.866 | |
| Avg. | 53.720 | 64.663 | 69.068 | 69.424 | ||
| Std. | 1.264 | 3.383 | 1.999 | 1.802 | ||
| Case 2 | WA | Best. | 0.710 | 0.690 | 0.600 | 0.620 |
| Avg. | 0.702 | 0.648 | 0.592 | 0.598 | ||
| Std. | 0.012 | 0.021 | 0.019 | 0.028 | ||
| PLV | Best. | 5.626 | 16.186 | 25.946 | 20.026 | |
| Avg. | 10.612 | 33.983 | 51.695 | 55.754 | ||
| Std. | 5.113 | 13.326 | 21.837 | 26.416 | ||
| Case 3 | WA | Best. | 0.650 | 0.620 | 0.600 | 0.600 |
| Avg. | 0.627 | 0.620 | 0.582 | 0.584 | ||
| Std. | 0.015 | 0 | 0.031 | 0.018 | ||
| PLV | Best. | 19.280 | 24.480 | 66.582 | 60.720 | |
| Avg. | 45.088 | 54.560 | 83.964 | 100.624 | ||
| Std. | 12.503 | 21.056 | 16.966 | 31.059 | ||
| Objective Functions | Evaluating Indicators | MR Tasks |  | ||
| Case 1 | Case 2 | Case 3 | |||
| WA | Best. | 0.520 | 0.492 | 0.450 | |
| Avg. | 0.520 | 0.461 | 0.430 | ||
| Std. | 0 | 0.023 | 0.008 | ||
| PLV | Best. | 57.862 | 16.580 | 6.400 | |
| Avg. | 65.7 | 21.337 | 11.447 | ||
| Std. | 3.276 | 2.789 | 2.686 | ||
| Time/s | Avg. | 173.2 | 240.8 | 321.8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhang, Y.; Su, X.; Wang, X. An Improved Optimization Algorithm for Aeronautical Maintenance and Repair Task Scheduling Problem. Mathematics 2022, 10, 3777. https://doi.org/10.3390/math10203777
Li C, Zhang Y, Su X, Wang X. An Improved Optimization Algorithm for Aeronautical Maintenance and Repair Task Scheduling Problem. Mathematics. 2022; 10(20):3777. https://doi.org/10.3390/math10203777
Chicago/Turabian StyleLi, Changjiu, Yong Zhang, Xichao Su, and Xinwei Wang. 2022. "An Improved Optimization Algorithm for Aeronautical Maintenance and Repair Task Scheduling Problem" Mathematics 10, no. 20: 3777. https://doi.org/10.3390/math10203777
APA StyleLi, C., Zhang, Y., Su, X., & Wang, X. (2022). An Improved Optimization Algorithm for Aeronautical Maintenance and Repair Task Scheduling Problem. Mathematics, 10(20), 3777. https://doi.org/10.3390/math10203777






