Some New Existence Results for Positive Periodic Solutions to First-Order Neutral Differential Equations with Variable Coefficients
Abstract
1. Introduction
- (1)
- (2)
2. Preliminaries
- (1)
- If is a constant c with then A has a continuous inverse on satisfying
- (2)
3. Main Results
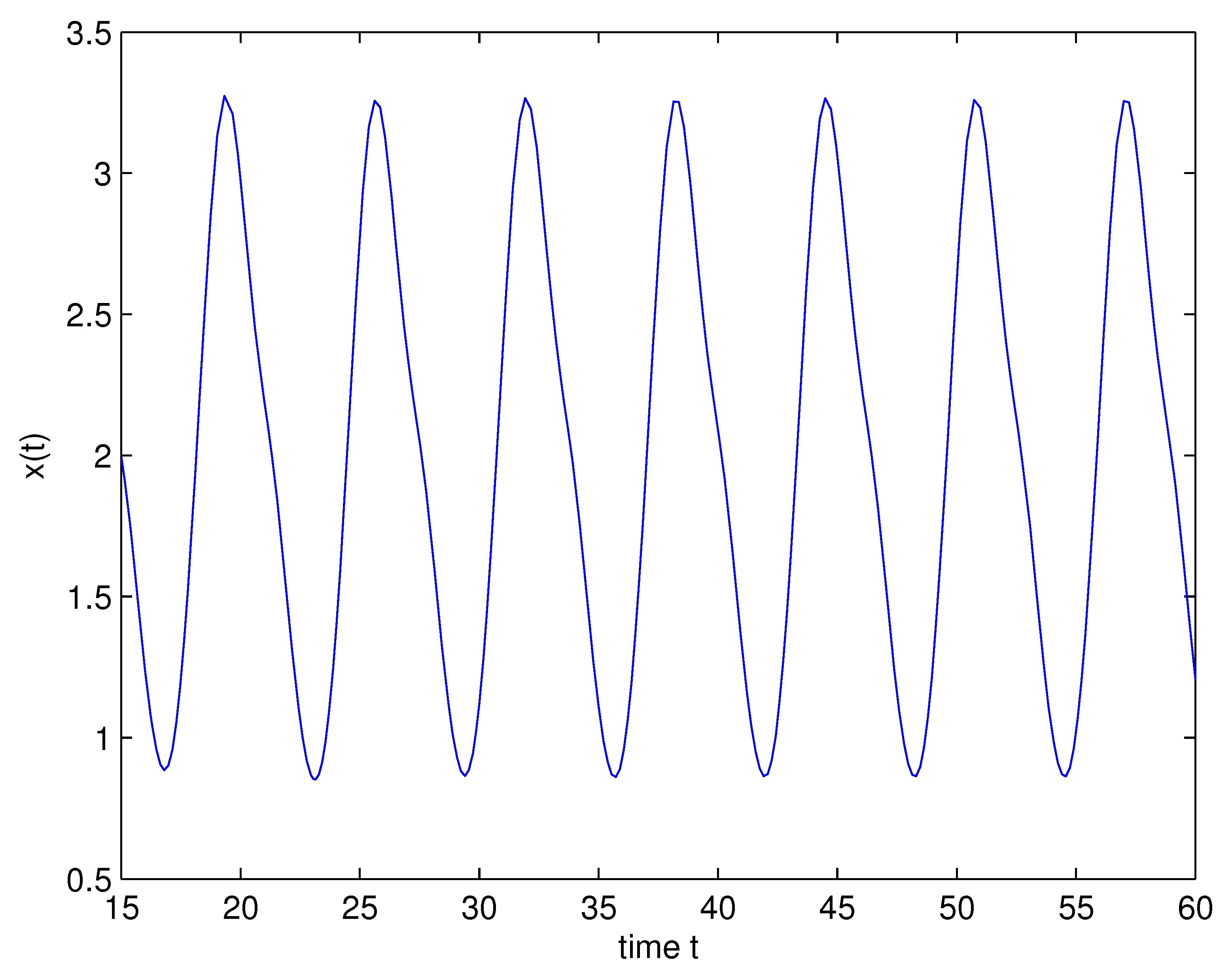
4. Example
5. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, Y.; Wang, W.; Shen, J. Existence of positive periodic solutions for two kinds of neutral functional differential equations. Appl. Math. Lett. 2008, 21, 581–587. [Google Scholar] [CrossRef]
- Candan, T. Existence of positive periodic solutions of first order neutral differential equations with variable coefficients. Appl. Math. Lett. 2016, 52, 142–148. [Google Scholar] [CrossRef]
- Luo, J.; Yu, J. Global asymptotic stability of nonautonomous mathematical ecological equations with distributed deviating arguments. Acta Math. Sin. 1998, 41, 1273–1282. [Google Scholar]
- Weng, P.; Liang, M. The existence and behavior of periodic solution of Hematopoiesis model. Math. Appl. 1995, 4, 434–439. [Google Scholar]
- Wan, A.; Jiang, D. Existence of positive periodic solutions for functional differential equations. Kyushu J. Math. 2002, 1, 193–202. [Google Scholar] [CrossRef][Green Version]
- Huang, C.; Yang, X.; Cao, J. Stability analysis of Nicholson’s blowfies equation with two different delays. Math. Comput. Simul. 2020, 171, 201–206. [Google Scholar] [CrossRef]
- Long, Z. Exponential convergence of a non-autonomous Nicholson’s blowfies model with an oscillating death rate. Electron. J. Qual. Theory Differ. Equ. 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Huang, Z. New results on global asymptotic stability for a class of delayed Nicholson’s blowfies model. Math. Meth. Appl. Sci. 2014, 37, 2697–2703. [Google Scholar] [CrossRef]
- Shu, H.; Wang, L.; Wu, J. Global dynamics of Nicholson’s blowflies equation revisited: Onset and termination of nonlinear oscillations. J. Differ. Equ. 2013, 255, 2565–2586. [Google Scholar] [CrossRef]
- Wang, W. Positive periodic solutions of delayed Nicholson’s blowflies models with a nonlinear density-dependent mortality term. Appl. Math. Model. 2012, 36, 4708–4713. [Google Scholar] [CrossRef]
- Gopalsamy, K. Stability and Oscillation in Delay Differential Equations of Population Dynamics; Kluwer Academic Press: Boston, MA, USA, 1992. [Google Scholar]
- Jiang, D.; Wei, J. Existence of positive periodic solutions for Volterra integro-differential equations. Acta Math. Sci. 2002, 21, 553–560. [Google Scholar] [CrossRef]
- Li, Y. Existence and global attractivity of a positive periodic solution of a class of delay differential equation. Sci. China 1998, 41, 273–284. [Google Scholar] [CrossRef]
- Lobo, J.; Valaulikar, Y. Group methods for first order neutral differential equations. Indian J. Math. 2021, 63, 263–282. [Google Scholar]
- Berezansky, L.; Braverman, E. Solution estimates and stability tests for linear neutral differential equations. Appl. Math. Lett. 2020, 108, 1–8. [Google Scholar] [CrossRef]
- Ghalia, S.; Affane, D. Control problem governed by an iterative differential inclusion. Rend. Del Circ. Mat. Palermo Ser. 2022, 2, 1–22. [Google Scholar] [CrossRef]
- Ngoc, L.; Long, N. On a first-order differential system with initial and nonlocal boundary conditions. Demonstr. Math. 2022, 55, 277–296. [Google Scholar] [CrossRef]
- Du, B.; Guo, L.; Ge, W.; Lu, S. Periodic solutions for generalized Liénard neutral equation with variable parameter. Nonlinear Anal. 2009, 70, 2387–2394. [Google Scholar] [CrossRef]
- Hale, J. Theory of Functional Differential Equations; Springer: New york, NY, USA, 1977. [Google Scholar]
- Zhang, M. Periodic solutions of linear and quasilinear neutral functional differential equations. J. Math. Anal. Appl. 1995, 189, 378–392. [Google Scholar] [CrossRef]
- Krasnoselskii, M.A. Positive Solutions of Operator Equations; Noordhoff: Gorninggen, The Netherlands, 1964. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Du, B. Some New Existence Results for Positive Periodic Solutions to First-Order Neutral Differential Equations with Variable Coefficients. Mathematics 2022, 10, 3770. https://doi.org/10.3390/math10203770
Zhang L, Du B. Some New Existence Results for Positive Periodic Solutions to First-Order Neutral Differential Equations with Variable Coefficients. Mathematics. 2022; 10(20):3770. https://doi.org/10.3390/math10203770
Chicago/Turabian StyleZhang, Lingping, and Bo Du. 2022. "Some New Existence Results for Positive Periodic Solutions to First-Order Neutral Differential Equations with Variable Coefficients" Mathematics 10, no. 20: 3770. https://doi.org/10.3390/math10203770
APA StyleZhang, L., & Du, B. (2022). Some New Existence Results for Positive Periodic Solutions to First-Order Neutral Differential Equations with Variable Coefficients. Mathematics, 10(20), 3770. https://doi.org/10.3390/math10203770





