A Revised Continuous Observation Length Model of Rough Contact without Adhesion
Abstract
1. Introduction
2. Theoretical Framework
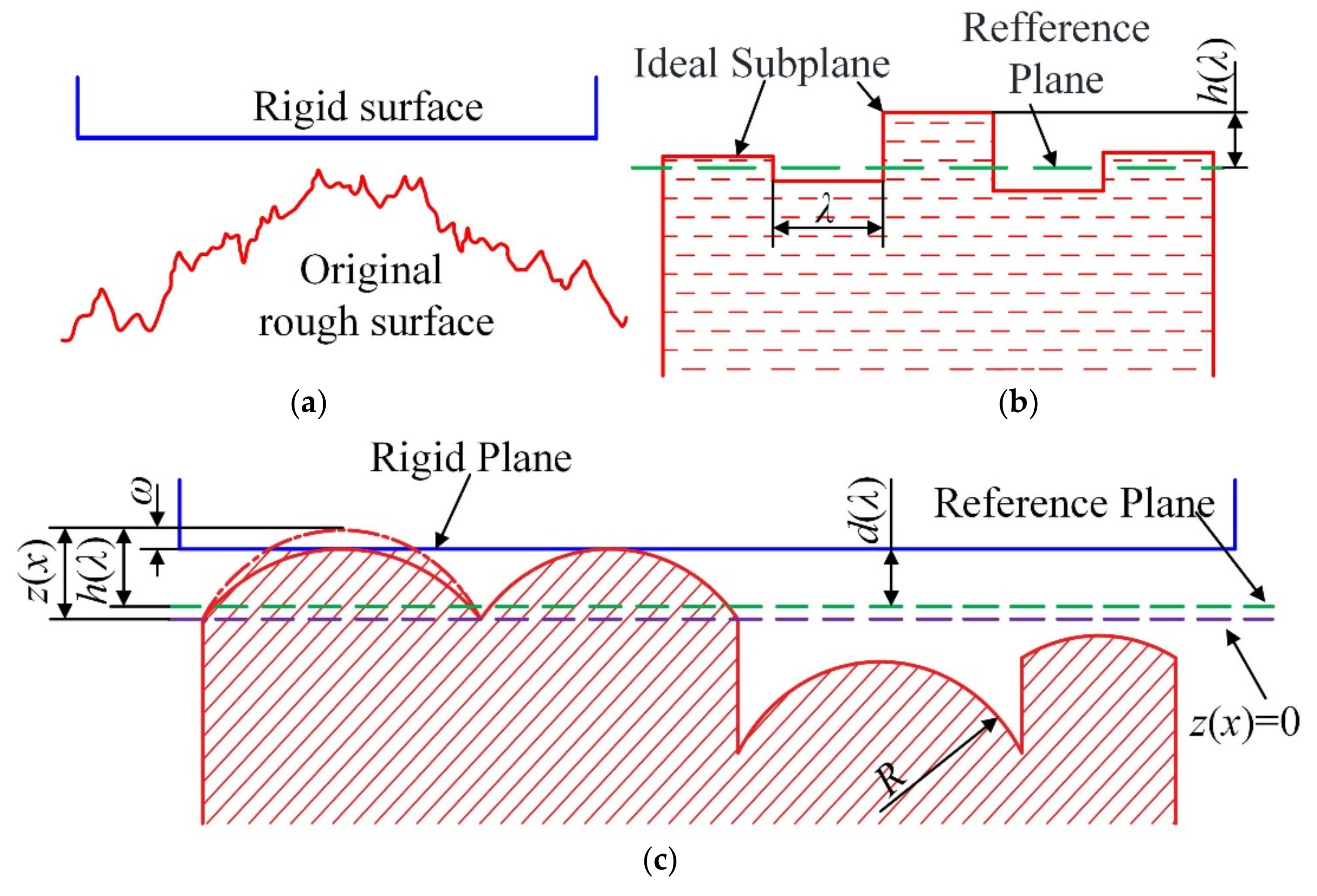
2.1. The OLD Model
2.1.1. The Standard Deviation
2.2. The Revised Continuous Observation Length Model
2.2.1. The Standard Deviation
2.2.2. Establishment of Contact Mechanics Model
2.3. Contact Areas and Mechanics
2.3.1. The Areas in Different Stages
2.3.2. The Relationship between F and ωe of Single Asperity
2.3.3. The Contact Force of the Surfaces in Different Stages
3. Numerical Results and Discussion
3.1. Surface Fractal Parameters
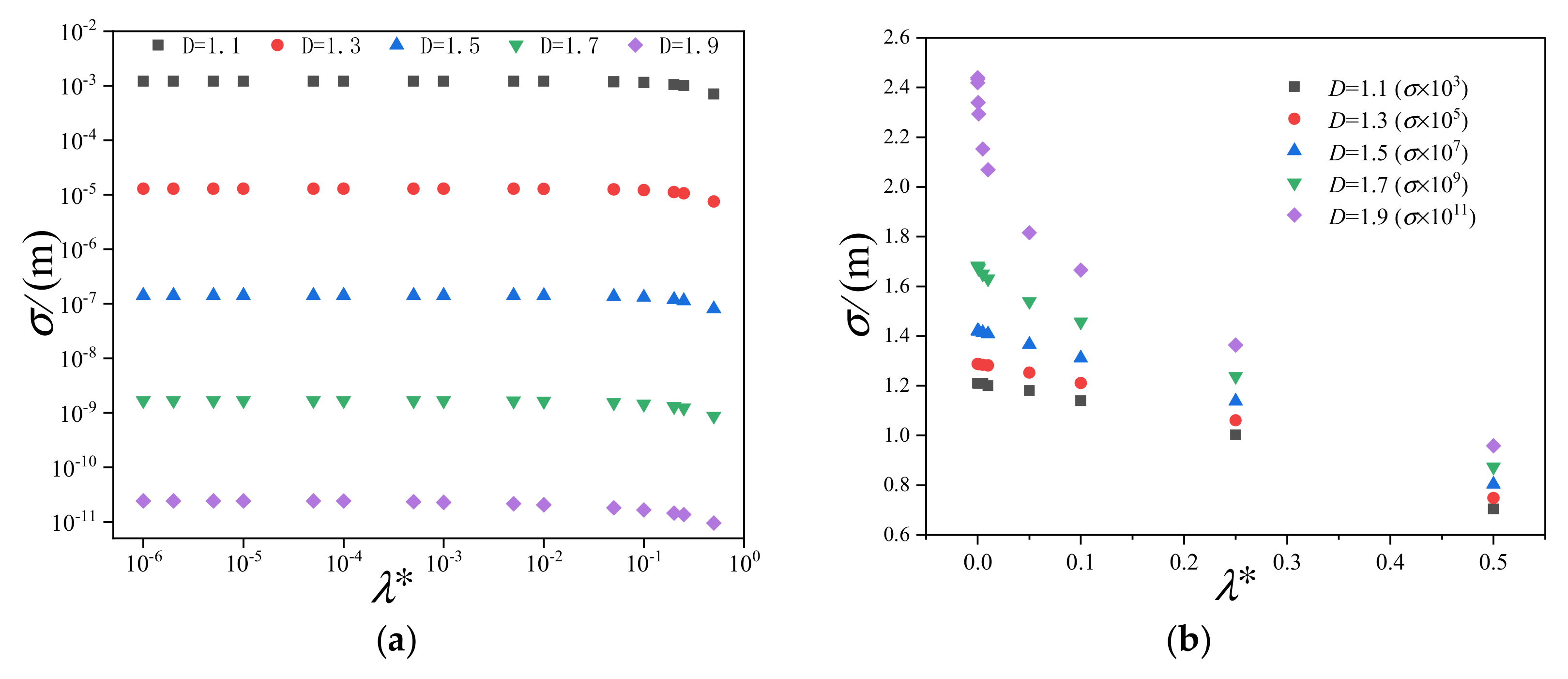
3.1.1. The Influence of the Fractal Dimension
3.1.2. The Influence of the Equivalent Modulus
3.2. Model Comparison
4. Conclusions
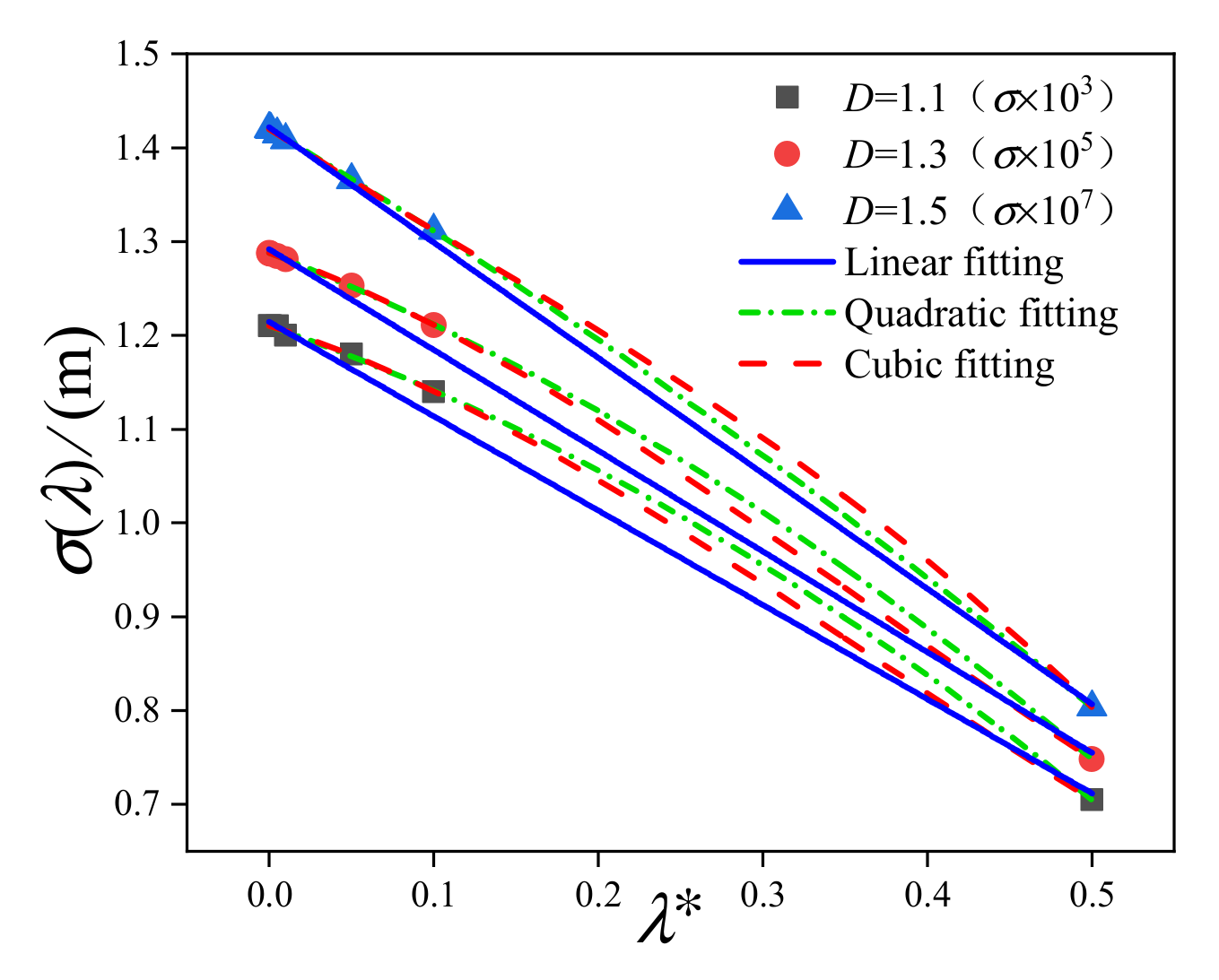
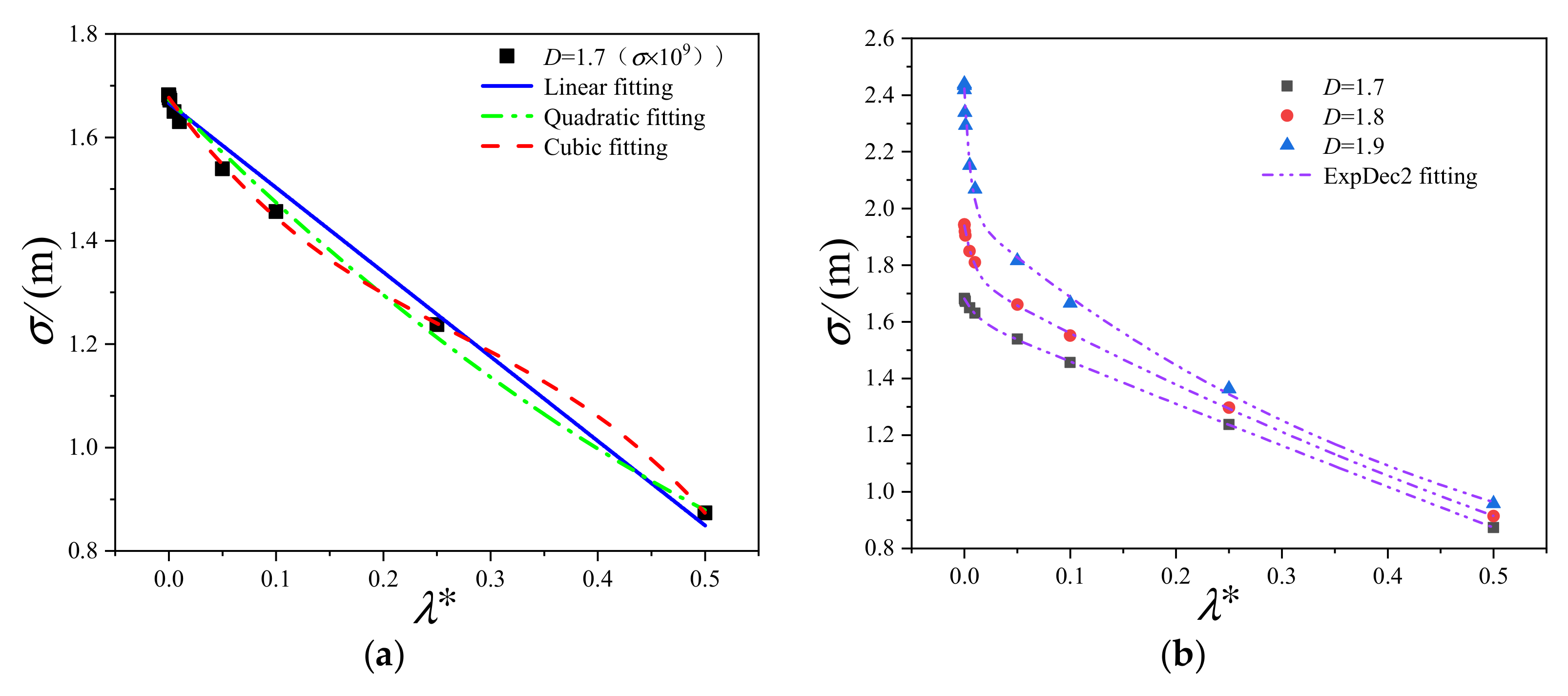
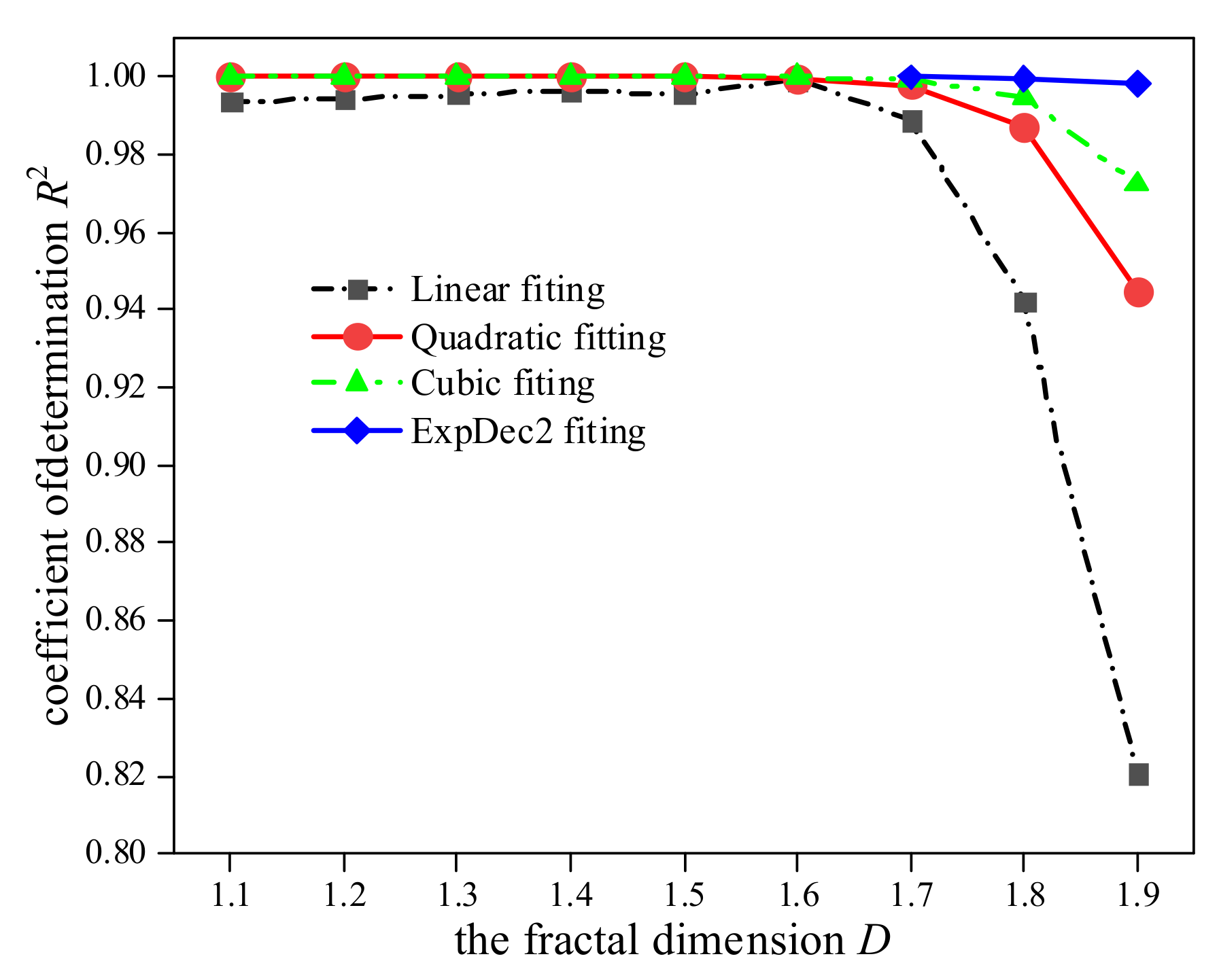
- When the fractal dimension D is different, the fitting relationship between the standard deviation and observation length is also different. For D ≤ 1.5, the polynomial fitting is the best. For D = 1.6, the quadratic polynomial fitting is more in line. For D ≥ 1.7, the ExpDec2 function fitting is better than the other fitting methods. The larger the D, the larger the error of the linear fitting.
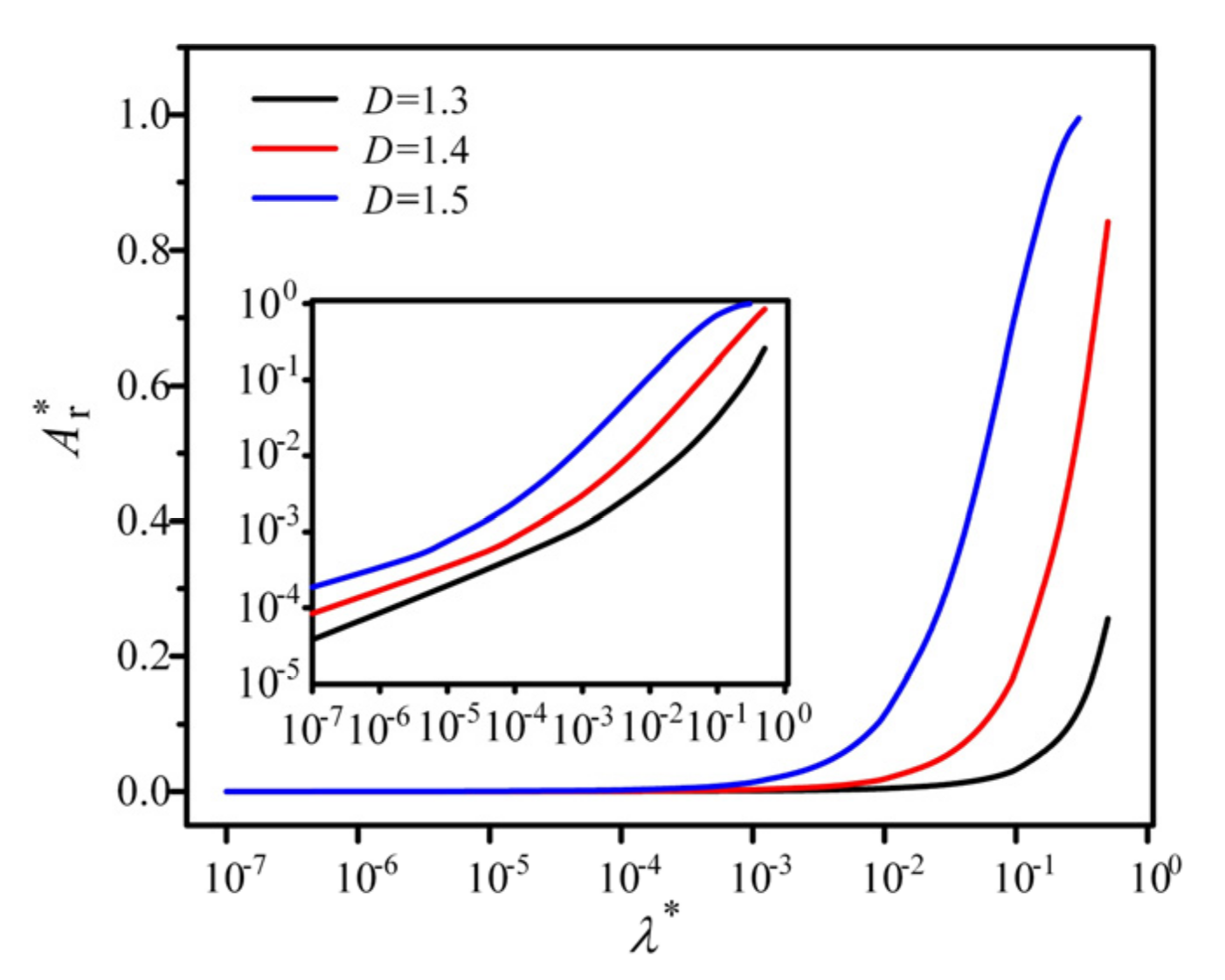
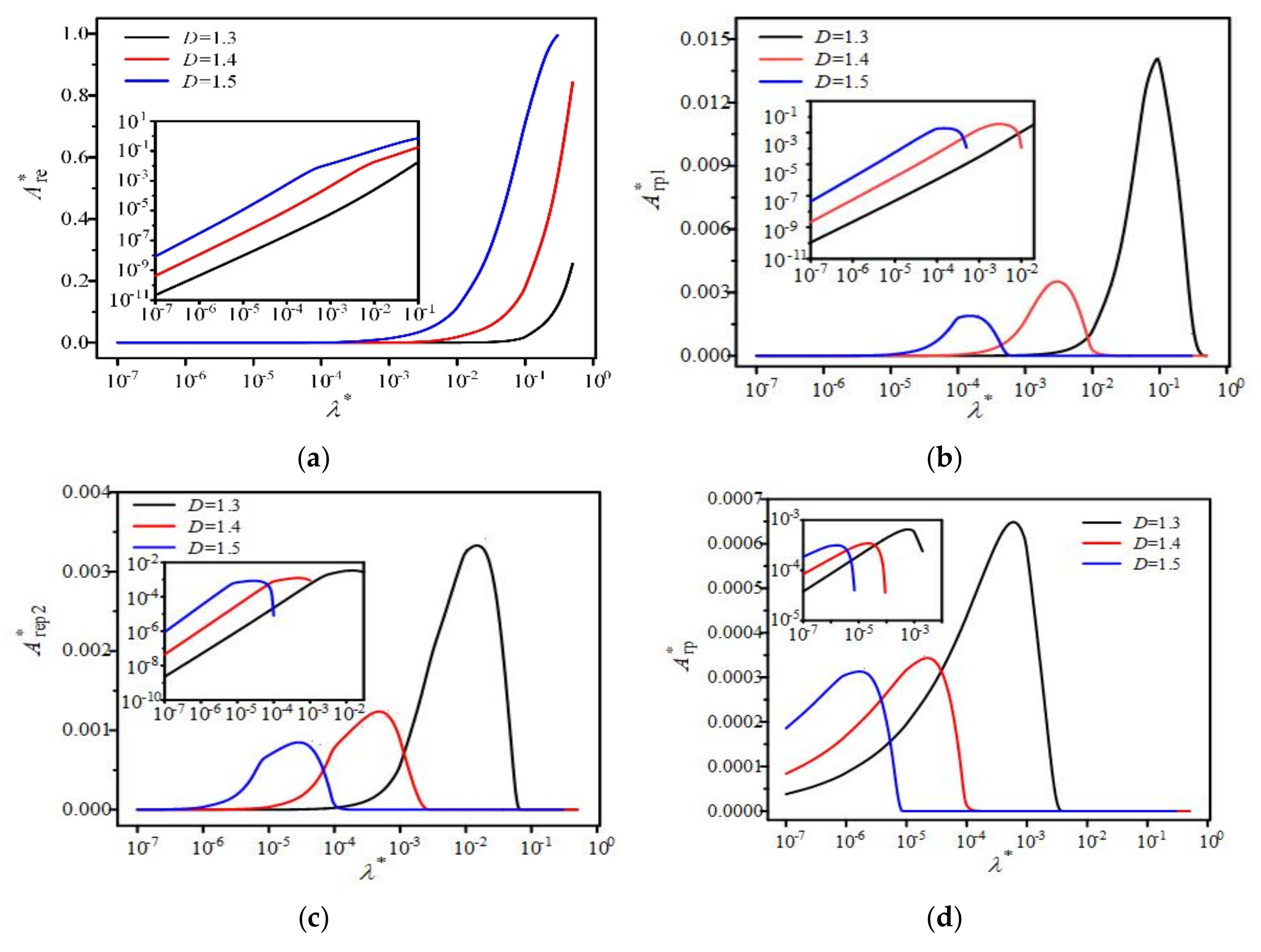
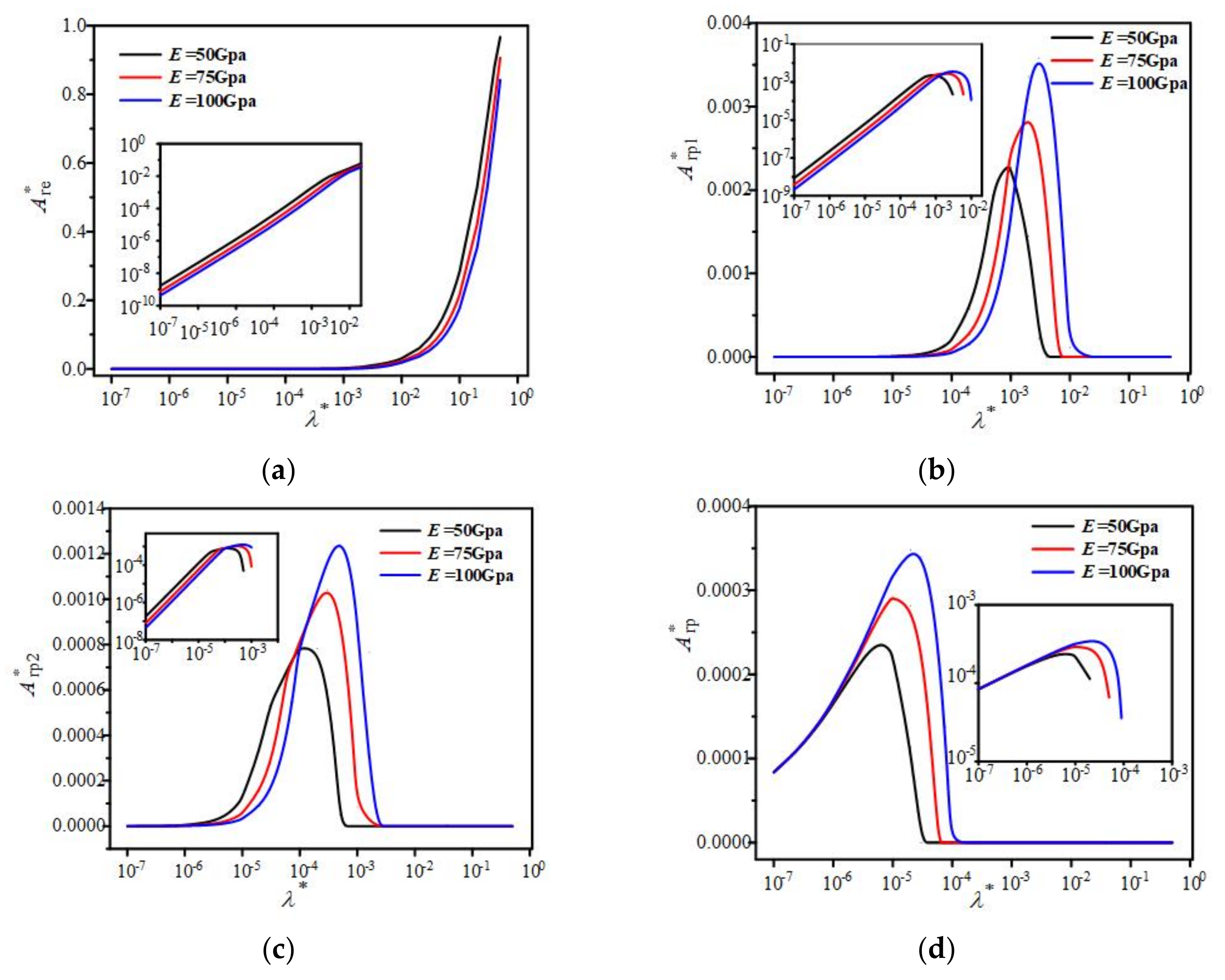
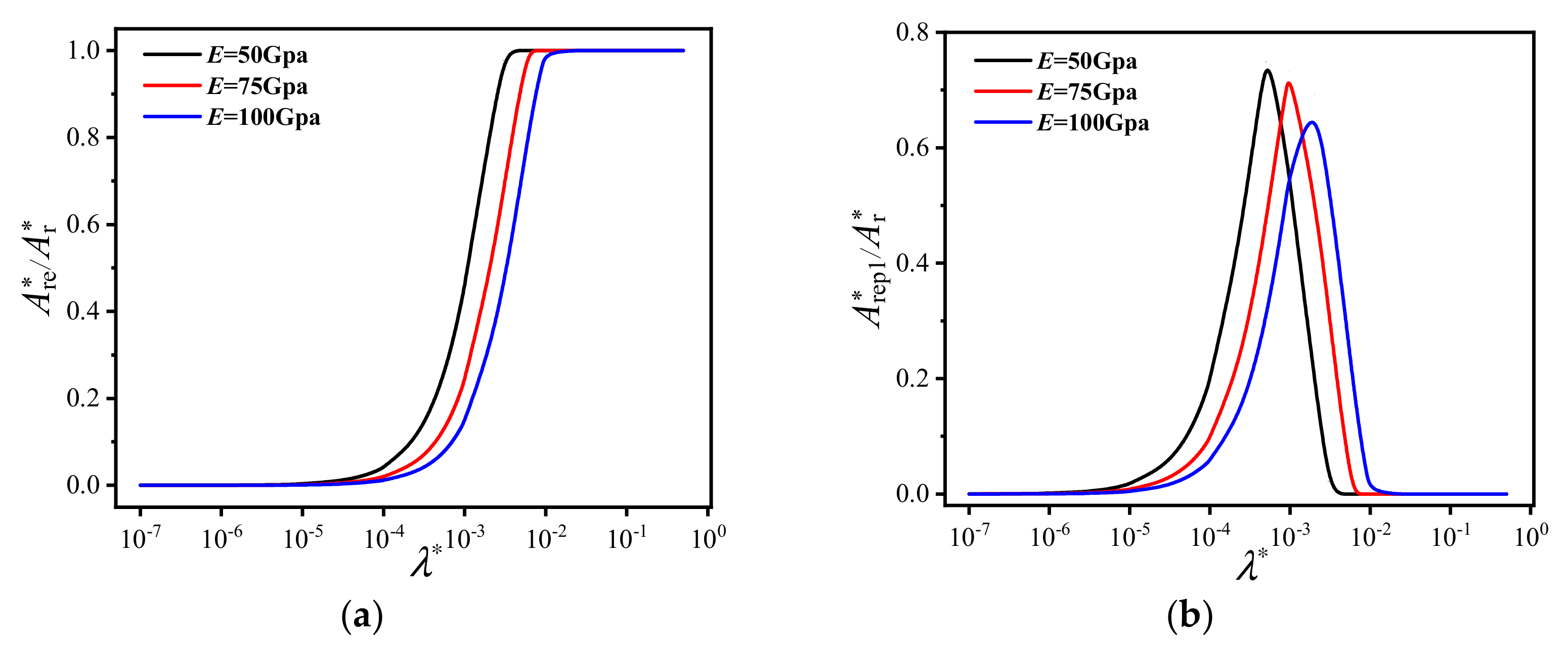
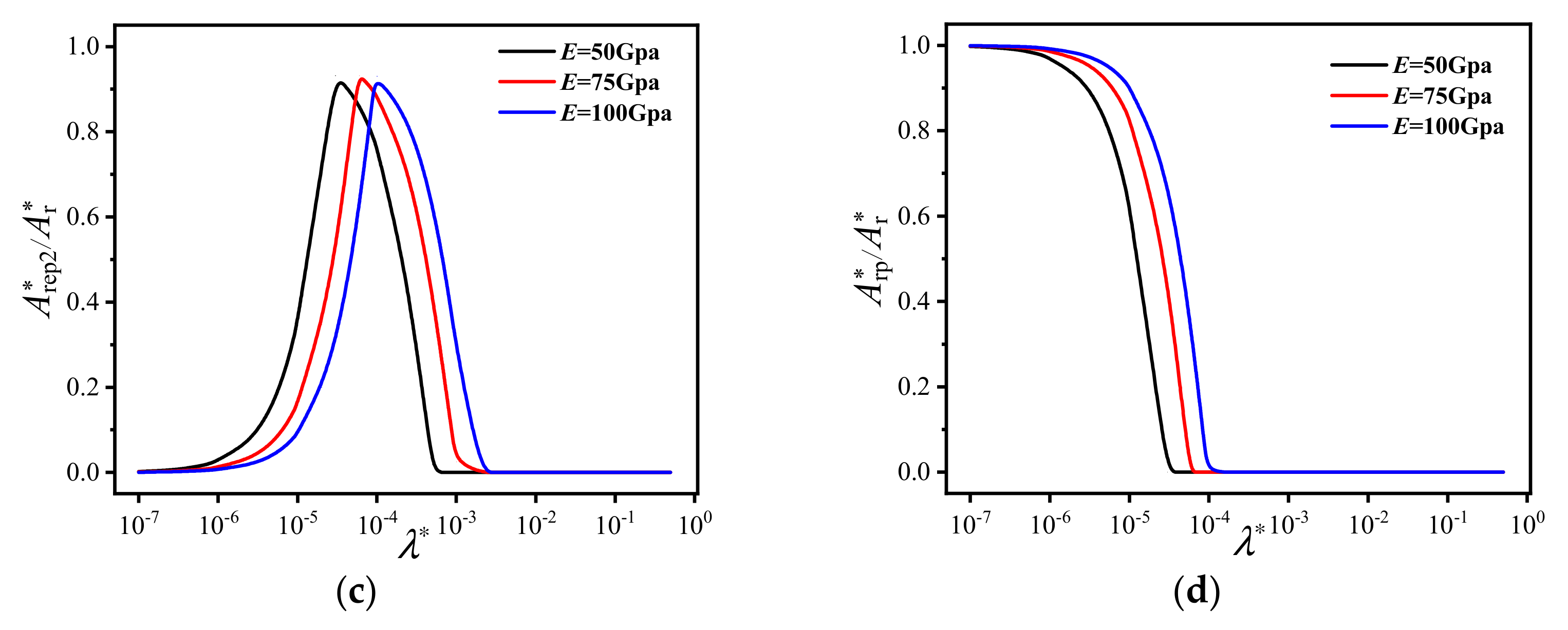
- As λ* reduces, the areas Ar* and Are* decrease, and in the other three stages, the areas rise to the peaks before decreasing to a small value. The values of the peaks and the values of λ* where peaks occur are related to D and E. As λ* reduces, the proportion of Are* decreases, the proportion of Arep* rises to the peak before similarly decreasing to a small value, and the proportion of Arp* increases. When λ* reduces to a certain value, the proportion of Arp* approaches 1, and the proportion of Arep1* is larger than Arep2*.
- As D increases, the area Ar* increases. The values of the peaks and λ* where peaks occur reduce with rising D. As E increases, the area Are* drops quicker when λ* decreases. Additionally, the values of the peaks and λ* where peaks occur decrease with the increase in E.
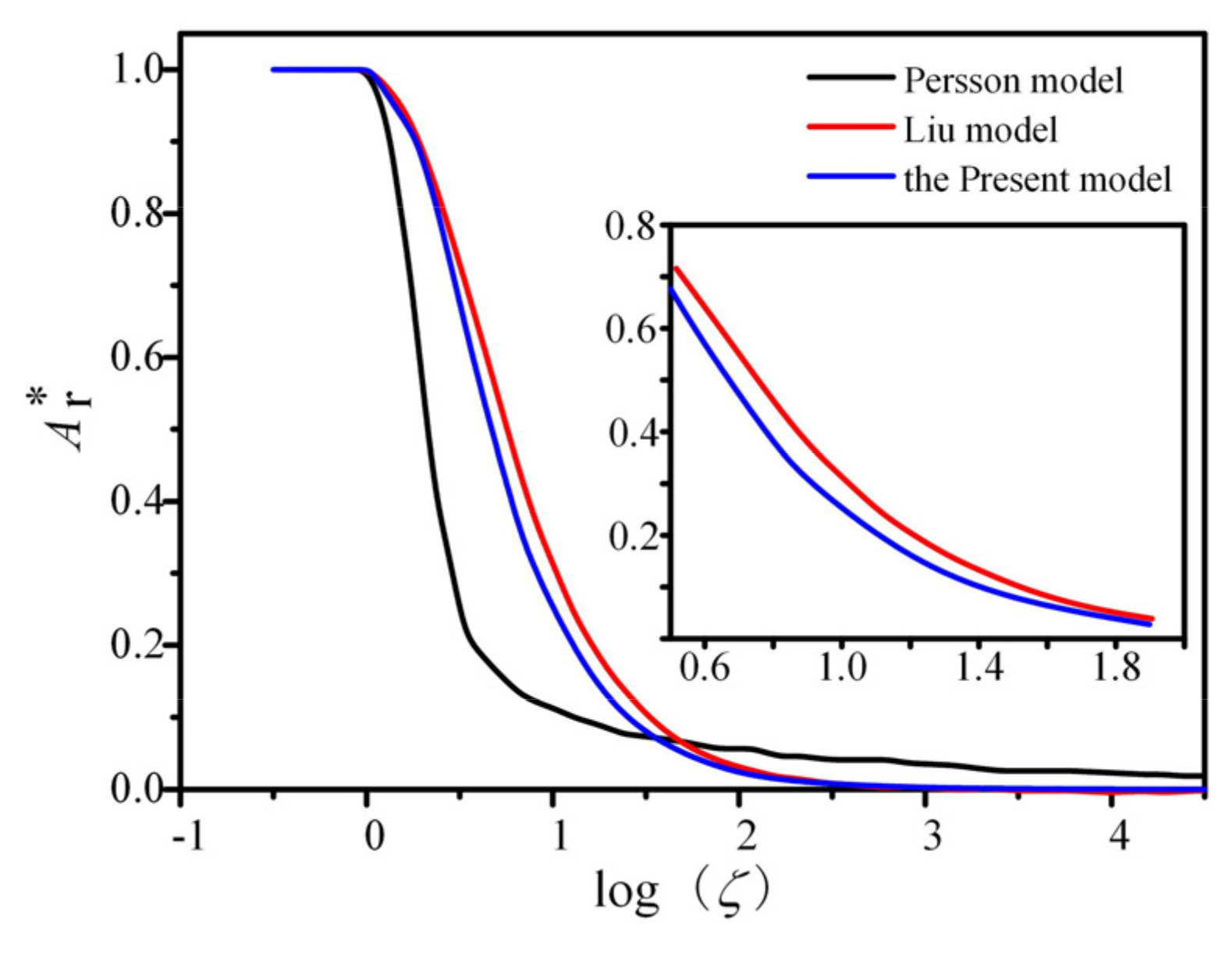
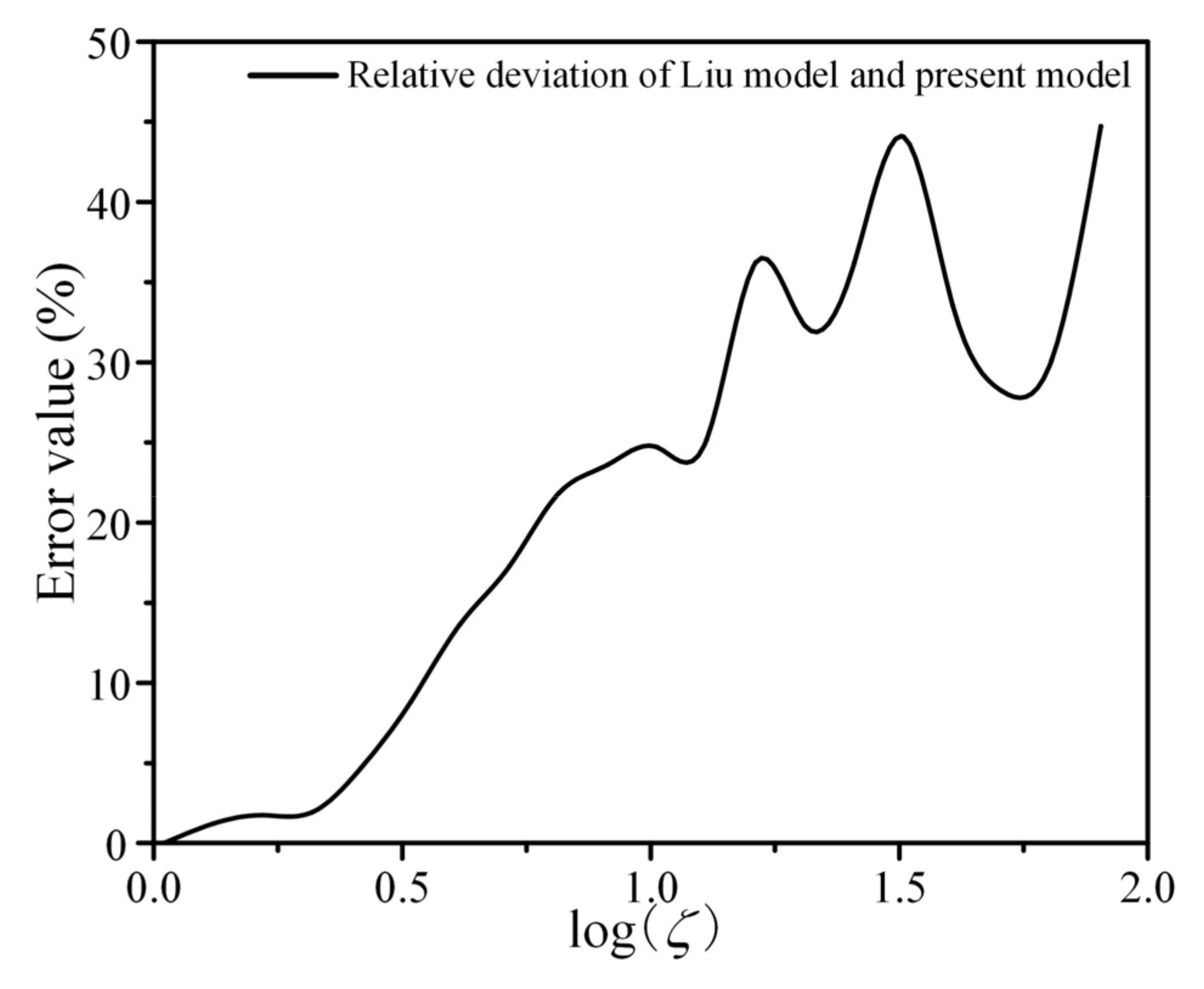
- The dimensionless real contact area of the present model is in good agreement with the Persson model and the Liu model in terms of variation patterns.
- The present model can accurately describe the contact characteristics of rough surfaces and the monotonicity and continuity in contact processes. The research results provide a theoretical basis for analyzing the contact characteristics on rough surfaces and designing a contact surface topography.
5. The Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| λ | the observation length, m |
| λ* | the observation scale |
| λ0 | the critical value of observation length |
| x | the height of the ideal subplane |
| σ | the standard deviation |
| σ (λ) | the standard deviation of the ideal subplane |
| h(λ) | the height of the ideal subplane |
| h(λ) | the average height of the ideal subplane |
| d(λ) | the separation at the observation length λ, m |
| R2 | the coefficient of determination |
| z(x) | the height of the surface profile |
| L0 | the sample length, m |
| nl | the minimum frequency index |
| γn | spatial frequency |
| D | the surface fractal dimension |
| G | the fractal roughness, m |
| K | the hardness coefficient |
| ν | the Poisson ratio |
| H | the hardness of the softer material, MPa |
| σY | the yield strength, MPa |
| R | the asperity curvature radius, m |
| E1, E2 | Young’s modulus of two contacting surfaces |
| ν1, ν2 | Poisson’s ratios of two contacting surfaces |
| E | the equivalent modulus of Hertzian elasticity |
| Ar | the real area of contact surface, m2 |
| Are | the elastic contact area, m2 |
| Arep1 | the real area in the first stage of elastoplastic contact, m2 |
| Arep2 | the real area in the second stage of elastoplastic contact, m2 |
| Arp | the real plastic contact area, m2 |
| A0 | the nominal area, m2 |
| A | the elastic dimensionless contact area |
| Arep1* | the dimensionless area in the first stage of elastoplastic contact |
| Arep2* | the dimensionless area in the second stage of elastoplastic contact |
| Arp* | the plastic dimensionless contact area |
| Ar* | the total dimensionless contact area |
| Fec | the critical contact force, N |
| Fre | the contact force of single asperity in elastic contact, N |
| Frep1 | the contact force of single asperity in the first stage of elastoplastic contact, N |
| Frep2 | the contact force of single asperity in the second stage of elastoplastic contact, N |
| Frp | the contact force of single asperity in plastic contact, N |
| Pr | the total surface contact force |
| Pre | the plastic contact forces, N |
| Prep1* | the dimensionless force in the first stage of elastoplastic contact |
| Prep2* | the dimensionless force in the second stage of elastoplastic contact |
| Prp* | the plastic dimensionless contact force |
| Pr* | the total dimensionless contact force |
| σ0 | the mean contact stress, MPa |
| RMS | the root mean square of rough surface |
| ζ | the magnification |
References
- Bowden, F.P.; Tabor, D. The Hardness of Metals; Clarendon Press: Oxford, UK, 1951; pp. 279–281. [Google Scholar]
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Chang, W.; Etsion, I.; Bogy, D.B. An Elastic-Plastic Model for the Contact of Rough Surfaces. J. Tribol. 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Xu, Y.; Jackson, R.L.; Marghitu, D.B. Statistical model of nearly complete elastic rough surface contact. Int. J. Solids Struct. 2014, 51, 1075–1088. [Google Scholar] [CrossRef]
- Bhushan, B.; Majumdar, A. Role of Fractal Geometry in Roughness Characterization and Contact Mechanics of Surface. J. Tribol. 1990, 112, 205–216. [Google Scholar] [CrossRef]
- Zhao, Y.; Maietta, D.M.; Chang, L. An Asperity Microcontact Model Incorporating the Transition from Elastic Deformation to Fully Plastic Flow. J. Tribol. 2000, 122, 86–93. [Google Scholar] [CrossRef]
- Liou, J.L.; Lin, J.F. A modified fractal microcontact model developed for asperity heights with variable morphology parameters. Wear 2010, 268, 133–144. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. Trans. ASME 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Morag, Y.; Etsion, I. Resolving the contradiction of asperities plastic to elastic mode transition in current contact models of fractal rough surfaces. Wear 2007, 262, 624–629. [Google Scholar] [CrossRef]
- Yuan, Y.; Gan, L.; Liu, K.; Yang, X. Elastoplastic contact mechanics model of rough surface based on fractal theory. Chin. J. Mech. Eng. 2017, 30, 207–215. [Google Scholar] [CrossRef]
- Hanaor, D.A.H.; Gan, Y.X.; Einav, I. Contact mechanics of fractal surfaces by spline assisted discretisation. Int. J. Solids Struct. 2015, 59, 121–131. [Google Scholar] [CrossRef]
- Pan, W.; Song, C.; Ling, L.; Qu, H.; Wang, M. Unloading contact mechanics analysis of elastic–plastic fractal surface. Arch. Appl. Mech. 2021, 91, 2697–2712. [Google Scholar] [CrossRef]
- Wen, Y.; Tang, J.; Zhou, W.; Li, L.; Zhu, C. New analytical model of elastic-plastic contact for three-dimensional rough surfaces considering interaction of asperities. Friction 2021, 10, 217–231. [Google Scholar] [CrossRef]
- Zhang, W.; Jin, F.; Zhang, S.L.; Guo, X. Adhesive Contact on Randomly Rough Surfaces Based on the Double-Hertz Model. J. Appl. Mech. Trans. ASME 2014, 81, 051008. [Google Scholar] [CrossRef]
- Song, H.; Van der Giessen, E.; Liu, X. Strain gradient plasticity analysis of elasto-plastic contact between rough surfaces. J. Mech. Phys. Solids 2016, 96, 18–28. [Google Scholar] [CrossRef]
- Song, H.; Vakis, A.I.; Liu, X.; Van der Giessen, E. Statistical model of rough surface contact accounting for size-dependent plasticity and asperity interaction. J. Mech. Phys. Solids 2017, 106, 1–14. [Google Scholar] [CrossRef]
- Kuzkin, V.A.; Kachanov, M. Contact of rough surfaces: Conductance-stiffness connection for contacting transversely isotropic half-spaces. Int. J. Eng. Sci. 2015, 97, 1–5. [Google Scholar] [CrossRef]
- Jin, F.; Wan, Q.; Guo, X. Plane Contact and Partial Slip Behaviors of Elastic Layers With Randomly Rough Surfaces. J. Appl. Mech. Trans. ASME 2015, 82, 091006. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, F.; Liu, P.; Fan, H. Research on fractal model of normal contact stiffness between two spheroidal joint surfaces considering friction factor. Tribol. Int. 2016, 97, 253–264. [Google Scholar] [CrossRef]
- Pan, W.; Li, X.; Wang, L.; Guo, N.; Mu, J. A normal contact stiffness fractal prediction model of dry-friction rough surface and experimental verification. Eur. J. Mech. A Solids 2017, 66, 94–102. [Google Scholar] [CrossRef]
- Wang, R.; Zhu, L.; Zhu, C. Research on fractal model of normal contact stiffness for mechanical joint considering asperity interaction. Int. J. Mech. Sci. 2017, 134, 357–369. [Google Scholar] [CrossRef]
- Zhai, C.; Hanaor, D.; Gan, Y. Contact stiffness of multiscale surfaces by truncation analysis. Int. J. Mech. Sci. 2017, 131, 305–316. [Google Scholar] [CrossRef]
- Yuan, Y.; Chen, J.J.; Zhang, L.H. Loading-unloading contact model between three-dimensional fractal rough surfaces. AIP Adv. 2018, 8, 075017. [Google Scholar] [CrossRef]
- Wang, H.H.; Jia, P.; Wang, L.Q.; Yun, F.H.; Wang, G.; Liu, M.; Wang, X.Y. Modeling of the Loading-Unloading Contact of Two Cylindrical Rough Surfaces with Friction. Appl. Sci. 2020, 10, 742. [Google Scholar] [CrossRef]
- Persson, B.N.J. Contact Mechanics for Randomly Rough Surfaces. Surf. Sci. Rep. 2006, 61, 201–227. [Google Scholar] [CrossRef]
- Afferrante, L.; Bottiglione, F.; Putignano, C.; Persson, B.N.J.; Carbone, G. Elastic Contact Mechanics of Randomly Rough Surfaces: An Assessment of Advanced Asperity Models and Persson’s Theory. Tribol. Lett. 2018, 66, 75. [Google Scholar] [CrossRef]
- Ciavarella, M. An approximate JKR solution for a general contact, including rough contacts. J. Mech. Phys. Solids 2018, 114, 209–218. [Google Scholar] [CrossRef]
- Guo, X.; Ma, B.B.; Zhu, Y.C. A magnification-based multi-asperity (MBMA) model of rough contact without adhesion. J. Mech. Phys. Solids 2019, 133, 103724. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, L.; Wang, L.Q.; Liu, H.X.; Sun, Y.Q.; Wang, Y.J. The leakage analysis of submarine pipeline connecter based on a new fractal porous media model. Desalin. Water Treat. 2020, 188, 390–399. [Google Scholar] [CrossRef]
- Lorenz, B.; Persson, B.N.J. Leak rate of seals: Effective-medium theory and comparison with experiment. Eur. Phys. J. E 2010, 31, 159–167. [Google Scholar] [CrossRef]
- Persson, B.N.J. Leakage of Metallic Seals: Role of Plastic Deformations. Tribol. Lett. 2016, 63, 42. [Google Scholar] [CrossRef]
- Lorenz, B.; Rodriguez, N.; Mangiagalli, P.; Persson, B.N.J. Role of hydrophobicity on interfacial fluid flow: Theory and some applications. Eur. Phys. J. E 2014, 37, 57. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, N.; Dorogin, L.; Chew, K.T.; Persson, B.N.J. Adhesion, friction and viscoelastic properties for non-aged and aged Styrene Butadiene rubber. Tribol. Int. 2018, 121, 78–83. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Scaraggi, M. Theory of adhesion: Role of surface roughness. J. Chem. Phys. 2014, 141, 124701. [Google Scholar] [CrossRef] [PubMed]
- Persson, B.N.J. The dependency of adhesion and friction on electrostatic attraction. J. Chem. Phys. 2018, 148, 144701. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, A.; Dorogin, L.; Tahir, M.; Stockelhuber, K.W.; Heinrich, G.; Espallargas, N.; Persson, B.N.J. Rubber contact mechanics: Adhesion, friction and leakage of seals. Soft Matter 2017, 13, 9103–9121. [Google Scholar] [CrossRef] [PubMed]
- Persson, B.N.J.; Scaraggi, M. Some Comments on Hydrogel and Cartilage Contact Mechanics and Friction. Tribol. Lett. 2018, 66, 23. [Google Scholar] [CrossRef]
- Lorenz, B.; Persson, B.N.J. Leak rate of seals: Comparison of theory with experiment. Europhys. Lett. 2009, 86, 44006. [Google Scholar] [CrossRef]


| Parameters | Values and Units |
|---|---|
| D | 1.1~1.9 |
| G | 10−12 m |
| L0 | 0.01 m |
| λmin | 1.0 × 10−9 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wen, J.; Liu, M.; Xing, G. A Revised Continuous Observation Length Model of Rough Contact without Adhesion. Mathematics 2022, 10, 3764. https://doi.org/10.3390/math10203764
Zhang L, Wen J, Liu M, Xing G. A Revised Continuous Observation Length Model of Rough Contact without Adhesion. Mathematics. 2022; 10(20):3764. https://doi.org/10.3390/math10203764
Chicago/Turabian StyleZhang, Lan, Jing Wen, Ming Liu, and Guangzhen Xing. 2022. "A Revised Continuous Observation Length Model of Rough Contact without Adhesion" Mathematics 10, no. 20: 3764. https://doi.org/10.3390/math10203764
APA StyleZhang, L., Wen, J., Liu, M., & Xing, G. (2022). A Revised Continuous Observation Length Model of Rough Contact without Adhesion. Mathematics, 10(20), 3764. https://doi.org/10.3390/math10203764






