Signorini-Type Problems over Non-Convex Sets for Composite Bodies Contacting by Sharp Edges of Rigid Inclusions

Abstract

A new type of non-classical 2D contact problem formulated over non-convex admissible sets is proposed. Specifically, we suppose that a composite body in its undeformed state touches a wedge-shaped rigid obstacle at a single contact point. Composite bodies under investigation consist of an elastic matrix and a rigid inclusion. In this case, the displacements on the set, corresponding to a rigid inclusion, have a predetermined structure that describes possible parallel shifts and rotations of the inclusion. The rigid inclusion is located on the external boundary and has the form of a wedge. The presence of the rigid inclusion imposes a new type of non-penetration condition for certain geometrical configurations of the obstacle and the body near the contact point. The sharp-shaped edges of the obstacle effect such sets of admissible displacements that may be non-convex. For the case of a thin rigid inclusion, which is described by a curve and a volume (bulk) rigid inclusion specified in a subdomain, the energy minimization problems are formulated. The solvability of the corresponding boundary value problems is proved, based on analysis of auxiliary minimization problems formulated over convex sets. Qualitative properties of the auxiliary variational problems are revealed; in particular, we have found their equivalent differential formulations. As the most important result of this study, we provide justification for a new type of mathematical model for 2D contact problems for reinforced composite bodies.

1. Introduction

There are various studies related to problems describing contact of elastic bodies with rigid or elastic obstacles, see for example [1,2,3,4,5,6,7,8,9,10]. For an overview of contact problems we refer to [11,12,13,14,15]. The classical Signorini-type condition supposes sufficient regularity for a part of a body boundary, where non-penetration conditions are imposed. We refer to the paper [16], in which free boundary problems for elastic bodies with a rigid inclusion being in contact with another rigid non-deformable punch were proposed and investigated for the first time. Crack problems with unilateral non-penetration conditions between crack faces (see, for example [17,18,19,20,21,22,23,24,25,26]) are a special subclass of contact problems. Furthermore, by passages to the limits when rigidity parameters for a family of crack problems go to infinity, convergences of corresponding solutions to appropriate solutions of contact problems with the Signorini-type conditions were established in [27,28,29].

In this article, we pay attention to variational problems describing a point contact of composite objects having sharp-shaped edges. Specifically, we study mathematical models describing the equilibrium of elastic bodies containing a rigid inclusion in the form of an external wedge. In contrast to [16], we propose a class of non-linear contact problems, where non-penetration conditions can be written for a single point located on the sharp edge. Due to the presence of rigid inclusions, we can rewrite the non-penetration condition in the form of three sets of inequalities, where each system describes three possible cases of rigid body deformations.

The contact problems are formulated as minimization problems of the energy functional over sets of admissible displacements. The existence of variational solutions (at least one and at most three) has been proved. For three auxiliary problems, each set of admissible displacements is convex and closed and the energy functional is coercive, strictly convex and weakly lower semi-continuous on a suitable Sobolev space. These properties allow us to establish the existence and uniqueness of solutions for each auxiliary minimization problem over sole sets. The issue of uniqueness of a solution for the reference minimization problem over all three sets simultaneously is an open question. For the auxiliary variational problems formulated over sole sets, equivalent differential conditions have been derived.

2. The Case of a Thin Rigid Inclusion

Let us formulate a contact problem for an elastic body containing a rigid inclusion on the external boundary. Such configuration may describe bodies covered by coatings. Consider a bounded simply connected domain $\Omega \subset {\mathbb{R}}^2$ with the boundary $\Gamma \in C^{0,1}$, which consists of two continuous curves $\Gamma ={\Gamma }_1\cup {\Gamma }_2$, ${\Gamma }_1\cap {\Gamma }_2=\varnothing$, $\mathrm{meas}\left({\Gamma }_1\right)>0$. We suppose that the curve comprised of two line segments

$$\gamma =[0,1]\times \left\{0\right\}\cup \left\{(x_1,x_2)\right|0\le x_1\le 1,x_2=\alpha x_1\},0<\alpha <\infty ,$$

is a part of ${\Gamma }_2$, such that $\gamma \subset \mathrm{int}\left({\Gamma }_2\right)$ (see Figure 1). For the construction of rigid displacements in what follows, the domain $\Omega$ is considered to be part of the planar wedge, which continues the sides of $\gamma$. We assume that a thin rigid inclusion is given by $\gamma$, and a rigid obstacle is given by the other planar wedge

$$O=\{-\infty <x_1\le 0,k_2{x}_1\le x_2\le k_1{x}_1\},-\infty <k_1<0<\alpha \le k_2<\infty .$$

Denote by $W=(w_1,w_2)$ the displacement vector. We suppose that the body is fixed on the part ${\Gamma }_1$ of the boundary, i.e.,

$$W=(0,0)\mathrm{on}{\Gamma }_1.$$

(1)

Introduce the Sobolev spaces

$$H_{{\Gamma }_1}^{1,0}(\Omega )=\{w\in H^1(\Omega )\mid w=0\mathrm{on}{\Gamma }_1\},H(\Omega )=H_{{\Gamma }_1}^{1,0}{(\Omega )}^2.$$

From the plane elasticity, we recall the strain and stress tensors describing deformation of the body

$${\epsilon }_{ij}\left(W\right)=\frac{1}{2}(w_{i,j}+w_{j,i}),{\sigma }_{ij}\left(W\right)=c_{ijkl}{\epsilon }_{kl}\left(W\right),i,j=1,2,$$

(2)

where the comma in the first formula in (2) implies a convention for derivatives, and summation over repeated indexes is assumed. The tensor of elastic coefficients is given by entries $c_{ijkl}$ assumed to be symmetric and positive definite:

$$c_{ijkl}=c_{klij}=c_{jikl},i,j,k,l=1,2,c_{ijkl}\in L^{\infty }(\Omega ),$$

$$c_{ijkl}{\xi }_{ij}{\xi }_{kl}\ge c_0{\left|\xi \right|}^2,\forall \xi ,{\xi }_{ij}={\xi }_{ji},i,j=1,2,c_0=const>0.$$

The well-known Korn inequality has the following form:

$$\underset{\Omega }{\int }{\sigma }_{ij}\left(W\right){\epsilon }_{ij}\left(W\right)\ge c{\parallel W\parallel }_{H(\Omega )}^2,\forall W\in H(\Omega ),$$

(3)

where the constant $c>0$ is independent of W. To provide a variational formulation describing the equilibrium state for the body with the rigid inclusion $\gamma$, we introduce the energy functional

$$\Pi \left(W\right)=\frac{1}{2}\underset{\Omega }{\int }{\sigma }_{ij}\left(W\right){\epsilon }_{ij}\left(W\right)-\underset{\Omega }{\int }FW,$$

where the vector $F=(f_1,f_2)\in L^2{(\Omega )}^2$ describes the external forces acting on the body, $FW=f_i{w}_i$. The Korn inequality (3) guarantees coercivity for the energy functional $\Pi$.

Let us provide arguments justifying non-penetration conditions between the rigid inclusion $\gamma$ and the rigid obstacle O in the specific geometry configuration. Here, we should note that our reasoning relies on assumption of the infinitesimal displacements within linearized elasticity. We assume that the body in the undeformed state lies in front of the sharp-shaped obstacle O (see Figure 1). The space of infinitesimal rigid displacements $R\left(\gamma \right)$ is defined according to the following general relations [14]:

$$R\left(Z\right)=\{\rho =({\rho }_1,{\rho }_2)|\rho \left(x\right)=b(x_2,-x_1)+(c_1,c_2);b,c_1,c_2\in \mathbb{R},x\in Z\},$$

(4)

where Z is some subset of $\overline{\Omega }$. The non-penetration of $\gamma$ into obstacle O requires that

$$x+\rho \left(x\right)\notin int\left(O\right)forx\in \gamma .$$

(5)

According to (4) points $x=(x_1,x_2)\in \gamma$ of the rigid inclusion are displaced to those points with the following coordinates

$$x+\rho \left(x\right)=(x_1+b{x}_2+c_1,x_2-b{x}_1+c_2),x_2\in \{0,\alpha x_1\},x_1\in [0,1].$$

(6)

Here the term $c=(c_1,c_2)$ implies dilatation, whereas the term $b(x_2,-x_1)$ describes linearized rotation in a counterclockwise fashion around the point $x+c$ at the right angle $\pi /2$ for $b<0$, and $-\pi /2$ for $b>0$.

For $c_1\ge 0$ the condition (5) is satisfied within the representation (6) as $x_2=0$ and $x_2=\alpha x_1$ if

$$x_1\ge 0,x_1+b\alpha x_1\ge 0\mathrm{for} \mathrm{all}{x}_1\in [0,1],$$

which holds as $b\ge -1/\alpha$. Indeed, this provides non-negativeness of the first component $x_1+{\rho }_1\left(x\right)$ for $x\in \gamma$, thus the shift of $\gamma$ to the right from O. Therefore, in the case of $c_1\ge 0$, the corresponding set of admissible displacements takes the following form

$$K_1={\{W\in H(\Omega )|W|}_{\gamma }=\rho ,\rho \left(x\right)\in R\left(\gamma \right),b\ge -\frac{1}{\alpha },c_1\ge 0\}.$$

For $c_1\le 0$, we should distinguish two cases depending on the parameters $c_2$ and b. This first case corresponds to a configuration when the inclusion is displaced above the obstacle O after the deformation. When $b\ge 0$ describes the clockwise rotation, from (5) and (6) as $x_2=0$, we have the condition

$$-b{x}_1+c_2\ge k_1(x_1+c_1)\mathrm{for} \mathrm{all}{x}_1\in [0,1].$$

(7)

Setting $x_1=0$, we get $c_2\ge k_1{c}_1$. Assuming that $c_2\ge k_1{c}_1$ holds, we reveal that (7) is valid for all $0\le b\le -k_1$ since $k_1<0$. In order to restrict possible rotations of the inclusion in the counterclockwise direction ($b\le 0$), we should consider the angle lying in the upper half-plane between the rectilinear lines $x_2=k_1{x}_1$ and $x_2=\alpha x_1$. If the angle is acute, i.e., $1+\alpha k_1<0$, then conditions (5) and (6) as $x_2=\alpha x_1$ require to satisfy

$$k_1(x_1+b\alpha x_1)\le \alpha x_1-x_{1}b\mathrm{for} \mathrm{all}{x}_1\in [0,1],$$

which holds as

$$b\ge \frac{\alpha -k_1}{1+\alpha k_1},\mathrm{where}\frac{\alpha -k_1}{1+\alpha k_1}<0.$$

For the right or obtuse angle, arbitrary b is admissible since it rotates not more than $\pi /2$. As a result, we have the following admissible set

$$K_2={\{W\in H(\Omega )|W|}_{\gamma }=\rho ,\rho \left(x\right)\in R\left(\gamma \right),\phantom{ssssssssssseeeeeesssssssssssss}$$

$$\phantom{sssssss}{b}_{min}\le b\le -k_1{c}_1\le 0,c_2\ge k_1{c}_1\},$$

where $b_{min}=\frac{\alpha -k_1}{1+\alpha k_1}$ if $1+\alpha k_1<0$, otherwise $b_{min}=-\infty .$

The second possibility to fulfill (5) for $c_1\le 0$ corresponds to displacement of the inclusion $\gamma$ below the obstacle O after the deformation. Rotation in the counterclockwise direction case needs to fulfill the non-penetration condition as $x_2=\alpha x_1$

$$\alpha x_1-b{x}_1+c_2\le k_2(x_1+b\alpha x_1+c_1)\mathrm{for} \mathrm{all}{x}_1\in [0,1].$$

(8)

As $x_1=0$, it follows $c_2\le k_2{c}_1$. Then (8) is valid for b such that

$$\alpha x_1-b{x}_1\le k_2(x_1+b\alpha x_1)\mathrm{for} \mathrm{all}{x}_1\in [0,1],$$

following the restriction on b

$$\frac{\alpha -k_2}{1+\alpha k_2}\le b,\mathrm{where}\frac{\alpha -k_2}{1+\alpha k_2}<0$$

due to $k_2\ge \alpha$. Rotating in the clock-wise direction, for every positive b it holds

$$-b{x}_1+c_2\le k_2(x_1+c_1)\mathrm{for} \mathrm{all}{x}_1\in [0,1].$$

In this case, the admissible set is given by

$$K_3={\{W\in H(\Omega )|W|}_{\gamma }=\rho ,\rho \left(x\right)\in R\left(\gamma \right),\phantom{ssssssssssssssssssssssss}$$

$$\phantom{ssssssssssssssssss}b\ge \frac{\alpha -k_2}{1+\alpha k_2},c_1\le 0,c_2\le k_2{c}_1\}.$$

Consider the minimization problem:

$$\mathrm{find}U\in K_1\cup K_2\cup K_3\mathrm{such} \mathrm{that}\Pi \left(U\right)=\underset{W\in K_1\cup K_2\cup K_3}{inf}\Pi \left(W\right).$$

(9)

It is obvious that each of sets $K_i$, $i=1,2,3$ is convex and closed [21]. At the same time, one can note that the union $K_1\cup K_2\cup K_3$ is closed, but not convex.

Example 1.

Indeed, consider two functions $W_1\in K_2$ and $W_2\in K_3$ such that

$$W_1{|}_{\gamma }={\rho }^1=(c_1^1,c_2^1),(b=0)on\gamma ,with{c}_1^1=-a,c_2^1=k_1(-a);$$

$$W_2{|}_{\gamma }={\rho }^2=(c_1^2,c_2^2),(b=0)on\gamma ,with{c}_1^2=-a,c_2^2=k_2(-a),$$

where $a>0$. Let us consider the sum $W_s=\frac{1}{2}(W_1+W_2)$, as we can see

$$W_s=(c_1^s,c_2^s)=\left(-a,\frac{1}{2}(k_1+k_2)(-a)\right)on\gamma ,$$

where $c_1^s=-a$ and $c_2^s=\frac{1}{2}(k_1+k_2)(-a)$ are constant. In view of relations

$$c_1^s<0,k_1{c}_1^s>c_2^s>k_2{c}_1^s$$

due to $k_1<0<k_2$, we conclude that $W_s\notin K_1\cup K_2\cup K_3.$ Namely, $W_s\notin K_1$ since $c_1^s<0$, and $W_s\notin K_2$ because of $c_2^s<k_1{c}_1^s$, analogously $c_2^s>k_2{c}_1^s$ infer the relation $W_s\notin K_3.$ This example provides non-convexity of $K_1\cup K_2\cup K_3.$

The non-convexity of the admissible set does not allow application of the standard variational theory. Therefore, we prove the following existence theorem based on splitting into convex sets. In the framework of the previous assumptions, the following assertion holds.

Theorem 1.

There exists at least one, and at most three, solutions U of the variational problem (9) over the non-convex set $K_1\cup K_2\cup K_3$.

Proof. 

Along with the reference problem (9), we consider the following three auxiliary problems

$$\mathrm{find}{U}_i\in K_i\mathrm{such} \mathrm{that}\Pi \left(U_i\right)=\underset{W\in K_i}{inf}\Pi \left(W\right),i=1,2,3.$$

(10)

Coercivity and weak lower semi-continuity of $\Pi \left(W\right)$ on the Hilbert space $H(\Omega )$ implies that $\Pi \left(W\right)$ attains its minimums over $K_i$, $i=1,2,3$, at some functions $U_1\in K_1$, $U_2\in K_2$, $U_3\in K_3$, respectively. Furthermore, by strict convexity of the energy functional, it follows that for each fixed $i\in \{1,2,3\}$ the corresponding auxiliary problem (10) has a unique solution $U_i$, $i=1,2,3$. We can find the sought function U as a function providing a minimum over the three optimal values, i.e.,

$$\Pi \left(U\right)=\min \{\Pi \left(U_1\right),\Pi \left(U_2\right),\Pi \left(U_3\right)\},$$

(11)

where $U_i$ are the solutions to (10) for corresponding sole admissible sets $K_i$, $i=1,2,3.$ Indeed, let us suppose that $U_l$ with some $l\in \{1,2,3\}$ is a minimizer of the right hand of (11), then we have

$$\Pi \left(U_l\right)\le \Pi \left(W\right),\forall W\in K_1\cup K_2\cup K_3.$$

This proves the theorem. □

One can note that the solution of (9) may be non-unique, e.g., when $\Pi \left(U_1\right)=\Pi \left(U_2\right)<\Pi \left(U_3\right)$ and $U_1\ne U_2$.

Remark 1.

The well-posedness analysis can be adapted to the case when the straight part $[0,1]\times \left\{0\right\}$ of γ is re-specified by an inclined segment given by

$$\left\{(x_1,x_2)\right|x_1\in [0,1],x_2=\beta x_1\},k_1<\beta <0,\beta =const.$$

Let us reveal some qualitative properties of the auxiliary problems. Under an assumption of additional regularity of the solutions $U_i$, $i=1,2,3$, we can obtain from (10) equivalent differential relations. We first note that the Gateaux differentiability of $\Pi \left(W\right)$ provides the equivalence of each problem of (10) to one of the following variational inequalities

$$U_l\in K_l,\underset{\Omega }{\int }{\sigma }_{ij}\left(U_l\right){\epsilon }_{ij}(W-U_l)\ge \underset{\Omega }{\int }F(W-U_l)\forall W\in K_l,l=1,2,3.$$

For example, let us consider in detail the problem corresponding to the variational inequality for the set $K_2$

$$U_2\in K_2,\underset{\Omega }{\int }{\sigma }_{ij}\left(U_2\right){\epsilon }_{ij}(W-U_2)\ge \underset{\Omega }{\int }F(W-U_2)\forall W\in K_2.$$

(12)

By substituting the test functions of the following form $W=U_2+\varphi$, $\varphi \in C_0^{\infty }{(\Omega )}^2$ we get

$$\underset{\Omega }{\int }{\sigma }_{ij}\left(U_2\right){\epsilon }_{ij}\left(\varphi \right)\ge \underset{\Omega }{\int }F\varphi \forall \varphi \in C_0^{\infty }{(\Omega )}^2.$$

In the sense of distributions, this means that

$$-{\sigma }_{ij,j}\left(U_2\right)=F_i\mathrm{in}\Omega ,i=1,2.$$

(13)

In the following, we will apply the following Green formula, which holds for sufficiently smooth functions V and $\overline{V}\in H(\Omega )$ [14]

$$\underset{\Omega }{\int }{\sigma }_{ij}\left(V\right){\epsilon }_{ij}\left(\overline{V}\right)=-\underset{\Omega }{\int }{\sigma }_{ij,j}\left(V\right){\overline{v}}_i+\underset{\Gamma }{\int }({\sigma }_{\nu }\left(V\right)\overline{V}\nu +{\sigma }_{\tau }\left(V\right)\overline{V}\tau ),$$

(14)

where $\nu =({\nu }_1,{\nu }_2)$ is a unit normal vector to $\Gamma$,

$${\sigma }_{\nu }\left(V\right)={\sigma }_{ij}\left(V\right){\nu }_i{\nu }_j,{\sigma }_{\tau }\left(V\right)=({\sigma }_{\tau }^1\left(V\right),{\sigma }_{\tau }^2\left(V\right))=({\sigma }_{1j}\left(V\right){\nu }_j,{\sigma }_{2j}\left(V\right){\nu }_j)-{\sigma }_{\nu }\left(V\right)\nu ,$$

$$\overline{V}\nu ={\overline{v}}_i{\nu }_i,\overline{V}\tau =({\overline{V}}_{\tau }^1,{\overline{V}}_{\tau }^2),{\overline{v}}_i=\left(\overline{V}\nu \right){\nu }_i+{\overline{V}}_{\tau }^i,i=1,2.$$

Applying the Green formula (14) and (13), we can rewrite the corresponding variational inequality (12) in the following form

$$\underset{{\Gamma }_2}{\int }\left({\sigma }_{\nu }\left(U_2\right)(W-U_2)\nu +{\sigma }_{\tau }\left(U_2\right)(W-U_2)\tau \right)\ge 0,\forall W\in K_2.$$

(15)

Then, substituting into (15) functions $W=U_2+\tilde{W}$, with $\tilde{W}\in H(\Omega )$, $\tilde{W}=0$ on ${\Gamma }_1$ and $\tilde{W}=U_2$ on $\gamma$, and applying (14), we infer

$$\underset{{\Gamma }_2\backslash \gamma }{\int }({\sigma }_{\nu }\left(U_2\right)\tilde{W}\nu +{\sigma }_{\tau }\left(U_2\right)\tilde{W}\tau )\ge 0.$$

(16)

From (16) it follows that

$${\sigma }_{\tau }\left(U_2\right)=0,{\sigma }_{\nu }\left(U_2\right)=0on{\Gamma }_2\backslash \gamma .$$

(17)

We insert the test functions $W=0$ and $W=2U_2$ into (15) and obtain

$$\underset{\gamma }{\int }({\sigma }_{\nu }\left(U_2\right){\rho }^2\nu +{\sigma }_{\tau }\left(U_2\right){\rho }^2\tau )=0,$$

(18)

where ${\rho }^2=U_2$ a.e. on $\gamma$. Finally, bearing in mind (17) and (18) we have

$$\underset{\gamma }{\int }({\sigma }_{\nu }\left(U_2\right)\rho \nu +{\sigma }_{\tau }\left(U_2\right)\rho \tau )\ge 0,$$

(19)

for all rigid displacements $\rho$ described in $K_2$. The integral formulas (18) and (19) imply a consequence of the principle of virtual displacements [20,30]. Following the same line of reasoning of [16], the converse can be proved, namely, that the differential setting consisting of (1), (2), (13), (17)–(19) leads to the variational formulation (12).

Remark 2.

The differential formulation of (12) can be obtained without additional regularity assumptions on the solution $U_2$. However, in this case, the expressions for the boundary conditions take the form of duality relations in the space of distributions.

Analogously, we can obtain the following differential conditions for the variational inequality corresponding to the set $K_1$

$$-{\sigma }_{ij,j}\left(U_1\right)=F_i\mathrm{in}\Omega ,i=1,2,$$

(20)

$${\sigma }_{ij}\left(U_1\right)=c_{ijkl}{\epsilon }_{kl}\left(U_1\right)\mathrm{in}\Omega ,i,j=1,2,$$

(21)

$$U_1=(0,0)\mathrm{on}{\Gamma }_1,$$

(22)

$$\underset{\gamma }{\int }({\sigma }_{\nu }\left(U_1\right){\rho }^1\nu +{\sigma }_{\tau }\left(U_1\right){\rho }^1\tau )=0,\mathrm{where}{\rho }^1=U_1\mathrm{on}\gamma ,$$

(23)

$${\sigma }_{\tau }\left(U_1\right)=0,{\sigma }_{\nu }\left(U_1\right)=0\mathrm{on}{\Gamma }_2\backslash \gamma ,$$

(24)

$$\underset{\gamma }{\int }({\sigma }_{\nu }\left(U_1\right)\rho \nu +{\sigma }_{\tau }\left(U_1\right)\rho \tau )\ge 0,$$

(25)

for all $\rho$ described in $K_1$.

The differential formulation for the variational inequality over the set $K_3$ has the analogous form as the previous conditions (20)–(25) wherein the last relation (25) transforms to

$$\underset{\gamma }{\int }({\sigma }_{\nu }\left(U_3\right)\rho \nu +{\sigma }_{\tau }\left(U_3\right)\rho \tau )\ge 0,$$

for all $\rho$ from $K_3$.

3. The Case of a Volume Rigid Inclusion

We can consider a problem for a rigid volume inclusion, which may describe reinforcement of the body by an external wedge. Let us assume that a simply connected subdomain $\omega \subset \Omega$ has the boundary $\partial \omega$ satisfying $\partial \omega \cap \Gamma =\gamma$ (see Figure 2).

The space of infinitesimal rigid displacements $R\left(\omega \right)$ is defined according to (4). Now, we introduce the following sets of possible displacements

$$\begin{gathered} K_1^{\omega }={\{W\in H(\Omega )|W|}_{\omega }=\rho ,\rho \left(x\right)\in R\left(\omega \right),b\ge -\frac{1}{\alpha },c_1\ge 0\}, \\ {K}_2^{\omega }={\{W\in H(\Omega )|W|}_{\omega }=\rho ,\rho \left(x\right)\in R\left(\omega \right), \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{b}_{min}\le b\le -k_1,c_1\le 0,c_2\ge k_1{c}_1\}, \\ {K}_3^{\omega }={\{W\in H(\Omega )|W|}_{\omega }=\rho ,\rho \left(x\right)\in R\left(\omega \right), \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}b\ge \frac{\alpha -k_2}{1+\alpha k_2},c_1\le 0,c_2\le k_2{c}_1\}. \end{gathered}$$

Consider the minimization problem:

$$\mathrm{find}{U}^{\omega }\in K_1^{\omega }\cup K_2^{\omega }\cup K_3^{\omega }\mathrm{such} \mathrm{that}\Pi \left(U^{\omega }\right)=\underset{W\in K_1^{\omega }\cup K_2^{\omega }\cup K_3^{\omega }}{inf}\Pi \left(W\right).$$

(26)

As in the previous case, each set $K_i^{\omega }$, $i=1,2,3$, is convex and closed [21]. The optimal $U^{\omega }$ can be found as a function providing minimum solutions over the three values, i.e.,

$$\Pi \left(U^{\omega }\right)=\min \{\Pi \left(U_1^{\omega }\right),\Pi \left(U_2^{\omega }\right),\Pi \left(U_3^{\omega }\right)\},$$

where $U_i^{\omega }$ are solutions of the three variational problems corresponding to sole admissible sets $K_i^{\omega }$, $i=1,2,3,$

$$\mathrm{find}{U}_i^{\omega }\in K_i^{\omega }\mathrm{such} \mathrm{that}\Pi \left(U_i^{\omega }\right)=\underset{W\in K_i^{\omega }}{inf}\Pi \left(W\right),i=1,2,3.$$

(27)

If the boundary of the domain $\Omega \backslash \overline{\omega }$ belongs to the class $C^{1,1}$, then for each of three of auxiliary variational problem (27), equivalent differential relations can be obtained provided that solutions $U_i^{\omega }$, $i=1,2,3,$ are sufficiently smooth in $\Omega \backslash \overline{\omega }$. For example, in the case of the set $K_2^{\omega }$, we have

$$\begin{gathered} -{\sigma }_{ij,j}\left(U_2^{\omega }\right)=F_i\mathrm{in}\Omega \backslash \overline{\omega },i=1,2, \\ {\sigma }_{ij}\left(U_2^{\omega }\right)=c_{ijkl}{\epsilon }_{kl}\left(U_2^{\omega }\right)\mathrm{in}\Omega ,i,j=1,2, \\ {U}_2^{\omega }=(0,0)\mathrm{on}{\Gamma }_1, \end{gathered}$$

$$\underset{\partial \omega \backslash \gamma }{\int }({\sigma }_{\nu }{\left(U_2^{\omega }\right)}^{-}{\rho }_{\omega }^2\nu +{\sigma }_{\tau }{\left(U_2^{\omega }\right)}^{-}{\rho }_{\omega }^2\tau )=\underset{\omega }{\int }F{\rho }_{\omega }^2,\mathrm{where}{\rho }_{\omega }^2=U_2^{\omega }in\omega ,$$

(28)

$${\sigma }_{\tau }{\left(U_2^{\omega }\right)}^{-}=0,{\sigma }_{\nu }{\left(U_2^{\omega }\right)}^{-}=0\mathrm{on}{\Gamma }_2\backslash \gamma ,$$

(29)

$$\underset{\partial \omega \backslash \gamma }{\int }({\sigma }_{\nu }{\left(U_2^{\omega }\right)}^{-}\rho \nu +{\sigma }_{\tau }{\left(U_2^{\omega }\right)}^{-}\rho \tau )\ge \underset{\omega }{\int }F\rho ,$$

(30)

for all $\rho$ from $K_2$. Here, the relations (28)–(30) are written for the unit external normal vector $\nu$ to the boundary of the domain $\Omega \backslash \overline{\omega }$. The traces ${\sigma }_{\nu }{\left(U_2^{\omega }\right)}^{-}$ and ${\sigma }_{\tau }{\left(U_2^{\omega }\right)}^{-}$ are defined on the negative side ${(\partial \omega \backslash \gamma )}^{-}$. The negative ${(\partial \omega \backslash \gamma )}^{-}$ and positive side ${(\partial \omega \backslash \gamma )}^{+}$ of the curve $\partial \omega \backslash \gamma$ are selected with respect to the normal $\nu$ such that the positive side is a part of the boundary of inclusion $\omega$. Then ${\sigma }_{\nu }{\left(U_2^{\omega }\right)}^{-}$ and ${\sigma }_{\tau }{\left(U_2^{\omega }\right)}^{-}$ are defined on the boundary of the deformed body $\Omega \backslash \overline{\omega }$. In addition, we note that the values ${\sigma }_{\nu }{\left(U_2^{\omega }\right)}^{-}$, ${\sigma }_{\tau }{\left(U_2^{\omega }\right)}^{-}$ can be non-zero on ${(\partial \omega \backslash \gamma )}^{-}$, despite of ${\sigma }_{\nu }{\left(U_2^{\omega }\right)}^{+}=0$, ${\sigma }_{\tau }{\left(U_2^{\omega }\right)}^{+}=0$ on ${(\partial \omega \backslash \gamma )}^{+}$ due to ${\epsilon }_{ij}\left(U_2^{\omega }\right)=0$ in the rigid inclusion $\omega$, $i,j=1,2$. This case arises when the jumps of functions ${\sigma }_{ij}\left(U_2^{\omega }\right)$, $i,j=1,2$, are not equal to zero on ${(\partial \omega \backslash \gamma )}^{-}$ provided that $U_2^{\omega }\in H(\Omega )$, but $U_2^{\omega }\notin H^2{(\Omega )}^2$.

4. The Case of Two-Hinged Thin Rigid Inclusions

In this section, we suppose that the curve $\gamma$ is divided by the point $(0,0)$ into two curves ${\gamma }^d=[0,1]\times \left\{0\right\}$ and ${\gamma }^t=\left\{(x_1,x_2)\right|0\le x_1\le 1,x_2=\alpha x_1\}$ that corresponds to two rigid inclusions. This setting has an additional degree of freedom allowing rotation at the origin. If we require that a sought function U satisfies ${U|}_{{\gamma }^t}={\rho }^t$, ${U|}_{{\gamma }^d}={\rho }^d$ with some linear functions

$${\rho }^t=b^t(x_2,-x_1)+(c_1^t,c_2^t)\in R\left({\gamma }^t\right),{\rho }^d=b^d(x_2,-x_1)+(c_1^d,c_2^d)\in R\left({\gamma }^d\right),$$

where $b^d,c_1^d,c_2^d\in \mathbb{R}$, $b^t,c_1^t,c_2^t\in \mathbb{R}$, then taking into account that $U\in H(\Omega )$, we have

$$c_1^d=c_1^t,c_2^d=c_2^t.$$

In this case admissible sets have been represented by the following relations

$$\begin{gathered} K_1^h={\{W\in H(\Omega )|W|}_{{\gamma }^d}={\rho }^d{,W|}_{{\gamma }^t}={\rho }^t,\phantom{eeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee} \\ {\rho }^d\in R\left({\gamma }^d\right),{\rho }^t\in R\left({\gamma }^t\right),b^t\ge -\frac{1}{\alpha },c_1^t\ge 0\}, \\ {K}_2^h={\{W\in H(\Omega )|W|}_{{\gamma }^d}={\rho }^d{,W|}_{{\gamma }^t}={\rho }^t,\phantom{eeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee} \\ {\rho }^d\in R\left({\gamma }^d\right),{\rho }^t\in R\left({\gamma }^t\right),c_1^t\le 0,b^d\le -k_1,b^t\ge b_{min},c_2^t\ge k_1{c}_1^t\}, \\ {K}_3^h={\{W\in H(\Omega )|W|}_{{\gamma }^d}={\rho }^d{,W|}_{{\gamma }^t}={\rho }^t,\phantom{eeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee} \\ {\rho }^d\in R\left({\gamma }^d\right),{\rho }^t\in R\left({\gamma }^t\right),b^t\ge \frac{\alpha -k_2}{1+\alpha k_2},c_1^t\le 0,c_2^t\le k_2{c}_1^t\}. \end{gathered}$$

The minimization problem:

$$\mathrm{find}{U}^h\in K_1^h\cup K_2^h\cup K_3^h\mathrm{such} \mathrm{that}\Pi \left(U\right)=\underset{W\in K_1^h\cup K_2^h\cup K_3^h}{inf}\Pi \left(W\right)$$

(31)

can be treated as the previous problem (9), since the admissible sets $K_i^h$, $i=1,2,3$, are convex closed cones and suitable test functions can be chosen in the same way as in the derivation of (20)–(25).

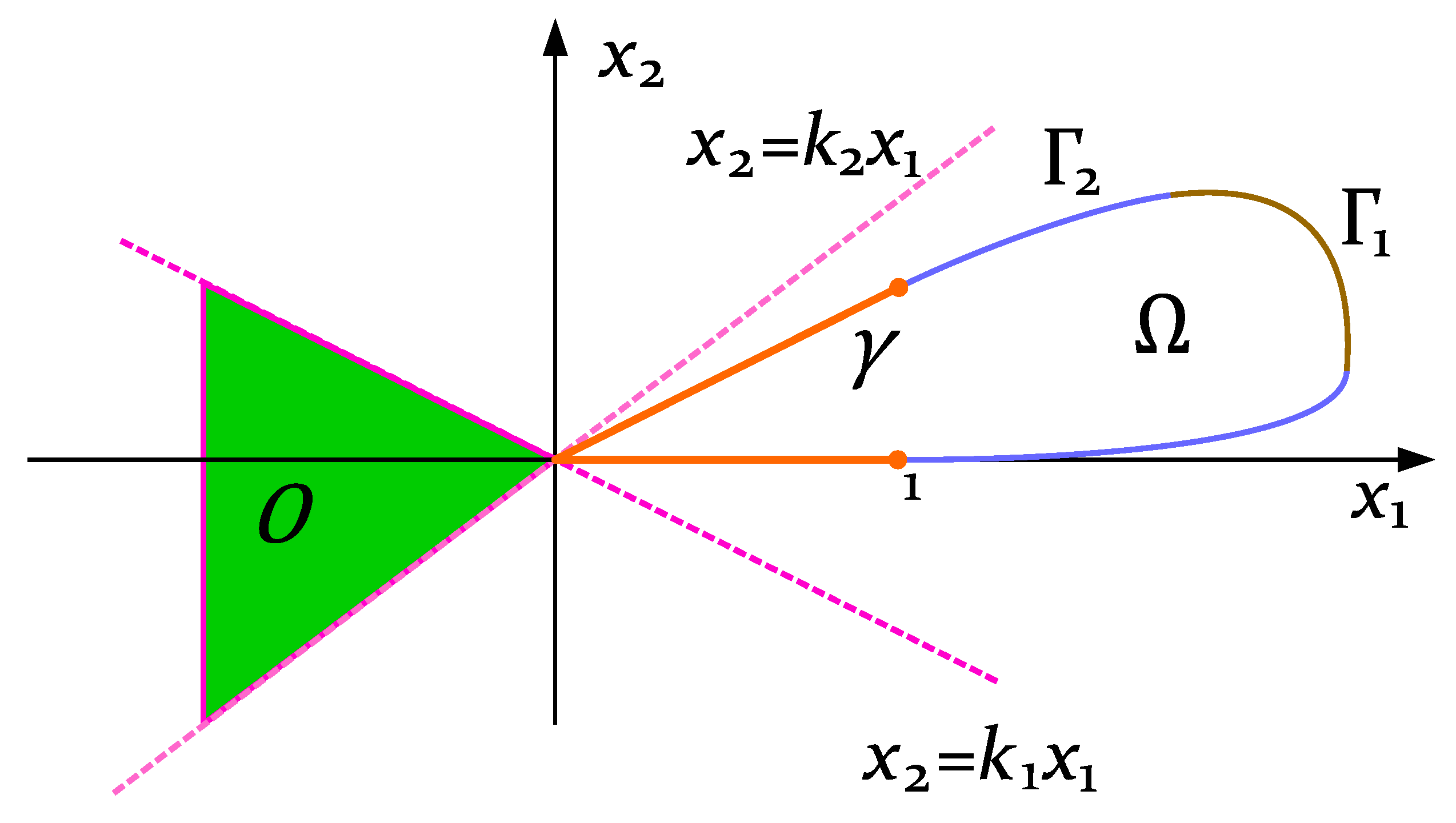
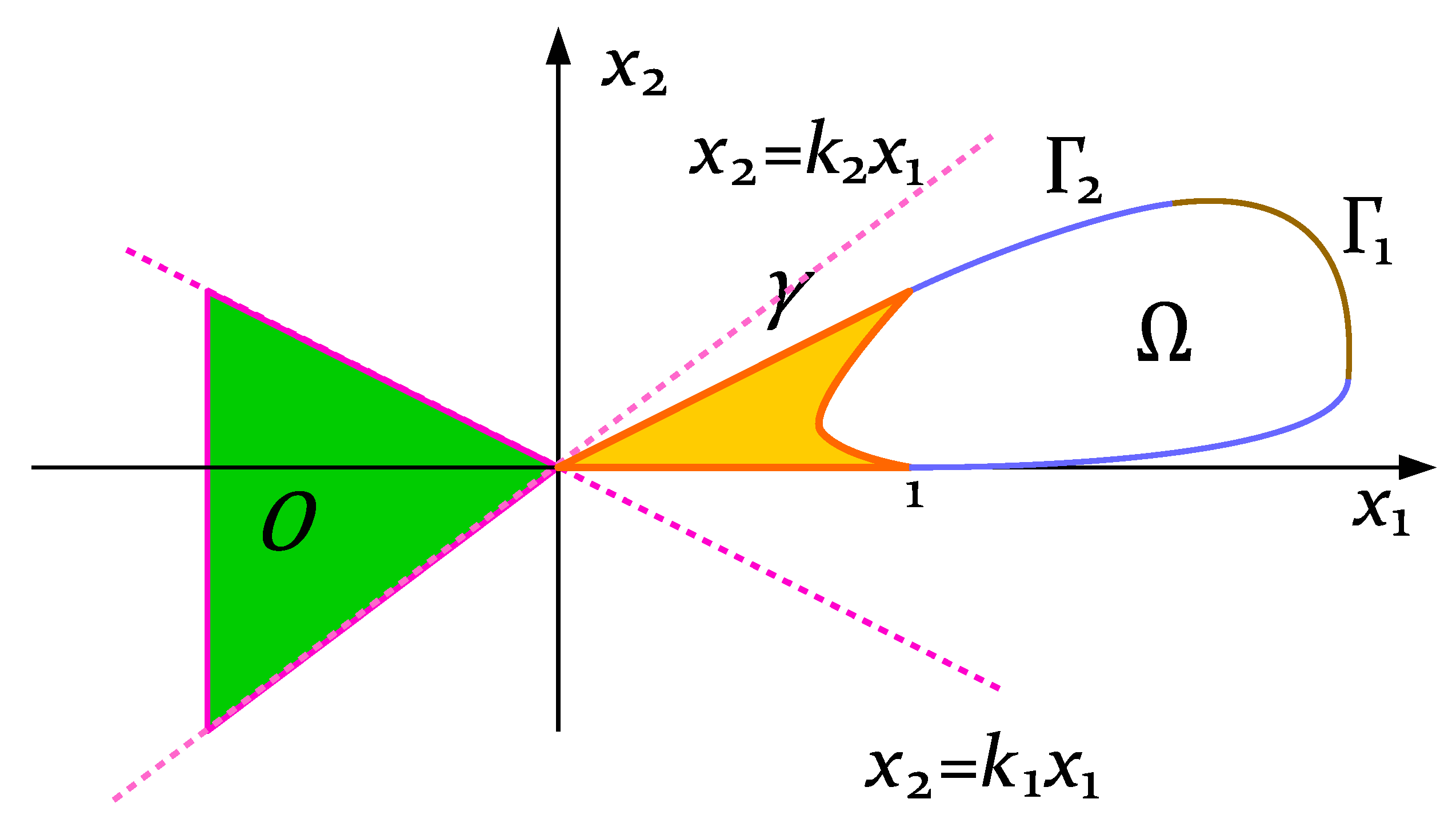
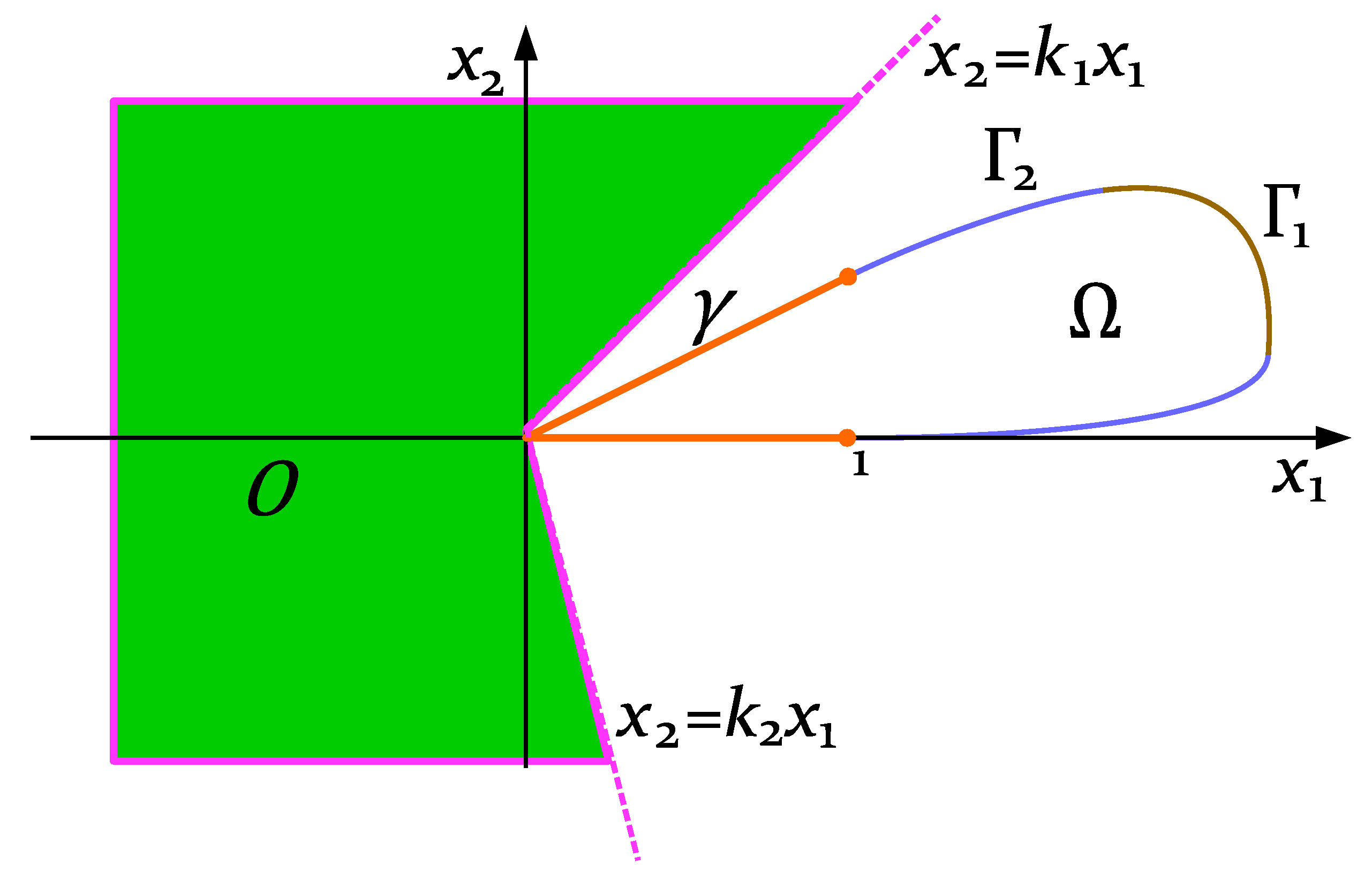
5. The Case of an Obstacle with an Obtuse Angle and a Body with Sharp-Shaped Edge

Let us suppose that near the contact point a part of the boundary of an obstacle O is comprised of two rectilinear lines given by $x_2=k_2{x}_1$, $x_2=k_1{x}_1$, $k_2\le 0$, $k_1\ge 0$ composing an obtuse angle, as shown in Figure 3.

In this case, we have to fulfill the following relations according to (5) and (6) at $x_2=0$

$$k_2(x_1+c_1)\le (-b{x}_1+c_2)\mathrm{for} \mathrm{all}{x}_1\in [0,1],$$

(32)

and at $x_2=\alpha x_1$

$$k_1(x_1+b\alpha x_1+c_1)\ge \alpha x_1-b{x}_1+c_2\mathrm{for} \mathrm{all}{x}_1\in [0,1].$$

(33)

Setting in the last two inequalities $x_1=0$, we get

$$k_2{c}_1\le c_2\le k_1{c}_1.$$

(34)

One can note that the last inequality holds only for non-negative values of $c_1$. Assuming that (34) holds, the inequality (32) is valid for $b\le -k_2$. As well as (33) holds when

$$b\ge \frac{\alpha -k_1}{1+k_1\alpha }.$$

In the framework of the previous consideration in Section 1, for the coefficient $\alpha$ satisfying $0<\alpha <k_1$, a minimization problem has the following form

$$\mathrm{find}\widehat{U}\in \widehat{K}\mathrm{such} \mathrm{that}\Pi \left(\widehat{U}\right)=\underset{W\in \widehat{K}}{inf}\Pi \left(W\right),$$

over the admissible set

$$\begin{gathered} \widehat{K}={\{W\in H(\Omega )|W|}_{\gamma }=\rho ,\rho \left(x\right)\in R\left(\gamma \right), \\ \frac{\alpha -k_1}{1+k_1\alpha }\le b\le -k_2,c_1\ge 0,k_2{c}_1\le c_2\le k_1{c}_1\}. \end{gathered}$$

One can confirm that the last problem has a unique solution $\widehat{U}$, since the set $\widehat{K}$ is convex.

6. Discussion

The obtained results justify the new class of point-contact problems. In contrast to the well-known Signorini condition, the proposed non-penetration condition is imposed for possible displacements of a single point located on a tip of a sharp-shaped rigid inclusion. Features of the variational problems (9), (26) and (31) are concerned with the non-convexity of corresponding admissible sets. The well-posedness property is investigated by using three auxiliary problems formulated over convex admissible sets. For the auxiliary problems obeying unique solutions, equivalent differential formulations have been obtained. The obtained rigorous mathematical results are subject to research from the point of view of applications of solid mechanics in the framework of contact problems for reinforced composite bodies. In particular, the results require numerical simulations and their subsequent comparison with experimental data. As possible directions for further research, we can highlight the following issues: uniqueness of solutions, approximation by a family of equilibrium problems for elastic bodies, inverse problems, etc. From the point of view of other constitutive relations, justification of contact problems, with the proposed non-penetration condition in the framework of composite bodies consisting of a plastic or viscoelastic matrix and a rigid inclusion with a sharp edge, is also an open problem.