Supply Restoration in Active Distribution Networks Based on Soft Open Points with Embedded DC Microgrids
Abstract
:1. Introduction
- Developing a supply restoration strategy based on MISOCP for ADNs, including SOPs and DC microgrids connected at the DC interface of a SOP,
- Extracting the most representative scenarios from the available load and generation data through the Fuzzy c-means algorithm,
- Applying the previously mentioned optimization model on a modified IEEE 33-bus system,
- Evaluating the benefits provided by SOPs and microgrids participation on the supply restoration strategy.
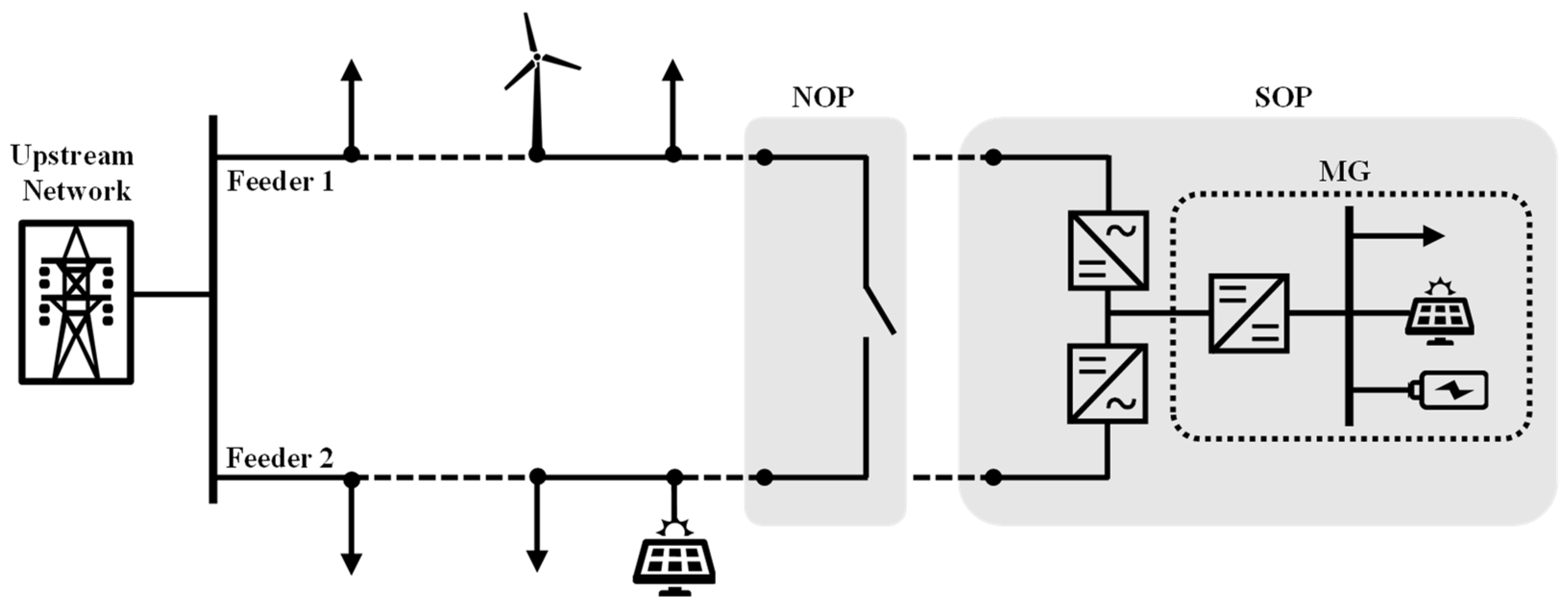
2. Soft Open Point
3. Problem Formulation
3.1. Uncertainty Modelling
| Algorithm 1. Pseudocode of Fuzzy c-means clustering method |
| Input: Number of clusters C, a set of N data points x1, x2,…, xN, the fuzzy parameter m and the maximum number of iterations itermax. Output: Positions of cluster centers c1, c2,…, cC.
|
3.2. The Optimal Restoration Model
3.2.1. Objective Functions
3.2.2. ADN Operational Constraints
3.2.3. DC-Microgrid Operation
3.2.4. SOP Operational Constraints
- (1)
- SOP active power constraints:
- (2)
- SOP reactive power constraints:
- (3)
- SOP capacity constraints:
4. Case Study
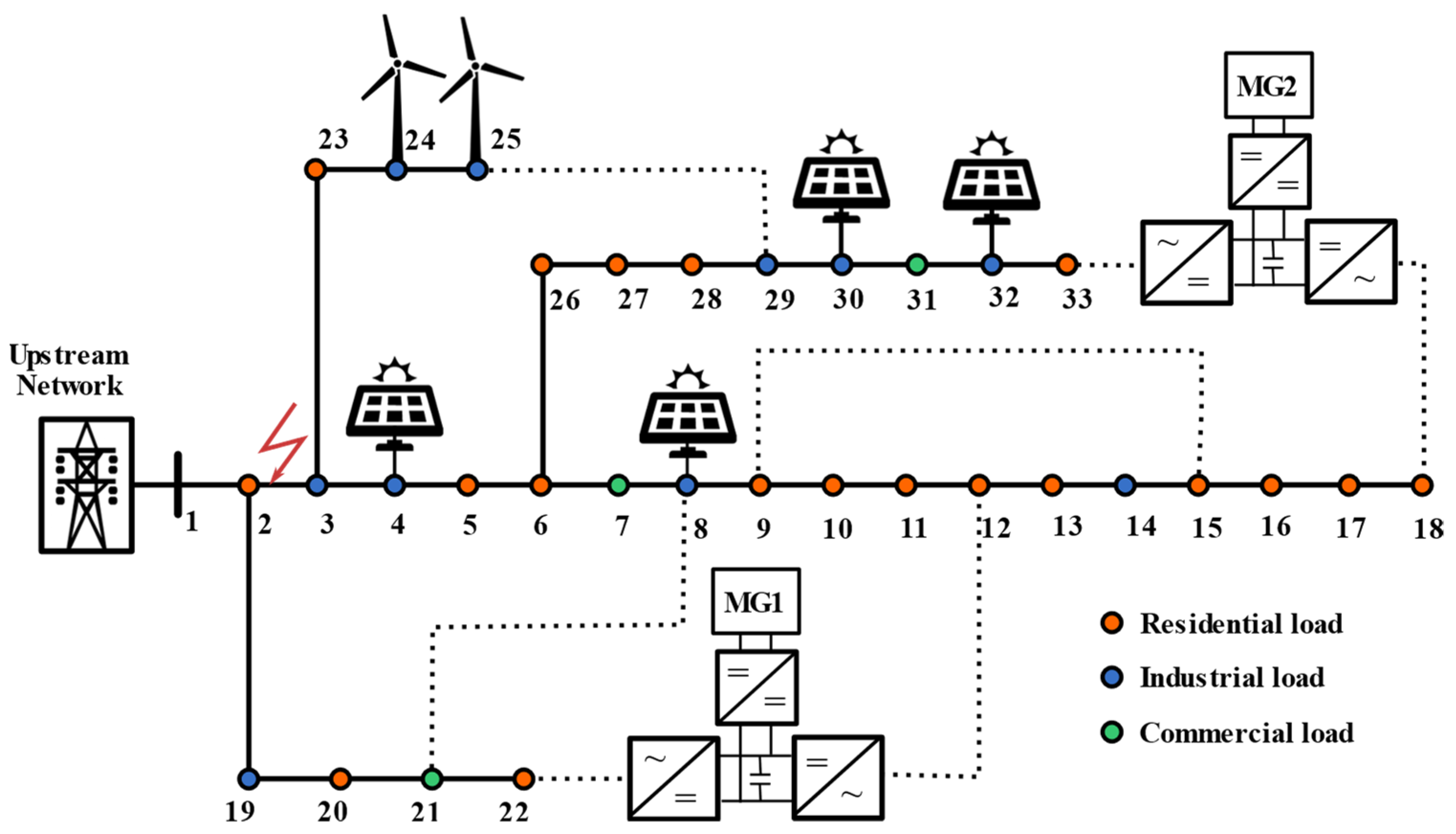
4.1. The Modified IEEE 33−Bus System
4.2. Load and Generation Uncertainties Modelling Results Based on FCM Clustering Technique
5. Discussion on Restoration Results
5.1. Scheme I Restoration Results
5.2. Scheme II Restoration Results
5.3. Overall Results and Scheme Comparison
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Davarzani, S.; Pisica, I.; Taylor, G.A.; Munisami, K.J. Residential Demand Response Strategies and Applications in Active Distribution Network Management. Renew. Sustain. Energy Rev. 2021, 138, 110567. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Thomas, L.; Jenkins, N. Optimal operation of soft open points in medium voltage electrical distribution networks with distributed generation. Appl. Energy 2016, 184, 427–437. [Google Scholar] [CrossRef] [Green Version]
- Qi, Q.; Wu, J.; Long, C. Multi-objective operation optimization of an electrical distribution network with soft open point. Appl. Energy 2017, 208, 734–744. [Google Scholar] [CrossRef]
- Cao, W.; Wu, J.; Jenkins, N.; Wang, C.; Green, T. Benefits analysis of Soft Open Points for electrical distribution network operation. Appl. Energy 2016, 165, 36–47. [Google Scholar] [CrossRef] [Green Version]
- Diaaeldin, I.; Abdel Aleem, S.; El-Rafei, A.; Abdelaziz, A.; Zobaa, A.F. Optimal Network Reconfiguration in Active Distribution Networks with Soft Open Points and Distributed Generation. Energies 2019, 12, 4172. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Song, G.; Li, P.; Ji, H.; Zhao, J.; Wu, J. Optimal siting and sizing of soft open points in active electrical distribution networks. Appl. Energy 2017, 189, 301–309. [Google Scholar] [CrossRef]
- Xiao, H.; Pei, W.; Li, K. Optimal Sizing and Siting of Soft Open Point for Improving the Three Phase Unbalance of the Distribution Network. In Proceedings of the 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018. [Google Scholar]
- Justo, J.J.; Mwasilu, F.; Lee, J.; Jung, J.W. AC-microgrids versus DC-microgrids with distributed energy resources: A review. Renew. Sustain. Energy Rev. 2013, 24, 387–405. [Google Scholar] [CrossRef]
- Lotfi, H.; Khodaei, A. AC Versus DC Microgrid Planning. IEEE Trans. Smart Grid 2017, 8, 296–304. [Google Scholar] [CrossRef]
- Habeeb, S.A.; Tostado-Véliz, M.; Hasanien, H.M.; Turky, R.A.; Meteab, W.K.; Jurado, F. DC Nanogrids for Integration of Demand Response and Electric Vehicle Charging Infrastructures: Appraisal, Optimal Scheduling and Analysis. Electronics 2021, 10, 2484. [Google Scholar] [CrossRef]
- Al-Ismail, F.S. DC Microgrid Planning, Operation, and Control: A Comprehensive Review. IEEE Access 2021, 9, 36154–36172. [Google Scholar] [CrossRef]
- Iovine, A.; Rigaut, T.; Damm, G.; De Santis, E.; Di Benedetto, M.D. Power management for a DC MicroGrid integrating renewables and storages. Control Eng. Pract. 2019, 85, 59–79. [Google Scholar] [CrossRef]
- Che, L.; Khodayar, M.; Shahidehpour, M. Only Connect: Microgrids for Distribution System Restoration. IEEE Power Energy Mag. 2014, 12, 70–81. [Google Scholar]
- Gao, H.; Chen, Y.; Xu, Y.; Liu, C. Resilience-Oriented Critical Load Restoration Using Microgrids in Distribution Systems. IEEE Trans. Smart Grid 2016, 7, 2837–2848. [Google Scholar] [CrossRef]
- Yao, C.; Zhou, C.; Yu, J.; Xu, K.; Li, P.; Song, G. A Sequential Optimization Method for Soft Open Point Integrated with Energy Storage in Active Distribution Networks. Energy Procedia 2018, 145, 528–533. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. State-of-the-art techniques for modelling of uncertainties in active distribution network planning: A review. Appl. Energy 2019, 239, 1509–1523. [Google Scholar] [CrossRef]
- Refaat, M.M.; Aleem, S.H.E.A.; Atia, Y.; Ali, Z.M.; El-Shahat, A.; Sayed, M.M. A Mathematical Approach to Simultaneously Plan Generation and Transmission Expansion Based on Fault Current Limiters and Reliability Constraints. Mathematics 2021, 9, 2771. [Google Scholar] [CrossRef]
- Neagu, B.C.; Grigoras, G. Uncertainty-Based Decision Making in the Planning of Electric Transmission Networks. In Proceedings of the 11th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Pitesti, Romania, 27–29 June 2019. [Google Scholar]
- Bloemink, J.M.; Green, T.C. Increasing Distributed Generation Penetration Using Soft Normally-Open Points. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar]
- Ali, Z.M.; Diaaeldin, I.M.; El-Rafei, A.; Hasanien, H.M.; Abdel Aleem, S.H.; Abdelaziz, A.Y. A novel distributed generation planning algorithm via graphically-based network reconfiguration and soft open points placement using Archimedes optimization algorithm. Ain Shams Eng. J. 2021, 12, 1923–1941. [Google Scholar] [CrossRef]
- Bai, L.; Jiang, T.; Li, F.; Chen, H.; Li, X. Distributed energy storage planning in soft open point based active distribution networks incorporating network reconfiguration and DG reactive power capability. Appl. Energy 2018, 210, 1082–1091. [Google Scholar] [CrossRef]
- Mudaliyar, S.; Mishra, S. Real-Time Coordinated Control of Low-Voltage DC Distribution Network with Soft Opening Point. IEEE Trans. Power Electron. 2021, 36, 7123–7137. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.; Long, C.; Wu, J.; Jenkins, N. Optimal Operation of Multi-Terminal Soft Open Point to Increase Hosting Capacity of Distributed Generation in Medium Voltage Networks. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018. [Google Scholar]
- Aithal, A.; Long, C.; Cao, W.; Wu, J.; Ugalde-Loo, C.E. Impact of soft open point on feeder automation. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016. [Google Scholar]
- Cao, W.; Wu, J.; Jenkins, N.; Wang, C.; Green, T. Operating Principle of Soft Open Points for Electrical Distribution Network Operation. Appl. Energy 2016, 164, 245–257. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Liu, J.; Li, F.; Liu, Y.; Liu, Y.; Xu, R.; Su, Y.; Ding, L. Optimal Active Distribution Network Planning: A Review. Electr. Power Compon. Syst. 2016, 44, 1075–1094. [Google Scholar] [CrossRef]
- Fathabadi, H. Power distribution network reconfiguration for power loss minimization using novel dynamic fuzzy c-means (dFCM) clustering based ANN approach. Int. J. Electr. Power Energy Syst. 2016, 78, 96–107. [Google Scholar] [CrossRef]
- Yan, R.; Wang, J.; Lu, S.; Ma, Z.; Zhou, Y.; Zhang, L.; Cheng, Y. Multi-objective two-stage adaptive robust planning method for an integrated energy system considering load uncertainty. Energy Build. 2021, 235, 110741. [Google Scholar] [CrossRef]
- Benmouiza, K.; Tadj, M.; Cheknane, A. Classification of hourly solar radiation using fuzzy c-means algorithm for optimal stand-alone PV system sizing. IEEE Syst. J. 2016, 82, 233–241. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, J.; Chen, C.; Tan, Y.; Cao, Y. Service Restoration Model with Mixed-Integer Second-Order Cone Programming for Distribution Network with Distributed Generations. IEEE Trans. Smart Grid 2019, 10, 4138–4150. [Google Scholar] [CrossRef]
- Lee, C.; Liu, C.; Mehrotra, S.; Bie, Z. Robust Distribution Network Reconfiguration. IEEE Trans. Smart Grid 2015, 6, 836–842. [Google Scholar] [CrossRef]
- Li, P.; Ji, H.; Wang, C.; Zhao, J.; Song, G.; Ding, F.; Wu, J. Coordinated Control Method of Voltage and Reactive Power for Active Distribution Networks Based on Soft Open Point. IEEE Trans. Sustain. Energy 2017, 8, 1430–1442. [Google Scholar] [CrossRef] [Green Version]
- Lou, C.; Yang, J.; Li, T.; Vega-Fuentes, E. New phase-changing soft open point and impacts on optimising unbalanced power distribution networks. IET Gener. Transm. Distrib. 2020, 14, 5685–5696. [Google Scholar] [CrossRef]
- Wan, C.; Lin, J.; Guo, W.; Song, Y. Maximum Uncertainty Boundary of Volatile Distributed Generation in Active Distribution Network. IEEE Trans. Smart Grid 2018, 9, 2930–2942. [Google Scholar] [CrossRef]
- Li, P.; Ji, H.; Wang, C.; Zhao, J.; Song, G.; Ding, F.; Wu, J. Optimal Operation of Soft Open Points in Active Distribution Networks Under Three-Phase Unbalanced Conditions. IEEE Trans. Smart Grid 2017, 10, 380–391. [Google Scholar] [CrossRef]
- Bokhari, A.; Alkan, A.; Dogan, R. Experimental Determination of the ZIP Coefficients for Modern Residential, Commercial, and Industrial Loads. IEEE Trans. Power Deliv. 2014, 29, 1372–1381. [Google Scholar] [CrossRef]
- Jardini, J.A.; Tahan, C.M.V.; Gouvea, M.R.; Ahn, S.U.; Figueiredo, F.M. Daily load profiles for residential, commercial and industrial low voltage consumers. IEEE Trans. Power Deliv. 2000, 15, 375–380. [Google Scholar] [CrossRef] [Green Version]
- Initiative Open Energy Data. Available online: Data.openei.org (accessed on 1 October 2021).
- Renewables.ninja. Available online: https://www.renewables.ninja/ (accessed on 1 October 2021).
- Li, K.; Cao, X.; Ge, X.; Wang, F.; Lu, X.; Shi, M.; Yin, R.; Mi, Z.; Chang, S. Meta-Heuristic Optimization-Based Two-Stage Residential Load Pattern Clustering Approach Considering Intra-Cluster Compactness and Inter-Cluster Separation. IEEE Trans. Ind. Appl. 2020, 56, 3375–3384. [Google Scholar]
- Yunjie, Z.; Weina, W.; Xiaona, Z.; Yi, L. A cluster validity index for fuzzy clustering. Inf. Sci. 2008, 178, 1205–1218. [Google Scholar]
- Zhou, J.; Zheng, Y.; Xu, Y.; Li, H.; Chen, D. A Heuristic T-S Fuzzy Model for the Pumped-Storage Generator-Motor Using Variable-Length Tree-Seed Algorithm-Based Competitive Agglomeration. Energies 2018, 11, 944. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Wu, W.; Zhang, B. Robust Restoration Method for Active Distribution Networks. IEEE Trans. Power Syst. 2016, 31, 4005–4015. [Google Scholar] [CrossRef]














| Priority Category | wj | Node of Load |
|---|---|---|
| I | 10 | 8, 11, 14, 21, 24, 30, |
| II | 5 | 7, 10, 19, 25, 27, 29, 32 |
| III | 1 | 2, 3, 4, 5, 6, 9, 12, 13, 15, 16, 17, 18, 20, 22, 23, 26, 28, 31, 33 |
| SOP Placement | Maximum Capacity | Reactive Power Limits | Active Power Losses |
|---|---|---|---|
| 12–22 | 1000 kVA | [−600, 600] kvar | 2% |
| 18–33 | 1000 kVA | [−600, 600] kvar | 2% |
| Component | Parameter | Value |
|---|---|---|
| Load | 150 kW | |
| Type | MG1–Commercial MG2–Industrial | |
| PV | 450 kWp | |
| Power factor (cosφ) | 1 | |
| ESS | EC | 1000 kWh |
| 0.2 | ||
| 0.98 | ||
| 0 | ||
| 0.2 | ||
| 0 | ||
| 0.35 | ||
| 0.9 | ||
| 0.85 | ||
| 0.4 | ||
| 2 | ||
| DC–DC converter | ADC | 1% |
| 200 kW |
| Reconfiguration | SOP with MG | |||||
|---|---|---|---|---|---|---|
| Priority I | Priority II | Priority III | Priority I | Priority II | Priority III | |
| Cluster 1 | 99.65 | 70.69 | 32.81 | 100 | 87.55 | 60.94 |
| Cluster 2 | 99.67 | 81.82 | 36.1 | 100 | 91.47 | 64.91 |
| Cluster 3 | 99.3 | 74.08 | 29.53 | 100 | 84.55 | 57.88 |
| Reconfiguration | SOP with MG | |||
|---|---|---|---|---|
| Total | Average (p.u.) | Total | Average (p.u.) | |
| Cluster 1 | 14.8651 | 0.0188 | 8.7164 | 0.011 |
| Cluster 2 | 15.4687 | 0.0195 | 12.1674 | 0.0153 |
| Cluster 3 | 14.8256 | 0.0187 | 11.2003 | 0.0141 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Picioroaga, I.I.; Tudose, A.M.; Sidea, D.O.; Bulac, C. Supply Restoration in Active Distribution Networks Based on Soft Open Points with Embedded DC Microgrids. Mathematics 2022, 10, 211. https://doi.org/10.3390/math10020211
Picioroaga II, Tudose AM, Sidea DO, Bulac C. Supply Restoration in Active Distribution Networks Based on Soft Open Points with Embedded DC Microgrids. Mathematics. 2022; 10(2):211. https://doi.org/10.3390/math10020211
Chicago/Turabian StylePicioroaga, Irina I., Andrei M. Tudose, Dorian O. Sidea, and Constantin Bulac. 2022. "Supply Restoration in Active Distribution Networks Based on Soft Open Points with Embedded DC Microgrids" Mathematics 10, no. 2: 211. https://doi.org/10.3390/math10020211
APA StylePicioroaga, I. I., Tudose, A. M., Sidea, D. O., & Bulac, C. (2022). Supply Restoration in Active Distribution Networks Based on Soft Open Points with Embedded DC Microgrids. Mathematics, 10(2), 211. https://doi.org/10.3390/math10020211






