Research on Dynamic Assessment Method of Earthquake Scene Rescue Performance Based on AHP and Cloud Model

Abstract

In view of the ambiguity and randomness of the assessment of earthquake scene rescue performance, this paper proposes an integrated assessment method considering quantitative and qualitative influencing factors from three levels: search, rescue and medical treatment. Firstly, this study constructs an assessment index system of rescue performance at the earthquake scene based on the International Search and Rescue Advisory Group (INSARAG) guidelines set by International Search and Response. Secondly, the subjective weights and objective weights of each index were calculated using the hierarchical analysis process (AHP) and cloud model, respectively. The comprehensive weights were calculated using weighted analysis, and the performance assessment results were visually expressed by cloud model images. Finally, the study was applied to an earthquake rescue case with an initial assessment of 4.0065, and its performance was improved by 4.36% when the rescue process was optimized. The assessment results show that earthquake rescue performance can be estimated, and the rationality and effectiveness of the method was validated.

1. Introduction

The vulnerability of cities and societies to large-scale disasters is one of the most urgent and serious challenges common to all countries, and natural disasters such as earthquakes pose a great threat to people’s lives [1,2,3], while post-earthquake urban search and rescue (US&R) is the most effective way to reduce human casualties [4]. Governments and departments at all levels need to conduct a scientific and rational assessment of the whole process of emergency relief after each earthquake. Wang Wei et al. [5] constructed an earthquake emergency response capability assessment index system by seeking expert opinions through a questionnaire. Xie Lili et al. [6] used AHP to construct an assessment index system for urban seismic mitigation capacity. Deng Yan et al. [7] used the AHP to construct an earthquake assessment index system consisting of four primary indexes and 47 secondary indexes based on the cases of earthquake rescue in provincial administrative units and Chinese regulations. The Federal Emergency Management Agency (FEMA)’s US&R developed the State Capability Assessment for Readiness (CAR) [8] in 1997 and revised it in 2000. The performance system has 13 primary assessment indexes to assess the weaknesses of national emergency readiness capabilities. INSARAG Guidelines are used to guide international urban search and rescue operations [9]. A reasonable dynamic assessment of earthquake rescue performance can quickly identify weaknesses in rescue operations and rationalize the allocation of rescue resources to improve earthquake rescue effectiveness.

AHP is a multi-objective decision analysis method that integrates qualitative and quantitative analysis, and it is widely used in performance assessment problems [10,11,12,13,14,15,16,17]. For example, in [12], AHP has been successfully applied to assess the operation performance of public transport network; that is, to build a system of indexes that include economic, social, ecological and other aspects. Scoring each index and applying hierarchical analysis can visually evaluate its efficiency, promote the optimization of resource allocation and improve operational efficiency. However, the disadvantage of the AHP is that it is influenced by subjective factors, causing the assessment results to depend on expert opinions; and, the results obtained are not accurate if the scores given are not reasonable.

Some studies focus on the combination of AHP and other methods [18,19,20,21,22,23,24], explored their application areas, and demonstrated that the combination of AHP and other methods can improve the performance of the overall method. For example, Shi Qu et al. [20] used a combination of AHP and the combined weighted TOPSIS method for quantitative assessment and comparative analysis of different operational scenarios to overcome the shortcomings of a single subjective assessment method for the operational performance of anti-missile warning and achieved a more scientific assessment of operational performance. Yan Zhou et al. [22] used a combination of AHP and cloud model to achieve a more scientific assessment of green building operational performance, and the paper reflects the influence of subjective opinions of building managers in the assessment of green building operational performance, while retaining the uncertainty and ambiguity of each index in operational performance assessment. In addition, the AHP combined with the cloud model was also applied to the roof risk assessment [25] to achieve accurate identification of the accident risk of the roof of the comprehensive mining workings. The successful application of this method in the fields of ecological environment assessment [26], comprehensive risk assessment of computer host safety [27] and slope stability assessment [28,29] proves that the method can assess the fusion of qualitative and quantitative indexes in multiple dimensions and provide a scientific and objective description of the fuzziness and uncertainty of each index.

Throughout the literature review, most of the studies on earthquake rescue effectiveness have been conducted from the regional perspective and the preparation stage of earthquake rescue, and there is no index system for assessing the whole process of earthquake emergency response at the national level and from the perspective of response subjects. Although researchers have used AHP combined with cloud model to conduct a comprehensive assessment of a problem, fewer studies have been conducted to assess the performance of earthquake rescue. In this paper, we fully utilize the advantages of AHP combined with cloud model in assessment and apply it to solve the problem of earthquake scene rescue performance assessment.

2. Research Methodology

2.1. Analytic Hierarchy Process

AHP is a method of qualitative and quantitative analysis for decision making proposed by T.L. Saaty in 1980 [30]. The AHP to solve practical problems can be carried out in the following four steps:

1.

Build a recursive hierarchy model. When applying AHP to analyze a decision problem, the problem is first organized and hierarchized. The decision problem is divided into a gradually refined hierarchy of goal layer, system layer, criterion layer and measure layer, and the factors influencing the decision goal and the internal links are modeled.

2.

Construct all judgment matrices in each layer. The relative importance values between attributes are assigned according to the relative importance scale developed by Saaty (see Table 1) [30]. And the importance scale is used to define the judgment matrix $A={\left(a_{ij}\right)}_{n\times n}$.

Table 1. Importance level and its assignment value.

Level of Importance	Assignment
Two elements of equal importance	1
The former is slightly more important than the latter	3
The former is obviously more important than the latter	5
The former is strongly more important than the latter	7
The former is extremely more important than the latter	9
The former is slightly unimportant compared to the latter	1/3
The former is obviously unimportant compared to the latter	1/5
The former is strongly unimportant compared to the latter	1/7
The former is extremely unimportant compared to the latter	1/9

Note: 2,4,6 and 8 represent the assignments of importance between 1, 3, 5, 7 and 9 respectively. 1/2, 1/4, 1/6 and 1/8 represent that they are less unimportant than 1/3, 1/5, 1/7 and 1/9 respectively.

3.

Calculate the subjective weights $k_i^S$ [31]. Computing the product of elements of i-th row of judgment matrix $A$, taking the n-th root of each product, and normalizing these roots to be the subjective weight component. The specific calculation is as follows

$$k_i^S=\frac{{\left({\prod }_{j=1}^n{a}_{ij}\right)}^{1/n}}{{\sum }_{i=1}^n{\left({\prod }_{j=1}^n{a}_{ij}\right)}^{1/n}}, i,j=1,2,\dots ,n$$

(1)

where $k_i^S$ represents the subjective weight of this layer relative to the previous layer.

4.

Consistency test. The consistency test is used to verify the internal conflicts in the pairwise judgement matrix. According to the maximum eigenvalue of judgement matrix $A$, the consistency index CI is obtained in Equation (2). Table 2 shows the random index RI. By Equation (3) the consistency ratio CR is calculated. When $CR<0.10$, the consistency of judgment matrix $A$ is accepted. Otherwise, the judgment matrix should be modified.

$$CI=\frac{{\lambda }_{max}-n}{n-1}$$

(2)

$$CR=\frac{CI}{RI}$$

(3)

where ${\lambda }_{max}$ is the maximum eigenvalue of matrix $A$.

Table 2. Random indicator RI value.

n	1	2	3	4	5	6	7	8	9
RI	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45

Commonly, the subjective weight of each lower layer index relative to the higher layer index is obtained through the judgment matrix with AHP. The system, criterion, and measure layers are represented by A, B and C, respectively. So, the combined subjective weight of each measure layer C index under the goal layer is computed as follows:

$$\left\{\begin{array}{c}{k}_{A_j}^S={\displaystyle \sum _m}{k}_{B_m}^S\\ k_{B_m}^S={\displaystyle \sum _i}{k}_{C_i}^S\end{array}\right.$$

(4)

$$k_{C_i}^S=k_{A_j }^S\times k_{B{A}_m}^S\times k_{C{B}_i}^S$$

(5)

$$\left\{\begin{array}{c}{\displaystyle \sum _j}{k}_{A_j }^S=1\\ {\displaystyle \sum _m}{k}_{B{A}_m}^S=1\\ {\displaystyle \sum _i}{k}_{C{B}_i}^S =1\end{array}\right.$$

(6)

where $k_{A_j}^S$, $k_{B_m}^S$, $k_{C_i}^S$ respectively represent the combined subjective weight of the system layer A, criterion layer B and measure layer C under the goal layer. $k_{B{A}_m}^S$ and $k_{C{B}_i}^S$ respectively represent the weight of the criterion layer under the system layer and the weight of the measure layer under the criterion layer, and $i, j,m$ correspond to the index number of each layer respectively.

2.2. Cloud Model

2.2.1. Definition of Cloud Model

Cloud model is a mathematical model of uncertainty conversion between qualitative concepts and quantitative representations based on traditional fuzzy mathematics and probability statistics proposed by academician Deyi Li [32,33,34], which preserves the randomness and fuzziness of uncertain events in objective reality and realizes the conversion between qualitative concepts to quantitative data.

Definition 1

([33]). Supposing U is the quantitative universe expressed by accurate value, T is a qualitative concept in U. For arbitrary $\mathit{x}\mathit{\in }\mathit{U}$ for T is a random number with a steady tendency, there exists a corresponding certainty degree ${\mathit{C}}_{\mathit{T}}\left(\mathit{x}\right)$ as shown in Equation (6).

$$\forall x\in U⟶C_T\left(x\right)\in \left[0,1\right]$$

(7)

Then, the distribution of$\mathit{x}$in the universe$U$can be defined as a cloud and$x$can be called a cloud drop.

A normal cloud [32] is a model of uncertainty transformation between a qualitative concept expressed in terms of linguistic values and its quantitative representation, with a set of mutually independent parameters that together express the numerical characteristics of a qualitative concept, reflecting the uncertainty of the concept. Based on the normal distribution function and normal membership function, these three parameters are characterized by the expectation of $Ex$, entropy $En$ and hyper-entropy $He$ (see Figure 1).

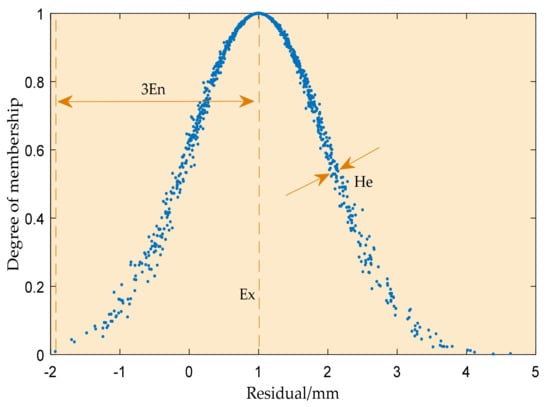
Figure 1. Different digital characteristics of cloud model.

Definition 2

([33]). Let U be the universe of discourse and T be a qualitative concept in U. If $x\in U$ is a random instantiation of concept T, which satisfies $\mathit{x}\mathit{\sim }\mathit{N}\left(\mathit{E}\mathit{x}\mathit{,} \mathit{E}{\mathit{n}}^{\prime \mathit{2}}\right)$, $\mathit{E}{\mathit{n}}^{\prime }\mathit{\sim }\mathit{N}\left(\mathit{E}\mathit{n}\mathit{,} \mathit{H}{\mathit{e}}^{\mathit{2}}\right)$, and the certainty degree of $\mathit{x}$ belonging to concept $\mathit{T}$ satisfies

$$f\left(x\right)=e^{-{\left(x-Ex\right)}^2/2{\left(E{n}^{\prime }\right)}^2},$$

(8)

then the distribution of x in the universe $U$ is called a normal cloud.

The parameter $Ex$ expresses the central value of the qualitative concept in the universe space, represents the value of the qualitative concept at 100% membership and is the center of gravity of the cloud drop group corresponding to the qualitative concept. The parameter $En$ represents the fuzzy degree of the corresponding numerical range of the problem described by cloud model, which is defined as standard deviation. The range of values that can be accepted by qualitative concepts in the universe space is expressed. Parameter $He$ reflects the randomness of the occurrence of samples representing qualitative concept values, which is defined as the standard deviation of entropy. It is the uncertainty measure of entropy, which reveals the relationship between fuzziness and randomness. The cloud model schematic diagram of different $Ex, En, He$ are shown in Figure 2.

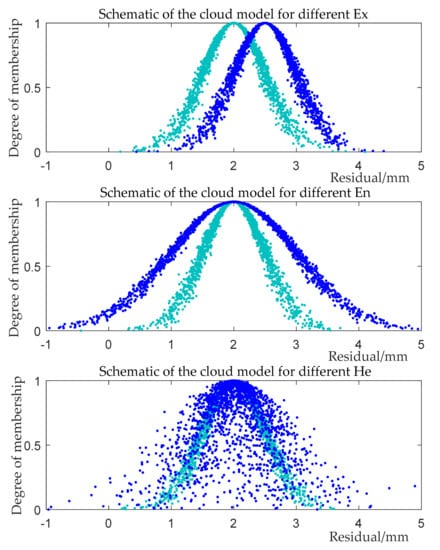
Figure 2. Schematic diagram of the different digital characteristics of cloud model.

2.2.2. Cloud Generator

The cloud generator is the key algorithm [35,36,37] for converting qualitative and quantitative cloud models and is the basis for uncertainty inference rule building. The cloud drop generation process is shown in Figure 3 and Figure 4.

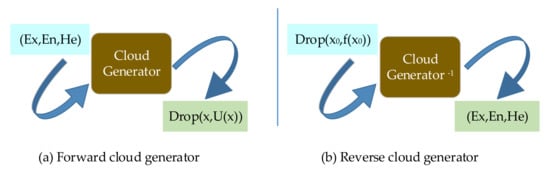
Figure 3. Cloud generator.

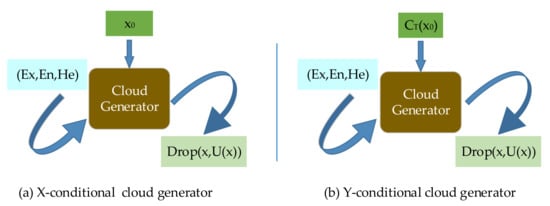
Figure 4. Conditional cloud generator.

Forward cloud generator is the uncertainty conversion algorithm from qualitative to quantitative representations. The forward cloud generator is the logical process of forwardness.

$$E{n}_i^{\prime }=normrnd\left(Ex,He\right)$$

(9)

$$x_i=normrnd\left(Ex,E{n}_i^{\prime }\right)$$

(10)

where $normrnd$ function is a normal random number generation function.

Reverse cloud generator converts a quantitative representation that conforms to the structure of the cloud model into a qualitative conceptual language and is an uncertain conversion algorithm from a quantitative to a qualitative representation.

$$Ex=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{x}_i$$

(11)

$$En=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(x_i-Ex\right)}^2}$$

(12)

$$E{n}_i^{\prime }=\frac{\left|x_i-Ex\right|}{\sqrt{-2ln{C}_T\left(x_i\right)}}$$

(13)

$$He=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(E{n}_i^{\prime }-En\right)}^2}$$

(14)

The specific algorithm of cloud generator is shown in Algorithm 1.

Algorithm 1: Cloud Generator
Forward Cloud Generator		Reverse Cloud Generator
Input	Digital feature $\left(Ex,En,He\right)$ and number of cloud drops $n$.	$Drop\left(x_i,f\left(x_i\right)\right)$, $i=1, 2,\dots ,n$.
Output	$Drop\left(x_i,f\left(x_i\right)\right)$, $i=1, 2,\dots ,n$.	The 3 main parameters $\left(Ex,En,He\right)$ corresponding to the $n$ cloud drops.
1. The normal random number $E{n}_i^{\prime }$ satisfying with as expectation and $En$ as variance is calculated from Equation (9).		1. Computing the expectation $Ex$ from Equation (11).
2. The Normal random number $x_i$ with $Ex$ as the expectitaion and $E{n}^{\prime }$ as the variance is calculated from Equation (10).		2. Computing the entropy $En$ from Equation (12).
3. The membership of $x_i$ corresponding to the qualitative concept $T$ is calculated from Equation (8).		3. Computing $E{n}_i^{\prime }$ corresponding to $Drop\left(x_i,f\left(x_i\right)\right)$ from Equation (13).
4. Get a cloud drop $Drop\left(x_i,f\left(x_i\right)\right)$.		4. Computing the hyper-entropy $He$ corresponding to $E{n}_i^{\prime }$ from Equation (14) (see Figure 3).
5. Repeat steps until the set number of $n$ cloud drops are obtained (see Figure 3).

The X-conditional cloud generator is an algorithm that applies the forward cloud generator on the theoretical universe $U$ and performs the calculation under the given specified condition $x=x_0$. That is, given the parameter $x$, the membership $C_T\left(x\right)$ corresponding to $x$ on the theoretical universe $U$ can be obtained by the forward cloud generator operation, and its membership $C_T\left(x\right)$ has uncertainty in each operation.

The Y-conditional cloud generator is an algorithm that applies a forward cloud generator on the theoretical universe $U$ to perform computation under the given specified condition $C_T\left(x\right)=C_T\left(x_0\right)$. The Y-conditional cloud generator is the basis of the regular posterior representation.

$$x_i=Ex+E{n}_i^{\prime }\sqrt{-2lnf\left(x_0\right)}$$

(15)

The uncertainty inference algorithm of the cloud model is based on the X-conditional cloud generator and the Y-conditional cloud generator, and the specific algorithms of both are shown in Algorithm 2.

Algorithm 2: Conditional Cloud Generator
X-Conditional Cloud Generator		Y-Conditional Cloud Generator
Input	Digital feature $\left(Ex,En,He\right)$, $x_0$ and number of cloud drops $n$.	Digital feature $\left(Ex,En,He\right)$, $f\left(x_0\right)$ and number of cloud drops $n$.
Output	$Drop\left(x_0,f\left(x_i\right)\right)$, $i=1, 2,\dots ,n$.	$Drop\left(x_i,f\left(x_0\right)\right)$, $i=1, 2,\dots ,n$.
1. The normal random number $E{n}_i^{\prime }$ satisfying $E{n}_i^{\prime }$ as the expectation and $He$ as the variance is calculated from Equation (9).		1. The normal random number $E{n}_i^{\prime }$ satisfying $En$ as the expectation and $He$ as the variance is calculated from Equation (9).
2. Computing the membership from Equation (8) to generate a cloud drop.		2. A cloud drop is obtained from Equation (15).
3. Repeat steps until the set number of $n$ cloud drops are obtained (see Figure 4).		3. Repeat steps until the set number of $n$ cloud drops are obtained (see Figure 4).

2.2.3. Cloud Rule Generator

Cloud rule generator is a tool for causal logic rule transformation reasoning among multiple concepts, and logic rules usually consist of multiple rule precursors and one rule successor.

In this paper, we use single-rule reasoning (if A then B) to combine X-conditional cloud generator and Y-conditional cloud generator to form a single-rule cloud generator (see Figure 5). $C{G}_A$ is the X-conditional cloud generator and is the Y-conditional cloud generator. When $x=x_0$ is specified, $C{G}_A$ generates a random membership that satisfies the cloud model, and this membership can output a random cloud drop $Drop\left(x_B,U\left(x_A\right)\right)$ that satisfies the cloud model of the posterior part of the rule through $C{G}_B$.

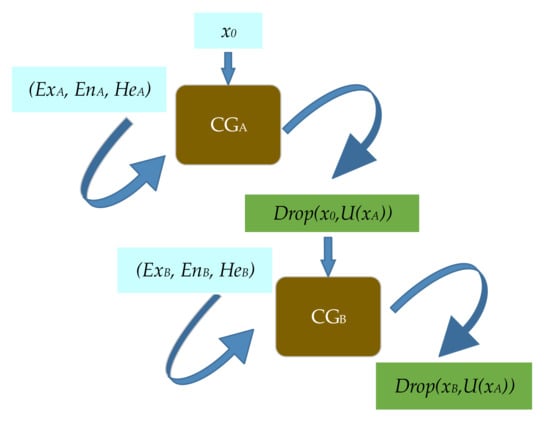
Figure 5. Single-rule cloud generator.

2.2.4. Objective Weight Calculation

Using the realistic data of each index as input, multiple sets of random and different cloud drops conforming to the cloud model can be obtained through the forward cloud generator to form an extended sample matrix. The uncertainty inference rules of the cloud model are used to convert the raw data into the impact intensity of each index on the assessment target, and then objective weights are computed according to the gray correlation equation [38].

That is, the extended sample data will be used as the initial input parameters of the X-conditional cloud generator, the membership under the X-conditional cloud generator will be computed and the data with the largest membership will be selected as the input parameters of the Y-conditional cloud generator. The output value of the Y-conditional cloud generator is the impact intensity of the initial score of each index, and forms the impact intensity matrix $P\left(p_{ij}\right), i=1, 2,\dots ,n, j=1, 2,\dots ,m$.

The gray correlation Equations (16)–(18) are used to compute the influence weight of the degree of association of each influence factor among the indexes on the results. That is, the objective weights.

$${\xi }_{0i}=\frac{\underset{i}{\min } \underset{j}{\min }\left|P_{0j}-P_{ij}\right|+\rho \underset{i}{\max } \underset{j}{\max }\left|P_{0j}-P_{ij}\right|}{\left|P_{0j}-P_{ij}\right|+\rho \underset{i}{\max } \underset{j}{\max }\left|P_{0j}-P_{ij}\right|}$$

(16)

$$r_i=\frac{{{\displaystyle \sum }}_{j=1}^m{\xi }_{0i}}{m}$$

(17)

$$k_{C_i}^O=\frac{r_i}{{{\displaystyle \sum }}_{i=1}^n{r}_i}$$

(18)

where $P_{ij}$ is the factor score value, which is determined by the output value of Y-condition generator.$P_{0j}$ is the sample index parameter. ${\xi }_{0i}$ is the correlation coefficient of each factor score on the index parameter. $\rho$ is the resolution coefficient, $\rho \in \left[0,1\right]$.$r_i$ is the correlation between the factors of each index, and $k_{C_i}^O$ is the objective weight of the i-th index.

2.3. Weighted Analysis Method

In order to obtain the comprehensive weight, the weighted analysis method is used to compute it as follows

$$k_{C_i}^C=q_S{k}_{C_i}^S+q_O{k}_{C_i}^O, i=1, 2,\dots ,n$$

(19)

where $k_{C_i}^C$ is the comprehensive weight of the i-th index, $q_S, q_O\in \left[0,1\right]$ and $q_S+q_O=1$.

3. Case Analysis

The method was applied to the assessment of rescue performance at an earthquake site. The rescue performance was calculated using an earthquake scene rescue as an example. The assessment process is shown in Figure 6.

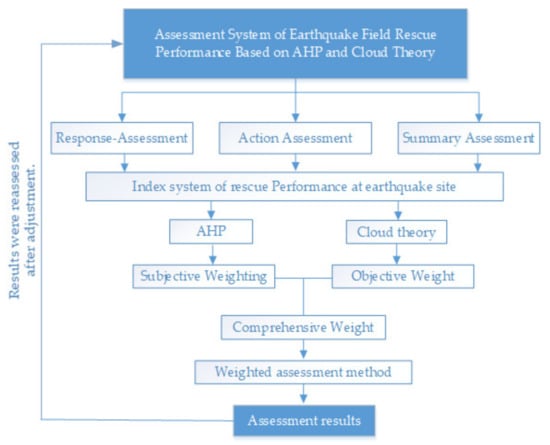
Figure 6. Flow chart of rescue performance assessment model.

3.1. Earthquake Rescue Performance Index System

This paper uses AHP to construct an assessment index system [8,9] from three aspects: search, rescue and medical treatment, based on the characteristics of the earthquake site and combined with the task requirements of on-site rescue.

According to the rescue performance assessment indexes given in the INSARAG guidelines [9], an index system—including search and rescue medical integrated earthquake scene rescue performance as the goal layer, the search system, rescue system and medical system as the system layer, 12 indexes, such as mobilization preparation B1 and action phase B2 as the criterion layer, and 54 indexes as the measure layer—was established. All indexes and their subordinate relationships are shown in Figure 7.

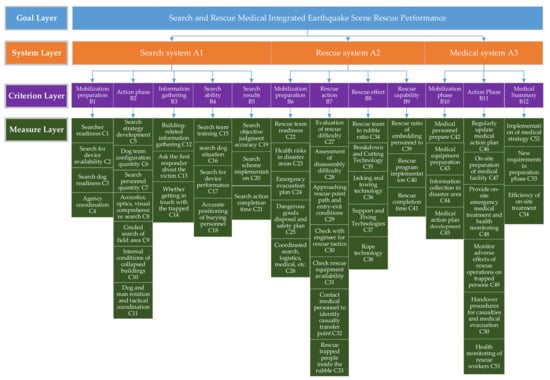
Figure 7. Performance assessment index system of search and rescue medical integrated earthquake scene rescue.

3.2. Quantitative Score of Rescue Performance

When assessing the performance of earthquake rescue, the initial score of indexes is based on the degree of completion of the index. The quantitative scoring criteria for the indexes are shown in Figure 8.

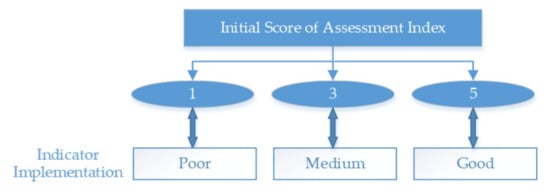
Figure 8. Description of initial scoring value of assessment index.

3.3. Determining the Weight of Each Earthquake Rescue Index

3.3.1. Computation of Subjective Weights of Indexes

Based on the questionnaires filled out by rescue experts from the Institute of Engineering Mechanics, China Earthquake Administration, Institute of Disaster and Medicine and National US & R Training Centre of Lanzhou, a judgment matrix was constructed, and the subjective weights of each index were computed. The importance of search system A1, rescue system A2 and medical system A3 were considered equally, that is $k_{A_j}^S=1/3$.

The index weights of the criterion layer under the system layer are computed. According to Table 1, a judgment matrix from the system layer to the criterion layer is established for each index under the search system A1, and the subjective weights of each index are calculated according to Equation (1). The results of the judgment matrix and index weights are recorded in Table 3.

Table 3. Search system A1 indexes judgment matrix and subjective weights.

Importance of Criteria Layer Indexes		B1	B2	B3	B4	B5	${\mathit{k}}_{\mathit{B}{\mathit{A}}_{\mathit{m}}}^{\mathit{S}}$
Search system A1	B1	1	1/5	1/7	1/5	1/7	0.0329
	B2	5	1	1/3	1/3	1/6	0.0846
	B3	7	3	1	1	1/5	0.1815
	B4	5	3	1	1	1/4	0.1774
	B5	7	6	5	4	1	0.5236

The weights corresponding to each index in rescue system A2 and medical system A3 were calculated, and the results are shown in Table 4 and Table 5.

Table 4. Rescue system A2 indexes judgment matrix and subjective weights.

Importance of Criteria Layer Indexes		B6	B7	B8	B9	$k_{B{A}_m}^S$
Rescue system A2	B6	1	1/3	1/5	1/7	0.0592
	B7	3	1	2	1/3	0.2255
	B8	5	1/2	1	1/3	0.1811
	B9	7	3	3	1	0.5342

Table 5. Medical system A3 indexes judgment matrix and subjective weights.

Importance of Criteria Layer Indexes		B10	B11	B12	${\mathit{k}}_{\mathit{B}{\mathit{A}}_{\mathit{m}}}^{\mathit{S}}$
Medical system A3	B10	1	1/2	1/3	0.1571
	B11	2	1	1/2	0.2493
	B12	3	2	1	0.5936

The initial judgment matrix was tested for consistency according to Equations (2) and (3), and the results are shown in Table 6.

Table 6. Consistency test results of judgment matrix.

System Layer	Characteristic Value ${\mathit{\lambda }}_{\mathit{m}\mathit{a}\mathit{x}}$	Consistency Ratio CR	Whether Conformity Is Met (CR < 0.1)?
Search system A1	5.3766	0.0841	Y
Rescue system A2	4.1634	0.0612	Y
Medical system A3	3.0536	0.0516	Y

The process of calculating the weights of the measure layer indexes under the criterion layer is consistent with the above, and Table 7 demonstrates the process of calculating the weights of the measure layer indexes C1 to C4 under the criterion layer index B1, the $CR<0.1$; that is, the judgement matrix is reasonable, and $k_{C_1}^S$ to $k_{C_4}^S$ can be calculated according to equations (4), (5) and (6). The weights $k_{C_i}^S$ of all indexes in the measure layer under the goal layer is shown in Table 8 are computed.

Table 7. Mobilization preparation B1 index judgment matrix and subjective weights.

Importance of Measure Layer Indexes		C1	C2	C3	C4	${\mathit{k}}_{\mathit{C}{\mathit{B}}_{\mathit{i}}}^{\mathit{S}}$
Mobilization preparation B1	C1	1	1	5	3	0.4199
	C2	1	1	2	3	0.3339
	C3	1/5	1/2	1	2	0.1427
	C4	1/3	1/3	1/2	1	0.1036

Table 8. Initial score of indexes and their weights.

System Layer	Criteria Layer	Measure Layer	Index Score $C_i$	Subjective Weight $k_{C_i}^S$	Objective Weight $k_{C_i}^O$	Comprehensive Weight $k_{C_i}^O$
Search system A1	Mobilization preparation B1	C1	5	0.0046	0.0276	0.0161
		C2	3	0.0037	0.0138	0.0087
		C3	5	0.0016	0.0276	0.0146
		C4	1	0.0011	0.0092	0.0052
	Action phase B2	C5	3	0.0067	0.0138	0.0103
		C6	1	0.0061	0.0092	0.0076
		C7	3	0.0017	0.0138	0.0077
		C8	5	0.0044	0.0276	0.0160
		C9	5	0.0039	0.0276	0.0157
		C10	3	0.0024	0.0178	0.0081
		C11	5	0.0030	0.0276	0.0153
	Information collection B3	C12	5	0.0063	0.0276	0.0170
		C13	3	0.0156	0.0138	0.0147
		C14	1	0.0385	0.0092	0.0239
	Search capability B4	C15	3	0.0256	0.0138	0.0202
		C16	5	0.0074	0.0276	0.0175
		C17	5	0.0082	0.0276	0.0179
		C18	3	0.0169	0.0138	0.0154
	Search effect B5	C19	5	0.0873	0.0118	0.0495
		C20	3	0.0436	0.0138	0.0287
		C21	5	0.0436	0.276	0.0356
Rescue system A2	Mobilization preparation B6	C22	1	0.0072	0.0092	0.0082
		C23	3	0.0046	0.0138	0.0092
		C24	5	0.0038	0.0276	0.0157
		C25	5	0.0020	0.0276	0.0148
		C26	1	0.0021	0.0092	0.0057
	Rescue action B7	C27	5	0.0143	0.0276	0.0209
		C28	3	0.0036	0.0138	0.0087
		C29	3	0.0111	0.0138	0.0124
		C30	1	0.0086	0.0092	0.0089
		C31	3	0.0082	0.0138	0.0110
		C32	5	0.0054	0.0276	0.0165
		C33	5	0.0240	0.0276	0.0258
	Rescue capability B8	C34	3	0.0039	0.0138	0.0088
		C35	5	0.0223	0.0276	0.0250
		C36	1	0.0111	0.0092	0.0102
		C37	3	0.0165	0.0138	0.0152
		C38	1	0.0065	0.0092	0.0078
	Rescue effect B9	C39	5	0.1134	0.0276	0.0705
		C40	3	0.0186	0.0138	0.0162
		C41	5	0.0460	0.0276	0.0368
Medical system A3	Mobilization phase B10	C42	3	0.0182	0.0138	0.0160
		C43	5	0.0182	0.0276	0.0229
		C44	3	0.0051	0.0138	0.0094
		C45	3	0.0108	0.0138	0.0123
	Action phase B11	C46	1	0.0061	0.0092	0.0076
		C47	1	0.0044	0.0092	0.0068
		C48	5	0.0262	0.0276	0.0269
		C49	5	0.0247	0.0276	0.0261
		C50	3	0.0094	0.0138	0.0116
		C51	3	0.0124	0.0276	0.0200
	Medical summary B12	C52	3	0.0454	0.0138	0.0296
		C53	3	0.0241	0.0138	0.0190
		C54	5	0.1283	0.0276	0.0779

3.3.2. Computation of Objective Weights of Indexes

The ambiguity of the qualitative concept can be expressed by cloud model when conducting the assessment of earthquake scene rescue performance. Take measure layer index C2 as an example—it mainly includes five influencing factors: (1) equipment quantity supply; (2) equipment type suitability; (3) equipment maintenance good; (4) equipment available for urgent repair; (5) equipment transportation convenience. If the site situation meets five of them, the score is 5; if it meets 3–4 of them, the score is 3; if it meets 0–2 of them, the score is 1. Using the data of the realistic situation of each index as input, multiple sets of random cloud drops conforming to the cloud model can be obtained according to the forward cloud generator, and the number of cloud drops $n=1000$, thus expanding the data sample of the original single score to form the extended sample. The 54 indexes in the index system are assigned with values according to the field situation, and the data are extended according to the extended sample computation model to form the extended sample matrix.

The impact intensity matrix $P\left(p_{ij}\right)$ is derived from the cloud rule generator according to the relationship between indexes. According to equations (16) to (18), take $\rho =0.5$ to compute the objective weight. The computation results are shown in Table 8.

3.4. Weighted Analysis of Rescue Performance Assessment

Based on Equation (19), taking $q_S=q_O=0.5$, the comprehensive weight of earthquake rescue performance is calculated. The results of the measure layer index scores and comprehensive weights calculations are shown in Table 8.

According to the index scores and weights computed in Table 8, the performance value of the whole system was computed as follows

$$y={\displaystyle \sum }_{i=1}^n{C}_i{k}_i$$

(20)

where $n$ represents the number of measures layer indexes. $C_i$ represents the corresponding quantitative score of the i-th index in the initial assessment state. $k_i$ is the weight of i-th index and $y$ is the performance score.

According to Equation (20), take $k_i=k_{C_i}^S$, and compute the composite score $y_S=4.0132$ in the subjective state. Take $k_i=k_{C_i}^O$, and compute the composite score $y_O=4.0012$ in the objective state.

In the same principle, the comprehensive performance value of this earthquake scene rescue is $y_C=4.0065$, and the assessment result is shown in the form of cloud model image in Figure 9, combining with the scoring standard of Figure 8, it can be concluded that the performance of the earthquake rescue is between medium and good.

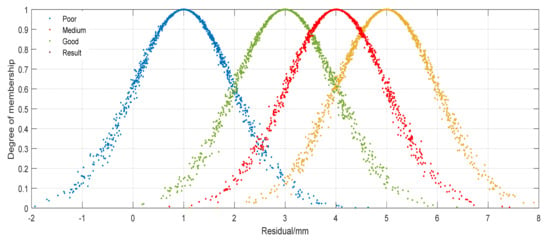
Figure 9. Initial assessment results.

The rescue performance is optimized in two levels, and the first level selects the action indexes with high weight share but low scores, such as C52, C20 and C15, for optimization. The second level for the lower scoring indexes, taking C30, for example, identifies the type of structure before rescue, assesses the damage and danger of the structure and monitors the structure during rescue so that it meets the requirements of the three indicators and the score reaches 5. Combined with the actual situation on site, the indexes that are realistic, feasible and easy to improve are optimized. The optimized scores of indexes C52, C20, C15 and C30 are 5, 5, 5 and 3 respectively, and only these four items are optimized, and the optimized comprehensive performance value $y_C=4.1813$, and the assessment results are represented as cloud model images as shown in Figure 10.

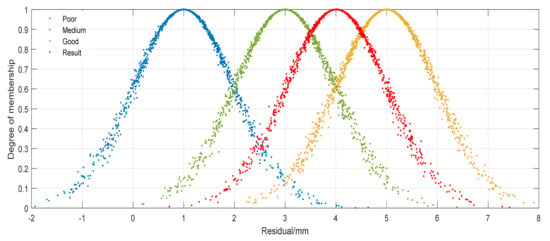
Figure 10. Optimized assessment results.

The optimized comprehensive assessment results show an improvement of 4.36% relative to the initial assessment results, which is closer to the rating of good. This assessment methodology can provide technical guidance for the allocation of resources for subsequent earthquake rescue operations and also give targeted requirements for the daily training of search and rescue teams.

4. Conclusions

In this paper, we systematically reviewed the previous assessment methods of earthquake rescue performance and the research of AHP and cloud theory in assessment. In order to better assess the performance of rescue after an earthquake, and to recognize the factors that limit the performance of earthquake rescue, this study uses AHP and cloud model, establishes a search and rescue medical integrated earthquake scene rescue performance assessment system through a weighted analysis method and validates the method with an earthquake rescue case. The main results are as follows:

• On the basis of a large number of on-site research and expert consultation, a rescue performance assessment index system was constructed, setting up a total of 54 indexes that basically cover the specific requirements of scene rescue, taking into account the scientific nature, hierarchy, independence and evaluability each index needs to have.
• Based on the performance characteristics of different stages of earthquake scene rescue, the application of AHP and cloud model in the assessment of earthquake scene rescue performance is realized. Through the cloud model, the sample set of assessment candidates was reasonably filled with missing data values, data anomaly processing and optimal selection of the sample set to expand the sample set of the assessment cloud model, thus providing a more accurate assessment basis for rescue performance assessment. Combined with the results of the questionnaire given by the rescue experts, a judgment matrix was constructed to derive the index weight values, which realized the application of AHP and cloud model in the assessment of earthquake scene rescue performance.
• Take an earthquake rescue case to calculate. The weighted analysis method is used to integrate the weights calculated by the AHP and the cloud model to score each index at the measure layer and apply the method to calculate the rescue performance value, and optimize the assessment results of the example in two levels to derive a better rescue performance assessment value to provide an improvement reference for subsequent rescues. The results show that the method of assessing the performance of search and rescue medical integrated earthquake scene rescue offers good practicality, and can provide training guidance and assessment indexes for rescue teams and provide reference for further optimization of earthquake emergency rescue in the world.

5. Limitations and Future Research Directions

The AHP method relies on expert questionnaires to calculate subjective weights. In future research, expanding the number of expert questionnaires can make the calculation of subjective weight more accurate. In addition, the method proposed in this paper can be compared with the existing performance assessment methods, such as the entropy weight method or the combination weighted TOPSIS method, to obtain the optimal assessment method.