On Asymptotics of Optimal Stopping Times

Abstract

We consider optimal stopping problems, in which a sequence of independent random variables is drawn from a known continuous density. The objective of such problems is to find a procedure which maximizes the expected reward. In this analysis, we obtained asymptotic expressions for the expectation and variance of the optimal stopping time as the number of drawn variables became large. In the case of distributions with infinite upper bound, the asymptotic behaviour of these statistics depends solely on the algebraic power of the probability distribution decay rate in the upper limit. In the case of densities with finite upper bound, the asymptotic behaviour of these statistics depends on the algebraic form of the distribution near the finite upper bound. Explicit calculations are provided for several common probability density functions.

1. Introduction

Optimal stopping problems pose the challenge of deciding when to stop some stochastic process in order to maximise some objective, or utility. This problem has arisen in a number of contexts, such as deciding how many candidates for a job should be interviewed before deciding upon one particular candidate, known in literature as the secretary problem [1,2,3]. Optimal stopping has been used to determine when assets should be bought and sold in order to maximize profits; this has been described as the house-selling problem and is discussed in [4,5,6]. Optimal stopping has been incorporated into the theory of online auctions, as in [7]. In this study, the authors linked the analysis of the secretary problem to the design of a mechanism for online auctions. Related analyses may be found in [8,9]. Optimal stopping also features in financial and economic applications, such as in the pricing of American options [10], games [11], operational risk insurance [12], dynamic pricing [13] and more complicated buying–selling problems [14,15,16].

Optimal stopping problems are formulated in terms of observing random variables and determining the stopping point in order to maximize a particular reward function. The problem considered here involved observing a sequence of random variables $y_1,y_2,\cdots ,y_N$ and making the decision to stop after a particular number of observations, denoted by m, where $1\le m\le N$, based on the variables that had been previously observed at that stage. After stopping, we receive a reward which is a function of the already observed values $y_1,\dots ,y_m$. This problem is one representative of a class of optimal stopping problems that consists of finding a sequential procedure that maximizes the expected reward. For a more extensive discussion of this class of problems, see Section 13.4 [17].

While there exists extensive literature on the theory of optimal stopping problems [17,18], less attention has been paid to the asymptotic properties of stopping times. Most existing asymptotic results focus on “no-information” problems in which the distribution of the observations is unknown.

In no-information problems, an observer determines the relative rank of each observation and the reward function is a function of these ranks. An example of a no-information problem is the secretary problem [1,19]. In this problem, the reward function is the indicator variable of the best object, which means that the observer aims to maximise the probability that the best object is selected. As a consequence, the secretary problem is sometimes referred to as the no-information best-choice problem.

There are many other variations of the no-information problem and significant work exists on the asymptotic properties of the stopping time (see, for example, [19,20,21]). It was shown in [22] that, in the secretary problem with a sequence of N observations, the asymptotic expectation and variance for the stopping time is $2N/\mathrm{e}$ and $\left(2/\mathrm{e}-5/{\mathrm{e}}^2\right)N^2$, respectively, where e is taken to be Euler’s constant. Asymptotic descriptions of statistical properties for other no-information problem variants can be found in [20,23], where the techniques used are dependent on the structure and variation of each problem. The asymptotics where the number of observations is random has also been studied in [24].

There is substantially less literature describing the asymptotic behaviour of statistical properties for “full-information” problems, when the distribution of random variables is known beforehand. Gilbert and Mosteller [23] studied the optimal stopping strategy for the full-information problem in which the objective is identical to that of the secretary problem, known as the full-information best-choice problem [25]. In this setting, the optimal stopping strategy was shown to consist of stopping and choosing the m-th observation $y_m$ if it is the highest ranked out of all observations made at this point and has a value exceeding a threshold, which depends on m. Asymptotically, it was shown that $v_n$, the value of a sequence with n steps remaining, $v_n\sim 1-c/n$, where $c\approx 0.804352$. An intermediate classification of the “partial information” problem occurs when the observations are taken from a known distribution but containing one, or potentially more, unknown parameters. For example, DeGroot (see Section 13.6; [17]) analysed the stopping problem involving sampling from a normal distribution with unknown mean. Such problems are dealt with using sequential estimation methodologies and Bayesian methods. As we focus on full-information problems in this paper, these methods are not needed and are deemed out of scope. In best-choice settings, variables that do not follow the uniform distribution can be re-scaled by applying the cumulative density function of the particular distribution to achieve a uniform distribution that is monotonically equivalent, as far as the best-choice is concerned. The asymptotic probability of finding the best object (see Section 3 of [23,26]) is independent of the distribution of the variables, tending to approximately 0.58 as the number of observations in the sequence becomes large.

The best-choice problems that are described above are interested in finding the very best object. For the full-information case, this condition can be relaxed by instead setting our reward at stopping time m to $y_m$ and seeking to maximise the expected reward. A special case of this problem, called the uniform game (Section 5a of [23]), is related to the well-known Cayley’s problem (see, for example, [1,27]). In [23], the authors showed that the expected reward of a sequence of n independent and identically distributed (iid) random variables having the standard uniform distribution can be approximated in the following way (see also [27]):

$$v_n\sim 1-\frac{2}{n+log(n+1)+1.767}\mathrm{as}n\to \infty .$$

(1)

In [22], the authors found the asymptotics of the expected value and the variance of the stopping time as $N/3$ and $N^2/18$, respectively, for the uniform game. The asymptotic techniques used to compute this behaviour are highly dependent on the distribution and cannot be easily generalized to more general classes of distribution. In [28,29], using the extreme value theory, the authors proved limit theorems for threshold-stopped random variables and derived the asymptotic distribution of the reward sequence of the optimal stopping (iid) random variables.

In the full-information problem, where the reward at time m is $y_m$, such as that considered in the present study, the distribution of the observations plays a significant role in the asymptotic behaviour of the outcome statistics. This study offers a general asymptotic technique for calculating the asymptotic behaviour of $E\left({\tau }_N\right)$ and $\mathrm{Var}\left({\tau }_N\right)$ as $N\to \infty$ for general classes of probability distributions in the full-information problem where we wish to maximise the expected reward $y_m$. The value $y_m$ could be interpreted as an offer for an asset (e.g., a house), at some time m, which the decision maker would like to sell. Having simple asymptotic results for $E\left({\tau }_N\right)$ and $\mathrm{Var}\left({\tau }_N\right)$ can be useful in analysing properties of the asymptotic distribution. For example, we may substitute for the expected value and variance in inequalities such as the Chebyshev’s and Markov’s to obtain probability bounds and avoid the need for simulation, which can save time and resources. It is worth noting that the asymptotic behaviour of the optimal stopping problem can be useful in understanding resource allocation in situations where there may be a fixed cost per observation, i.e., the decision maker would be able to have a conservative understanding of how much cost they would incur before their stopping strategy is completed, hence being able to allocate their resources accordingly. In addition to recovering existing results from [22] for the uniform distribution, we extended the analysis to consider the effect of drawing elements of the sequence from a wide range of common distributions.

2. Formulation

Let $y_1,y_2,\cdots ,y_N$ be a sequence of independent, identically distributed (iid) random variables from a known distribution. We are allowed to observe the $y_n$ sequentially, stopping at any variable we choose. If we stop at time m after observations $(y_1,\dots ,y_m)$, then we receive reward $y_m$. This decision to stop depends solely on the values of the random sequence already observed and not on any future values. We are interested in the problem where we find an optimal stopping rule that maximises our expected gain. More formally, we assume we have (i) a probability space $(\mathrm{\Omega },\mathcal{F},{\left\{{\mathcal{F}}_n\right\}}_{n=1,\dots ,N},P)$, (ii) an increasing sequence ${\left\{{\mathcal{F}}_n\right\}}_{n=1,\dots ,N}$ of sub-$\sigma$-algebras of $\mathcal{F}$ and (iii) that the sequence $y_1,\dots ,y_N$ of random variables is such that $y_n$ is measurable with respect to ${\mathcal{F}}_n$ for each $n=1,\dots ,N$. Note that, here, we take ${\mathcal{F}}_{\mathcal{n}}=\mathcal{B}(y_1,\dots ,y_n)$, where $\mathcal{B}\left(\mathcal{A}\right)$ is the $\sigma$-algebra generated by $\mathcal{A}$. The optimal stopping problem can be formulated as finding the value process

$$V_n=\mathrm{ess}{\sup }_{\tau \in S_n}E\left\{y_{\tau }\right|{\mathcal{F}}_n\},$$

where $S_n$ is the class of all $\mathcal{F}$-measurable stopping times with values in $\{n,\dots ,N\}$ and $E\{·|{\mathcal{F}}_n\}$ is the conditional expectation with respect to ${\mathcal{F}}_n$. We note that the (iid) assumption allows us to drop this conditional.

A well-known method to solve such optimal stopping problems is to use a recursive scheme called the Snell envelope. This is the main tool to derive optimal solutions and to characterise them; see, for example, [30]. In the present study, the problem of finding the optimal stopping rule can be solved by backward induction using the Snell envelope (see, for example, [17,18]).

$$v_n=E\left(\max \{y_{N-n+1},v_{n-1}\}\right),n=1,\cdots ,N,v_0=-\infty ,$$

(2)

where $v_n$ is the value of a sequence with n steps and $v_N$ is the expected reward. Here, $\max \{y_{N-n+1},v_{n-1}\}$ represents the maximum gain that is possible to obtain having n steps left. If $n=1$, we have to stop and our gain would be $y_N$. If $1<n⩽N$, we can either stop or continue. If we stop, our gain is $y_{N-n+1}$ and if we continue, our expected gain is $v_{n-1}$.

If $y_1,y_2,\cdots ,y_N$ are iid continuous random variables with common probability density function (pdf) $f\left(y\right)$, then

$$v_n={\int }_{-\infty }^{\infty }\max \{y,v_{n-1}\}f\left(y\right)dy,n=1,\cdots ,N,v_0=-\infty .$$

(3)

The optimal stopping rule ${\tau }_N$ is

$${\tau }_N=\min \{m:1⩽m⩽N,y_m⩾v_{N-m}\}.$$

(4)

This optimal stopping rule formulation is for single stopping. It can be extended for multiple stopping for sums of random variables; see [31,32].

3. Computing ${\mathbf{v}}_{\mathbf{n}}$ Behaviour

3.1. Recurrence Relation for $v_n$

Let us assume that $y_n$ is drawn from a continuous pdf $f\left(y\right)$, which has unbounded support in the positive direction. This function has a cumulative distribution function (cdf) $F\left(y\right)$ and a survival function $h\left(y\right)=1-F\left(y\right)$.

Theorem 1.

Let Y be an integrable random variable whose expectation exists and which is drawn from a continuous distribution $f\left(y\right)$.

The value of a sequence with $n+1$ steps is given by

$$v_{n+1}=v_n+{\int }_{v_n}^{\infty }h\left(y\right)dy.$$

(5)

Proof. 

We recall that, for any integrable random variable X, we have that

$$E\left(X\right)={\int }_0^{\infty }(1-F\left(x\right))dx-{\int }_{-\infty }^{0}F\left(x\right)dx.$$

(6)

Thus,

$$\begin{array}{cc}\hfill v_{n+1}& =-{\int }_{-\infty }^{0}P(\max (Y,v_n)\le x)dx+{\int }_0^{v_n}P(\max (Y,v_n)>x)dx+\hfill \\ & {\int }_{v_n}^{\infty }P(\max (Y,v_n)>x)dx\hfill \\ & =0+{\int }_0^{v_n}1dx+{\int }_{v_n}^{\infty }P(Y>x)dx\hfill \\ & =v_n+{\int }_{v_n}^{\infty }h\left(y\right)dy.\hfill \end{array}$$

□

We note that, if $f\left(y\right)$ has bounded support in the positive direction such that $f\left(y\right)=0$ for $y>y_{\max }$, it follows, from above, that

$$v_{n+1}=v_n+{\int }_{v_n}^{y_{\max }}h\left(y\right)dy.$$

(7)

3.2. Asymptotics of $v_n$ as $n\to \infty$

Using the asymptotic controlling factor method (found in Section 5.3 of [33]), we know that, if a function $v_n$ grows no more rapidly than ${\mathrm{e}}^{a{n}^b}$ with $b<1$ as $n\to \infty$, then the leading-order asymptotic solution for $v_n$ satisfies

$$v_{n+1}-v_n\sim v_n^{\prime }\mathrm{as}n\to \infty ,$$

(8)

where asymptotic equivalence is defined in the usual fashion and ${}^{\prime }$ denotes differentiation with respect to n. It is straightforward to obtain a finite upper bound for the integral in (5), which implies that the growth of $v_n$ can be no faster than linear in n. Hence, this theorem holds.

Therefore, we can use (5) to write the asymptotic relation

$$v_n^{\prime }\sim {\int }_{v_n}^{\infty }h\left(y\right)\mathrm{d}y\mathrm{as}n\to \infty ,$$

(9)

with the upper bound replaced by b in the finite upper support case, corresponding to (7).

Remark 1.

The expression in (9) can be manipulated to obtain a convenient asymptotic representation for $v_n$, subject to some additional assumptions. Let us suppose that $v_n^{\prime \prime }$ exists, is integrable for sufficiently large values of n and has an asymptotic series representation. These conditions are sufficient to allow both sides of (9) to be differentiated (see, for example, the discussion in Section 3.8 of [33]) to give

$$v_n^{\prime \prime }\sim -h\left(v_n\right)v_n^{\prime }\mathrm{as}n\to \infty .$$

(10)

Let us assume that there exists some k such that $v_n^{\prime }\ne 0$ for $n>k$. Therefore, Equation (10) gives

$$h\left(v_n\right)\sim -\frac{v_n^{\prime \prime }}{v_n^{\prime }}\mathrm{as}n\to \infty .$$

(11)

The assumptions required for (11) to be valid hold for all distributions considered in the present study. Therefore, this relationship is used to simplify a later result for a collection of common distributions.

3.3. Example Calculations

We illustrate the application of these ideas to some common distributions, such as the exponential distribution, which is studied in Example 1. In Example 2, we demonstrate that the same method can be applied to heavy-tailed distributions by considering the Pareto distribution and, in Example 3, we show that this method can be easily applied to distributions with finite support by considering the uniform distribution.

Finally, in Example 4, we consider a broad class of distributions with exponential upper tails and show that the asymptotic behaviour of $v_n$ is fully determined for this class of distribution, subject to the assumption that $v_n$ increases without bound.

Example 1.

The exponential distribution is given by

$$f\left(y\right)=\frac{1}{\beta }{\mathrm{e}}^{-y/\beta },$$

(12)

with $y\in [0,\infty )$ and $\beta >0$.

The survival function $h\left(y\right)$ is given by $h\left(y\right)={\mathrm{e}}^{-y/\beta }$. Hence, (9) becomes

$$\frac{\mathrm{d}{v}_n}{\mathrm{d}n}\sim \beta {\mathrm{e}}^{-v_n/\beta }\mathrm{as}n\to \infty .$$

(13)

Solving this formal equation gives the large-n asymptotic behaviour as

$$v_n\sim \beta log\left(n\right)\mathrm{as}n\to \infty .$$

(14)

Note that the constant term obtained by solving the ordinary differential equation does not contribute to the leading-order expression in the large-n limit.

Example 2.

The Pareto distribution is given by

$$f\left(y\right)=\frac{\alpha {\beta }^{\alpha }}{y^{\alpha +1}},$$

(15)

on $y\in [\beta ,\infty )$, where $\beta >0$. We assume that $\alpha >1$.

The survival function is given by $h\left(y\right)={(\beta /y)}^{\alpha }$. Therefore, the differential equation for the large-n asymptotic behaviour is given by

$$\frac{\mathrm{d}{v}_n}{\mathrm{d}n}\sim \left(\frac{{\beta }^{\alpha }}{\alpha -1}\right)v_n^{1-\alpha }.$$

(16)

Solving this formal equation gives the asymptotic behaviour in the large-n limit as

$$v_n\sim \beta {\left(\frac{\alpha n}{\alpha -1}\right)}^{1/\alpha }\mathrm{as}n\to \infty .$$

(17)

Example 3.

The uniform distribution is given by

$$f\left(y\right)=\frac{1}{b-a},$$

(18)

on $y\in [a,b]$, where $b>a$.

The survival function is given by $h\left(y\right)=\frac{b-y}{b-a}$. Therefore, the differential equation for the large-n asymptotic behaviour is given from (7) by

$$\frac{\mathrm{d}{v}_n}{\mathrm{d}n}\sim \frac{{(b-v)}^2}{2(b-a)}\mathrm{as}n\to \infty .$$

(19)

Solving this formal equation gives the asymptotic behaviour in the large-n limit as

$$v_n\sim b-\frac{2(b-a)}{n}\mathrm{as}n\to \infty .$$

(20)

Example 4.

A distribution $f\left(y\right)$ is given with a survival function that, for sufficiently large values of y, satisfies

$$\left|h\left(y\right)-\gamma {\mathrm{e}}^{-{(y/\beta )}^{\alpha }}\right|<\frac{{\mathrm{e}}^{-{(y/\beta )}^{\alpha }}}{y^{\Delta }},$$

(21)

for positive Δ and where α, β and γ are positive constants. Let us assume that $v_n$ increases without bound (i.e., for any N, there exists an n such that $v_n>N$).

The condition in (21) gives the asymptotic behaviour of $h\left(y\right)$ for large values of y. Assuming that $v_n$ increases without bound as n increases, there must be some sufficiently large n such that this inequality holds. Therefore, we may replace the full expression for $h\left(y\right)$ in (9) with its asymptotic value in the large-n limit, giving the ordinary differential equation

$$\begin{array}{c}\hfill \frac{\mathrm{d}{v}_n}{\mathrm{d}n}\sim {\int }_{v_n}^{\infty }h\left(y\right)\mathrm{d}y=\frac{\gamma \beta }{\alpha }\mathrm{\Gamma }\left(\frac{1}{\alpha },\frac{v_n^{\alpha }}{{\beta }^{\alpha }}\right)+g\left(n\right),\end{array}$$

(22)

where $\mathrm{\Gamma }$ represents the upper incomplete gamma function and

$$\left|g\left(n\right)\right|<{\int }_{v_n}^{\infty }\frac{{\mathrm{e}}^{-{(y/\beta )}^{\alpha }}}{y^{\Delta }}\mathrm{d}y<\frac{1}{v_n^{\Delta }}{\int }_{v_n}^{\infty }{\mathrm{e}}^{-{(y/\beta )}^{\alpha }}\mathrm{d}y.$$

(23)

As $v_n$ is assumed to increase without bound, this integral is asymptotically subdominant compared to the right-hand side of (22) as $n\to \infty$. Therefore, the solution to the differential Equation (22) may be approximated using standard asymptotic methods to give the formal asymptotic relation

$$v_n\sim \beta log{\left(n\right)}^{1/\alpha }\mathrm{as}n\to \infty .$$

(24)

It is straightforward to show, using (11), that large-n asymptotics of $h\left(v_n\right)$ are independent of $\alpha$ and $\beta$ to leading order, giving $h\left(v_n\right)\sim 1/n$ in the limit $n\to \infty$.

3.4. Tabulation of Further Examples

Using methods similar to the previous examples, the asymptotic behaviour of $v_n$ may be computed for a wide range of common distributions.

Table 1. This table details the behaviour of $v_n$ in the large-n limit for several common probability density functions. For each example, the table contains the pdf equation $f\left(y\right)$ and the density domain. The next column contains the survival function $h\left(y\right)$. The final column shows the asymptotic behaviour of $v_n$ in the limit $n\to \infty .$ In each case, $v_n$ increases without bound.

Distribution	$\mathit{h}\left(\mathit{y}\right)$	Tail Asymptotics as $\mathit{n}\to \mathit{\infty }$
Normal, $y\in (-\infty ,\infty )$:
$f\left(y\right)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{\mathrm{e}}^{-{(y-\mu )}^2/2{\sigma }^2}$	$\frac{1}{2}-\frac{1}{2}\mathrm{erf}\left(\frac{y-\mu }{\sigma \sqrt{2}}\right)$	$v_n\sim \mu +\sigma \sqrt{W\left(\frac{n^2}{2\pi }\right)}$
Gamma, $y\in (0,\infty )$:
$f\left(y\right)=\frac{{\beta }^{-\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}{y}^{\alpha -1}{\mathrm{e}}^{-y/\beta }$	$1-\frac{\gamma (\alpha ,y/\beta )}{\mathrm{\Gamma }\left(\alpha \right)}$	$\begin{array}{cc}\hfill v_n\sim \beta & (\alpha -1)W\left. [\frac{1}{\alpha -1}{\left(\frac{n}{\mathrm{\Gamma }\left(\alpha \right)}\right)}^{1/(\alpha -1)}\right]\hfill \end{array}$
Triangular, $y\in [a,b]$:
$\begin{array}{cc}\hfill y\le c:& \frac{2(y-a)}{(b-a)(c-a)}\hfill \\ \hfill y>c:& \frac{2(b-y)}{(b-a)(b-c)}\hfill \end{array}$	$\begin{array}{cc}\hfill y\le c:& \frac{{(y-a)}^2}{(b-a)(c-a)}\hfill \\ \hfill y>c:& \frac{{(b-y)}^2}{(b-a)(b-c)}\hfill \end{array}$	$v_n\sim b-\sqrt{\frac{3(b-a)(b-c)}{2n}}$
Wigner, $y\in [-R,R]$:
$f\left(y\right)=\frac{2\sqrt{R^2-y^2}}{\pi R^2}$	$\frac{1}{2}-\frac{y\sqrt{R^2-y^2}}{\pi R^2}-\frac{1}{\pi }\arcsin \left(\frac{y}{R}\right)$	$v_n\sim R\left(1-\frac{1}{2}{\left(\frac{5\pi }{2n}\right)}^{2/3}\right)$
Beta, $y\in (0,1)$:
$f\left(y\right)=\frac{y^{\alpha -1}{(1-y)}^{\beta -1}}{B(\alpha ,\beta )}$	$1-\frac{B(y;\alpha ,\beta )}{B(\alpha ,\beta )}$	$v_n\sim 1-{\left(\frac{(\beta +1)B(\alpha ,\beta )}{n}\right)}^{1/\beta }$

contains the large-n asymptotics for a number of common distributions.

These densities contain a number of parameters, some of which are required to satisfy particular conditions. The normal distribution permits arbitrary $\mu$, but requires $\sigma >0$. The gamma distribution requires $\alpha >0$ and $\beta >0$ and the function $\gamma$ represents the lower incomplete gamma function, found in [34]. We also assume that $\alpha \ne 1$ for the purposes of the calculation shown here. The $\alpha =1$ case requires a different analysis and corresponds to the exponential distribution. The Pareto distribution requires $\beta >0$ and $\alpha >1$.

The uniform distribution requires $a<b$, while the triangular distribution requires $a<c<b$. The Wigner distribution requires $R>0$ and the beta distribution requires $\alpha >0$ and $\beta >0$. In the expression for the beta distribution, the function $B(\alpha ,\beta )$ represents the standard beta function, while $B(y;\alpha ,\beta )$ represents the incomplete beta function (see [34]).

The function W denotes the Lambert-W function. The asymptotic expressions for $v_n$ associated with the normal and gamma distributions can be further simplified by observing that the argument of the Lambert-W function becomes large in the asymptotic limit and

$$W\left(x\right)=log\left(x\right)-log(log\left(x\right))+\frac{log(log(x\left)\right)}{log\left(x\right)}+o\left(\frac{1}{log\left(x\right)}\right)\mathrm{as}x\to \infty .$$

(25)

Using the first two terms of this expansion produces an asymptotic expression for $v_n$ with error that is $o\left(1\right)$ as $n\to \infty$ for both the normal and gamma distributions.

We note that the results obtained using this asymptotic formulation for the uniform distribution are consistent with previous analyses from [20,22].

Importantly, we see that $v_n$ approaches a maximum value for each distribution with compact support, corresponding to the maximum possible value of y in the domain, as assumed and subsequently confirmed in the previous analysis. In contrast, for each pdf on a domain with unbounded upper support, $v_n$ increases monotonically without bound. The asymptotic behaviour of $v_n$ is subsequently used to determine the expectation and variance of ${\tau }_N$ for each example.

4. Calculating Optimal Stopping Statistics

4.1. Calculating the Expectation

Let $w_i=P(y<v_i)=1-h\left(v_i\right)$. The expectation is now given by

$$\begin{array}{cc}\hfill E\left({\tau }_N\right)& =\sum _{n=1}^{N}nP(y_1<v_{N-1},\cdots ,y_{n-1}<v_{N-n+1},y_n⩾v_{N-n})\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & =(1-w_{N-1})+2w_{N-1}(1-w_{N-2})+\dots +N{w}_{N-1}\dots w_1\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & =1+\sum _{n=1}^{N-1}\prod _{i=n}^{N-1}{w}_i.\hfill \end{array}$$

(28)

We select a value k such that $0\ll k\ll N$; a representative choice is $k=\lfloor \sqrt{N}\rfloor$. This choice does not affect the asymptotic values computed here, but would impact the form of higher-order corrections. We write the sum of products as

$$E\left({\tau }_N\right)=1+\sum _{n=1}^{k-1}\prod _{i=n}^{N-1}{w}_i+\sum _{n=k}^{N-1}\prod _{i=n}^{N-1}{w}_i.$$

(29)

We now consider the first summation term in (29). Recalling that $w_n$ is non-negative and bounded above by one, we see that

$$0<\sum _{n=1}^{k-1}\prod _{i=n}^{N-1}{w}_i<\sum _{n=1}^{k-1}\prod _{i=n}^{N-1}1=k-1.$$

(30)

The purpose of (29) is to split the sum such that an asymptotic expression can be used for $w_i$ in order to approximate the second summation term. As k is large in the limit $N\to \infty$, we may use the asymptotic approximation for $v_n$ in the large n limit for each term in the product. Consequently, if $v_n$ satisfies the requirements for (11) to hold, we find that

$$\begin{array}{c}\hfill \sum _{n=k}^{N-1}\prod _{i=n}^{N-1}{w}_i\sim \sum _{n=k}^{N-1}\prod _{i=n}^{N-1}\left(1+\frac{v_i^{\prime \prime }}{v_i^{\prime }}\right)\mathrm{as}N\to \infty .\end{array}$$

(31)

In fact, for many distributions, this may be further simplified, using the large-n asymptotics for $v_n$ and its derivatives. For the distributions in Examples 1–4, as well as each distribution from Table 1, it is straightforward to show, by direct calculation using (11), that

$$h\left(v_n\right)\sim \frac{\lambda }{n}\mathrm{as}n\to \infty ,$$

(32)

for some positive constant $\lambda$. In fact, from Example 4, we see that any distribution with an exponential upper tail has $\lambda =1$. For distributions where $v_n$ satisfies (32),

$$\begin{array}{cc}\hfill \sum _{n=k}^{N-1}\prod _{i=n}^{N-1}{w}_i& \sim \sum _{n=k}^{N-1}\prod _{i=n}^{N-1}\left(1-\frac{\lambda }{i}\right)=\sum _{n=k}^{N-1}\frac{{(n-\lambda )}_{N-n}}{{\left(n\right)}_{N-n}}=\frac{\mathrm{\Gamma }(N-\lambda )}{\mathrm{\Gamma }\left(N\right)}\sum _{n=k}^{N-1}\frac{\mathrm{\Gamma }\left(n\right)}{\mathrm{\Gamma }(n-\lambda )},\hfill \end{array}$$

(33)

in the limit $N\to \infty$, where ${\left(a\right)}_n$ is the Pochhammer symbol [34]. The asymptotic behaviour of this expression is given by

$$\frac{\mathrm{\Gamma }(N-\lambda )}{\mathrm{\Gamma }\left(N\right)}\sum _{n=k}^{N-1}\frac{\mathrm{\Gamma }\left(n\right)}{\mathrm{\Gamma }(n-\lambda )}\sim \frac{N}{\lambda +1}\mathrm{as}N\to \infty .$$

(34)

By comparing (34) with (30), we see that the second summation term dominates the expression for large N. Hence,

$$E\left({\tau }_N\right)\sim \frac{N}{\lambda +1}\mathrm{as}N\to \infty .$$

(35)

We note that, while this leading-order approximation is correct in the limit $N\to \infty$, for practical purposes, it is often necessary to retain the first correction term in the approximation for $w_n$ in the limit $n\to \infty$. While this does not give an expression as simple as (35), it does significantly increase the accuracy of the approximation for moderately large values of N.

For example, in Section 5, we compute the expectation (and variance) of ${\tau }_N$ for the normal distribution. Computing only the leading-order expression for the expectation and variance of ${\tau }_N$ causes this computation to converge to the asymptotic value extremely slowly, due to the $log(log(n\left)\right)$ terms present in the first correction to $w_n$ as $n\to \infty$. By including these terms in the asymptotic expansion for $w_n$, we are able to show that the simulations agree with the asymptotic predictions within the simulated range of N.

4.2. Calculating the Variance

A similar process may be used to determine the square expectation, hence the variance. The square expectation is given by

$$\begin{array}{cc}\hfill E\left({\tau }_N^2\right)& =\sum _{n=1}^N{n}^{2}P(y_1<v_{N-1},\cdots ,y_{n-1}<v_{N-n+1},y_n⩾v_{N-n})\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & =(1-w_{N-1})+2^2{w}_{N-1}(1-w_{N-2})+\dots +N^2{w}_{N-1}\dots w_1\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & =1+\sum _{n=1}^{N-1}(2N+1-2n)\prod _{i=n}^{N-1}{w}_i.\hfill \end{array}$$

(38)

We again define k such that $0\ll k\ll N$ and split this series to obtain

$$E\left({\tau }_N^2\right)=1+\sum _{n=1}^{k-1}(2N+1-2n)\prod _{i=n}^{N-1}{w}_i+\sum _{n=k}^{N-1}(2N+1-2n)\prod _{i=n}^{N-1}{w}_i.$$

(39)

We now consider the first summation term in (39). As before, we note that $w_i$ is positive and less than one, giving

$$0<\sum _{n=1}^{k-1}(2N+1-2n)\prod _{i=n}^{N-1}{w}_i<\sum _{n=1}^{k-1}(2N+1-2n)\prod _{i=n}^{N-1}1=2kN-2N-k^2+2k-1.$$

(40)

We have again split the sum such that an asymptotic expression can be used for $w_i$ in order to approximate the second summation term using the asymptotic approximation for $v_n$ in the large n limit for each term in the product. If $v_n$ satisfies the requirements for (11) to hold, we find that

$$\begin{array}{c}\hfill \sum _{n=k}^{N-1}(2N+1-2n)\prod _{i=n}^{N-1}{w}_i\sim \sum _{n=k}^{N-1}(2N+1-2n)\prod _{i=n}^{N-1}\left(1+\frac{v_i^{\prime \prime }}{v_i^{\prime }}\right)\mathrm{as}N\to \infty .\end{array}$$

(41)

We again observe that, for many distributions, including those in Examples 1–4 and each distribution from Table 1, the asymptotic behaviour of $v_n$ and its derivatives may be used to simplify $h\left(v_n\right)$, giving the expression in (32). Noting this result, the sum can be evaluated to give

$$\begin{array}{cc}\hfill \sum _{n=k}^{N-1}(2N+1-2n)\prod _{i=n}^{N-1}{w}_i& \sim \sum _{n=k}^{N-1}(2N+1-2n)\prod _{i=n}^{N-1}\left(1-\frac{\lambda }{i}\right)\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & =\sum _{n=k}^{N-1}\frac{(2N+1-2n){(n-\lambda )}_{N-n}}{{\left(n\right)}_{N-n}}\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill & =\frac{\mathrm{\Gamma }(N-\lambda )}{\mathrm{\Gamma }\left(N\right)}\sum _{n=k}^{N-1}\frac{(2N+1-2n)\mathrm{\Gamma }\left(n\right)}{\mathrm{\Gamma }(n-\lambda )}.\hfill \end{array}$$

(44)

The asymptotic behaviour of this expression can be evaluated to give

$$\frac{\mathrm{\Gamma }(N-\lambda )}{\mathrm{\Gamma }\left(N\right)}\sum _{n=k}^{N-1}\frac{(2N+1-2n)\mathrm{\Gamma }\left(n\right)}{\mathrm{\Gamma }(n-\lambda )}\sim \frac{2N^2}{(\lambda +1)(\lambda +2)}$$

(45)

in the limit $N\to \infty$. This expression dominates the sum in (40). Hence, the evaluation of the asymptotic behaviour of the variance as $N\to \infty$ gives

$$\mathrm{Var}\left({\tau }_N\right)=E\left({\tau }_N^2\right)-E{\left({\tau }_N\right)}^2\sim \frac{2N^2}{(\lambda +1)(\lambda +2)}-{\left(\frac{N}{\lambda +1}\right)}^2.$$

(46)

This expression may be simplified to give an asymptotic approximation for the variance.

$$\mathrm{Var}\left({\tau }_N\right)\sim \frac{\lambda N^2}{{(\lambda +1)}^2(\lambda +2)}\mathrm{as}N\to \infty .$$

(47)

As before, it is sometimes of practical value to retain higher corrections in the approximation for $w_n$ as $n\to \infty$, such as in the computations performed in Section [5] (Figure 1) on the normal distribution. This allows the asymptotic prediction to be compared with the simulations for the moderately large values of N considered here.

4.3. Higher Moments

We note that it is possible to calculate the statistics comprising of higher moments, since the above calculations for the first and second moment are easily generalised through the following expression for the $j^{\mathrm{th}}$ raw moment:

$$E\left({\tau }_N^j\right)=1+\sum _{n=1}^{N-1}\left({(N-n+1)}^j-{(N-n)}^j\right)\prod _{i=n}^{N-1}{w}_i.$$

(48)

Finding asymptotic expressions for moments of interest can be performed by using a very similar approach as above.

4.4. Example Calculations

In

Table 2. This table contains the asymptotic behaviour of optimal stopping statistics for several common probability density functions, as well as the intermediate quantities used to compute these statistics. For each distribution, the table describes the pdf name and domain, the asymptotic behaviour of $h\left(y\right)$ in the limit $y\to \infty$ or $y\to y_{\max }$ for domains with infinite and finite upper support, respectively, and the value of $\lambda$ associated with this asymptotic behaviour. The final two columns contain the expectation and variance of ${\tau }_N$ in the limit $N\to \infty$.

Distribution	Domain	$\mathit{h}\left(\mathit{y}\right)$ as $\mathit{y}\to \mathit{\infty }$	$\mathit{\lambda }$	$\mathit{E}\left({\mathit{\tau }}_{\mathit{N}}\right)$	Var(${\mathit{\tau }}_{\mathit{N}}$)
Exponential	$[0,\infty )$	${\mathrm{e}}^{-y/\beta }$	1	$\frac{N}{2}$	$\frac{N^2}{12}$
Gamma	$[0,\infty )$	$\frac{{\beta }^{1-\alpha }}{\mathrm{\Gamma }\left(\alpha \right)}{y}^{\alpha -1}{\mathrm{e}}^{-y/\beta }$	1	$\frac{N}{2}$	$\frac{N^2}{12}$
Pareto	$[\beta ,\infty )$	${\left(\frac{\beta }{y}\right)}^{\alpha }$	$\frac{\alpha -1}{\alpha }$	$\frac{\alpha N}{2\alpha -1}$	$\frac{{\alpha }^2(\alpha -1)N^2}{{(2\alpha -1)}^2(3\alpha -1)}$
Distribution	Domain	$\mathbf{h}\left(\mathbf{y}\right)$ as $\mathbf{y}\to {\mathbf{y}}_{\max }$	$\mathbf{\lambda }$	$\mathbf{E}\left({\mathbf{\tau }}_{\mathbf{N}}\right)$	Var(${\mathbf{\tau }}_{\mathbf{N}}$)
Uniform	$[a,b]$	$\frac{b-y}{b-a}$	2	$\frac{N}{3}$	$\frac{N^2}{18}$
Triangular	$[a,b]$	$\frac{{(b-y)}^2}{(b-a)(b-c)}$	$\frac{3}{2}$	$\frac{2N}{5}$	$\frac{12N^2}{175}$
Wigner	$[-R,R]$	$\frac{4\sqrt{2}{(R-y)}^{3/2}}{3\pi R^{3/2}}$	$\frac{5}{3}$	$\frac{3N}{8}$	$\frac{45N^2}{704}$
Beta	$(0,1)$	$\frac{\mathrm{\Gamma }(\alpha +\beta ){(1-y)}^{\beta }}{\mathrm{\Gamma }\left(\alpha \right)\mathrm{\Gamma }(\beta +1)}$	$\frac{\beta +1}{\beta }$	$\frac{\beta N}{2\beta +1}$	$\frac{{\beta }^2(\beta +1)N^2}{{(2\beta +1)}^2(3\beta +1)}$

, we compute the expectation and variance for the common pdfs computed in Examples 1–3 and those shown in Table 2. This table illustrates the asymptotics of $h\left(y\right)$ in the limit $y\to \infty$ for pdfs with infinite upper support and in the limit $y\to y_{\max }$ for domains with finite upper support. For each pdf, the expectation and variance of ${\tau }_N$ are obtained using the expectation formula from (35) and the variance formula from (47).

In each of the densities with exponentially decaying tails (exponential and gamma), the expectation and variance are identical, corresponding to setting $\lambda =1$ in the expectation and variance formulae. This is consistent with the result of Example 4, which showed that the large-n asymptotics are identical for any pdf with an exponentially decaying upper tail, corresponding to $\lambda =1$.

However, in the remaining pdfs, the expectation and variance are not identical. For distributions with heavy tails or a finite upper bound, the optimal stopping statistics are determined by the rate at which the distribution function decays as the upper bound is approached, characterised by the asymptotic behaviour of $h\left(y\right)$ in this limit. Consequently, the expectation and variance associated with each of these distributions take different values.

We can see that setting $\beta =1$ in the beta distribution gives identical expectation and variance to the uniform distribution, while setting $\beta =2$ or $\beta =3/2$ give identical expectation and variance to the triangular and Wigner distributions, respectively. This is caused by the fact that the asymptotic decay of $h\left(y\right)$ in the limit $y\to y_{\max }$ occurs at the same algebraic power in each case and these statistics depend entirely on the algebraic power of the decay rate.

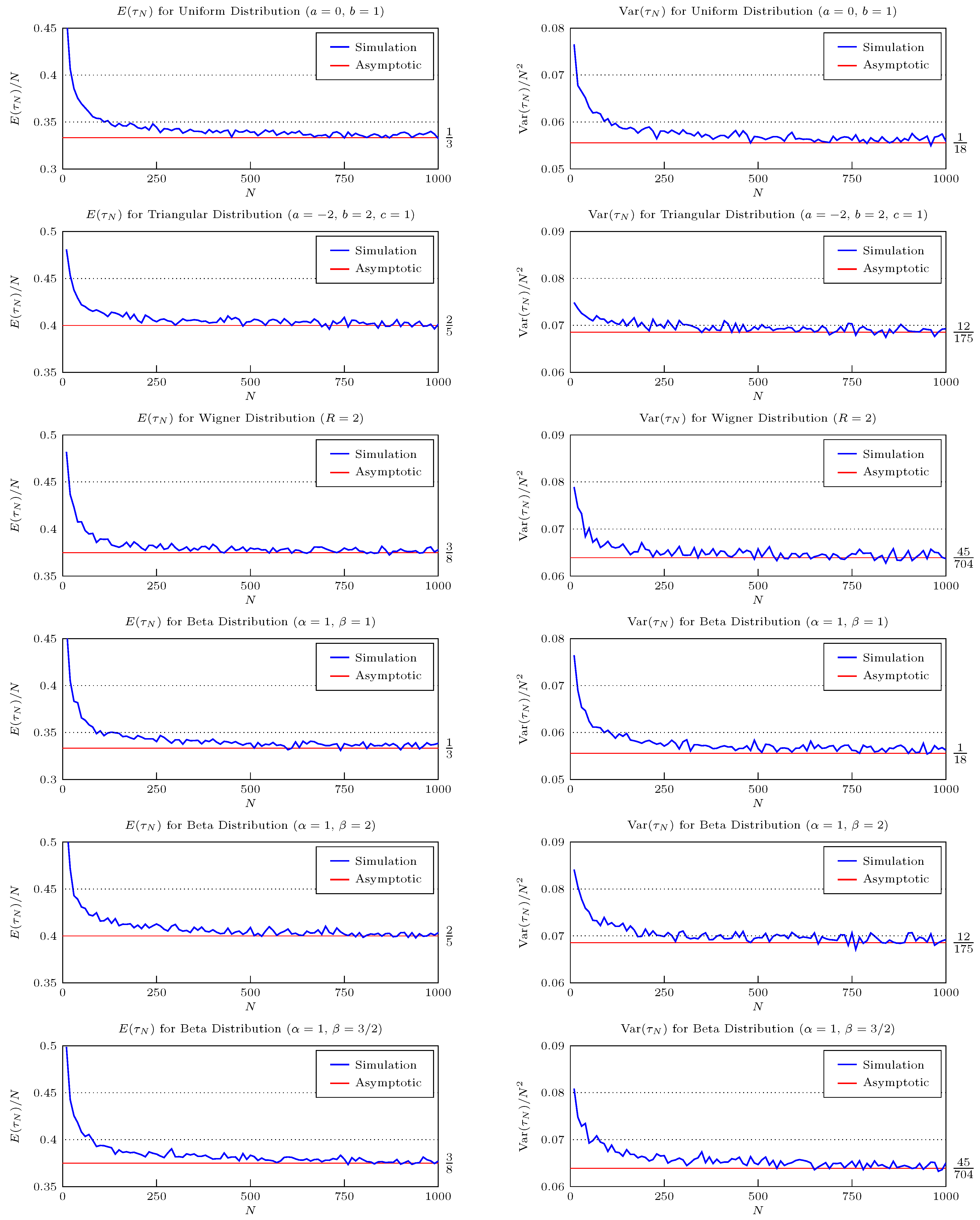
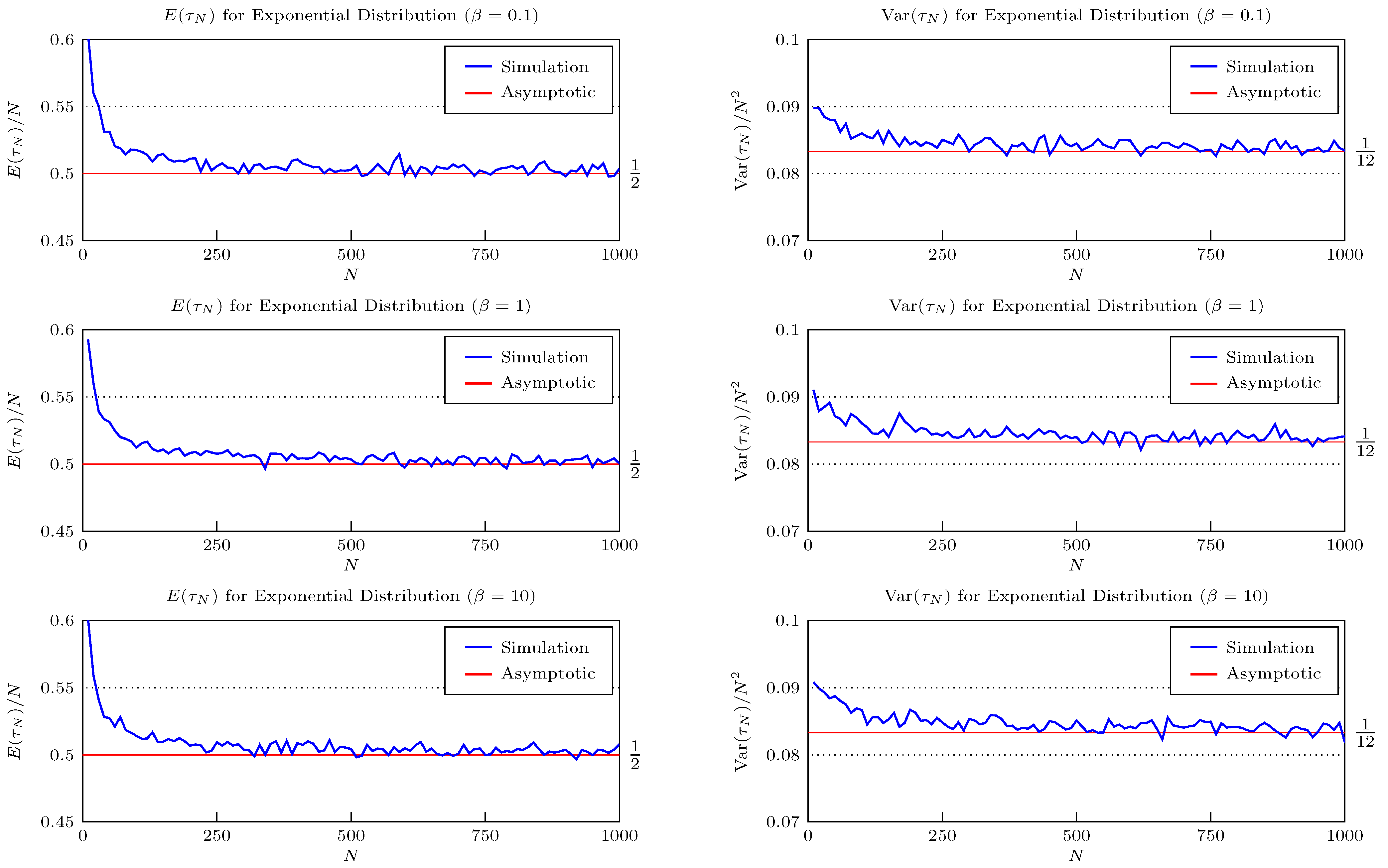
5. Numerical Comparisons

For each of the distributions in Table 2, we validated the asymptotic predictions for the expectation and variance of ${\tau }_N$ for large N by comparing against numerical simulations. These results were simulated using the R programming language [35], with graphs plotted using Tikz [36]. For each value of N from 10 to 1000, in increments of 10, we simulated the optimal stopping problem 10,000 times, using the optimal stopping rule from (4) to determine the stopping point. The expected value and variance were then estimated for each of these N. The results of these computations are illustrated in Figure 1 and Figure 2 for a range of unbounded and bounded distributions, respectively.

We note that the calculated expectation and variance were scaled by a factor of N and $N^2$, respectively, so that they tended to constant asymptotic values. The variance of the simulations for these calculated values appeared constant under this scaling, which indicates that the simulated expectation and variance both varied more significantly about the asymptotic predicted values as N increased.

In each computation, the numerical results support the corresponding asymptotic predictions. As N increased, the expectation and variance of each set of trials approached the value predicted by the asymptotic calculations. For the Pareto and beta distributions, the numerical comparisons were performed for three different sets of distribution parameters. We saw that changing the parameters of the Pareto and beta distributions had the effect of changing the asymptotic expectation and variance, as predicted by the calculated values in Table 2.

In contrast, Figure 3 contains the simulated results for the exponential function with $\beta =0.1$, $\beta =1$ and $\beta =10$. In each of these figures, the asymptotic behaviour of the expectation and variance of ${\tau }_N$ tended to identical values for the expectation and variance. These figures support the predictions from Section 4, in which it is determined that the leading-order large-N approximation of the expectation and variance do not depend on the distribution parameters for distributions with exponential upper tails.

In our asymptotic prediction for the mean and variance of the normal distribution, we retained the first correction term for $h\left(v_n\right)$ as $n\to \infty$, which corresponded to taking the first correction in the expansion of the Lambert-W function (25). This gave

$$h\left(v_n\right)\sim \frac{1}{n}+\frac{1}{nlog(n^2/2\pi )}\mathrm{as}n\to \infty ,$$

(49)

which allowed us to more accurate estimate $E\left({\tau }_N\right)$ using (34) and $\mathrm{Var}\left({\tau }_N\right)$ using (31). This first correction was small compared to the leading-order behaviour as $N\to \infty$, but decayed so slowly that it had to be included in order to obtain accurate predictions for the expectation and variance of ${\tau }_N$ for even moderately large values of N. By comparing the behaviour of the simulated and asymptotic results, we saw that the computations agreed with this more accurate asymptotic prediction.

6. Applications

Historically, asymptotics are used alongside numerical computation in order to understand the long-term behaviour of such problems that are difficult to analyse with exact results. While the asymptotic approximation of optimal stopping moments in this study does not assist with computation, these results can provide insight into the long-term structure of how these optimal decisions might be made. Typically, decision makers are risk-averse and tend to make sub-optimal decisions that are made too early [37]. Therefore, understanding the basic long-term behaviour of what might happen would benefit how decision makers perceive risk and their expected profits alongside with any losses they would incur before making profit.

Example 5.

In some processes, such as in the selling of the asset, the decision maker may receive a sequence of offers that follow some distribution. Additionally, there may be some fixed cost $\$\frac{c}{N}$ of observing each offer in the sequence; therefore, we must factor in the cumulative increase in these costs into the decision making. This may be especially true in the situation where there are limited resources that would prevent the ability to wait until an optimal decision can be made. The problem can be remodelled by creating the cumulative sequence ${\left\{c_n\right\}}_{n=1}^N$, where $c_n$ corresponds to the amount paid in costs when there are n steps remaining. Here, we would have that $c_n=(N-n)\times \frac{c}{N}$ and the recurrent equations for $v_n$ would now be a function of $c_n$, which requires a new consideration of the problem. However, the asymptotics for the stopping time in the basic problem (without cost) can provide a conservative insight into how much money might be spent, or lost, before the stopping rule has been actioned. For example, if we observe a sequence of uniformly distributed variables on the interval $[a,b]$, under the basic optimal stopping strategy, we may expect to lose roughly $\$\frac{c}{3}$ before arriving at a decision. Under this strategy, we would expect a profit of

$$v_N-\frac{c}{3}\sim b-\frac{2(b-a)}{N}-\frac{c}{3}.$$

These would be, in fact, underestimates of the strategy, since the optimal strategy would change. Nevertheless, very simple (conservative) estimates of the expected profit and cost can be obtained from this theory.

Example 6.

In this study, we calculated asymptotics for the expected value and variance of ${\tau }_N$. These can now be substituted into well-known inequalities, such as the Chebyshev’s and Markov’s inequalities, to obtain bounds for probabilities concerning the duration of the optimal stopping rule. This is useful when the underlying probability distribution is unknown and not roughly normal, which is the case for the stopping duration. We recall that, if X is an integrable non-negative random variable with finite expectation and finite non-zero variance and $a>0$ is a real number, then the probability that X is at least a is, at most, the expectation of X divided by a. We note that ${\tau }_N$ satisfies these conditions; thus, we apply Markov’s inequality to obtain

$$P\left({\tau }_N\ge \frac{N}{\delta }\right)\le \frac{\delta E\left({\tau }_N\right)}{N}\sim \frac{\delta }{\lambda +1}.$$

We may apply Chebyshev’s inequality to provide a bound for probability that the stopping time exceeds a certain distance from its mean.

$$P\left(\left|{\tau }_N-E\left({\tau }_N\right)\right|\ge \frac{N}{\delta }\right)\le \frac{{\delta }^2\mathrm{Var}\left({\tau }_N\right)}{N^2}.$$

For large values of N, we obtain

$$P\left(\left|{\tau }_N-\frac{N}{\lambda +1}\right|\ge \frac{N}{\delta }\right)\le \frac{\lambda {\delta }^2}{{(\lambda +1)}^2(\lambda +2)}$$

By the corresponding substitution for $\lambda$, these calculations can be performed for any of the distributions highlighted in this study. We note that these bounds are not incredibly precise; for example, in the case for optimal stopping on the uniform distribution, we have that $\lambda =2$ and so

$$P\left(\left|{\tau }_N-\frac{N}{3}\right|\ge \frac{N}{\delta }\right)\le \frac{{\delta }^2}{18},$$

which would only be useful on $\frac{3}{2}<\delta <3\sqrt{2}$. We simulated the uniform stopping problem for $N=5000$ (conducting 10,000 simulations) to obtain the theoretical and simulated bounds (see

Table 3. Values for the standard uniform distribution.

$\mathit{\delta }$	1.75	2	2.25	2.5	2.75	3	3.25	3.5
Chebyshev Bound	0.1701	0.2222	0.2813	0.3472	0.4201	0.5000	0.5868	0.6806
Simulated Result	0.0103	0.0318	0.0541	0.0790	0.0977	0.1148	0.1834	0.2401

).

7. Conclusions

In this paper, we derived asymptotics of optimal stopping times for sequences of independent identically distributed continuous random variables. In particular, we found the asymptotics of the expected value and the variance of the stopping time for large classes of density functions whose domains have either infinite or finite upper bounds.

Asymptotic calculations were performed on a number of probability distributions, on both bounded and unbounded domains. Numerical simulations were subsequently performed to calculate the expectation and variance of the optimal stopping rule for a range of values of N, ranging from 10 to 1000. In each case, the simulated results tended towards the asymptotic prediction in the large-N limit, validating the asymptotic approach.

One particularly interesting observation is that, if a density function $f\left(y\right)$ has no upper bound and the upper tail decays at certain exponential rate as $y\to \infty$, the expectation and variance of the optimal stopping rule are given by $E\left({\tau }_N\right)=N/2$ and $\mathrm{Var}\left({\tau }_N\right)=N^2/12$. These asymptotic values do not depend on any other features of the distribution and hold for any distribution with exponentially decaying upper tail behaviour. This parameter independence was tested for the exponential distribution, for which the simulated values converged to the large-N asymptotic prediction given a range of different parameter choices.

The independence of the expectation and variance of the optimal stopping rule from distribution parameters does not hold for distributions with algebraically decaying upper tails, such as the Pareto distribution. We found, in our analyses, that the expectation and variance of the optimal stopping rule, in this case, depends on the algebraic power of the tail decay rate, which was supported by numerical computation for a range of different parameter values.

In most cases, the leading-order asymptotic behaviour was sufficient to explain the simulated results; however, this is not necessarily true. Comparing the leading-order asymptotic approximation with the simulated results for the normal distribution showed a significant error between the predicted and simulated values. This error was resolved by including an extra correction term in the asymptotic calculations, leading to agreement between the asymptotic and simulated results. It is important to note that, for some distributions, higher correction terms to the value of a sequence can be required in order for the asymptotics to be useful in predicting statistical properties for moderately large values of the asymptotic parameter.

The key contribution from this study is outlining a general strategy for obtaining the asymptotic behaviour of the expectation and variance of the optimal stopping rule that can be applied to a wide range of distributions in a consistent fashion. This method recovers existing results from [22], while also making predictions for many other distributions that were subsequently validated through comparison with simulated results.