About AutoGraphiX Conjecture on Domination Number and Remoteness of Graphs

Abstract

A set $D\subseteq V\left(G\right)$ is called a dominating set if $N\left[v\right]\cap D\ne \varnothing$ for every vertex v in graph G. The domination number $\gamma \left(G\right)$ is the minimum cardinality of a dominating set of G. The proximity $\pi \left(v\right)$ of a vertex v is the average distance from it to all other vertices in graph. The remoteness $\rho \left(G\right)$ of a connected graph G is the maximum proximity of all the vertices in graph G. AutoGraphiX Conjecture A.565 gives the sharp upper bound on the difference between the domination number and remoteness. In this paper, we characterize the explicit graphs that attain the upper bound in the above conjecture, and prove the improved AutoGraphiX conjecture.

1. Introduction

We only consider finite, simple and connected graphs in the present paper. Denote by $G=\left(V\right(G),E(G\left)\right)$ the finite, simple and connected graph, where $V\left(G\right)$ is the vertex set and $E\left(G\right)$ is the edge set. The open neighborhood of v is the set $N_G\left(v\right)=\{u\in V\left(G\right)\mid uv\in E\left(G\right)\}$, and the closed neighborhood of v is $N_G\left[v\right]=N_G\left(v\right)\cup \left\{v\right\}$. The degree $d_G\left(v\right)$ of a vertex v is the number of edges incident with v in G. The minimum and maximum vertex degree of G are denoted by $\delta \left(G\right)$ and $\Delta \left(G\right)$, respectively. The distance of two vertices u and v is the length of a shortest path between u and v, denoted by $d(u,v)$. The eccentricity $\epsilon \left(v\right)$ of a vertex v is defined as $\epsilon \left(v\right)=max\{d_G(u,v)\mid u\in V\left(G\right)\}$. The proximity $\pi \left(v\right)$ of a vertex v is the average distance from it to all other vertices in graph. Based on this, the proximity $\pi \left(G\right)$ and remoteness $\rho \left(G\right)$ of a connected graph G denote the minimum and maximum proximities of vertices in graph G, respectively. Namely,

$$\pi \left(G\right)=mi{n}_{v\in V\left(G\right)}\pi \left(v\right)\mathrm{and}\rho \left(G\right)=ma{x}_{v\in V\left(G\right)}\pi \left(v\right).$$

As we know, the transmission of a vertex is the sum of distances from it to all others in graph. In other words, $\pi \left(G\right)$ and $\rho \left(G\right)$ can be considered as the minimum and maximum normalized transmission of vertices in graph G, respectively. For more excellent results on proximity and remoteness, the readers please refer to [1,2,3,4,5,6].

The AutoGraphiX (AGX) is an automated system that is mainly used for finding conjectures and extremal graphs for some graph invariant [7]. Aouchiche [8] presented 760 conjectures with regard to 20 graph invariants, and these invariants include proximity and remoteness. Many conjectures on remoteness or proximity were proved. Each one of proximity and remoteness was compared to the diameter, radius, average eccentricity, average distance, independence number and matching number [9,10]. The authors proved lower and upper bounds on the distance spectral radius using proximity and remoteness, and lower bounds on the difference between the largest distance eigenvalue and proximity(remoteness) [11]. The difference, the sum, the ratio and the product of the proximity and the girth were researched [12]. Four AutoGraphiX conjectures on the quotient of proximity and average distance, the quotient of remoteness and girth, the sum of remoteness and maximum degree, the product of proximity and average degree were studied [13]. The upper bound on the difference between the average eccentricity and proximity was determined [14]. The authors established maximal trees and graphs for the difference of average distance and proximity(remoteness), as well as minimal trees for the difference of remoteness and radius [15].

A set $D\subseteq V\left(G\right)$ is called a dominating set if $N\left[v\right]\cap D\ne \varnothing$ for every $v\in V\left(G\right)$. A classical upper bound on the domination number of G is presented by Ore [16] in 1962, that is $\gamma \left(G\right)\le \lfloor \frac{n}{2}\rfloor$. The domination number $\gamma \left(G\right)$ is the minimum cardinality of a dominating set of G. Although determining the domination number is NP-complete [17], studies on domination number have attracted graph theorists for their applications and interest [18,19]. Recently, we focus on the relationship between the domination number and other graph invariants [20,21,22,23]. And this includes some AGX conjectures on domination number. Furthermore, some other AGX conjectures about domination number have been studied [24,25,26]. In this paper, we will continue to study the following AGX conjecture which is related to the domination number and remoteness.

Denote by $K_{a,b}$ the graph of order n obtained from a complete graph $K_a$ by attaching a pendent vertex to each of the b vertices of $K_a$, where $a+b=n$ and $0\le b\le a$.

Conjecture 1 (Conjecture A.565)

([8]).

$$\gamma \left(G\right)-\rho \left(G\right)\le \left\{\begin{array}{cc}\frac{n-5}{2}+\frac{3}{2n-2},\hfill & niseven\hfill \\ \frac{n-6}{2}+\frac{2}{n-1},\hfill & nisodd\hfill \end{array}\right.$$

with equality if and only if $rad\left(G\right)=2$ and $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor$. For instance, the equality is attained for the graph $K_{\lceil \frac{n}{2}\rceil ,\lfloor \frac{n}{2}\rfloor }$.

Based on the Conjecture 1, we will characterize the explicit graphs that satisfy the equation in Conjecture 1, and prove an improved AutoGraphiX conjecture.

2. Results and Discussion

Lemma 1.

If G is a connected graph with $n\le 6$ vertices and $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor -1$, then $n\ge 4$ and

$$\gamma \left(G\right)-\rho \left(G\right)\le \left\{\begin{array}{cc}\frac{4}{5},\hfill & n=6\hfill \\ 0,\hfill & 4\le n\le 5\hfill \end{array}\right.$$

with equality if and only if G is 4-regular when $n=6$, and $G\cong K_n$ when $4\le n\le 5$.

Proof. 

It is obvious that $n\ge 4$ since $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor -1\ge 1$.

Let $n=6$ and $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor -1=2$. It is well-known that $\gamma \left(G\right)\le n-▵\left(G\right)$ ([27]). Then $\delta \left(G\right)\le ▵\left(G\right)\le n-\gamma \left(G\right)=4$. If $\delta \left(G\right)=4$, then $▵\left(G\right)=4$. It implies that G is 4-regular, and thus $\rho \left(G\right)=\pi \left(v\right)=\frac{1}{5}·(1+1+1+1+2)=\frac{6}{5}$, where v is any vertex of G. Assume that $\delta \left(G\right)\le 3$ and v is the vertex with $d\left(v\right)=\delta \left(G\right)\le 3$, then $\epsilon \left(v\right)\ge 2$. Therefore,

$$\rho \left(G\right)\ge \pi \left(v\right)\ge \frac{1}{5}·[d\left(v\right)+2(n-1-d\left(v\right))]\ge \frac{7}{5}.$$

To sum up, $\gamma \left(G\right)-\rho \left(G\right)\le 2-\frac{6}{5}=\frac{4}{5}$ with equality if and only if G is 4-regular.

Let $4\le n\le 5$ and $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor -1=1$. Then $\rho \left(G\right)\ge 1=\rho \left(K_n\right)$, which implies that $\gamma \left(G\right)-\rho \left(G\right)\le 0$, the equality holds if and only if $G\cong K_n$. The result follows. □

Lemma 2

([28]). If a graph G has no isolated vertices and $\gamma \left(G\right)\ge 3$, then $\gamma \left(G\right)\le \frac{n+1-\delta \left(G\right)}{2}$.

Lemma 3.

Let G be a connected graph of order $n\ge 7$ with $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor -1$. Then

$$\gamma \left(G\right)-\rho \left(G\right)<\left\{\begin{array}{cc}\frac{n-5}{2}+\frac{3}{2n-2},\hfill & niseven\hfill \\ \frac{n-6}{2}+\frac{2}{n-1},\hfill & nisoddandn\ge 9\hfill \\ \frac{n-3}{4},\hfill & n=7\hfill \end{array}\right..$$

Proof. 

Assume that $v\in V\left(G\right)$ is a vertex with $d\left(v\right)=\delta \left(G\right)$. Since $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor -1\ge 3$, one has that $\gamma \left(G\right)\le \frac{n+1-\delta \left(G\right)}{2}$ by Lemma 2. It follows that

$$d\left(v\right)=\delta \left(G\right)\le n+1-2\gamma \left(G\right)=\left\{\begin{array}{cc}3,\hfill & niseven\hfill \\ 4,\hfill & nisodd\hfill \end{array}\right.<n-1.$$

Thus $\epsilon \left(v\right)\ge 2$ and

$$\rho \left(G\right)\ge \pi \left(v\right)\ge \frac{d\left(v\right)+2(n-1-d(v\left)\right)}{n-1}\ge \left\{\begin{array}{cc}2-\frac{3}{n-1},\hfill & niseven\hfill \\ 2-\frac{4}{n-1},\hfill & nisodd\hfill \end{array}\right..$$

Therefore

$$\begin{array}{ccc}\hfill \gamma \left(G\right)-\rho \left(G\right)& \le & \left\{\begin{array}{cc}\frac{n-6}{2}+\frac{3}{n-1},\hfill & niseven\hfill \\ \frac{n-7}{2}+\frac{4}{n-1},\hfill & nisodd\hfill \end{array}\right.\hfill \\ & <& \left\{\begin{array}{cc}\frac{n-5}{2}+\frac{3}{2n-2},\hfill & niseven\hfill \\ \frac{n-6}{2}+\frac{2}{n-1},\hfill & nisoddandn\ge 9\hfill \\ \frac{n-3}{4},\hfill & n=7\hfill \end{array}\right..\hfill \end{array}$$

This completes the proof. □

Lemma 4.

Suppose that G is an n-vertex connected graph with $1\le \gamma \left(G\right)\le \lfloor \frac{n}{2}\rfloor -2$. Then

$$\gamma \left(G\right)-\rho \left(G\right)<\left\{\begin{array}{cc}\frac{n-5}{2}+\frac{3}{2n-2},\hfill & niseven\hfill \\ \frac{n-6}{2}+\frac{2}{n-1},\hfill & nisoddandn\ge 9\hfill \\ \frac{n-3}{4},\hfill & nisoddandn\le 7\hfill \end{array}\right..$$

Proof. 

It is obvious that $\rho \left(G\right)\ge 1$. So

$$\gamma \left(G\right)-\rho \left(G\right)\le \lfloor \frac{n}{2}\rfloor -3=\left\{\begin{array}{cc}\frac{n-6}{2},\hfill & niseven\hfill \\ \frac{n-7}{2},\hfill & nisodd\hfill \end{array}\right.<\left\{\begin{array}{cc}\frac{n-5}{2}+\frac{3}{2n-2},\hfill & niseven\hfill \\ \frac{n-6}{2}+\frac{2}{n-1},\hfill & nisoddandn\ge 9\hfill \\ \frac{n-3}{4},\hfill & nisoddandn\le 7\hfill \end{array}\right..$$

The result follows. □

Lemma 5

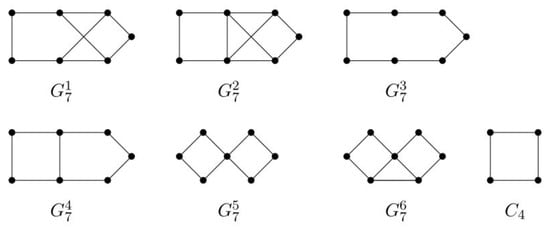
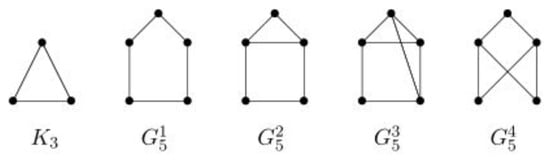
([29,30]). A connected graph G of order n satisfies $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor$ if and only if $G\in \mathcal{G}={\bigcup }_{i=1}^6{\mathcal{G}}_i$, where ${\mathcal{G}}_i$, $i=1,\dots ,6$, is the set defined in the following.

Let H be any graph with vertex set $\{v_1,\dots ,v_k\}$. Denote by $f\left(H\right)$ the graph obtained from H by adding new vertices $u_1,\dots ,u_k$ and the edges $v_i{u}_i,i=1,\dots ,k.$ Define ${\mathcal{G}}_1=\left\{C_4\right\}\cup \{G\mid G=f\left(H\right)$ for some connected graph $H\}.$

Let $\mathcal{F}=\mathcal{A}\cup \mathcal{B}$ and ${\mathcal{G}}_2=\mathcal{F}-\left\{C_4\right\},$ where $\mathcal{A}=\{C_4,G_7^i\mid i=1,\dots ,6\}$ and $\mathcal{B}=\{K_3,G_5^i)\mid i=1,\dots ,4\}$, as shown in Figure 1 and Figure 2, respectively.

Figure 1. Graphs in family $\mathcal{A}$.

Figure 2. Graphs in family $\mathcal{B}$.

For any graph H, let $\phi \left(H\right)$ be the set of connected graphs, each of which can be formed from $f\left(H\right)$ by adding a new vertex x and edges joining x to one or more vertices of H. Then define ${\mathcal{G}}_3=\{G\mid G=\phi \left(H\right)$ for some graph $H\}.$

Let $G\in {\mathcal{G}}_3$ and y be a vertex of a copy of $C_4$. Denote by $\theta \left(G\right)$ the graph obtained by joining G to $C_4$ with the single edge $xy$, where x is the new vertex added in forming G. Then define ${\mathcal{G}}_4=\{G\mid G=\theta \left(H\right)$ for some graph $H\in {\mathcal{G}}_3\}.$

Let $u,v,w$ be the vertex sequence of a path $P_3$. For any graph H, let $\mathcal{P}\left(H\right)$ be the set of connected graphs which may be formed from $f\left(H\right)$ by joining each of u and w to one or more vertices of H. Then define ${\mathcal{G}}_5=\{G\mid G=\mathcal{P}\left(H\right)$ for some graph $H\}.$

For a graph $X\in \mathcal{B}$, let $U\subset V\left(X\right)$ be a set of vertices such that no fewer than $\gamma \left(X\right)$ vertices of X dominate $V\left(X\right)\setminus U$. Let $\mathcal{R}(H,X)$ be the set of connected graphs which may be formed from $f\left(H\right)$ by joining each vertex of U to one or more vertices of H for some set U as defined above and any graph H. Then define ${\mathcal{G}}_6=\{G\mid G\in \mathcal{R}(H,X)$ for some $X\in \mathcal{B}$ and some $H\}.$

Definition 1

([23]). Let $G^{\prime }\in \mathcal{P}(K_{\frac{n-3}{2}})\subseteq {\mathcal{G}}_5$ be the graph obtained from $f(K_{\frac{n-3}{2}})$ by joining each of u and w to every vertex of $K_{\frac{n-3}{2}}$, and $G^{″}\in \mathcal{R}(K_{\frac{n-3}{2}},K_3)\subseteq {\mathcal{G}}_6$ be the graph obtained from $f(K_{\frac{n-3}{2}})$ by joining each vertex of $U=\{x,y\}\subseteq V(K_3)$ to every vertex of $K_{\frac{n-3}{2}}$.

Denote by $K_{a,b}$ the graph of order n obtained from a complete graph $K_a$ by attaching a pendent vertex to each of the b vertices of $K_a$, where $a+b=n$ and $0\le b\le a$.

Lemma 6.

If G is a connected graph with order $n(\ge 2)$ and $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor$, then

$$\gamma \left(G\right)-\rho \left(G\right)\le \left\{\begin{array}{cc}\frac{2}{3},\hfill & n=4\hfill \\ \frac{n-5}{2}+\frac{3}{2n-2},\hfill & nisevenandn\ne 4\hfill \\ \frac{n-3}{4},\hfill & nisoddandn\le 7\hfill \\ \frac{n-6}{2}+\frac{2}{n-1},\hfill & nisoddandn\ge 9\hfill \end{array}\right.$$

with equality if and only if $G\in \{C_4,K_{\frac{n}{2},\frac{n}{2}}\mid n$ is even and $n\ne 4$$\}\cup ({\mathcal{G}}_2-\left\{G_7^5\right)\})\cup \{K_{\lceil \frac{n}{2}\rceil ,\lfloor \frac{n}{2}\rfloor },G^{\prime },G^{″}\mid n$ is odd and $n\ge 9\}$.

Proof. 

Since $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor$, $G\in \mathcal{G}={\bigcup }_{i=1}^6{\mathcal{G}}_i$ by Lemma 2.5. Moreover, the order is even for the graphs in ${\mathcal{G}}_1$ and odd for the graphs in ${\bigcup }_{i=2}^6{\mathcal{G}}_i$ by the definition of $\mathcal{G}$.

Claim 1.

$\rho \left(G\right)\ne \pi \left(v_i\right)$ for $n>2$, where $v_i\in V\left(H\right)$, $i=1,2,\dots ,k$, $k=\left|V\right(H\left)\right|$ and H is the graph in the definition of $\mathcal{G}$. Since

$$\begin{array}{ccc}\hfill \pi \left(u_i\right)& =& \frac{1}{n-1}(d(u_i,v_i)+\sum _{s\in V\left(G\right)\setminus \{u_i,v_i\}}d(u_i,s))\hfill \\ & =& \frac{1}{n-1}[d(v_i,u_i)+\sum _{s\in V\left(G\right)\setminus \{u_i,v_i\}}(d(u_i,v_i)+d(v_i,s))]\hfill \\ & =& \frac{1}{n-1}(d(v_i,u_i)+\sum _{s\in V\left(G\right)\setminus \{u_i,v_i\}}d(v_i,s))+\frac{n-2}{n-1}\hfill \\ & =& \pi \left(v_i\right)+\frac{n-2}{n-1}>\pi \left(v_i\right).\hfill \end{array}$$

Hence, the claim is true. By the way, $G\cong P_2$ and $\pi \left(u_i\right)=\pi \left(v_i\right)$ for $n=2$. In what follows, we prove the lemma in terms of the parity of n.

Case 1.

n is even, that is, $G\in {\mathcal{G}}_1$.

Let $n\ne 4$. Then $G=f\left(H\right)$ for some connected graph H and $\left|V\left(H\right)\right|=\frac{n}{2}$ by the definition of ${\mathcal{G}}_1$. Claim 1 implies that $\rho \left(G\right)=\pi \left(u_{i_0}\right)$ for some $i_0\in \{1,2,\dots ,k\}$. If $G\cong f(K_{\frac{n}{2}})$, then

$$\begin{array}{ccc}\hfill \rho \left(G\right)& =& \pi \left(u_{i_0}\right)\hfill \\ & =& \frac{1}{n-1}[d(u_{i_0},v_{i_0})+\sum _{j\in \{1,\dots ,i_0-1,i_0+1,\dots ,k\}}(d(u_{i_0},u_j)+d(u_{i_0},v_j))]\hfill \\ & =& \frac{1}{n-1}[d(u_{i_0},v_{i_0})+\sum _{j\in \{1,\dots ,i_0-1,i_0+1,\dots ,k\}}(2d(u_{i_0},v_{i_0})+2d(v_{i_0},v_j)+d(v_j,u_j))]\hfill \\ & =& \frac{1}{n-1}·[1+5(k-1)]=\frac{5n-8}{2(n-1)}.\hfill \end{array}$$

If $G\ncong f(K_{\frac{n}{2}})$, then $v_s{v}_t\notin E\left(G\right)$ for some $s,t\in \{1,\cdots ,\frac{n}{2}\}$. Thus

$$\rho \left(G\right)\ge \pi \left(u_s\right)>\frac{1}{n-1}·[1+5(k-1)]=\frac{5n-8}{2(n-1)}.$$

Moreover,

$$\gamma \left(G\right)-\rho \left(G\right)\le \frac{n}{2}-\frac{5n-8}{2(n-1)}=\frac{n-5}{2}+\frac{3}{2n-2},$$

the equality holds if and only if $G\cong f(K_{\frac{n}{2}})\cong K_{\frac{n}{2},\frac{n}{2}}$.

Let $n=4$. Then $G\in \{C_4,P_4\}$. And just by doing a direct calculation, we get that

$$\gamma \left(G\right)-\rho \left(G\right)\le 2-\frac{4}{3}=\frac{2}{3}$$

with the equality if and only if $G\cong C_4$.

Case 2.

n is odd, that is, $G\in {\bigcup }_{i=2}^6{\mathcal{G}}_i$.

Subcase 2.1.

$G\in {\mathcal{G}}_2$, where ${\mathcal{G}}_2=\mathcal{A}+\mathcal{B}-\left\{C_4\right\}$.

When $G\cong K_3\in \mathcal{B}$, we get that $\gamma \left(G\right)-\rho \left(G\right)=0$.

When $G\in \mathcal{B}-\left\{K_3\right\}=\{G_5^1,G_5^2,G_5^3,G_5^4\}$, one has that $\epsilon \left(v\right)=2$ for any vertex $v\in V\left(G\right)$. Then $\pi \left(v\right)=\frac{2n-2-d\left(v\right)}{n-1}$. It follows that $\rho \left(G\right)=\frac{2n-2-\delta \left(G\right)}{n-1}=\frac{3}{2}$ and $\gamma \left(G\right)-\rho \left(G\right)=\frac{1}{2}$.

When $G\in {\mathcal{G}}_2-\mathcal{B}$,

$$\rho \left(G\right)=\left\{\begin{array}{cc}2,\hfill & ifG\in \{G_7^1,G_7^2,G_7^3,G_7^4,G_7^6\}\hfill \\ \frac{7}{3},\hfill & ifG\cong G_7^5\hfill \end{array}\right.$$

by direct calculation. Hence, $\gamma \left(G\right)-\rho \left(G\right)\le 1$ with the equality if and only if $G\in \{G_7^1,G_7^2,G_7^3,G_7^4,G_7^6\}$.

In all, $\gamma \left(G\right)-\rho \left(G\right)\le \frac{n-3}{4}$ with the equality if and only if $G\in {\mathcal{G}}_2-\left\{G_7^5\right\}$ in this case.

Subcase 2.2.

$G\in {\mathcal{G}}_3$. Then $G=\phi \left(H\right)$ for some connected graph H and $\left|V\left(H\right)\right|=k=\frac{n-1}{2}$ by the definition of ${\mathcal{G}}_3$.

In consideration of $K_{\lceil \frac{n}{2}\rceil ,\lfloor \frac{n}{2}\rfloor }\in {\mathcal{G}}_3$, where $K_{\lceil \frac{n}{2}\rceil ,\lfloor \frac{n}{2}\rfloor }$ is the graph obtained from $f(K_{\lfloor \frac{n}{2}\rfloor })$ by adding a new vertex x and edges joining x to every vertex of $K_{\lfloor \frac{n}{2}\rfloor }$. Assume that $G\cong K_{\lceil \frac{n}{2}\rceil ,\lfloor \frac{n}{2}\rfloor }$. Then Firstly, $\rho \left(G\right)\ne \pi \left(v_i\right)$, $i=1,\dots ,k,$ by Claim 1. Secondly, for each $i\in \{1,\dots ,k\}$, we have that

$$\begin{array}{ccc}\hfill \pi \left(u_i\right)& =& \frac{1}{n-1}[d(u_i,x)+d(u_i,v_i)+\sum _{j\in \{1,\dots ,i-1,i+1,\dots ,k\}}(d(u_i,u_j)+d(u_i,v_j))]\hfill \\ & =& \frac{1}{n-1}[2+1+5(k-1)]\hfill \\ & =& \frac{5}{2}-\frac{2}{n-1}.\hfill \end{array}$$

(1)

Finnally, for the vertex x appeared in the definition of ${\mathcal{G}}_3$,

$$\begin{array}{c}\hfill \pi \left(x\right)=\frac{1}{n-1}·\sum _{i=1}^k(d(x,v_i)+d(x,u_i))=\frac{1}{n-1}·3k=\frac{3}{2}.\end{array}$$

(2)

Since $\frac{5}{2}-\frac{2}{n-1}\ge \frac{3}{2}$ always true for $n\ge 3$, $\gamma \left(G\right)-\rho \left(G\right)=\frac{n-1}{2}-(\frac{5}{2}-\frac{2}{n-1})=\frac{n-6}{2}+\frac{2}{n-1}.$

Assume that $G\ncong K_{\lceil \frac{n}{2}\rceil ,\lfloor \frac{n}{2}\rfloor }$. Then $v_s{v}_t\notin E\left(G\right)$ or $v_{m}x\notin E\left(G\right)$ for some $s,t,m\in \{1,\cdots ,k\}$. Combining with Equation (1), we get that $\rho \left(G\right)\ge \pi \left(u_s\right)>\frac{5}{2}-\frac{2}{n-1}$ and $\rho \left(G\right)\ge \pi \left(u_m\right)>\frac{5}{2}-\frac{2}{n-1}$, respectively. As a result, $\gamma \left(G\right)-\rho \left(G\right)<\gamma \left(G\right)-\pi \left(u_s\right)<\frac{n-6}{2}+\frac{2}{n-1}.$

In brief, $\gamma \left(G\right)-\rho \left(G\right)\le \frac{n-6}{2}+\frac{2}{n-1}$ with equality if and only if $G\cong K_{\lceil \frac{n}{2}\rceil ,\lfloor \frac{n}{2}\rfloor }$.

Subcase 2.3.

$G\in {\mathcal{G}}_4$.

We notice that $k=\frac{n-5}{2}$ and a cycle $C_4$ is mentioned in constructing ${\mathcal{G}}_4$. Let $V\left(C_4\right)=\{y,y_1,y_2,y_3\}$, where $y_1$ and $y_2$ be the neighbors of vertex y in the cycle $C_4$. It is obvious that $\pi \left(y_3\right)$ is greater than $\pi \left(y_1\right),\pi \left(y_2\right),\pi \left(y\right)$ and $\pi \left(x\right)$, by the definition of ${\mathcal{G}}_4$. Therefore, $\rho \left(G\right)\notin \{\pi \left(y_1\right),\pi \left(y_2\right),\pi \left(y\right),\pi \left(x\right)\}$. Furthermore,

$$\begin{array}{ccc}\hfill \pi \left(y_3\right)& =& \frac{1}{n-1}[d(y_3,y_1)+d(y_3,y_2)+d(y_3,y)+d(y_3,x)+\sum _{j=1}^k(d(y_3,u_j)+d(y_3,v_j))]\hfill \\ & =& \frac{1}{n-1}\{1+1+2+3+\sum _{j=1}^k[(d(y_3,x)+d(x,u_j))+(d(y_3,x)+d(x,v_j))]\}\hfill \\ & \ge & \frac{1}{n-1}[7+k·(3+2+3+1)]\hfill \\ & =& \frac{9}{2}-\frac{11}{n-1},\hfill \end{array}$$

with the equality if and only if $\{x{v}_j\mid j=1,\dots ,k\}\subseteq E\left(G\right).$ And for $i\in \{1,\dots ,k\}$,

$$\begin{array}{ccc}\hfill \pi \left(u_i\right)& =& \frac{1}{n-1}[d(u_i,x)+d(u_i,y)+d(u_i,y_1)+d(u_i,y_2)+d(u_i,y_3)\hfill \\ & & +d(u_i,v_i)+\sum _{j\in \{1,\dots ,i-1,i+1,\dots ,k\}}(d(u_i,u_j)+d(u_i,v_j))]\hfill \\ & \ge & \frac{1}{n-1}[2+3+4+4+5+1+5(k-1)]\hfill \\ & =& \frac{5}{2}+\frac{4}{n-1},\hfill \end{array}$$

the equality holds if and only if $\{v_{i}x,v_i{v}_j\mid j=1,\dots ,i-1,i+1,\dots ,k\}\subseteq E\left(G\right).$ Considering $\left|V\right(G\left)\right|\ge 7$ for $G\in {\mathcal{G}}_4$, and

$$\left\{\begin{array}{cc}\frac{9}{2}-\frac{11}{n-1}<\frac{5}{2}+\frac{4}{n-1},\hfill & if7\le n\le 8\hfill \\ \frac{9}{2}-\frac{11}{n-1}>\frac{5}{2}+\frac{4}{n-1},\hfill & ifn\ge 9,\hfill \end{array}\right.$$

we get that

$$\rho \left(G\right)\ge \left\{\begin{array}{cc}\frac{5}{2}+\frac{4}{n-1},\hfill & if7\le n\le 8\hfill \\ \frac{9}{2}-\frac{11}{n-1},\hfill & ifn\ge 9,\hfill \end{array}\right.$$

which follows that

$$\begin{array}{ccc}\hfill \gamma \left(G\right)-\rho \left(G\right)& \le & \left\{\begin{array}{cc}\frac{n-1}{2}-\frac{5}{2}-\frac{4}{n-1},\hfill & if7\le n\le 8\hfill \\ \frac{n-1}{2}-\frac{9}{2}+\frac{11}{n-1},\hfill & ifn\ge 9\hfill \end{array}\right.\hfill \\ & <& \frac{n-6}{2}-\frac{2}{n-1}.\hfill \end{array}$$

Subcase 2.4.

$G\in {\mathcal{G}}_5$.

By the definition of ${\mathcal{G}}_5$, one gets that $V\left(G\right)=\{u,v,w,v_1,\dots ,v_k,u_1,\dots ,u_k\}$, where $k=\frac{n-3}{2}$. We analyze the proximity of all the vertices in graph G one by one.

For each $i\in \{1,\dots ,k\}$,

$$\begin{array}{ccc}\hfill \pi \left(u_i\right)& =& \frac{1}{n-1}[d(u_i,u)+d(u_i,v)+d(u_i,w)+\sum _{s\in \{v_1,\dots ,v_k,u_1,\dots ,u_k\}}d(u_i,s)]\hfill \\ & \ge & \frac{1}{n-1}[2+3+2+(5k-4)]\hfill \\ & =& \frac{5}{2}-\frac{2}{n-1},\hfill \end{array}$$

(3)

the equality holds if and only if $\{v_{i}u,v_{i}w,v_i{v}_j\mid j=1,\dots ,i-1,i+1,\dots ,k\}\subseteq E\left(G\right)$. For the vertex u of path $P_3$,

$$\begin{array}{ccc}\hfill \pi \left(u\right)& =& \frac{1}{n-1}[d(u,v)+d(u,w)+\sum _{i=1}^k(d(u,v_i)+d(u,u_i))]\hfill \\ & \ge & \frac{1}{n-1}(1+2+3k)=\frac{3}{2},\hfill \end{array}$$

(4)

the equality holds if and only if $\{u{v}_i\mid i=1,\dots ,k\}\subseteq E\left(G\right).$ Analogously, $\pi \left(w\right)\ge \frac{3}{2}$. Moreover,

$$\begin{array}{ccc}\hfill \pi \left(v\right)& =& \frac{1}{n-1}[d(v,u)+d(v,w)+\sum _{i=1}^k(d(v,v_i)+d(v,u_i))]\hfill \\ & \ge & \frac{1}{n-1}(1+1+5k)\hfill \\ & =& \frac{5}{2}-\frac{3}{n-1},\hfill \end{array}$$

(5)

and the equality holds if and only if $d(v,v_i)=2,i=1,\dots ,k$, that is, $u{v}_i\in E\left(G\right)$ or $w{v}_i\in E\left(G\right)$ for each $i=1,\dots ,k$.

Since max$\{\frac{5}{2}-\frac{2}{n-1},\frac{3}{2},\frac{5}{2}-\frac{3}{n-1}\}=\frac{5}{2}-\frac{2}{n-1}$ and $\rho \left(G\right)\ne \pi \left(v_i\right)$ for $i=1,\dots ,k,$ by Claim 1,

$$\rho \left(G\right)\ge \frac{5}{2}-\frac{2}{n-1},$$

the equality holds if and only if (3), (4) and (5) are tight. Namely $G\cong G^{\prime }$, where $G^{\prime }$ is defined in Definition 1. Otherwise, $v_s{v}_t\notin E\left(G\right)$ or $v_{m}u\notin E\left(G\right)$ or $v_{k}w\notin E\left(G\right)$ or $d\left(v_{l}v\right)>2$ for some $s,t,m,k,l\in \{1,\cdots ,k\}$. It follows that $\rho \left(G\right)\ge \pi \left(u_i\right)>\frac{5}{2}-\frac{2}{n-1}$, where i is equal to $s,m,k$ and l, respectively. As a result,

$$\gamma \left(G\right)-\rho \left(G\right)\le \frac{n-1}{2}-\frac{5}{2}+\frac{2}{n-1}=\frac{n-6}{2}+\frac{2}{n-1},$$

with equality if and only if $G\cong G^{\prime }$.

Subcase 2.5.

$G\in {\mathcal{G}}_6$.

By the proof of Lemma 3.4 in [23], we derive that $\left|U\right|\le 2$, where U is the set in the definition of ${\mathcal{G}}_6$.

Subcase 2.5.1.

$X=K_3$.

In this case, $\rho \left(G\right)\ne \pi \left(v_i\right)$ still holds by Claim 1 for $i=1,\dots ,k$, and $k=\frac{n-3}{2}$.

Suppose that $s\in U$ and $s^{*}\in V\left(K_3\right)-U$. Similar to the proof of Claim 1, we can obtain that $\pi \left(s\right)<\pi \left(s^{*}\right)$, and thus $\rho \left(G\right)\ne \pi \left(s\right)$.

Besides,

$$\begin{array}{ccc}\hfill \pi \left(s^{*}\right)& =& \frac{1}{n-1}[\sum _{s^{\prime }\in V\left(K_3\right)-\left\{s^{*}\right\}}d(s^{*},s^{\prime })+\sum _{i=1}^k(d(s^{*},v_i)+d(s^{*},u_i))]\hfill \\ & \ge & \frac{1}{n-1}·(2+5k)=\frac{5}{2}-\frac{3}{n-1},\hfill \end{array}$$

(6)

with the equality if and only if $\{s{v}_i\mid i=1,\dots ,k\}\subseteq E\left(G\right).$ Furthermore, for each $i\in \{1,\dots ,k\}$,

$$\begin{array}{ccc}\hfill \pi \left(u_i\right)& =& \frac{1}{n-1}[\sum _{z\in V\left(K_3\right)}d(u_i,z)+\sum _{j=1}^k(d(u_i,u_j)+d(u_i,v_j))]\hfill \\ & \ge & \frac{1}{n-1}[2+2+3+(5k-4)]\hfill \\ & =& \frac{5}{2}-\frac{2}{n-1},\hfill \end{array}$$

(7)

the equality holds if and only if

$$\{s{v}_i,v_i{v}_j\mid s\in U,|U|=2,j=1,\dots ,i-1,i+1,\dots ,k\}\subseteq E\left(G\right).$$

Combining the inequalities (6) and (7), and using the analysis similar to Subcase 2.4, we get that $\rho \left(G\right)\ge \frac{5}{2}-\frac{2}{n-1}$ and

$$\gamma \left(G\right)-\rho \left(G\right)\le \frac{n-1}{2}-\frac{5}{2}+\frac{2}{n-1}=\frac{n-6}{2}+\frac{2}{n-1}$$

with equality if and only if $G\cong G^{″}$, where $G^{″}$ is the graph defined in Definition 1.

Subcase 2.5.2.

$X\in {\bigcup }_{i=1}^4{G}_5^i$.

In this case $k=\frac{n-5}{2}$. For each $i\in \{1,\dots ,k\}$, let

$$\pi \left(u_i\right)=\frac{1}{n-1}[\sum _{s\in U}d(u_i,s)+\sum _{s^{*}\in V\left(X\right)-U}d(u_i,s^{*})+\sum _{i=1}^k(d(u_i,u_j)+d(u_i,v_j))].$$

It is easy to know that $d(u_i,s)\ge 2$ and $d(u_i,s^{*})\ge 3$, so

$$\begin{array}{ccc}\hfill \pi \left(u_i\right)& \ge & \frac{1}{n-1}\left[2\right|U|+3(5-\left|U\right|)+(5k-4)]\hfill \\ & \ge & \frac{1}{n-1}[4+9+(5k-4)]\hfill \\ & =& \frac{5}{2}-\frac{1}{n-1},\hfill \end{array}$$

(8)

the equality holds if and only if $\{s{v}_i,v_i{v}_j\mid s\in U,|U|=2,UisadominatingsetofX,j=1,\dots ,i-1,i+1,\dots ,k\}\subseteq E\left(G\right).$

Let $s\in U$. Then $\pi \left(s\right)=\frac{1}{n-1}[{\sum }_{z\in X}d(s,z)+{\sum }_{i=1}^k(d(s,v_i)+d(s,u_i))].$ If $X=G_5^1$, then

$$\begin{array}{ccc}\hfill \pi \left(s\right)& =& \frac{1}{n-1}[\sum _{z\in G_5^1}d(s,z)+\sum _{i=1}^k(d(s,v_i)+d(s,u_i))]\hfill \\ & =& \frac{1}{n-1}[1+1+2+2+\sum _{i=1}^k(d(s,v_i)+d(s,u_i))]\hfill \\ & \ge & \frac{1}{n-1}(1+1+2+2+3k)\hfill \\ & =& \frac{3}{2}\hfill \end{array}$$

(9)

with equality if and only if $\{s{v}_i\mid i=1,\dots ,k\}\subseteq E\left(G\right)$. If $X=G_5^l,l=2,3,4$, then

$$\begin{array}{ccc}\hfill \pi \left(s\right)& =& \frac{1}{n-1}[\sum _{z\in G_5^l}d(s,z)+\sum _{i=1}^k(d(s,v_i)+d(s,u_i))]\hfill \\ & \ge & \frac{1}{n-1}(1+1+1+2+3k)\hfill \\ & =& \frac{3}{2}-\frac{1}{n-1},\hfill \end{array}$$

(10)

the equality holds if and only if $\{s{v}_i\mid i=1,\dots ,k\}\subseteq E\left(G\right)$ and s be the vertex with $d\left(s\right)=3$ in U.

Let $s^{*}\in V\left(X\right)-U$. Then $\pi \left(s^{*}\right)=\frac{1}{n-1}[{\sum }_{z\in V\left(X\right)-\left\{s^{*}\right\}}d(s^{*},z)+{\sum }_{i=1}^k(d(s^{*},v_i)$$+d(s^{*},u_i)\left)\right]$. Since $\epsilon \left(v\right)=2$ for each $v\in V\left(G_5^i\right),i=1,\dots ,4$, which follows that $\epsilon \left(s^{*}\right)=2$. Hence,

$$\begin{array}{ccc}\hfill \sum _{z\in V\left(X\right)-\left\{s^{*}\right\}}d(s^{*},z)& =& d\left(s^{*}\right)+2\left(\right|V\left(X\right)|-1-d\left(s^{*}\right))=2|V\left(X\right)|-2-d\left(s^{*}\right)\hfill \\ & \ge & 2\times 5-2-3=5\hfill \end{array}$$

with the equality if and only if $d\left(s^{*}\right)=3$. In view of $d(s^{*},v_i)\ge 2$ and $d(s^{*},u_i))\ge 3$, thus

$$\begin{array}{c}\hfill \pi \left(s^{*}\right)\ge \frac{5+5k}{n-1}=\frac{5}{2}-\frac{5}{n-1}.\end{array}$$

(11)

Combine with (8)–(11), we obtain that $\rho \left(G\right)\ge \frac{5}{2}-\frac{1}{n-1}$. And $\gamma \left(G\right)-\rho \left(G\right)\le \frac{n-1}{2}-\frac{5}{2}+\frac{2}{n-1}=\frac{n-6}{2}+\frac{1}{n-1}.$

In conclusion,

$$\gamma \left(G\right)-\rho \left(G\right)\le \frac{n-1}{2}-\frac{5}{2}+\frac{2}{n-1}=\frac{n-6}{2}+\frac{2}{n-1}$$

with the equality if and only if $X=K_3$ and $G\cong G^{″}$ by Subcases 2.5.1 and 2.5.2.

Here’s a quick rundown of the above proof. If n is even, then

$$\gamma \left(G\right)-\rho \left(G\right)\le \left\{\begin{array}{cc}\frac{2}{3},\hfill & n=4\hfill \\ \frac{n-5}{2}+\frac{3}{2n-2},\hfill & nisevenandn\ne 4\hfill \end{array}\right.$$

with equality if and only if $G\in \{C_4,K_{\frac{n}{2},\frac{n}{2}}\mid n$ is even and $n\ne 4\}$ by case 1. If n is odd, then $\gamma \left(G\right)-\rho \left(G\right)\le \frac{n-6}{2}+\frac{2}{n-1}$ with equality if and only if $G\in \{K_{\lceil \frac{n}{2}\rceil ,\lfloor \frac{n}{2}\rfloor },G^{\prime },G^{″}\}$ by Subcases 2.2–2.5. And it is worth mentioning that for n is odd and $n\le 7$, we get a better bound in Subcase 2.1. Namely, $\gamma \left(G\right)-\rho \left(G\right)\le \frac{n-3}{4}$ with the equality if and only if $G\in {\mathcal{G}}_2-\left\{G_7^5\right\}$. Therefore,

$$\gamma \left(G\right)-\rho \left(G\right)\le \left\{\begin{array}{cc}\frac{n-3}{4},\hfill & nisoddandn\le 7\hfill \\ \frac{n-6}{2}+\frac{2}{n-1},\hfill & nisoddandn\ge 9\hfill \end{array}\right.$$

with equality if and only if $G\in ({\mathcal{G}}_2-\left\{G_7^5\right)\})\cup \{K_{\lceil \frac{n}{2}\rceil ,\lfloor \frac{n}{2}\rfloor },G^{\prime },G^{″}\mid n$ is odd and $n\ge 9\}$ This completes the proof. □

3. Conclusions

Many of the AutoGraphiX conjectures were studied, but some of them remained as conjectures. The existing research mainly focus on proving the correct AutoGraphiX conjectures; improving the not-quite correct AutoGraphiX conjectures; disproving the incorrect AutoGraphiX conjectures by counter examples. The aim of this note is to improve the AutoGraphiX conjecture A. 565.

Recall that $1\le \gamma \left(G\right)\le \lfloor \frac{n}{2}\rfloor$ [16], Lemmas 1, 3, 4 and 6 prove the upper bounds on $\gamma \left(G\right)-\rho \left(G\right)$ with $1\le \gamma \left(G\right)\le \lfloor \frac{n}{2}\rfloor -2$, $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor -1$ and $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor$, respectively. The maximum value of $\gamma \left(G\right)-\rho \left(G\right)$ can be obtained immediately by comparing the results in Lemmas 1, 3, 4 and 6. It can not be reached for $1\le \gamma \left(G\right)\le \lfloor \frac{n}{2}\rfloor -2$ by Lemmas 4 and 6. But it can be reached for $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor$ and $\gamma \left(G\right)=\lfloor \frac{n}{2}\rfloor -1$ with $n=6$, by Lemmas 1, 3 and 6. On this basis, we are obtain Theorem 1 in the following, which implies that Conjecture 1 is not entirely true. In Theorem 1, we are improve the bound for $n=3,4,5,7$, and recharacterize the extremal graphs that satisfy the equation in Conjecture 1.

Theorem 1.

Let G be a connected graph of order $n(\ge 2)$. Then

$$\gamma \left(G\right)-\rho \left(G\right)\le \left\{\begin{array}{cc}\frac{2}{3},\hfill & n=4\hfill \\ \frac{n-5}{2}+\frac{3}{2n-2},\hfill & nisevenandn\ne 4\hfill \\ \frac{n-3}{4},\hfill & nisoddandn\le 7\hfill \\ \frac{n-6}{2}+\frac{2}{n-1},\hfill & nisoddandn\ge 9\hfill \end{array}\right.$$

with equality if and only if $G\in \left\{C_4\right\}\cup \{$4-regular 6-vertices graph, $K_{\frac{n}{2},\frac{n}{2}}\mid n$ is even and $n\ne 4$$\}\cup ({\mathcal{G}}_2-\left\{G_7^5\right)\})\cup \{K_{\lceil \frac{n}{2}\rceil ,\lfloor \frac{n}{2}\rfloor },G^{\prime },G^{″}\mid n$ is odd and $n\ge 9\}$.

In this paper, we present the sharp upper bound on the difference between the domination number and remoteness. AutoGraphiX conjectures A.566, A.567, A.568 in [8] give the bounds on the sum, the ratio and the product of the domination number and remoteness, which are still open. It is very meaningful to study the above conjectures. This research method is, in all probability, available in the AutoGraphiX conjectures about the domination number and proximity.