A Fixed Point Approach to Lattice Fuzzy Set via F-Contraction

Abstract

In this work, we design and demonstrate the occurrence of L-fuzzy common fixed points of L-fuzzy mappings (L-FM) meeting contractive criteria in the framework of complete b-metric spaces (b-MS) employing F-contractions and a certain class of continuous functions. We also conduct a case study to determine the implementation of our derived principles. A few other concepts which are the direct consequences of our findings are explained in this paper.

1. Introduction

In 1965, Zadeh [1] presented the concept of fuzzy set (FS) that expands on the idea of a crisp set by giving all of its elements membership values between [0, 1]. The levels of possession of a particular property are described using hazy ideas. Because it is effective at solving control problems, FS theory has the potential to address situations that crisp set theory finds troublesome. Systems that are vague, complicated, and nonlinear in nature are governed by fuzzy sets. FS theory has made it simpler to resolve real-world issues since it defines and simplifies the concept of fuzziness and flaws. It is currently a generally recognized theory. Due to the flexibility in solving real-world problems with this theory, a number of researchers modified fuzzy concepts in many other fields of science, such as [2,3,4] and references therein.

By replacing the interval [0, 1] with a complete distributive lattice L later in 1967, Goguen [2] advanced this concept to L-FS theory. An FS is a special type of L-FS where L = [0, 1]. For ${\alpha }_L$-cut sets of L-FM, Rashid et al. [5] studied FP theorems for L-FMs to the discovery of the Hausdorff distance. Common FP results on L-FPs can be seen in [5,6,7] and references therein. Heilpern [8] introduced the theory of FM and established a theorem on FP for FM in metric linear space, which serves as a fuzzy generalization of Banach’s contraction principle [9].

The most active and vigorous area of research in pure mathematics is fixed point (FP) theory. For nonlinear analysis, FP theory is an effective technique. Numerous disciplines, including biosciences, chemistry, commerce, finances, astronomy, and game scheme, use FP methods. The most significant result of Banach’s work in metric FP theory is Banach’s principle [9], which was published in 1922. This rule provides a reliable way of finding FPs of a function that satisfies certain conditions on complete metric spaces (MS) as well as guaranteeing their existence and uniqueness.

Nadler [10] improved Banach’s principle for multivalued mappings in complete MS in 1969.

Backhtin [11] proposed the concept of a b-MS for the first time in 1989. The b-MS results were first conceptualized by Czerwik [12] in 1993. By adopting this theory, several researchers have expanded Banach’s principle in b-MSs, including Boriceanu [13], Kanwal et al. [14], Czerwik [12,15], Kir and Kiziltunc [16], Kumam et al. [17], and Phiangsungnoen et al. [18].

Many works appear to ensure the existence of FPs and common FPs of FMs and L-FMs that meet a condition (see [5,6,7,8,19,20] and references therein). Moreover, in 2012, Wardowski [21] obtained a new fixed point theorem concerning F-contraction for single-valued mapping.

Theorem 1

[21]. Let (X,d) be a complete metric space and T: X → X be an F-contraction. Then, T has a unique fixed point x∗ ∈ X, and for every $x_0$∈ X, a sequence {$T^n{x}_0$} _n∈N is convergent to x∗. Ample research regarding the existence of FP and common FP for single-valued and set-valued mappings satisfying F-contraction has been conducted (see [22,23,24,25,26,27] and references therein).

In this paper, we construct and establish the existence of ${\alpha }_L$-fuzzy common FPs of L-FMs satisfying a contraction in the setting of complete b-MSs using F-contractions and a certain kind of continuous function. Additionally, a case study is provided to show the applicability of our findings. A few well-known consequences are expanded.

2. Materials and Methods

Some important definitions and lemmas are given here for understanding.

Definition 1

[11]. Let$\Psi$be a non-empty set and $w\ge 1$ be any real number. A map $d:\Psi \times \Psi \to R^{+}{{\displaystyle \cup }}^{}\left\{0\right\}$ is called a b-metric if the following axioms are satisfied for all $\iota ,\vartheta ,\zeta \in \Psi$:

• $d\left(\iota ,\vartheta \right)\ge 0$ and $d\left(\vartheta ,\iota \right)=0$ iff $\iota =\vartheta$;
• $d\left(\iota ,\vartheta \right)=d\left(\vartheta ,\iota \right)$; and
• $d\left(\iota ,\zeta \right)\le w\left[d\left(\iota ,\vartheta \right)+d\left(\vartheta ,\zeta \right)\right]$.

Here, $\left(\mathsf{\Psi },d\right)$ is called a b-MS.

For $w=1$, a b-MS becomes an ordinary MS.

Example 

[13]. The set ${\varsigma }_t$ with $0<t<1$, together with the function $d:{\varsigma }_t\times {\varsigma }_t \to [0,\infty ),$ defined as

$$d\left(s,r\right)={\left({\displaystyle \sum }_{j=1}^{\infty }{\left|s_j-r_j\right|}^t\right)}^{\frac{1}{t}},$$

where ${\varsigma }_t=\left\{\left\{s_j\right\}\subset ℝ: {\displaystyle \sum }_{j=1}^{\infty }{\left|s_j\right|}^t<\infty \right\},$ s $=\left\{s_j\right\},r=\left\{r_j\right\}\in {\varsigma }_t$ is a b-MS with $w=2^{\frac{1}{t}}>1$.

Definition 2

[13]. Consider that $\left(\Psi ,d\right)$ is a b-MS and $\left\{s_j\right\}$ is a sequence in $\Psi$. Then,

(1)

$\left\{s_j\right\}$ is called a convergent sequence to some$s\in \mathsf{\Psi }$, iff for all $ϵ>0, \exists n_0\left(ϵ\right)\in \mathbb{N}$ such that for all $j\ge n_0\left(ϵ\right)$, we have $d\left(s_j,s\right)<ϵ$. Then, we write $\underset{j\to \infty }{\lim }{s}_j=s$.

(2)

$\left\{s_j\right\}$ is said to be a Cauchy sequence iff for all $ϵ>0, \exists n_0\left(ϵ\right)\in \mathbb{N}$ such that for each $k, j\ge n_0\left(ϵ\right)$, we have $d\left(s_j,s_k\right)<ϵ$.

(3)

A b-MS is called complete if every Cauchy sequence is convergent in it.

Note: Throughout this paper, we denote $CB\left(\mathsf{\Psi }\right)$ as the set of non-empty closed and bounded subsets of $\mathsf{\Psi }$ and $CL\left(\mathsf{\Psi }\right)$ as the set of all non-empty closed subsets of$\mathsf{\Psi }$.

Definition 3

[15]. Consider that $\left(\Psi ,d\right)$ is a b-MS; for$z\in \Psi$and$M,N\in CL\left(\Psi \right)$, we define

$$d\left(z,M\right)=\underset{a\in M}{\inf }d\left(z,a\right)$$

$$d\left(M,N\right)=inf\left\{d\left(a,b\right):a\in M , b \in N\right\}$$

The Hausdorff b-metric induced by $d$can be defined on $CB\left(\mathsf{\Psi }\right)$ as:

$$H\left(M,N\right)=max\left\{\underset{u\in A}{\sup }d\left(u,N\right),\underset{v\in N}{\sup }d\left(M,v\right)\right\}$$

for all $M,N,\in CB\left(\mathsf{\Psi }\right)$.

Lemma 1

[18]. Suppose that $\left(\Psi ,d\right)$ is a b-MS. For any $M,N,O\in CB\left(\Psi \right)$ and any $l, m\in \Psi$, we have the following:

(1)

$d\left(l,N\right)\le H\left(M,N\right)$ for all $l\in M;$

(2)

$d\left(M,N\right)\le H\left(M,N\right)$;

(3)

$H\left(N,N\right)=0$;

(4)

$H\left(M,N\right)=H\left(N,M\right)$;

(5)

$H\left(M,O\right)\le w\left[H\left(M,N\right)+H\left(N,O\right)\right]$; and

(6)

$d\left(l,N\right)\le w\left[d\left(l,b\right)+d\left(b,N\right)\right]$.

Lemma 2

[18]. Let $\left(\Psi ,d\right)$ be a b-MS. For $M\in CB\left(\Psi \right)$ and $a\in \Psi$, we have

$$d\left(a,M\right)=0\iff a\in \overline{M}=M,$$

where $\overline{M}$ is the closure of the set M in $\mathsf{\Psi }$.

Lemma 3

[18]. For a b-MS $\left(\Psi ,d\right)$ and $M,N\in CB\left(\Psi \right),$consider $q>1$; then, for each $a\in M$, there exists $b\in N$, such that

$$d\left(a,b\right)\le qH\left(M,N\right)$$

Lemma 4

[19]. Suppose that $\left(\Psi ,d\right)$ is a b-MS. For $M,N\in CB\left(\Psi \right)$ and $0<\delta \in R$. Then, for $a\in M$, there exists $b\in N$, such that

$$d\left(a,b\right)\le H\left(M,N\right)+\delta .$$

Lemma 5

[19]. If $M, N\in CB\left(\Psi \right)$ with $H\left(M,N\right)<ϵ$, then for each$a\in M$, there exists $b\in N$, such that $d\left(a,b\right)<ϵ$.

Definition 4

[1]. Let $\Psi$ be a universal set. A function $G: \Psi \to \left[0,1\right]$ is known as an FS in $\Psi$. The value $G\left(u\right)$ of $G$ at $u\in \Psi$ stands for the degree of membership of $u$ in $G$. The set of all FSs in $\Psi$ will be denoted by $F\left(\Psi \right).$ $G\left(u\right)=1$ means full membership, $G\left(u\right)=0$ means no membership, and intermediate values between $0$ and $1$ mean partial membership.

Example. 

Let A denote the old and B denote the young and$\Psi$= [0, 100]. Then, A and B both are fuzzy sets that are defined by

$$A\left(x\right)=\{\begin{array}{c}{\left[1+{\left(\frac{x-50}{5}\right)}^{-2}\right]}^{-1}, if 50<x\le 100\\ 0 , otherwise \end{array}$$

$$B\left(x\right)=\{\begin{array}{c}{\left[1+{\left(\frac{x-25}{5}\right)}^2\right]}^{-1}, if 25<x\le 100\\ 0 , otherwise\\ \end{array}$$

The $\alpha$-level set of $G$ is denoted by ${\left[G\right]}_{\alpha }$ and defined as

$$\left[G\right]{ }_{\alpha }=\left\{u\in \mathsf{\Omega }: G\left(u\right)\ge \alpha \right\};\alpha \in \left(0, 1\right].$$

Definition 5

[7]. A partially ordered set (poset) is a set$\mathcal{X}$ with a binary relation $⪯$ such that for all $m, n, q\in \mathcal{X}$,

(1)

$m⪯m$ (reflexive);

(2)

$m⪯n$ and $n⪯m$ implies $m=n$ (anti-symmetric); and

(3)

$m⪯n$ and $n⪯q$ implies $m⪯q$ (transitivity).

Definition 6

[7]. A poset$\left(L,{⪯}_L\right)$ is said to be a

(1)

Lattice if $\xi \wedge \eta \in L, \xi \vee \eta \in L$ for all $\xi ,\eta \in L$.

(2)

Complete lattice if it is lattice and $\vee Q\in L,\wedge Q\in L$for all$Q\subseteq L$.

(3)

Distributive lattice if it is lattice and

$$\xi \vee \left(\eta \wedge t\right)=\left(\xi \vee \eta \right)\wedge \left(\xi \vee t\right), \xi \wedge \left(\eta \vee t\right)=\left(\xi \wedge \eta \right)\vee \left(\xi \wedge t\right)$$

for all $\xi ,\eta ,t\in L$.

(4)

Complete distributive lattice if it is lattice and

$$\xi \vee \left({\wedge }_i{\eta }_i\right)={\wedge }_i\left(\xi \vee {\eta }_i\right),\xi \wedge \left({\vee }_i{\eta }_i\right)={\vee }_i\left(\xi \wedge {\eta }_i\right)$$

for all ${\xi }_i,{\eta }_i\in L$.

(5)

Bounded lattice if it is a lattice along with a maximal element$1_L$ and a minimal element$0_L,$ which satisfies $0_L{⪯}_{L}x{⪯}_L{1}_L$ for every $x\in L$.

Note:$\vee$ means least upper bound and $\wedge$ means greatest lower bound.

Example 1.

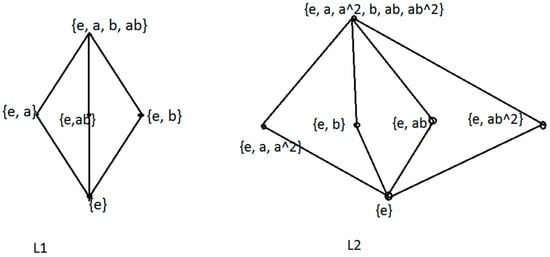
Lattice of Klein four group (L1) and lattice of dihedral group of order 6 (L2) are shown in Figure 1, which are complete and bounded but not distributive lattices.

Figure 1. Complete bounded but non-distributive lattices.

Example 2.

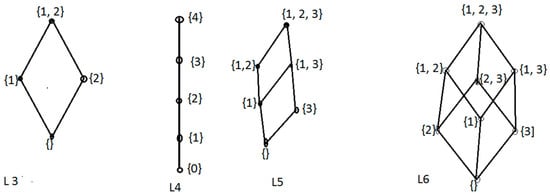
Power set of any non-empty set is a complete bounded distributive lattice; in Figure 2, L3 and L6 are the lattices of power sets of sets containing elements two and three, respectively. L4 is the lattice of the set$\left\{x:x\in \mathbb{Z}\wedge 0\le x\le 4\right\}$and L5 is the lattice of subsets of the set {1, 2, 3}, which are other examples of complete bounded distributive lattices.

Figure 2. Complete bounded distributive lattices.

Definition 7

[2]. An L-FS $G$ on a non-empty set $\Psi$ is a function $G:\Psi \to L,$ where $L$ is a bounded complete distributive lattice, along with $1_L$ and $0_L$.

Remark 1.

If $L=\left[0,1\right]$, then the$L$-FS becomes an FS in the sense of Zadeh. Hence, the class of$L$-FSs is larger than the class of FSs.

Definition 8

[2]. The ${\alpha }_L$-level set of an L-FS $G$ is denoted by ${[G]}_{{\alpha }_L}$and is defined as below:

$${\left[G\right]}_{{\alpha }_L}=\left\{u\in \mathsf{\Psi } : {\alpha }_L{⪯}_{L}G\left(u\right), \mathrm{for}{\alpha }_L\in L\backslash \left\{0_L\right\}\right\}$$

$${\left[\mathrm{G}\right]}_{0_L}=\overline{\left\{u\in \mathsf{\Psi } :0_L{⪯}_{L}G\left(u\right)\right\}}$$

where $\overline{S}$ is the closure of the set $S$ (crisp set).

Let $F_L\left(\mathsf{\Psi }\right)$be the set of all L-FSs in $\mathsf{\Psi }$. Now, for $x\in \mathsf{\Psi },A,B\in F_L\left(\mathsf{\Psi }\right),{\alpha }_L\in L\backslash \left\{0_L\right\}$ and ${\left[A\right]}_{{\alpha }_L},{\left[B\right]}_{{\alpha }_L}\in CB\left(\mathsf{\Psi }\right),$ we define:

$$p_{{\alpha }_L}\left(x,A\right)=inf\left\{d\left(x,a\right).;a.\in {\left[A\right]}_{{\alpha }_L}\right\}$$

$$p_{{\alpha }_L}\left(A,B\right)=inf\left\{d\left(a,b\right).; a\in {\left[A\right]}_{{\alpha }_L},b.\in {\left[B\right]}_{{\alpha }_L}\right\}$$

$$p\left(A,B\right)=\underset{{\alpha }_L}{\sup }{p}_{{\alpha }_L}\left(A,B\right)$$

$$H\left({\left[A\right]}_{{\alpha }_L},{\left[B\right]}_{{\alpha }_L}\right)=max\left\{\underset{a\in {\left[A\right]}_{{\alpha }_L}}{\sup }d\left(a,{\left[B\right]}_{{\alpha }_L}\right),\underset{b\in {\left[B\right]}_{{\alpha }_L}}{\sup }d\left(b,{\left[A\right]}_{{\alpha }_L}\right)\right\}$$

Define $Q_L\left(\mathsf{\Psi }\right)\subset F_L\left(\mathsf{\Psi }\right)$ as below:

$$Q_L\left(\mathsf{\Psi }\right)=\left\{A\in F_L\left(\mathsf{\Psi }\right) : {\left[A\right]}_{{\alpha }_L}\mathrm{is}\mathrm{nonempty}\mathrm{and}\mathrm{compact},{\alpha }_L\in L\backslash \left\{0_L\right\}\right\}$$

Definition 9

[7]. Let ${\Psi }_1$ be any set and${\Psi }_2$ be a metric space. A function $g:{\Psi }_1\to F_L\left({\Psi }_2\right)$ is called an $L$-FM. An $L$-FM $g$ is an L-FS on ${\Psi }_1\times {\Psi }_2$ with membership function $g\left(x\right)\left(y\right).$ The image $g\left(x\right)\left(y\right)$ is the grade of membership of $y$ in $g\left(x\right)$.

Definition 10

[19]. Suppose that $\left(\Psi ,d\right)$ is an MS and $T:\Psi \to F_L\left(\Psi \right).$ A point $z\in \Psi$ is an $L$-fuzzy FP of $T$ if $z\in {\left[Tz\right]}_{{\alpha }_L}$ for some ${\alpha }_L\in L\backslash \left\{0_L\right\}$.

Definition 11

[5]. Consider a b-MS$\left(\Psi , d\right)$ and $T_1,T_2:\Psi \to F_L\left(\Psi \right)$. A point $z\in \Psi$ is an$L$-fuzzy common FP of $T_1 and T_2$ if $z\in {\left[T_{1}z\right]}_{{\alpha }_{T_1}}{{\displaystyle \cap }}^{}{\left[T_{2}z\right]}_{{\alpha }_{T_2}}$ for some ${\alpha }_{T_1},{\alpha }_{T_2}\in L\backslash \left\{0_L\right\}$.

Banach Contraction Theorem

[9]. Consider a complete metric space ($\Psi ,d$) and a self-map T on $\Psi .$ If T satisfies the following contraction condition, then it has a unique fixed point in $\Psi :$

$$d\left(Tx, T y\right) \le \alpha d\left(x, y\right) for all x, y \in \mathsf{\Psi }\mathrm{and}\mathrm{for}\mathrm{some}\mathsf{\alpha }\in \left[0,1\right).$$

F-Contraction 

[20]. $F_s$ denotes the collection of functions $F:\left(0,+\infty \right)\to \left(-\infty ,+\infty \right),$satisfying:

(1)

$F$is strictly increasing;

(2)

$\forall \left\{{\mu }_n\right\}\subseteq \left(0,+\infty \right), \underset{n\to \infty }{\lim }{\mu }_n=0\iff \underset{n\to \infty }{\lim }F\left({\mu }_n\right)=-\infty$;

(3)

$\exists 0<r<1$ such that $\underset{n\to 0^{+}}{\lim }{\mu }^{r}F\left(\mu \right)=0$; and

(4)

For each sequence $\left\{{\mu }_n\right\}\subseteq R^{+}$ of positive numbers such that

$$\varrho +F\left(s{\mu }_n\right)\le F\left({\mu }_{n-1}\right),n\in \mathbb{N}$$

and some $\varrho >0$, we have

$$\varrho +F\left(s^n{\mu }_n\right)\le F\left(s^{n-1}{\mu }_{n-1}\right)$$

for all $n\in \mathbb{N} \mathrm{and}s\ge 1$.

A mapping G : $\Psi$ → CB($\Psi$) is said to be an F-contraction if there exists τ > 0 such that H(Gx,Gy) > 0 ⇒ τ + F(H(Gx,Gy)) $\le$ F(d(x,y)), for all x,y ∈ $\Psi$.

Example 

[27]. If F(a) = lna+a for all a > 0 and H : (CB($\Psi$))² → [0,+∞] is the Hausdorff metric on CB($\Psi$), then F satisfies 1–3 and each mapping G : $\Psi$ → CB($\Psi$) is an F-contraction such that H(Gx,Gy)$e^{H\left(Gx,Gy\right)-d\left(x,y\right)}$ $\le$ e−τd(x,y) for all x,y ∈ $\Psi$.

For more details on F-contraction, see [22,23,24,25,26,27] and references therein.

Remark 2.

Throughout the paper, we assume that functions $F\in F_s$ are continuous from the right.

Constantin [28] initiated a new collection $P$of continuous functions $\sigma :{\left(R^{+}\right)}^5\to R^{+}$ satisfying these conditions:

(1)

$\sigma \left(1,1,1,2,0\right),\sigma \left(1,1,1,0,2\right),\sigma \left(1,1,1,1,1\right)\in (0,1]$.

(2)

$\sigma$ is sub-homogeneous; that is, for all $\left({\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4,{\mu }_5\right)\in {\left(R^{+}\right)}^5$ and $\alpha \ge 0$, we have

$$\sigma \left(\alpha {\mu }_1,\alpha {\mu }_2,\alpha {\mu }_3,\alpha {\mu }_4,\alpha {\mu }_5\right)\le \alpha \left({\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4,{\mu }_5\right).$$

(3)

$\sigma$ is a non-decreasing function, i.e., ${\mu }_i,{\omega }_i\in R^{+},{\mu }_i\le {\omega }_i,i=1,2,\dots ,5,$ we obtain

$$\sigma \left({\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4,{\mu }_5\right)\le \alpha \left({\omega }_1,{\omega }_2,{\omega }_3,{\omega }_4,{\omega }_5\right)$$

and if ${\mu }_i,{\omega }_i\in R^{+},i=1,2,3,4,$ then

$$\sigma \left({\mu }_1,{\mu }_2,{\mu }_3,{\mu }_4,0\right)\le \alpha \left({\omega }_1,{\omega }_2,{\omega }_3,{\omega }_4,0\right)$$

and

$$\sigma \left({\mu }_1,{\mu }_2,{\mu }_3,0,{\mu }_4\right)\le \alpha \left({\omega }_1,{\omega }_2,{\omega }_3,0,{\omega }_4\right).$$

Lemma 6

[20]. If $\sigma \in P$ and $\mu ,\omega \in R^{+}$ are such that

$$\mu <max\left\{\begin{array}{c}\sigma \left(\omega ,\omega ,\mu ,\omega +\mu ,0\right),\sigma \left(\omega ,\omega ,\mu ,0,\omega +\mu \right),\sigma \left(\omega ,\mu ,\omega ,\omega +\mu ,0\right)\\ ,\sigma \left(\omega ,\mu ,\omega ,0,\omega +\mu \right)\end{array}\right\},$$

then $\mu <\omega$.

3. Results

This section deals with our investigations regarding the existence of L-fuzzy common fixed points via F-contractions in the environment of complete b-MSs. Moreover, the results are supported with an example. A few corollaries are assembled to generalize our results.

Theorem 2.

Suppose that $\left(\Psi ,d,s\right)$ is a complete b-MS with coefficient $s\ge 1$ and $T_1 , T_2:\Psi \to {ℱ}_L\left(\Psi \right)$ are two L-FMs, and for each $x,y\in \Omega , there are {\alpha }_{L{T}_1\left(x\right)} and {\alpha }_{L{T}_2\left(y\right)}\in L\backslash \left\{0_L\right\}$, such that${\left[T_{1}x\right]}_{{\alpha }_{L{T}_1\left(x\right)}} and {\left[T_{2}y\right]}_{{\alpha }_{L{T}_2\left(y\right)}}\in CB\left(\Psi \right).$Assume that there are $F\in F_s , a$ constant$e>0$, and$\sigma \in P$, such that

$$2e+F\left(sH\left({\left[T_{1}x\right]}_{{\alpha }_{L{T}_1\left(x\right)}}, {\left[T_{2}y\right]}_{{\alpha }_{L{T}_2\left(y\right)}}\right)\right)\le F\left(\sigma \left(\begin{array}{c}d\left(x,y\right),d\left(x,{\left[T_{1}x\right]}_{{\alpha }_{L{T}_1\left(x\right)}}\right),d\left(y,{\left[T_{2}y\right]}_{{\alpha }_{L{T}_2\left(y\right)}}\right),d\left(x,{\left[T_{2}y\right]}_{{\alpha }_{L{T}_2\left(y\right)}}\right),\\ d\left(y,{\left[T_{1}x\right]}_{{\alpha }_{L{T}_1\left(x\right)}}\right)\end{array}\right)\right),$$

(1)

for all $x,y\in \mathsf{\Psi }$ with $H\left({\left[T_{1}x\right]}_{{\alpha }_{L{T}_1\left(x\right)}},{\left[T_{2}y\right]}_{{\alpha }_{L{T}_2\left(y\right)}}\right)>0$. Then, there is$x^{*}\in \mathsf{\Psi }$ such that $x^{*}\in {\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}{{\displaystyle \cap }}^{}{\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}.}$

Proof. 

Let$x_o\in \Psi ;$then, by hypothesis, there exists${\alpha }_{L{T}_{1\left(x_o\right)}}\in L$, such that${\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}}\in CB\left(\Psi \right).$Let$x_1\in {\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}}.$For this$x_1, \exists {\alpha }_{L{T}_{2\left(x_1\right)}}\in L$, such that${\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\in CB\left(\Psi \right).$As,  □

$$d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\le H\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}} , {\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),$$

Then

$$\mathrm{F}\left(d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)\le F\left(H\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}} , {\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)$$

That is,

$$2e+\mathrm{F}\left(d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)\le 2e+F\left(H\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}}, {\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right),$$

and so

$$2e+\mathrm{F}\left(d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)\le 2e+F\left(sH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}} , {\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right),$$

$\mathrm{where}s\ge 1$. Inequality (1) implies that

$$\begin{gathered} 2e+\mathrm{F}\left(d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right) \le F\left(\sigma \left(\begin{array}{c}d\left(x_o,x_1\right),d\left(x_o,{\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}}\right),d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),d\left(x_o,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\\ ,d\left(x_1,{\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}}\right)\end{array}\right)\right) \\ \le F\left(\sigma \left(d\left(x_o,x_1\right),d\left(x_o,x_1\right),d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),d\left(x_o,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),0\right)\right). \end{gathered}$$

Thus,

$$2e+\mathrm{F}\left(d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)\le F\left(\sigma \left(d\left(x_o,x_1\right),d\left(x_o,x_1\right),d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),d\left(x_o,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),0\right)\right).$$

(2)

Since$F$ is strictly increasing, it implies that

$$d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)<\sigma \left(d\left(x_o,x_1\right),d\left(x_o,x_1\right),d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),d\left(x_o,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),0\right).$$

By Lemma 6,

$$d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)<d\left(x_o,x_1\right).$$

(3)

By using (3) along with inequality (2),

$$2e+F\left(sH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)\le F\left(\sigma \left(d\left(x_o,x_1\right),d\left(x_o,x_1\right),d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),d\left(x_o,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),0\right)\right).$$

By using triangle inequality,

$$\begin{gathered} 2e+F\left(sH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right) \\ \le F\left(\sigma \left(d\left(x_o,x_1\right),d\left(x_o,x_1\right),d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),d\left(x_o,x_1\right)+d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),0\right)\right). \end{gathered}$$

By (3), we have

$$\begin{gathered} 2e+F\left(sH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)\le F\left(\sigma \left(d\left(x_o,x_1\right),d\left(x_o,x_1\right),d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),d\left(x_o,x_1\right)+d\left(x_o,x_1\right),0\right)\right) \\ \le F\left(\sigma \left(d\left(x_o,x_1\right),d\left(x_o,x_1\right),d\left(x_1,x_o\right),2d\left(x_o,x_1\right),0\right)\right) \\ \le F\left(d\left(x_o,x_1\right)\sigma \left(1,1,1,2,0\right)\right). \end{gathered}$$

Since$F$ is strictly increasing and $\sigma \in (0,1]$, it implies that

$$2e+F\left(sH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)\le F\left(d\left(x_o,x_1\right)\right).$$

(4)

Since $F\in F_s,$ there is $h>1$, such that

$$F\left(hsH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)<F\left(sH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)+e.$$

(5)

$$d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)<hH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),$$

there exists$x_2\in {\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}$ (obviously $x_1\ne x_2$) such that

$$d\left(x_1,x_2\right)\le hH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right).$$

Thus, we have

$$F\left(sd\left(x_1,x_2\right)\right)\le F\left(hsH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)$$

$$<F\left(sH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)+e.$$

Hence,

$$F\left(sd\left(x_1,x_2\right)\right)<F\left(sH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)+e.$$

Thus,

$$2e+F\left(sd\left(x_1,x_2\right)\right)<2e+F\left(sH\left({\left[T_1{x}_o\right]}_{{\alpha }_{L{T}_1\left(x_o\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)+e.$$

By (4), one obtains

$$2e+F\left(sd\left(x_1,x_2\right)\right)\le F\left(d\left(x_o,x_1\right)\right)+e,$$

and so

$$e+F\left(sd\left(x_1,x_2\right)\right)\le F\left(d\left(x_o,x_1\right)\right).$$

(6)

For this $x_2,\exists {\alpha }_{L{T}_{1\left(x_2\right)}}\in L$ such that ${\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\in CB\left(\mathsf{\Psi }\right).$ Since we have,

$$\begin{gathered} 2e+\mathrm{F}\left(d\left(x_2,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\right)\le 2e+\mathrm{F}\left(H\left({\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right), \\ 2e+\mathrm{F}\left(d\left(x_2,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\right)\le 2e+\mathrm{F}\left(sH\left({\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right), \mathrm{where}s\ge 1. \end{gathered}$$

By (1),

$$\begin{gathered} 2e+\mathrm{F}\left(d\left(x_2,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\right)\le F\left(\sigma \left(\begin{array}{c}d\left(x_2,x_1\right),d\left(x_2,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right),d\left(x_1,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right),d\left(x_2,{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\\ ,d\left(x_1,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\end{array}\right)\right) \\ \le F\left(\sigma \left(d\left(x_2,x_1\right),d\left(x_2,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right),d\left(x_1,x_2\right),0,d\left(x_1,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\right)\right). \end{gathered}$$

Thus,

$$d\left(x_2,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)<\sigma \left(d\left(x_2,x_1\right),d\left(x_2,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right),d\left(x_1,x_2\right),0,d\left(x_1,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\right).$$

By Lemma 6,

$$d\left(x_2,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)<d\left(x_1,x_2\right).$$

(7)

By using (1) and (7), we obtain

$$\begin{gathered} 2e+\mathrm{F}\left(sH\left({\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)\le F\left(\sigma \left(d\left(x_2,x_1\right),d\left(x_2,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right),d\left(x_1,x_2\right),0,d\left(x_1,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\right)\right) \\ \le F\left(\sigma \left(d\left(x_1,x_2\right),d\left(x_1,x_2\right),d\left(x_1,x_2\right),0,2d\left(x_1,x_2\right)\right)\right) \\ \le F\left(d\left(x_1,x_2\right)\sigma \left(1,1,1,0,2\right)\right)\le F\left(d\left(x_1,x_2\right)\right). \end{gathered}$$

(8)

Since $F\in F_s,$ there is$h>1$, such that

$$F\left(hsH\left({\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}},{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\right)<F\left(sH\left({\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}},{\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}}\right)\right)+e.$$

(9)

$$d\left(x_2,{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_{1\left(x_2\right)}}}\right)<hH\left({\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}},{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right),$$

we deduce that there exists$x_3\in {\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}$ (obviously $x_3\ne x_2$), such that

$$d\left(x_2,x_3\right)\le hH\left({\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}},{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right).$$

Thus, we have

$$\begin{gathered} F\left(sd\left(x_2,x_3\right)\right)\le F\left(hsH\left({\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}},{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\right) \\ <F\left(sH\left({\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}},{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\right)+e. \end{gathered}$$

Consequently,

$$\begin{gathered} F\left(sd\left(x_2,x_3\right)\right)<F\left(sH\left({\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}},{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\right)+e, \\ 2e+F\left(sd\left(x_2,x_3\right)\right)<2e+F\left(sH\left({\left[T_2{x}_1\right]}_{{\alpha }_{L{T}_2\left(x_1\right)}},{\left[T_1{x}_2\right]}_{{\alpha }_{L{T}_1\left(x_2\right)}}\right)\right)+e. \end{gathered}$$

By $\left(8\right)$, $2e+F\left(sd\left(x_2,x_3\right)\right)\le F\left(d\left(x_1,x_2\right)\right)+e,$ which implies that

$$e+F\left(sd\left(x_2,x_3\right)\right)\le F\left(d\left(x_1,x_2\right)\right).$$

(10)

Thus, pursuing in this way, we obtain a sequence$\left\{x_n\right\}$ in$\Omega ,$such that

$$x_{2n+1}\in {\left[T_1{x}_{2n}\right]}_{{\alpha }_{L{T}_1\left(x_{2n}\right)}},x_{2n+2}\in {\left[T_2{x}_{2n+1}\right]}_{{\alpha }_{L{T}_2\left(x_{2n+1}\right)}}$$

with

$$e+F\left(sd\left(x_{2n+1},x_{2n+2}\right)\right)\le F\left(d\left(x_{2n},x_{2n+1}\right)\right),$$

(11)

and

$$e+F\left(sd\left(x_{2n+2},x_{2n+3}\right)\right)\le F\left(d\left(x_{2n+1},x_{2n+2}\right)\right),$$

(12)

for all$n\in \mathbb{N}.$By $\left(11\right)$ and $\left(12\right)$, we obtain

$$e+F\left(sd\left(x_n,x_{n+1}\right)\right)\le F\left(d\left(x_{n-1},x_n\right)\right),$$

(13)

for all$n\in \mathbb{N}. \mathrm{By} \left(13\right)$ and the fourth property of $F$-contractions,

$$e+F\left(s^{n}d\left(x_n,x_{n+1}\right)\right)\le F\left(s^{n-1}d\left(x_{n-1},x_n\right)\right).$$

(14)

Thus, by $\left(14\right)$, we obtain

$$F\left(s^{n}d\left(x_n,x_{n+1}\right)\right)\le F\left(s^{n-1}d\left(x_{n-1},x_n\right)\right)-e,$$

$$F\left(s^{n}d\left(x_n,x_{n+1}\right)\right)\le F\left(s^{n-2}d\left(x_{n-1},x_n\right)\right)-2e,$$

$$F\left(s^{n}d\left(x_n,x_{n+1}\right)\right)\le F\left(d\left(x_o,x_1\right)\right)-ne.$$

(15)

Taking $n\to \infty$, we obtain $\underset{n\to \infty }{\lim }F\left(s^{n}d\left(x_n,x_{n+1}\right)\right)\le -\infty .$

By the second property of $F$-contractions, $\underset{n\to \infty }{\lim }F\left(s^{n}d\left(x_n,x_{n+1}\right)\right)=0.$

By the third property of F-contractions, there is$r\in \left(0,1\right),$ so that $\underset{n\to \infty }{\lim }{\left(s^{n}d\left(x_n,x_{n+1}\right)\right)}^{r}F\left(s^{n}d\left(x_n,x_{n+1}\right)\right)=0$. From $\left(15\right)$, we have

$$\begin{gathered} {\left(s^{n}d\left(x_n,x_{n+1}\right)\right)}^{r}F\left(s^{n}d\left(x_n,x_{n+1}\right)\right)-{\left(s^{n}d\left(x_n,x_{n+1}\right)\right)}^{r}F\left(d\left(x_o,x_1\right)\right) \\ \le {\left(s^{n}d\left(x_n,x_{n+1}\right)\right)}^{r}F\left(d\left(x_o,x_1\right)-ne\right)-{\left(s^{n}d\left(x_n,x_{n+1}\right)\right)}^{r}F\left(d\left(x_o,x_1\right)\right) \\ \le -ne{\left(s^{n}d\left(x_n,x_{n+1}\right)\right)}^r\le 0. \end{gathered}$$

Taking $n\to \infty$ in the above inequality, we obtain

$$\underset{n\to \infty }{\lim }n{\left(s^{n}d\left(x_n,x_{n+1}\right)\right)}^r=0.$$

(16)

Hence, $\underset{n\to \infty }{\lim }{n}^{\frac{1}{r}}{s}^{n}d\left(x_n,x_{n+1}\right)=0$.

Now, the last limit implies that the series ${\displaystyle \sum }_{n=1}^{\infty }{s}^{n}d\left(x_n,x_{n+1}\right)$ is convergent.

Thus,$\left\{x_n\right\}$ is a Cauchy sequence in$\mathsf{\Psi }.$ Since$\left(\mathsf{\Psi },d,s\right)$ is a complete b-metric space, there exists $x^{*}\in \mathsf{\Psi }$, such that

$$\underset{n\to \infty }{\lim }{x}_n=x^{*}.$$

(17)

Now, we prove that $x^{*}\in {\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}.$ We assume, on the contrary, that $x^{*}$ does not belong to ${\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}$. By (17), there are $n_o\in \mathbb{N}$ and $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$, such that $d\left(x_{2n_k+2},{\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}\right)>0,\forall n_k\ge n_o.$Now, using $\left(1\right)$ with $x=x_{2n_k+2}$ and $y=x^{*},$ we obtain

$$2e+\mathrm{F}\left(d\left(x_{2n_k+2},{\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}\right)\right)\le 2e+F\left(sH\left({\left[T_2{x}_{2n_k+1}\right]}_{{\alpha }_{L{T}_2\left(x_{2n_k+1}\right)}} , {\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}\right)\right)$$

$$\le F\left(\sigma \left(\begin{array}{c}d\left(x_{2n_k+2},x^{*}\right),d\left(x_{2n_k+1},{\left[T_1{x}_{2n_k+1}\right]}_{{\alpha }_{L{T}_1\left(x_{2n_k+1}\right)}}\right),d\left(x^{*},{\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}\right),\\ d\left(x_{2n_k+1},{\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}\right),d\left(x^{*},{\left[T_2{x}_{2n_k+1}\right]}_{{\alpha }_{L{T}_2\left(x_{2n_k+1}\right)}}\right)\end{array}\right)\right).$$

As $e>0,$ by the first property of $F$-contractions, we obtain

$$d\left(x_{2n_k+2},{\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}\right)<\sigma \left(\begin{array}{c}d\left(x_{2n_k+2},x^{*}\right),d\left(x_{2n_k+1},{\left[T_1{x}_{2n_k+1}\right]}_{{\alpha }_{L{T}_1\left(x_{2n_k+1}\right)}}\right),d\left(x^{*},{\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}\right),\\ d\left(x_{2n_k+1},{\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}\right),d\left(x^{*},{\left[T_2{x}_{2n_k+1}\right]}_{{\alpha }_{L{T}_2\left(x_{2n_k+1}\right)}}\right)\end{array}\right).$$

Letting $n\to \infty$ in the above expression, we have $d\left(x^{*},{\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}\right)\le 0$.

Hence,

$$x^{*}\in {\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}}.$$

(18)

Now, we prove that $x^{*}\in {\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}.$ We assume, on the contrary, that $x^{*}$ does not belong to ${\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}$. By $\left(17\right)$, there are $n_o\in \mathbb{N}$ and $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$, such that $d\left(x_{2n_k+1},{\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}\right)>0,\forall n_k\ge n_o.$ Now, using $\left(1\right)$ with $x=x_{2n_k+1}$ and $y=x^{*},$ we obtain

$$2e+\mathrm{F}\left(d\left(x_{2n_k+1},{\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}\right)\right)\le 2e+F\left(sH\left({\left[T_1{x}_{2n_k}\right]}_{{\alpha }_{L{T}_1\left(x_{2n_k}\right)}} , {\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}\right)\right)$$

$$\le F\left(\sigma \left(\begin{array}{c}d\left(x_{2n_k},x^{*}\right),d\left(x_{2n_k},{\left[T_1{x}_{2n_k}\right]}_{{\alpha }_{L{T}_1\left(x_{2n_k}\right)}}\right),d\left(x^{*},{\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}\right),\\ d\left(x_{2n_k},{\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}\right),d\left(x^{*},{\left[T_1{x}_{2n_k}\right]}_{{\alpha }_{L{T}_1\left(x_{2n_k}\right)}}\right)\end{array}\right)\right).$$

As $e>0,$ by the first property of $\mathrm{F}$-contractions, we obtain

$$d\left(x_{2n_k+1},{\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}\right)<\sigma \left(\begin{array}{c}d\left(x_{2n_k},x^{*}\right),d\left(x_{2n_k},{\left[T_1{x}_{2n_k}\right]}_{{\alpha }_{L{T}_1\left(x_{2n_k}\right)}}\right),d\left(x^{*},{\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}\right),\\ d\left(x_{2n_k},{\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}\right),d\left(x^{*},{\left[T_1{x}_{2n_k}\right]}_{{\alpha }_{L{T}_1\left(x_{2n_k}\right)}}\right)\end{array}\right).$$

Letting $n\to \infty$ in the above expression, we have $d\left(x^{*},{\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}\right)\le 0$.

Hence,

$$x^{*}\in {\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2}\left(x^{*}\right)}.$$

(19)

By (18) and (19), $x^{*}\in {\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1}\left(x^{*}\right)}{{\displaystyle \cap }}^{}{\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2}\left(x^{*}\right).}$

Example. 

Let$\Psi =\left\{0,1,2\right\}$and define the metric$d:\Psi \times \Psi \to R^{+}{{\displaystyle \cup }}^{}\left\{0\right\}$by

$$d\left(\mathsf{\omega },\mathsf{\mu }\right)=\{\begin{array}{c}\begin{array}{c}0 , if \mathsf{\omega }=\mathsf{\mu }\\ \frac{1}{4} ,if \mathsf{\omega }\ne \mathsf{\mu } and \mathsf{\omega },\mathsf{\mu }\in \left\{0,1\right\}\end{array}\\ \begin{array}{c}\frac{25}{33} ,if \mathsf{\omega }\ne \mathsf{\mu } and \mathsf{\omega },\mathsf{\mu }\in \left\{0,2\right\}\\ 1 ,if \mathsf{\omega }\ne \mathsf{\mu } and \mathsf{\omega },\mathsf{\mu }\in \left\{1,2\right\}\end{array}\end{array}.$$

Note that $\left(\mathsf{\Psi }, d, s\right)$ is a complete b-metric space with coefficient $s=\frac{3}{2}$.

Define $T_1:\mathsf{\Psi }\to {ℱ}_L\left(\mathsf{\Psi }\right)$ by

$$\left(T_{1}0\right)\left(t\right)=\left(T_{1}1\right)\left(t\right)=\{\begin{array}{c}5 if t=0 \\ 1 if t=1,2\end{array}$$

$$\left(T_{1}2\right)\left(t\right)=\{\begin{array}{c}1 if t=0,2 \\ 5 if t=1 \end{array}$$

Define ${\alpha }_{T_1}:\mathsf{\Psi }\to L=\left[1, 10\right]$ by ${\alpha }_{T_1}\left(\mathsf{\omega }\right)=5,$ for all $\mathsf{\omega }\in \mathsf{\Psi }.$ Now, we obtain that

$${\left[T_1\mathsf{\omega }\right]}_5=\{\begin{array}{c}\left\{0\right\} , if \omega =0,1 \\ \left\{1\right\} , if \omega =2 \end{array}.$$

Define $T_2:\mathsf{\Psi }\to {ℱ}_L\left(\mathsf{\Psi }\right)$ by

$$\begin{gathered} \left(T_{2}0\right)\left(t\right)=\{\begin{array}{c}4 , if t=0 \\ 2 , if t=1,2\end{array} \\ \left(T_{2}1\right)\left(t\right)=\{\begin{array}{c}3 , if t=1,2 \\ 4 , if t=0 \end{array} \\ \left(T_{2}2\right)\left(t\right)=\{\begin{array}{c}4 , if t=1 \\ 1 , if t=0,2\end{array}. \end{gathered}$$

Define ${\alpha }_{T_2}:\mathsf{\Psi }\to L=\left[1, 10\right]$ by ${\alpha }_{T_2}\left(\mathsf{\omega }\right)=4,$ for all $\mathsf{\omega }\in \mathsf{\Psi }.$ Now, we obtain that

$${\left[T_2\mathsf{\omega }\right]}_4=\{\begin{array}{c}\left\{0\right\} , if \omega =0,1 \\ \left\{1\right\} , if \omega =2 \end{array}.$$

For $\mathsf{\omega },\mathsf{\mu }\in \mathsf{\Psi },$ we obtain

$$\begin{gathered} H\left({\left[T_{1}0\right]}_5,{\left[T_{2}0\right]}_4\right)=H\left(\left\{0\right\},\left\{0\right\}\right)=0; \\ H\left({\left[T_{1}0\right]}_5,{\left[T_{2}1\right]}_4\right)=H\left(\left\{0\right\},\left\{0\right\}\right)=0; \\ H\left({\left[T_{1}0\right]}_5,{\left[T_{2}2\right]}_4\right)=H\left(\left\{0\right\},\left\{1\right\}\right)=\frac{1}{4}; \\ H\left({\left[T_{1}1\right]}_5,{\left[T_{2}0\right]}_4\right)=H\left(\left\{0\right\},\left\{0\right\}\right)=0; \\ H\left({\left[T_{1}1\right]}_5,{\left[T_{2}1\right]}_4\right)=H\left(\left\{0\right\},\left\{0\right\}\right)=0; \\ H\left({\left[T_{1}1\right]}_5,{\left[T_{2}2\right]}_4\right)=H\left(\left\{0\right\},\left\{1\right\}\right)=\frac{1}{4}; \\ H\left({\left[T_{1}2\right]}_5,{\left[T_{2}0\right]}_4\right)=H\left(\left\{1\right\},\left\{0\right\}\right)=\frac{1}{4}; \\ H\left({\left[T_{1}2\right]}_5,{\left[T_{2}1\right]}_4\right)=H\left(\left\{1\right\},\left\{0\right\}\right)=\frac{1}{4}; \\ H\left({\left[T_{1}2\right]}_5,{\left[T_{2}2\right]}_4\right)=H\left(\left\{1\right\},\left\{1\right\}\right)=0. \end{gathered}$$

We only considered a non-zero Hausdorff distance. Thus, for $\mathsf{\omega },\mathsf{\mu }\in \mathsf{\Psi },$ we obtain

$$H\left({\left[T_{1}0\right]}_5,{\left[T_{2}2\right]}_4\right)=H\left({\left[T_{1}1\right]}_5,{\left[T_{2}2\right]}_4\right)=H\left(\left\{0\right\},\left\{1\right\}\right)=\frac{1}{4}.$$

Taking $F\left(\vartheta \right)=\vartheta +\ln \vartheta ,$for $\vartheta >0$ and $e=\frac{101}{528}>0,$ then

$$2e+F\left(sH\left({\left[T_{1}0\right]}_5,{\left[T_{2}2\right]}_4\right)\right)=\frac{101}{264}+\frac{3}{8}+\ln \left(\frac{25}{33}·\frac{99}{200}\right)\le \frac{25}{33}+\ln \frac{25}{33}=F\left(d\left(0,2\right)\right).$$

Furthermore,

$$\begin{gathered} 2e+F\left(sH\left({\left[T_{1}1\right]}_5,{\left[T_{2}2\right]}_4\right)\right)=\frac{101}{264}+\frac{3}{8}+\ln \left(\frac{25}{33}·\frac{99}{200}\right)\le \frac{25}{33}+\ln \frac{25}{33} \\ =F\left(d\left(1,2\right)\right). \end{gathered}$$

Thus, all the assumptions of Theorem 2 hold by considering $\sigma \in P$ as $\sigma \left({\mathsf{\omega }}_1,{\mathsf{\omega }}_2,{\mathsf{\omega }}_3,{\mathsf{\omega }}_4,{\mathsf{\omega }}_5\right)={\mathsf{\omega }}_1$. Here, $0\in \Omega$ and $0\in {\left[T_{1}0\right]}_5\cap {\left[T_{2}0\right]}_4$ is an ${\alpha }_L$-common fuzzy fixed point of $T_1$ and $T_2$.

Corollary 1.

Let$\left(\Psi ,d\right)$be a complete MS and$T_1, T_2:\Psi \to {ℱ}_L\left(\Psi \right)$be two$L$-FMs, and for each$x,y\in \Psi , there are {\alpha }_{L{T}_1\left(x\right)} and {\alpha }_{L{T}_2\left(y\right)}\in L\backslash \left\{0_L\right\}$, such that${\left[T_{1}x\right]}_{{\alpha }_{L{T}_1\left(x\right)}} and {\left[T_{2}y\right]}_{{\alpha }_{L{T}_2\left(y\right)}}\in CB\left(\Psi \right).$Assume that there are$F\in F_s , a$constant$e>0$, and$\sigma \in P$, such that

$$\begin{array}{c}2e+F\left(sH\left({\left[T_{1}x\right]}_{{\alpha }_{L{T}_1\left(x\right)}} , {\left[T_{2}y\right]}_{{\alpha }_{L{T}_2\left(y\right)}}\right)\right)\hfill \\ \le F\left(\sigma \left(d\left(x,y\right),d\left(x,{\left[T_{1}x\right]}_{{\alpha }_{L{T}_1\left(x\right)}}\right),d\left(y,{\left[T_{2}y\right]}_{{\alpha }_{L{T}_2\left(y\right)}}\right),d\left(x,{\left[T_{2}y\right]}_{{\alpha }_{L{T}_2\left(y\right)}}\right),d\left(y,{\left[T_{1}x\right]}_{{\alpha }_{L{T}_1\left(x\right)}}\right)\right)\right),\end{array}$$

for all $x,y\in \mathsf{\Psi }$ with $H\left({\left[T_{1}x\right]}_{{\alpha }_{L{T}_1\left(x\right)}},{\left[T_{2}y\right]}_{{\alpha }_{L{T}_2\left(y\right)}}\right)>0$. Then, there is$x^{*}\in \mathsf{\Psi }$, such that $x^{*}\in {\left[T_1{x}^{*}\right]}_{{\alpha }_{L{T}_1\left(x^{*}\right)}} {{\displaystyle \cap }}^{} {\left[T_2{x}^{*}\right]}_{{\alpha }_{L{T}_2\left(x^{*}\right)}}$.

Corollary 2.

Let$\left(\Psi ,d,s\right)$be a complete b-MS with coefficient$s\ge 1$and$T_1 , T_2:\Psi \to ℱ\left(\Psi \right)$be two FMs, and for each$x,y\in \Psi , there are {\alpha }_{T_1\left(x\right)} and {\alpha }_{T_2\left(y\right)}\in (0, 1],$such that${\left[T_{1}x\right]}_{{\alpha }_{T_1\left(x\right)}} and {\left[T_{2}y\right]}_{{\alpha }_{T_2\left(y\right)}}\in CB\left(\Psi \right).$ Assume that there are$F\in F_s ,$a constant$e>0$, and$\sigma \in P$, such that

$$2e+F\left(sH\left({\left[T_{1}x\right]}_{{\alpha }_{T_1\left(x\right)}}, {\left[T_{2}y\right]}_{{\alpha }_{T_2\left(y\right)}}\right)\right)\le F\left(\sigma \left(\begin{array}{c}d\left(x,y\right),d\left(x,{\left[T_{1}x\right]}_{{\alpha }_{T_1\left(x\right)}}\right),d\left(y,{\left[T_{2}y\right]}_{{\alpha }_{T_2\left(y\right)}}\right),d\left(x,{\left[T_{2}y\right]}_{{\alpha }_{T_2\left(y\right)}}\right),\\ d\left(y,{\left[T_{1}x\right]}_{{\alpha }_{T_1\left(x\right)}}\right)\end{array}\right)\right),$$

for all $x,y\in \mathsf{\Psi }$ with $H\left({\left[T_{1}x\right]}_{{\alpha }_{T_1\left(x\right)}},{\left[T_{2}y\right]}_{{\alpha }_{T_2\left(y\right)}}\right)>0$. Then, there is $x^{*}\in \mathsf{\Psi }$, such that $x^{*}\in {\left[T_1{x}^{*}\right]}_{{\alpha }_{T_1\left(x^{*}\right)}} {{\displaystyle \cap }}^{} {\left[T_2{x}^{*}\right]}_{{\alpha }_{T_2\left(x^{*}\right)}.}$.

Theorem 3.

Let$\left(\Psi ,d,s\right)$be a complete b-MS with coefficient$s\ge 1$and$T:\Psi \to {ℱ}_L\left(\Psi \right)$, and for each$x,y\in \Psi , there are {\alpha }_{LT\left(x\right)} and {\alpha }_{LT\left(y\right)}\in L\backslash \left\{0_L\right\}$, such that${\left[Tx\right]}_{{\alpha }_{LT\left(x\right)}} and {\left[Ty\right]}_{{\alpha }_{LT\left(y\right)}}\in CB\left(\Psi \right).$Assume that there are$F\in F_s ,$a constant$e>0$, and$\sigma \in P$, such that

$$\begin{gathered} 2e+F\left(sH\left({\left[Tx\right]}_{{\alpha }_{LT\left(x\right)}} , {\left[Ty\right]}_{{\alpha }_{LT\left(y\right)}}\right)\right) \\ \le F\left(\sigma \left(d\left(x,y\right),d\left(x,{\left[Tx\right]}_{{\alpha }_{LT\left(x\right)}}\right),d\left(y,{\left[Ty\right]}_{{\alpha }_{LT\left(y\right)}}\right),d\left(x,{\left[Ty\right]}_{{\alpha }_{LT\left(y\right)}}\right),d\left(y,{\left[Tx\right]}_{{\alpha }_{LT\left(x\right)}}\right)\right)\right), \end{gathered}$$

for all with $H\left({\left[Tx\right]}_{{\alpha }_{LT\left(x\right)}},{\left[Ty\right]}_{{\alpha }_{LT\left(y\right)}}\right)>0$. Then, there is $x^{*}\in \mathsf{\Psi },$such that

$$x^{*}\in {\left[T{x}^{*}\right]}_{{\alpha }_{LT\left(x^{*}\right)}}.$$

Proof. 

By replacing T₁ = T₂ = T in Theorem 2, the required result will be obtained. □

Corollary 3.

Let$\left(\Psi ,d\right)$be a complete MS and let$T:\Psi \to {ℱ}_L\left(\Psi \right)$be an L-FM, and for each$x,y\in \Psi , there are {\alpha }_{LT\left(x\right)} and {\alpha }_{LT\left(y\right)}\in L\backslash \left\{0_L\right\}$, such that${\left[Tx\right]}_{{\alpha }_{LT\left(x\right)}} and {\left[Ty\right]}_{{\alpha }_{LT\left(y\right)}}\in CB\left(\Psi \right).$Assume that there are$F\in F_s ,$a constant$e>0$, and$\sigma \in P$, such that

$$\begin{gathered} 2e+F\left(sH\left({\left[Tx\right]}_{{\alpha }_{LT\left(x\right)}} , {\left[Ty\right]}_{{\alpha }_{LT\left(y\right)}}\right)\right) \\ \le F\left(\sigma \left(d\left(x,y\right),d\left(x,{\left[Tx\right]}_{{\alpha }_{LT\left(x\right)}}\right),d\left(y,{\left[Ty\right]}_{{\alpha }_{LT\left(y\right)}}\right),d\left(x,{\left[Ty\right]}_{{\alpha }_{LT\left(y\right)}}\right),d\left(y,{\left[Tx\right]}_{{\alpha }_{LT\left(x\right)}}\right)\right)\right), \end{gathered}$$

for all $x,y\in \mathsf{\Psi }$ with $H\left({\left[Tx\right]}_{{\alpha }_{LT\left(x\right)}},{\left[Ty\right]}_{{\alpha }_{LT\left(y\right)}}\right)>0$. Then, there is $x^{*}\in \mathsf{\Psi }$, such that $x^{*}\in {\left[T{x}^{*}\right]}_{{\alpha }_{LT\left(x^{*}\right)}}.$

Corollary 4.

Let$\left(\Psi ,d,s\right)$be a complete b-MS with coefficient$s\ge 1$and let$T:\Psi \to ℱ\left(\Psi \right)$be an FM, and for each$x,y\in \Psi , there are {\alpha }_{T\left(x\right)} and {\alpha }_{T\left(y\right)}\in (0, 1]$, such that${\left[Tx\right]}_{{\alpha }_{T\left(x\right)}} and {\left[Ty\right]}_{{\alpha }_{T\left(y\right)}}\in CB\left(\Psi \right).$Assume that there are$F\in F_s ,$a constant$e>0$, and$\sigma \in P$, such that

$$\begin{gathered} 2e+F\left(sH\left({\left[Tx\right]}_{{\alpha }_{T\left(x\right)}} , {\left[Ty\right]}_{{\alpha }_{T\left(y\right)}}\right)\right) \\ \le F\left(\sigma \left(d\left(x,y\right),d\left(x,{\left[Tx\right]}_{{\alpha }_{T\left(x\right)}}\right),d\left(y,{\left[Ty\right]}_{{\alpha }_{T\left(y\right)}}\right),d\left(x,{\left[Ty\right]}_{{\alpha }_{T\left(y\right)}}\right),d\left(y,{\left[Tx\right]}_{{\alpha }_{T\left(x\right)}}\right)\right)\right), \end{gathered}$$

for all $x,y\in \mathsf{\Psi }$ with $H\left({\left[Tx\right]}_{{\alpha }_{T\left(x\right)}},{\left[Ty\right]}_{{\alpha }_{T\left(y\right)}}\right)>0$. Then, there is $x^{*}\in \mathsf{\Psi }$, such that $x^{*}\in {\left[T{x}^{*}\right]}_{{\alpha }_{T\left(x^{*}\right)}}.$

Corollary 5.

Let$\left(\Psi ,d\right)$be a complete MS and let$T:\Psi \to ℱ\left(\Psi \right)$be an FM, and for each$x,y\in \Psi , there are {\alpha }_{T\left(x\right)} and {\alpha }_{T\left(y\right)}\in (0, 1]$, such that${\left[Tx\right]}_{{\alpha }_{T\left(x\right)}} and {\left[Ty\right]}_{{\alpha }_{T\left(y\right)}}\in CB\left(\Psi \right).$Assume that there are$F\in F_s ,$a constant$e>0$, and$\sigma \in P$, such that

$$\begin{gathered} 2e+F\left(sH\left({\left[Tx\right]}_{{\alpha }_{T\left(x\right)}} , {\left[Ty\right]}_{{\alpha }_{T\left(y\right)}}\right)\right) \\ \le F\left(\sigma \left(d\left(x,y\right),d\left(x,{\left[Tx\right]}_{{\alpha }_{T\left(x\right)}}\right),d\left(y,{\left[Ty\right]}_{{\alpha }_{T\left(y\right)}}\right),d\left(x,{\left[Ty\right]}_{{\alpha }_{T\left(y\right)}}\right),d\left(y,{\left[Tx\right]}_{{\alpha }_{T\left(x\right)}}\right)\right)\right), \end{gathered}$$

for all $x,y\in \mathsf{\Psi }$ with $H\left({\left[Tx\right]}_{{\alpha }_{T\left(x\right)}},{\left[Ty\right]}_{{\alpha }_{T\left(y\right)}}\right)>0$. Then, there is $x^{*}\in \mathsf{\Psi }$, such that $x^{*}\in {\left[T{x}^{*}\right]}_{{\alpha }_{T\left(x^{*}\right)}}.$

4. Discussion

Many problems arising in engineering, economics, and other fields of science are solved by converting them into differential or integral equations. The fixed point technique provides an effective environment in which these functional inclusions can be solved by fixed point methods. In the context of complete b-metric spaces applying F-contractions and a certain class of continuous functions, we develop and illustrate the presence of L-fuzzy common fixed points of L-fuzzy mappings (L-FM) satisfying a contractive criterion. A prime example is also provided to show how our derived concepts are put into practice, as well as the explanation of a few additional ideas that directly follow our findings. b-metric space is a generalized form of a metric space and L-fuzzy mapping is a more general form of fuzzy mapping and multivalued mappings. Thus, our results are helpful for future researchers.

5. Conclusions

In the setting of b-metric spaces, we studied the presence of L-fuzzy common fixed points using F-contractions. Furthermore, the results are backed up by examples. To generalize our result, we assembled a few corollaries.