On the Dynamics of New 4D and 6D Hyperchaotic Systems
Abstract
1. Introduction
2. Mathematical Models
3. Ultimate Bound Set for the New 6D Hyperchaotic System
- When , we can obtain
- and
- or
- and
- When , and , we can obtain
- and .
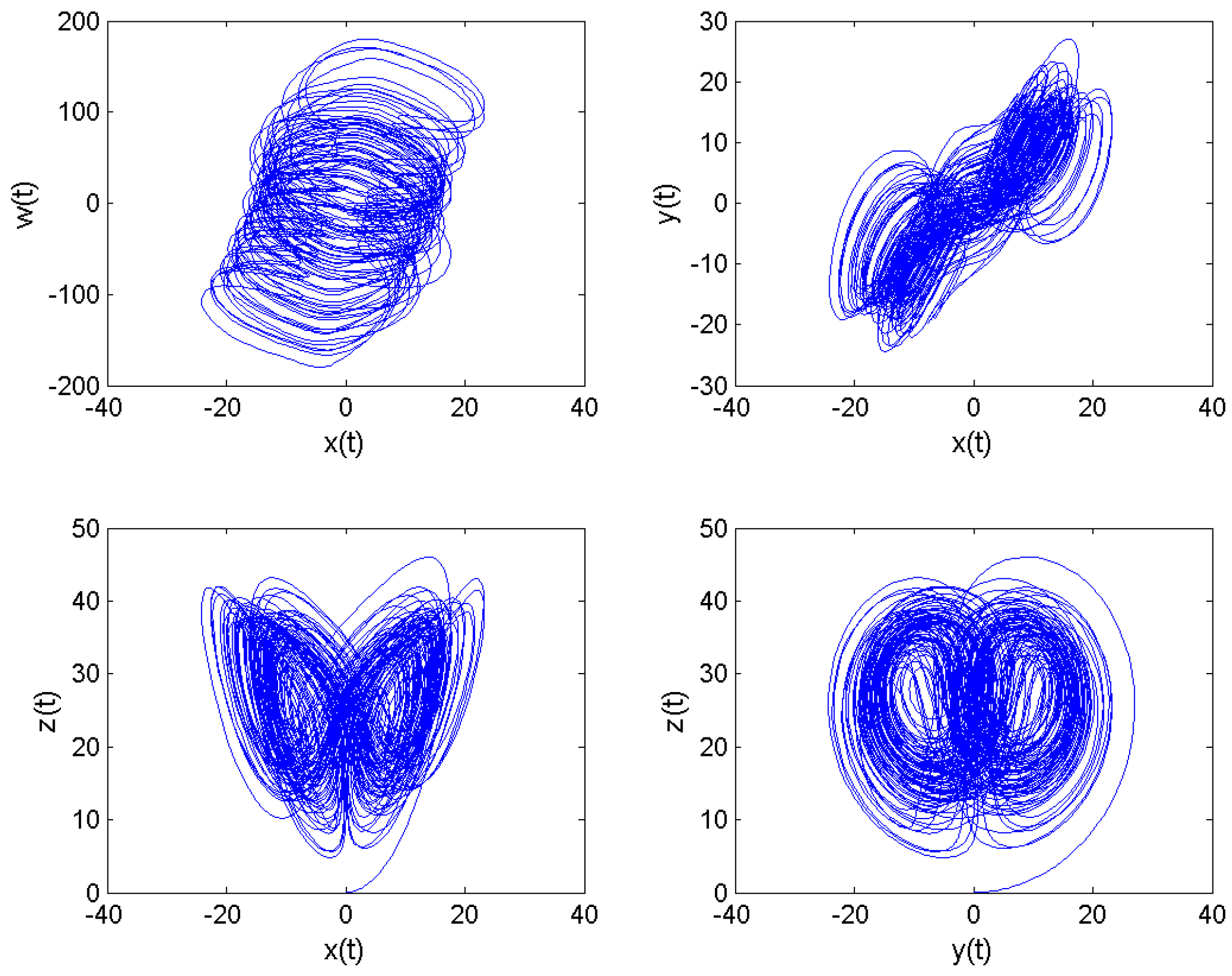
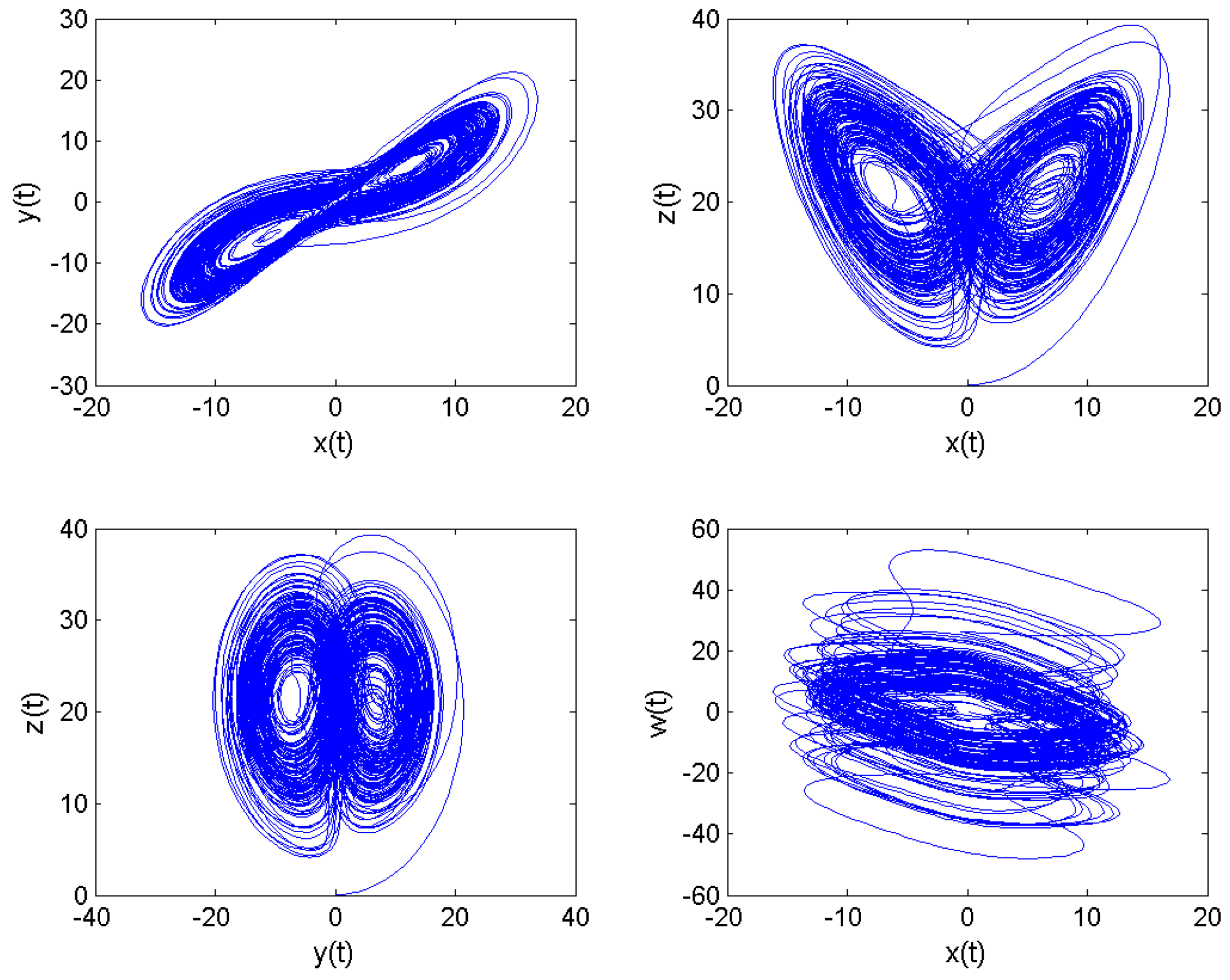
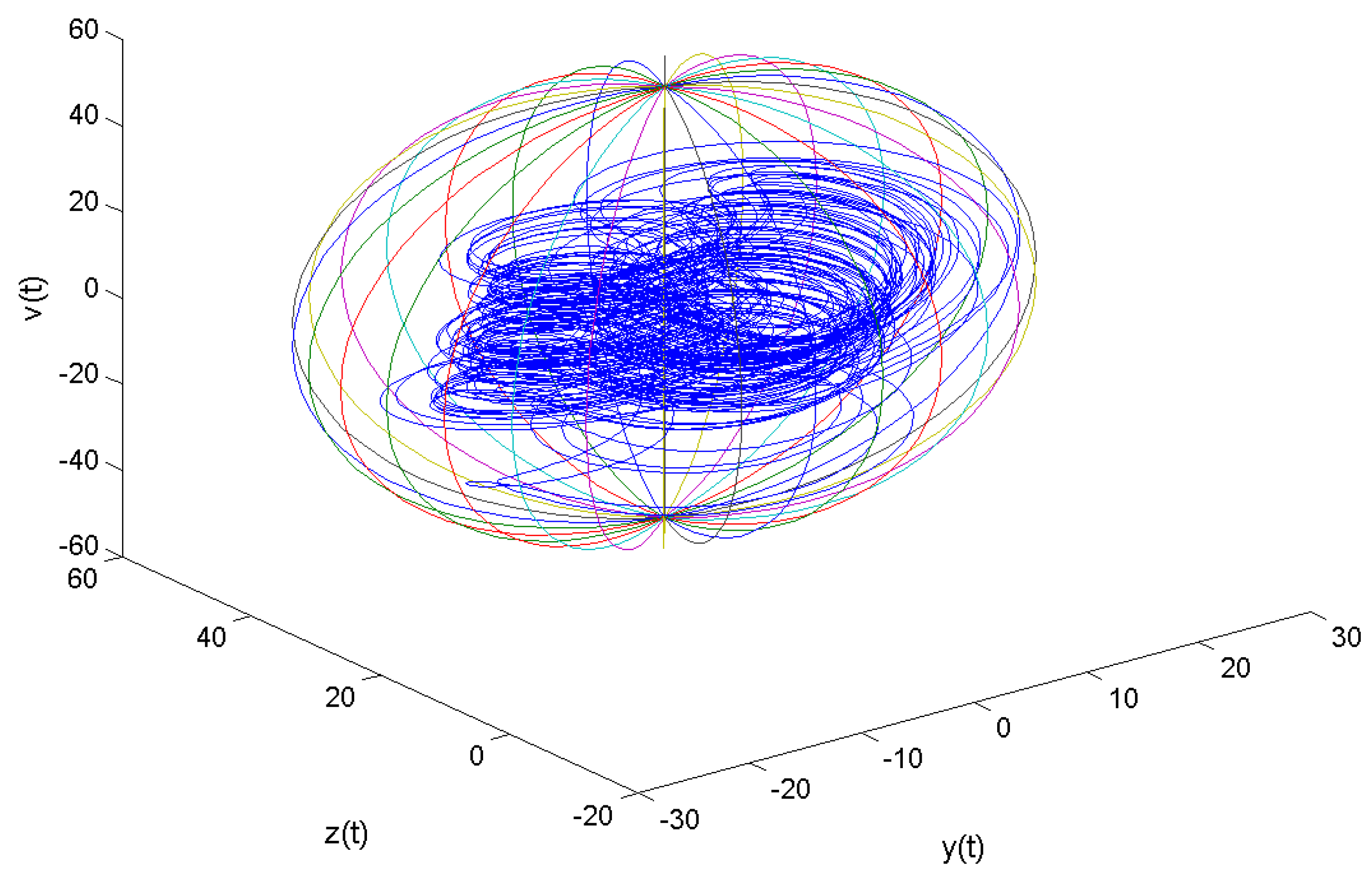
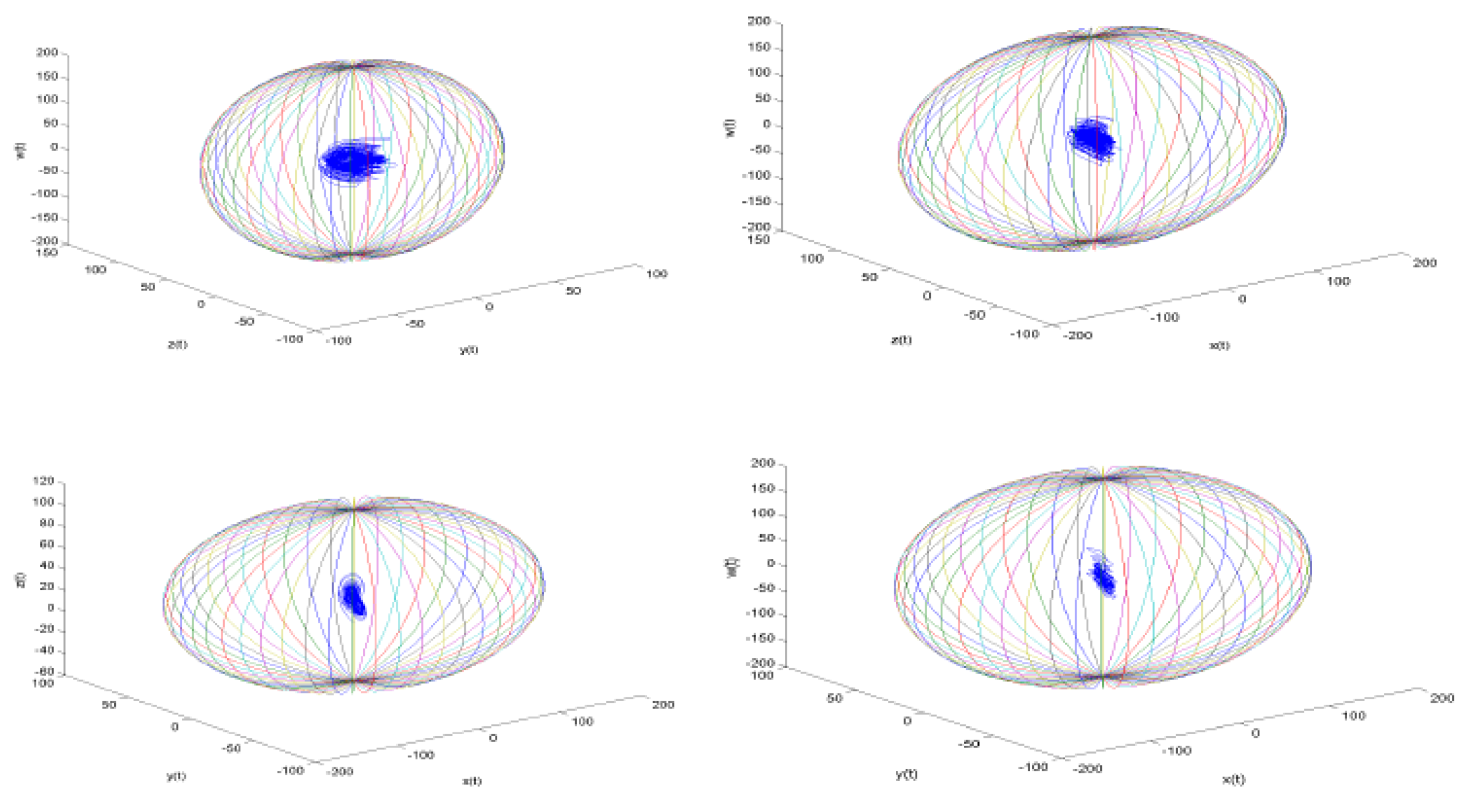
Numerical Simulations
4. The Globally Exponentially Attractive Set for the New 4D Lorenz-Type Hyperchaotic System
Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rössler, O.E. An equation for hyperchaos. Phys. Lett. A 1979, 71, 155–157. [Google Scholar] [CrossRef]
- Udaltsov, V.; Goedgebuer, J.; Larger, L.; Cuenot, J.; Levy, P. Communicating with hyperchaos: The dynamics of a DNLF emitter and recovery of transmitted information. Opt. Spectrosc. 2003, 95, 114–118. [Google Scholar] [CrossRef]
- Cenys, A.; Tamaservicius, A.; Baziliauskas, A.; Krivickas, R.; Lindberg, E. Hyperchaos in coupled Colpitts oscillators. Chaos Solitons Fractals 2003, 17, 349–353. [Google Scholar] [CrossRef]
- Vicente, R.; Daudén, J.; Colet, P.; Toral, R. Analysis and characterization of thehyperchaos generated by a semiconductor laser subject to delayed feedbackloop. IEEE J. Quantum Electron 2005, 41, 541–548. [Google Scholar] [CrossRef]
- Arena, P.; Baglio, S.; Fortuna, L.; Manganaro, G. Hyperchaos from cellularnetworks. Electron. Lett. 1995, 31, 250–251. [Google Scholar] [CrossRef]
- Sixiao, K.; Chunbiao, L.; Shaobo, H.; Serdar, ç.; Qiang, L. A memristive map with coexisting chaos and hyperchaos. Chin. Phys. B 2021, 30, 110502. [Google Scholar]
- Hsieh, J.; Hwang, C.; Wang, A.; Li, W. Controlling hyper-chaos of the Rossler system. Int. J. Control 1999, 72, 882–886. [Google Scholar] [CrossRef]
- Jiang, P.; Wang, B.; Bu, S.; Xia, Q.; Luo, X. Hyperchaotic synchronizationin deterministic small-world dynamical networks. Int. Mod. Phys. B 2004, 18, 2674–2679. [Google Scholar] [CrossRef]
- Liao, X.; Fu, Y.; Xie, S.; Yu, P. Globally exponentially attractive sets of the family of Lorenz systems. Sci. China Ser. F 2008, 51, 283–292. [Google Scholar] [CrossRef]
- Kuznetsov, N.; Mokaev, T.; Vasilyev, P. Numerical justification of Leonov conjecture on Lyapunov dimension of Rossler attractor. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1027–1034. [Google Scholar] [CrossRef]
- Saberi Nik, H.; Effati, S.; Saberi-Nadjafi, J. Ultimate bound sets of a hyperchaotic system and its application in chaos synchronization. Complexity 2014, 20, 30–44. [Google Scholar]
- Saberi Nik, H.; Golchaman, M. Chaos control of a bounded 4D chaotic system. Neural Comput. Appl. 2014, 25, 683–692. [Google Scholar] [CrossRef]
- Gao, W.; Yan, L.; Saeedi, M.; Saberi Nik, H. Ultimate bound estimation set and chaos synchronization for a financial risk system. Math. Comput. Simul. 2018, 154, 19–33. [Google Scholar] [CrossRef]
- Jian, J.; Zhao, Z. New estimations for ultimate boundary and synchronization control for a disk dynamo system. Nonlinear Anal. Hybrid Syst. 2013, 9, 56–66. [Google Scholar] [CrossRef]
- Karimov, A.; Tutueva, A.; Karimov, T.; Druzhina, O.; Butusov, D. Adaptive generalized synchronization between circuit and computer implementations of the Rössler system. Appl. Sci. 2020, 11, 81. [Google Scholar] [CrossRef]
- Leonov, G.; Bunin, A.; Koksch, N. Attractor localisation of the Lorenz system. Z. Angew. Math. Mech. 1987, 67, 649–656. [Google Scholar] [CrossRef]
- Leonov, G.; Reitmann, V. Attraktoreingrenzung fur Nichtlineare System; Tenbner: Leipzing, Germany, 1987. [Google Scholar]
- Sun, Y. Solution bounds of generalized Lorenz chaotic system. Chaos Solitons Fractals 2009, 40, 691–696. [Google Scholar] [CrossRef]
- Li, D.; Lu, J.; Wu, X.; Chen, G. Estimating the bounds for the Lorenz family of chaotic systems. Chaos Solitons Fractals 2005, 23, 529–534. [Google Scholar] [CrossRef]
- Pogromsky, A.; Santoboni, G.; Nijmeijer, H. An ultimate bound on the trajectories of the Lorenz systems and its applications. Nonlinearity 2003, 16, 1597–1605. [Google Scholar] [CrossRef]
- Wang, P.; Li, D.; Hu, Q. Bounds of the hyper-chaotic Lorenz-Stenflo system. Commun. Nonlinear Sci. Numer. 2010, 15, 2514–2520. [Google Scholar] [CrossRef]
- Rezzag, S. Boundedness of the new modified hyperchaotic Pan System. Nonlinear Dyn. Syst. Theory 2017, 17, 402–408. [Google Scholar]
- Zhang, F.; Xiao, M. Complex dynamical behaviors of Lorenz-Stenflo equations. Mathematics 2019, 7, 513. [Google Scholar] [CrossRef]
- Lingzhi, Y.; Weihong, X.; Wenxin, Y.; Binren, W. Dynamical analysis, circuit implementation and deep belief network control of new six-dimensional hyperchaotic system. J. Algorithms Comput. Technol. 2018, 12, 361–375. [Google Scholar]
- Yuxia, L.; Xuezhen, L.; Guanrong, C.; Xiaoxin, L. A new hyperchaotic Lorenz-type system: Generation, analysis, and implementation. Int. J. Circuit Theory Appl. 2011, 39, 865–879. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezzag, S.; Zhang, F. On the Dynamics of New 4D and 6D Hyperchaotic Systems. Mathematics 2022, 10, 3668. https://doi.org/10.3390/math10193668
Rezzag S, Zhang F. On the Dynamics of New 4D and 6D Hyperchaotic Systems. Mathematics. 2022; 10(19):3668. https://doi.org/10.3390/math10193668
Chicago/Turabian StyleRezzag, Samia, and Fuchen Zhang. 2022. "On the Dynamics of New 4D and 6D Hyperchaotic Systems" Mathematics 10, no. 19: 3668. https://doi.org/10.3390/math10193668
APA StyleRezzag, S., & Zhang, F. (2022). On the Dynamics of New 4D and 6D Hyperchaotic Systems. Mathematics, 10(19), 3668. https://doi.org/10.3390/math10193668











