1. Introduction
The emergence of deep convolutional networks [
1,
2,
3,
4] has greatly developed image recognition. However, the realistic category distribution is imbalanced, as some categories have few or even no samples for training, which severely limits the performance of networks on unseen classes. Zero-shot learning [
5] is proposed to solve this problem by recognizing novel classes (unseen classes) solely through class-level semantic attributes and knowledge learned from the existing training set (seen classes). Conventional zero-shot learning has the strong assumption that all test samples are from unseen classes. In adaptation to realistic scenarios, generalized zero-shot learning (GZSL) [
6,
7] has been proposed, where seen classes and semantic attributes are used to train the model, and both seen and unseen classes participate in the test.
The current mainstream solution to GZSL is feature generative methods [
8,
9,
10,
11] that use semantic attributes as the cues to train a visual feature generator. The trained feature generator can be used to synthesize unseen-class visual features by the attributes of unseen classes. The synthetic unseen-class features and existing seen-class features are used to train a softmax classifier in a supervised way. The synthetic features make up for the lack of unseen classes and effectively avoid overfitting on seen classes. The generative methods use only semantic attributes as cues for synthesizing visual features, which can be considered attribute-to-feature mapping. However, the visual features contain richer information than the semantic attributes, thus the semantic attributes can only represent visual features that are highly relevant to the category. Current generative methods concatenate Gaussian noises on the attributes to balance the gap between the attributes and the features, but the introduction of a large amount of noise seriously affects the mining of attributes, which restricts the attribute-to-feature inference of the generative model.
Through the discussion above, a residual-prototype-generating network (RPGN) is proposed, which consists of prototype generating and residual feature generating. Specifically, considering that different dimensions of semantic attributes represent different category information, such as white, furry, paws, etc., we propose a disentangle regressor that first chunks the semantic attributes and regresses them separately and then regresses the visual feature prototype. Through the disentangling operation, the visual feature prototype can fully explore the different information in the attribute and has excellent category differentiation. Meanwhile, to ensure consistency between feature prototypes and semantic attributes, the feature prototypes are reverted to the original semantic attributes as the reconstruction constraint. In addition, we propose a residual variational auto-encoder (rVAE) to extract the part of visual features (residual features) that cannot be represented by semantic attributes from the original visual features. The residual features extracted from original features have realistic and rich visual features and do not affect the mining of attribute information. To finish, the feature prototypes and the residual features are added to obtain the synthesized visual features, the category of which is determined by the category to which the prototype belongs, and the residuals used to synthesize the features can be synthesized with any visual features. This residual-prototype generation ensures that the feature prototypes contain attribute-associated information, and the residual features contain only attribute-independent information, which is indeed indispensable for constructing a real visual feature.
The work and contributions in this paper are threefold:
We propose a disentangle regressor to generate class prototypes by first chunking the attributes and regressing them separately for fully mining visual information.
We design a residual-prototype-generating network (RPGN) that can synthesize diverse unseen-class features with the help of real seen-class features, greatly enhancing the diversity of synthesized features.
The proposed method achieves state-of-the-art (SOTA) results on four public GZSL datasets.
2. Related Work
2.1. Conventional Zero-Shot Learning
Zero-shot learning (ZSL) relies on class-level semantic descriptions or features, such as semantic attributes and word vectors, which are used to transfer models from seen classes to unseen classes. Early ZSL research work focused on traditional ZSL problems, in which semantic embedding was the most important approach. Semantic embedding methods can learn to embed visual features into semantic space. By doing this, visual features and semantic features are located in the same space, and ZSL classification can be accomplished by searching for the nearest semantic descriptor.
2.2. Generalized Zero-Shot Learning
Currently, generative approaches dominate in GZSL [
6,
7]; these exploit existing adversarial generative networks (GAN) [
12,
13,
14] or variational auto-encoders (VAE) [
15,
16] to synthesize visual features from class-level semantic attributes and random noise. Examples such as f-CLSWGAN [
8], cycle-UWGAN [
11] and LisGAN [
10] introduce the Wasserstein generative adversarial network (WGAN) [
17] paired with a pre-trained classifier to synthesize visual features for unseen classes, transforming the GZSL task into a fully supervised classification issue. RFF [
18] combines the traditional projection method and GAN to initially map visual features to a new redundancy-free feature space and then to judge the veracity of the mapped features. To enhance the performance of the generator, some works [
9,
19,
20,
21] formulate GAN into the variational auto-encoder (VAE) model to fit the class-specific latent distribution and highly discriminative feature representations. The combination of GAN and VAE greatly enhances the performance of the generative model in GZSL and becomes the benchmark method for many new methods [
22,
23].
To enhance the generalization of the model from seen classes to unseen classes, some studies introduce meta-learning. Meta-learning methods for GZSL [
24,
25,
26] simulate the setting of zero-shot learning in the training stage so that the model can effectively learn the ability to transfer knowledge. ZSML [
25] first introduces meta-learning into GZSL and combines meta-learning with GAN, which gives the generator better knowledge transfer capability. E-PGN [
24] first introduces an episode-based paradigm in the training phase; this divides the training set into pseudo-multiple zero-shot learning subsets and then takes these subsets as multiple tasks to train the model. By training on multiple tasks, the model can effectively transfer the knowledge learned from the seen classes to the task of the unseen classes. Furthermore, to solve the problem of task inconsistency in the meta-learning model, TGMZ [
26] proposed a task alignment module to make the tasks of seen classes and unseen classes more similar.
3. Method
3.1. Notations and Definitions
In the GZSL task, we define the dataset of seen classes as , where , and represent the set of visual features, labels and attributes of seen classes, respectively. Similarly, the unseen class dataset is denoted as , where , and denote the set of visual features, labels and attributes of unseen classes, respectively. Note that the label set of seen and unseen classes do not intersect, which is . The main goal of the GZSL task is to train a classifier that can recognize both seen and unseen classes by only using the seen-class dataset () and attributes of unseen classes () for training.
3.2. Overview
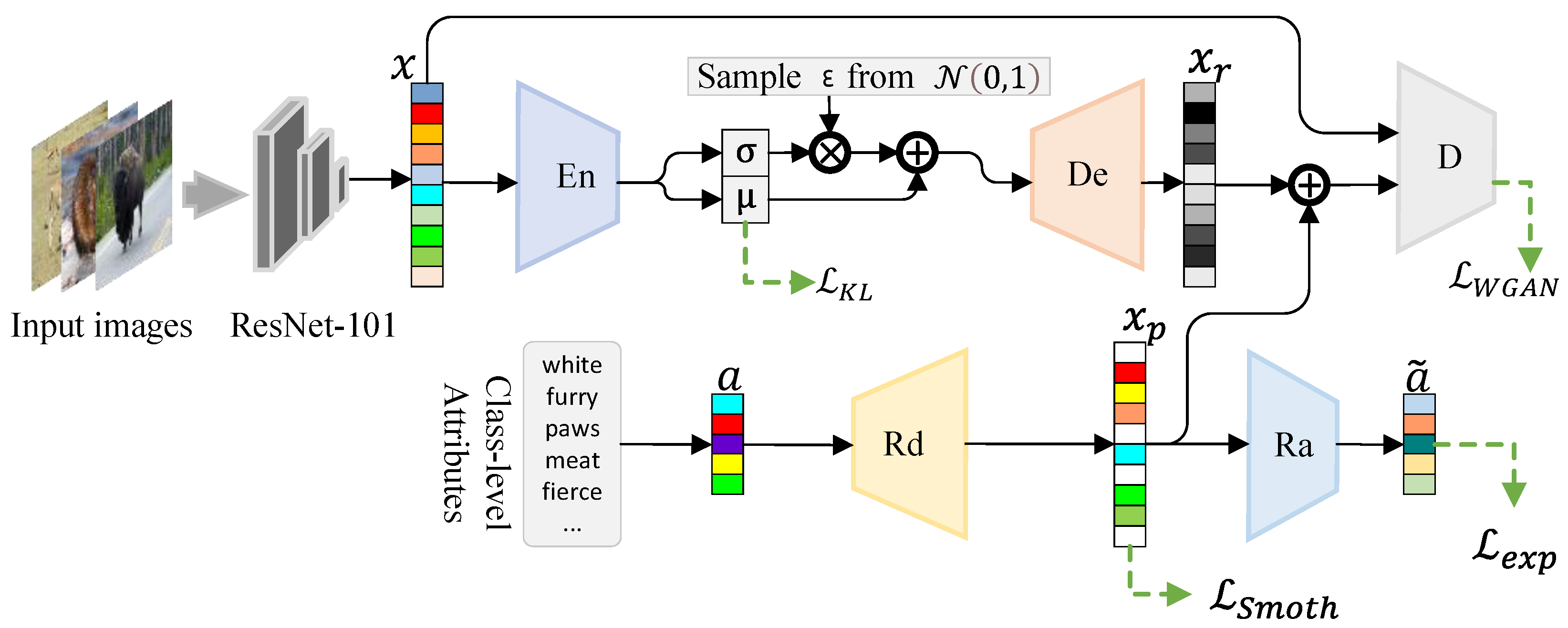
The framework of the proposed approach, called residual-prototype-generating network (RPGN), is shown in
Figure 1 and contains five modules: ResNet-101 [
4] as a backbone, an encoder (
), a decoder (
), a disentangle regressor (
), an attribute regressor (
), and a discriminator (
D).
The backbone is ResNet-101 pre-trained on ImageNet to extract visual features of images, and its parameters are fixed and no longer fine-tuned in any of the experiments.
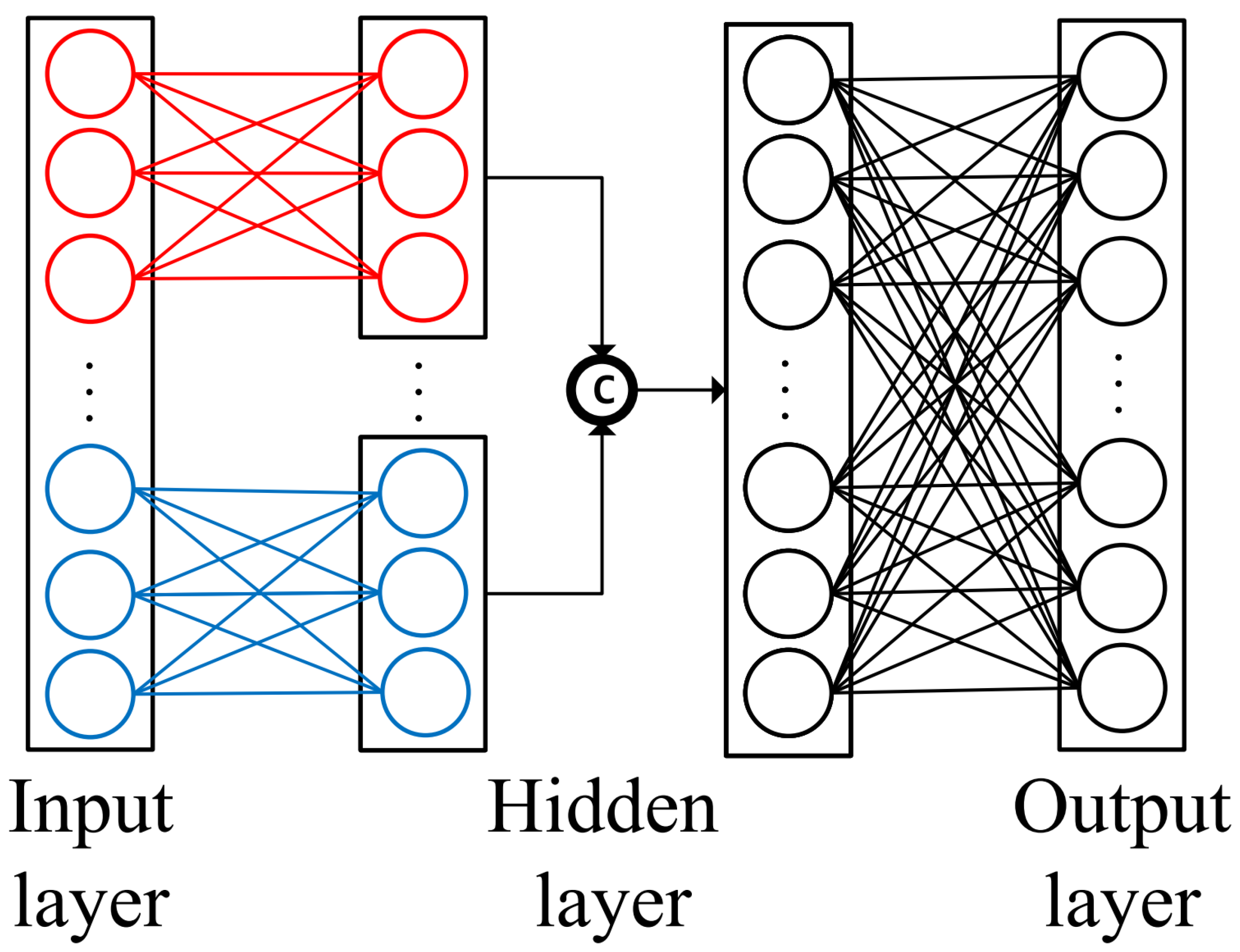
The main function of disentangling regressor
is to generate a prototype feature of a certain class based on attributes, and its structure is a block connection multilayer perceptron (MLP) (see
Figure 2 for details) for capturing complex semantic relationships between attributes. To contain richer information on attributes, the generated prototype feature reconstructs the attributes through an attribute regressor (
).
The encoder () and decoder () form the proposed residual variational auto-encoder (rVAE), which generates residual features. Unlike the traditional variational auto-encoder that synthesizes features directly, the proposed rVAE is used to extract semantically irrelevant visual feature residuals from real features. The prototype features synthesized by the disentangle regressor () only have semantic information and do not contain other information that constitutes visual features; thus the residual features can be used to compensate for the missing prototype feature information. Further, through generating prototype features and residual features, RPGN can make the final synthesized visual features contain more semantic information and be more realistic.
The discriminator (D) mainly distinguishes between real features and synthetic features and makes the distribution of synthetic features converge to the distribution of real features through adversarial learning loss. The attribute regressor reconstructs the prototypes back to the attributes, ensuring that the prototypes and attributes are strongly correlated.
3.3. Prototype Generation
The prototype feature is generated through the proposed disentangle regressor (
), which is illustrated in
Figure 2. The reason for this design is that there are strong dependencies between attributes; for example, the presence of a bird’s beak in an attribute necessarily results in the presence of a bird’s claw, which leads to coupling between attributes. To solve this problem, the attributes (
a) are divided into
K blocks (
) randomly to reduce the dependencies between attributes. Each attribute block (
) is input to the hidden layer (
to get the result, and then all of them are concatenated together and input to the output layer (
) to get the prototype feature
with the following equation:
where
denotes the attribute of the i-th block, and
.
To make the prototype contain the common features of a certain class, all the visual features (
x) of this class are used to constrain the prototype (
). Usually, L2 loss is used to achieve this, but each class has only one prototype, which will inevitably lead to some features of this class being greatly different from the prototype, causing too much L2 loss; that is, it is easy to have a gradient explosion. To avoid this problem, smooth L1 loss [
27] is used here, which is as follows:
where
is a hyper-parameter and is set to 1 in all the experiments according to the suggestion of [
27].
To further constrain the prototype features to be as relevant as possible to the attributes and to contain all the attribute information, the prototype is reconstructed back to the attributes, and an exponential loss function is used to make the projected attributes to be as similar as possible to the real attributes:
The purpose of exponential loss is to produce a high dot-product similarity between the reconstructed attributes and the real ones.
3.4. Residual Generation
Residual generation is implemented through the proposed residual variational auto-encoder (rVAE), which first encodes visual feature (
x) as a hidden variable (denoted as
h). Here, we use the re-parameterization trick in VAE [
28] to represent
h as
, where
, and the distribution of
h is consistent with the standard normal distribution through the following Kullback–Leibler divergence loss:
where
are the i-th dimension values of
and
, respectively.
The latent variables are used to decode the residual features with the following equation:
where
z is Gaussian noise; that is,
. In the absence of confusion, the process of synthesizing residual features by the residual generator is abbreviated as
. Here, the final residual features are not expected to be the same as the initial visual features as in traditional VAE, but are expected to contain the attribute-independent part of a visual feature, which is precisely the part that makes the final synthesized visual features more realistic and more diverse. The information of residual features cannot be obtained by traditional generators through random noise alone, and the proposed method greatly avoids the problem of missing the diversity of synthetic features by traditional generators.
3.5. Generative Adversarial Network
The final synthetic features combine the results of the prototype generator and the residual generator as follows:
Note that the residual features are synthesized using the real features of any seen classes, not necessarily the same class as the prototype features , and the final synthesized features x are determined by the class to which the prototype belongs. This way of synthesizing residual features without using visual features of the same class can significantly improve residual generation to capture attribute-independent feature information, which can greatly enhance the authenticity of the synthesized features. For convenience, the overall generation process is denoted as , where x is the real feature used to extract the residual feature, z is sampled from for re-parameterization, and a is the attribute vector to control the class of synthesized feature .
To improve the authenticity of the synthetic features and to make their distribution closer to that of the real features, the generative adversarial loss is introduced as:
where
is a hyper-parameter. The last term is the Wasserstein loss [
17] by enforcing the Lipschitz constraint [
29], where
with
. As suggested in [
17], we fix
.
In summary, the total objective loss is as follows:
where
is a hyper-parameter to control the effect of attribute reconstruction.
3.6. Classification
In the classification stage, the goal is to train a classifier capable of classifying both seen and unseen classes. To compensate for the lack of unseen class data, a synthetic unseen class dataset is forged through feature generation. Specifically, given the of any unseen class , and with sampling noise z and seen-class feature , the visual features of unseen classes can be synthesized through . After repeating this feature-generation process for every unseen class, a synthetic unseen dataset is obtained. As the last step, synthetic unseen classes and real seen classes are used to train a classifier in a supervised way.
4. Experimental Results
4.1. Experimental Setup
Datasets. The proposed method is evaluated on four benchmark datasets: Animals with Attributes (AWA1) [
30], renewed Animals with Attributes (AWA2) [
6], Caltech USCD Birds-2011 (CUB) [
31] and Oxford Flowers (FLO) [
32]. We use the category splitting strategy in [
6]. Concretely, AWA1 and AWA2 are two coarse-grained datasets that consist of different visual images from the same 50 animal classes; each class is labeled with 85-dimensional category attributes. Forty classes in AWA1 and 2 are split into seen classes, and the other 10 classes are split into unseen classes. CUB is a fine-grained dataset with 11,788 images from 200 different classes of birds with 1024-dimensional attributes extracted by CNN-RNN [
33]. A total of 150 classes in CUB are split into seen classes, and the other 50 classes are split into unseen classes. FLO is a fine-grained dataset that consists of 8189 images from 102 flower classes with 1024-dimensional attributes extracted by CNN-RNN [
33], similar to CUB. A total of 82 classes in FLO are split into visible classes, and another 20 classes are split into unseen classes. A summary of the datasets is given in
Table 1.
Evaluation Protocol. The proposed method is evaluated in terms of the average per-class Top-1 accuracy (ACC). In addition, we follow the protocol proposed in [
6] for the GZSL task, in which the ACCs of both seen class
S and unseen class
U are calculated, as well as the harmonic mean
.
Implementation Details. Following [
6], we use the 2048-dimensional global features extracted by ResNet-101 [
4], which is pre-trained on ImageNet for visual features. As a pre-processing step, we also normalize the visual features such as that of f-CLSGAN [
8].
,
,
D and
all adopt a three-layer multilayer perceptron (MLP), which employs 4096 units in the hidden layer. Meanwhile, they all apply LeakReLU as the activation function on the hidden layer. The difference is that the
,
and
apply ReLU [
34,
35] as the activation function of the output layer, while
D and
do not use the activation function on the output layer. For all datasets,
,
,
D,
and
are optimized by Adam [
36] with learning rate 0.0001, batch size 512,
and
.
4.2. Comparison with SOTA Methods
Results on public zero-shot learning datasets are reported in
Table 2. RPGN outperforms all generative and non-generative methods on AWA2, a coarse-grained dataset, and FLO, a dataset with non-manually labeled attributes, especially on the FLO dataset, where the proposed method is only 3% away from reaching 80% accuracy. On AWA1, RPGN outperforms all the generative methods by 1.1% over the second place CE-GZSL [
37], which is a very big improvement. On CUB, a fine-grained dataset, RPGN is below CE-GZSL [
37] in the generative method, but it is much better than the algorithm on other datasets, which shows that the proposed method can be applied to all datasets and does not cause significant performance degradation due to changes in the dataset. In addition, the unseen class accuracy
U of RPG is the highest on AWA2 compared with the generative method; our method is higher than TGMZ [
26] by 4.2%, which is a good indication that our model is able to synthesize more truly diverse unseen-class features, and although the unseen-class accuracy of our method is not the highest on FLO, we have the highest seen-class accuracy, which also shows that our synthesized unseen-class features are not strongly biased towards the seen class; therefore, they do not affect the accuracy of the seen class too much.
As for the reason why our method is not in the leading position on CUB, a fine-grained dataset, but is superior on AWA1, AWA2 and coarse-grained datasets, the analysis is as follows. Other generative methods only use attributes and Gaussian noise to synthesize unseen class data. If the attributes are coarse-grained and provide less information, the Gaussian noise alone cannot provide other information about a visual feature; therefore, the unseen-class features synthesized by other generative methods are bound to face problems of poor realism and lack of diversity. In contrast, our RPGN uses the residuals generated by real seen-class features. Due to the authenticity and richness of seen-class features, the generated residuals must also contain a large amount of information on real features, which can make up for the lack of information provided by attributes. As for CUB, a fine-grained dataset, the attributes already provide sufficient information; therefore, other generative methods obtain better performance. In summary, our method is more suitable for coarse-grained datasets than other methods. In addition, it is observed that many non-generative methods [
44,
46] can obtain very good performance on CUB, which is also because the attributes of CUB contain enough information that extra synthetic unseen-class features are not necessary to compensate for the absence of the unseen class, and the model can infer the relationship between features and attributes to complete zero-shot recognition.
4.3. Ablation Study
We perform ablation experiments to determine whether or not to use the following key components: (a) residual variational auto-encoder to generate residual features; (b) the disentangle regressor to synthesize the prototype; and (c) smooth L1 loss [
27]. Results of the ablation study are reported in
Table 3.
Residual feature generation: If only Gaussian noise is used to synthesize the residual features, this synthesis is similar to other generative methods, but the authenticity and diversity of the visual features synthesized by relying only on random noise to obtain information other than attributes of a visual feature are deficient because random noise does not provide as much information as the real visual features. In contrast, our method synthesizes residual features by random noise and real seen-class features; these residual features contain information other than the attributes in real visual features, and the richness and authenticity of the visual features synthesized with this residual feature method are guaranteed. Thus, comparing the first and second columns of
Table 3 after using our method to synthesize visual features shows improvements of 5.0%, 6.2% and 6.1% on CUB, AWA2 and FLO, respectively. Comparing the fifth and eighth rows reveals that removing the innovation reduces performance by 3.6%, 4.0% and 5.2% on the three datasets, respectively, which fully illustrates the effectiveness of the innovation.
Disentangle regressor: If only ordinary MLP is used to capture the semantic relationships between attributes, there will be strong dependencies between some attributes and confusion will arise between them, and some attributes will even be useless. The proposed disentangle regressor first randomizes attributes to different blocks, reducing the probability of having attributes with strong dependency in the same block and thus achieving better mining of the semantic relationships between attributes. This enables the synthesized prototype to make full use of all the attributes. Comparing the first and third rows of
Table 3 shows that the model improves by 4.3%, 5.9% and 5.6% for CUB, AWA2 and FLO, respectively, after using the multi-headed MLP. Comparing the sixth and eighth rows reveals that the model’s performance decreases by 1.8%, 1.3% and 1.4% for the three datasets, respectively, after removing the innovation, which fully indicates that the more complex structure can better generate prototypes containing attribute information, thus improving the zero-shot recognition performance of the model.
Smooth L1 loss: If the traditional L2 loss is used to constrain the prototypes and training features, there are bound to be many features that are far different from the prototypes, for there is only one prototype for each class. This will result in larger loss and will potentially lead to gradient explosion. In fact, the prototypes are expected to represent the universal and common information of a class, so if some features are more different than other features of the same class, then such features should not provide too much reference to the prototype. L2 loss would give such features more attention, which is obviously unreasonable. Comparing the first and third rows of
Table 3, the model improves by 3.3%, 4.6% and 3.2% on CUB, AWA2 and FLO, respectively, after using the smooth L1 loss, while comparing the seventh and eighth rows after removing the innovation, the model’s performance decreases by 1.1%, 1.0% and 1.1% on the three datasets, respectively, which fully illustrates the effectiveness of the loss and shows that the loss is more helpful to synthesize better prototypes.
4.4. Hyper-Parameter Analysis
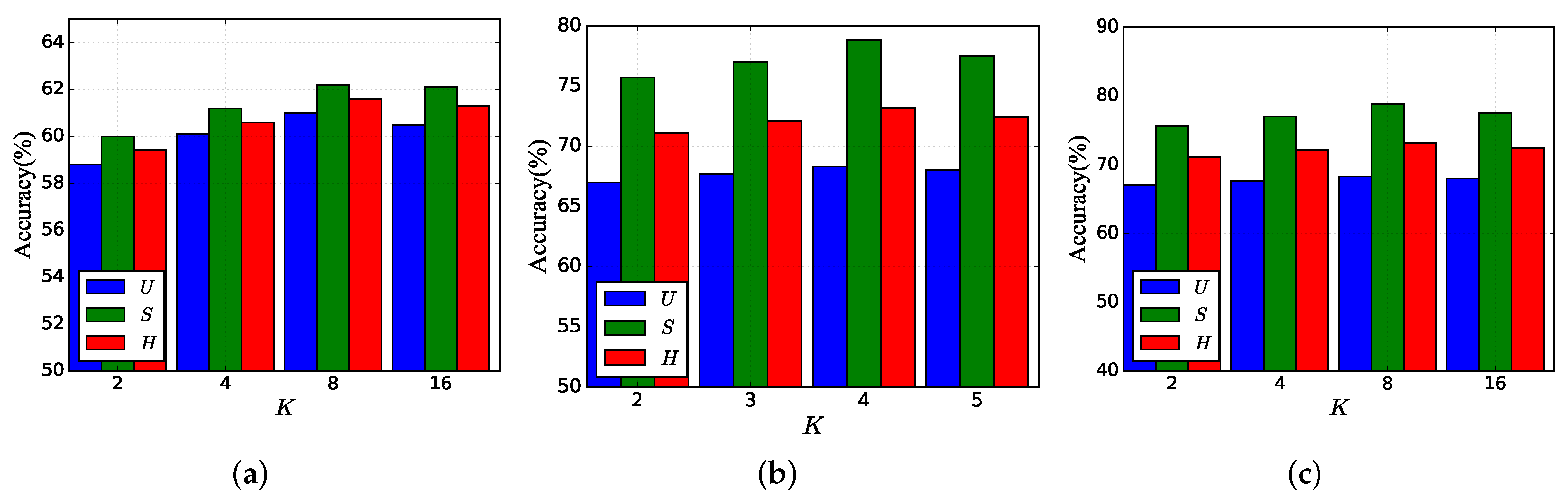
Hyper-parameter K: We evaluate the effect of
K as shown in
Figure 3. We found that the effect of
K on the accuracy of the model is smaller in a certain range. On the AWA2 datasets, the model gets the best performance when
K is four, but on FLO and CUB, the model gets the best performance when
K is 8. This is because the attributes of FLO and CUB are 1024 dimensions, which is far more than the other datasets, so they should be divided into more groups for the attributes. It can be seen that the number of groups should be positively correlated with the dimensionality of the attributes, and the larger the dimensionality of the attributes, the more the number of groups should be appropriately increased.
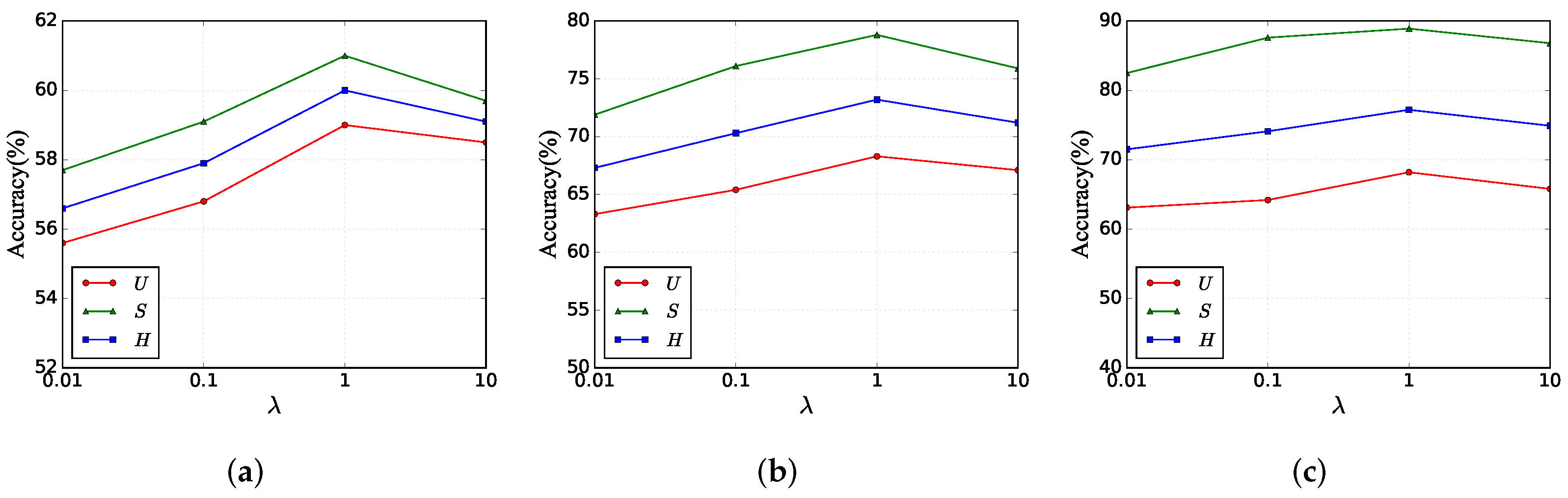
Hyper-parameter : We evaluate the effect of
as shown in
Figure 4. This hyper-parameter controls the regression loss of the prototype projected back to the attribute space, and by the same token, the prototype is also controlled by the adversarial loss. If this hyper-parameter is too large, it will lead to a lower percentage of adversarial loss, which will lead to lower authenticity of the final synthesized features. If this hyper-parameter is too small, then it will lead to a lower correlation between the prototype and the attributes. Thus,
is set to one to achieve the best results on all datasets.
4.5. Zero-Shot Bai Character Recognition
In addition to the public datasets, we create a new zero-shot dataset: the Chinese and Bai Character (CBC) dataset. Bai script is an ancient script similar to Chinese script and is composed of 32 strokes, similar to Chinese (see
Figure 5). Specifically, we take 503 Chinese characters as seen classes and 400 Bai characters as unseen classes and use the 32-stroke information of each character as attributes.
Results on CBC are reported in
Table 4. We transplanted eight of the latest GZSL methods (ZSML [
25], f-CLSGAN [
8], LisGAN [
10], f-VAEGAN [
9], RFF [
18], CE-GZSL [
37] and FREE [
23]) to the CBC dataset, and the best-performing RFF [
18] has a recognition accuracy of 80.9% on the term of
H. This is because these generative methods use Gaussian noise plus attribute-synthesized features; therefore, these synthesized features are less realistic and less diverse, while our RGPN uses residual features generated by real seen classes and prototype-synthesized features generated by attributes; therefore, our model synthesizes features that are more realistic and diverse. In addition, our method obtains an accuracy of 79.4% on the unseen class and is 5.4% higher than FREE [
23], which fully illustrates that the unseen-class features synthesized by our method are far better than other methods. Finally, on the index
H, our method is also higher than the second place by 3.1%, which shows the superiority of our method. To be as fair as possible, the above eight GZSL methods all require careful hyper-parameter tuning to obtain comparable results.
5. Conclusions
Current generative methods for GZSL are facing bottlenecks as a consequence of the fact that these methods use only Gaussian noise and attributes to synthesize unseen-class features. To get out of this predicament, we propose a novel residual-prototype adversarial generation network that can use real seen-class features to assist in synthesizing unseen-class features, greatly improving the richness and authenticity of unseen-class features. Experiments on multiple datasets, rich ablation experiments and hyper-parameter analysis experiments show that our method is comparable or superior to existing methods. Furthermore, we constructed a GZSL-compliant task with the Chinese and Bai character (CBC) dataset and applied eight SOTA methods to the CBC dataset to compare the performance.
Author Contributions
Conceptualization, Z.Z., X.L. and Z.G.; methodology, Z.Z. and X.L.; validation, Z.Z., X.L. and Z.G.; formal analysis, Z.Z. and X.L.; investigation, X.L. and Z.G.; resources, Z.Z. and T.M.; writing—original draft preparation, Z.Z. and X.L.; writing—review and editing, Z.G., C.L. and W.L.; visualization, X.L.; funding acquisition, T.M. All authors have read and agreed to the published version of the manuscript.
Funding
Project supported by the Science and Technology Planning Project of Yunnan Provincial Science and Technology Department (grant no. 2018FD058).
Data Availability Statement
Data will be provided upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition, 2015. Tech Report. arXiv 2014, arXiv:1512.03385. [Google Scholar]
- Lampert, C.H.; Nickisch, H.; Harmeling, S. Attribute-based classification for zero-shot visual object categorization. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 453–465. [Google Scholar] [CrossRef] [PubMed]
- Xian, Y.; Lampert, C.H.; Schiele, B.; Akata, Z. Zero-shot learning—A comprehensive evaluation of the good, the bad and the ugly. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2251–2265. [Google Scholar] [CrossRef] [PubMed]
- Pourpanah, F.; Abdar, M.; Luo, Y.; Zhou, X.; Wang, R.; Lim, C.P.; Wang, X.Z.; Wu, Q.J. A review of generalized zero-shot learning methods. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Xian, Y.; Lorenz, T.; Schiele, B.; Akata, Z. Feature generating networks for zero-shot learning. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 5542–5551. [Google Scholar]
- Xian, Y.; Sharma, S.; Schiele, B.; Akata, Z. F-VAEGAN-D2: A feature generating framework for any-shot learning. In Proceedings of the CVPR, Long Beach, CA, USA, 16–20 June 2019; pp. 10275–10284. [Google Scholar]
- Li, J.; Jing, M.; Lu, K.; Ding, Z.; Zhu, L.; Huang, Z. Leveraging the Invariant Side of Generative Zero-Shot Learning. In Proceedings of the CVPR, Long Beach, CA, USA, 16–20 June 2019; pp. 7402–7411. [Google Scholar]
- Felix, R.; Kumar, B.G.V.; Reid, I.D.; Carneiro, G. Multi-modal cycle-consistent generalized zero-shot learning. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.C.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional Generative Adversarial Nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Nguyen, T.D.; Le, T.; Vu, H.; Phung, D.Q. Dual discriminator generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 2670–2680. [Google Scholar]
- Doersch, C. Tutorial on Variational Autoencoders. arXiv 2016, arXiv:1606.05908. [Google Scholar]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. Beta-VAE: Learning basic visual concepts with a constrained variational framework. In Proceedings of the 5th International Conference on Learning Representations ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the 34th International Conference on Machine Learning, ICML, PMLR 2017, Seoul, Korea, 15–17 November 2017; Volume 70, pp. 214–223. [Google Scholar]
- Han, Z.; Fu, Z.; Yang, J. Learning the redundancy-free features for generalized zero-shot object recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 12862–12871. [Google Scholar]
- Schonfeld, E.; Ebrahimi, S.; Sinha, S.; Darrell, T.; Akata, Z. Generalized zero- and few-shot learning via aligned variational autoencoders. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8247–8255. [Google Scholar]
- Peirong, M.; Xiao, H. A variational autoencoder with deep embedding model for generalized zero-shot learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Keshari, R.; Singh, R.; Vatsa, M. Generalized Zero-Shot Learning Via Over-Complete Distribution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Narayan, S.; Gupta, A.; Khan, F.S.; Snoek, C.G.; Shao, L. Latent embedding feedback and discriminative features for zero-shot classification. In Proceedings of the ECCV 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 479–495. [Google Scholar]
- Chen, S.; Wang, W.; Xia, B.; Peng, Q.; You, X.; Zheng, F.; Shao, L. Free: Feature refinement for generalized zero-shot learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11 October 2021; pp. 122–131. [Google Scholar]
- Yu, Y.; Ji, Z.; Han, J.; Zhang, Z. Episode-based prototype generating network for zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 14032–14041. [Google Scholar]
- Verma, V.K.; Brahma, D.; Rai, P. A Meta-Learning Framework for Generalized Zero-Shot Learning. arXiv 2020, arXiv:1909.04344. [Google Scholar]
- Liu, Z.; Li, Y.; Yao, L.; Wang, X.; Long, G. Task aligned generative meta-learning for zero-shot learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021. [Google Scholar]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Caterini, A.L.; Doucet, A.; Sejdinovic, D. Hamiltonian variational auto-encoder. In Proceedings of the Advances in Neural Information Processing Systems 31 (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018; pp. 8178–8188. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved training of wasserstein GANs. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Lampert, C.H.; Nickisch, H.; Harmeling, S. Learning to detect unseen object classes by between-class attribute transfer. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition CVPR, Miami, FL, USA, 20–25 June 2009; pp. 951–958. [Google Scholar]
- Wah, C.; Branson, S.; Welinder, P.; Perona, P.; Belongie, S. The Caltech-UCSD Birds-200-2011 Dataset; Computation & Neural Systems Technical Report, 2010-001; California Institute of Technology: Pasadena, CA, USA, 2011. [Google Scholar]
- Nilsback, M.E.; Zisserman, A. Automated flower classification over a large number of classes. In Proceedings of the 2008 Sixth Indian Conference on Computer Vision, Graphics & Image Processing, ICVGIP, Bhubaneswar, India, 16–19 December 2008; pp. 722–729. [Google Scholar]
- Reed, S.; Akata, Z.; Lee, H.; Schiele, B. Learning deep representations of fine-grained visual descriptions. In Proceedings of the 2008 Sixth Indian Conference on Computer Vision, Graphics & Image Processing CVPR, Bhubaneswar, India, 16–19 December 2008; pp. 49–58. [Google Scholar]
- Agarap, A.F. Deep Learning using Rectified Linear Units (ReLU). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Maennel, H.; Bousquet, O.; Gelly, S. Gradient Descent Quantizes ReLU Network Features. arXiv 2018, arXiv:1803.08367. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Han, Z.; Fu, Z.; Chen, S.; Yang, J. Contrastive embedding for generalized zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 19–25 June 2021. [Google Scholar]
- Verma, V.K.; Arora, G.; Mishra, A.; Rai, P. Generalized Zero-shot learning via synthesized examples. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 4281–4289. [Google Scholar]
- Zhu, Y.; Xie, J.; Liu, B.; Elgammal, A. Learning feature-to-feature translator by alternating back-propagation for generative zero-shot learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 9843–9853. [Google Scholar]
- Atzmon, Y.; Chechik, G. Adaptive confidence smoothing for generalized zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 11671–11680. [Google Scholar]
- Huynh, D.; Elhamifar, E. Fine-grained generalized zero-shot learning via dense attribute-based attention. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–20 June 2020; pp. 4482–4492. [Google Scholar]
- Min, S.; Yao, H.; Xie, H.; Wang, C.; Zha, Z.J.; Zhang, Y. Domain-aware Visual Bias Eliminating for Generalized Zero-Shot Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Zhongqi, Y.; Tan, W.; Hanwang, Z.; Qianru, S.; Xian-Sheng, H. Counterfactual Zero-Shot and Open-Set Visual Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–20 June 2021. [Google Scholar]
- Ge, J.; Xie, H.; Min, S.; Zhang, Y. Semantic-guided reinforced region embedding for generalized zero-shot learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 1406–1414. [Google Scholar]
- Chou, Y.Y.; Lin, H.T.; Liu, T.L. Adaptive and generative zero-shot learning. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Liu, L.; Zhou, T.; Long, G.; Jiang, J.; Dong, X.; Zhang, C. Isometric propagation network for generalized zero-shot learning. arXiv 2021, arXiv:2102.02038. [Google Scholar]
- Zhu, Y.; Elhoseiny, M.; Liu, B.; Peng, X.; Elgammal, A. A generative adversarial approach for zero-shot learning from noisy texts. In Proceedings of the CVPR, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1004–1013. [Google Scholar]
- Chen, S.; Xie, G.; Liu, Y.; Peng, Q.; Sun, B.; Li, H.; You, X.; Shao, L. Hsva: Hierarchical semantic-visual adaptation for zero-shot learning. In Proceedings of the Advances in Neural Information Processing Systems 34 (NeurIPS 2021), Virtual, 6–14 December 2021; Volume 34. [Google Scholar]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).