Solution of Second- and Higher-Order Nonlinear Two-Point Boundary-Value Problems Using Double Decomposition Method
Abstract
1. Introduction
2. Analysis of the Method
3. Numerical Examples
4. Discussion of Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Duan, J.S.; Wang, Z.; Zhong, S.; Temuer, C. Parameterized temperature distribution and efficiency of convective straight fins with temperature dependent thermal conductivity by a new modified decomposition method. Int. J. Heat Mass Transf. 2013, 59, 137–143. [Google Scholar] [CrossRef]
- Duan, J.S.; Rach, R.; Wazwaz, A. Solution of the model of beam-type micro-and nano-scale electrostatic actuators by a new modified Adomian decomposition method for nonlinear boundary value problems. Int. J. Nonlinear Mech. 2013, 49, 159–169. [Google Scholar] [CrossRef]
- Bishop, R.E.D.; Cannon, S.M.; Miao, S. On Coupled bending and torsional vibration of uniform beams. J. Sound Vibr. 1989, 131, 457–464. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Dover: New York, NY, USA, 1981. [Google Scholar]
- Djidjeli, K.; Twizell, E.H.; Boutayeb, A. Numerical methods for special nonlinear boundary value problem of order 2 m. J. Comput. Appl. Math. 1993, 47, 35–45. [Google Scholar] [CrossRef]
- Dzhumabaev, D.S.; Temesheva, S.M. A parametrization method for solving nonlinear two-point boundary value problems. Comput. Math. Math. Phys. 2007, 47, 37–61. [Google Scholar] [CrossRef]
- Dzhumabaev, D.S.; Temesheva, S.M. Criteria for the Existence of an Isolated Solution of a Nonlinear Boundary-Value Problem. Ukr. Math. J. 2018, 70, 410–421. [Google Scholar] [CrossRef]
- Dzhumabaev, D.S. New General Solutions of Ordinary Differential Equations and The Methods for The Solution of Boundary-Value Problems. Ukr. Math. J. 2019, 71, 1006–1031. [Google Scholar] [CrossRef]
- Myint, U. Ordinary Differential Equations; Elsevier: North-Holland, The Netherlands, 1978. [Google Scholar]
- Edwards, C.H.; Penney, D.E. Elementary Differential Equations with Boundary Value Problems, 6th ed.; Pearson Education International, Pearson Prentice Hill: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Agarwal, R.P. Boundary Value Problems for Higher Order Differential Equations; World Scientific: Singapore, 1986. [Google Scholar]
- Siddiqi, S.S.; Twizell, E.H. Spline solutions of linear eighth-order boundary value problems. Comput. Meth. Appl. Mech. Eng. 1996, 131, 309–325. [Google Scholar] [CrossRef]
- Boutayeb, A.; Twizell, E.H. Finite difference methods for the solution of special eighth-order boundary value problems. Int. J. Comp. Math. 1993, 48, 63–75. [Google Scholar] [CrossRef]
- Baldwin, P. Asymptotic estimates of the eigenvalues of a sixth order boundary value problem obtained by using global phase-integral methods. Phil. Trans. R. Soc. Lond. A 1987, 322, 281–305. [Google Scholar]
- Chawla, M.M.; Katti, C.P. Finite difference methods for two-point boundary value problems involving high order differential equations. BIT 1979, 19, 27–33. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer: Boston, MA, USA, 1994. [Google Scholar]
- Cherruault, Y. Convergence of Adomian’s method. Kybernetes 1989, 18, 31–38. [Google Scholar] [CrossRef]
- Abbaoui, K.; Cherruault, Y. Convergence of Adomian’s method applied to differential equations. Comp. Math. Appl. 1994, 28, 103–109. [Google Scholar] [CrossRef]
- Rach, R. On the Adomian decomposition method and comparisons with Picard’s method. J. Math. Anal. Appl. 1987, 128, 480–483. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A comparison between Adomian decomposition method and Taylor series method in the series solutions. Appl. Math. Comput. 1998, 97, 37–44. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Approximate solutions to boundary value problems of higher order by the modified decomposition method. Comput. Math. Appl. 2000, 40, 679–691. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The numerical Solution of fifth order boundary value problems by the decomposition method. J. Comput. Appl. Math. 2001, 136, 259–270. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The numerical solution of sixth-orders boundary value problems by the modified decomposition method. Appl. Math. Comput. 2001, 118, 311–325. [Google Scholar] [CrossRef]
- Duan, J.S.; Rach, R. A new modification of the Adomian decomposition method for solving boundary value problems for higher order nonlinear differential equations. Appl. Math. Comput. 2011, 218, 4090–4118. [Google Scholar] [CrossRef]
- Adomian, G.; Rach, R. Analytic solution of nonlinear boundary value problems in several dimensions by decomposition. J. Math. Anal. Appl. 1993, 174, 118–137. [Google Scholar] [CrossRef]
- Aminataei, A.; Hosseini, S.S. Comparison of Adomian decomposition method and double decomposition methods for boundary value problems. Eur. J. Sci. Res. 2005, 2, 48–56. [Google Scholar]
- Bello, N.; Alkali, A.J.; Roko, A. A fixed point iterative method for the solution of two-point boundary value problems for a second order differential equations. Alex. Eng. J. 2018, 57, 2515–2520. [Google Scholar] [CrossRef]
- Noor, M.A.; Mohyud-Din, S.T. An efficient method for fourth-order boundary value problems. Comput. Math. Appl. 2007, 54, 1101–1111. [Google Scholar] [CrossRef][Green Version]
- Noor, M.A.; Mohyud-Din, S.T. Variational iteration method for fifth-order boundary value problems using He’s polynomials. Math. Probl. Eng. 2008, 2008, 954794. [Google Scholar] [CrossRef]
- Siddiqi, S.S.; Iftikhar, M. Variational iteration method for the solution of seventh order boundary value problems using He’s polynomials. J. Assoc. Arab Univ. Basic Appl. Sci. 2015, 18, 60–65. [Google Scholar] [CrossRef]
- Viswanadham, K.K.; Reddy, S.M. Numerical solution of ninth order boundary value problems by Petrov-Galerkin method with Quintic B-splines as basis functions and Septic B-splines as weight functions. Procedia Eng. 2015, 127, 1227–1234. [Google Scholar] [CrossRef]
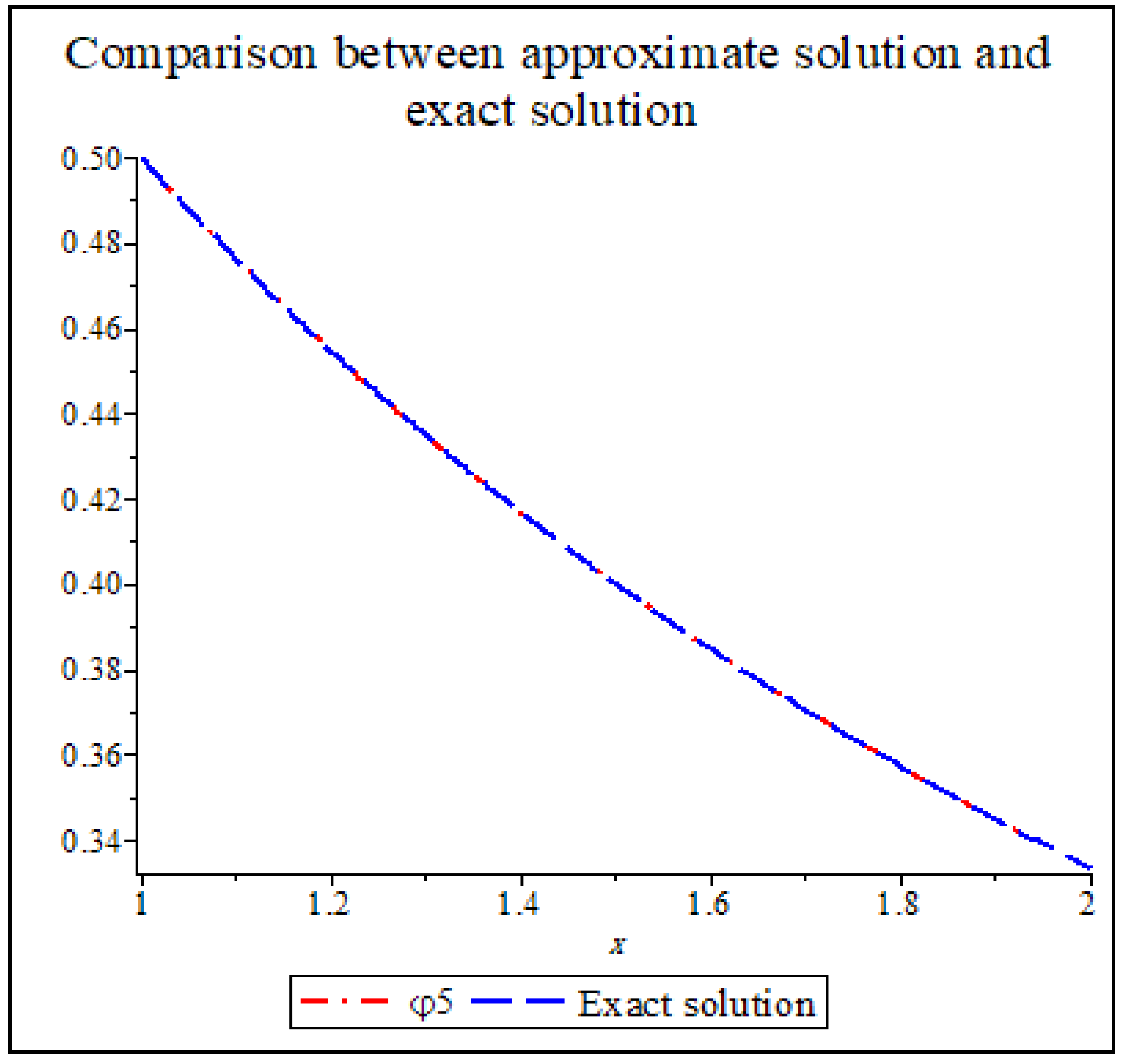
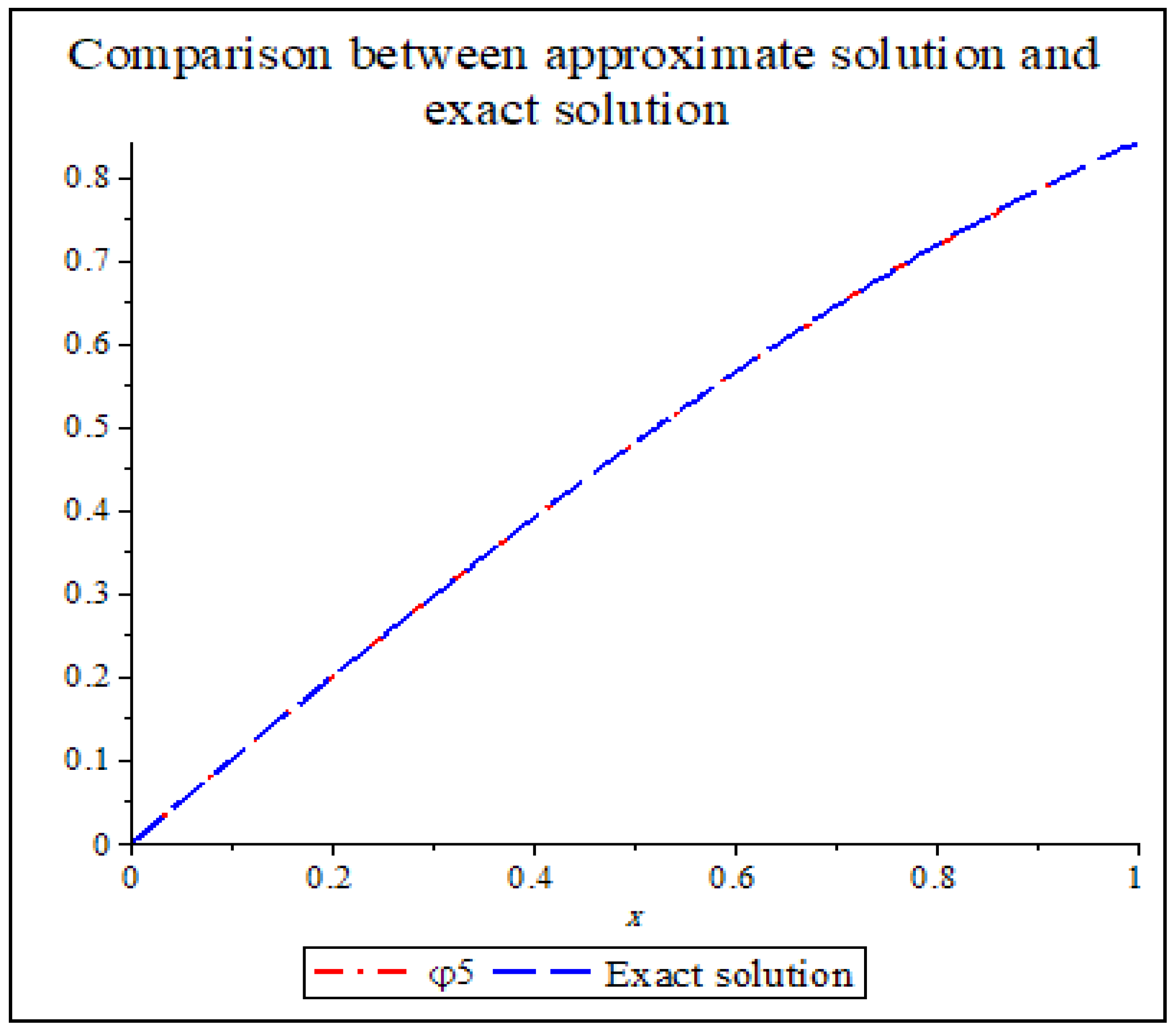



| Error in [27] | ||
|---|---|---|
| 1.0 | 1.5 | |
| 1.1 | ||
| 1.2 | ||
| 1.3 | ||
| 1.4 | . | |
| 1.5 | ||
| 1.6 | ||
| 1.7 | ||
| 1.8 | ||
| 1.9 | ||
| 2.0 |
| Error in [28] | ||
|---|---|---|
| 0.0 | 1.64899441 | 9.5923 |
| 0.1 | 7.7856 | |
| 0.2 | 2.7231 | |
| 0.3 | ||
| 0.4 | 7.7730 | |
| 0.5 | 9.7145 | |
| 0.6 | 1.0502 | |
| 0.7 | ||
| 0.8 | 6.8407 | |
| 0.9 | 2.7069 | |
| 1.0 | 1.5676 |
| VIMHP [29] | ||
|---|---|---|
| 0.0 | 3.00000000 | 0.0 |
| 0.1 | 1.28946045 | 1.0 |
| 0.2 | 8.71505433 | |
| 0.3 | 2.40516757 | 1.0 |
| 0.4 | 4.45866002 | 2.0 |
| 0.5 | 6.400647286 | 3.1 |
| 0.6 | 7.43254934 | |
| 0.7 | 6.90319620 | 4.1 |
| 0.8 | 4.71067442 | 3.1 |
| 0.9 | 1.70573303 | 1.4 |
| 1.0 | 2.52865000 | 0.0 |
| VIMHP [30] | ||
|---|---|---|
| 0.0 | 7.24695891 | 0.0 |
| 0.1 | 3.05370438 | 5.28944 |
| 0.2 | 3.23715191 | 6.44606 |
| 0.3 | 1.12228840 | 2.38427 |
| 0.4 | 2.14964709 | 5.20559 |
| 0.5 | 2.80162697 | 8.11431 |
| 0.6 | 2.62088240 | 9.55209 |
| 0.7 | 1.73155372 | 8.30543 |
| 0.8 | 7.37260050 | 4.67351 |
| 0.9 | 1.0113907 | 1.04882 |
| 1.0 | 1.0000000 | 3.90259 |
| Error in [31] | ||
|---|---|---|
| 0.1 | 1.862645 | |
| 0.2 | 7.301569 | |
| 0.3 | 9.834766 | |
| 0.4 | 1.221895 | |
| 0.5 | 8.344650 | |
| 0.6 | ||
| 0.7 | ||
| 0.8 | ||
| 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AL-Zaid, N.; AL-Refaidi, A.; Bakodah, H.; AL-Mazmumy, M. Solution of Second- and Higher-Order Nonlinear Two-Point Boundary-Value Problems Using Double Decomposition Method. Mathematics 2022, 10, 3519. https://doi.org/10.3390/math10193519
AL-Zaid N, AL-Refaidi A, Bakodah H, AL-Mazmumy M. Solution of Second- and Higher-Order Nonlinear Two-Point Boundary-Value Problems Using Double Decomposition Method. Mathematics. 2022; 10(19):3519. https://doi.org/10.3390/math10193519
Chicago/Turabian StyleAL-Zaid, Nawal, Amani AL-Refaidi, Huda Bakodah, and Mariam AL-Mazmumy. 2022. "Solution of Second- and Higher-Order Nonlinear Two-Point Boundary-Value Problems Using Double Decomposition Method" Mathematics 10, no. 19: 3519. https://doi.org/10.3390/math10193519
APA StyleAL-Zaid, N., AL-Refaidi, A., Bakodah, H., & AL-Mazmumy, M. (2022). Solution of Second- and Higher-Order Nonlinear Two-Point Boundary-Value Problems Using Double Decomposition Method. Mathematics, 10(19), 3519. https://doi.org/10.3390/math10193519





