Extra Edge Connectivity and Extremal Problems in Education Networks

Abstract

Extra edge connectivity and diagnosability have been employed to investigate the fault tolerance properties of network structures. The p-extra edge connectivity ${\lambda }_p(\Gamma )$ of a graph $\Gamma$ was introduced by Fàbrega and Fiol in 1996. In this paper, we find the exact values of p-extra edge connectivity of some special graphs. Moreover, we give some upper and lower bounds for ${\lambda }_p(\Gamma )$, and graphs with ${\lambda }_p(\Gamma )=1,2,⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-1,⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋$ are characterized. Finally, we obtain the three extremal results for the p-extra edge connectivity.

1. Introduction

The concept of education networks was proposed by Vicki A. Davis during the Economist debate on social networking technologies in education [1]. Networks with a small-world topology are distinguished by the characteristics of their connections, allowing two nodes, distant from each other, to be linked by a shorter path. Arcos-Argudo [2] studied a small-world network in the area of education sciences in particular in the integration of teaching cloisters in the world system of higher education. Such an education network plays a central role within a multi-processor systems, and many efforts have been made to investigate various fault tolerance properties of these network structures; see [3].

Networks can be summarized as nodes and linkages. This means that they are components of various kinds (people, schools, universities, and other kinds of organizations) that are connected in some larger pattern, whether consciously or unconsciously, by one or more types of connectedness, such as values, ideas, friends, and acquaintances, likes, exchange, routes of transportation, and communications channels. An education network is a process of developing and maintaining connections with people and information and communicating in such a way so as to support one another’s learning. This definition’s key concept is connections. It adopts a relational stance in which learning takes place both in relation to others and in relation to learning resources. An education network is meant to assist in developing relationships between learners and their interpersonal communities, knowledge contexts, and digital tools in both theory and practice.

For any subset Y of $V(\Gamma )$, let $\Gamma \left[Y\right]$ denote the subgraph induced by Y, and $E\left[Y\right]$ the edge set of $\Gamma \left[Y\right]$. Similarly, for any subset Z of $E(\Gamma )$, let $\Gamma \left[Z\right]$ denote the subgraph induced by Z. We use $\Gamma -Y$ to denote the subgraph of $\Gamma$ obtained by deleting all the vertices of Y and the edges incident with them. Similarly, we use $\Gamma -Z$ to denote the subgraph of $\Gamma$ obtained by deleting all the edges of Z. If $Y=\left\{v\right\}$ and $Z=\left\{e\right\}$, the subgraphs $\Gamma -Y$ and $\Gamma -Z$ will be written as $\Gamma -v$ and $\Gamma -e$ for short, respectively. To denote the path, cycle, wheel, complete, and complete bipartite graphs of order n, we use $P_n$, $C_n$, $W_n$, $K_n$, and $K_{a,b}(a+b=n,a\ge b)$, respectively. The connectivity of a graph $\Gamma$, written $\kappa (\Gamma )$, is the order of a minimum vertex subset $S\subseteq V(\Gamma )$ such that $\Gamma -S$ is disconnected or has only one vertex. The edge connectivity of $\Gamma$, written $\lambda (\Gamma )$, is the minimum size of an edge subset $M\subseteq E(\Gamma )$ such that $\Gamma -M$ is disconnected. The extremal graphs with respect to various topological descriptors of graphs with given connectivity and edge connectivity have been studied in [4,5] and the references therein. We skip the definitions of other standard graph-theoretical notions, as these can be found in [6] and other textbooks.

The concept of p-extra connectivity was introduced by Fàbrega and Fiol [7]. A vertex set S is said to be a cutset if $\Gamma -S$ is disconnected. If every component of $\Gamma -S$ has at least $p+1$ vertices (p is a non-negative integer), then the cutset S is called an $R_p$ cutset. The p-extra connectivity of a graph $\Gamma$, denoted by ${\kappa }_p(\Gamma )$, is defined as the minimum cardinality over all $R_p$ cutsets of $\Gamma$ when $\Gamma$ has at least one $R_p$ cutset.

As a natural counterpart of p-extra connectivity, Fàbrega and Fiol introduced the concept of p-extra edge connectivity in [7]. Let $X\subseteq E(\Gamma )$. If $\Gamma -X$ is disconnected, then the subset of edges X is said to be an edge cutset. If every component of $\Gamma -X$ has at least $p+1$ vertices (p is a non-negative integer), then the edge cutset X is called an $R_p$-edge cutset. The p-extra edge connectivity of $\Gamma$, denoted by ${\lambda }_p(\Gamma )$, is then defined as the minimum cardinality over all $R_p$-edge cutsets of $\Gamma$ when $\Gamma$ has at least one $R_p$-edge cutset. It is clear that $\kappa (\Gamma )={\kappa }_0(\Gamma )$ and $\lambda (\Gamma )={\lambda }_0(\Gamma )$ for any connected non-complete graph $\Gamma$.

The maximum number of identifiable faulty vertices following a specific fault-tolerant model is referred to as its associated diagnosability, which has attracted much attention in the research community, and several results, including those of p-extra diagnosability related to p-extra connectivity for various network structures, have been obtained. For more details of the mathematical properties, we refer to [3,7,8,9,10,11,12,13,14,15,16,17].

Proposition 1.

Let Γ be a connected graph with a non-negative integer p. Then,

$${\lambda }_p(\Gamma )\le {\lambda }_{p+1}(\Gamma ).$$

Proof. 

By deleting ${\lambda }_{p+1}(\Gamma )$ edges from $\Gamma$, one can see that the resulting graph is disconnected and each connected component has at least $p+2$ vertices. It is clear that each connected component has at least $p+1$ vertices. So, ${\lambda }_p(\Gamma )\le {\lambda }_{p+1}(\Gamma )$. □

Proposition 2.

Let H be a spanning subgraph of connected graph Γ. Then, ${\lambda }_0\left(H\right)\le {\lambda }_0(\Gamma )$.

The property in Proposition 2 is not true for $p\ge 1$.

Remark 1.

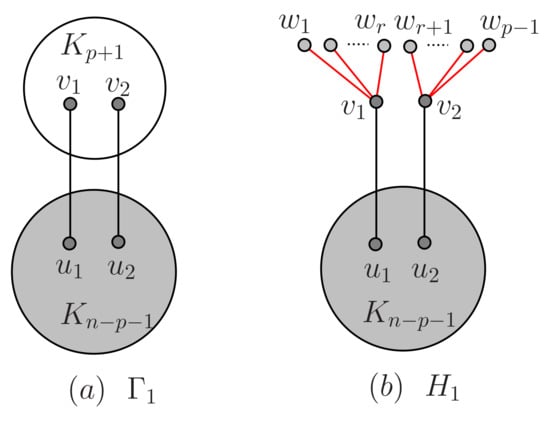
Let ${\Gamma }_1$ be a graph obtained from two cliques $K_{n-p-1},K_{p+1}$ by adding two edges $u_1{v}_1,u_2{v}_2$, where $1\le p\le \lfloor \frac{n-2}{2}\rfloor$, $u_1,u_2\in V\left(K_{n-p-1}\right)$, and $v_1,v_2\in V\left(K_{p+1}\right)$; see Figure 1a. Let $H_1$ be a graph obtained from a clique $K_{n-p-1}$ and two stars $K_{1,r},K_{1,p-r-1}$ with centres of $v_1,v_2$, respectively, by identifying one leaf $u_1$ and a vertex of $K_{n-p-1}$ and another leaf $u_2$ and another vertex of $K_{n-p-1}$ (see Figure 1b). It is clear that $H_1$ is a spanning subgraph of ${\Gamma }_1$. Note that ${\lambda }_p\left({\Gamma }_1\right)\ge \lambda \left({\Gamma }_1\right)=2$. By deleting two edges $u_1{v}_1,u_2{v}_2$, the remaining graph is the disjoint union of $K_{n-p-1}$ and $K_{p+1}$, and hence ${\lambda }_p\left({\Gamma }_1\right)\le 2$. Therefore, ${\lambda }_p\left({\Gamma }_1\right)=2$. For any two edges $e_1,e_2\in E\left(H_1\right)$, if neither $e_1$ nor $e_2$ are cut edges, then $H_1-e_1-e_2$ is connected. Suppose that one of them $e_1,e_2$ is a cut edge. Then, there is an isolated vertex in $H_1-e_1-e_2$ or there is a component of $H_1-e_1-e_2$ having at most p vertices. Since $p\ge 1$, it follows that there is a component of $H_1-e_1-e_2$ having at most p vertices. It is clear that ${\lambda }_p\left(H_1\right)\ge 3>2={\lambda }_p\left({\Gamma }_1\right)$.

Figure 1. Graphs ${\Gamma }_1$ and $H_1$.

Proposition 3.

Let Γ be a graph with p-extra edge connectivity. Then,

$$0\le p\le ⌊\frac{n-2}{2}⌋.$$

Proof. 

From the definition of ${\lambda }_p(\Gamma )$, we delete some edges, and the resulting graph has exactly two components, and each component has at least $p+1$ vertices. Then, $n\ge 2(p+1)$, and hence $0\le p\le \lfloor \frac{n-2}{2}\rfloor$. □

The solutions to the following problems will provide insights into designing interconnection networks with respect to the number of edges and p-extra edge connectivity of the networks.

• Problem 1. Let $\Theta (n,k)$ be the set of all graphs of order n with p-extra edge connectivity k (n and k are positive integers). Determine the minimum integer $s(n,k)$ such that $s(n,k)=\min \left\{\right|E(\Gamma )|:\Gamma \in \Theta (n,k\left)\right\}$.
• Problem 2. Determine the minimum integer $f(n,k)$ such that for every connected graph $\Gamma$ of order n (n and k are positive integers), so that if $f(n,k)\le \left|E\right(\Gamma \left)\right|$, then ${\lambda }_p(\Gamma )\ge k$.
• Problem 3. Determine the maximum integer $g(n,k)$ such that for every graph $\Gamma$ of order n (n and k are positive integers), so that if $g(n,k)\ge \left|E\right(\Gamma \left)\right|$, then ${\lambda }_p(\Gamma )\le k$.

In Section 2, we first give the exact values of the p-extra edge connectivity of complete graphs, complete bipartite graphs, complete multipartite graphs, paths, cycles, and wheels. We prove that ${\lambda }_p(\Gamma )\le \lceil \frac{n}{2}\rceil \lfloor \frac{n}{2}\rfloor -\lceil \frac{diam(\Gamma )+1}{2}\rceil \lfloor \frac{diam(\Gamma )+1}{2}\rfloor +1$ for $diam(\Gamma )\ge 2p+1$; and ${\lambda }_p(\Gamma )\le \lceil \frac{n}{2}\rceil \lfloor \frac{n}{2}\rfloor -(\lceil \frac{diam(\Gamma )+1}{2}\rceil -3)(p+1)$ for $5\le diam(\Gamma )\le 2p$. We also prove that ${\lambda }_p(\Gamma )\le (p+1)(n-p-1)$ for $\kappa (\Gamma )\ge p+2$; and ${\lambda }_p(\Gamma )\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-(n-p-1)(p+1-\kappa (\Gamma ))$ for $1\le \kappa (\Gamma )\le p+1$. For a connected graph $\Gamma$ of order n, we prove that $1\le {\lambda }_p(\Gamma )\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋$ for $0\le p\le ⌊\frac{n-3}{2}⌋$ in Section 3. Graphs with ${\lambda }_p(\Gamma )=1,2,⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-1,⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋$ are characterized in Section 4. Finally, we obtain the extremal results for the p-extra connectivity in Section 5.

2. On $\mathit{p}$-Extra Edge Connectivity of Some Special Graphs

In this section, we obtain the exact values for ${\lambda }_p\left(G\right)$ when G is a special graph.

Proposition 4.

Let p be a non-negative integer with $0\le p\le ⌊\frac{n-2}{2}⌋$. Then,

$${\lambda }_p\left(K_n\right)=(p+1)(n-p-1).$$

Proof. 

It is easy to see that ${\lambda }_p\left(K_n\right)\le (p+1)(n-p-1)$. From the definition of ${\lambda }_p\left(K_n\right)$, there exists an edge set X of $K_n$ such that $K_n-X$ has two components, say $C_1,C_2$, such that $\left|V\right(C_i\left)\right|\ge p+1$, where $\left|X\right|={\lambda }_p\left(K_n\right)$. Therefore, we have

$${\lambda }_p\left(K_n\right)=\left|X\right|\ge |V\left(C_1\right)\left|\right|V\left(C_2\right)| \ge (p+1)(n-p-1),$$

and hence ${\lambda }_p\left(K_n\right)=(p+1)(n-p-1)$. □

Proposition 5.

$\left(1\right)$Let $\Gamma =K_{a,b}(a\ge b\ge 2)$. Then, $p=0$ and ${\lambda }_p(\Gamma )=b$.

$\left(2\right)$Let $K_{n_1,n_2,\dots ,n_r}$ $(n_1\le n_2\le \cdots \le n_r)$ be a complete multipartite graph with integer $r\ge 3$. Then, $p=0$ and

$${\lambda }_p\left(K_{n_1,n_2,\dots ,n_r}\right)=\sum _{i=1}^{r-1}{n}_i.$$

Proof. 

$\left(1\right)$ By deleting any edge in $K_{a,b}$, the resulting graph is a connected bipartite graph. If we require the resulting graph to not be connected, then we must delete all the edges that are incident with one vertex. Then, $p=0$ and hence ${\lambda }_p\left(K_{a,b}\right)=b$ as $a\ge b\ge 2$.

$\left(2\right)$ This part of the proof is very similar to the proof of $\left(1\right)$. □

Proposition 6.

Let p be a non-negative integer.

$\left(1\right)$If $\Gamma =P_n(n\ge 3)$, then $0\le p\le \lfloor \frac{n-2}{2}\rfloor$ and ${\lambda }_p(\Gamma )=1$.

$\left(2\right)$If $\Gamma =C_n(n\ge 3)$, then $0\le p\le \lfloor \frac{n-2}{2}\rfloor$ and ${\lambda }_p(\Gamma )=2$.

$\left(3\right)$If $\Gamma =W_n(n\ge 5)$, then $0\le p\le \lfloor \frac{n-3}{2}\rfloor$ and ${\lambda }_p(\Gamma )=p+3$.

Proof. 

$\left(1\right)$ From the definition of ${\lambda }_p\left(P_n\right)$, we have ${\lambda }_p\left(P_n\right)\ge \lambda \left(P_n\right)=1$. Now we have to prove that ${\lambda }_p\left(P_n\right)\le 1$. For this, let $P_n=u_1{u}_2\dots u_n$. Choose $e=u_{\lceil n/2\rceil }{u}_{\lfloor n/2\rfloor }$. Since $0\le p\le \lfloor \frac{n-2}{2}\rfloor$, one can easily see that each component of $\Gamma -e$ has $p+1$ vertices, and hence ${\lambda }_p\left(P_n\right)\le 1$. So, ${\lambda }_p\left(P_n\right)=1$.

$\left(2\right)$ From the definition of ${\lambda }_p\left(C_n\right)$, we have ${\lambda }_p\left(C_n\right)\ge \lambda \left(C_n\right)=2$. It suffices to show ${\lambda }_p\left(C_n\right)\le 2$. Let $C_n=u_1{u}_2\dots u_n{u}_1$. Choose $e=u_n{u}_1$ and $e^{\prime }=u_{\lfloor n/2\rfloor }{u}_{\lceil n/2\rceil }$. Since $0\le p\le \lfloor \frac{n-2}{2}\rfloor$, one can easily see that each component of $\Gamma -e-e^{\prime }$ has $p+1$ vertices, and hence ${\lambda }_p\left(C_n\right)\le 2$. So, ${\lambda }_p\left(C_n\right)=2$.

$\left(3\right)$ Let u be the center of $W_n$, and $W_n-u=C_{n-1}$, and $V\left(C_{n-1}\right)=\{v_1,v_2,\dots ,v_{n-1}\}$. To show ${\lambda }_p\left(W_n\right)\ge p+3$, we need to show that for any $Y\subseteq E(\Gamma )$ and $\left|Y\right|\le p+2$, there are two components of $W_n-Y$, say $C_1,C_2$. Clearly, $u\in V\left(C_1\right)$ or $u\in V\left(C_2\right)$. Without loss of generality, we can assume that $u\in V\left(C_1\right)$. Then, the edges from u to $C_1$ must belong to $C_2$, and we have at least $p+1$ edges. Since there are at least two edges from $C_2$ to $C_1-u$, it follows that there are at least $p+3$ edges in Y, a contradiction. Now, we have to prove that ${\lambda }_p\left(W_n\right)\le p+3$. Choose $Y=\left\{u{v}_i\right|1\le i\le p+1\}\cup \{v_1{v}_{n-1},v_{p+1}{v}_{p+2}\}$. Since $0\le p\le \lfloor \frac{n-3}{2}\rfloor$, one can see easily that each component has $p+1$ vertices, and hence ${\lambda }_p\left(W_n\right)\le p+3$. So, ${\lambda }_p\left(W_n\right)=p+3$. □

3. Bounds on ${\mathbf{\lambda }}_{\mathit{p}}\left(\mathsf{\Gamma }\right)$

We now give some bounds on ${\lambda }_p(\Gamma )$.

Proposition 7.

Let Γ be a connected graph of order n with a non-negative integer p such that $0\le p\le ⌊\frac{n-3}{2}⌋$. Then,

$$\lambda (\Gamma )\le {\lambda }_p(\Gamma )\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋.$$

Moreover, the bounds are sharp.

Proof. 

From the definition of ${\lambda }_p(\Gamma )$, we have ${\lambda }_p(\Gamma )\ge \lambda (\Gamma )$. From the definition, by deleting ${\lambda }_p(\Gamma )$ edges in $\Gamma$, there are exactly two components, say $C_1,C_2$, such that each of them has at least $p+1$ vertices. Then,

$${\lambda }_p(\Gamma )\le |C_1\left|\right|C_2| = |C_1\left|\right(n-|C_1\left|\right)\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋.$$

□

Corollary 1.

Let Γ be a connected graph of order n with a non-negative integers p such that $0\le p\le ⌊\frac{n-3}{2}⌋$. Then,

$$1\le {\lambda }_p(\Gamma )\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋.$$

Moreover, the bounds are sharp.

We obtain some upper bounds on ${\lambda }_p(\Gamma )$ in terms of n, p, and $diam(\Gamma )$.

Theorem 1.

Let Γ be a connected graph of order n with a non-negative integer p such that $0\le p\le ⌊\frac{diam(\Gamma )}{2}⌋-1$.

$\left(1\right)$If $diam(\Gamma )\ge 2p+1$, then

$${\lambda }_p(\Gamma )\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-⌈\frac{diam(\Gamma )+1}{2}⌉⌊\frac{diam(\Gamma )+1}{2}⌋+1.$$

Moreover, the bound is sharp.

$\left(2\right)$If $5\le diam(\Gamma )\le 2p$, then

$${\lambda }_p(\Gamma )\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-\left(⌈\frac{diam(\Gamma )+1}{2}⌉-3\right)(p+1).$$

Proof. 

$\left(1\right)$ Let $diam(\Gamma )=d$ and let $P_{d+1}=v_1{v}_2\dots v_{d+1}$ be a diametral path in $\Gamma$. Choose the edge cutset $X\subseteq E(\Gamma )$ such that $\Gamma -X$ has exactly two components $C_1,C_2$ such that $C_1$ contains that sub-path $v_1{v}_2\dots v_{\lfloor \frac{d+1}{2}\rfloor }$ and $C_2$ contains that sub-path $v_{\lfloor \frac{d+1}{2}\rfloor +1}{v}_{\lfloor \frac{d+1}{2}\rfloor +2}\dots v_{d+1}$. Since $d\ge 2p+1$, one can easily see that $C_i(i=1,2)$ has at least $p+1$ vertices. It is clear that

$$\begin{array}{ccc}\hfill \left|X\right|& \le & |V\left(C_1\right)\left|\right|V\left(C_2\right)| -⌊\frac{d+1}{2}⌋⌈\frac{d+1}{2}⌉+1\hfill \\ & \le & ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-⌈\frac{diam(\Gamma )+1}{2}⌉⌊\frac{diam(\Gamma )+1}{2}⌋+1.\hfill \end{array}$$

$\left(2\right)$ From the definition of ${\lambda }_p(\Gamma )$, there exists an edge cutset X such that $\Gamma -X$ has two components $C_1,C_2$ and each component $C_i$ has at least $p+1$ vertices. Let $diam(\Gamma )=d$ and let $P_{d+1}=v_1{v}_2\dots v_{d+1}$ be a diametral path in $\Gamma$. Then, there exists a component $C_1$ containing at least $\lceil \frac{d+1}{2}\rceil$ vertices in $V\left(P_{d+1}\right)$, say $v_{i_1},v_{i_2},\dots ,v_{i_t}$, where $t\ge \lceil \frac{d+1}{2}\rceil$. For any vertex $w\in V\left(C_2\right)$, there exists at most three vertices in $\{v_{i_1},v_{i_2},\dots ,v_{i_t}\}$ adjacent to w, and hence there are at least $t-3$ vertices in $\{v_{i_1},v_{i_2},\dots ,v_{i_t}\}$ not adjacent to w. Since $\left|V\right(C_2\left)\right|\ge p+1$, it follows that there are at least $(p+1)(t-3)$ edges from $C_1$ to $C_2$ in $\overline{\Gamma }$. Thus, we have

$$\left|X\right|\le |V\left(C_1\right)\left|\right|V\left(C_2\right)| -(p+1)(t-3)\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-\left(⌈\frac{diam(\Gamma )+1}{2}⌉-3\right)(p+1).$$

□

Example 1.

Let $\Gamma =P_n$. Then, $diam(\Gamma )=n-1$ and

$${\lambda }_p(\Gamma )=1=⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-⌈\frac{diam(\Gamma )+1}{2}⌉⌊\frac{diam(\Gamma )+1}{2}⌋+1,$$

which means that the upper bound in$\left(1\right)$of Theorem 1 is sharp.

Theorem 2.

Let Γ be a connected graph of order n with a non-negative integer p such that $0\le p\le ⌊\frac{n-2}{2}⌋$.

$\left(1\right)$If $\kappa (\Gamma )\ge p+2$, then

$${\lambda }_p(\Gamma )\le (p+1)(n-p-1).$$

Moreover, the bound is sharp.

$\left(2\right)$If $1\le \kappa (\Gamma )\le p+1$, then

$${\lambda }_p(\Gamma )\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-(n-p-1)(p+1-\kappa (\Gamma )).$$

Proof. 

$\left(1\right)$ Choose $S\subseteq V(\Gamma )$ and $\left|S\right|=p+1$ such that $\Gamma \left[S\right]$ is connected. Let $X=E_{\Gamma }[S,\overline{S}]$, where $\overline{S}=V(\Gamma )-S$. Clearly, $\Gamma -X$ is not connected. Since $\kappa (\Gamma )\ge p+2$, it follows that $\Gamma \left[\overline{S}\right]$ is also connected. It is clear that $|\overline{S}|=n-p-1$ and ${\lambda }_p(\Gamma )\le \left|X\right| = |E_{\Gamma }[S,\overline{S}]| \le (p+1)(n-p-1)$.

$\left(2\right)$ From the definition of ${\lambda }_p(\Gamma )$, there exists an edge cutset X such that $\Gamma -X$ has two components $C_1,C_2$ and each component $C_i$ has at least $p+1$ vertices. Let $\kappa (\Gamma )=r$. Then, there exists a vertex set $S\subseteq V(\Gamma )$ with $\left|S\right|=r$ such that $\Gamma -S$ is not connected. Let $|S\cap V(C_1\left)\right|=x$. Then, $|S\cap V(C_2\left)\right|=r-x$, and hence

$$\begin{array}{ccc}\hfill {\lambda }_p(\Gamma )& \le & |V\left(C_1\right)\left|\right|V\left(C_2\right)| - (|V\left(C_1\right)| - x)\left(\right|V\left(C_2\right)| - r + x)\hfill \\ & \le & ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-(n-p-1)(p+1-\kappa (\Gamma )).\hfill \end{array}$$

□

Example 2.

Let $\Gamma =K_n$. From Proposition 4, we have ${\lambda }_p(\Gamma )=(p+1)(n-p-1)$, which means that the upper bound in$\left(1\right)$of Theorem 2 is sharp.

4. Graphs with Given $\mathit{p}$-Extra Edge Connectivity

From Corollary 1, for $0\le p\le ⌊\frac{n-3}{2}⌋$, we have $1\le {\lambda }_p(\Gamma )\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋$. We first characterize graphs with ${\lambda }_p(\Gamma )=⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋$.

Theorem 3.

Let Γ be a connected graph of order $n(n\ge 4)$ with a non-negative integer p such that $0\le p\le ⌊\frac{n-2}{2}⌋$. Then, ${\lambda }_p(\Gamma )=⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋$ if and only if Γ is a complete graph of order n and $p=⌊\frac{n}{2}⌋-1$.

Proof. 

Suppose that $\Gamma$ is a complete graph of order n and $p=⌊\frac{n}{2}⌋-1$. From the definition of ${\lambda }_p(\Gamma )$, there exists an edge cutset Y such that each component has $p+1=⌊\frac{n}{2}⌋$ vertices, and hence there are exactly two components: one of them has $⌊\frac{n}{2}⌋$ vertices, and the other has $⌈\frac{n}{2}⌉$ vertices. So, we have ${\lambda }_p(\Gamma )=⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋$.

Suppose that ${\lambda }_p(\Gamma )=⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋$. Then, there exists an edge set $\left|Y\right|=⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋$ such that each component of $\Gamma -Y$ has at least $p+1$ vertices. We will then analyse the number of components, the exact value of p, and the structure of each component.

Claim 1.

There are exactly two components in $\Gamma -Y$.

Proof. 

Assume, to the contrary, that there are at least three components in $\Gamma -Y$. Choose $e\in Y$. Then, $\Gamma -Y+e$ has at least two components and each component has at least $p+1$ vertices, and hence ${\lambda }_p(\Gamma )\le \left|Y\right|-1=⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-1$, a contradiction. □

From Claim 1, there are exactly two components, say $C_1,C_2$, in $\Gamma -Y$. Then we can assume $|V\left(C_1\right)|=⌈\frac{n}{2}⌉$ and $|V\left(C_2\right)|=⌊\frac{n}{2}⌋$. Then, $Y=E_{\Gamma }[V\left(C_1\right),V\left(C_2\right)]$.

Claim 2.

$p=⌊\frac{n}{2}⌋-1$.

Proof. 

Assume, to the contrary, that $p\le ⌊\frac{n}{2}⌋-2$. Then, we choose $v\in V\left(C_2\right)$ such that $C_2-v$ is connected. Let $Y^{\prime }=E_{\Gamma }[V\left(C_1\right)\cup \left\{v\right\},V\left(C_2\right)-v]$. Then, $|Y^{\prime }|<⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋=\left|Y\right|$ and $\Gamma -Y^{\prime }$ is disconnected and each component has $p+1$ vertices, a contradiction. □

From Claim 2, $p=⌊\frac{n}{2}⌋-1$.

Claim 3.

For each $C_i(i=1,2)$, $C_i$ is complete.

Proof. 

Assume, to the contrary, that $C_i$ is not complete. Without loss of generality, we assume that $C_1$ is not complete. Then, there exist two vertices $u,v\in V\left(C_1\right)$ such that $uv\notin E(\Gamma )$. Choose $w\in V\left(C_2\right)$. Let $C_1^{\prime }=C_1-v+w$, $C_2^{\prime }=C_2-w+v$, and $Y^{\prime }=E_{\Gamma }[V\left(C_1^{\prime }\right),V\left(C_2^{\prime }\right)]$. It is clear that $\Gamma -Y^{\prime }$ has two components and each component has at least $p+1$ vertices, and hence ${\lambda }_p(\Gamma )\le \left|Y^{\prime }\right|\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-1$, a contradiction. □

From Claim 3, $\Gamma$ is a complete graph of order n. □

Next, we characterize graphs with ${\lambda }_p(\Gamma )=⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-1$.

Theorem 4.

Let Γ be a connected graph of order $n(n\ge 6)$ with a non-negative integer p such that $0\le p\le ⌊\frac{n-2}{2}⌋$. Then, ${\lambda }_p(\Gamma )=⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-1$ if and only if $p=⌊\frac{n}{2}⌋-1$ and $\Gamma =K_n-e$, where $e\in E\left(K_n\right)$.

The proof for Theorem 4 is similar to the proof of Theorem 3, since we characterize the graphs by deleting edges from the complete graph $K_n$.

We now characterize the graphs when ${\lambda }_p(\Gamma )=1$.

Observation 1.

Let Γ be a connected graph of order n with a non-negative integer p such that $0\le p\le ⌊\frac{n-2}{2}⌋$. Then, ${\lambda }_p(\Gamma )=1$ if and only if there exists a cut edge e in Γ such that each component of $\Gamma -e$ has at least $p+1$ vertices.

We characterize the graphs when ${\lambda }_p(\Gamma )=2$ in the following theorem.

Theorem 5.

Let Γ be a connected graph of order n with a non-negative integer p such that $0\le p\le ⌊\frac{n-2}{2}⌋$. Then, ${\lambda }_p(\Gamma )=2$ if and only if Γ satisfies one of the following conditions:

$\left(1\right)$$\lambda (\Gamma )=2$and there exist cut edge set with $e_1,e_2$ in Γ such that each component of $\Gamma -e_1-e_2$ has at least $p+1$ vertices.

$\left(2\right)$$\lambda (\Gamma )=1$, and for each cut edge e, there exists a component of $\Gamma -e$ such that it has at most p vertices, and there exist two non-cut edges $e_1,e_2$ in Γ such that each component of $\Gamma -e_1-e_2$ has at least $p+1$ vertices.

Proof. 

Suppose that $\left(1\right)$ holds. It is clear that ${\lambda }_p(\Gamma )\ge \lambda (\Gamma )=2$. Since there exist two edges $e_1,e_2$ in $\Gamma$ such that each component of $\Gamma -e_1-e_2$ has at least $p+1$ vertices, it follows that ${\lambda }_p(\Gamma )\le 2$, and so ${\lambda }_p(\Gamma )=2$. Suppose that $\left(2\right)$ holds. Since for each cut edge e, there exists a component of $\Gamma -e$ such that it has at most p vertices, it follows that ${\lambda }_p(\Gamma )\ge 2$. Since there exist two non-cut edges $e_1,e_2$ in $\Gamma$ such that each component of $\Gamma -e_1-e_2$ has at least $p+1$ vertices, it follows that ${\lambda }_p(\Gamma )\le 2$, and so ${\lambda }_p(\Gamma )=2$.

Conversely, we suppose ${\lambda }_p(\Gamma )=2$. Then $\lambda (\Gamma )=2$ or $\lambda (\Gamma )=1$. If $\lambda (\Gamma )=2$, then it follows from ${\lambda }_p(\Gamma )=2$ that there exist two cut edges $e_1,e_2$ in $\Gamma$ such that each component of $\Gamma -e_1-e_2$ has at least $p+1$ vertices.

Suppose $\lambda (\Gamma )=1$. Then, we have the following claim.

Claim 4.

For each cut edge e, there exists a component of $\Gamma -e$ such that it has at most p vertices.

Proof. 

Assume, to the contrary, that there exists a cut edge $e^{\prime }$ such that each component of $\Gamma -e^{\prime }$ has $p+1$ vertices, which contradicts the fact ${\lambda }_p(\Gamma )=2$. □

From Claim 4, $\left(1\right)$ holds. Since ${\lambda }_p(\Gamma )=2$, it follows that there exist two edges $e_1,e_2$ in $\Gamma$ such that each component of $\Gamma -e_1-e_2$ has at least $p+1$ vertices.

Claim 5.

Neither $e_1$ nor $e_2$ are cut edges.

Proof. 

Assume, to the contrary, that there is at least one cut edge, say $e_1$. Then, there are two components of $\Gamma -e_1$, say $C_1,C_2$. From Claim 4, there exists a component of $\Gamma -e_1$, say $C_1$, such that $C_1$ has at most p vertices in $\Gamma -e_1$. It is clear that $C_1$ has at most p vertices in $\Gamma -e_1-e_2$ or there exists a component of $C_1-e_2$ such that it has at most p vertices in $\Gamma -e_1-e_2$, which contradicts the fact there exist two edges $e_1,e_2$ in $\Gamma$ such that each component of $\Gamma -e_1-e_2$ has at least $p+1$ vertices. □

From Claim 5, $\left(2\right)$ holds. □

Example 3.

Let F be a graph of order n obtained from two complete graphs $K_{\lceil n/2\rceil }$ and $K_{\lfloor n/2\rfloor }$ by adding two edges between them. One can easily check that ${\lambda }_p\left(F\right)=2$.

5. On Problems 1, 2 and 3

We now discuss Problems 1, 2 and 3.

Let $F_n^k$ be a graph obtained from two stars $K_{1,p+k},K_{1,n-p-3}$ with centres $u,v$, respectively, by identifying $k-1$ leaves, say $w_1,w_2,\dots ,w_{k-1}$ and then adding a new edge $uv$ (Figure 2).

Figure 2. Graph $F_n^k$.

Lemma 1.

For three integers $n,p,k$ with $1\le p\le ⌊\frac{n-2}{2}⌋$ and $1\le k\le n-p-1$, we have

$${\lambda }_p\left(F_n^k\right)=k.$$

Proof. 

Choose $Y=\left\{uv\right\}\cup \left\{u{w}_i\right|1\le i\le k-1\}$. Clearly, $F_n^k-Y$ is disconnected, each component of $F_n^k-Y$ has at least $p+1$ vertices, and hence ${\lambda }_p\left(F_n^k\right)\le k$. It suffices to show that ${\lambda }_p\left(F_n^k\right)\ge k$. We only need to prove that for any $Y\subseteq E\left(F_n^k\right)$ with $\left|Y\right|\le k-1$, if $F_n^k-Y$ is disconnected, then there is a component of $F_n^k-Y$ having at most p vertices. Since $p\ge 1$, it follows that there is no pendent edge in $F_n^k$ belonging to Y, that is, $Y\cap Z=\varnothing$, where $Z=\left\{u{u}_i\right|1\le i\le p+1\}\cup \left\{v{v}_i\right|1\le i\le n-k-p-2\}$. Furthermore, we have the following fact.

Fact 1.

For each $i(1\le i\le k-1)$, at most one of $u{w}_i,v{w}_i$ belongs to Y.

From Fact 1, $F_n^k-Y$ is connected, a contradiction. So, we have ${\lambda }_p\left(F_n^k\right)=k$. □

Proposition 8.

For three integers $n,p,k$ with $1\le p\le ⌊\frac{n-2}{2}⌋$ and $1\le k\le n-p-1$, we have

$$s(n,k)=n+k-2.$$

Proof. 

Let $\Gamma =F_n^k$. From Lemma 1, we obtain ${\lambda }_p\left(F_n^k\right)=k$, and so $s(n,k)\le n+k-2$.

Let $\Gamma$ be any connected graph of order n with ${\lambda }_p(\Gamma )=k$. Then, there exists an edge set $X\subseteq E(\Gamma )$ with $\left|X\right|=k$ such that $\Gamma -X$ has two components, say $C_1,C_2$. Therefore, $e(\Gamma )\ge e\left(C_1\right)+e\left(C_2\right)+k\ge \left(\right|V\left(C_1\right)|-1)+\left(\right|V\left(C_2\right)|-1)+k=n+k-2$, and so $s(n,k)\ge n+k-2$. Hence $s(n,k)=n+k-2$. □

From [14], $g(n,k)=s(n,k+1)-1$, and so the following result is immediate.

Corollary 2.

For three integers $n,p,k$ with $1\le p\le ⌊\frac{n-2}{2}⌋$ and $1\le k\le n-p-1$, we have

$$g(n,k)=n+k-2.$$

Lemma 2.

Let $n,k,p$ be three integers with $1\le p\le ⌊\frac{n-k-2}{2}⌋$. Let $H_k$ be a graph obtained from two cliques $K_{n-p-1},K_{p+1}$ by adding $k-1$ edges between them. Then,

$${\lambda }_p\left(H_k\right)=k-1.$$

Proof. 

Since $1\le p\le ⌊\frac{n-k-2}{2}⌋$, there exists a subset $Y=V\left(K_{k-1}\right)\subseteq V\left(H_k\right)$ such that $\Gamma -Y$ is not connected and each component has at least $p+1$ vertices, and hence ${\lambda }_p\left(H_k\right)\le k-1$. Clearly, ${\lambda }_p\left(H_k\right)\ge \kappa \left(H_k\right)=k-1$. So, ${\lambda }_p\left(H_k\right)=k-1$. □

Theorem 6.

Let $n,p,k$ be three integers with $1\le p\le ⌊\frac{n-k-2}{2}⌋$ and $1\le k\le (n-p-1)(p+1)$. Then,

$$f(n,k)=\left(\genfrac{}{}{0pt}{}{n}{2}\right)-(n-p-1)(p+1)+k.$$

Proof. 

We consider a graph $H_k$ defined in Lemma 2. Then, ${\lambda }_p\left(H_k\right)=k-1$. Since $|E\left(H_k\right)|=\left(\genfrac{}{}{0pt}{}{n}{2}\right)-(n-p-1)(p+1)+k-1$, it follows that $f(n,k)\ge \left(\genfrac{}{}{0pt}{}{n}{2}\right)-(n-p-1)(p+1)+k$.

Let $\Gamma$ be a graph with n vertices and $\left|E(\Gamma )\right|\ge \left(\genfrac{}{}{0pt}{}{n}{2}\right)-(n-p-1)(p+1)+k$. We have to prove that ${\lambda }_p(\Gamma )\ge k$. Assume, to the contrary, that ${\lambda }_p(\Gamma )\le k-1$. Then, there exists an edge set $Y\subseteq E(\Gamma )$ and $\left|Y\right|\le k-1$ such that each connected component of $\Gamma -Y$ has at least $p+1$ vertices. Let $C_1,C_2$ be the connected components of $\Gamma -Y$. Clearly, $\left|V\right(C_i\left)\right|\ge p+1$ for each $i=1,2$. Clearly, $\left|E(\Gamma )\right|\le \left(\genfrac{}{}{0pt}{}{n}{2}\right)-(n-p-1)(p+1)+k-1$, which contradicts $\left|E(\Gamma )\right|\ge \left(\genfrac{}{}{0pt}{}{n}{2}\right)-(n-p-1)(p+1)+k$. So, ${\lambda }_p(\Gamma )\ge k$, and hence $f(n,k)\le \left(\genfrac{}{}{0pt}{}{n}{2}\right)-(n-p-1)(p+1)+k$.

From the above, we conclude that $f(n,k)=\left(\genfrac{}{}{0pt}{}{n}{2}\right)-(n-p-1)(p+1)+k$. □

6. Concluding Remark

In this research, we studied the connectivity parameter to measure the reliability of education networks formed by education resources, including teachers, students, types of equipment, etc. The extremal problem studied in this paper shows that education networks keep their connections but use as few as links as possible to save education resources. This work can be used to design minimal education networks under some conditions.

In this paper, we presented several results including the upper and lower bounds on the p-extra edge connectivity of general graphs. We have proved that $1\le {\lambda }_p(\Gamma )\le ⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋$ for $0\le p\le ⌊\frac{n-2}{2}⌋$. Graphs with ${\lambda }_p(\Gamma )=⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋,⌈\frac{n}{2}⌉⌊\frac{n}{2}⌋-1,2,1$ for general $p(0\le p\le ⌊\frac{n-2}{2}⌋)$ are characterized in this paper. From Theorem 1, the classical $diam(\Gamma )$ is a natural upper bound of ${\lambda }_p(\Gamma )$, but there is no lower bound of ${\lambda }_p(\Gamma )$ in terms of $diam(\Gamma )$. From Theorem 1, the classical $\lambda (\Gamma )$ is a natural lower bound of ${\lambda }_p(\Gamma )$, but there is no upper bound of ${\lambda }_p(\Gamma )$ in terms of $\lambda (\Gamma )$.