An Extended Multi-Attributive Border Approximation Area Comparison Method for Emergency Decision Making with Complex Linguistic Information

Abstract

In recent years, different types of emergency events have taken place frequently around the world. Emergencies need to be addressed in the shortest possible time since inappropriate or delayed decisions may result in severe secondary disasters and economic losses. To make emergency decisions effectively within a limited time, a new emergency decision-making model is proposed in this study based on double hierarchy hesitant linguistic term sets (DHHLTSs) and the multi-attributive border approximation area comparison (MABAC) method. First, the performance assessment information on emergency solutions provided by domain experts is represented by the DHHLTSs, which are very useful for managing complex linguistic expressions in a prominent manner. Then, we make an extension of the MABAC method to determine the priority of alternative solutions and find out the optimal one for an emergency event. Furthermore, the criteria weights for emergency decision making are determined objectively with a maximum comprehensive method. Finally, a practical public health example is provided and a comparative analysis is performed to illustrate the applicability and advantages of the proposed emergency decision-making model.

1. Introduction

Over recent decades, many emergency events occurred unexpectedly all over the world, which brought about enormous losses of life and property, social and economic damage, and environment degradation [1,2,3]. For example, the Super Typhoon Lekima disaster in 2019 was characterized by a wide scope of influence and long duration. The direct economic losses amounted to CNY 53 billion, and 57 people unfortunately died. In the same year, the Sichuan forest fire accident caused the death of 31 firefighters. Because of high uncertainty and complex evolution, emergency events could hardly be prevented with the help of limited warning approaches [4,5]. To reduce the casualties, economic losses, and environment disruption caused by emergencies, it is of great significance for decision makers to make a timely emergency response and take immediate actions [6,7]. However, because of the dynamic environment, time urgency, and incomplete information, it is difficult to deal with complex emergency events effectively using conventional emergency management methods [8,9]. Therefore, how to select the optimal rescue plan to address an emergency decision-making (EDM) problem has become a pressing and important research topic in the last few years [10,11,12].

Regarding EDM problems, experts are usually unable to give precise evaluations on alternative solutions since emergencies are characterized by high uncertainty, complex evolution, and strong time constraints [13,14,15]. Instead, they prefer to use natural language to express their assessment information [16,17,18]. Moreover, experts may hesitate about their assessments due to the ambiguity as well as intangibility arising from human qualitative judgments [19,20]. To describe the evaluation information of decision makers flexibly and in detail, the double hierarchy hesitant linguistic term set (DHHLTS) was introduced by Gou et al. [21]. A DHHLTS is constructed by two independent hierarchy linguistic term sets, in which the second hierarchy serves as the supplement to the first one by a set of adverbs. It is particularly valuable and pragmatic to reflect complicated linguistic information completely [22,23,24], and provides a rich and flexible data structure for decision information elicitation [25,26]. Because of these advantages, the DHHLTSs have been widely used to address practical decision-making problems with uncertain linguistic information. For example, the DHHLTS theory has been utilized for the performance analysis of financial logistics enterprises [27], the public-private-partnership’s advancement evaluation [28], the failure model risk analysis [29], the passenger satisfaction evaluation of public transport [30], and the sustainable supplier selection [31].

The problem-solving process in EDM often involves conflicting criteria and thus can be regarded as a multiple-criteria decision-making (MCDM) problem [10,32,33]. Hence, the MCDM techniques are a useful and effective tool for solving the EDM problems [13,20,32]. The multi-attributive border approximation area comparison (MABAC) is a new MCDM method recently put forward by Pamučar and Ćirović [34]. Its basic principle is to divide alternatives into the border, upper, and lower approximation regions, and compute the distances between all alternatives and the margin approximation matrix with respect to each criterion [35,36]. This approach makes the decision-making results as precise as possible by computing the potential gains and losses values [37]. Compared with other MCDM methods, the MABAC is a particularly pragmatic and reliable technique for rational decision making, which has a simple computation process and a well-structured analytical framework [38,39]. In view of its distinct merits, the MABAC method has been widely applied to solve many practical decision-making problems, which include risk investment assessment [40], unmanned aircraft selection [41], supplier selection-order allocation [42], design alternative assessment [43], occupational health risk assessment [44], and green supplier selection [45].

The MABAC method has its merits in ranking different alternative actions to respond to emergency events. However, the classical MABAC technique lacks the mechanism to deal with multiple factors of uncertainty in EDM problems. Therefore, considering the advantages of the DHHLTSs and MABAC method, in this study, we combine them to develop a new EDM model for the evaluation and selection of the most desirable response plan for an emergency. To sum up, the contributions of this study to the EDM literature are as follows: First, the DHHLTSs are used to portray the uncertain evaluation information of decision makers in complex emergency environments. Second, the MABAC method is extended to determine the ranking of emergency solutions and identify the optimal one to handle an emergency event. Third, a maximum comprehensive method is employed to calculate criteria weights with incomplete weighting information. Finally, an empirical example is presented to demonstrate the effectiveness and applicability of the proposed EDM model. It is shown that the proposed method integrating DHHLTSs with the MABAC method is practicable and can obtain higher-quality decisions for EDM.

The remainder of this paper is arranged as follows. Section 2 provides a detailed review of the EDM methods proposed in previous studies. Section 3 deals with basic definitions and operational laws of the DHHLTSs. In Section 4, a new framework of EDM based on DHHLTSs and the MABAC method is described. In Section 5, a practical public health emergency case and a comparative analysis are provided to verify the proposed EDM model. Finally, Section 6 ends the paper with conclusions and directions of future studies.

2. Literature Review

In the literature, a lot of EDM models have been established in order to handle emergency events effectively [32]. For the time starved in emergency response, decision information is usually uncertain, especially in the early stages. To address this issue, many fuzzy theories and methods have been utilized for the uncertainty analysis of EDM. For example, the fuzzy set [46], the intuitionistic fuzzy set [15], the rough fuzzy set [17], the interval type-2 fuzzy sets [11], the hesitant fuzzy set [47], the Pythagorean fuzzy set [48], the picture fuzzy set [12], and the spherical fuzzy set [49] were employed to characterize the fuzziness and hesitation of decision information in EDM. In addition, to quantify the linguistic decision information of experts, a variety of linguistic computational methods were incorporated into EDM, which include the probabilistic linguistic term sets [8], the linguistic intuitionistic fuzzy sets [2], the proportional hesitant fuzzy linguistic sets [14], the 2-dimension uncertain linguistic variables [19], the probabilistic linguistic preference relations [9], the Pythagorean fuzzy uncertain linguistic variables [16], the interval-valued Pythagorean fuzzy linguistic variables [50], the 2-tuple linguistic method [45], the interval 2-tuple linguistic method [1], and the 2-tuple spherical linguistic term sets [10].

To find out the optimal emergency solution for an emergency event, many MCDM methods have been adopted for EDM in previous studies. For example, Zheng et al. [18] proposed a heterogeneous multi-attribute case retrieval approach for EDM based on bidirectional projection and TODIM (an acronym in Portuguese of interactive and multi-attribute decision making) method. Qin and Ma [11] proposed an EDM method based on the third generation prospect theory and the multiple multi-objective optimization by ratio analysis (MULTIMOORA) for the evaluation of emergency response plans. Qi et al. [1] introduced a collaborative EDM approach considering the synergy among different department alternatives based on the best-worst method (BWM) and the TODIM method. Lv et al. [50] investigated the emergency group decision-making problem with the technique for order performance by similarity to ideal solution (TOPSIS) and kernel principal component analysis methods. Huang et al. [10] suggested a framework for EDM with an integrated regret theory and the evaluation based on the distance from average solution (EDAS) method.

In addition, a dynamic reference point method based on the regret theory was introduced by Xue et al. [5] to support public health emergency decision making. An extended picture fuzzy axiomatic design technique was proposed by Ding et al. [33] for determining the optimal rescue plan to reduce the damages of emergencies. A dynamic approach based on prospect theory was introduced by Ding et al. [13] to solve EDM problems in the uncertain and time starved circumstance. Ren et al. [47] suggested a hesitant fuzzy thermodynamic method based on the prospect theory to comprehensively reflect the EDM process. In [19], an integrated prospect theory-VIKOR (VIsekriterijumska optimizacija i KOm-promisno Resenje) approach was proposed to determine the optimal solution for unconventional events. In [16], a combined approach using zero-sum game and the BWM was presented to ensure effective EDM in real-life circumstances. In [4], an extended TODIM method based on the bidirectional projection was developed to offer emergency group support in responding to emergency events.

The literature review above shows that a lot of achievements have been made to handle the uncertainty of decision information and determine an effective response action for emergency events. On the one hand, different kinds of linguistic representation methods have been utilized to describe the expressions and cognitions of decision makers in EDM. However, these methods are incapable of expressing decision makers’ complex linguistic information in a precise way. To address this problem, the DHHLTSs have been proposed, which can describe hesitation more accurately and reasonably than other linguistic representation models by adding a second hierarchy hesitant fuzzy linguistic term set. Hence, the DHHLTSs are of significant value when describing diverse and uncertain linguistic judgements provided by decision makers in EDM. On the other hand, a variety of MCDM methods have been applied to rank several alternatives and make reasonable decisions in the group multi-criteria EDM. However, the MABAC as a more recent and effective MCDM method has not been used for EDM yet. The mission of this method is to make the evaluation results as accurate as possible by calculating the potential gain and loss values. Considering the distinct advantages, it is expected to utilize the MABAC method to evaluate different alternatives to identify the ideal solution in real-world EDM problems. Based on the above research gaps, this paper aims to introduce an innovative EDM method by integrating the DHHLTSs and MABAC method for describing complex emergency decision information accurately and obtaining robust ranking results with simple but logical computational procedure. Furthermore, a maximum comprehensive technique is designed to determine criteria weights objectively.

3. Preliminaries

The DHHLTSs were introduced by Gou et al. [21] to express complex linguistic information in decision-making problems.

Definition 1 

([21]).Let X be a fixed set and$S_O=\left\{s_{t<o_k>}|t=-\tau ,\dots ,-1,0,1,\dots ,\tau ;k=-\zeta ,\dots ,-1,0,1,\dots \zeta \right\}$be a double hierarchy linguistic term set, then a DHHLTS on X, $H_{S_O}$, is in the form of

$$H_{S_O}=\left\{<x_i,h_{S_O}(x_i)>|x_i\in X\right\},$$

(1)

where$h_{S_O}(x_i)$represents a set of some values in$S_O$, and it can be defined as

$$h_{S_O}(x_i)=\{s_{{\varphi }_l<o_{{\phi }_l}>}\left(x_i\right)|s_{{\varphi }_l<o_{{\phi }_l}>}\in S_O;l=1,2,\dots ,L;{\varphi }_l=-\tau ,\dots ,-1,0,1,\dots ,\tau ;{\phi }_l=-\varsigma ,\dots ,-1,0,1,\dots ,\varsigma \}.$$

(2)

with L being the number of double hierarchy linguistic terms in $h_{S_O}(x_i)$, and$s_{{\varphi }_l<o_{{\phi }_l}>}$being the continuous terms in$S_O$. For convenience,$h_{S_O}(x_i)$is named as the double hierarchy hesitant linguistic element (DHHLE).

Definition 2 

([21]). Let$S_O=\left\{s_{t<o_k>}|t=-\tau ,\dots ,-1,0,1,\dots ,\tau ;k=-\zeta ,\dots ,-1,0,1,\dots \zeta \right\}$be a double hierarchy linguistic term set, and$h_{S_O}=\left\{s_{{\varphi }_l<o_{{\phi }_l}>}|s_{{\varphi }_l<o_{{\phi }_l}>}\in {\overline{S}}_O;l=1,2,\dots ,L;{\varphi }_l\in \left[-\tau ,\tau \right];{\phi }_l\in \left[-\varsigma ,\varsigma \right]\right\}$be a DHHLE. Then, the subscript${\varphi }_l<{\phi }_l>$of the$s_{{\varphi }_l<o_{{\phi }_l}>}$and the real value${\gamma }_l\in \left[0,1\right]$can be converted into each other by

$$f:\left[-\tau ,\tau \right]\times \left[-\varsigma ,\varsigma \right]\to \left[0,1\right],f\left({\varphi }_l,{\phi }_l\right)=\frac{{\phi }_l+\left(\tau +{\varphi }_l\right)\varsigma }{2\varsigma \tau }={\gamma }_l,$$

(3)

$$\begin{array}{ll}{f}^{-1}:\left[0,1\right]\to \left[-\tau ,\tau \right]\times \left[-\varsigma ,\varsigma \right],f^{-1}\left({\gamma }_l\right)& =\left[2\tau {\gamma }_l-\tau \right]<o_{\varsigma \left(2\tau {\gamma }_l-\tau -\left[2\tau {\gamma }_l-\tau \right]\right)}>\\ & =\left[2\tau {\gamma }_l-\tau \right]+1<o_{\varsigma \left(\left(2\tau {\gamma }_l-\tau -\left[2\tau {\gamma }_l-\tau \right]\right)-1\right)}>.\end{array}$$

(4)

The conversion between the DHHLE$h_{S_O}$and the numerical value$h_{\gamma }$is determined by

$$\begin{array}{ll}F\left(h_{S_O}\right)& =F\left\{\left(s_{{\varphi }_l<o_{{\phi }_l}>}|s_{{\varphi }_l<o_{{\phi }_l}>}\in {\overline{S}}_O;l=1,2,\dots ,L;{\varphi }_l\in \left[-\tau ,\tau \right];{\phi }_l\in \left[-\varsigma ,\varsigma \right]\right)\right\}\\ & =\left\{{\gamma }_l|{\gamma }_l=f\left({\varphi }_l,{\phi }_l\right);l=1,2,\dots ,L\right\}=h_{\gamma },\end{array}$$

(5)

$$\begin{array}{ll}{F}^{-1}\left(h_{\gamma }\right)& =F^{-1}\left(\left\{{\gamma }_l|{\gamma }_l\in \left[0,1\right];l=1,2,\dots ,L\right\}\right)\\ & =\left\{s_{{\varphi }_l<o_{{\phi }_l}>}|{\varphi }_{l<o_{{\phi }_l}>}=f^{-1}\left({\gamma }_l\right)\right\}=h_{S_O}.\end{array}$$

(6)

Definition 3 

([21]). Suppose that$h_{S_O}^1=\left\{s_{{\varphi }_l{}^1}{}_{<o_{{\phi }_l}^1>}|s_{{\varphi }_l{}^1}{}_{<o_{{\phi }_l}^1>}\in S_O;l=1,2,\dots ,L\right\}$and$h_{S_O}^2=\left\{s_{{\varphi }_l{}^2}{}_{<o_{{\phi }_l}^2>}|s_{{\varphi }_l{}^2}{}_{<o_{{\phi }_l}^2>}\in S_O;l=1,2,\dots ,L\right\}$are two DHHLEs, and$\lambda$is a real number. Then, the operational laws of DHHLEs are defined as follows:

(1)

$h_{S_O}^1\oplus h_{S_O}^2={\displaystyle \underset{s_{{\varphi }_l^i<O_{{\phi }_l^i}>}\in h_{S_{O1}},s_{{\varphi }_l^i<O_{{\phi }_l^i}>}\in h_{S_{O2}}}{\cup }\left\{s_{{\displaystyle {\sum }_{i=1}^L{\varphi }_l^i}<O_{{\displaystyle {\sum }_{i=1}^L{\phi }_l^i}}>}\right\}};{\displaystyle {\sum }_{i=1}^L{\varphi }_l^i}\le \tau ,{\displaystyle {\sum }_{i=1}^L{\phi }_l^i}\le \varsigma$;

(2)

$\lambda h_{S_O}^1={\displaystyle \underset{{\varphi }_l^1<o_{{\phi }_l}^1>\in h_{S_O}^1}{\cup }\left\{s_{\lambda {\varphi }_l^1<o_{{\phi }_l}^1>}\right\}},0\le \lambda \le 1$;

(3)

${\left(h_{S_O}^1\right)}^C={\displaystyle \underset{{\varphi }_l^1<o_{{\phi }_l}^1>\in h_{S_O}^1}{\cup }\left\{s_{{\varphi }_l^1<o_{{\phi }_l}^1>}\right\}}.$

Definition 4 

([21]). Let$h_{S_O}=\left\{s_{{\varphi }_l<o_{{\phi }_l}^{}>}|s_{{\varphi }_l<o_{{\phi }_l}^{}>}\in S_O;l=1,2,\dots ,L\right\}$be a DHHLE, then the expect value of$h_{S_O}$is defined as

$$E\left(h_{S_O}\right)=\frac{1}{L}{\displaystyle \sum _{l=1}^{L}F\left(s_{{\varphi }_l<o_{{\phi }_l}>}\right)},$$

(7)

and the variance value of$h_{S_O}$is defined as

$$V\left(h_{S_O}\right)=\sqrt{\frac{1}{L}{{\displaystyle \sum _{l=1}^L\left(F\left(s_{{\varphi }_l<o_{{\phi }_l}>}\right)-E\left(h_{S_O}\right)\right)}}^2}.$$

(8)

Definition 5 

([21]). Let$h_{S_O}^1$and$h_{S_O}^2$be any two DHHLEs, then

(1)

If$E\left(h_{S_O}^1\right)\succ E\left(h_{S_O}^2\right)$, then$h_{S_O}^1\succ h_{S_O}^2$;

(2)

If$E\left(h_{S_O}^1\right)=E\left(h_{S_O}^2\right)$, then

(a)

If$V\left(h_{S_O}^1\right)\prec V\left(h_{S_O}^2\right)$, then$h_{S_O}^1\succ h_{S_O}^2$;

(b)

If$V\left(h_{S_O}^1\right)=V\left(h_{S_O}^2\right)$, then$h_{S_O}^1=h_{S_O}^2$.

Definition 6 

([26]). Let$h_{S_O}^i=\left\{s_{{\varphi }_l^i}{}_{<o_{{\phi }_l^i}>}|s_{{\varphi }_l^i}{}_{<o_{{\phi }_l^i}>}\in S_O;l=1,2,\dots ,L\right\}\left(i=1,2,\dots ,n\right)$be a set of DHHLEs. Then, the double hierarchy hesitant linguistic weighted average (DHHLWA) operator is defined as:

$$\begin{array}{ll}\mathrm{DHHLWA}\left(h_{S_O}^1,h_{S_O}^2,\dots ,h_{S_O}^n\right)& =\underset{i=1}{\overset{n}{\oplus }}\left(w_i{h}_{S_O}^i\right)\\ & =\underset{i=1}{\overset{n}{\oplus }}\left[w_i\left(s_{\left({\displaystyle {\sum }_{l=1}^L{\varphi }_l^i}/L\right)}{}_{<o_{\left({\displaystyle {\sum }_{l=1}^L{\phi }_l^i}/L\right)}>}\right)\right],\end{array}$$

(9)

where$w={\left(w_1,w_2,\dots ,w_n\right)}^T$is the weight vector of DHHLEs, satisfying$0\le w_i\le 1\left(i=1,2,\dots ,n\right)$and${\displaystyle {\sum }_{i=1}^n{w}_i}=1$.

Definition 7 

([24]). Let$h_{S_O}^1=\left\{s_{{\varphi }_l{}^1}{}_{<o_{{\phi }_l}^1>}|s_{{\varphi }_l{}^1}{}_{<o_{{\phi }_l}^1>}\in S_O;l=1,2,\dots ,L\right\}$and$h_{S_O}^2=\left\{s_{{\varphi }_l{}^2}{}_{<o_{{\phi }_l}^2>}|s_{{\varphi }_l{}^2}{}_{<o_{{\phi }_l}^2>}\in S_O;l=1,2,\dots ,L\right\}$be two DHHLEs. Then, the Hamming distance between them is computed by

$$d\left(h_{S_O}^1,h_{S_O}^2\right)=\frac{1}{L}{\displaystyle \sum _{l=1}^L\left|F\left(s_{{\varphi }_l^1<o_{{\phi }_l}^1>}^{}\right)-F\left(s_{{\varphi }_l^2<o_{{\phi }_l}^2>}^{}\right)\right|.}$$

(10)

where L is the number of double hierarchy linguistic terms in$h_{S_O}^1$and$h_{S_O}^2$.

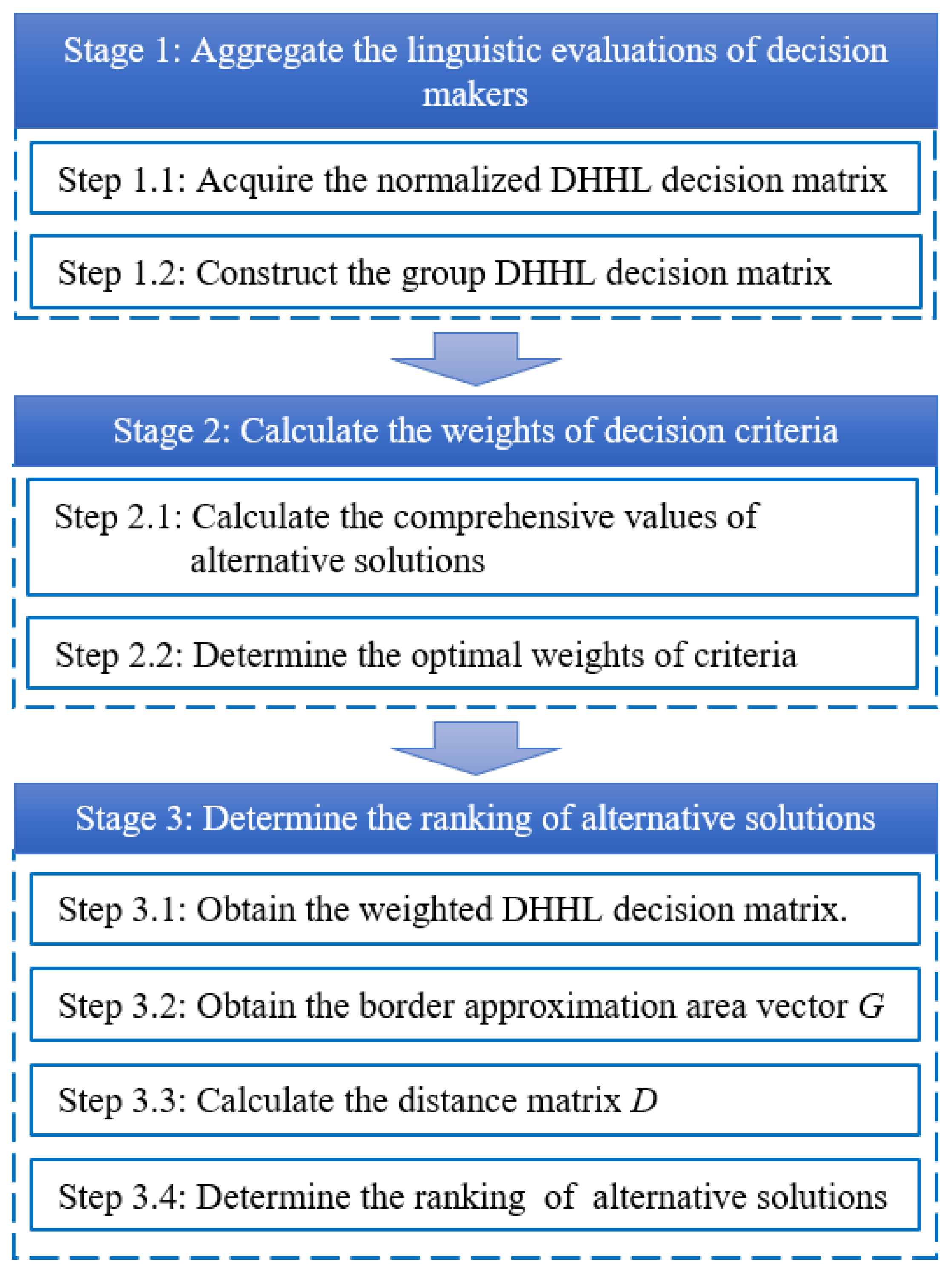
4. The Proposed EDM Model

In this section, a new EDM model based on the DHHLTSs and MABAC method is introduced to evaluate and determine the optimal response action for an emergency event. This model is composed of three stages: (1) evaluating the performance of alternative solutions by utilizing the DHHLTSs; (2) computing the weights of decision criteria using a maximum comprehensive method; (3) determining the priority of emergency solutions with an extended MABAC method. The flow diagram shown in Figure 1 depicts the main stages and detailed steps of the proposed EDM model.

For an EDM problem, suppose that $A=\left\{A_1,A_2,\dots ,A_m\right\}$ represents a set of alternative solutions, $C=\left\{C_1,C_2,\dots ,C_n\right\}$ is a set of decision criteria, and $DM=\left\{D_1,D_2,\dots ,D_p\right\}$ be a set of decision makers. The decision makers are assigned with different weights expressed by the vector $\lambda ={\left({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_p\right)}^T$, where $0\le {\lambda }_r\le 1\left(r=1,2,\dots ,p\right)$ and ${\displaystyle {\sum }_{r=1}^p{\lambda }_r}=1.$ Each expert is requested to provide his/her evaluations to $A_i$ regarding $C_j$ on the basis of the linguistic term sets $S=\left\{s_t|t=-\tau ,\dots ,-1,0,1,\dots ,\tau \right\}$ and $O=\left\{s_k|k=-\varsigma ,\dots ,-1,0,1,\dots ,\varsigma \right\}$. Let $H_r={\left(h_{S_{Oij}}^r\right)}_{m\times n}$ be the double hierarchy hesitant linguistic (DHHL) decision matrix of the rth decision maker for $r=1,2,\dots ,p.$

In the following subsections, the proposed DHHL-MABAC method for dealing with the EDM problem is described in detail.

4.1. Aggregate the Linguistic Evaluations of Decision Makers

The DHHLTSs are a newly developed complex linguistic expression model which can effectively model experts’ linguistic information in natural language forms. Therefore, the DHHLT method is applied here to describe the complex performance assessments of alternatives given by decision makers. In this stage, the individual DHHL performance evaluations provided by decision makers are normalized and aggerated to obtain the group DHHL evaluation matrix.

Step 1.1: Acquire the normalized DHHL decision matrix.

Considering that both benefit and cost criteria may be existed in a EDM problem, the DHHL evaluations of decision makers should be normalized first. The normalized DHHL decision matrix of each decision maker ${\overline{H}}_r={\left({\overline{h}}_{S_{Oij}}^r\right)}_{m\times n}\left(r=1,2,\dots ,p\right)$ can be calculated with

$${\overline{h}}_{S_{Oij}}^r=\{\begin{array}{c}{h}_{S_{Oij}}^r,\mathrm{for}\mathrm{benefit}\mathrm{criteria},\\ {\left(h_{S_{Oij}}^r\right)}^C,\mathrm{for}\mathrm{cost}\mathrm{criteria}.\end{array}$$

(11)

Step 1.2: Construct the group DHHL decision matrix.

In this step, the normalized DHHL decision matrices ${\overline{H}}_r\left(r=1,2,\dots ,p\right)$ are aggregated for computing the group DHHL decision matrix $H={\left(h_{S_{Oij}}\right)}_{m\times n}$, in which

$$h_{S_{Oij}}=\mathrm{DHHLWA}\left({\overline{h}}_{S_{Oij}}^1,{\overline{h}}_{S_{Oij}}^2,\dots ,{\overline{h}}_{S_{Oij}}^p\right)=\underset{r=1}{\overset{p}{\oplus }}\left({\lambda }_r{\overline{h}}_{S_{Oij}}^r\right),\hspace{1em}i=1,2,\dots ,m;j=1,2,\dots ,n.$$

(12)

4.2. Calculate the Weights of Decision Criteria

In the realistic EDM process, the weights of decision criteria may be partially known or even completely unknown because of time pressure, lack of knowledge or data, and the experts’ limited expertise about the problem. Therefore, an interesting and important issue is how to utilize the known weight information to find the relative weights of decision criteria. In this stage, the maximum comprehensive method introduced in [51] is employed for determining criteria weights when the weighting data is incomplete.

Let $w={\left(w_1,w_2,\dots ,w_n\right)}^T$ be the weight vector of the n decision criteria, with $0\le w_j\le 1\left(j=1,2,\dots ,n\right)$ and ${\displaystyle {\sum }_{j=1}^n{w}_j}=1$. Normally, the known weight information on decision criteria can be expressed as V using the following forms [52]:

(1)

A weak raking: $V_1=\left\{w_i\ge w_j\right\}$;

(2)

A strict ranking: $V_2=\left\{w_i-w_j\ge {\gamma }_i\left({\gamma }_i>0\right)\right\}$;

(3)

A ranking of difference: $V_3=\left\{w_i-w_j\ge w_k-w_l\right\}\left(j\ne k\ne l\right)$;

(4)

A ranking with multiples: $V_4=\left\{w_i\ge {\gamma }_i{w}_j\right\}\left(0\le {\gamma }_i\le 1\right)$;

(5)

An interval form: $V_5=\left\{{\gamma }_i\le w_i\le {\gamma }_i+{\epsilon }_i\right\}\left(0\le {\gamma }_i\le {\gamma }_i+1\le 1\right)$.

Based on the maximum comprehensive method, the weights of decision criteria can be derived by the following steps:

Step 2.1: Acquire the comprehensive values of alternative solutions.

The comprehensive value related to each alternative solution is computed by

$$T_i=\underset{j=1}{\overset{n}{\oplus }}\left(w_{j}E\left(h_{S_{Oij}}\right)\right),\hspace{1em}i=1,2,\dots ,m.$$

(13)

Step 2.2: Determine the optimal weights of decision criteria.

The larger the comprehensive value T_i, the better the alternative A_i. It is reasonable to maximize the comprehensive values of all alternatives for the purpose of determining criteria weights. Therefore, the following multi-objective programming model can be established:

$$\begin{array}{l}\max Z\left(w\right)=\frac{1}{m}{\displaystyle \sum _{i=1}^m{T}_i}\\ s.t.\{\begin{array}{l}w\in V,\\ {\displaystyle \sum _{j=1}^n{w}_j}=1,w_j\ge 0,j=1,2,\dots ,n.\end{array}\end{array}$$

(14)

By solving the above model, the optional solution $w^{\ast }={\left(w_1^{*},w_2^{*},\dots ,w_n^{*}\right)}^T$ can be used as the weight vector of decision criteria.

4.3. Determine the Ranking of Alternative Solutions

The MABAC is a new method proposed by Pamučar and Ćirović [34] for solving MCDM problems. In view of its simplicity and stability, this method is a particularly effective and reliable tool for rational EDM. However, the traditional MABAC method is limited to crip values and unable to handle complex linguistic expressions of decision makers. Thus, in this stage, we extend the MABAC method within the DHHL environment and apply it for ranking the alternative solutions in EDM. Specific steps of the DHHL-MABAC approach are explained as follows:

Step 3.1: Obtain the weighted DHHL decision matrix $H^{\prime }$.

Based on the criteria weights w, the weighted DHHL decision matrix $H^{\prime }={\left({h^{\prime }}_{S_{Oij}}\right)}_{m\times n}$ is determined by

$${h^{\prime }}_{S_{Oij}}=w_j{h}_{S_{Oij}},i=1,2,\dots ,m;j=1,2,\dots ,n.$$

(15)

Step 3.2: Compute the border approximation area vector G.

The border approximation area vector G can be formed as $G=\left(g_1,g_2,\dots ,g_n\right),$ in which

$$g_j=F^{-1}\left(\prod _{i=1}^{m}F{\left({h^{\prime }}_{S_{Oij}}\right)}^{1/m}\right),j=1,2,\dots ,n.$$

(16)

Step 3.3: Calculate the distance matrix D.

The distance matrix $D={\left(d_{ij}\right)}_{m\times n}$ is constructed by computing the distance of each alternative from the border approximation area G. That is,

$$d_{ij}=\{\begin{array}{cc}d\left({h^{\prime }}_{S_{Oij}},g_i\right),& \mathrm{if}{h^{\prime }}_{S_{Oij}}>g_i,\\ -d\left({h^{\prime }}_{S_{Oij}},g_i\right),& \mathrm{if}{h^{\prime }}_{S_{Oij}}<g_i.\end{array}$$

(17)

Step 3.4: Determine the ranking of alternative solutions.

Finally, the priority value to the border approximation area for each alternative solution is calculated using

$$P{V}_i={\displaystyle \sum _{j=1}^n{d}_{ij}},i=1,2,\dots ,m.$$

(18)

The bigger the value of $P{V}_i$ is, the better the alternative solution A_i would be. Therefore, the best alternative corresponding to the maximum $P{V}_i$ value can be selected for EDM.

5. Illustrative Example

In this section, we address a practical EDM problem about an earthquake to illustrate the implementation process and availability of the proposed DHHL-MABAC model.

5.1. Implementation and Results

At approximately 21:20 on 8 August 2017, a serious 7.0-magnitude earthquake occurred in Aba prefecture, Sichuan province, China. As both the worst-hit area and the core scenic area of the country, Jiuzhaigou valley scenic and historic interest area, a world-famous tourist spot, was densely populated due to peak tourist season. More than 7000 tourists and migrant workers were trapped and needed to be relocated. In addition, the tourist spot is located in a mountainous area where the elevation is over 2000 m and the forest cover is as high as 80%. High altitude and dense trees may not only cause serious secondary geological disasters, but also increase the difficulty of rescue and relocation. According to the national meteorological center, there was going to be moderate rain on the night of August 10. Therefore, the organization of emergency capacity and scientific arrangement were required to evacuate and transfer the stranded people urgently within 48 h.

Based on the current situation, the transportation ways of transferring people can be divided into the following three modes: road transportation, air transportation, and railway transportation. Through interviewing the experts from emergency management agency, we reviewed the emergency solutions used in handling previous earthquake cases and analyzed the problems encountered in EDM. After preliminary screening, the following emergency solutions are put forward: transfer people and transport relief materials by aircraft (A₁), eliminate security risks of railway lines and transfer people (A₂), repair and clear damaged roads and transfer people by car (A₃), and large numbers of people evacuate the disaster area on foot (A₄). Many quantitative and qualitative factors should be taken into consideration in determining the most preferred emergency plan. As a result of literature review and expert interview, five criteria are taken into consideration for the EDM problem. They are comfort level (C₁), anti-earthquake level (C₂), personal injury (C₃), transfer cost (C₄), and building difficulty (C₅). Among these criteria, C₁ and C₂ belong to benefit criteria, while the remaining three are cost criteria.

To find the most desirable plan for the given emergency, five decision makers $DM=\left\{D_1,D_2,\dots ,D_5\right\}$ are involved in EDM process. They are requested to provide the weight information about criteria with incomplete information structure and the performance evaluations of alternative solutions by using DHHLTSs. The five decision makers are given equal weights and thus $\lambda ={\left(0.2,0.2,0.2,0.2,0.2\right)}^T$. Note that the proposed EDM approach is applicable to any number of decision makers and the five decision makers selected in this case example are for demonstration purpose only. The linguistic term sets used are:

$$\begin{array}{ll}S=& \{s_{-3}=Verybad,s_{-2}=Bad,s_{-1}=Slightlybad,s_0=Fair,s_1=slightlygood,s_2=good,s_3=Verygood\},\\ O=& \{o_{-3}=Farfrom,o_{-2}=Onlyalittle,o_{-1}=Alittle,o_0=Justright,o_1=Much,o_2=Verymuch,\\ & o_3=Extremely\}.\end{array}$$

Based on the linguistic evaluations of decision makers, the DHHL decision matrices $H_r\left(r=1,2,\dots ,5\right)$ are obtained as shown in

Table 1. DHHL decision matrices given by the decision makers.

Decision Makers	Alternative Solutions	Criteria
		C1	C2	C3	C4	C5
D1	A1	$\left\{s_{2<o_2>},s_{3<o_0>}\right\}$	$\left\{s_{2<o_0>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{2<o_0>}\right\}$
	A2	$\left\{s_{1<o_1>},s_{1<o_2>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{-1<o_1>},s_{1<o_{-3}>}\right\}$	$\left\{s_{1<o_{-3}>},s_{0<o_2>}\right\}$	$\left\{s_{-2<o_2>},s_{0<o_{-3}>}\right\}$
	A3	$\left\{s_{0<o_1>}\right\}$	$\left\{s_{-2<o_1>},s_{-1<o_{-1}>}\right\}$	$\left\{s_{-1<o_0>},s_{0<o_{-2}>},s_{0<o_0>}\right\}$	$\left\{s_{0<o_0>},s_{0<o_1>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$
	A4	$\left\{s_{-3<o_0>},s_{-2<o_{-3}>}\right\}$	$\left\{s_{0<o_{-2}>},s_{0<o_0>},s_{0<o_1>}\right\}$	$\left\{s_{1<o_1>},s_{2<o_{-1}>}\right\}$	$\left\{s_{1<o_1>}\right\}$	$\left\{s_{1<o_0>},s_{1<o_2>}\right\}$
D2	A1	$\left\{s_{2<o_2>},s_{3<o_0>}\right\}$	$\left\{s_{2<o_1>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{-2<o_1>},s_{-1<o_{-1}>},s_{-1<o_0>}\right\}$	$\left\{s_{2<o_2>},s_{3<o_0>}\right\}$
	A2	$\left\{s_{1<o_{-1}>},s_{1<o_1>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_1>}\right\}$	$\left\{s_{-2<o_2>}\right\}$	$\left\{s_{1<o_1>},s_{1<o_2>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$
	A3	$\left\{s_{2<o_0>}\right\}$	$\left\{s_{-2<o_1>},s_{-1<o_{-1}>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{0<o_0>},s_{0<o_1>}\right\}$	$\left\{s_{-2<o_1>},s_{-1<o_{-1}>}\right\}$
	A4	$\left\{s_{-3<o_0>},s_{-2<o_{-3}>}\right\}$	$\left\{s_{-1<o_0>},s_{0<o_{-2}>}\right\}$	$\left\{s_{1<o_1>},s_{2<o_{-1}>}\right\}$	$\left\{s_{2<o_1>}\right\}$	$\left\{s_{2<o_{-3}>},s_{3<o_{-3}>}\right\}$
D3	A1	$\left\{s_{1<o_2>},s_{2<o_2>}\right\}$	$\left\{s_{2<o_0>},s_{2<o_1>}\right\}$	$\left\{s_{0<o_0>},s_{0<o_1>}\right\}$	$\left\{s_{-1<o_0>},s_{0<o_{-3}>}\right\}$	$\left\{s_{0<o_0>},s_{0<o_1>}\right\}$
	A2	$\left\{s_{1<o_2>}\right\}$	$\left\{s_{-1<o_2>},s_{1<o_{-3}>}\right\}$	$\left\{s_{1<o_1>}\right\}$	$\left\{s_{1<o_1>},s_{1<o_2>}\right\}$	$\left\{s_{0<o_2>},s_{2<o_{-3}>}\right\}$
	A3	$\left\{s_{0<o_2>},s_{2<o_{-3}>}\right\}$	$\left\{s_{0<o_{-1}>}\right\}$	$\left\{s_{0<o_2>},s_{2<o_{-3}>}\right\}$	$\left\{s_{0<o_2>},s_{1<o_0>}\right\}$	$\left\{s_{0<o_2>},s_{2<o_{-3}>}\right\}$
	A4	$\left\{s_{0<o_{-3}>},s_{-1<o_1>}\right\}$	$\left\{s_{0<o_2>},s_{2<o_{-3}>},s_{2<o_{-1}>}\right\}$	$\left\{s_{-1<o_{-1}>}\right\}$	$\left\{s_{-1<o_{-1}>},s_{-1<o_0>}\right\}$	$\left\{s_{-1<o_{-1}>}\right\}$
D4	A1	$\left\{s_{2<o_2>},s_{3<o_0>}\right\}$	$\left\{s_{2<o_0>},s_{2<o_1>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{-3<o_1>},s_{-2<o_2>},s_{-2<o_3>}\right\}$	$\left\{s_{2<o_2>},s_{3<o_0>}\right\}$
	A2	$\left\{s_{0<o_0>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{1<o_1>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$
	A3	$\left\{s_{2<o_0>},s_{2<o_1>}\right\}$	$\left\{s_{-1<o_{-1}>}\right\}$	$\left\{s_{-1<o_{-1}>},s_{-1<o_0>}\right\}$	$\left\{s_{0<o_2>},s_{2<o_{-3}>},s_{2<o_{-1}>}\right\}$	$\left\{s_{-2<o_1>},s_{-1<o_{-1}>}\right\}$
	A4	$\left\{s_{-3<o_0>},s_{-2<o_{-3}>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{2<o_0>},s_{2<o_1>}\right\}$	$\left\{s_{2<o_0>},s_{2<o_1>}\right\}$	$\left\{s_{2<o_{-3}>},s_{3<o_{-3}>}\right\}$
D5	A1	$\left\{s_{2<o_2>},s_{3<o_0>}\right\}$	$\left\{s_{2<o_0>},s_{2<o_1>}\right\}$	$\left\{s_{-2<o_2>}\right\}$	$\left\{s_{-1<o_{-1}>}\right\}$	$\left\{s_{2<o_2>},s_{3<o_0>}\right\}$
	A2	$\left\{s_{0<o_0>},s_{0<o_1>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{1<o_1>},s_{1<o_2>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$
	A3	$\left\{s_{2<o_0>},s_{2<o_1>}\right\}$	$\left\{s_{-1<o_{-1}>},s_{-1<o_0>}\right\}$	$\left\{s_{-1<o_{-1}>},s_{-1<o_0>}\right\}$	$\left\{s_{0<o_2>},s_{2<o_{-3}>}\right\}$	$\left\{s_{-2<o_1>},s_{-1<o_{-1}>},s_{-1<o_0>}\right\}$
	A4	$\left\{s_{-3<o_0>},s_{-2<o_{-3}>},s_{-2<o_{-1}>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{2<o_0>}\right\}$	$\left\{s_{2<o_0>}\right\}$	$\left\{s_{2<o_{-3}>},s_{3<o_{-3}>}\right\}$

.

The above EDM problem can be tackled with the application of the proposed DHHL-MABAC model for identifying the optimal alternative solution. In what follows, the decision process and calculation results are summarized.

Stage 1: Aggregate the linguistic evaluations of decision makers.

First, by utilizing Equation (11), the normalized DHHL decision matrices of the five decision makers ${\overline{H}}_r={\left({\overline{h}}_{S_{Oij}}^r\right)}_{4\times 5}\left(r=1,2,\dots ,5\right)$ can be obtained. For example, the ${\overline{H}}_1$ of the first decision maker is displayed in

Table 2. The normalized DHHL decision matrix ${\overline{H}}_1$ .

Alternative solutions	C1	C2	C3	C4	C5
A1	$\left\{s_{2<o_2>},s_{3<o_0>}\right\}$	$\left\{s_{2<o_0>}\right\}$	$\left\{s_{2<o_{-2}>},s_{1<o_0>}\right\}$	$\left\{s_{2<o_{-2}>},s_{1<o_0>}\right\}$	$\left\{s_{-2<o_0>}\right\}$
A2	$\left\{s_{1<o_1>},s_{1<o_2>}\right\}$	$\left\{s_{-2<o_2>},s_{-1<o_0>}\right\}$	$\left\{s_{1<o_{-1}>},s_{-1<o_3>}\right\}$	$\left\{s_{-1<o_3>},s_{0<o_{-2}>}\right\}$	$\left\{s_{2<o_{-2}>},s_{0<o_3>}\right\}$
A3	$\left\{s_{0<o_1>}\right\}$	$\left\{s_{-2<o_1>},s_{-1<o_{-1}>}\right\}$	$\left\{s_{1<o_0>},s_{0<o_2>},s_{0<o_0>}\right\}$	$\left\{s_{0<o_0>},s_{0<o_{-1}>}\right\}$	$\left\{s_{2<o_{-2}>},s_{1<o_0>}\right\}$
A4	$\left\{s_{-3<o_0>},s_{-2<o_{-3}>}\right\}$	$\left\{s_{0<o_{-2}>},s_{0<o_0>},s_{0<o_1>}\right\}$	$\left\{s_{-1<o_{-1}>},s_{-2<o_1>}\right\}$	$\left\{s_{-1<o_{-1}>}\right\}$	$\left\{s_{-1<o_0>},s_{-1<o_{-2}>}\right\}$

. Next, based on Equation (12), the individual DHHL evaluations from decision makers are aggregated to construct the group DHHL decision matrix $H={\left(h_{S_{Oij}}\right)}_{4\times 5}$ as presented in

Table 3. The group DHHL decision matrix H.

Alternatives	C1	C2	C3	C4	C5
A1	$\left\{s_{2.3<o_{1.2}>}\right\}$	$\left\{s_{2<o_{0.5}>}\right\}$	$\left\{s_{1.4<o_{-1.1}>}\right\}$	$\left\{s_{1.3<o_{-0.1}>}\right\}$	$\left\{s_{-1.9<o_{-0.7}>}\right\}$
A2	$\left\{s_{0.6<o_{0.8}>}\right\}$	$\left\{s_{-1.2<o_{0.8}>}\right\}$	$\left\{s_{0.8<o_{-0.8}>}\right\}$	$\left\{s_{-0.9<o_{-1}>}\right\}$	$\left\{s_{0.9<o_{-0.4}>}\right\}$
A3	$\left\{s_{1.4<o_{0.3}>}\right\}$	$\left\{s_{-1<o_{-0.5}>}\right\}$	$\left\{s_{0.6<o_{0.2}>}\right\}$	$\left\{s_{-0.6<o_{-0.2}>}\right\}$	$\left\{s_{1<o_{-0.1}>}\right\}$
A4	$\left\{s_{-2.1<o_{-1.4}>}\right\}$	$\left\{s_{-0.4<o_{-0.0}>}\right\}$	$\left\{s_{-1.2<o_{-0.1}>}\right\}$	$\left\{s_{-1.2<o_{-0.4}>}\right\}$	$\left\{s_{-1.5<o_{1.8}>}\right\}$

.

Stage 2: Calculate the weights of decision criteria.

The incomplete information on criteria importance given by the decision makers is listed as follows:

$$V=\{w_1\le w_4;w_2\ge 0.35;w_3\ge 0.1;w_3+w_4\le 0.3;w_5\ge 0.15;{\displaystyle {\sum }_1^5{w}_j=1,w_j\ge 0,j=1,2,\dots ,5}\}.$$

Next, by using Equation (13), the comprehensive values of the four alternative solutions are computed as:

$$\begin{array}{l}{T}_1=0.950w_1+0.861w_2+0.672w_3+0.711w_4+0.144w_5,\\ T_2=0.644w_1+0.344w_2+0.589w_3+0.294w_4+0.628w_5,\\ T_3=0.750w_1+0.306w_2+0.607w_3+0.396w_4+0.656w_5,\\ T_4=0.080w_1+0.428w_2+0.306w_3+0.278w_4+0.350w_5.\end{array}$$

For the comprehensive value T₁, the calculation process is as follows:

$$\begin{gathered} E\left(h_{S_{O_{11}}}\right)=F\left(S_{2.3\langle O_{1.2}\rangle }\right)=f\left(2.3,1.2\right)=\frac{1.2+\left(3+2.3\right)\times 3}{2\times 3\times 3}=0.950, \\ E\left(h_{S_{O_{12}}}\right)=F\left(S_{2\langle O_{0.5}\rangle }\right)=f\left(2,0.5\right)=\frac{0.5+\left(3+2\right)\times 3}{2\times 3\times 3}=0.861, \\ E\left(h_{S_{O_{13}}}\right)=F\left(S_{1.4\langle O_{-1.1}\rangle }\right)=f\left(1.4,-1.1\right)=\frac{-1.1+\left(3+1.4\right)\times 3}{2\times 3\times 3}=0.672, \\ E\left(h_{S_{O_{14}}}\right)=F\left(S_{1.3\langle O_{-0.1}\rangle }\right)=f\left(1.3,-0.1\right)=\frac{-0.1+\left(3+1.3\right)\times 3}{2\times 3\times 3}=0.711, \\ E\left(h_{S_{O_{15}}}\right)=F\left(S_{-1.9\langle O_{-0.7}\rangle }\right)=f\left(-1.9,-0.7\right)=\frac{-0.7+\left(3-1.9\right)\times 3}{2\times 3\times 3}=0.144. \end{gathered}$$

Then, based on (14), we can establish the following programming model:

$$\begin{array}{c}\max Z\left(w\right)=0.606w_1+0.485w_2+0.544w_3+0.421w_4+0.444w_5\\ s.t.\{\begin{array}{l}w\in V,\\ {\displaystyle \sum _{j=1}^n{w}_j}=1,w_j\ge 0,j=1,2,\dots ,n.\end{array}\end{array}$$

By solving this model, the relative weights of decision criteria are derived as $w={\left(0.20,0.35,0.10,0.20,0.15\right)}^T$.

Stage 3: Determine the ranking of alternative solutions.

First, the weighted DHHL decision matrix $H^{\prime }={\left({h^{\prime }}_{S_{Oij}}\right)}_{4\times 5}$ is determined via Equation (15) and the results are listed in

Table 4. The weighted DHHL decision matrix $H^{\prime }$ .

Alternatives	C1	C2	C3	C4	C5
A1	$\left\{s_{0.46<o_{0.24}>}\right\}$	$\left\{s_{0.7<o_{0.175}>}\right\}$	$\left\{s_{0.13<o_{-0.09}>}\right\}$	$\left\{s_{0.28<o_{-0.02}>}\right\}$	$\left\{s_{-0.29<o_{-0.12}>}\right\}$
A2	$\left\{s_{0.12<o_{0.16}>}\right\}$	$\left\{s_{-0.42<o_{0.28}>}\right\}$	$\left\{s_{0.07<o_{-0.07}>}\right\}$	$\left\{s_{-0.18<o_{0.22}>}\right\}$	$\left\{s_{0.14<o_{-0.06}>}\right\}$
A3	$\left\{s_{0.28<o_{0.06}>}\right\}$	$\left\{s_{-0.35<o_{-0.11}>}\right\}$	$\left\{s_{0.06<o_{0.03}>}\right\}$	$\left\{s_{-0.1<o_{-0.04}>}\right\}$	$\left\{s_{0.15<o_{-0.02}>}\right\}$
A4	$\left\{s_{-0.42<o_{-0.28}>}\right\}$	$\left\{s_{-0.18<o_{-0.44}>}\right\}$	$\left\{s_{-0.12<o_{-0.01}>}\right\}$	$\left\{s_{-0.24<o_{-0.1}>}\right\}$	$\left\{s_{-0.23<o_{0.255}>}\right\}$

. Second, the border approximation area vector G is obtained with Equation (16) as: $G=\left(\left\{s_{0<o_{0.304}>}\right\},\left\{s_{0<o_{-0.196}>}\right\},\left\{s_{0<o_{0.075}>}\right\},\left\{s_{0<o_{-0.306}>}\right\},\left\{s_{0<o_{-0.169}>}\right\}\right).$ Third, the distance matrix $D={\left(d_{ij}\right)}_{4\times 5}$ is obtained with Equation (17) and displayed in

Table 5. The distance matrix D.

Alternatives	C1	C2	C3	C4	C5
A1	0.073	0.137	0.013	0.060	−0.044
A2	0.012	−0.044	0.005	−0.024	0.029
A3	0.033	−0.057	0.007	−0.004	0.033
A4	−0.101	−0.014	−0.024	−0.027	−0.013

. Finally, the priority values of the four alternative solutions are calculated using Equation (18) as: PV₁ = 0.240, PV₂ = −0.022, PV₃ = 0.011, and PV₄ = −0.180.

According to the descend order of the priority values $P{V}_i\left(i=1,2,3,4\right)$, the four alternative solutions can be ranked as: A₁ > A₃ > A₂ > A₄. Thus, A₁ is the best solution for the emergency event. In the first 48 h after the earthquake, transferring the trapped people by aircraft is the best rescue plan.

5.2. Comparison Analysis

To verify the effectiveness of the proposed EDM model, we conducted a comparison analysis with some closely related EDM methods, including the spherical fuzzy GRA [49], the Pythagorean fuzzy TOPSIS [48], the linguistic VIKOR [19], and the interval TODIM [3]. The reasons of choosing these methods are as follows. On the one hand, the MCDM methods (GRA, TOPSIS, VIKOR, and TODIM) are the most commonly used for dealing with EDM problems in the literature. On the other hand, the four methods adopted different fuzzy theories, i.e., spherical fuzzy numbers [53], Pythagorean fuzzy numbers [54], linguistic variables [55], and interval-valued fuzzy numbers [56], to describe the uncertain EDM information. Thus, by comparing with these methods, the potentials of the proposed DHHL-MABAC model in capturing decision makers’ diversity opinions and prioritizing alternative solutions can be analyzed. The ranking results of alternative solutions derived by the four approaches and the proposed EDM model are listed in Figure 2.

From Figure 2, it can be found that the priority orders of emergency alternatives based on the spherical fuzzy GRA is consistent with the one by using the proposed DHHL-MABAC model. Moreover, A₁ is always determined as the optimal emergency alternative in the listed EDM methods. The important goal of EDM is to obtain the optimal response to an emergency event. Therefore, these observations demonstrate the feasibility and effectiveness of the proposed approach for EDM.

The ranking result of alternative solutions by the Pythagorean fuzzy TOPSIS shows that A₂ is the last emergency solution. However, A₄ is regarded as the worst emergency alternative in our proposed model. The main reasons for this difference are as follows: First, Pythagorean fuzzy numbers are used by the Pythagorean fuzzy TOPSIS to represent the evaluations from decision makers, which cannot reflect uncertain decision information precisely. Second, criteria weights are designated in the Pythagorean fuzzy TOPSIS, and the subjective randomness is not able to reflect actual importance of criteria. Third, the Pythagorean fuzzy TOPSIS method makes no distinction between benefit criteria and cost criteria. When determining positive or negative solutions by selecting the maximum or minimum values, there may exist contradiction in actual situations.

Based on the linguistic VIKOR and the interval TODIM methods, A₂ has a higher priority than A₃, which is different from our proposed model. The explanations of the inconsistent ranking result lie in the following aspects. In the linguistic VIKOR, group 2-dimension uncertain decision matrix is converted into crisp values before normalization. This can cause the loss of original evaluation information and leads to biased ranking results. In addition, the basic elements of interval-valued fuzzy numbers in the interval TODIM method are fuzzy numbers and the accuracy of evaluation information is highly dependent on decision makers’ experience. The lacking experience and restricted time will always lead to inaccurate information and decision failure.

The priority of the alternative solutions obtained with our proposed model is more reasonable and the reasons are as follows: As mentioned above, 48 h after the earthquake broke out are the most critical time to rescue. To rescue more lives, the trapped people need to be transported to the safe area as soon as possible. Unfortunately, the considered area is located in the mountains, the terrain is very complex and many roads leading to the safe area were damaged after the earthquake. It is necessary to transport people by air within time limit, and to organize manpower to repair the damage road leading to the disaster area as quickly as possible; once the road is repaired, transporting the trapped people by cars is possible. Therefore, it is reasonable for ranking A₃ as the second choice. In addition, the best emergency solution A₁ is agree with the emergency measure taken by the emergency management office to the earthquake occurred in the area in reality. Therefore, the reliability of our proposed EDM approach is confirmed.

From the above analysis, it can be concluded that the ranking result of emergency alternatives obtained with our introduced DHHL-MABAC approach is more acceptable and reasonable. Compared with other methods to address the EDM problem, the advantages of the proposed EDM model using DHHLTSs and the MABAC method are summarized as follows:

(1)

The proposed EDM model can express complex linguistic decision information in a more prominent manner and reduce the loss of information in fusing multiple-expert evaluations. This enables decision makers to express their judgments more realistically and easily.

(2)

The proposed EDM model is able to assign the weights of decision criteria when their weighting information is partially known. This is particularly useful for EDM since precise data is usually unavailable or unreliable under strong time constraints.

(3)

The proposed EDM model is more efficient in the EDM process and can assist decision makers in achieving more reasonable and credible ranking results of alternative solutions. This makes the proposed DHHL-MABAC method more realistic and practical.

In addition, detailed comparisons between the relevant EDM methods and the proposed model are provided in

Table 6. Characteristics of the considered EDM methods.

Characteristics	The Spherical Fuzzy GRA	The Pythagorean Fuzzy TOPSIS	The Linguistic VIKOR	The Interval TODIM	The Proposed DHHL-MABAC
Whether model uncertainty more powerful	No	No	YES	No	Yes
Whether considers quantity of both gains and losses	No	YES	No	No	Yes
Whether handles partial weighting information	No	No	No	No	Yes

to further explain the superiorities of the proposed approach.

6. Conclusions

In this paper, we develop a new EDM model based on the DHHLTSs and MABAC method to determine an effective response action to an emergency event. The DHHLTSs are employed to describe the complex uncertain evaluation information on emergency solutions from decision makers. The method of MABAC is extended for the ranking of alternative solutions and the determination of optimal one for emergency response. A maximum comprehensive method is adopted to calculate criteria weights based on limited weight information. Finally, a practical EDM case of earthquake is performed to demonstrate the proposed DHHL-MABAC approach. Moreover, the effectiveness and rationality of the proposed EDM model are validated through a comparison analysis with existing methods.

However, there are several limitations in the proposed EDM model, which can be addressed in the future research. First, the consensus among decision makers is not considered, which is vital to achieving a consensus solution in some real situations. Hence, one orientation for future research is to develop an efficient EDM method by considering the consensus issue of decision makers. Second, many other variables including vulnerabilities that are associated with uncertainties and emergencies are not considered in the case study. In the future, it is recommended to take the operational thinking aspect into account to further improve the practicability of the proposed DHHL-MABAC model. In addition, it is necessary to include the optimization of the multicriteria evaluation system in EDM to make the proposed model more robust.