From Multi- to Univariate: A Product Random Variable with an Application to Electricity Market Transactions: Pareto and Student’s t-Distribution Case
Abstract
1. Introduction
2. State of the Art
3. Pareto Distribution
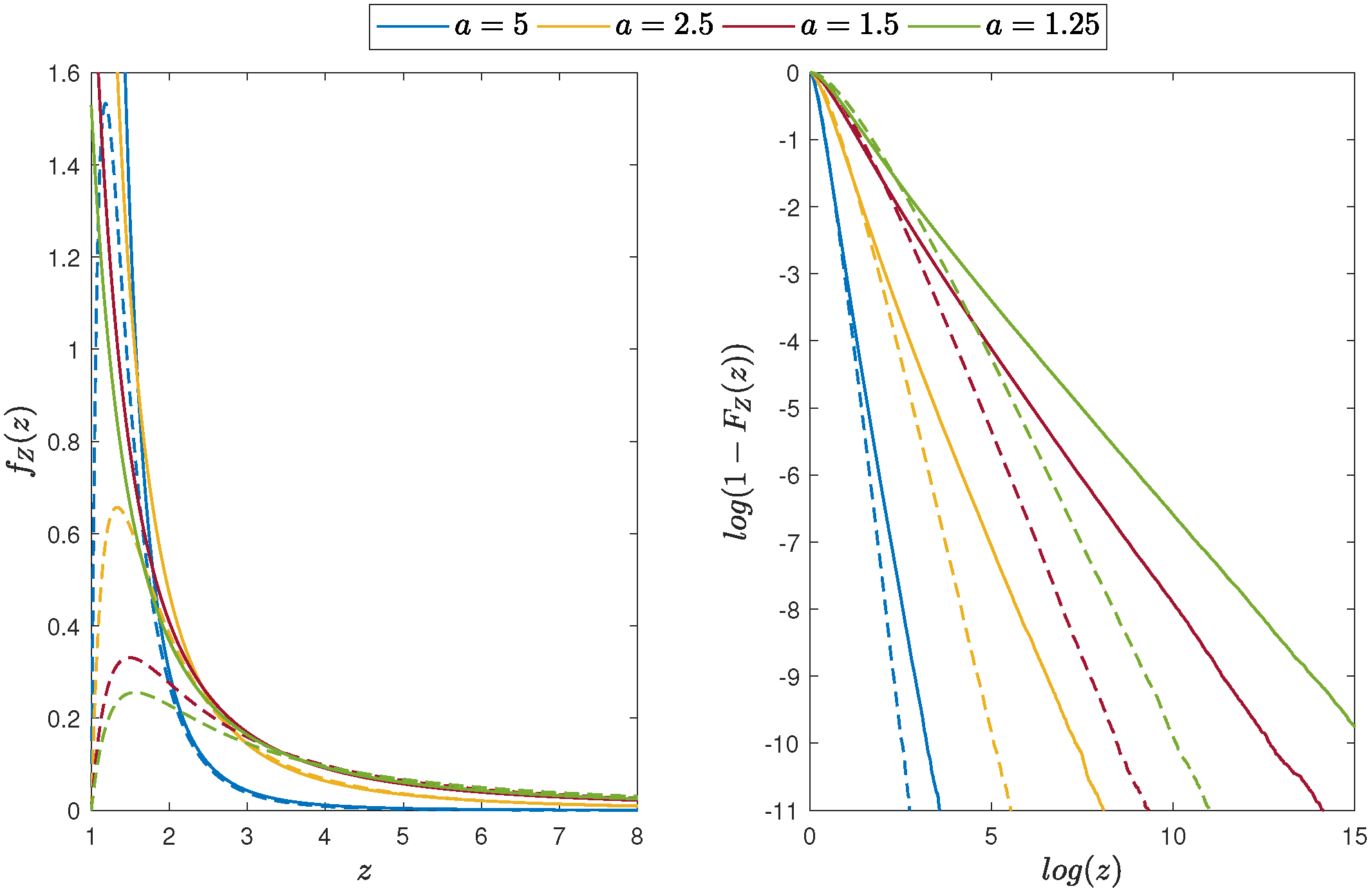
3.1. Product of Two Pareto Distributed Random Variables
3.2. Product of Gaussian and Pareto Distributed Random Variables
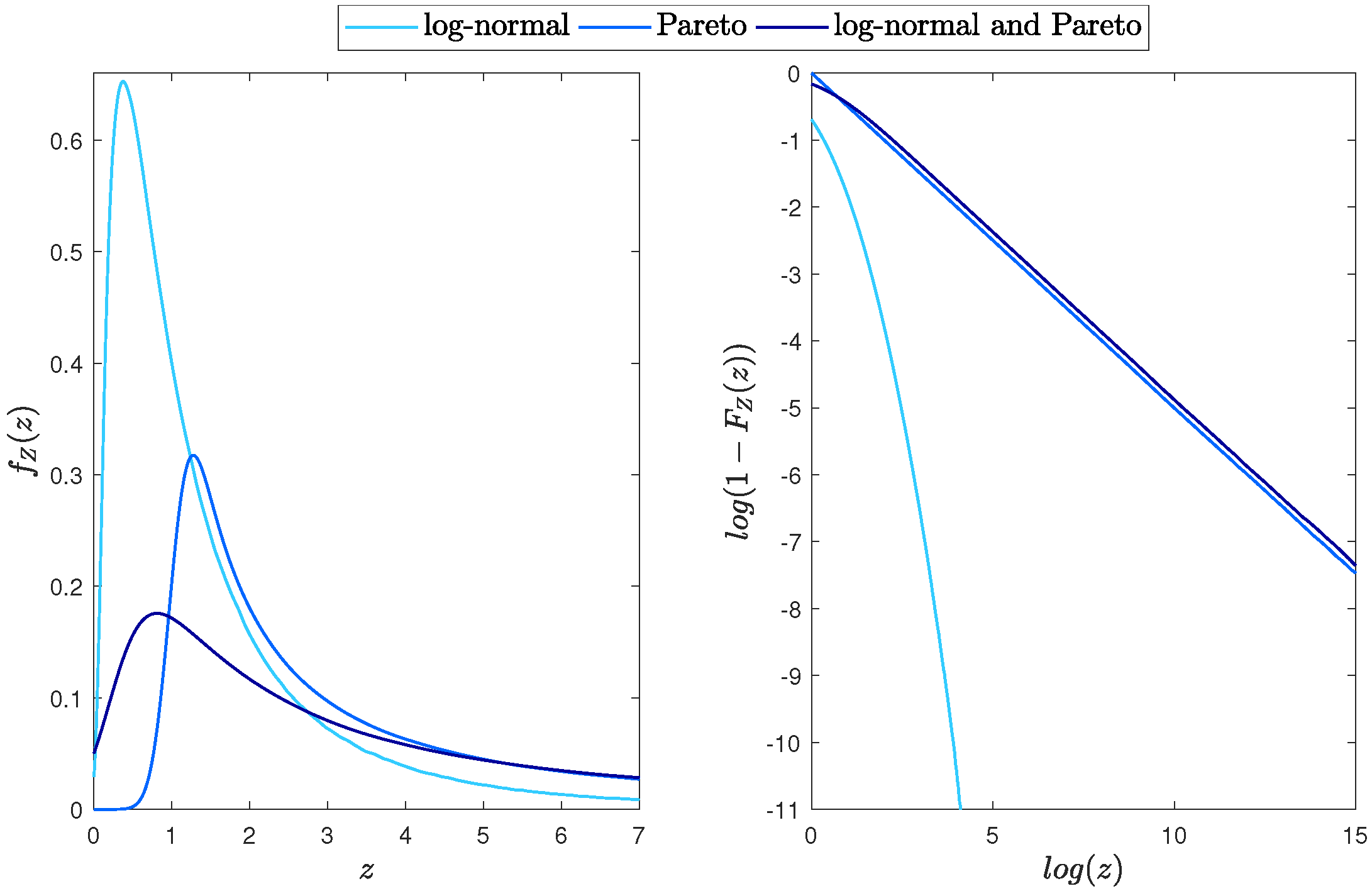
3.3. Product of Log-Normal and Pareto Distributed Random Variables
4. Student’s t Distribution
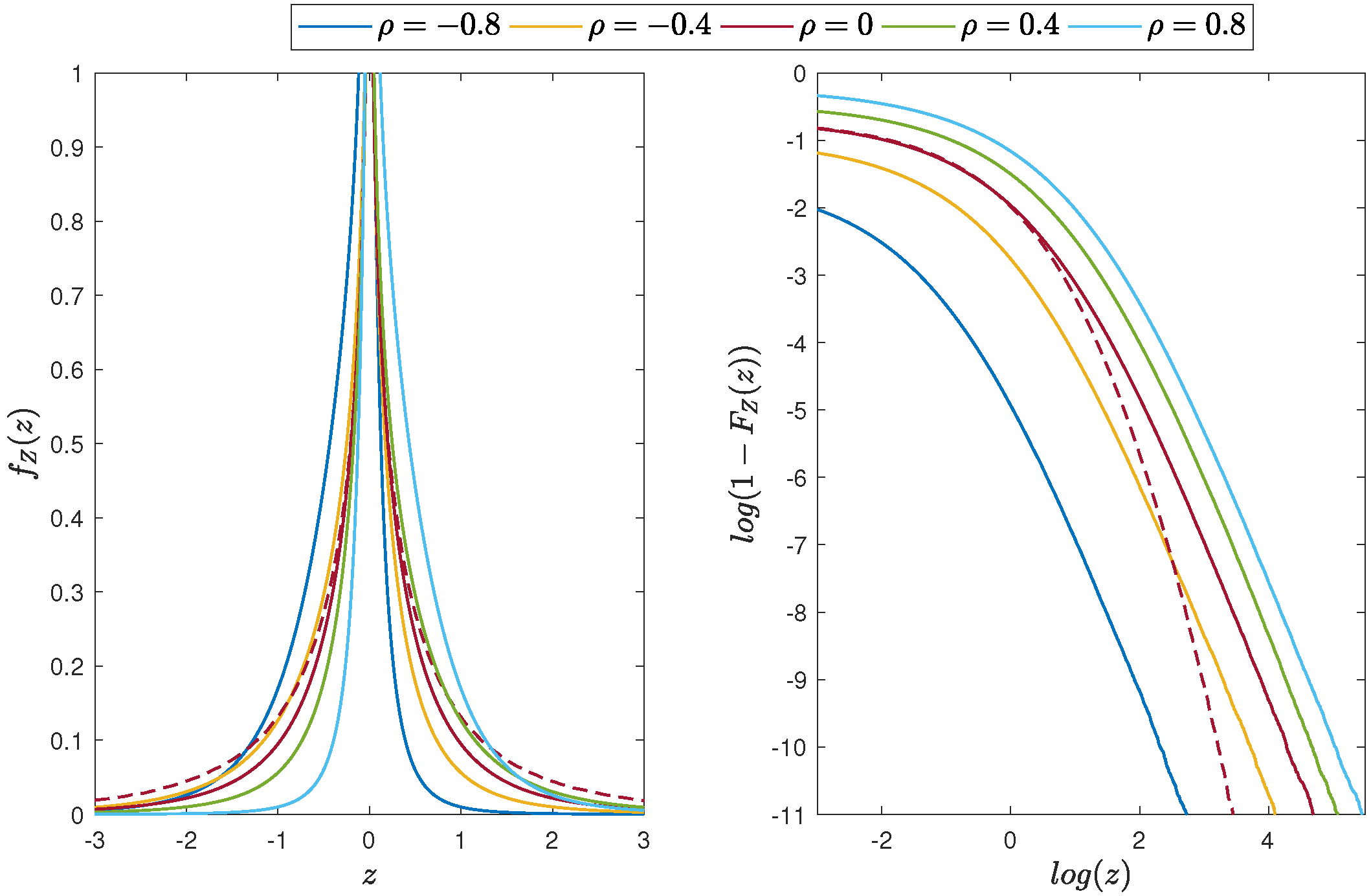
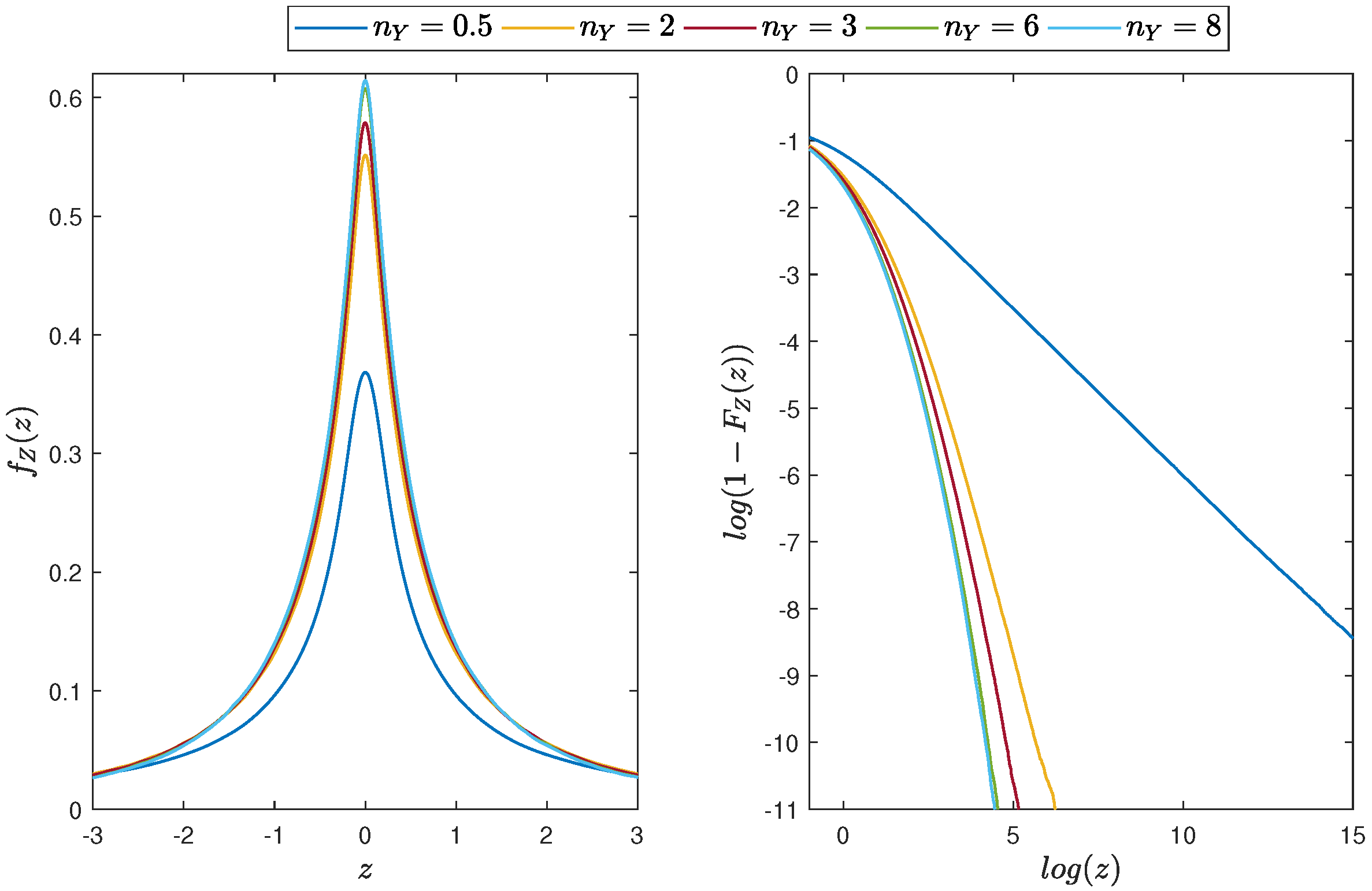
4.1. Product of Two Student’s t Distributed Random Variables
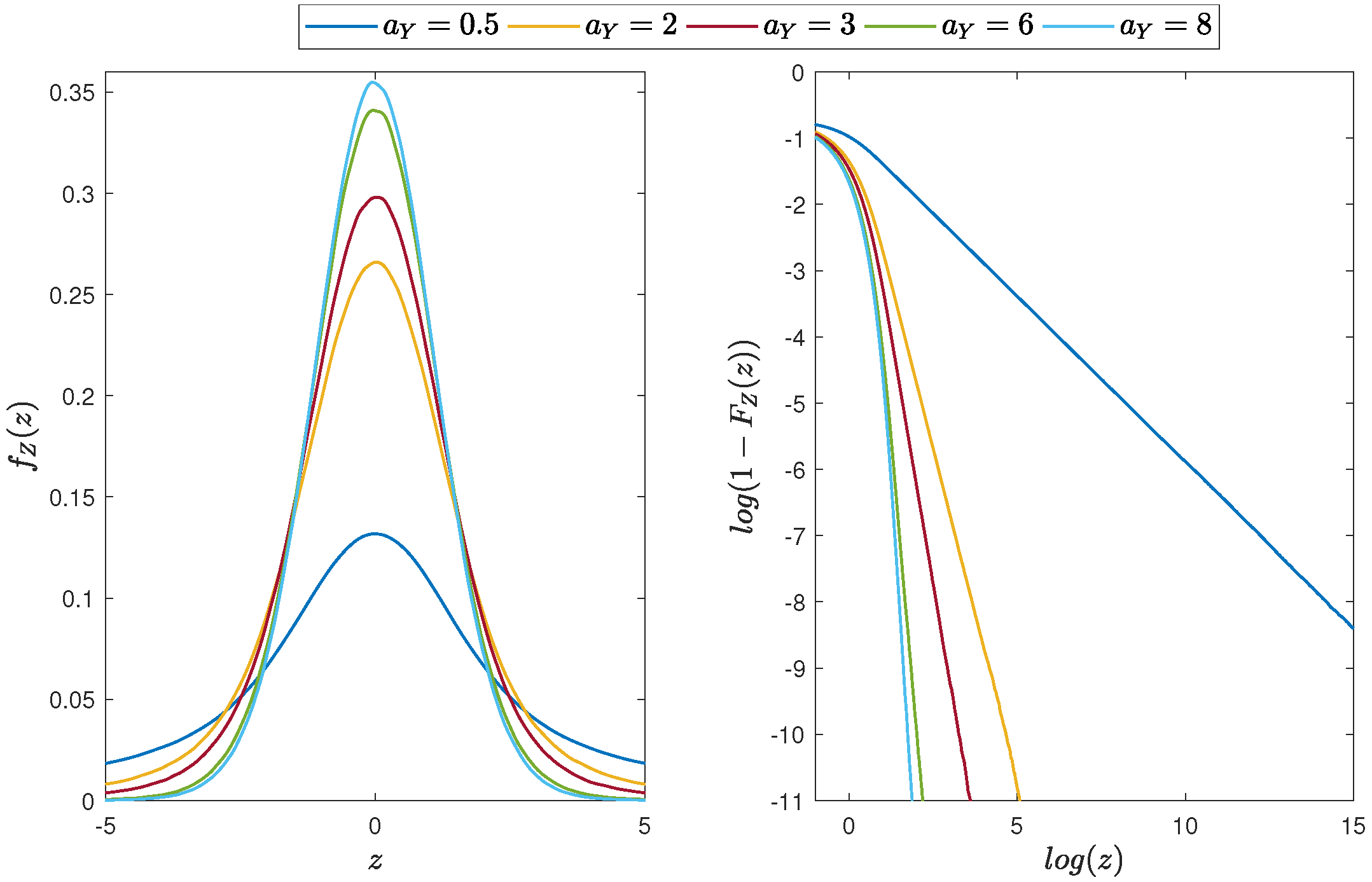
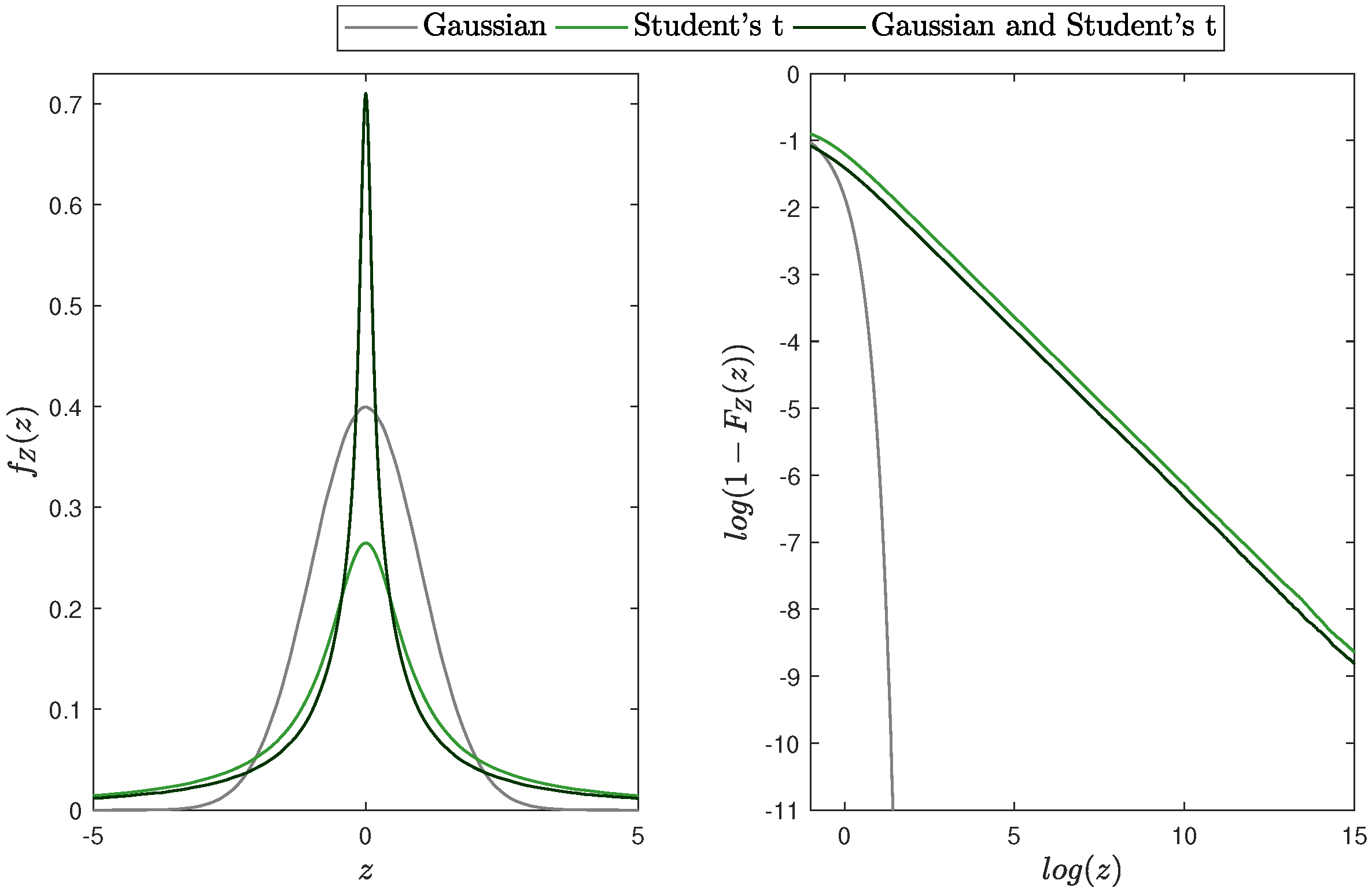
4.2. Product of Gaussian and Student’s t Distributed Random Variables
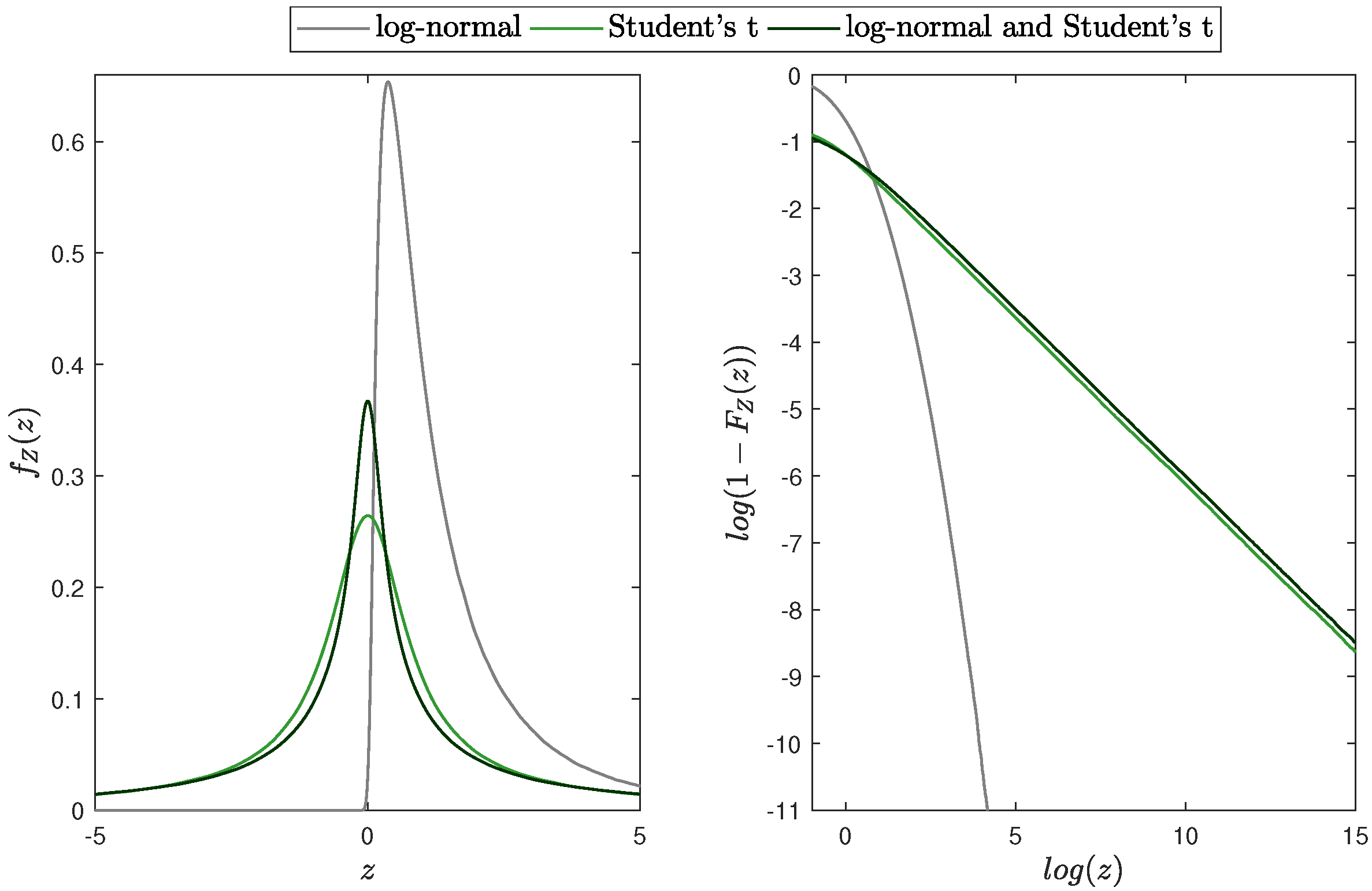
4.3. Product of Log-Normal and Student’s t Distributed Random Variables
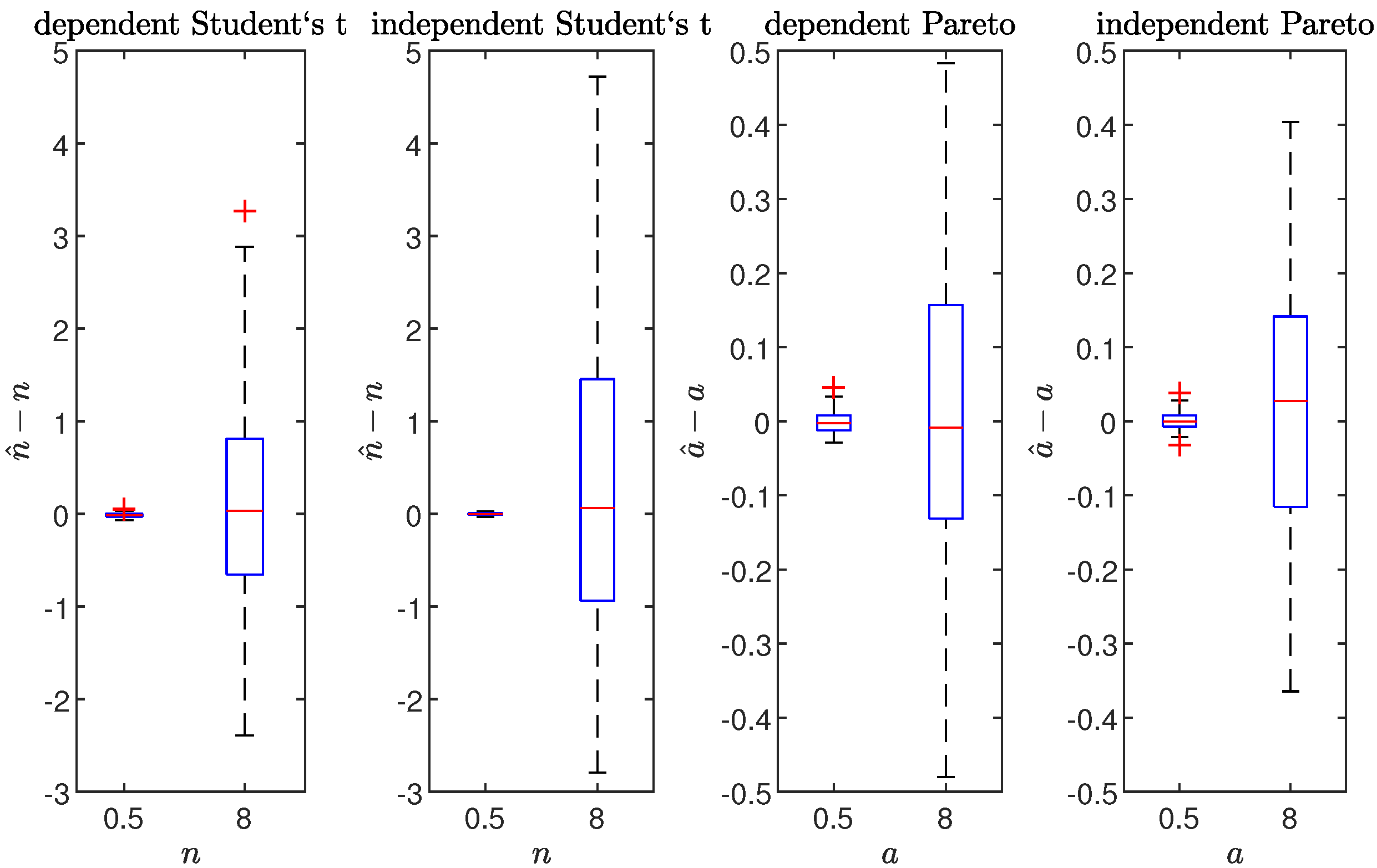
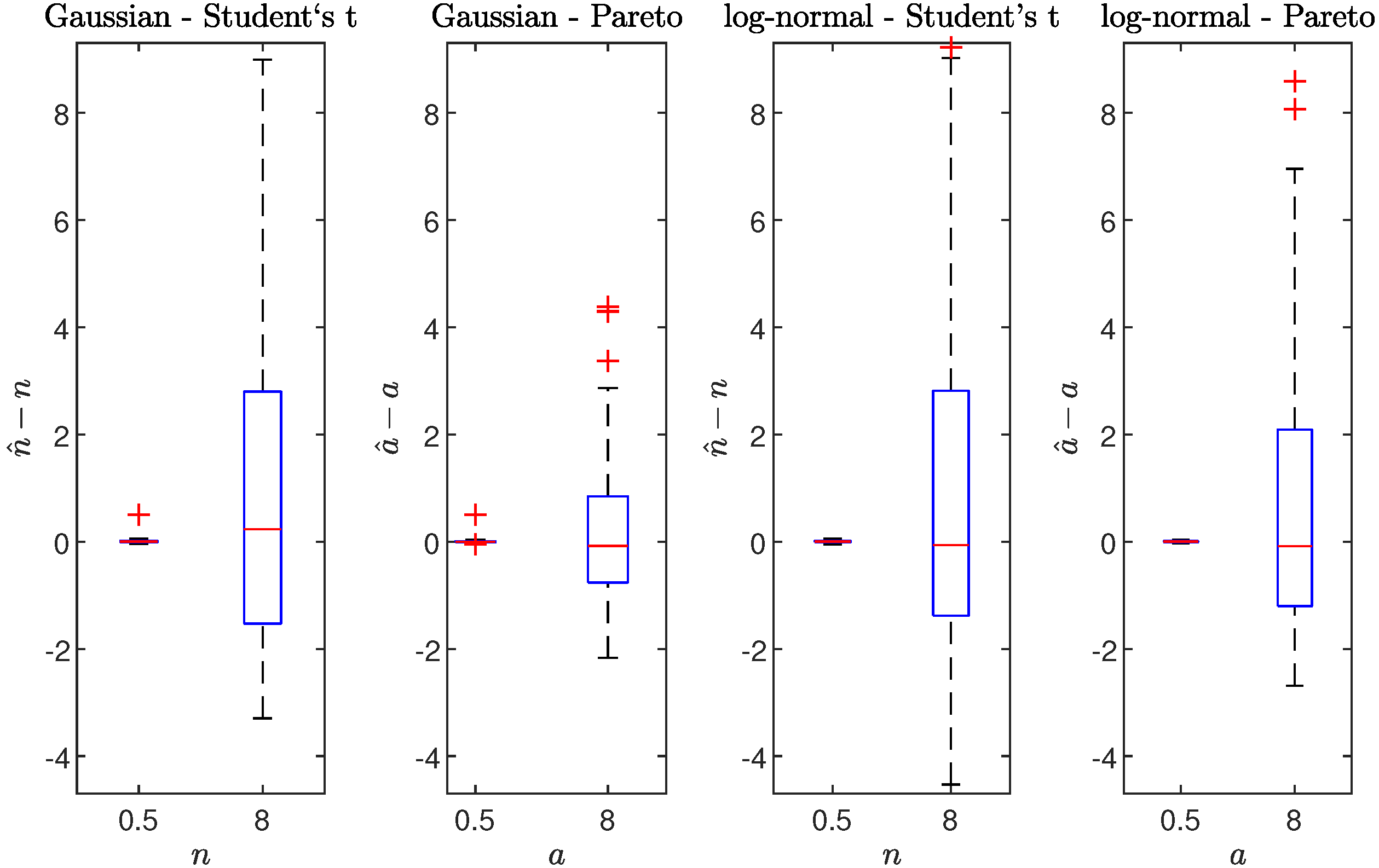
5. Parameters Estimation–Simulation Study
6. Real Data Application—Distribution of Electricity Transaction Values
7. Conclusions
8. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Gaussian and Log-Normal Distributions
Appendix A.1. Product of Two Gaussian Distributed Random Variables
Appendix A.2. Product of Two Log-Normally Distributed Random Variables
Appendix B. Proofs
Appendix B.1. Proof of Lemma 2
Appendix B.2. Proof of Lemma 3
References
- Bielak, Ł.; Grzesiek, A.; Janczura, J.; Wyłomańska, A. Market risk factors analysis for an international mining company. Multi-dimensional heavy-tailed-based modelling. Resour. Policy 2021, 74, 102308. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y. Tail behavior of the product of two dependent random variables with applications to risk theory. Extremes 2013, 16, 55–74. [Google Scholar] [CrossRef]
- Nadarajah, S. Exact distribution of the product of m gamma and n Pareto random variables. J. Comput. Appl. Math. 2011, 235, 4496–4512. [Google Scholar] [CrossRef]
- Seijas-Macías, A.; Oliveira, A. An Approach to Distribution of the Product of Two Normal Variables. Discuss. Math. Probab. Stat. 2012, 32, 87–99. [Google Scholar]
- Rohatgi, V.K.; Saleh, A.K.M.E. An Introduction to Probability and Statistics; Wiley Series in Probability and Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Mardia, K.V. Multivariate Pareto Distributions. Ann. Math. Stat. 1962, 33, 1008–1015. [Google Scholar] [CrossRef]
- Ahsanullah, M.; Kibria, B.M.G.; Shakil, M. Normal and Student’s t Distributions and Their Applications; Atlantis Press: Paris, France, 2014; pp. 7–102. [Google Scholar]
- Holmes, J.D.; Moriarty, W.W. Application of the generalized Pareto distribution to extreme value analysis in wind engineering. J. Wind. Eng. Ind. Aerodyn. 1999, 83, 1–10. [Google Scholar] [CrossRef]
- Mahmoudi, E. The beta generalized Pareto distribution with application to lifetime data. Math. Comput. Simul. 2011, 81, 2414–2430. [Google Scholar] [CrossRef]
- Li, R.; Nadarajah, S. A review of Student’s t distribution and its generalizations. Empir. Econ. 2020, 58, 1461–1490. [Google Scholar] [CrossRef]
- Stępniak, P.; Wyłomańska, A. The maximum likelihood method for Student’s t-distributed autoregressive model with infinite variance. Math. Appl. 2020, 48, 133–156. [Google Scholar]
- Ahmad, B.; Jun, S.; Palade, V.; You, Q.; Mao, L.; Zhongjie, M. Improving skin cancer classification using heavy-tailed Student t-distribution in generative adversarial networks (TED-GAN). Diagnostics 2021, 11, 2147. [Google Scholar] [CrossRef]
- Uchiyama, Y.; Nakagawa, K. TPLVM: Portfolio construction by Student’s t-process latent variable model. Mathematics 2020, 8, 449. [Google Scholar] [CrossRef]
- Kwon, O.K.; Satchell, S. The distribution of cross sectional momentum returns when underlying asset returns are Student’s t distributed. J. Risk Financ. Manag. 2020, 13, 27. [Google Scholar] [CrossRef]
- Wang, Y.; Tsay, R.S. On diagnostic checking of Vector ARMA-GARCH Models with Gaussian and Student-t innovations. Econometrics 2013, 1, 1–31. [Google Scholar] [CrossRef]
- Huang, C.; Zhao, X.; Cheng, W.; Ji, Q.; Duan, Q.; Han, Y. Statistical inference of Dynamic Conditional Generalized Pareto distribution with weather and air quality factors. Mathematics 2022, 10, 1433. [Google Scholar] [CrossRef]
- Bhati, D.; Calderín-Ojeda, E.; Meenakshi, M. A new heavy tailed class of distributions which includes the Pareto. Risks 2019, 7, 99. [Google Scholar] [CrossRef]
- Li, C.; Li, X. On the optimal risk sharing in reinsurance with random recovery rate. Risks 2018, 6, 114. [Google Scholar] [CrossRef]
- Loke, S.H.; Thomann, E. Numerical ruin probability in the dual risk model with risk-free investments. Risks 2018, 6, 110. [Google Scholar] [CrossRef]
- Nadarajah, S. Exact Distribution of the Product of Two or More Logistic Random Variables. Methodol. Comput. Appl. Probab. 2008, 11, 651–660. [Google Scholar] [CrossRef]
- Nadarajah, S. Some algebra for Pearson type VII random variables. Bull. Korean Math. Soc. 2008, 45, 339–353. [Google Scholar] [CrossRef]
- Nadarajah, S. On the product XY for some elliptically symmetric distributions. Stat. Probab. Lett. 2005, 75, 67–75. [Google Scholar] [CrossRef]
- Garg, M.; Sharma, A.; Manohar, P. The distribution of the product of two independent generalized trapezoidal random variables. Commun. Stat.-Theory Methods 2016, 45, 6369–6384. [Google Scholar] [CrossRef]
- Krstic, D.; Mihajlo, S.; Jovanovic, Z.; Gerov, R.; Milenkovic, V. Statistical characteristic of ratio and product of rician random variables and its application in analysis of wireless communication cystems. Int. J. Math. Comput. Methods 2016, 1, 79–86. [Google Scholar]
- Nadarajah, S.; Dey, D.K. On the product and ratio of t random variables. Appl. Math. Lett. 2006, 19, 45–55. [Google Scholar] [CrossRef]
- Li, Y.; He, Q.; Blum, R.S. On the Product of Two Correlated Complex Gaussian Random Variables. IEEE Signal Process. Lett. 2020, 27, 16–20. [Google Scholar] [CrossRef]
- Nadarajah, S. The product t density distribution arising from the product of two Student’s t PDFs. Stat. Pap. 2009, 50, 605–615. [Google Scholar] [CrossRef]
- Seijas-Macias, A.; Oliveira, A.; Oliveira, T.A. The skewness and kurtosis of the product of two normally distributed random variables. Commun. Stat.-Theory Methods 2021, 1–37. [Google Scholar] [CrossRef]
- Malik, H.J.; Trudel, R. Probability Density Function of the Product and Quotient of Two Correlated Exponential Random Variables. Can. Math. Bull. 1986, 29, 413–418. [Google Scholar] [CrossRef]
- Homei, H. The stochastic linear combination of Dirichlet distributions. Commun. Stat.-Theory Methods 2019, 50, 2354–2359. [Google Scholar] [CrossRef]
- Tang, J.; Gupta, A. On the distribution of the product of independent beta random variables. Stat. Probab. Lett. 1984, 2, 165–168. [Google Scholar] [CrossRef]
- Bhargava, R.; Khatri, C. The distribution of product of independent beta random variables with application to multivariate analysis. Ann. Inst. Stat. Math. 1981, 33, 287–296. [Google Scholar] [CrossRef]
- Nadarajah, S. On the product of generalized Pareto random variables. Appl. Econ. Lett. 2008, 15, 253–259. [Google Scholar] [CrossRef]
- Pham-Gia, T.; Turkkan, N. The product and quotient of general beta distributions. Stat. Pap. 2002, 43, 537–550. [Google Scholar] [CrossRef]
- Lin, G.D.; Stoyanov, J. Moment Determinacy of Powers and Products of Nonnegative Random Variables. J. Theor. Probab. 2014, 28, 1337–1353. [Google Scholar] [CrossRef]
- Glen, A.G.; Leemis, L.M.; Drew, J.H. Computing the distribution of the product of two continuous random variables. Comput. Stat. Data Anal. 2004, 44, 451–464. [Google Scholar] [CrossRef]
- Hamedani, G.G.; Walter, G.G. On the product of symmetric random variables. Stat. Probab. Lett. 1985, 3, 251–253. [Google Scholar] [CrossRef]
- Xu, H.; Cheng, F.; Wang, Y.; Cheng, D. A necessary and sufficient condition for the subexponentiality of the product convolution. Adv. Appl. Probab. 2018, 50, 57–73. [Google Scholar] [CrossRef]
- Cui, Z.; Omey, E.; Wang, W.; Wang, Y. Asymptotics of convolution with the semi-regular-variation tail and its application to risk. Extremes 2018, 21, 509–532. [Google Scholar] [CrossRef]
- Leonardo, E.J.; Mafra, S.B.; Montejo-Sánchez, S.; Fernández, E.M.G. Approximations for the product, ratio, and sum of alpha-mu random variables with application in the analysis of cognitive radio networks. Int. J. Commun. Syst. 2021, 34, e4756. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. A note on the product of normal and Laplace random variables. Braz. J. Probab. Stat. 2005, 19, 33–38. [Google Scholar]
- Nadarajah, S.; Kotz, S. On the linear combination, product and ratio of normal and Laplace random variables. J. Frankl. Inst. 2011, 348, 810–822. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. On the Product and Ratio of Gamma and Weibull Random Variables. Econom. Theory 2006, 22, 338–344. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. On the Product and Ratio of Gamma and Beta Random Variables. Allg. Stat. Arch. 2005, 89, 435–449. [Google Scholar] [CrossRef]
- Nadarajah, S. Sum, product and ratio of Pareto and gamma variables. J. Stat. Comput. Simul. 2010, 80, 1071–1082. [Google Scholar] [CrossRef]
- Shakil, M.; Kibria, B.G. On the Product of Maxwell and Rice Random Variables. J. Mod. Appl. Stat. Methods 2007, 6, 19. [Google Scholar] [CrossRef]
- Tang, Q. From light tails to heavy tails through multiplier. Extremes 2008, 11, 379–391. [Google Scholar] [CrossRef]
- Idrizi, L. On the product and ratio of Pareto and Kumarswamy random variables. Math. Theory Model. 2014, 4, 137–146. [Google Scholar]
- Nadarajah, S.; Kotz, S. On the Product and Ratio of Pearson Type VII and Laplace Random Variables. Austrian J. Stat. 2016, 34, 11–23. [Google Scholar] [CrossRef]
- Obeid, N.; Kadry, S. On the product and ratio of Pareto and Rayleigh random variables. Pak. J. Stat. 2019, 35, 285. [Google Scholar]
- Springer, M.D.; Thompson, W. The distribution of products of Beta, Gamma and Gaussian random variables. SIAM J. Appl. Math. 1970, 18, 721–737. [Google Scholar] [CrossRef]
- Cline, D.B.; Samorodnitsky, G. Subexponentiality of the product of independent random variables. Stoch. Process. Their Appl. 1994, 49, 75–98. [Google Scholar] [CrossRef]
- Su, C.; Chen, Y. On the behavior of the product of independent random variables. Sci. China Ser. A 2006, 49, 342–359. [Google Scholar] [CrossRef]
- Springer, M.D.; Thompson, W. The distribution of products of independent random variables. SIAM J. Appl. Math. 1966, 14, 511–526. [Google Scholar] [CrossRef]
- Cui, G.; Yu, X.; Iommelli, S.; Kong, L. Exact distribution for the product of two correlated Gaussian random variables. IEEE Signal Process. Lett. 2016, 23, 1662–1666. [Google Scholar] [CrossRef]
- Gaunt, R.E. A note on the distribution of the product of zero-mean correlated normal random variables. Stat. Neerl. 2018, 73, 176–179. [Google Scholar] [CrossRef]
- Kan, R. From moments of sum to moments of product. J. Multivar. Anal. 2008, 99, 542–554. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, Y. On the long tail property of product convolution. Lith. Math. J. 2020, 60, 315–329. [Google Scholar] [CrossRef]
- Maksimov, V.M. A convergence property of products of independent random variables on compact Lie groups. Math. USSR-Sbornik 1970, 11, 423–440. [Google Scholar] [CrossRef]
- Webb, E.L.R. Note on the product of random variables. Can. J. Phys. 1962, 40, 1394–1396. [Google Scholar] [CrossRef]
- Williams, E.J. Some representations of stable random variables as products. Biometrika 1977, 64, 167–169. [Google Scholar] [CrossRef]
- Galambos, J.; Simonelli, I. Products of Random Variables: Applications to Problems of Physics and to Arithmetical Functions, 1st ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Podolski, H. The distribution of a product of n independent random variables with generalized Gamma distribution. Demonstr. Math. 1972, 4, 119–124. [Google Scholar] [CrossRef]
- Wilson, P.S.; Toumi, R. A fundamental probability distribution for heavy rainfall. Geophys. Res. Lett. 2005, 32, L14812. [Google Scholar] [CrossRef]
- Cigizoglu, H.K.; Bayazit, M. A generalized seasonal model for flow duration curve. Hydrol. Process. 2000, 14, 1053–1067. [Google Scholar] [CrossRef]
- Ly, S.; Pho, K.H.; Ly, S.; Wong, W.K. Determining Distribution for the Product of Random Variables by Using Copulas. Risks 2019, 7, 23. [Google Scholar] [CrossRef]
- Salo, J.; El-Sallabi, H.; Vainikainen, P. The distribution of the product of independent Rayleigh random variables. IEEE Trans. Antennas Propag. 2006, 54, 639–643. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. Comments on “On the Distribution of the Product of Independent Rayleigh Random Variables”. IEEE Trans. Antennas Propag. 2006, 54, 3570–3571. [Google Scholar] [CrossRef]
- Bhargav, N.; da Silva, C.R.N.; Chun, Y.J.; Leonardo, E.J.; Cotton, S.L.; Yacoub, M.D. On the Product of Two κ − μ Random Variables and its Application to Double and Composite Fading Channels. IEEE Trans. Wirel. Commun. 2018, 17, 2457–2470. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. Sociological Models Based on Fréchet Random Variables. Qual. Quant. 2008, 42, 89–95. [Google Scholar] [CrossRef]
- Hossain, A.M.; Zimmer, W.J. Comparisons of methods of estimation for a Pareto distribution of the first kind. Commun. Stat.-Theory Methods 2000, 29, 859–878. [Google Scholar] [CrossRef]
- Lai, C.D.; Balakrishnan, N. Continuous Bivariate Distributions; Springer: New York, NY, USA, 2009. [Google Scholar]
- Cochran, W.G. The distribution of quadratic forms in a normal system, with applications to the analysis of covariance. Math. Proc. Camb. Philos. Soc. 1934, 30, 178–191. [Google Scholar] [CrossRef]
- Nadarajah, S. Exact distribution of the product of n Student’s t RVs. Methodol. Comput. Appl. Probab. 2012, 14, 997–1009. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Daalhuis, A.B.; Lozier, D.W.; Schneider, B.I.; Boisvert, R.F.; Clark, C.W.; Miller, B.R.; Saunders, B.V.; Cohl, H.S.; McClain, M.A. (Eds.) NIST Digital Library of Mathematical Functions. Release 1.1.4 of 15 January 2022. 2022. Available online: http://dlmf.nist.gov/ (accessed on 30 June 2022).
- Weron, R. Modeling and Forecasting Electricity Loads and Prices: A Statistical Approach/Rafał Weron; Wiley Finance Series; John Wiley & Sons: Chichester, UK; Hoboken, NJ, USA; New York, NY, USA, 2006. [Google Scholar]
- August, B.; Horsch, A. Negative market prices on power exchanges: Evidence and policy implications from Germany. Electr. J. 2020, 33, 106716. [Google Scholar]
- Stephens, M.A. EDF statistics for goodness of fit and some comparisons. J. Am. Stat. Assoc. 1974, 69, 730–737. [Google Scholar] [CrossRef]
- Joyce, J.M. Kullback–Leibler Divergence. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 720–722. [Google Scholar]
- Wecker, W.E. A note on the time series which is the product of two stationary time series. Stoch. Process. Their Appl. 1978, 8, 153–157. [Google Scholar] [CrossRef]
- White, H.; Granger, C.W. Consideration of trends in time series. J. Time Ser. Econom. 2011, 3. [Google Scholar] [CrossRef]
- Roussas, G.G. Joint and conditional p.d.f.’s, conditional expectation and variance, moment generating function, covariance, and correlation coefficient. In An Introduction to Probability and Statistical Inference; Elsevier: San Diego, CA, USA, 2015; pp. 135–186. [Google Scholar]
- Aroian, L.A.; Taneja, V.S.; Cornwell, L.W. Mathematical forms of the distribution of the product of two normal variables. Commun. Stat.-Theory Methods 1978, 7, 165–172. [Google Scholar] [CrossRef]
- Craig, C.C. On the Frequency Function of xy. Ann. Math. Stat. 1936, 7, 1–15. [Google Scholar] [CrossRef]
- Aitchison, J.; Ho, C.H. The Multivariate Poisson-Log Normal Distribution. Biometrika 1989, 76, 643–653. [Google Scholar] [CrossRef]
- Yerel, S.; Konuk, A. Bivariate lognormal distribution model of cutoff grade impurities: A case study of magnesite ore deposit. Sci. Res. Essay 2009, 4, 1500–1504. [Google Scholar]

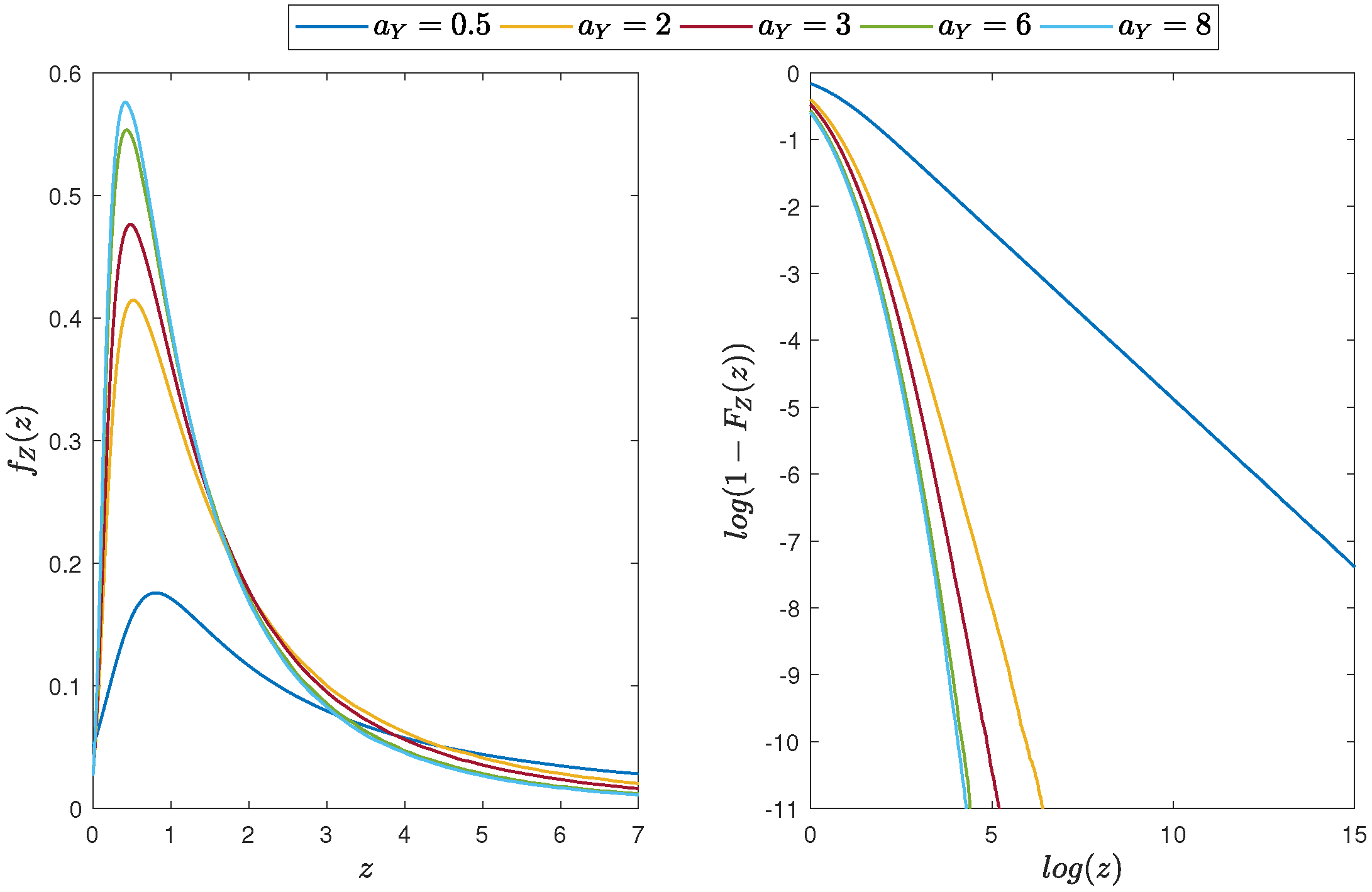

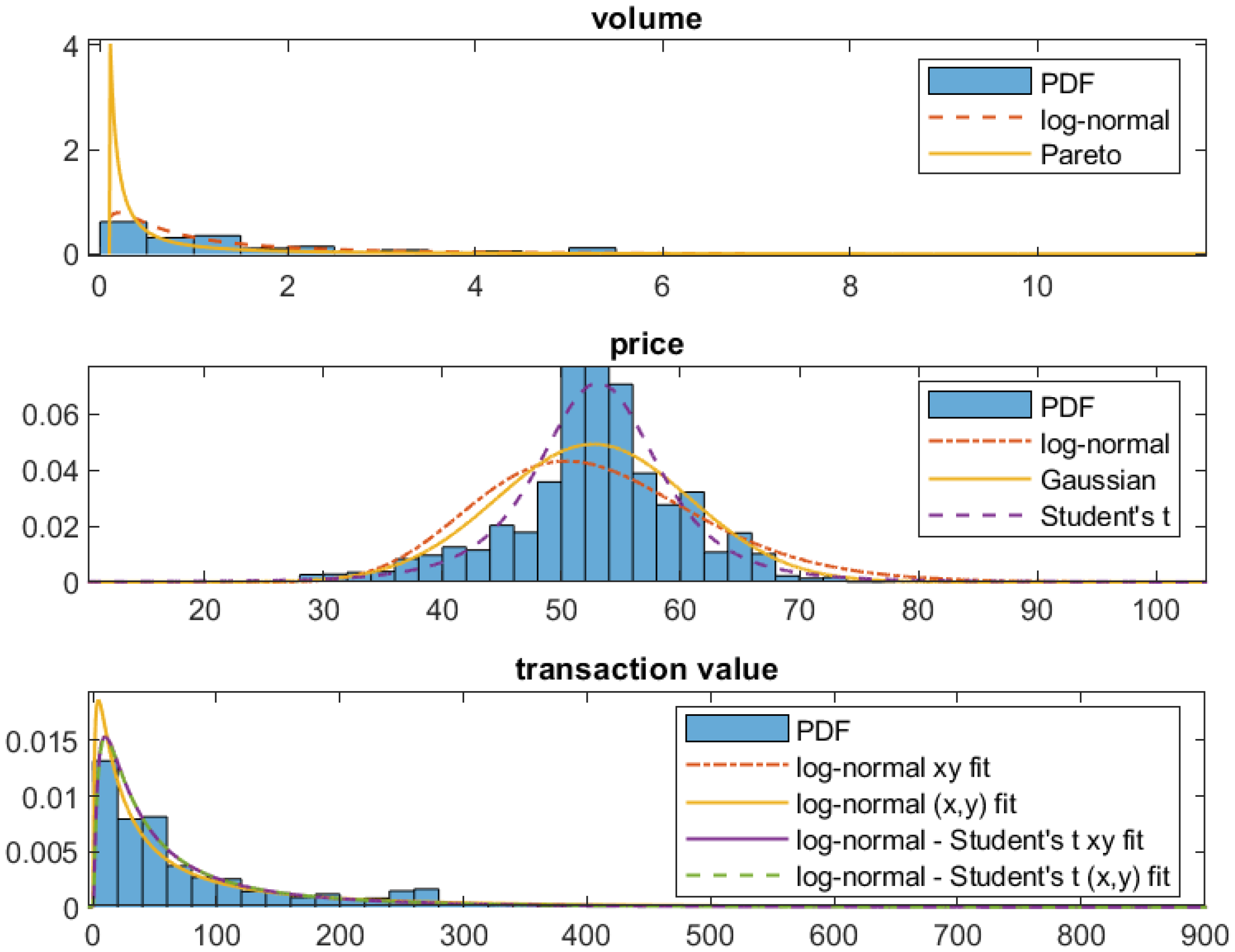
| 20 December | ||||
| Variable | Distribution | KS statistic | RMSE | KLD |
| Volume | log-normal | 0.0810 | 0.0359 | 0.1367 |
| Pareto | 0.2263 | 0.1350 | 0.5717 | |
| Price | log-normal | 0.1719 | 0.0813 | 3.1737 |
| Gaussian | 0.1305 | 0.0560 | 2.5211 | |
| Student’s t | 0.0523 | 0.0206 | 2.5304 | |
| Value | log-normal (x, y) | 0.0501 | 0.0247 | 0.0819 |
| log-normal xy | 0.0498 | 0.0247 | 0.0208 | |
| log-normal—Student’s t (x, y) | 0.0487 | 0.0242 | 0.0214 | |
| log-normal—Student’s t xy | 0.0500 | 0.0245 | 0.0214 | |
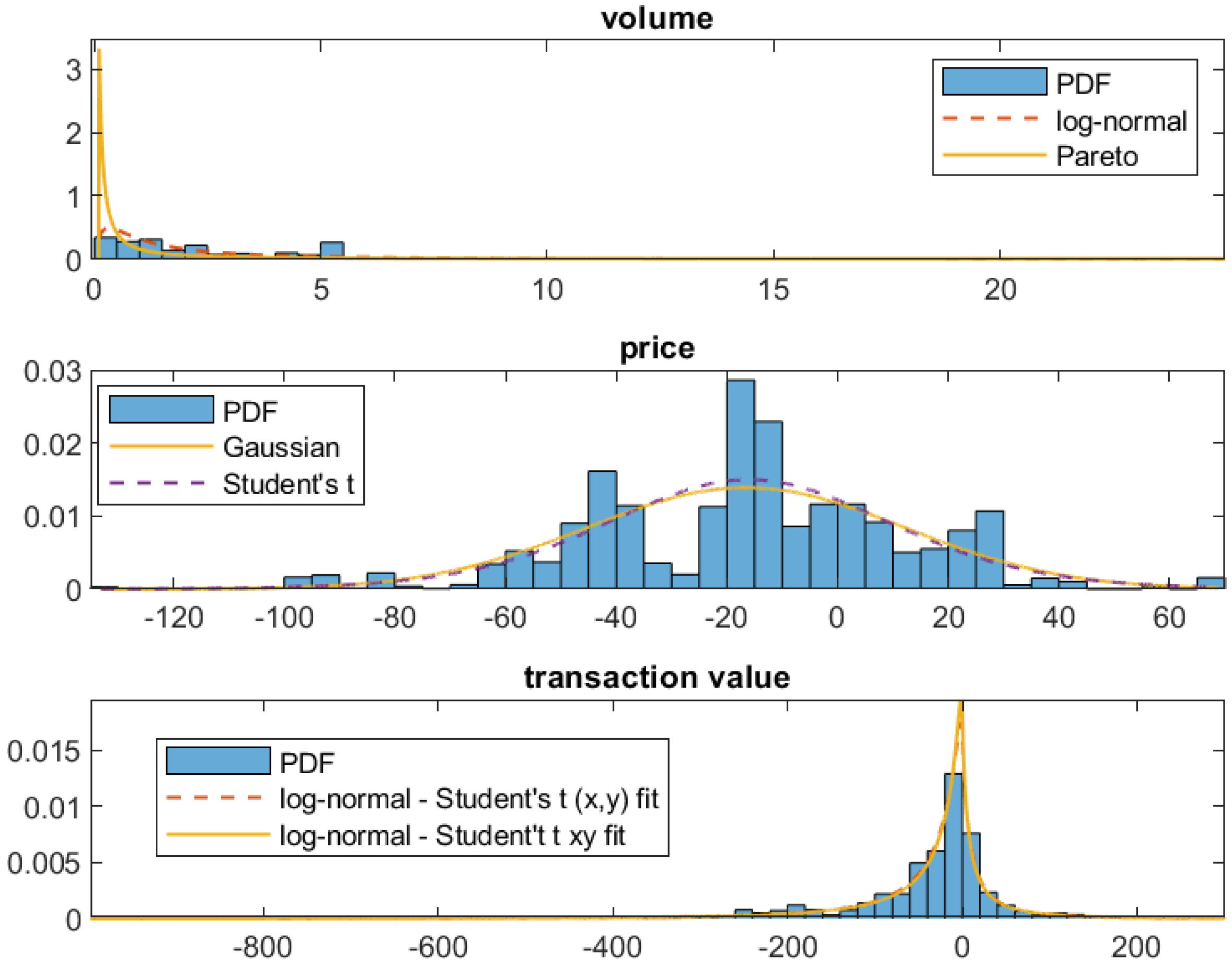
| 15 March | ||||
| Volume | log-normal | 0.0952 | 0.0501 | 0.2868 |
| Pareto | 0.2881 | 0.1702 | 0.9211 | |
| Price | Gaussian | 0.1014 | 0.0333 | 1.4262 |
| Student’s t | 0.0891 | 0.0308 | 1.4707 | |
| Value | log-normal—Student’s t (x, y) | 0.0414 | 0.0167 | 1.4370 |
| log-normal—Student’s t xy | 0.0369 | 0.0148 | 1.4202 | |
| Multivariate Pareto |
| Independent Pareto |
| Gaussian-Pareto |
| Log-normal-Pareto |
| Multivariate Student’s t |
| Independent Student’s t |
| Gaussian-Student’s t |
| Log-normal-Student’s t |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adamska, J.; Bielak, Ł.; Janczura, J.; Wyłomańska, A. From Multi- to Univariate: A Product Random Variable with an Application to Electricity Market Transactions: Pareto and Student’s t-Distribution Case. Mathematics 2022, 10, 3371. https://doi.org/10.3390/math10183371
Adamska J, Bielak Ł, Janczura J, Wyłomańska A. From Multi- to Univariate: A Product Random Variable with an Application to Electricity Market Transactions: Pareto and Student’s t-Distribution Case. Mathematics. 2022; 10(18):3371. https://doi.org/10.3390/math10183371
Chicago/Turabian StyleAdamska, Julia, Łukasz Bielak, Joanna Janczura, and Agnieszka Wyłomańska. 2022. "From Multi- to Univariate: A Product Random Variable with an Application to Electricity Market Transactions: Pareto and Student’s t-Distribution Case" Mathematics 10, no. 18: 3371. https://doi.org/10.3390/math10183371
APA StyleAdamska, J., Bielak, Ł., Janczura, J., & Wyłomańska, A. (2022). From Multi- to Univariate: A Product Random Variable with an Application to Electricity Market Transactions: Pareto and Student’s t-Distribution Case. Mathematics, 10(18), 3371. https://doi.org/10.3390/math10183371






