Abstract
The first person to introduce possibility theory was Lotfi A. Zadeh, in 1977. It was, of course, of no coincidence that he directly combined it with the theory of fuzzy sets. Later, several researchers dealt with the mathematical foundations of the theory of possibilities. They introduced possibility distribution as a concept, and they directly combined it with fuzzy numbers. A fuzzy number corresponds to a possibility distribution and vice versa. This correspondence gave a key advantage to possibility theory over probability theory. This advantage is the facility of operations. However, there is also a basic: problem how is a possibility distribution generated? In this paper, we introduce a method of constructing a possibility distribution via a cumulative probability function. The advantage of this method is the simplicity of construction, which is nothing more than the construction of a fuzzy triangular or trapezoidal number via a cumulative probability function. This construction introduces a way to determine a fuzzy number without relying on the experience or intuition of the researcher. We should, of course, emphasize that this specific construction is within the framework of a theoretical model. We do not apply it to specific data. We also considered that the theoretical construction model should be presented through the theory of possibilities, thus avoiding the theory of probabilities.
Keywords:
fuzzy numbers; possibility measure; necessity measure; cumulative distribution function; possibility distributions MSC:
28E10; 03E72; 94D05
1. Introduction
The possibility theory initiated by Zadeh in [1] is a generalization of probability theory. Many authors had a hand in the development of possibility theory, especially Dubois and Prade [2]. It has been successfully applied in decision-making problems in conditions of uncertainty [3], in fuzzy cooperative games [4], fuzzy neural networks [5], etc. An important role in the development of possibility theory was played by the concept of fuzzy numbers. In general, fuzzy numbers represent an important class of possibility measure. The main reasons why fuzzy numbers make a very good instrument both for theoretical approaches and applications are as follows: Fuzzy numbers generalize real numbers, and by Zadeh’s extension principle [6], the operations of fuzzy numbers are extensions of the operations of real numbers [6]. Moreover, the operations with fuzzy numbers have good arithmetical properties [2]. The link that connects the two concepts of fuzzy numbers and possibility is the possibility distribution of an event. This possibility distribution is most often expressed by a fuzzy number. This fuzzy number plays a role in corresponding to the probability distribution. In other words, it works in a similar way, but instead of probabilities, it uses the concept of possibility. The above procedure has been used quite effectively in risk theory [7]. The main disadvantage of this procedure is the choice of the fuzzy number. This disadvantage is usually covered by the researcher’s experience. In this work, we construct the fuzzy number with the help of a cumulative distribution function. That is, from basic data, we produce the cumulative distribution function and then transform it into a fuzzy number, which we can use as a possibility distribution. The process of transformation is simple and produces triangular or trapezoidal fuzzy numbers retaining all the properties of these numbers.
This paper is organized as follows: In Section 2, we present fundamental concepts regarding the formulation of fuzzy numbers and possibility distribution. In Section 3, we show the construction of fuzzy numbers through the cumulative distribution function, and we also give several examples of its operation. General comments and concluding remarks are set out in Section 4 and Section 5.
2. Definitions and Basic Properties
In this section, we present the most basic concepts concepts used in this paper and their definitions and properties drawn from the relevant literature, starting with fuzzy numbers. It should also be noted that the definitions and properties of fuzzy numbers have been drawn from the book by G. Klir and B. Yuan, titled Fuzzy sets and fuzzy logic [6].
2.1. Fuzzy Numbers
Definition 1
(See [6,7]). A fuzzy subset of is a function . For , the real number from the interval is called the degree of membership of in and represents the degree of truth of the statement “x belongs to A”.
We demote by the family of fuzzy subsets of . Let us give an example.
Example 1.
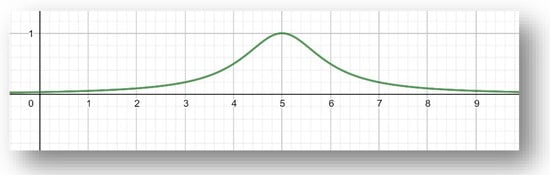
Let us consider the statement “the real numbers close to 5”. This statement is represented by a fuzzy set. For this purpose, we define the function with the form:
where A is a fuzzy subset of and represents the degree to which the real number x is “close to 5”. For the graph of the membership function , see Figure 1.

Figure 1.
Membership function graph .
As we have seen, a fuzzy set is essentially a function . If, in addition, , then it is possible to have the graph of the fuzzy set as we saw in Example 1. The fuzzy sets for which applies are, in essence, the fuzzy numbers we will define below.
Definition 2
(See [6]). A subset A of is called a fuzzy number if the following conditions are fulfilled:
- a.
- The function is continuous;
- b.
- A is normal, i.e., there exists such that ;
- c.
- A is fuzzy convex;
- d.
- is a bounded subset of .
We will denote by the set of fuzzy numbers.
Remark 1.
We recall that support of A is the crisp subset of defined by .
Usually, the triangular and trapezoidal shapes of membership functions shown in Figure 2 most often represent fuzzy numbers. Other shapes may be preferable in some applications.
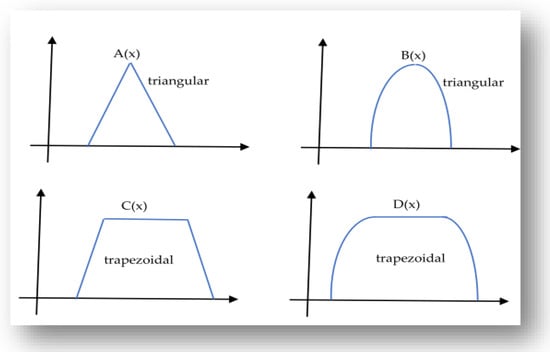
Figure 2.
Basic types of fuzzy numbers.
The following theorem shows that membership functions of fuzzy numbers may be, in general, piece-defined functions.
Theorem 1
(For proof, see Theorem 4.1 in [8]). Let . Then, is a fuzzy number if and only if there exists a closed interval such that
where is a function from to that is monotonic increasing, continuous from the right, and such that for , is a function to that is monotonic degreasing, continuous from the left that for .
So, the construction of a fuzzy number should satisfy the conditions of Theorem 1.
2.2. Cumulative Distribution Function and Possibility Distribution
In this paragraph, we will give the definitions of the cumulative distribution function or simple distribution function and the main properties of possibility measure. It should also be noted that the definitions and properties have been drawn from [9,10,11].
Definition 3.
Let be a random variable with respect to the probability space . The cumulative distribution function or simple distribution function of is the function defined by for any .
Remark 2.
A distribution function is a function with domain such that:
- a.
- F is monotonic increasing;
- b.
- and ;
- c.
- If the random variable is discrete, the cumulative distribution function will be discontinuous, and the discontinuity points will correspond to the values of the random variable that have a positive probability.
Definition 4.
Let be a nonempty set and its powerset. Then,
- a.
- the elements of will be called events;
- b.
- a possibility measure on is a function such that the following conditions are verified:
- (Pos1) and
- (Pos2) , for any family of subsets of .
Proposition 1
(For proof, see [7]). Let be a possibility measure on . For any , if , then .
Definition 5.
A possibility distribution on is a function such that ; is said to be normalized if for some .
Next, we will see how close these two concepts are. Additionally, we should emphasize that the distribution function of probability has nothing to do with the probability distribution. They are completely different concepts. Their differences have been highlighted in [1,2,11]. In the paper, we will not emphasize these differences, and neither will we develop a philosophical view of these concepts. However, the conceptual framework of the possibility distribution function should be made clear. The possibility distribution does not refer to the random variable of the population and, therefore, has nothing to do with the probability. The possibility distribution refers to a fuzzy variable and measures the degree of possibility of a value of the variable belonging to a set.
Definition 6.
Let be a possibility measure on and a possibility distribution. Then, we define the functions:
- a.
- such that for any ;
- b.
- such thatfor any .
According to the functions we defined in Definition 5, we have the results of the following proposition:
Proposition 2
(For proof, see Proposition 3.2.7 in [9]).
- a.
- is a possibility distribution on ;
- b.
- is a possibility measure on ;
- c.
- and.
Next, we will define the fuzzy variable. For this, we should assume that .
Definition 7.
A fuzzy variable is an arbitrary function . If is a fuzzy variable, and , then we will define the following concepts: , , , etc. Furthermore, we will say that a possibility distribution is associated with the fuzzy variable if
for any .
Proposition 3
(For Proof, see Proposition 3.2.9 [7]). Let be a fuzzy variable with possibility distribution . For any we have:
So, according to Equation (4), we have the following corresponding equations. Let be a fuzzy variable with possibility distribution . For any the following applies:
With the above equations, we are now able to connect the two basic concepts that we presented above—fuzzy numbers and the possibility distribution [2,7,12]. This connection will be best seen with two examples. The first example is with a triangular number, and the second example is with a trapezoidal number.
Example 2.
Let be a triangular number with form:
where is a function from to that is monotonic increasing, is a function from to [0, 1] that is monotonic decreasing, and and . Furthermore, let be a fuzzy variable such that the triangular fuzzy number of Equation (10) is the possibility distribution associated with . We denote by the possibility measure associated with . For any we have
Example 3.
Let be a trapezoidal number with the form:
where is a function from to that is monotonic increasing, is a function from to [0, 1] that is monotonic decreasing, and and . Furthermore, let be a fuzzy variable such that the triangular fuzzy number of Equation (13) is the possibility distribution associated with . We denote by the possibility measure associated with . For any we have
3. Results
As we know, probability theory and possibility theory try to express randomness and fuzziness, respectively. Both randomness and fuzziness, despite their diversity, in essence, attempt to “capture” uncertainty, so a collaboration between random variables (probability theory) and fuzzy numbers (possibility theory) in practice is very useful [12,13,14]. However, fοr this cooperation, the best representative of fuzziness is the fuzzy number. For the most part, real-world uncertainty problems contain fuzziness and randomness together. A characteristic example of the coexistence of randomness and fuzziness was given by Zadeh in [14]. Nevertheless, the question of how a fuzzy number is determined remains. By what mechanism will we assign a degree of possibility (degree of truth) to our data? Is the experience of researchers enough? The answers are not easily found. However, some efforts gave results [11,13,15,16]. Following these efforts, we propose a way to convert the cumulative distribution function to a fuzzy number. Specifically, from research data, we construct the cumulative distribution function and then convert it into a fuzzy number. This fuzzy number also serves as the distribution of the possibility of this research. Below, we give the conversion form of a given cumulative distribution function to a fuzzy number as well as some examples of this conversion using possibility theory.
3.1. Construction of a Fuzzy Number via Cumulative Distribution Function
According to Definition 3, suppose we have a cumulative distribution function defined by for any . In addition, is continuous and nondecreasing, so the following proposition applies:
Proposition 4.
If is a cumulative distribution function, then the function given by the form
is a triangular fuzzy number.
Proof of Proposition 4.
- For the function is increasing since is increasing (from Definition 3 and ), and for the function is decreasing since is decreasing;
- is a continuous function since is continuous for and
Therefore, the conditions of Theorem 1 are satisfied. Hence, the function is a fuzzy number and triangular as in Equation (10). □
Remark 3.
The choice of the real number can be a measure of location. In other words, it can be the average median mode, etc. A typical example of converting a cumulative distribution function into a fuzzy triangular number is a uniform distribution. The cumulative distribution function of the continuous uniform distribution is
The above function has average and variance . With the help of Equation (16), we want to create a triangular fuzzy number “close to μ”, meaning we will obtain the fuzzy number with the membership function
This conversion is shown in Figure 3.
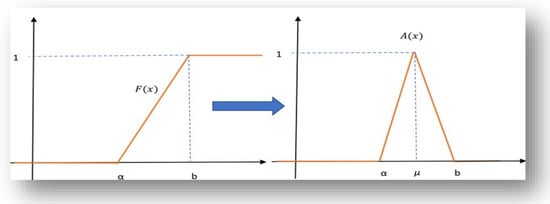
Figure 3.
Conversion from F(x) to A(x).
In a similar way, we can construct a trapezoidal fuzzy number with a variant of Proposition 4. In this case, we determine two points at which we will break the cumulative distribution function. So, we have the following proposition:
Proposition 5.
If is a cumulative distribution function, then the functions given by the form
is a trapezoidal fuzzy number.
Proof of Proposition 5.
The proof is like the proof in Proposition 4. □
Remark 4.
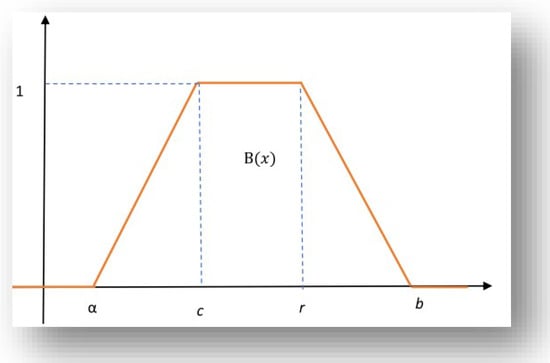
If, in the example of Remark 3, instead of triangular, we wanted to construct trapezoidal fuzzy number , then according to Equation (19) we would have the following graph of the trapezoidal fuzzy number, Figure 4.

Figure 4.
The trapezoidal fuzzy number created via the cumulative uniform distribution function .
3.2. A Simple Paradigm in the Theory of Possibility of Fuzzy Numbers Created by Cumulative Distribution Function
Let us look at the paradigm below linking the construction of Proposition 4 to the theory of possibilities and suppose the following:
Paradigm 1.
The duration in minutes of telephone conversations follows a distribution with a cumulative function
When a subscriber was asked how long a call is, the answer was about 1 min. The questions that arise are:
- a.
- How possible is it for the subscriber's call to be longer than 5 min?
- b.
- How possible is it to be between 3 min and 5 min?
Proof of Paradigm 1.
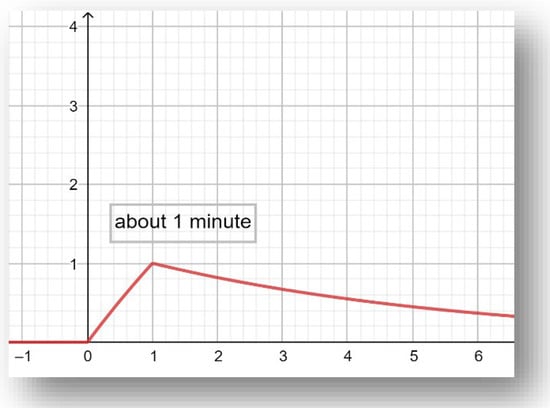
It is difficult for probability theory alone to give an answer since we have a fuzzy “about 1 min” variable, but we can use the cumulative distribution function, see Equation (16). According to Proposition 4, we have the fuzzy triangular number we need to measure the possibilities. So, we create the fuzzy number “about 1 min” from the Equation (16) with and we have
where is the membership function of the fuzzy number “about 1 min” and graph, Figure 5.

Figure 5.
The fuzzy number “about 1 min” according to F(x).
This fuzzy number will play the role of possibility distribution according to Proposition 3 and Example 2. For question (a.), from Equation (15), we have
while for question (b.), according to Equation (9) we have
□
4. Discussion
It becomes obvious that the construction of the fuzzy triangular number via a cumulative distribution function is a simple process; it does not have difficult calculations, and it is applied in a very simple way. It is understood through the last paradigm that fuzziness, as Zadeh defined it, has much to offer to the theory of possibilities. The main advantage of this construction is that it minimizes the arbitrary choice of the fuzzy number, which will then play the role of possibility distribution. In future research, we will extend the theoretical results to the expected average and variance by minimizing our reference to probability theory. It should also be understood that our goal is to use the primary concept of statistics free from the concept of probability. How is this achieved? We use the tool of descriptive statistics. This is free from probability as a measure of uncertainty. Hereafter we define the possibility distribution and, consequently, the concept of the fuzzy number. In many works that use fuzzy numbers [17,18,19], their construction is based on intuitive or empirical data [20,21]. Therefore, in addition to the simplicity, the construction we propose would also have the following advantage: from the collection of project data (for example, a questionnaire), we could obtain the cumulative distribution function, and then, through the construction, propose to extract the fuzzy number, essentially turning the experience into a countable quantity and then a fuzzy number.
5. Conclusions
Throughout history, one of the main goals of science was to measure and consequently compare quantities. Since the middle of the last century, it became evident that some sizes are unquantifiable. Spoken languages have adapted to this fact, and we have been able to discuss and understand concepts such as medium, good, very good, etc. These concepts have become conceptual constants innate in our logic. Similarly, the future fuzzy numbers will be an important tool in scientific endeavors. We believe this paper gives a sound basis for constructing fuzzy numbers by linking them to research data. The construction we propose is a step towards determining the fuzzy numbers not based only on the intuition or experience of the researchers but through a construction method based on research data. Because the method we presented in this work has a clear theoretical background, we will be able to orient our future studies to research data and make our results comparable with other research studies.
Author Contributions
G.S. and Y.A. conceptualized and designed the study. G.S. and Y.A. wrote the manuscript. G.S., Y.A. and B.P. revised the manuscript. Y.A. and B.P. attributed the final approval of the version to be submitted. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goguen, J.A. L. A. Zadeh. Fuzzy sets. Information and control, vol. 8 (1965), pp. 338–353.—L. A. Zadeh. Similarity relations and fuzzy orderings. Information sciences, vol. 3 (1971), pp. 177–200. J. Symb. Log. 1973, 38, 656–657. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Possibility theory. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 6927–6939. [Google Scholar] [CrossRef]
- Carlsson, C.; Fullér, R. Fuzzy Reasoning in Decision Making and Optimization; Physica: Heidelberg, Germany, 2001; Volume 82. [Google Scholar]
- Mareš, M. Fuzzy shapley value. In Fuzzy Cooperative Games: Cooperation with Vague Expectations; Physica-Verlag HD: Heidelberg, Germany, 2001; pp. 89–93. [Google Scholar] [CrossRef]
- Fullér, R. Artificial neural networks. In Introduction to Neuro-Fuzzy Systems; Physica-Verlag HD: Heidelberg, Germany, 2000; pp. 133–170. [Google Scholar] [CrossRef]
- Klir, G.; Yuan, B. Fuzzy Sets and Fuzzy Logic; Prentice Hall: Hoboken, NJ, USA, 1995; Volume 4. [Google Scholar]
- Georgescu, I. Possibility Theory and the Risk; Springer: Berlin/Heidelberg, Germany, 2012; Volume 274. [Google Scholar] [CrossRef]
- Park, K. Fundamentals of Probability and Stochastic Processes with Applications to Communications; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Carlsson, C.; Fullér, R. On possibilistic mean value and variance of fuzzy numbers. Fuzzy Sets Syst. 2001, 122, 315–326. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Sugeno, M. Fuzzy measures and fuzzy integrals—A survey. In Readings in Fuzzy Sets for Intelligent Systems; Elsevier: Amsterdam, The Netherlands, 1993; pp. 251–257. [Google Scholar]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Sfiris, D.S.; Papadopoulos, B.K. Fuzzy estimators in expert systems. Appl. Math. Sci. 2012, 6, 1695–1718. [Google Scholar]
- Yager, R.R.; Zadeh, L.A. An Introduction to Fuzzy Logic Applications in Intelligent Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 165. [Google Scholar]
- Mylonas, N.; Papadopoulos, B. Unbiased Fuzzy Estimators in Fuzzy Hypothesis Testing. Algorithms 2021, 14, 185. [Google Scholar] [CrossRef]
- Murofushi, T.; Sugeno, M. Fuzzy measures and fuzzy integrals. Fuzzy Meas. Integrals Theory Appl. 2000, 2000, 3–41. [Google Scholar]
- Hatefi, S.M.; Tamošaitienė, J. An integrated fuzzy DEMATEL-fuzzy ANP model for evaluating construction projects by considering interrelationships among risk factors. J. Civ. Eng. Manag. 2019, 25, 114–131. [Google Scholar] [CrossRef]
- Marín, L.G.; Cruz, N.; Sáez, D.; Sumner, M.; Núñez, A. Prediction interval methodology based on fuzzy numbers and its extension to fuzzy systems and neural networks. Expert Syst. Appl. 2019, 119, 128–141. [Google Scholar] [CrossRef]
- Peddi, P. Defuzzification method for ranking fuzzy numbers based on centroids and maximizing and minimizing set. Decis. Sci. Lett. 2019, 8, 411–428. [Google Scholar] [CrossRef]
- Li, M.; Wang, H.; Wang, D.; Shao, Z.; He, S. Risk assessment of gas explosion in coal mines based on fuzzy AHP and bayesian network. Process Saf. Environ. Prot. 2020, 135, 207–218. [Google Scholar] [CrossRef]
- Seiti, H.; Hafezalkotob, A.; Martínez, L. R-numbers, a new risk modeling associated with fuzzy numbers and its application to decision making. Inf. Sci. 2019, 483, 206–231. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).