Knowledge and Beliefs on Mathematical Modelling Inferred in the Argumentation of a Prospective Teacher When Reflecting on the Incorporation of This Process in His Lessons

Abstract

Mathematical modelling enjoys affirmed relevance in educational curricula worldwide, and teacher education programs consider that this process should also be experienced during educational internships. The interest of this study focuses on the argumentation of a prospective teacher to justify the incorporation (or not) of mathematical modelling in his lessons. To do this, we analyzed the reflection of a prospective mathematics teacher on the design of a modelling task during his educational internship. Methodologically, it is a case study in which, based on the didactic suitability criteria tool, the study subject structured the reflection on his educational internship in his master’s degree final project (MFP), whose central axis was modelling. We collected data from video recordings of group reflection sessions with the study subject and other prospective teachers of a professionalizing master’s program, and from the analysis of his MFP. The results evidenced the prospective teacher’s arguments to justify the design of a modelling task, his knowledge, and his beliefs about this process, among other aspects. We conclude that the specialized knowledge that is inferred from this argumentation is of different types and is part of a conglomerate formed, in addition, by values, beliefs, and guidelines for action.

1. Introduction

The study of knowledge and competences that a mathematics teacher should have to perform correctly in his/her professional practice is one of the topics that has been investigated by the mathematics education community. International research has led to conceptualizations (and models) about the components of knowledge that teachers use to teach mathematics (see [1,2,3,4,5,6,7]). Some studies have focused on the characterization and development of the professional competences necessary for the mathematics teacher (see [8,9,10]). Other studies explore the assessment of teachers’ knowledge as one of the most critical parameters of teaching quality (see [11,12,13]). However, researchers devoted to delving into teaching competences have given particular emphasis to the role of reflection on educational practice, perceiving the reflective component as a critical competence for professional development and improvement of teaching (see [14,15,16,17,18,19]).

The initial and continuing mathematics teachers’ education is still one of the greatest challenges facing the research community in mathematics education. In this area, several research agendas have been proposed and developed, among which the characterization and development of didactic and mathematical knowledge that allows teachers to favor the management of their lessons stands out.

There is currently a broad consensus regarding both the importance of including mathematical modelling in school curricula and the development of competences related to this process [20]. In the same way, it is considered that the integration of modelling helps students to improve their understanding of mathematics, provides real contexts for their learning and, consequently, contributes to the development of different mathematical competences, among other benefits [21]. Given the importance attributed to modelling, teachers are required to have the knowledge and teaching strategies to implement this process in the classroom [22].

Several studies have addressed the prospective mathematics teachers’ knowledge and beliefs about modelling in different countries and contexts. In some cases, researchers follow a very common structure (for example, see [23]), which consists of presenting hypothetical student resolutions to problems (in this case, modelling problems), and then asking prospective teachers what types of simulated interactions they would manage to address a certain student resolution. For example, in the Australian context, Stillman and Brown [24] analyze the professional knowledge and beliefs of prospective secondary school teachers on the use of modelling tasks, and the influences of receiving parallel (at undergraduate level) versus specific (at postgraduate level) modelling preparation. In this study, knowledge and beliefs are analyzed based on the prospective teachers’ responses to student resolutions, and how they would manage potential errors and difficulties. In this way, findings are reported regarding the diagnostic and didactic-reflexive competencies, and the affinity with modelling at the educational level in which the prospective teachers will work.

In other cases, researchers analyze the teacher’s practice in order to infer their knowledge and beliefs. For example, in the American context, Doerr [25] discusses the results of two studies, one of which was developed with prospective teachers. This study was conducted during a modelling course, focusing on the knowledge and beliefs about this process, and on the changes that the participants experienced during their practice throughout the course. We highlight two results of this study: on one hand, the participants experienced changes in their conception of modelling, from a linear perspective to one of the ‘non-linear cycle’ type; and, on the other hand, the importance of individuals reflecting on their own modelling process in order to better understand its cyclical nature.

Several studies have been conducted in the German context in this regard, due to its long tradition of research in modelling. For example, Kaiser and Maaß [26] present the results of two studies, one of which was developed with servicing teachers. This study focused on teachers’ beliefs about mathematical modelling and applications tasks, within the framework of a teacher professional development program promoted by the German government. Through the application of in-depth interviews, the participants manifested a weak relationship between the mathematical knowledge of the subject with the real world and considered that applications and modelling play a minor role, both in mathematics and in its teaching. For their part, Kaiser and collaborators [27] study the prospective teachers’ professional knowledge on modelling competences, from the perspectives of mathematical content knowledge, pedagogical content knowledge, and general pedagogical knowledge. Through the application of questionnaires on the areas ‘modelling and real-world context’ and ‘argumentation and proof’, and interviews with the participants, the following results were obtained: (a) there is a direct relationship between knowledge about the modelling process and the modelling competencies, and between comprehension of modelling and understanding real-world situations; (b) curricular times affect the way in which modelling can be implemented in the classroom; and (c) the predominance of pedagogical content knowledge in developing professional content knowledge on modelling. Lastly, Wendt and collaborators [28] conducted a case study about a teacher, who showed a broadening of her perception of the use of metacognition by students in mathematical modelling processes.

Finally, in the Colombian context, Villa-Ochoa [29] identifies some arguments of servicing teachers about the use of modelling in their classes, observing a tendency of teachers to use word problem to work on this process. Through direct observations, interviews, questionnaires, and the study of lesson episodes, the need to prepare teachers to integrate more realistic situations in the use of modelling that considers everyday aspects and culture in school mathematics is stated conclusively.

In the Spanish context, prospective mathematics teachers must take a professionalizing master’s degree to teach at secondary and baccalaureate education (students aged 12 to 18). The admission profile for this master’s degree program is made up of professionals from different areas related to mathematics who are interested in teaching. To obtain the degree, prospective teachers must prepare a master’s degree final project (MFP), which consists of an original, autonomous, and individual work that, on one hand, reflects the formative content received and the skills acquired during the master’s program in an integrated way and, on the other hand, contributes to the reflection, analysis, and improvement of the own practice. In terms of research with MFPs, studies such as the conducted by Ledezma and collaborators [30,31] have focused on the aspects of the teaching and learning process that prospective teachers relate to modelling, through the analysis of these documents.

Given this background, it is interesting to ask whether prospective teachers, on one hand, have relevant theoretical-methodological preparation in modelling and its teaching, or whether they only have vague notions to implement this process in the classroom; and, on the other hand, in the case they have specialized education in modelling and its teaching, if the context in which they implement their didactic proposals leads them to make decisions that privilege other aspects to the detriment of modelling (curricular times, sociocultural level of the students, etc.). In this line, for this study, we posed the following research questions:

• What argumentation does a prospective teacher make to justify the incorporation (or not) of mathematical modelling in his lessons?
• What knowledge, values, beliefs, and guidelines for action, among other aspects, are inferred in this argumentation?

To answer them, we studied the reflection process of a prospective teacher on the design, implementation, and redesign of a mathematical modelling task, both during his educational internship and in the preparation of his MFP. This prospective teacher organized the reflection in his MFP using the didactic suitability criteria tool, proposed by the onto-semiotic approach [32]. In methodological terms, it is a case study with a student of a professionalizing master’s program for mathematics teacher education. In this way, we propose the following objective: to infer, based on the argumentation made in his teaching reflection on the design, implementation, and redesign of a modelling task, the knowledge, beliefs, values, and guidelines for action on mathematical modelling of a prospective teacher.

An innovative aspect of this research is that we inferred the knowledge and beliefs based on the argumentation of the prospective teacher studied, which we analyzed from unusual theoretical references, namely, from the pragma–dialectical perspective [33] for the analysis of a critical discussion through four stages (confrontation, opening, argumentation, and concluding stages); and from the diagramming technique [34], which allows, on one hand, to make a spatial map of the argumentation, considering the language and, on the other hand, to shape the written reasoning. In the literature review, we have not found works that infer prospective teachers’ knowledge and beliefs from the analysis of the structure of the argumentation, which they realize when they reflect on their practice, with models other than Toulmin’s [35] (among others, the works of [36,37]). Similarly, unlike the research commented in the literature review [23,24,25,26,27,28,29], where knowledge and beliefs are extracted through the application of questionnaires and interviews with items aimed at individuals clearly expressing their knowledge and beliefs; in this study, we opted for argumentation as a means to infer these elements indirectly.

2. Theoretical References

In this section we present the theoretical references considered for this study.

2.1. Mathematical Modelling

Modelling can be understood, in general terms, as a process that transits from the «real world» to «mathematics» for the solving of a problem-situation taken from reality. From the theoretical plane, different cycles have been designed for its analysis [38] and different perspectives on its implementation have emerged [39]. This variety of approaches is mainly due to the theoretical diversity around modelling [40], although the proposed cycles tend to converge in similar phases (see [41]). In this study, we adopted the cycle proposed by [42], since it is adapted to our research context.

This modelling cycle, of a didactic-cognitive nature, has its roots in the theories by [43,44], and is focused on the individual who solves this type of problems. In terms of what is described by [42], the real situation is given by the wording of the problem, which must be understood to build a situation model. Then, this situation must be simplified and structured to form a real model of it. A product of the mathematization (translation into mathematical language) of the real model, it will be transformed into a mathematical model that, by working with it, will allow obtaining mathematical results. These results must be interpreted in the context of the problem to obtain real results that must be validated in real world terms. Finally, the solver exposes the answer obtained for the problem. (An illustrative example on the use of this cycle can be found in [42], pp. 225–227). The transit between the phases of the cycle described above is carried out through transitions or, in terms of [45], modelling sub-competences (numbered on the right of Figure 1).

Along with this cycle, we consider some attributes agreed upon by the mathematical modelling research community that characterize both the work with this process in the classroom and this type of task.

Modelling work in the classroom is usually carried out in small groups of students, who are presented with a real-world problem-situation that they must mathematise [46,47], that is, translate into mathematical language in order to work with it. Another way of working on modelling is through problem-oriented projects [48,49], which is a methodology understood as “a didactical situation where a group of students are working together on a problem during a longer period of time” [48] (p. 167). In both contexts, the modelling task must meet the following characteristics [50]:

• Open, that is, not limited to specific answers or procedures.
• Complex, that is, given the information in the wording of the task, students must search for the relevant data for its solving.
• Realistic, that is, incorporating elements taken from the real world.
• Authentic, that is, consistent with an event that has occurred or could occur in reality (in terms of [51]).
• A problem that should not be solved by applying known algorithms (in terms of [52]) and that required strategies for its solving.
• Solvable through a modelling cycle, in which all the phases are passed through.

The modelling problem that is posed, in the form of a question or task, must be challenging for the students and be solved in a period of time that allows both its assimilation and the search for information from different sources.

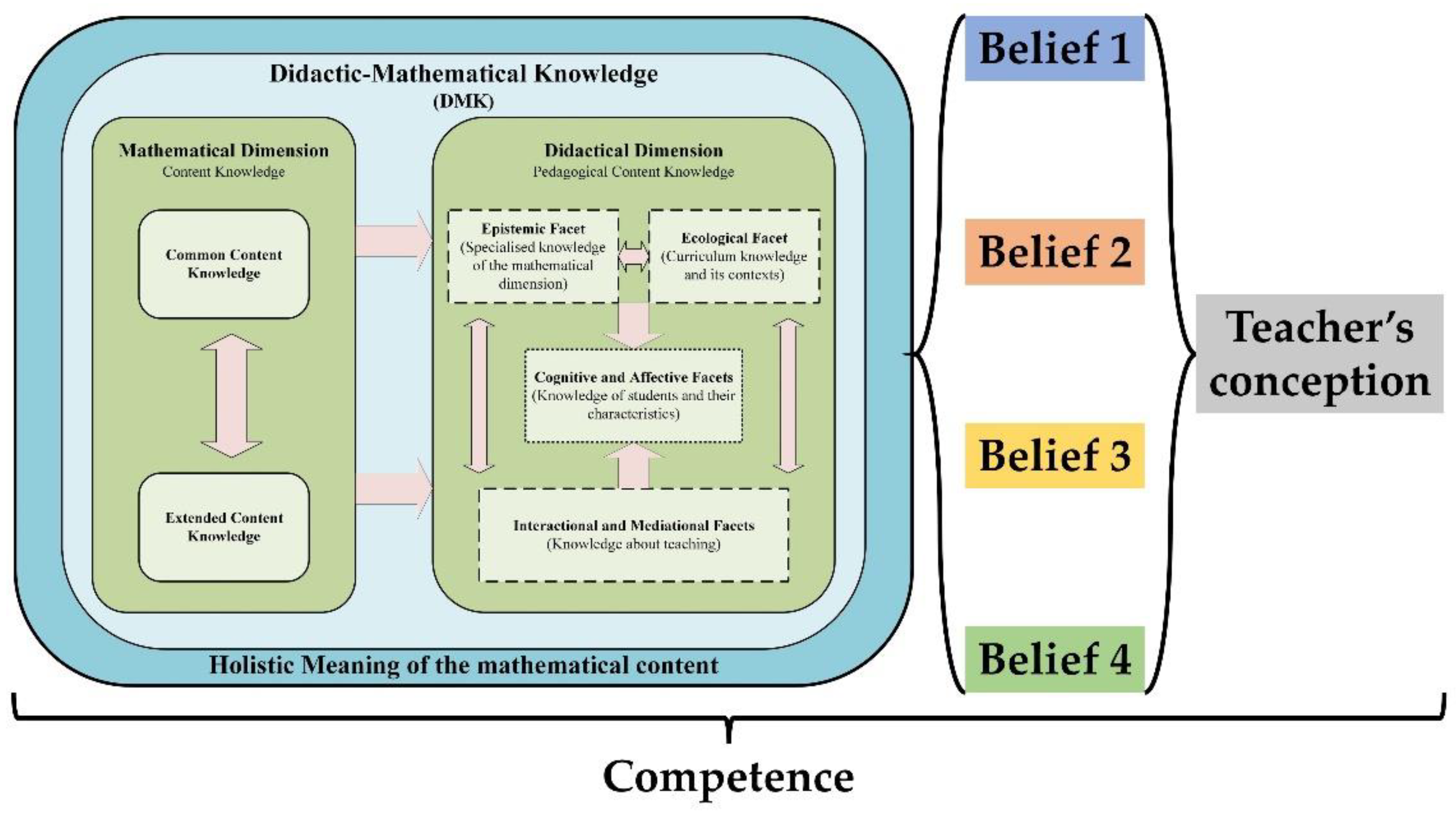
2.2. Didactic-Mathematical Knowledge and Competences Model (DMKC Model)

As we mentioned at the beginning, there are various models regarding the knowledge that a mathematics teacher should have in order to properly manage their student learning (for example, [1,2,3,4,5,6,7]). In the onto-semiotic approach (OSA), a theoretical model called didactic-mathematical knowledge and competences model (DMKC model) of the mathematics teacher has been developed [53,54,55,56]. In the DMKC model, it is considered that the two key competences of the mathematics teacher are the ‘mathematical competence’ and the ‘analysis and didactic intervention competence’. The fundamental core of this last competence is [53]: designing, applying, and assessing own learning sequences and those of others, through didactic analysis techniques and quality criteria, to establish cycles of planning, implementation, and evaluation, as well as to put forward improvement proposals. This general competence is made up of different sub-competences [53]:

• Analysis of mathematical activity: This sub-competence is made up of (a) analysis of global meanings competence and (b) onto-semiotic analysis of mathematical practices competence [54].
• Analysis and management of the interaction and its effect on student learning.
• Analysis of norms and meta-norms.
• Assessment of the didactic suitability of teaching and learning processes.

2.2.1. Assessment of the Didactic Suitability of Teaching and Learning Processes Sub-Competence: Didactic Suitability Criteria

For the assessment of teaching and learning processes, the OSA proposes the notion of didactic suitability [57] as an essential tool. Given a specific topic in a certain educational context, the notion of didactic suitability leads to being able to answer questions such as [58,59]: What is the degree of didactic suitability of the implemented teaching and learning process? What changes should be introduced in the design and implementation of the teaching and learning process to increase its didactic suitability in future implementations?

The didactic suitability of a teaching and learning process is defined as the degree to which such process (or a part of it) meets certain characteristics that allow it to be qualified as optimal or adequate to reach the adaptation between the personal meanings achieved by the students (learning) and the intended or implemented institutional meanings (teaching), considering the circumstances and available resources (environment). A teaching and learning process will achieve a high degree of didactic suitability if it is capable of articulating, in a coherent and systematic way, the following six partial criteria of didactic suitability, referring to each of the six facets involved in the teaching and learning process [53]:

• Epistemic criterion: To assess whether the mathematics that is taught is ‘good mathematics’.
• Cognitive criterion: To assess, before starting the teaching and learning process, whether what is intended to be taught is at a reasonable distance from what the students know.
• Interactional criterion: To assess whether the interaction solves students’ doubts and difficulties.
• Mediational criterion: To assess the adequacy of resources and time used in the teaching and learning process.
• Affective (or emotional) criterion: To assess the students’ involvement (interest, motivation) in the teaching and learning process.
• Ecological criterion: To assess the adaptation of the teaching and learning process to the educational project of the school, the curricular guidelines, the conditions of the social and professional environment, etc.

In turn, each didactic suitability criterion (DSC) has its respective components, and their utility requires defining a set of observable indicators that allow assessing the degree of suitability of each facet of the teaching and learning process.

Table 1. Didactic suitability criteria and their components.

Criteria	Components
Epistemic	- Errors. - Ambiguities. - Richness of processes. - Representativeness of the complexity of the mathematical object.
Cognitive	- Prior knowledge. - Curricular adaptation to individual differences. - Learning. - High cognitive demand.
Interactional	- Teacher-student interaction. - Student interaction. - Autonomy. - Formative assessment.
Mediational	- Material resources. - Number of students, class schedule, and classroom conditions. - Time.
Affective	- Interests and needs. - Attitudes. - Emotions.
Ecological	- Curriculum adaptation. - Intra and interdisciplinary connections. - Social and labor usefulness. - Didactic innovation.

Adapted from [53].

presents the components of each DSC, based on the guidelines by [53].

In the context of OSA [32], modelling is considered a hyper or mega process, since it includes other relevant processes of mathematical activity (representation, simplification, idealization, etc.). In addition, this framework has tools to analyze the mathematical activity underlying the modelling process (see [60]). Finally, the OSA considers that working on modelling in the classroom is an aspect that improves the didactic suitability of the teaching and learning process [61].

2.2.2. Knowledge, Beliefs, and Conceptions

The DMKC model considers that the teacher’s knowledge is organized in three large dimensions: mathematical, didactic, and meta didactic-mathematical.

The mathematical dimension of the DMKC model refers to the knowledge that allows teachers to solve mathematical problems or tasks specific to the educational level in which they will teach (common knowledge), and to link the mathematical objects of such educational level with mathematical objects that will be studied at later levels (expanded knowledge).

The authors of the different models of mathematics teacher’s knowledge agree that, in addition to the mathematical content, the teacher must have knowledge about the various factors that influence when the teaching of such mathematical content is planned and implemented. In this sense, the didactic dimension of the DMKC model proposes six subcategories of teacher’s knowledge:

• Epistemic facet: Refers to the specialized knowledge of the mathematical dimension (use of various representations, arguments, problem-solving strategies, and partial meanings of a mathematical object), and incorporates notions such as ‘knowing mathematics with depth and breadth’ [6] and ‘specialized content knowledge’ [1].
• Cognitive facet: Refers to the knowledge about the cognitive aspects of students (difficulties, errors, conflicts, learning, etc.).
• Interactional facet: Refers to the knowledge about the interactions that arise in the classroom (teacher–students, student–student, student–resources, etc.).
• Mediational facet: Refers to the knowledge about the resources and media that can enhance student learning, and about the times designated for teaching.
• Affective facet: Refers to the knowledge about the affective, emotional, and attitudinal aspects of the students.
• Ecological facet: Refers to the knowledge about the different aspects (curricular, contextual, social, political, economic, etc.) that influence the management of student learning.

The meta didactic-mathematical dimension of the DMKC model refers to the knowledge necessary to reflect on one’s own practice [6,62], which allows the teacher to assess the teaching and learning process and carry out a redesign that improves it in future implementations.

The three dimensions described above are present in the different phases of the teaching and learning process of a certain mathematical content, namely preliminary study, planning, implementation, and assessment [63].

In the DMKC model (see Figure 2), a belief (‘I believe P’), according to [64], is understood as a ‘disposition for action’, and a conception is understood as ‘a set of beliefs’. Likewise, beliefs are based on knowledge, accompanied by assessments, and are evidenced in a disposition for action in accordance with certain principles/criteria that are positively valued.

2.3. Argumentation

We analyzed a portion of the data of this study from the pragma–dialectical perspective [33] as a theoretical reference. Since pragma–dialectics proposes an ideal model for critical discussion, four stages can occur (or not) in this technique, namely:

• Confrontation stage: Establishes the difference of opinion. In a non-mixed difference of opinion, this simply means that one party’s point of view is not immediately accepted by the other, but instead is met with doubt or criticism. In a mixed difference of opinion, the other party advances its opposing point of view.
• Opening stage: Refers to the starting points of the discussion and assigns the roles of protagonist and antagonist (in a mixed difference of opinion there are two protagonists and two antagonists). Moreover, the rules of the debate and the starting points are agreed upon.
• Argumentation stage: The protagonist defends his/her point of view against the antagonist’s persistent criticism, advancing arguments to meet the antagonist’s objections or to remove the antagonist’s doubts.
• Concluding stage: The parties evaluate the extent to which the resolution of the difference of opinion reached and in favor of whom. If the protagonist withdraws the point of view, the difference of opinion is resolved in favor of the antagonist; if the antagonist abandons his/her doubts, it is resolved in favor of the protagonist.

We analyzed another portion of the data of this study using the diagramming technique [34]. This technique allows, on one hand, to make a spatial map of the possible ways that premises are linked to support a conclusion, considering the language and, on the other hand, to visually represent the written reasoning. In this technique, four basic structures of arguments are defined:

• Convergent structure: Two or more premises independently support the conclusion.
• Dependent structure: The premises are united to support the conclusion, i.e., both premises (or all of them) need each other to infer the conclusion.
• Divergent structure: The same premise is supporting more than one conclusion (it can be said that there are two or more unitary arguments).
• Chained structure: One of the propositions is the conclusion of a premise and, in turn, it is the premise of another conclusion.

3. Methodological Aspects

In this study, we followed a qualitative research methodology from an interpretative paradigm [65], which mainly consists of an intrinsic case study [66]. In this section, we describe the methodological aspects of this work.

3.1. Research Context

This research was developed in the context of a professionalizing master’s degree program for the education of secondary and baccalaureate education mathematics teachers taught by the public universities of Catalonia (Spain), during the 2020–2021 academic year. The admission profile for this master’s degree program is made up of professionals from different areas related to mathematics (mathematicians, architects, engineers, economists, etc.) who are interested in teaching.

Within the specific formation module, the study program of this master’s course includes a submodule on mathematical modelling. In this submodule, the cycle proposed by [42] is presented to the prospective teachers, along with some examples of modelling tasks. At the end of the submodule, the prospective teachers must expose a modelling problem (wording of the task, solving process, curricular location of the contents) as a final task.

Within the practicum module, the study program of this master’s course states that the prospective teachers must carry out educational internships. These internships must be realized in educational institutions established through agreements with universities, since they must be recognized as internship centers; as well as the mentor teachers (classroom teachers) who must guide the prospective teachers. During the internship period, the prospective teachers must design and implement a teaching and learning sequence (known as ‘didactic unit’), which is determined by: (a) the educational institution and the mentor teacher; (b) the educational level of the students; and (c) the time of the school year in which it is implemented. Due to these conditions, the prospective teachers cannot work exclusively on modelling in their didactic units. However, these restrictions are not considered in the redesign that they propose in their MFPs.

To obtain the master’s degree, the prospective teachers must prepare an MFP, which consists of an original, autonomous, and individual work. For its preparation, the prospective teachers are presented with the DSC, along with the guidelines of components and descriptors that allow their application (see [53]). Finally, the prospective teachers must use the DSC to assess in their MFPs the didactic unit that they implemented during their educational internships and, in this way, propose changes that aim to improve the didactic suitability of the implemented teaching and learning process.

3.2. Study Subject

In this work we constituted an intrinsic case study since our interest was focused on the study of the particular case [66]. The study subject of this research was the prospective teacher AD, who has an undergraduate degree in industrial engineering and a doctoral degree in his area. In addition, the study subject has 15 years of experience in university teaching and academic publications derived from research work in his area. In this context, the study subject has worked with the modelling of phenomena typical of his study area. However, in his experience as a university professor, he has not taught modelling.

As a student of the master’s program described in the previous section, the study subject expressed his interest in including the work with modelling in the didactic unit that he had to design to implement during his educational internship. In this way, the selection of this particular case is justified, firstly, by the interest of the study subject in implementing modelling during his educational internship; secondly, and as a result of the above, the master’s program assigned him two tutor professors (the first and the fourth author) for his supervision, which allowed us to accompany the study subject throughout the development of his work; and thirdly, in the possible analysis that the study subject would carry out in his MFP on the implementation of modelling. We consider these three reasons sufficient to be able to study the argumentation of this prospective teacher to justify the incorporation (or not) of mathematics modelling in his lessons and, in this way, infer his knowledge, values, beliefs, and guidelines for action from this argumentation.

During his educational internship, the study subject designed and implemented a didactic unit, consisting of 18 sessions of 60 min each, for the teaching of linear and affine functions in the third grade of secondary education (students aged 14–15), whose central axis was modelling [67]. According to what is described in his MFP, the study subject carried out his internship in an educational center under the supervision of a mentor teacher (teacher from the center), who introduced him to the system of articulated work of the mathematics department, which did not give much space to educational innovation. The mathematics class had four lessons a week (Monday, Tuesday, Thursday, and Friday), in one of which (Thursday) a workshop called ‘Món Matemàtic’ (‘Mathematical World’ in Catalan language) was implemented. In this workshop, the students solved ad hoc problems distinct from the mathematical content worked on in the regular lessons on the other days (Monday, Tuesday, and Friday), and for which the study subject designed a modelling task to implement in the workshop.

After his educational internship, the study subject began to elaborate his MFP under the supervision of his two tutor professors. In that document, the study subject made a series of evaluative comments about his didactic unit, guiding his reflection based on the DSC components (see Table 1), most of which he related to modelling. These evaluative comments are analyzed in Section 4.2.

3.3. Data Collection and Analysis

For this research, we collected data from two sources: on one hand, the video recordings of group reflection sessions in which the study subject participated with his tutor professors and, on the other hand, the study subject’s MFP. We applied specific analysis techniques for each of these sources.

3.3.1. Group Reflection Sessions

Regarding the group reflection sessions, since three prospective teachers from the master’s program (JL, RD, and the study subject AD) worked on the topic of functions at the same educational level (third grade of secondary education) during their internships, and their MFPs were under the supervision of one common tutor professor (the fourth author), six group reflection sessions were held with them. In these sessions, developed in a virtual format, each prospective teacher shared his experiences during two sessions by explaining the design, implementation, and redesign of his respective didactic unit, while the other participants (the remaining prospective teachers and the tutor professors) gave their opinions and suggested ideas. The study subject was the only one of the three prospective teachers who decided to include modelling work in his didactic unit, which is why he was under the supervision of two tutor professors (the first and the fourth author), to whom he shared the progress of his didactic unit prior to these sessions.

The dynamics of the two group reflection sessions in which he shared his experience was as follows:

• In the first session, the study subject described the context in which he was carrying out his educational internship and presented his didactic unit for the teaching of functions.
• In the second session, the content and considerations for the preparation of the MFP were discussed.

Although we reviewed the video recordings of the two group reflection sessions with the study subject, in this research we only considered the first session, since it was the design phase of the didactic unit, and its description allowed us to obtain a first reading of his knowledge, beliefs, and conception of modelling. On the other side, the second session was mainly focused on the formal aspects for the preparation of his MFP.

The analysis of the video recordings was carried out from the pragma–dialectical perspective [33] since, being a dialogue performed in an academic context, it can be considered as a critical discussion. We analyzed these data according to the four stages that pragma–dialectics proposes as an ideal model for a critical discussion: confrontation, opening, argumentation, and concluding stage (see Section 2.3). The analysis of the arguments was carried out with the following steps:

• We undertook a general review of the video recordings of the group reflection sessions, which allowed us to have a first appreciation of the development of this critical discussion and, at the same time, allowed us to make a timeless list of the ideas and positions of the participants.
• We transcribed the dialogues from the video recordings of the group reflection sessions, labelling each participant and their respective interventions.
• We identified the stages that appeared in the dialogue, according to the pragma–dialectics model. To do this, we justified each segment of dialogue with the definition of each stage of the model.

For the specific case of the argumentation stage, we identified the arguments taking into account two elements: on one hand, who defended the conclusion and, on the other hand, the conclusion and the premises that support it. Finally, we selected only the arguments related to modelling.

The unit of analysis was made up of segments of the dialogue between the study subject and his two tutor professors, excluding the interventions performed by the other two participating prospective teachers (JL and RD), since they were not of interest for this study.

3.3.2. Study Subject’s MFP

Regarding the study subject’s MFP, an important chapter within this document is the one in which he analyzed the implementation of his didactic unit and used the DSC tool to assess the didactic suitability of the implemented teaching and learning process. In the ‘Implementation analysis’ chapter, we found evaluative comments where the study subject related different DSC components with the modelling process, since he identified it as an aspect that would increase the degree of suitability for the redesign of the didactic unit implemented during his educational internship. Another element of interest for this study is the modelling task proposed by the study subject, which he described in his MFP, and which was part of the planning of his implemented didactic unit.

We analyzed the study subject’s MFP as follows:

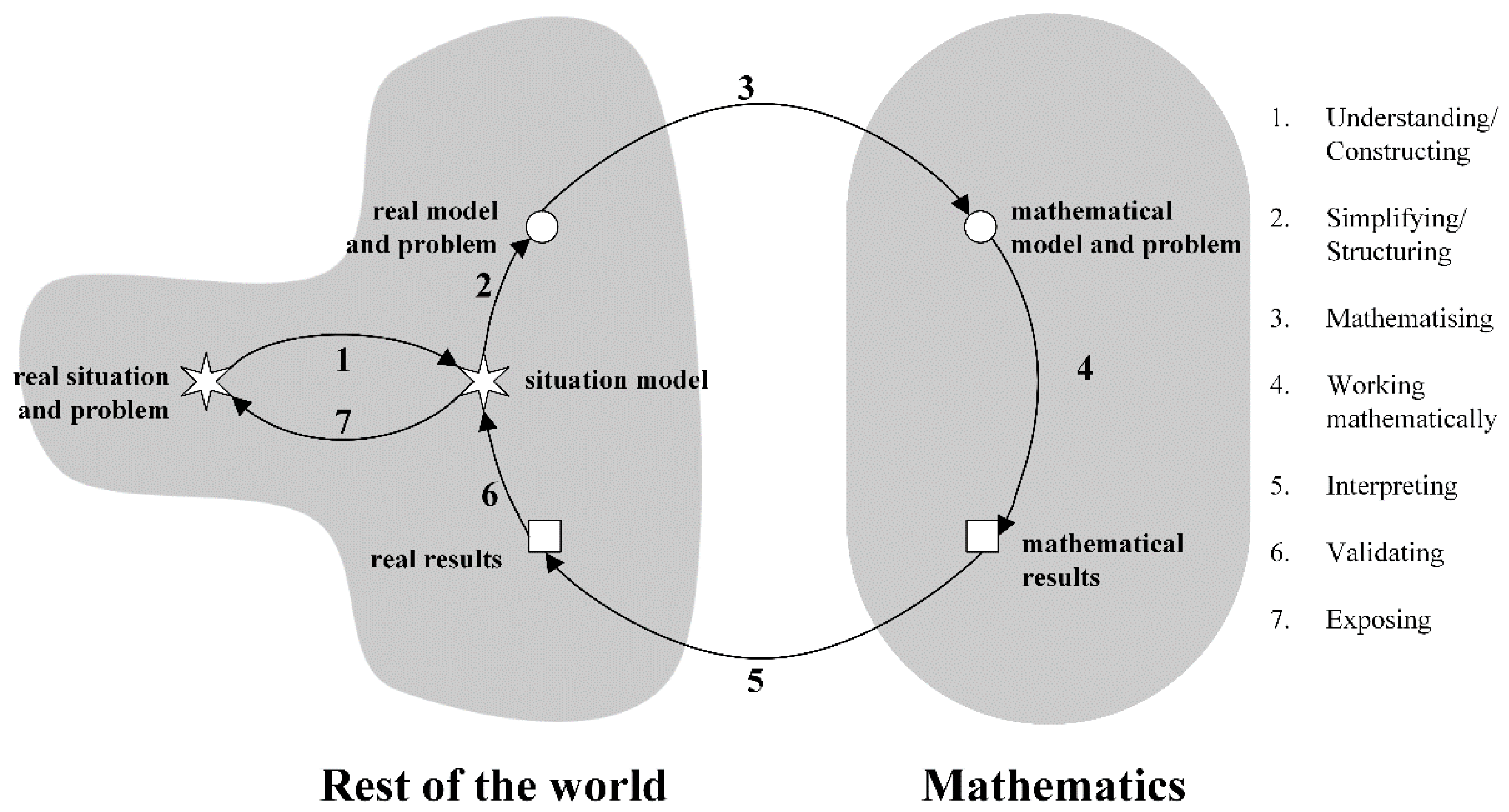
• Firstly, we identified the criteria and components of the DSC with which the study subject related his reflections on modelling when he assessed the suitability of his didactic unit in the ‘Implementation analysis’ chapter. Various works have studied teacher reflection during the mathematics teachers’ education from different points of view (see [68] from didactic analysis; [69] from self-regulation practices; [70] from creativity; [30,31] from mathematical modelling; among others), whose common denominator has been that, by using the DSC, the prospective teachers’ knowledge can also be inferred. In this sense, we followed a content analysis methodology like that used by [31], focused on the ‘Implementation analysis’ chapter of the MFP, which consisted of (1) carrying out a search for keywords related to modelling (model, context, problem, real); (2) identifying the criterion and component of the DSC in which we found the keywords and the comment that contained them.
• Secondly, to identify the different structures of the arguments in the assessment of the didactic suitability that the study subject made in his MFP, we used the diagramming technique [34], which is more appropriate for an argumentative text, such as is the case of the MFP. The steps for diagramming are: (1) all propositions in the text are enclosed in curly brackets; (2) propositions are listed in order of appearance; (3) the argument is structured, spatially locating the place of the conclusion; (4) a way in which the premises are related is proposed. Finally, in the diagrams of the arguments we distinguished the propositions that referred to modelling from those that did not.
• Thirdly, we analyzed the modelling task proposed in the MFP, using the characterization for a problem of this type, also considering the phases of the modelling cycle that occurred (or could occur) for its solving.

In both data sources, we looked for arguments that would make evident, on one hand, the study subject’s conception of the modelling process and, on the other hand, after his educational internship, how this experience allowed him to think—and rethink—modelling as an element to improve the didactic suitability of the implemented teaching and learning process.

4. Presentation and Analysis of Results

In this section, we present and analyze the results of this study. To do this, in the first subsection, we analyze the first group reflection session of the study subject with his tutor professors, from the perspective of pragma–dialectics. In the second subsection, we analyze the study subject’s MFP using the DSC, the diagramming technique, and the theoretical framework on mathematical modelling. In this work we consider argumentation as a means to resolve a difference of opinion, which can be manifested in a discussion, a meeting, or an essay.

4.1. Analysis of the First Group Reflection Session

In this section, we analyze the dialogues of the first group reflection session. To do this, first, we identified the four stages in a critical discussion, according to the pragma–dialectical model; and, secondly, we present the structures of the main arguments used by the study subject during the argumentation stage. The interlocutors mentioned in the following paragraphs are the two tutor professors (T1 and T2) and the study subject (AD). As mentioned above, we must take into account that, since pragma–dialectics proposes an ideal model, each of the stages may or may not appear within a critical discussion and not necessarily in the numbering order proposed by this model. Moreover, the interpretation of these stages is not unique, since some factors that influence it are part of the context in which the discussion took place. In this case, since it is an educational context, cordiality between the tutor professors and the students is different from, for instance, a political debate, so differences of opinion are not always shown in an explicit and impetuous way.

4.1.1. Confrontation Stage

At this stage, the parties establish that they have a difference of opinion. In this group reflection session, the confrontation stage can be evidenced from the following excerpt from the dialogue, where T1 asked AD a general question about how to introduce modelling with the topic of functions, and it is the one that guided the dialogue of the session.

“T1: How to introduce the topic of modelling with a topic of functions? Of course, when you reflect on this, there are many aspects to take into account, it does not only depend on your willingness to model, but it also depends on the conditions of the [educational] centre, on the type of students you will have, on the didactic unit… and that this problem is specific to each [educational] centre. We are going to take the opportunity to discuss the problem”.

4.1.2. Opening Stage

At this stage, the parties decide to try to resolve the difference of opinion and the roles of protagonist and antagonist are assigned. This difference of opinion is identified by the fact that the tutor professors had the progress of the AD’s didactic unit prior to the session. To solve it, the tutor professors decided to pose a series of questions to AD with the intention that he reflect on his definition of modelling and the way in which we would implement this process in his didactic unit. The role of protagonist was assigned to AD when T1 asked him to explain two things: the characteristics of the educational center where he carried out his internship and how he intended to implement modelling. The rules for the dialogue are implicit as it is a session that is part of a master’s program.

“T1: What is modelling? How can functions be introduced? And how can they be introduced in the specific case of your [educational] centre? Which has characteristics that are unique compared to other [educational institutions]. The reflection on the problem of modelling would be, to what extent can it be applied or not? And if it cannot be incorporated, why could it not be incorporated? Now, what we will do is that AD will explain to us a little about the characteristics of the [educational] centre in which he implements his didactic unit, […] and, later, he will explain his proposal of how he intends to introduce modelling”.

4.1.3. Argumentation Stage

At this stage, the protagonist defends his/her point of view. For this stage, we present some arguments put forward by AD in which posed some reasons that he considered for the implementation of modelling. We stress that, during this stage, AD mentioned a particular modelling task that he designed for his didactic unit, contextualized in the fuel consumption of a car during a family trip to the beach. This task and its redesign proposal are analyzed in Section 4.2.3.

Therefore, as a starting point, we infer that AD had a belief that can be formulated, more or less, in the following terms: ‘for the topic of functions, a modelling task can be implemented’. This belief disposed him to act in accordance with the principle that this process should be incorporated, which he valued positively. Furthermore, AD believed that the designed task was a modelling task, and he showed a common mathematical knowledge that allowed him to create and solve the task.

In the AD’s first Argument (see Figure 3) reasons about the difficulties for implementing modelling are given. On one hand, there is the work dynamics of the institution, and, on the other hand, there is limited access to technological resources.

“AD: The whole mathematics department works […] like a gear, that is, they all do exactly the same thing, the same exams, they coordinate even the dates of the exams, and that makes it a bit difficult to introduce something new. […]. The only problem that I have seen is that, based on what they have told me, during normal hours [sic], they do not have access to the computer room. So, certain modelling problems, for example, with GeoGebra or a spreadsheet where they can work with these tools, […] they will have to do it on their own and, at best, project with the computer on one of these [interactive] boards that they do have. That is right, but it cannot be an interactive thing with the students”.

Figure 3. Structure of the AD’s first Argument. Authors’ interpretation.

Figure 3. Structure of the AD’s first Argument. Authors’ interpretation.

In the AD’s second Argument (see Figure 4), it is declared that an advantage that the educational center where AD carried out his internship had was the ‘Món Matemàtic’ workshop, in which mathematical problems are posed in parallel to regular lessons of the subject. This space allowed AD, in principle, the implementation of modelling tasks with functions, particularly, that based on the family trip to the beach.

“AD: [In the mathematics department] They have a peculiarity and that is that, in parallel to the solving of problems in class and the usual dynamics, they pose some problems that they call ‘Món Matemàtic’, which is still a slightly broader plan, which accompanies all the topics. That is, each subject has its ‘Món Matemàtic’ and is like a problem a little more in context and is a little more extensive. This problem, in this case, my idea was to focus it towards modelling [continues in the next Argument]”.

Figure 4. Structure of the AD’s second Argument. Authors’ interpretation.

Figure 4. Structure of the AD’s second Argument. Authors’ interpretation.

In the AD’s third Argument (see Figure 5), we observe the intention, on the part of the study subject, to build an increasingly complex mathematical model with the students, enriching the context of the problem-situation posed as a modelling task, that is, that based on the family trip to the beach.

“AD: … and, therefore, with a modelling context with a specific topic, take advantage of a context that is a little richer and propose, because this was my idea, different problems or different questions that, step by step, address the entire topic of the functions section, so let them start with a single context: first, problems of graphical representation; next, we will begin with domain and range; to end up posing line equations and then solving something more complex using these tools. And that is more or less the idea I had”.

Figure 5. Structure of the AD’s third Argument. Authors’ interpretation.

Figure 5. Structure of the AD’s third Argument. Authors’ interpretation.

The AD’s fourth Argument (see Figure 6) emerges from a question posed by T2 to the study subject while the task of the family trip to the beach was shown on a shared screen ‘How did you see the topic of working on modelling? Did you give them the model and they worked on it? Was that your idea?’ In response to T2, AD gave the reasons why he gave the students a pre-set mathematical model and did not ask them to build it.

“AD: Yes, the idea is that, since it is the first time that they [the students] do functions, they can give the model that algebraic structure. Let them make the model themselves or let them look for information to make a model, unless the case is very simple, I am not very sure that they can do it. But, by giving them the model, by giving them the context and so that they can understand its parts, then apply it, I think it can be easier for them. And, also, that is why I have put in the last section that, precisely, it is that idea: once I give them the context, it is not that I give them the data that they fill in the model and they get an equation that they can represent, but it is the other way around, I give them the points and they, through those points, find the equation from which they can deduce the starting data, that is, as in the opposite direction. That would be the last thing, so in a way, they would not build the model, that is true, because the model and the context are fixed, but, at that level of complexity, I think they could not do it on their own [continues in the next Argument]”.

Figure 6. Structure of the AD’s fourth Argument. Authors’ interpretation.

Figure 6. Structure of the AD’s fourth Argument. Authors’ interpretation.

In the AD’s fifth Argument (see Figure 7), the study subject commented on some aspects that he considered as impediments to fully implement the modelling process (an entire cycle) in the institution where he carried out his educational internship.

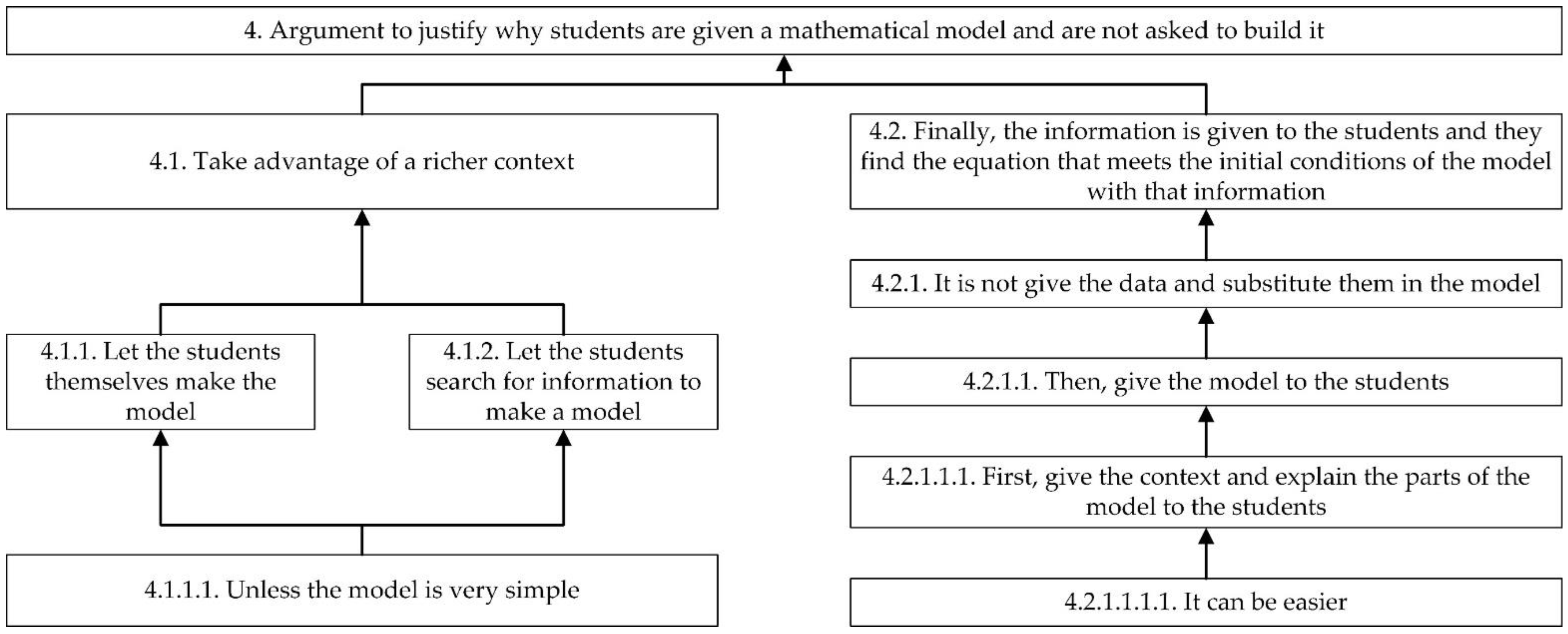
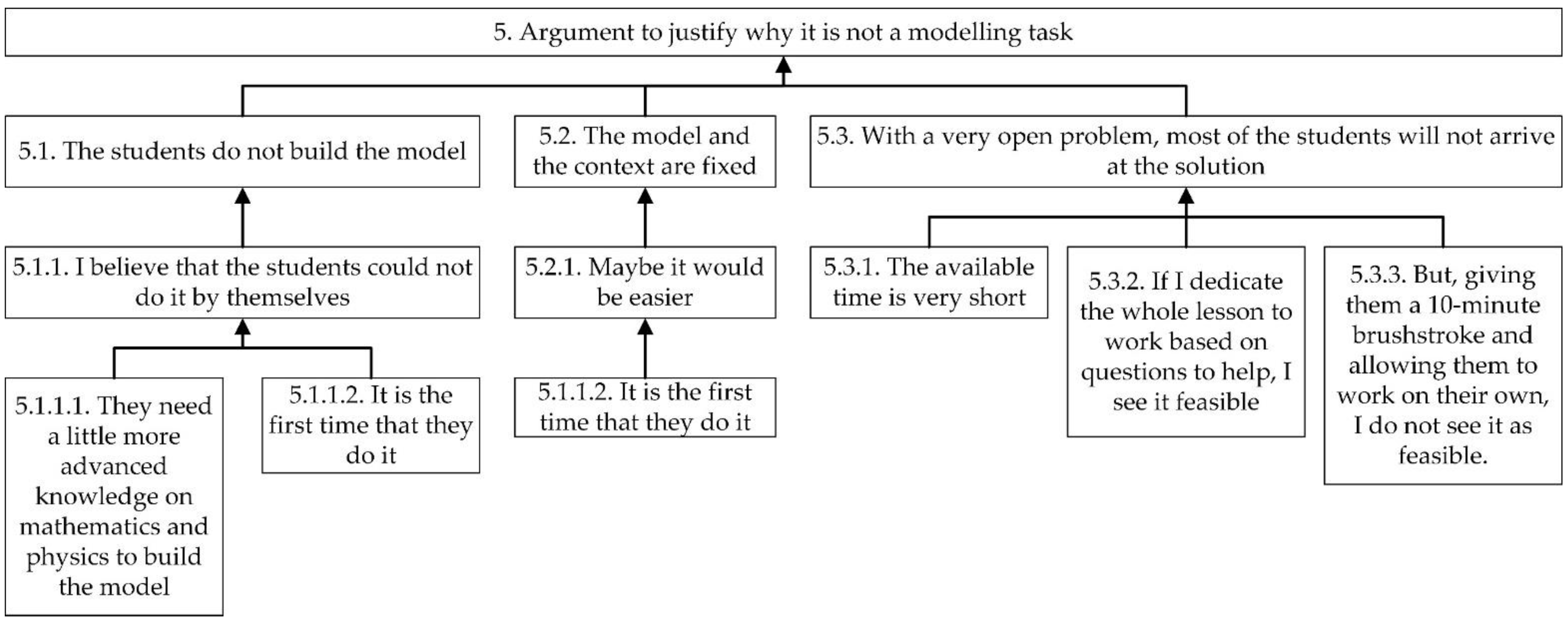
“AD: In that sense, perhaps this problem is not very creative for them, because they do not generate their own model, but adhere to an existing model, but, perhaps, since it is the first time they do it, surely, perhaps it is easier, because generating the model already means that they have a somewhat more advanced knowledge of mathematics, but also physics, I do not know, it could also be tried. […]. But, also, if you leave it [the problem] so open to them, I get the impression, from what I have seen, that maybe one or two of them will come up with a better or worse solution. I am not saying that it is good, but the rest, perhaps, surely, will not amount to anything. So, as a first stone in this world of modelling, perhaps it is better to give them a fixed context, that they handle themselves algebraically, understand a little and, perhaps in the fourth [grade of secondary education] or baccalaureate [education], then they already generate their own models. […]. What is a little more complicated for me is to leave them with such an open model but let them do it on their own. If I have them [the students] in class, and I dedicate the whole lesson to working on this based on questions that help them to build something, I do see that as more feasible, but give them a brushstroke of ten minutes and let that they on their own can develop an open work, perhaps it is more complicated, I do not know”.

Figure 7. Structure of the AD’s fifth Argument. Authors’ interpretation.

Figure 7. Structure of the AD’s fifth Argument. Authors’ interpretation.

In his argumentation, AD used knowledge from the different types proposed by the DMKC model. In this sense, in the first and second Arguments he used, above all, knowledge from the mediational facet; in the third Argument, knowledge from the epistemic facet is mainly inferred; in the fourth Argument, knowledge from the epistemic and cognitive facets is inferred; and in the fifth Argument, above all, they are knowledge from the cognitive facet.

4.1.4. Concluding Stage

At this stage, the parties evaluate the extent to which the resolution of the difference of opinion was reached and in favor of whom. In the case of this discussion, the one who made the conclusion was T1, for which he considered the comments of all the participants (T2, AD, JL, RD) and, in summary, raised the following points:

• Considering the cognitive level of the students, it is not possible to pose an open problem for modelling.
• It was decided to reduce the mathematical richness by giving the model to the students (this task and its redesign are analyzed in Section 4.2.3).
• For the redesign proposal, it is necessary to: (a) propose working on the task in a group, considering the advantages of this way of working; and (b) modify the wording of the modelling task to customize the situation to the students’ context.
• Considering the situation of the context in which the didactic unit was implemented, it can be assumed that the proposed modelling task did not necessarily meet all the characteristics of a modelling problem.

4.2. Analysis of the Study Subject’s MFP

In this section, we examine the ‘Implementation analysis’ chapter of the study subject’s MFP. To do this, first, we identified the criteria and components of the DSC with which AD related modelling (Section 4.2.1). Second, we analyzed the comments found through the diagramming technique (Section 4.2.2). Finally, we analyzed the modelling task incorporated in the didactic unit (Section 4.2.3).

Since, at the time of preparing his MFP, the study subject knew and used the DSC as a tool to guide his reflection, derived from his educative process in the master’s program, we can affirm that he mainly evidences knowledge from the meta didactic-mathematical dimension of the DMKC model. However, by studying his argumentation in detail, we also infer knowledge from the mathematical and didactic dimensions. In the diagramming that follows, we detail such knowledge, which allows us to affirm, metaphorically, that mathematical, didactic, and meta didactic-mathematical knowledge are ‘dense’ in their reflection guided by the DSC tool.

4.2.1. DSC Components Related to Modelling

From the search for keywords in the study subject’s MFP, we were able to identify the criteria and components of the DSC in which AD made evaluative comments on modelling, as listed below:

• Epistemic criterion: ‘Richness of processes’ and ‘Representativeness of the complexity of the mathematical object’ components.
• Cognitive criterion: ‘Prior knowledge’, ‘Learning’, and ‘High cognitive demand’ components.
• Interactional criterion: ‘Student interaction’ and ‘Autonomy’ components.
• Mediational criterion: We did not find keywords or comments on modelling in any of the components of this criterion.
• Affective criterion: ‘Interest and needs’ component.
• Ecological criterion: We found keywords and comments on modelling in the four components of this criterion.

After identifying these criteria and components, we selected the evaluative comments that were directly related to modelling and the purposes of this study for their consequent diagramming, as described in the following paragraphs.

4.2.2. Diagramming

Based on the criteria and components of the DSC identified in the previous paragraphs, here, we diagram the text of the MFP to identify the reasoning constructed by the study subject. For this, we present the text portions of the MFP in which we identified and numbered the propositions for their diagramming and, later, we specifically deal with those related to the modelling process. In the diagrams of Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, we represent in blue the propositions in the argumentation of the text that are not related to modelling, and in green those that are related to this process. After each diagram, we present an interpretation of the propositions about modelling to infer the study subject’s conceptions about this process.

The first criterion in which the suitability of the implemented didactic unit was assessed is the ‘epistemic criterion’. In this criterion we found evaluative comments on modelling in the ‘Richness of processes’ and ‘Representativeness of the complexity of the mathematical object’ components.

The diagram of the analysis of the ‘Richness of processes’ component is as follows:

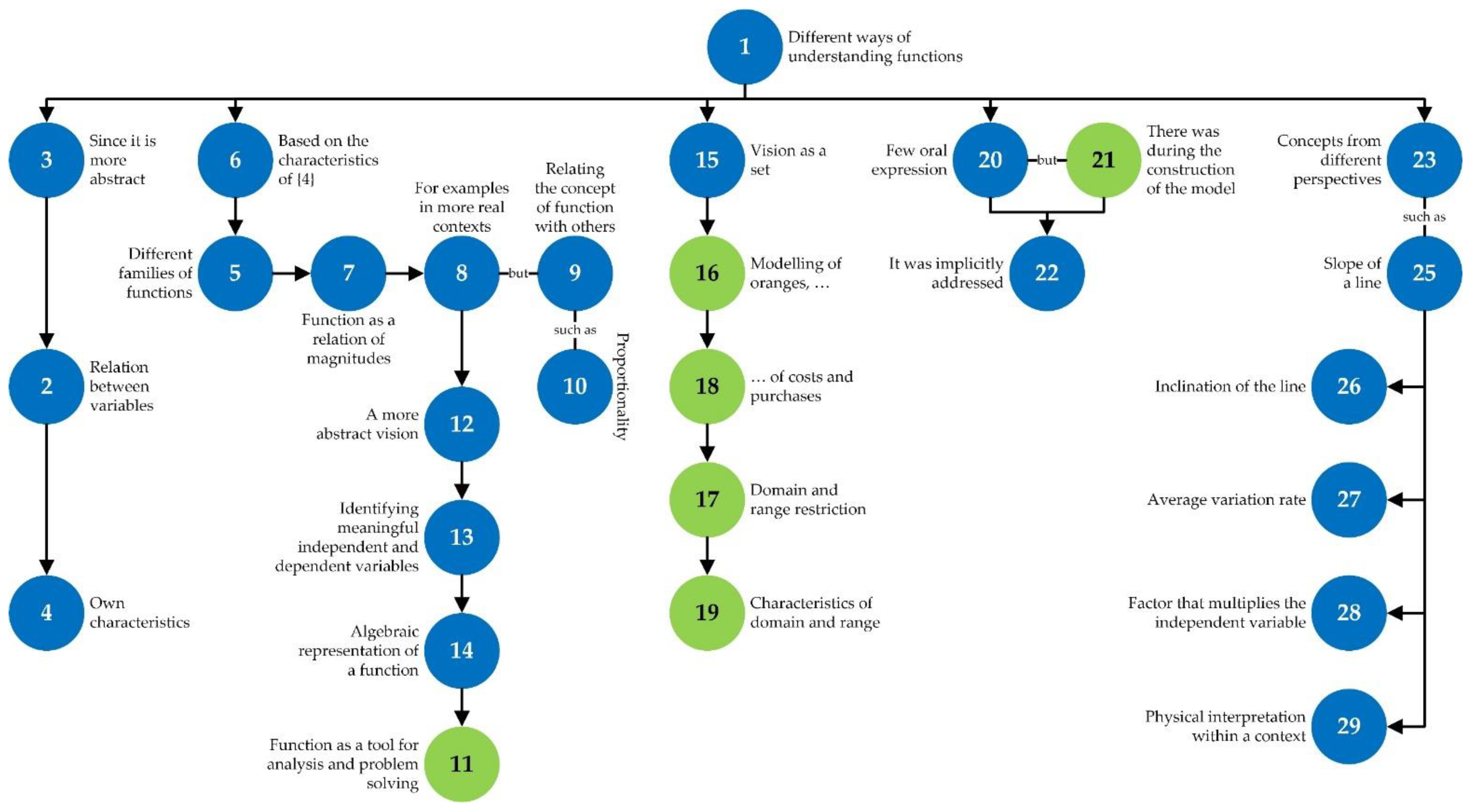
1 {It is clear that the proposed activities must not only represent an exemplification of mathematical concepts, but must also contribute to the work of competences that put into play the students’ abilities, knowledge, attitudes, and skills through cognitive processes}. 2 {In this sense, the central axis of the didactic unit is the modelling process that allows many tools to work on different competences}. […]. Competence 1. Translate a problem into mathematical language or mathematical representation using appropriate variables, symbols, diagrams, and models. 3 {This competence has been extensively worked on in all the modelling problems, especially in sessions 2, 7, and 8, as well as in the synthesis work, which in the end could not be taken to the classroom}. 4 {Here, the expression of the problems in algebraic, graphical, or table form stands out, which has been integrated into all the modelling problems}, 5 {not only in order to see the different forms of expression of the problem}, but also 6 {the student’s abstraction capability to understand a situation in a ‘real’ context} such as 7 {buying fruit in session 2, calculating the speed of a runner in session 7, or the choice of the best rate of mobile operators}. Related to this competence, 8 {intense work has been done on the processes of problem solving and conversion between different representations of functions}, 9 {in this case, between natural and mathematical languages (translation)}. In all cases 10 {it has been insisted that the mathematical translation be formally correct}, 11 {always trying that the student correctly assigns and defines the independent and dependent variable(s), considering the units and their compatibility and coherence, as well as unit conversion where appropriate}. Competence 5. Construct, express, and contrast arguments to justify and validate the statements made in mathematics. At the same time, the previous competence, and especially in the modelling problem posed in session 8, 12 {the student is encouraged to make small conjectures} about the rate behavior of a service or, at least, 13 {to propose a thesis and mathematically check it}, 14 {forcing the student to build a model}, 15 {to express more or less real situations through the model}, and 16 {to contrast information or check whether the statements are correct or not}. 17 {In terms of processes, mathematical argumentation has been worked on}. 18 {Modelling problems, in general, always propose not only to model, but also to apply this model to a situation, often very close to reality} 19 {(for which I would also work intensively on competences 6 and 7 from the mathematical area, that is ‘Use mathematical reasoning in non-mathematical environments’ and ‘Identify the mathematics involved in close and academic situations and look for situations that can be related to concrete mathematical ideas’)}. 20 {The process associated with these competences would be contextualization}.

([67], pp. 4–5)

Figure 8. Diagramming of the assessment of the ‘Richness of processes’ component. Authors’ interpretation.

Figure 8. Diagramming of the assessment of the ‘Richness of processes’ component. Authors’ interpretation.

The study subject made the assessment of the ‘Richness of processes’ component considering, furthermore, the competences established in the educational curriculum for mathematics [71]. In this line, proposition 3 shows that the study subject related competence 1 of the curriculum to work with modelling. More specifically, competence 1 is somewhat related to the definition of the ‘mathematization’ transition, which includes the modelling cycle (see Figure 1, no. 3). In terms of [72], there are tasks to work on certain transitions of the modelling cycle, which does not imply that a modelling process is being carried out as such, since their intention is to focus on some specific sub-competence(s). However, from his writing we can infer that the study subject considered the idea: ‘by working on competence 1, in addition, I am working on modelling’.

For its part, proposition 6 shows that the study subject, in one of the beliefs that form his conception of modelling, considered the understanding of the task in its context as a starting point to develop the modelling process. In particular, this idea can be related to the ‘understanding/constructing’ transition that includes the modelling cycle (see Figure 1, no. 1). Likewise, from proposition 12 to 17, we can interpret that the study subject considered different transitions of the modelling cycle. For example, proposition 12 can be related to the ‘simplifying/structuring’ transition (see Figure 1, no. 2), and proposition 16 to the ‘validating’ transition (see Figure 1, no. 6).

Finally, proposition 18 evidences certain limited interpretations of the study subject on modelling. On one hand, we can infer an overlap between the ‘mathematical modelling’ and ‘mathematical applications’ processes. In terms of [73], although both processes denote all kinds of relationships between the «real world» and «mathematics», modelling starts from the «real world» towards «mathematics», focused on the process; while applications start in the opposite direction, focused on the mathematical object. On the other hand, the study subject considered that modelling also implies applying a mathematical model to a situation close to reality. Although this idea is not wrong, it is imprecise in the sense that, as stated in Section 2.1, a modelling problem is characterized by coming from a ‘realistic’ and ‘authentic’ context, and its writing seems to show that calls into question—with the phrase ‘many times’—the condition of closeness to reality, and not as a sine qua non condition to pose this type of problem.

For the next diagrams of the analysis of the DSC components, we only show the text portions extracted from the study subject’s MFP that include numbered propositions related to modelling. However, the figure associated with each analysis includes the diagram of each component in its entirety.

The diagram of the analysis of the ‘Representativeness of the complexity of the mathematical object’ component is as follows:

11 {In the contextualized examples and, above all, in the modelling problems, the change in the conception of function has been used as a tool for analysis and problem solving}, 12 {starting from an abstract vision of function as a relation of variables}, 13 {adding meaning to these variables, in order to identify the independent and dependent variables of a problem in its context} to, 14 {finally, enable the algebraic representation of a function}. Beyond the conception of function as a relation of magnitudes or variables, 15 {a vision of function as a subset of the cartesian product of two sets has been introduced in class, that is, a vision as a set}. For example, 16 {in the modelling problem of buying oranges, when algebraically expressing the function, its domain and range as an abstract mathematical function was one}, but, 17 {if we conceive function as a relation of magnitudes, that domain and range are restricted}, since 18 {the purchase of a negative mass of oranges or obtaining negative costs of a purchase does not represent an easy interpretation}, (despite the fact that these could be interpreted as sales), so 19 {the characteristics of domain and range of a function can differ for the same algebraic representation, defining in itself different functions depending on the domain considered, that is, different functions that, despite having the same algebraic expression, they differ depending on the subset of independent variables considered (vision of a function as a subset of the cartesian product)}. 20 {To a lesser extent, the verbal expression of a function has been explicitly worked on, that is, it has not been asked as an objective to verbally express a function}, but 21 {the oral expression of a function has been worked on in the context of the model development}, so 22 {this representation has been worked on, albeit implicitly}.

([67], pp. 6–7)

Figure 9. Diagramming of the assessment of the ‘Representativeness of the complexity of the mathematical object’ component. Authors’ interpretation.

Figure 9. Diagramming of the assessment of the ‘Representativeness of the complexity of the mathematical object’ component. Authors’ interpretation.

In the assessment of this component, the study subject explicitly related the work with modelling to the treatment of the complexity of the mathematical object function, as evidenced in proposition 11, through the change of conception that one has of it (function as a ‘relation between variables’ and as a ‘subset of the cartesian product’). Likewise, from proposition 16 to 19, the study subject considered that, in a modelling problem, the context is what determines the behavior of the mathematical object involved. This idea of the study subject is related to the position of [60] on the epistemic (metamathematical) norms that regulate the modelling activity, in which the solution of the problem must make sense in the context of the problem-situation posed. One aspect that we stress is that, in the study subject’s reflection on this component, he repeatedly used the term ‘conception’. However, he did not specify what he means by such term. For this reason, we infer that sometimes he interprets its use as a ‘partial meaning’ (see [32]) of a mathematical object.

The second criterion in which the suitability of the implemented didactic unit was assessed is the ‘cognitive criterion’. In this criterion, we found evaluative comments on modelling in the ‘Prior knowledge’, ‘High cognitive demand’, and ‘Learning’ components. However, in the latter, we did not find a direct relationship with the purposes of this study, which is why we discarded it for analysis.

The diagram of the analysis of the ‘Prior knowledge’ component is as follows:

3 {The objective of this initial evaluation was focused on analyzing the student knowledge of units of measurement and unit conversion}, 4 {to see their mastery of the topic}, 5 {which is essential for modelling and contextualized exercises and problems}. In addition, 6 {it is where there may be more level of disparity between students}, since 7 {units of measurement and unit conversion are not only addressed in mathematics}. 8 {The assessed prior knowledge is the algebraic manipulation of linear equations}, 9 {to see if students will be able to work with functions algebraically expressed with sufficient ease so that, in modelling problems, the algebraic manipulation not be an impediment to exercise solving}. In general, 10 {it can be seen that, in terms of knowledge and unit conversion, six students have made two errors or more in the three-unit conversion questions} and that, therefore, 11 {may have problems when following the modelling problems}.

([67], p. 7)

Figure 10. Diagramming of the assessment of the ‘Prior knowledge’ component. Authors’ interpretation.

Figure 10. Diagramming of the assessment of the ‘Prior knowledge’ component. Authors’ interpretation.

In the assessment of this component, from proposition 3 to 5, we can evidence that the study subject attributed great importance to prior knowledge about the mathematical object function to, later, work on modelling and avoid difficulties during the solving of this kind of tasks (there ideas are reinforced in propositions 9 and 11). As mentioned above, modelling primarily focuses on the transition process between the «real world» and «mathematics», rather than on the mathematical object involved (as in the case of applications) [73]. However, the study subject’s position sheds light to the contrary. In the same way, we did not observe in his writing that he has considered the previous experiences of modelling that the students may have had as prior knowledge.

The diagram of the analysis of the ‘High cognitive demand’ component is as follows:

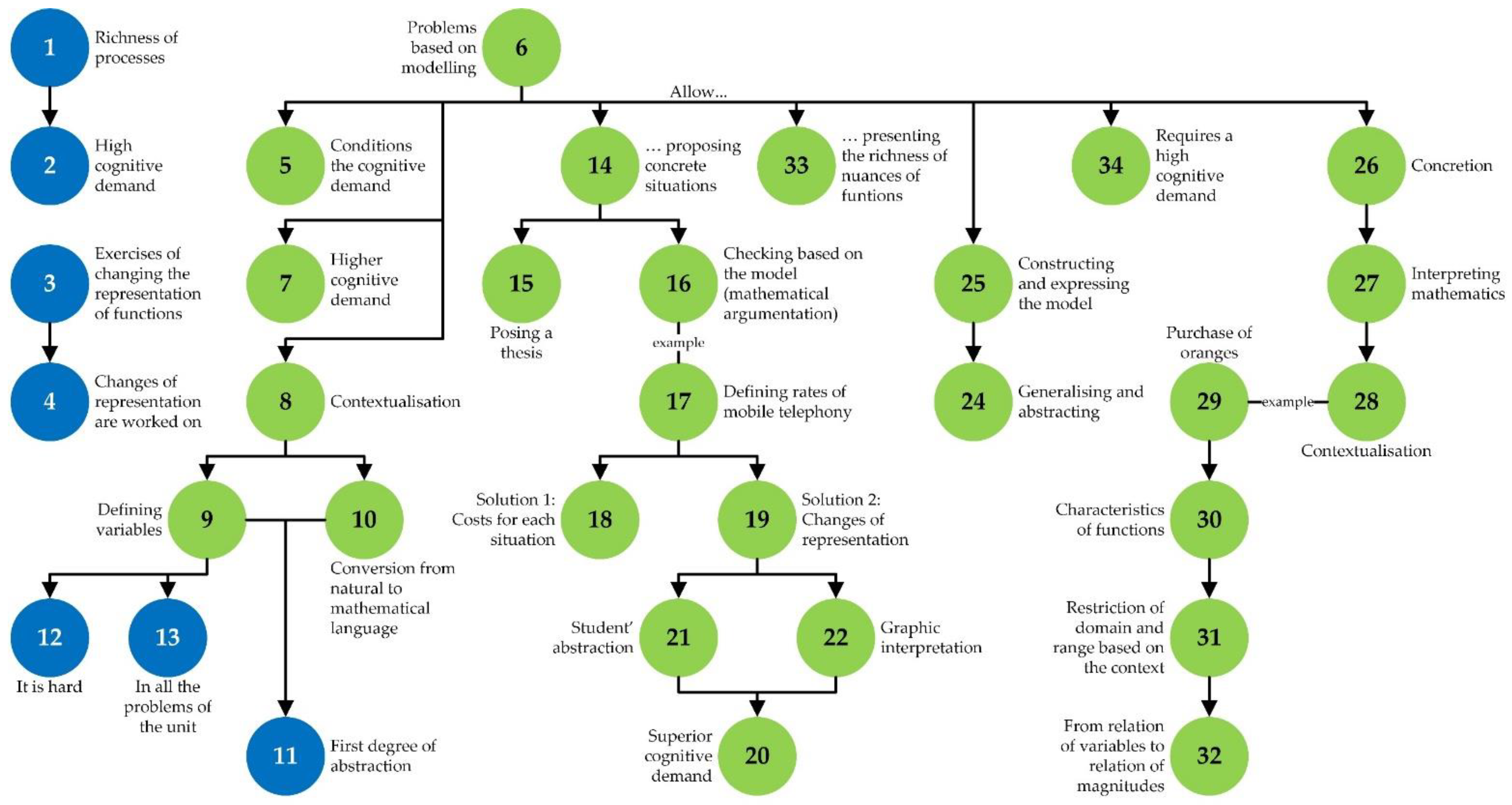
However, 5 {the cognitive demand is conditioned} by the 6 {structure of the didactic unit, with problems based on modelling processes}. 7 {In these problems is where the cognitive demand on the student is higher}. First of all, 8 {every modelling problem required a first phase of understanding the context (contextualization)} 9 {to define what the variables are {independent and dependent)} and 10 {in what units they want to be represented (conversion from natural to mathematical language)}. 11 {Here we already find a first degree of abstraction that, as verified in the final exam, many times modelling problems are solved}, but 12 {it is difficult for students to formally determine the variables and, therefore, they reach the maximum degree of abstraction of the problem, which will entail the representation of the problem in the form of a function, typically expressed in algebraic form, in order to be mathematically analyzed}. 13 {This conversion process is carried out in all the modelling problems proposed in this didactic unit that is analyzed}. Beyond the conversion, 14 {modelling problems allow the student to propose solving specific situations}, so that 15 {they must propose different situations or theses} and 16 {verify them from the model (mathematical argumentation)}, such as, for example, in the modelling problem of session 8, 17 {where the student is asked to determine which mobile rate is more convenient}. 18 {This problem can be solved by calculating the costs for each situation that the problem poses}, or 19 {by performing a change of representation, plotting the costs of the different companies (treatment) and, from the cut-off point of the functions, see from which mobile consumption one company or another pays better}. 20 {In this last resolution model, the cognitive demand is higher}, not only 21 {due to the higher degree of abstraction that the student needs}, but 22 {due to changes in representation} and 22 {the fact of correctly interpreting the cut-off points of the functions}, 23 {to make deductions of what happens in reality with the cost of the mobile}. Moreover, it is important to note that 24 {in the modelling process we have a first step of generalization and abstraction} 25 {when building and expressing the model}, but also, 26 {a concrete exercise} 27 {when the mathematical results must be interpreted} 28 {to draw conclusions in the context of the problem (contextualization)}. Many times, like, 29 {for example, in the problem proposed in session 2 about the purchase of oranges}, 30 {the purely mathematical analysis of the function represented by the model would have characteristics such as the domain and range} which, later, 31 {its concretion to the real context of the problem makes both the domain and the range make sense in more restricted intervals} (since the purchase of a negative mass of oranges or obtaining negative costs of a purchase does not present an easy interpretation), 32 {when passing from the interpretation of a function as a relation of variables to that of a relation of magnitudes}. 33 {It is therefore thanks to the modelling problems that this richness of nuances can be presented in the definition of function and to be able to exemplify what it is for taking them into account}. 34 {This process requires a high cognitive demand}.

([67], pp. 9–10)

Figure 11. Diagramming of the assessment of the ‘High cognitive demand’ component. Authors’ interpretation.

Figure 11. Diagramming of the assessment of the ‘High cognitive demand’ component. Authors’ interpretation.

In the assessment of this component, we can observe that many propositions posed by the study subject are related to modelling. This is fundamentally since he considered this process as the central axis of his implemented didactic unit. Proposition 8 explicitly considers the ‘understanding/constructing’ transition that the modelling cycle includes (see Figure 1, no. 1). For its part, proposition 12 evidences the ‘working mathematically’ transition (see Figure 1, no. 4), when specifically referring to the analysis of the problem with the tools of mathematics. From proposition 17 to 23, the study subject focused his analysis on some particular problems, where he alluded to the semiotic aspects (in terms of [74]) that working with modelling implies. These problems only consist of exercises of conversion between registers. Propositions 27 and 28 are related to the ‘interpreting’ and ‘validating’ transitions (see Figure 1, nos. 5 and 6). From the assessment of this component, we can highlight two aspects: on one hand, the study subject referred to different transitions of the modelling cycle, which he exemplified with the modelling problems that he included in his didactic unit; and, on the other hand, he considered that this process requires a high cognitive demand for its development, including other processes of mathematical activity (in line with the position of [32]).

The third criterion in which the suitability of the implemented didactic unit was assessed is the ‘interactional criterion’. In this criterion we found evaluative comments on modelling in the ‘Student interaction’ and ‘Autonomy’ components.

The diagram of the analysis of the ‘Student interaction’ component is as follows:

3 {Initially, I wanted that part of the synthesis work of the didactic unit (Annex 3) to be worked on in virtual groups among themselves}, but 4 {the lack of habit of the group in these work dynamics and the advice from the mentor teacher made me change my mind}. 5 {Unfortunately, the fact that some sessions were cancelled} 6 {because of students’ activities outside the classroom (outings and gymkhanas)}, 7 {meant that, finally, the synthesis work had to be suspended}, which is where 8 {it was expected to further enhance the student interaction}. In group meetings, 9 {the students commented on how they thought the problems were solved and tried to explain why they tried one way or another}. Finally, 10 {they reached consensus (or not) after consulting with the teacher}.

([67], pp. 11–12)

Figure 12. Diagramming of the assessment of the ’Student interaction’ component. Authors’ interpretation.

Figure 12. Diagramming of the assessment of the ’Student interaction’ component. Authors’ interpretation.

In the assessment of this component, the study subject made evident the greatest difficulty he had in implementing his didactic unit in the way he had planned it. Due to mismatches with the temporary organization of the educational center, there were two sessions (10 and 13) in which his class made extracurricular outings, and which were intended to develop the synthesis work of the didactic unit during the ‘Món Matemàtic’ workshop. More specifically, it was in these two sessions that he would implement the modelling task on which he reflected the most within his MFP, which ended up being hypothetical reflections. On the other hand, propositions 3 and 9 show that the study subject considered that an important aspect to work on modelling is to promote interactions between students through group work with this type of tasks, which is in line with the position of [46].

The diagram of the analysis of the ‘Autonomy’ component is as follows:

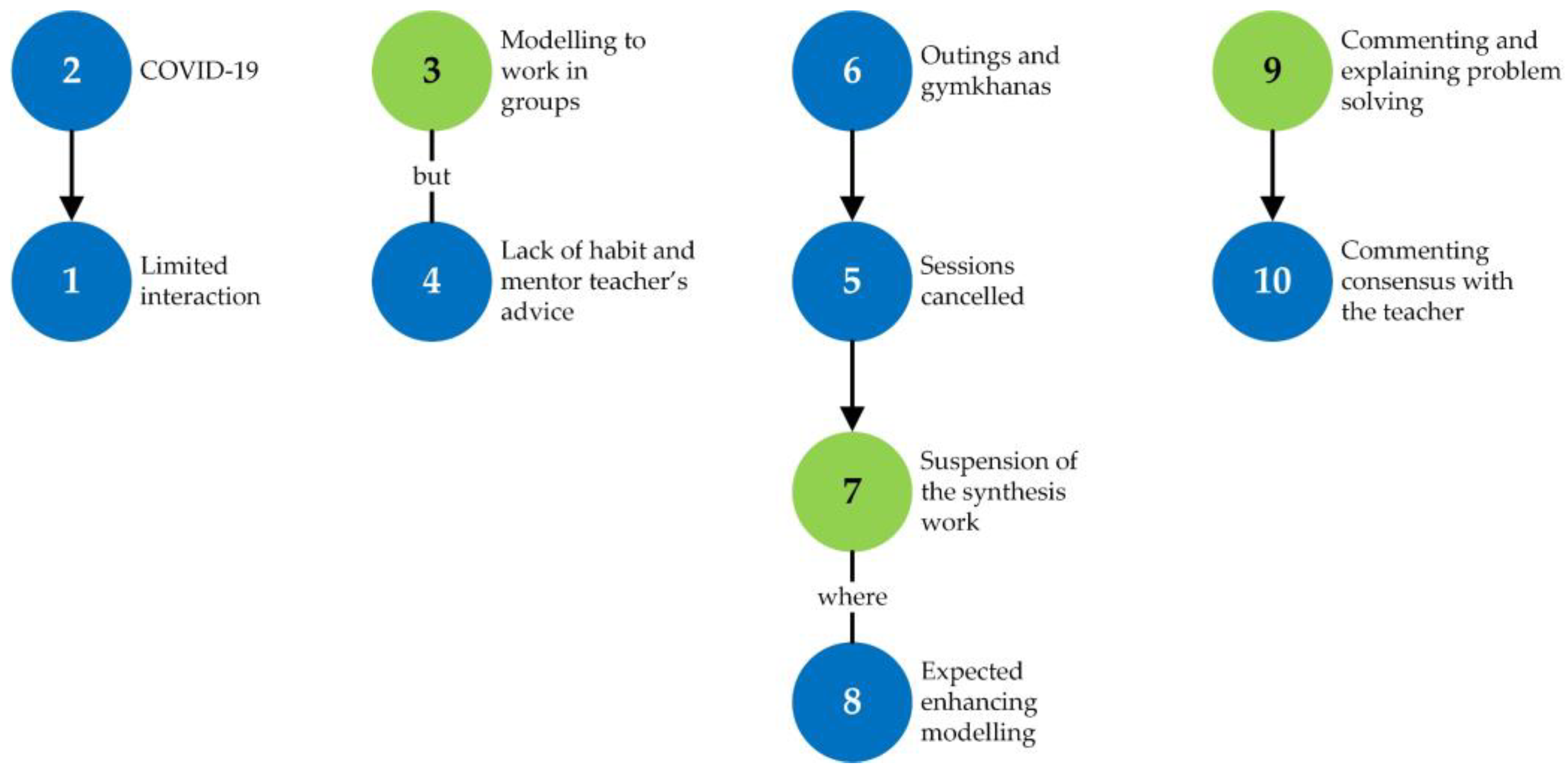
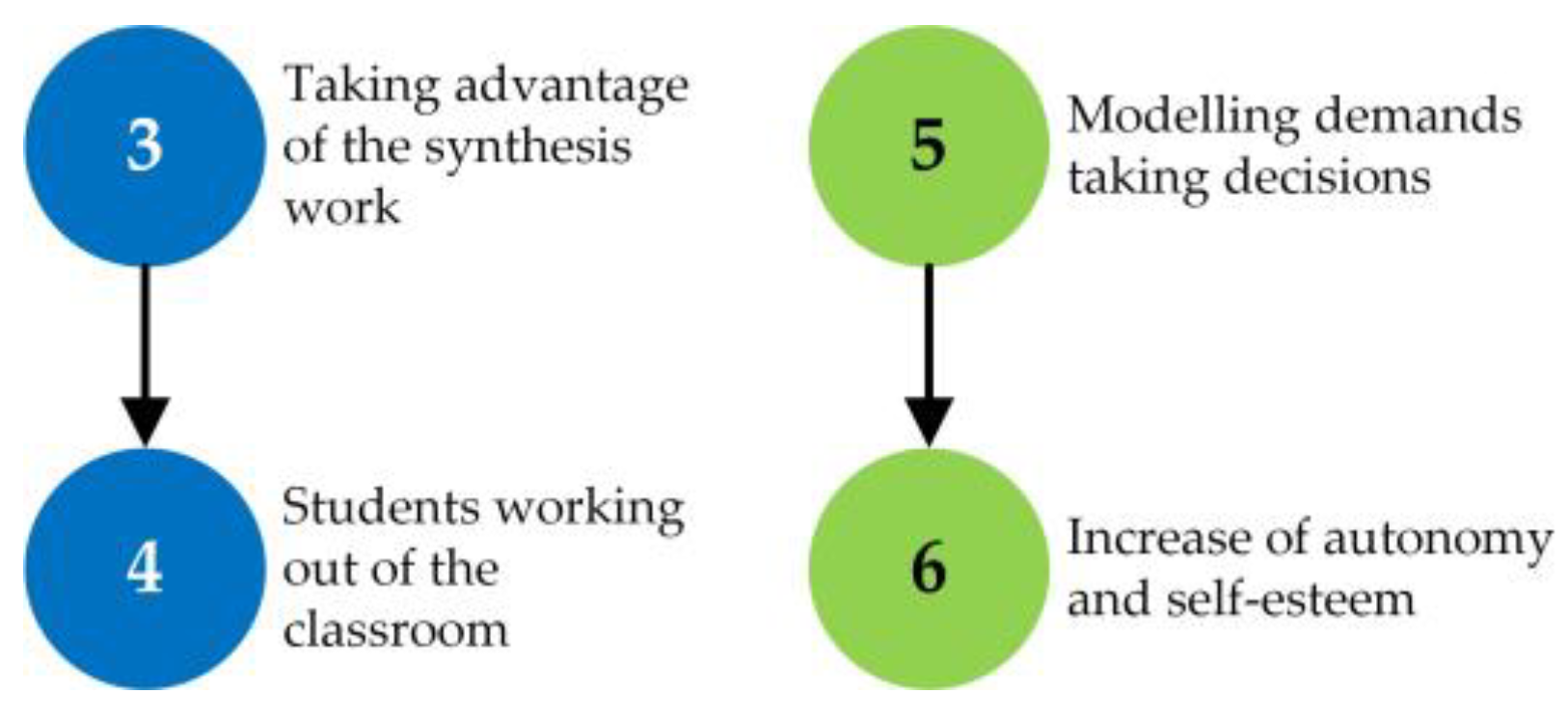
3 {Given this lack of autonomy during the classes, I wanted to take advantage of the synthesis work to increase this autonomy}, 4 {letting the students do part of this work on their own outside the classroom}. By not being able to introduce the synthesis work, it was not possible to enhance the autonomy of the group. 5 {Modelling problems, by requiring the student to make decisions in various processes}, 6 {tend to increase autonomy and, when reaching solutions, create a certain feeling of self-esteem for having solved a problem that, being contextualized, is perceived as something related to reality}.

([67], p. 12)

Figure 13. Diagramming of the assessment of the ‘Autonomy’ component. Authors’ interpretation.

Figure 13. Diagramming of the assessment of the ‘Autonomy’ component. Authors’ interpretation.

In the assessment of this component, the study subject considered that the work with modelling promotes decision-making, along with the improvement of the students’ autonomy and self-esteem. Although this is a hypothetical reflection, i.e., it is based on his notion of the positive aspects of modelling work by students, the idea is in line with the position of [21].

The fourth criterion in which the suitability of the implemented didactic unit was assessed was the ‘mediational criterion’. However, we did not find evaluative comments on modelling in any of the components of this criterion.

The fifth criterion in which the suitability of the implemented didactic unit was assessed is the ‘affective criterion’. In this criterion, we found evaluative comments on modelling in the ‘Interests and needs’ component.

The diagram of the analysis of the ‘Interests and needs’ component is as follows:

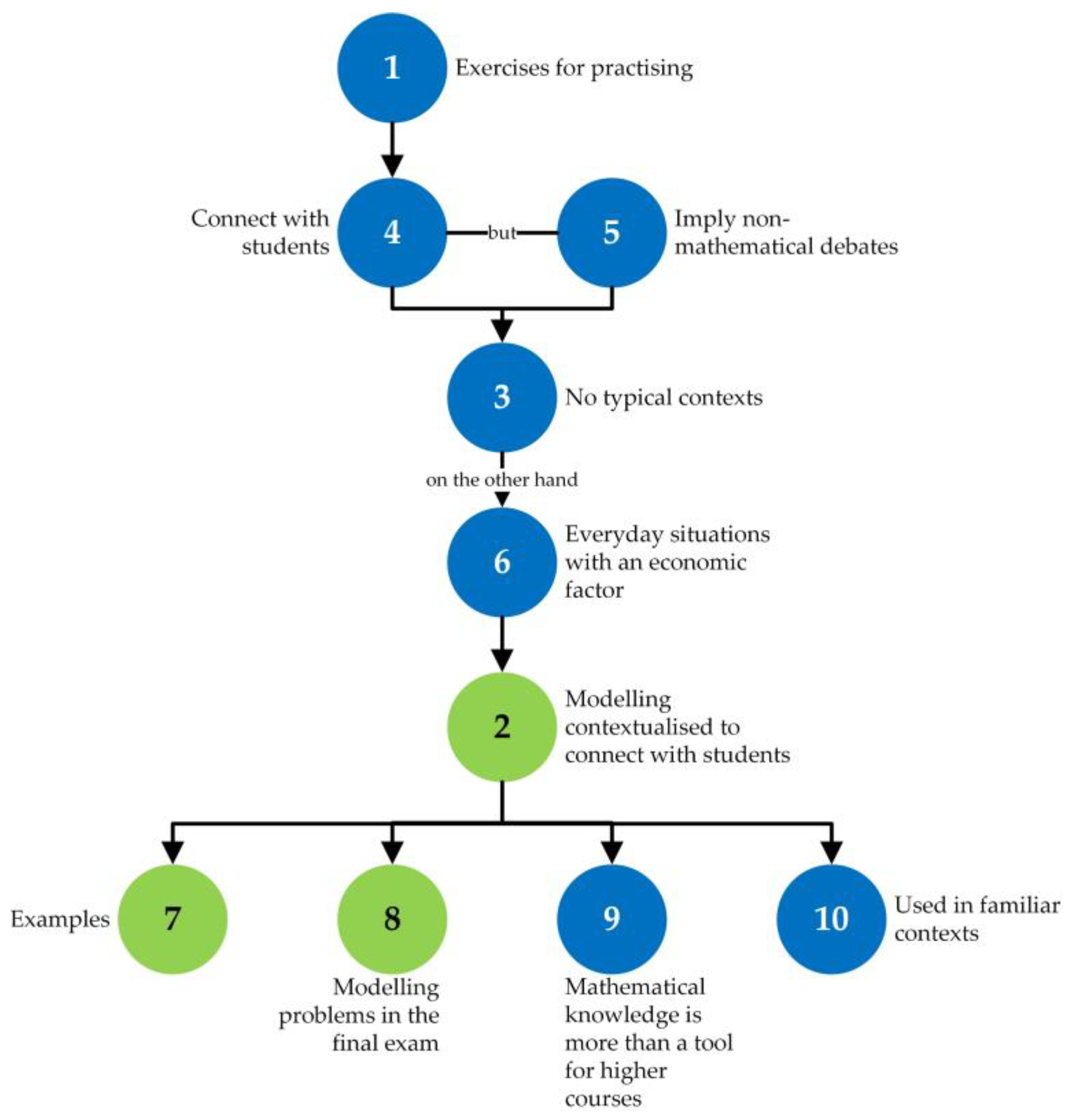
1 {The exercises in class, in general, were for practicing}, 2 {but the modelling problems, distributed throughout the didactic unit, were contextualized to appeal to everyday situations where the students felt identified}. 3 {No typical contexts have been introduced to attract the attention of the students such as football, movies, videogames, or something like that}. Although 4 {these topics connect with the interests of the vast majority of students}, 5 {they end up provoking non-mathematical debates that do not contribute to improving the work climate in the classroom}, on the other hand, 6 {everyday situations, where many times they identify themselves in adult situations, they also find them attractive and, above all, if they incorporate the economic factor}. This, 7 {the contexts proposed by the three modelling problems defined for the didactic unit are the purchase of products in bulk (oranges), the analysis of the speed of a runner in a race, and the choice of a rate of mobile telephony among different options}. Likewise, 8 {in the final exam, a contextualized modelling problem was included when looking for the most appropriate hiring rate for a gym service based on its use}. 9 {The objective of this contextualization of problems was also aimed at showing the students that mathematical knowledge is not only a tool for those who want to continue their studies in baccalaureate education}, but also 10 {is found and useful in close and everyday environments}.

([67], pp. 14–15)

Figure 14. Diagramming of the assessment of the ‘Interests and needs’ component. Authors’ interpretation.

Figure 14. Diagramming of the assessment of the ‘Interests and needs’ component. Authors’ interpretation.

In the assessment of this component, propositions 3 and 4 allow us to see some aspects that the study subject took into account to design the wording of their modelling problems. In these aspects, those focused on the students’ daily life were privileged, avoiding context that could produce disparities of opinions and, in this way, focusing on the mathematical aspects of the solving.

The sixth (and final) criterion in which the suitability of the implemented didactic unit was assessed is the ‘ecological criterion’. In this criterion, we found evaluative comments on modelling in its four components. We will make a general comment on this criterion at the end of the four diagrams, due to the fact that the assessments of the components are interrelated.

The diagram of the analysis of the ‘Curriculum adaptation’ component is as follows:

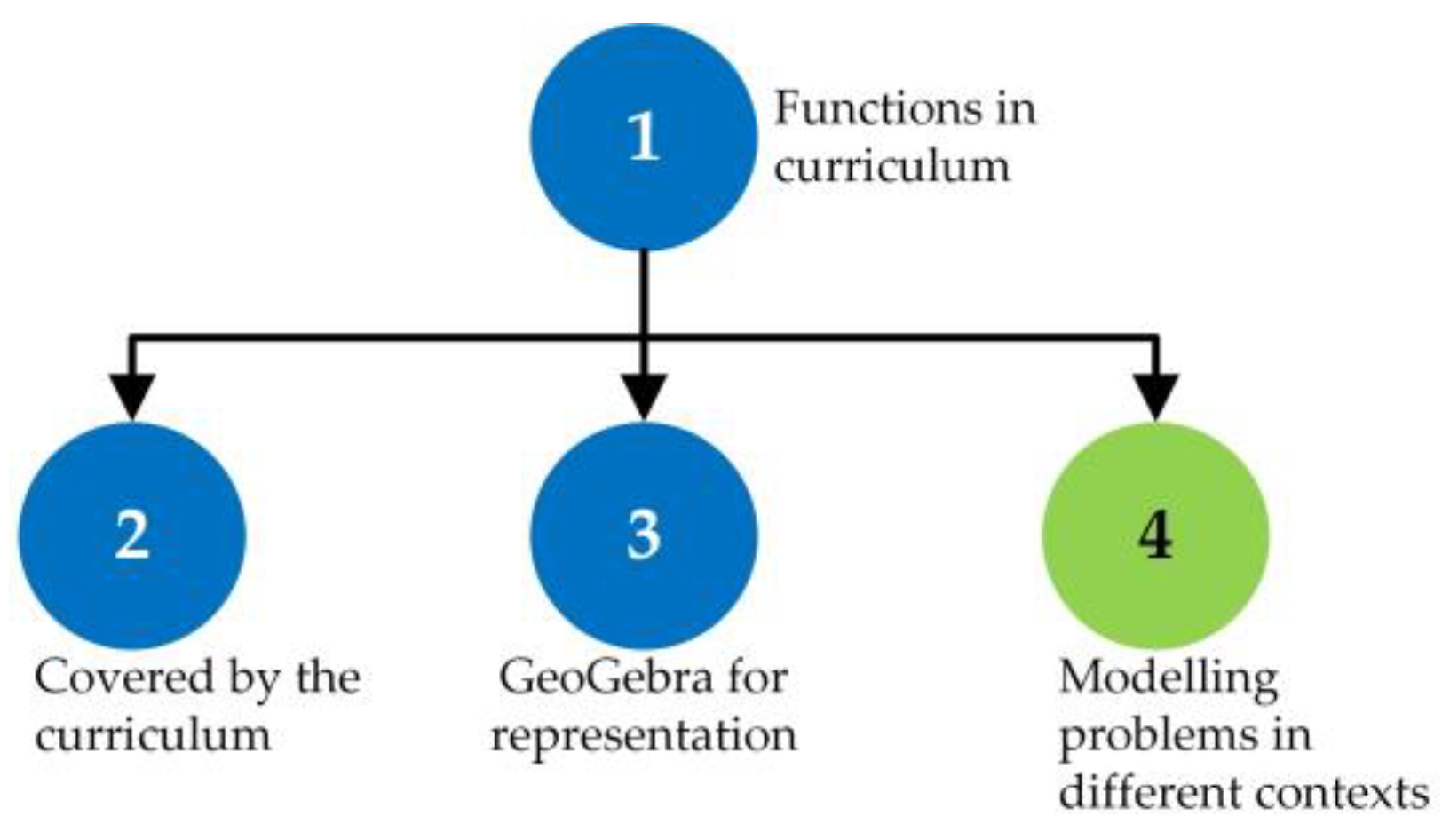
4 {Finally, the point use of functions for solving problems in different contexts is fully covered with the use of modelling problems, which have been solved in the didactic unit}.

([67], p. 16)

Figure 15. Diagramming of the assessment of the ‘Curriculum adaptation’ component. Authors’ interpretation.

Figure 15. Diagramming of the assessment of the ‘Curriculum adaptation’ component. Authors’ interpretation.

The diagram of the analysis of the ‘Intra and interdisciplinary connections’ component is as follows:

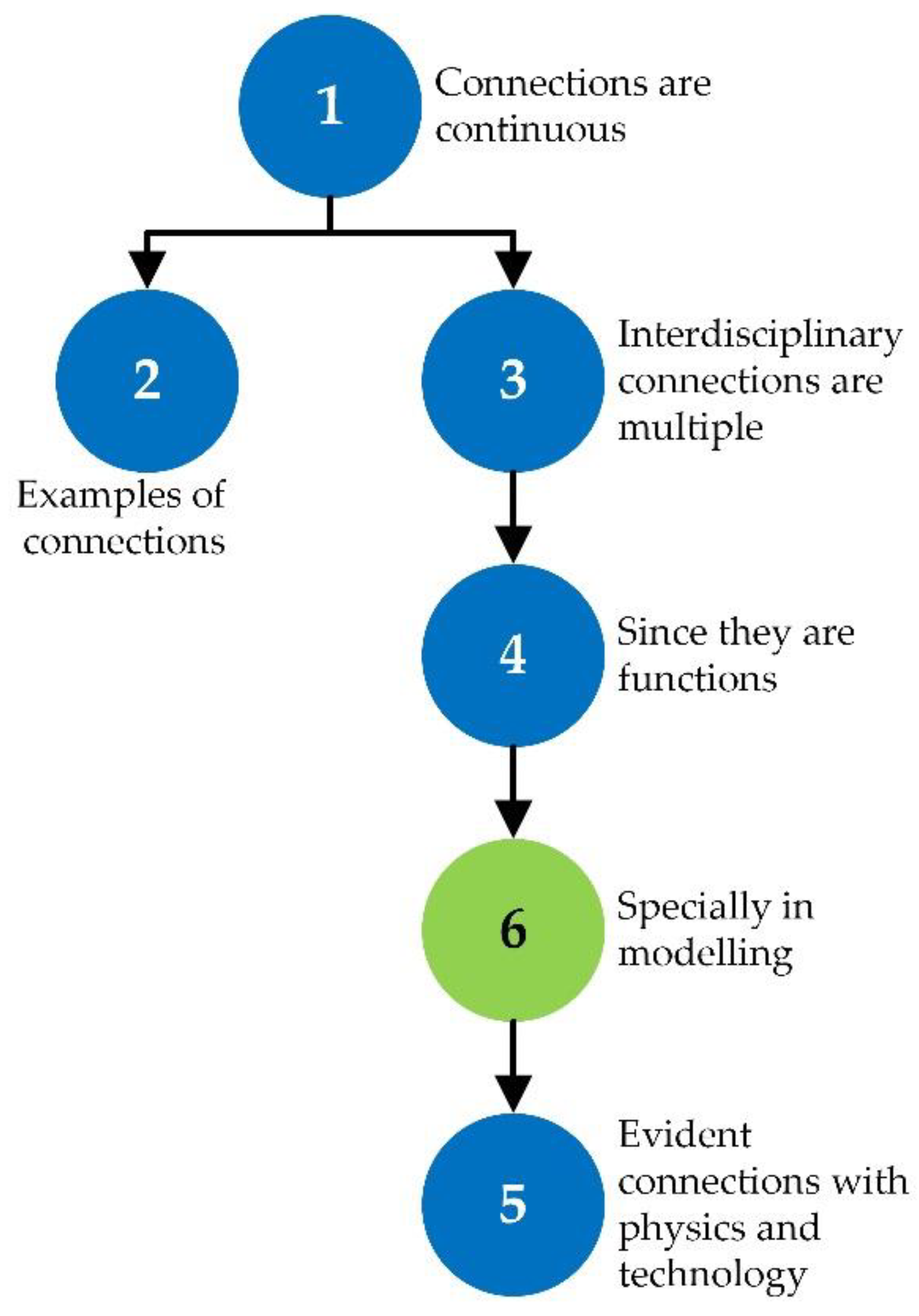
1 {The intradisciplinary connections (within mathematics) of the didactic unit are continuous}. […]. 3 {The interdisciplinary connections are also multiple}, 4 {given the nature of the didactic unit of functions}, 5 {there are obvious connections with the physics and technology subjects}, 6 {specially, due to the use of modelling in problems, which is natural in these disciplines}. […]. It has not been formally established in the development of the didactic unit, but it could be easily given the connection with social sciences or economics subjects.

([67], p. 17)

Figure 16. Diagramming of the assessment of the ‘Intra and interdisciplinary connections’ components. Authors’ interpretation.

Figure 16. Diagramming of the assessment of the ‘Intra and interdisciplinary connections’ components. Authors’ interpretation.

The diagram of the analysis of the ‘Social and labor usefulness’ component is as follows:

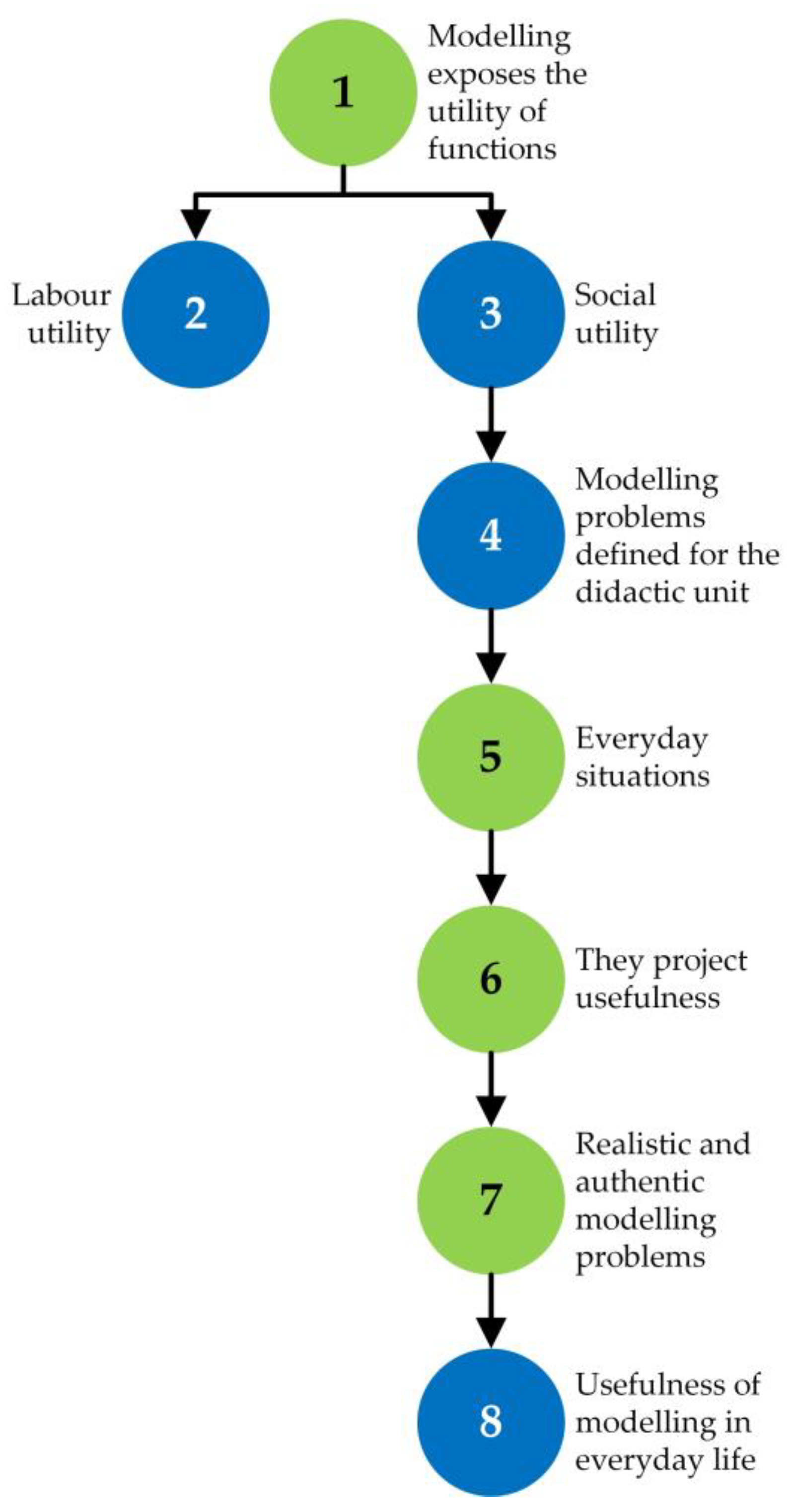
1 {The social and labor utility of functions has been exposed, mainly, from modelling problems, which have been contextualized in everyday situations}. 2 {The labor utility, perhaps, is further away from third grade of secondary education students} and, even so, it has been commented on. 3 {The social utility, which I believe may be closer to 3rd grade of secondary education students}, 4 {has been introduced from the contextualization of the contexts proposed by the three modelling problems defined for the didactic unit}, which are the purchase of products in bulk (oranges), the analysis of the speed of a runner in a race, and the choice of a mobile phone rate among different options. 5 {These are everyday situations, which avoid grandiloquent statements}, but which I believe 6 {project the image of the usefulness of mathematics on a day-to-day basis and, therefore, the need and convenience of learning them}. 7 {The problems based on modelling processes are usually realistic and authentic}, which 8 {shows their usefulness in everyday life and not only in special and professional situations}.

([67], p. 17)

Figure 17. Diagramming of the assessment of the ‘Social and labor utility’ component. Authors’ interpretation.

Figure 17. Diagramming of the assessment of the ‘Social and labor utility’ component. Authors’ interpretation.

The diagram of the analysis of the ‘Didactic innovation’ component is as follows:

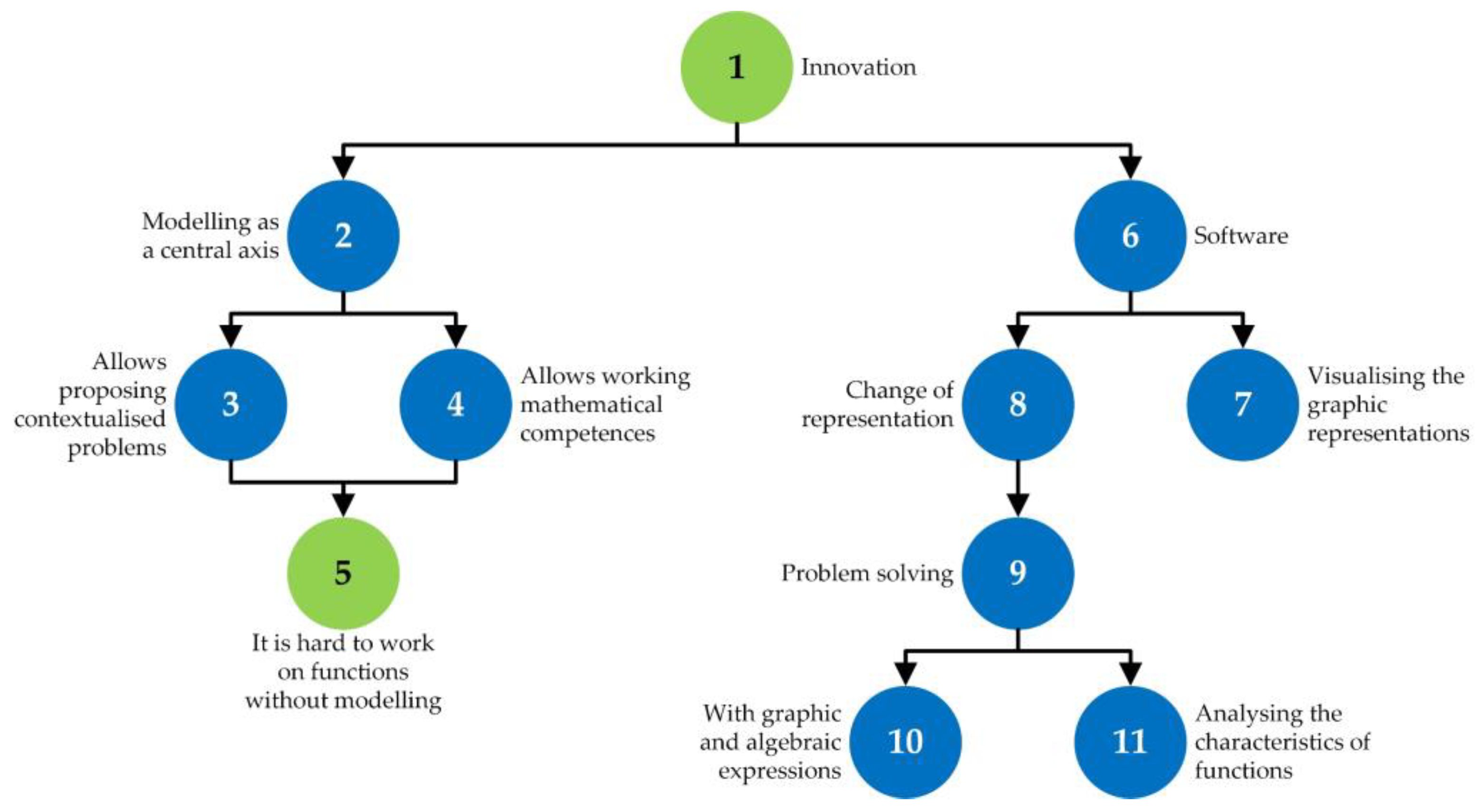
1 {The innovation in this didactic unit does not come from the content, which is the classic, but from two aspects}. 2 {Firstly, the use of modelling as a central axis of the didactic unit}, 3 {which allows to propose contextually rich problems to the students}, and 4 {which allow different mathematical competences to be worked on}, such as those discussed in Section 3.1.3 dedicated to the analysis of richness of processes. In this sense, 5 {it is difficult for me to imaging the fact of proposing this didactic unit of functions without using modelling}. Moreover, during the didactic unit, 6 {{software such as GeoGebra} 7 {was used to immediately visualize the graphical representations of functions} and 8 {encourage the change of representation} as a tool 9 {to solve problems or understand concepts in class}.

([67], p. 17)

Figure 18. Diagramming of the assessment of the ‘Didactic innovation’ component. Authors’ interpretation.

Figure 18. Diagramming of the assessment of the ‘Didactic innovation’ component. Authors’ interpretation.

In the assessment of the ‘Curriculum adaptation’ component, proposition 4 in Figure 15 shows that the study subject considered functions as an appropriate mathematical object to work on modelling (in line with the position of [75]) and, in this way, addressing both the content and the competences that are established in the educational curriculum. Hand in hand with the above, in the assessment of the ‘Intra and interdisciplinary connections’ component, propositions 5 and 6 in Figure 16 show that the study subject considered that, although functions naturally connect with other disciplines included in the educational curriculum, it was through modelling that he tried to make such connections more evident, which he considered to be an advantage. Regarding the assessment of the ‘Social and labor usefulness’ component, propositions 6 to 9 in Figure 17 reinforce the previous ideas about the benefits of contextualization as part of modelling, which highlights the social and labor utility of mathematics and, in particular, the concept of function. Finally, regarding the assessment of the ‘Didactic innovation’ component, proposition 2 in Figure 18 once again highlights that modelling, as a central axis of the didactic unit, allows the development of different mathematical competences, both those included in the curriculum (proposition 4) and those that are typical of working with this process.

4.2.3. Modelling Task

As we have stated throughout this article, the study subject’s didactic unit considered the modelling process as the central axis. To do this, in his MFP he repeatedly stated that he designed and implemented this type of tasks to work with his students. Moreover, during the first group reflection session, emphasis was placed on a task based on the fuel consumption of a car during a family trip to the beach. In the following paragraphs we present this task and its reformulation, which we analyzed from the theoretical framework of modelling described in Section 2.1.

The task initially proposed by the study subject was designed to be implemented during the ‘Món Matemàtic’ workshop and was part of a work guide for the students. The guide included an introductory text describing three formulas, considered as mathematical models, to calculate the fuel consumption of a car, explaining, in turn, the intervening variables.

Table 2. Formulas for the calculation of fuel consumption.

Description	Formulas
Real distance consumption $\left(C{D}_r\right)$	$C{D}_r=C{D}_e\cdot \left(\frac{m_v+{{\displaystyle \sum }}_{i=n}^{i=0}{m}_{ci}}{m_v}\right)$
Consumption at idle $\left(C_p\right)$	$c_p=\left(\frac{3l}{h}\right)\cdot t$
Total consumption $\left(C\right)$	$C=C_p+L\cdot \frac{C{D}_r}{100}$

Adapted from [67] (p. 80).

presents these three formulas that, in terms of the study subject, correspond to ‘simplified models’.

The variables involved in the three formulas in Table 2 and the magnitudes in which they are expressed are:

• $C{D}_r$: Fuel consumption per real distance (expressed in litres per 100 km).
• $C{D}_e$: Fuel consumption per standard distance (reported by the manufacturer; expressed in liters per 100 km).
• $m_v$: Mass of the vehicle (without additional load; expressed in kg).
• $m_{ci}$: Mass loaded by the vehicle (passengers, packages; expressed in kg).
• $C_p$: Fuel consumption at idle (expressed in litres; a constant of 3 liters per hour is estimated).
• $t$: Time that the vehicle is stopped (expressed in hours).
• $C$: Total fuel consumption (expressed in litres).
• $L$: Distances travelled (expressed in km).

The three statements after the introductory text (items (a) to (c)) consisted of tasks to mathematically work with the formulas and, in terms of the study subject, consisted of exercises with the ‘models’ previously presented. It is in item (d) where the modelling task designed by the study subject is introduced (see Figure 19), which is the same task that was discussed at length during the first group reflection session (see Section 4.1).

Figure 19. Modelling task designed for the didactic unit. Translated from [67] (p. 82).

Figure 19. Modelling task designed for the didactic unit. Translated from [67] (p. 82).

The solving of the task basically consisted of interpreting the data of the statement and placing them in the respective variable of the ‘mathematical models’ of the introductory text of the work guide (described in Table 2). After performing the corresponding mathematical operations, the results for the problem question would be (in rounded values): €10.89 (with Tere) and €10.88 (without Tere).

In his MFP, the study subject mentioned that this task corresponded to a modelling problem. Based on the characteristics for this type of problem that were described in Section 2.1, we can state the following:

• The situation is neither open nor complex because, on one hand, the solving procedure is determined by the application of the formulas—or ‘mathematical models’—that were mentioned in Table 2 and, on the other hand, the wording of the task provides all the information necessary for its solving.
• Although the wording of the task is realistic, by adding elements from the real world (the Puigventós family, the car, the trip to the beach), the situation described contains numerical values that were defined to obtain certain results, so we cannot consider it like an authentic situation.
• Finally, and taking into account the two points raised above, this task cannot be considered as a modelling problem, which is why its solving cannot be carried out or explained in terms of a modelling cycle.

On this last point, the statement in Figure 19 is more consistent with a task to work on the ‘work mathematically’ sub-competence given a mathematical model and the data necessary for its use, in accordance with the position of [72] and her proposed classification on modelling tasks.

The two tutor professors pointed out these observations to the study subject during the first group reflection session. However, due to the work dynamics of the educational center in which he carried out his educational internship, the study subject could not modify his work guide, which had been previously reviewed and approved by his mentor teacher. Despite this situation, the study subject redesigned the wording of the task in the question (see Figure 20) for his MFP, taking into account the observations and suggestions made by the tutor professors.

Figure 20. Modelling task redesigned for the MFP. Translated from [67] (p. 79).

Figure 20. Modelling task redesigned for the MFP. Translated from [67] (p. 79).

The redesign of the task kept the context of the original proposal, that is, the fuel consumption of a car during a family trip to the beach. However, the modifications to the wording of the task brought it closer to a modelling problem than in the initially designed proposal:

• The situation now is more open and complex since, although the procedure is still determined by the applications of the formulas in Table 2, now it is the students who must search for the necessary data to be able to solve the task.
• The wording of the task now includes a more realistic and authentic situation since, derived from the previous point, the opening of the problem now allows the information to be adapted to the context of each student, with variables, such as the price of a liter of fuel in their environment, the data of consumption and mass of the family vehicle, the distance from their home to a beach of free choice, etc.
• Finally, taking into account that this task was redesigned for a new hypothetical implementation of the didactic unit, it could be considered as a problem, as long as the students have not previously experimented with the originally designed task. In the same way, the solving of the redesigned task can be solvable through a modelling cycle.

On this last point, Figure 21 presents a hypothetical solving (elaborated by the authors) of the redesigned modelling task, which is explained using the modelling cycle of [42] and using our own reference values for the variables involved in the ‘mathematical models’ in Table 2.

Figure 21. Solving of the redesigned modelling task from the cycle by [42]. Authors’ interpretation.

Figure 21. Solving of the redesigned modelling task from the cycle by [42]. Authors’ interpretation.

The redesigned modelling task is much closer to a modelling problem, both in its wording and in its solving, than the originally designed task. For this hypothetical solving, we considered a hotel in the center of the city of Figueras (Spain) as a starting point and Garvet Beach as a destination, tracing the route by vehicle with a map application. In turn, we obtained the data on fuel consumption per standard distance and vehicle mass based on the car of one of the authors.

However, when solving the task, we could identify certain inconsistencies with the real context in which the task is situated. Firstly, the city center of Figueras is located at a linear distance of 15 km from the coast, with multiple road connections to get there; therefore, would traffic jams for 3 h make sense? Secondly, in the event that the solver’s vehicle was equipped with the ‘start-stop’ technology, would the calculation of the fuel consumption at idle make sense? Finally, in the case that the solver’s vehicle was hybrid or electric, would mathematical models make sense to solve the problem?

Although these aspects reduce the authenticity of the redesigned modelling task, these questions could be raised in class in order to reflect on the importance of real context in modelling processes.

5. Discussion and Conclusions

In this section, we discuss the results presented in the previous section. In a first subsection we return to the arguments put forward by the study subject during the first group reflection session (see Section 4.1), which were analyzed from the pragma–dialectical perspective. In a second subsection, we return to the arguments obtained through the diagramming technique of the assessment of the didactic unit made by the study subject in his MFP. Finally, we conclude the results of the study, establishing relationships in the argumentation of both subsections. The analysis of the argumentation in the reflection sessions and in the assessment of the MFP allowed inferring some beliefs that constitute the study subject’s conception regarding the modelling process, some of which coincide with the characteristics that this type of task should have and others that are not compatible.

5.1. On the Group Reflection Sessions

During the group reflection sessions, some comments regarding the interaction with students were repeatedly mentioned by the study subject to justify the design and implementation of his didactic unit. These comments referred to the fact that, in his role as a teacher, he was the one who should guide the modelling process that his students would develop, which suggests a double reading. On one hand, we can infer that a belief of the study subject about working with modelling is that, when problems of this type are posed for the first time, it is the teacher who directly guides their students in solving the task. Although this position is not fully shared by the mathematical modelling research community, it can be justified, to a certain extent, in the duality of teaching this process, first, from an atomistic approach, to then work from a holistic approach (see [76]). In other words, ‘teaching to model to be able to model’. On the other hand, this possible belief conflicts with the methodology suggested in the literature to work on the modelling process in the classroom where, among other aspects, a balance between maximum student autonomy and minimal teacher intervention must be achieved (see a discussion on these ‘dilemmas’ in [77]).

From the third Argument (Figure 5) we can infer that a belief of the study subject about modelling is that this process can be used to develop a topic such as, in this case, functions. That is, the modelling process can be used ‘as a vehicle’ to introduce a mathematical object, in line with the position of [78]. In this particular argument, the study subject raised a proposal that he considered would allow him to work with modelling as a means to introduce functions. In propositions 3.1.1.1.–3.1 in the third Argument, the study subject stated that he wanted to address the topic of functions from elementary mathematical concepts (graphical representations, domain, range) to the equation of a line, and ended by presenting a situation where he considered that he would be using modelling. However, what he was actually doing was posing a situation of application of a mathematical model. By raising his motivation for naively including this process in his didactic unit, his tutor professors began to question him about this idealistic vision. In this sense, the third Argument represents a turning point within the group reflection session.

The tutor professors’ questions about how to work modelling with the students were mainly based on the fact that there were aspects of this idealistic vision that were not compatible with the characteristics of a modelling problem, nor with the conditions for developing this process in the classroom. In other words, the students had no previous modelling experience, they did not know the heuristics of a cycle, there was not enough time to teach it (only the ‘Món Matemàtic’ workshop), etc. That said, in the fourth (Figure 6) and fifth (Figure 7) Argument, the study subject justified that the cognitive level of his students and the restrictions of the context would not allow him to develop modelling tasks with all these necessary characteristics and conditions. Although these two arguments showed that the study subject became more aware of the limitations to carry out a modelling process during his didactic unit, this did not imply making substantial changes in the modelling tasks proposed in his work program but had repercussion only in the redesign proposed in his MFP and in the assessment of his didactic unit.

From the fourth Argument (Figure 6), we can infer that the idea of the study subject to work on modelling was in phases (atomistic approach) and did not seek to develop a complete modelling process (holistic approach). This was justified by the fact that, on one hand, it was the first time that the students faced this type of problem and, on the other hand, that the model was not so simple that they could construct it on their own. For these reasons, the study subject decided to give the mathematical models to the students, which were described in the work guide and explained their intervening variables. On this last aspect we can infer another belief of the study subject, that a modelling process necessarily implies the construction of new mathematical models, beyond the knowledge acquired by students up to a certain educational level. This idea, somewhat voluntarist on the part of the study subject, is not fully consistent with the definition of ‘mathematical model’ that is considered in the cycle proposed by [42], where this concept is understood as the set of mathematical objects that allow to explain the phenomenon to be modelled (see [39], p. 4) and that, not necessarily, imply the generation of new objects, since it is equally valid that those already known by the problem solvers are used. In the same way, if they are students who, on one hand, did not have previous experiences of working on modelling and, on the other hand, were studying a third grade of secondary education (students aged 14–15), this idea of the study subject would have no basis in the educational context in which he developed his internship.

Finally, his intention was reduced to the fact that, once the students understood the model, they would be able to apply it to situations that were adjusted to the model for its solving. In other words, the study subject taught his students to apply a function in different situations, through a diversification strategy, in order to work on a representative sample of problems with the same mathematical model. These results partially coincide with the findings of [29], as far as the modelling problems posed by teachers are reduced to statements to evaluate the students’ skills to register, through a symbolic expression, a mathematical relationship covered in a, more or less, realistic word problem.

From the fifth Argument (Figure 7), we infer that one of the initial beliefs that form the conception of modelling of the study subject is that it is not necessary for this type of problem to be open, which is inconsistent with the characteristics of a modelling problem (as described in Section 2.1).

Finally, we stress that, in his argumentation, the study subject used knowledge from the different types proposed by the DMKC model, namely epistemic (third and fourth Argument), cognitive (fourth and fifth Argument), and mediational (first and second Argument) knowledge.

5.2. On the Assessment of the Didactic Unit in the MFP

The diagramming of the assessment of the didactic unit carried out in the MFP, guided by the DSC, allowed us to relate the arguments in the study subject’s reflection with some elements of the modelling cycle; as well as identify some ideas, conceptions, or beliefs of AD regarding modelling that are (or are not) compatible with the characteristics of both a modelling problem and the work with this process.

In the diagramming of the assessment of the ‘Richness of process’ component (Figure 8) of the epistemic criterion, we were able to relate some propositions with the ‘mathematization’, ‘understanding/constructing’, ‘simplifying/structuring’, and ‘validating’ transitions that include the modelling cycle (see Figure 1, nos. 1, 2, 3, 6). However, we evidenced certain limited interpretations of the study subject about this process. On one hand, we were able to infer an overlap between the ‘mathematical modelling’ and ‘mathematical applications’ processes. On the other hand, his conceptualization of modelling gives a greater weight to mathematical aspects (‘model’ and ‘mathematical work’) than to the interpretation and validation of results with the content of the problem-situation posed, calling into question the closeness of this process with the «real world». This idea is reinforced in the diagramming of the ‘Prior knowledge’ component (Figure 10) of the cognitive criterion, where the study subject showed greater interest in the students’ prior knowledge about the mathematical object function than in their knowledge about the modelling process. As this last aspect was not considered by the study subject, we infer that his conception of modelling does not focus its interest on the transition between «real world» and «mathematics» in a bidirectional way.

Regarding the aspects consistent with the literature about modelling, some propositions of the diagramming of the assessment of the ‘Representativeness of the complexity of the mathematical object’ component (Figure 9) of the epistemic criterion, are considered as a sign that the study subject considered that, in a modelling process, the mathematical object (model) is determined by the context of the problem-situation. Regarding the assessment of the ‘High cognitive demand’ component (Figure 11) of the cognitive criterion, we were able to identify that the study subject, in some way, considered the following transitions in a modelling process, at least within his reflection (not so in the design of the task originally proposed): ‘understanding/constructing’, ‘working mathematically’, ‘interpreting’, and ‘validating’. Similarly, the study subject considered that the modelling process implies a high cognitive demand, due to the multiplicity of mathematical processes involved.

Finally, in his MFP, the study subject made explicit some changes that he had from the conclusions of the first group reflection session, which were reflected both in the assessment of his didactic unit and in his redesign proposal. On one hand, in the diagramming of the assessment of the ‘Student interaction’ component (Figure 12) of the interactional criterion, the study subject considered as important that the modelling process promotes interactions between students through group work. On the other hand, in the diagramming of the assessment of the ‘Didactic innovation’ component (Figure 18) of the ecological criterion, the study subject downplayed the restrictions that he had in his implementation phase, e.g., the impossibility of using a computer room to work on the modelling task using GeoGebra software, since its reformulation made him dispense with these limitations. Now, first, this is innovating didactically in his context, such as in the educational center where he undertook his internship, and second, it is innovating with support from the literature of the didactics of mathematics. That is, innovation is relative to the context. In addition to that, we must take into account that, in terms of [79], the implementation of modelling in regular mathematics lessons is not usual, due to different restrictions presented by the educational context, such as those that occurred in the institutions where the study subject carried out his educational internship.

Given that, at the time of preparing his MFP, the study subject already knew and used the DSC as a tool to guide his reflection, we can affirm that he shows knowledge of the meta didactic-mathematical dimension of the DMKC model. However, the detailed study of his argumentation also allowed inferring knowledge of the mathematical and didactic dimensions.

5.3. Conclusions

In relation to the first research question, regarding what argumentation a prospective teacher makes to justify the incorporation (or not) of mathematical modelling in his lessons, in Section 5, we described the arguments used by the study subject in two different phases.

In relation to the second research question, regarding what knowledge, values, beliefs, and guidelines for action are inferred in this argumentation, we can make several affirmations. In the first place, the detailed analysis of the arguments present in the study subject’s reflection evidences the use of the three dimensions of knowledge proposed by the DMKC model (mathematical, didactic, and meta didactic-mathematical dimensions), while knowledge of the six facets of didactic knowledge (epistemic, cognitive, interactional, mediational, affective, and ecological facets) appear. In the second place, with respect to the study subject’s beliefs, we were able to observe a change from his initial reflections to those contemplated in his MFP. Initially, he considered that it was enough to translate the wording of a task from natural to mathematical language to talk about modelling, while, in his final reflection, he considered that there are certain necessary characteristics to be able to consider a modelling problem as such. This last belief disposed the study subject to redesign the originally proposed task so that, in the improvement proposal of his MFP, it meets many of these characteristics.

An additional conclusion is that the study subject showed both good knowledge and competent use of the DSC construct. In his initial proposal, the study subject had given great importance to epistemic suitability, since he considered incorporating modelling in his didactic unit on the teaching of functions, but without taking into account the other criteria. Finally, in the reflection of his MFP, the study subject assigned a determining weight to different DSC, even though the planned modelling task could not be implemented. In summary, his reflection organized with the DSC, on one hand, improves epistemic suitability by ensuring that the redesigned modelling task meets the characteristics of a modelling problem and, on the other hand, considers the rest of the criteria in a more balanced way.

Our last conclusion is that, based on the analysis of the group reflection sessions and the study subject’s MFP, we can suppose that AD’s education as an engineer influenced part of his beliefs about modelling. However, we need a deeper analysis to fully affirm this conclusion, with a study that includes, for instance, interviews or questionnaires with the study subject that focus on this specific aspect. In any case, there are some elements that partially reinforce this conclusion, e.g., the fact that AD has reduced the modelling process to the application of a mathematical model in a specific situation, consistent with the view of [80] on applied mathematics; in the design of a task contextualized in a problem from physics, where formulas, considered as ‘mathematical models’, were included for its analysis and solving; and, finally, that the interest of his tasks was that students understand and apply such formulas to a specific situation.

The results of this study may be useful for the master’s program in which we carried out this research, in the sense that a DSC guideline could be developed with more specific indicators to determine what will be understood by a modelling process or reconsider the way in which the incorporation of modelling is taught for secondary and baccalaureate education levels within the submodule dedicated to the teaching of such process. More specifically, the study subject, who had completed this submodule before designing his didactic unit, had the intention of working on modelling, but he was not aware that his students should have knowledge about the heuristics of the modelling process or, at least, having had previous modelling experiences, either with the complete cycle (holistic approach) or with some of its phases and transitions (atomistic approach). Because the study subject did not fully handle a modelling cycle either, what he ended up doing was a proposal to work on some of its elements (above all, ‘mathematization’ and ‘mathematical work’) and say that he worked with modelling.

Finally, this study opens a research line to infer teachers’ knowledge and beliefs from the argumentation made in their reflection, which differs from what is more common in this plane, such as the application of questionnaires or interviews, since we incorporate a new way of analyzing the teachers’ argumentation through pragma–dialectics and diagramming.