Dynamics of RK Iteration and Basic Family of Iterations for Polynomiography
Abstract
1. Introduction
2. Basic Family of Iterations and Other Iterative Methods
3. Escape Criterion Results
4. Polynomiograph Generation
4.1. Algorithms
| Algorithm 1 RK algorithm for generating polynomiography. |
Input: Choose
While:, compute
Stopping criterion:. Output: Colour c of |
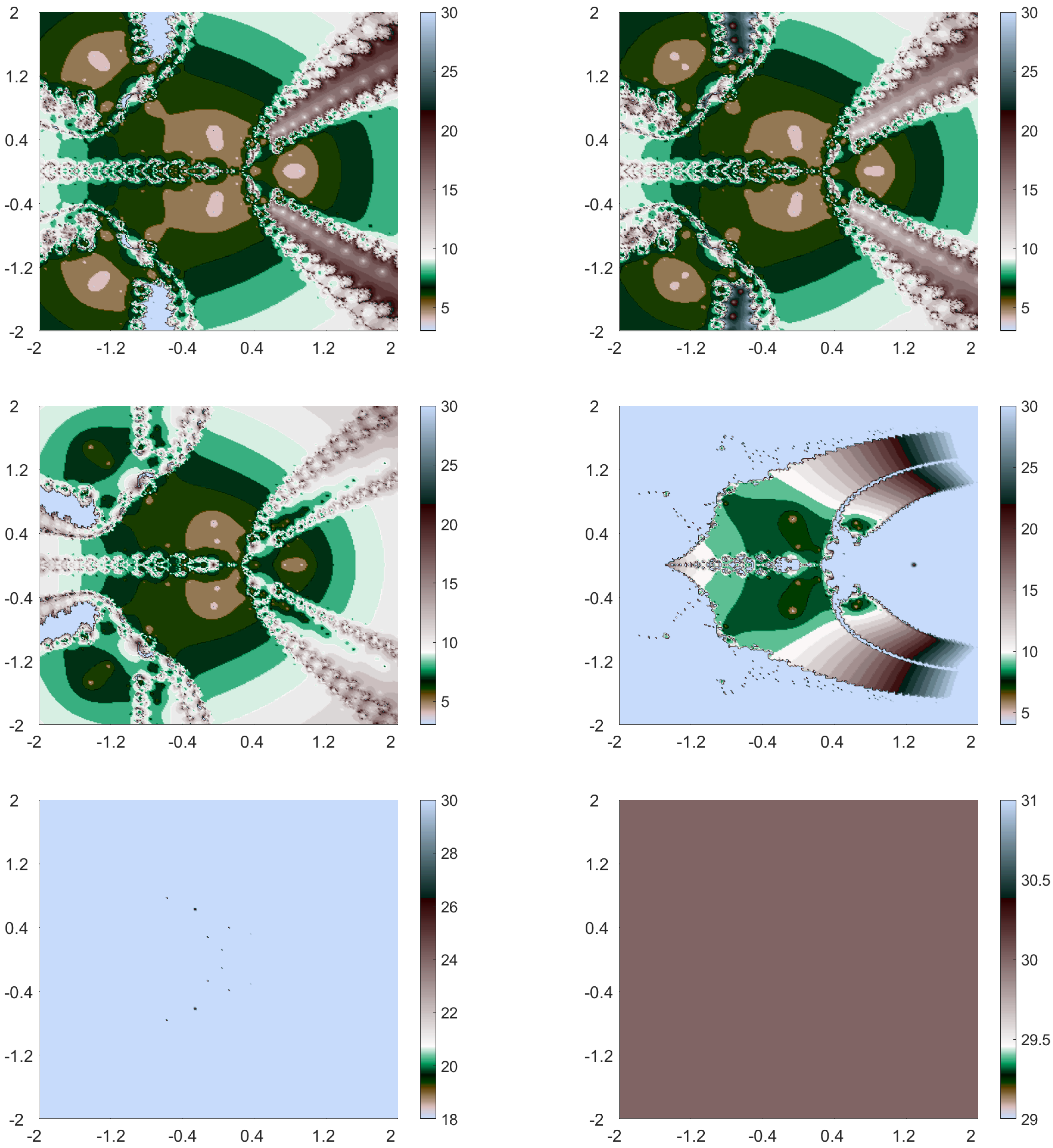
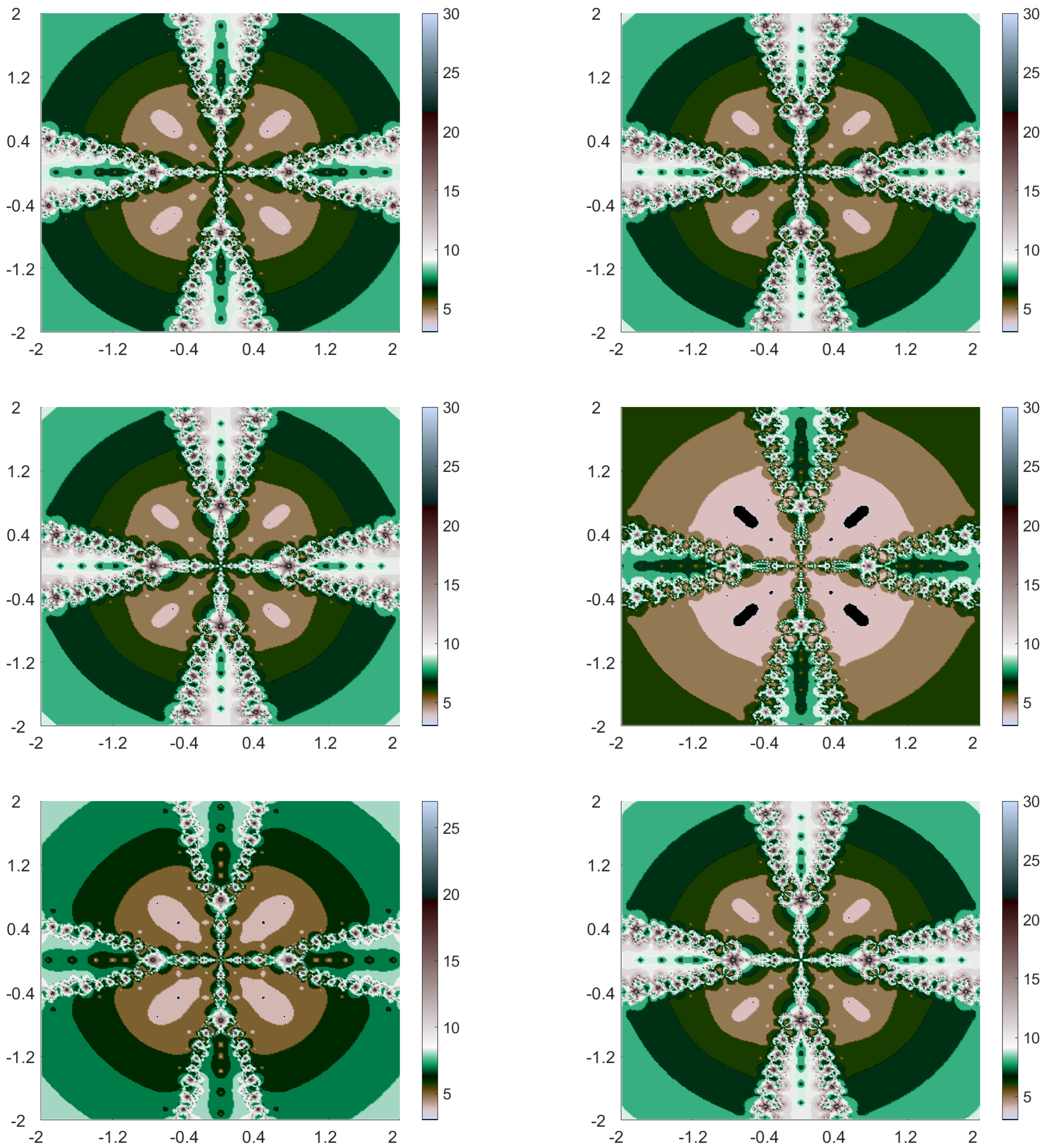
4.2. Visualisation of Polynomiographs
- Case I:
- Case II:
- Case III:
- Case IV:
- Case V:
- Case VI:
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalantari, B. Method of Creating Graphical Works Based on Polynomials. U.S. Patent 6,894,705, 17 May 2005. [Google Scholar]
- Kalantari, B. Polynomial Root-Finding and Polynomiography; World Scientific: Singapore, 2009. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: New York, NY, USA, 1983. [Google Scholar]
- Kalantari, B. Polynomiography: From the fundamental theorem of Algebra to art. Leonardo 2005, 38, 233–238. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 9th ed.; Brooks/Cole: Boston, MA, USA, 2011. [Google Scholar]
- Cayley, A. The Newton-Fourier imaginary problem. Am. J. Math. 1879, 2, 97. [Google Scholar] [CrossRef]
- Ardelean, G. Comparison between iterative methods by using the basins of attraction. Appl. Math. Comput. 2011, 218, 88–95. [Google Scholar] [CrossRef]
- Lotfi, T.; Sharifi, S.; Salimi, M.; Siegmund, S. A new class of three-point methods with optimal convergence order eight and its dynamics. Numer. Algorithms 2015, 68, 261–288. [Google Scholar] [CrossRef]
- Lotfi, T.; Soleymani, F.; Sharifi, S.; Shateyi, S.; Haghani, K. Multipoint iterative methods for finding all the simple zeros in an interval. J. Appl. Math. 2014, 2014, 601205. [Google Scholar] [CrossRef][Green Version]
- Cordero, A.; Torregrosa, J.R.; Vassileva, M.P. Three-step iterative methods with optimal eight-order convergence. J. Comput. Appl. Math. 2011, 235, 3189–3194. [Google Scholar] [CrossRef]
- Jolaoso, L.O.; Khan, S.H. Some Escape Time Results for General Complex Polynomials and Biomorphs Generation by a New Iteration Process. Mathematics 2020, 8, 2172. [Google Scholar] [CrossRef]
- Gdawiec, K.; Kotarski, W.; Lisowski, A. Polynomiography based on the nonstandard Newton-like root finding methods. Abstr. Appl. Anal. 2015, 2015, 797594. [Google Scholar] [CrossRef]
- Kang, S.M.; Alsulami, H.H.; Rafiq, A.; Shahid, A.A. S-iteration scheme and polynomiography. J. Nonlinear Sci. Appl. 2015, 8, 617–627. [Google Scholar] [CrossRef]
- Gdawiec, K.; Kotarski, W. Polynomiography for the polynomial infinity norm via Kalantari’s formula and nonstandard iterations. Appl. Math. Comput. 2017, 307, 17–30. [Google Scholar] [CrossRef]
- Rafiq, A.; Tanveer, M.; Nazeer, W.; Kang, M. Polynomiography via modified Jungck, modified Jungck Mann and modified Jungck Ishikawa iteration scheme. Panam. Am. Math. J. 2014, 24, 66–95. [Google Scholar]
- Gdawiec, K.; Shahid, A.A.; Nazeer, W. Higher order methods of the Basic Family of Iterations via S-iteration with s-convexity. Mediterr. J. Math. 2020, 17, 43. [Google Scholar] [CrossRef]
- Ritika, S.H. Khan, Convergence of RK-iterative process for generalized nonexpansive mapping in CAT(0) spaces. Asian-Eur. J. Math. 2019, 12, 13. [Google Scholar] [CrossRef]
- Kalantari, B. Generalization of Taylor’s theorem and Newton’s method via a new family of determinantal interpolation formulas and its applications. J. Comput. Appl. Math. 2000, 126, 287–318. [Google Scholar] [CrossRef]
- Kalantari, B. On the order of convergence of a determinantal family of rootfinding methods. BIT Numer. Math. 1999, 39, 96–109. [Google Scholar] [CrossRef]
- Kalantari, B. Alternating sign matrices and Polynomiography. Electr. J. Comb. 2011, 18, P24. [Google Scholar] [CrossRef]
- Kalantari, B.; Gerlach, J. Newton’s method and generation of a determinantal family of iteration functions. J. Comput. Appl. Math. 2000, 116, 195–200. [Google Scholar] [CrossRef]
- Banach, S. Sur les opérations dan les ensembles abstracts ey lear applications aux équations integrales. Fund. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Mann, W. Mean value methods in iteration. Proc. Am. Math. Soc. 1953, 4, 506–510. [Google Scholar] [CrossRef]
- Ishikawa, S. Fixed points by a new iteration method. Proc. Am. Math. Soc. 1974, 44, 147–150. [Google Scholar] [CrossRef]
- Khan, S.H. A Picard-Mann hybrid iterative process. Fixed Point Theory Appl. 2013, 2013, 69. [Google Scholar] [CrossRef]
- Agarwal, R.P.; O’Regan, D.; Sahu, D.R. Iterative construction of fixed points of nearly asymptotically nonexpansive mappings. J. Nonlinear Convex Anal. 2007, 8, 61–79. [Google Scholar]
- Abbas, M.; Iqbal, H.; Sen, M.D.L. Generation of Julia and Madelbrot sets via fixed points. Symmetry 2020, 12, 86. [Google Scholar] [CrossRef]
- Nazeer, W.; Kang, S.M.; Tanveer, M.; Shahid, A.A. Fixed point results in the generation of Julia and Mandelbrot sets. J. Inequalities Appl. 2015, 2015, 298. [Google Scholar] [CrossRef]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing: Principles, Algorithms and Applications, 4th ed.; Pearson: Bengaluru, India, 2007. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jolaoso, L.O.; Khan, S.H.; Aremu, K.O. Dynamics of RK Iteration and Basic Family of Iterations for Polynomiography. Mathematics 2022, 10, 3324. https://doi.org/10.3390/math10183324
Jolaoso LO, Khan SH, Aremu KO. Dynamics of RK Iteration and Basic Family of Iterations for Polynomiography. Mathematics. 2022; 10(18):3324. https://doi.org/10.3390/math10183324
Chicago/Turabian StyleJolaoso, Lateef Olakunle, Safeer Hussain Khan, and Kazeem Olalekan Aremu. 2022. "Dynamics of RK Iteration and Basic Family of Iterations for Polynomiography" Mathematics 10, no. 18: 3324. https://doi.org/10.3390/math10183324
APA StyleJolaoso, L. O., Khan, S. H., & Aremu, K. O. (2022). Dynamics of RK Iteration and Basic Family of Iterations for Polynomiography. Mathematics, 10(18), 3324. https://doi.org/10.3390/math10183324





