Abstract
Interdependent decisionmaking of individuals in social systems can be modelled by games played on complex networks. Players in such systems have bounded rationality, which influences the computation of equilibrium solutions. It has been shown that the ‘system rationality’, which indicates the overall rationality of a network of players, may play a key role in the emergence of scale-free or core-periphery topologies in real-world networks. In this work, we identify optimal topologies and mixing patterns of players which can maximise system rationality. Based on simulation results, we show that irrespective of the placement of nodes with higher rationality, it is the disassortative mixing of node rationality that helps to maximize system rationality in a population. In other words, the findings of this work indicate that the overall rationality of a population may improve when more players with non-similar individual rationality levels interact with each other. We identify particular topologies such as the core-periphery topology, which facilitates the optimisation of system rationality. The findings presented in this work may have useful interpretations and applications in socio-economic systems for maximizing the utility of interactions in a population of strategic players.
MSC:
91D30; 05C82
1. Introduction
Complex networks are increasingly used to model and represent large-scale systems which consist of a finite (and typically small) number of element types and connection types [1,2,3]. When represented using a complex network, these elements and connections are termed nodes and links, respectively. While the structure of the system can be represented by the topology of the complex network, there is a need to model the dynamics of the system and the interplay between its elements, including in decision making. Game theory is the study of interdependent decisionmaking in a system, where the best decision for one element (termed an agent or player) depends on the decisions made by other elements in the system [4,5,6,7,8]. Therefore, networked game theory, where games are played between players/nodes in a system modelled as a complex network, is increasingly used to model decisionmaking in large-scale systems [9,10,11,12].
The concept of ‘rationality’ in game theory denotes the ability of a player to make the best possible decision in a given situation based on available information about payoffs [4,5,7]. Classical game theory assumes that all players are perfectly rational, and the concept of Nash equilibrium is based on this assumption [6,8]. However, this assumption has been criticised [13,14] on the basis that in real-world situations players are seldom perfectly rational. The concept of ‘bounded rationality’ has been introduced to address this issue [13,15,16], and has been used to refer to a broad range of descriptive, normative, and prescriptive behaviors that deviate from the assumptions of perfect rationality. Several bounded rationality models have been proposed whereby a finite rationality parameter is assigned to each player [4,5,17]. The resultant bounded rationality distribution is superimposed on the underlying network topology, and it has been shown that the resultant decision making behaviour of the system is dependent on both the bounded rationality distribution itself and on the topological placement of nodes which are relatively more or less rational [17,18]. For example, a system with a certain bounded rationality distribution where the more rational nodes are the ‘hubs’ of that system may display different decisionmaking behaviour from another system with the same topology and the same bounded rationality distribution where the less rational nodes are at the hub. Therefore, the concept of ‘system rationality’, which alludes to the level of rational decisionmaking behaviour in a system, which is placement-dependent, is distinct from the ‘average rationality’ of that system, which is merely the average of the rationality parameters of all players in that system and is thus independent of topology and placement [17,19]. Therefore, system rationality can be optimised by rewiring a network even when the average rationality of the nodes in the network remains the same. This characteristic is important because of the implication that a socio-ecological networked system could be made to behave more rationally simply by rewiring it or rearranging its players, even when the average rationality of the players or even the rationality distribution itself cannot be changed.
It is beneficial for topological design of networks to identify certain topologies which aid in optimising system rationality while the average rationality or the rationality distribution itself remains constrained and cannot be changed. A set of interesting questions therefore arise: (1) Is there an optimal topology which maximises system rationality when the average rationality of the network is constrained, regardless of the relative placement of more and less rational players in the network in terms of its topology? (2) If there is such a topology, what is it? (3) If the optimisation of system rationality is dependent on both the topology of the network and the topological placement of players with respect to their rationality, what placement strategy maximises the system rationality when average rationality and topology are both constrained? (4) If placement does indeed matter, is there a network topology which maximises the ‘potential’ system rationality of a network, subject to re-arranging the placement of players? (5) What is the effect of the rationality distribution of players on the overall system rationality? We attempt to answer these questions in this paper.
In short, this paper addresses the optimisation of system rationality in a networked system by varying topology and placement while rationality distribution is constrained. In particular, we show that such an optimisation can be achieved by optimising disassortative mixing, either topologically or by placement (by maximising ‘scalar disassortativity’ based on node rationality) where topology is constrained. Such optimisation is important in systems where the attributes of the underlying population of players cannot be changed yet the players can be placed or connected in ways which aid the performance of the system. Examples of this include organisational hierarchies [20,21,22,23], military hierarchies [24,25,26,27], peer support networks [28,29,30], and other social networks that can be topologically designed for a given set of people.
The rest of this paper is organised as follows: in Section 2, we provide the background, discuss the relevant literature that motivated this study, and set out the problem addressed in this paper in more technical detail. In Section 3, we define the key concepts that are used in our analysis. In Section 4 we describe our simulation experiments and their methodology, while in Section 5, we describe the results. Finally, in Section 6 we discuss our results, summarise our conclusions, and point out directions for future work.
2. Background
Network science attempts to model and predict the structure and operations of entities that are connected over non-trivial topologies [1,2]. It has applications in myriad fields such as epidemiology, social network analysis, and biology.
Autonomous agents distributed over a topology may interact with their neighbors in making strategic decisions. These strategic interactions may be modelled as strategic games in game theory, where each agent acts in a self-interested manner to maximize its payoff. Strategic games that are played over a population of players that interact over a topology can be used to model biological and socio-economic systems. Evolutionary game theory utilizes such networked games to model the evolution of strategies over a network of players [31,32].
The effect of assortative mixing on the evolution of cooperation in networked games has been explored previously [11,33]. It has been shown that in networked prisoner’s dilemma and public goods games, degree-based disassortativity facilitates cooperation among players [11]. This is due to the tendency of cooperative hubs to be protected from other defective hubs in a disassortative network. However, the existing work on the evolution of cooperation [34,35,36] assumes that all nodes have optimal rationality in a network of players. However, real-world actors have rationality that is bounded (limited) by many factors.
2.1. Bounded Rationality
The Nash Equilibrium is one of the cornerstones of game theory; it theorizes that in every strategic interaction, there exist one or more equilibria which no player would benefit by deviating from [37]. However, most real-world strategic interactions deviate from the Nash equilibrium, as the Nash equilibrium assumes perfect or optimal rationality. Real-world players possess non-optimal or bounded rationality. Real-world players may have limited information, time, and cognitive capacity to choose a strategy [38]. In the quantal response equilibrium (QRE) model [39], this bounded rationality of players is quantified using a rationality parameter. In the QRE model, denotes the individual rationality of player i. The rationality parameter makes it possible to model player i’s level of bounded rationality. When , the quantal response equilibrium, converges to the corresponding Nash equilibrium, and as , the player operates in a totally random, that is, irrational, manner [40]. Thus, the logit function used in the QRE model provides a convenient mechanism to derive the mixed strategy equilibrium probability distributions of strategic agents that may possess non-optimal rationality values.
Even though there have been numerous attempts to quantify the bounded rationality of players, they have predominantly focused on quantifying bounded rationality as a population-specific uniform value that is applied to all players that operate in a given strategic decision making environment in a generic manner. For instance, Wolpert [41] proposed a method to analytically quantify the bounded rationality of a given player by solving the Maxent or maximum entropy Lagrangians by using the Boltzman distribution to derive the mixed strategy probability distribution of a human agent. However, both empirical evidence and theoretical frameworks such as the cognitive hierarchical model [42] strongly suggest that the bounded and non-optimal rationality of agents in a given population is typically distributed in a heterogeneous fashion and not as a population-specific uniform value. Numerous reasons, including the variability of the cognitive capacity of nodes and the varying degrees of information available to nodes due to the different levels of social interaction, may lead to this heterogeneity in bounded rationality [17]. Thus, it is necessary to account for the heterogeneity of the bounded rationality of players in order to better fit game-theoretical models to real-world strategic interactions
There have been numerous prior attempts made to quantify the heterogeneous rationality of players using the quantal response equilibrium model [43,44]. Examples of such models include the heterogeneous QRE model and the Truncated QRE model [43]. Furthermore, the cognitive hierarchical model [42] that operates under the same goal and can be considered as a special case of Truncated QRE model. However, such models operate by varying the player rationality in such a way that it fits with the empirical results in a given setting. The key limitation of using such an approach is that the rationality parameter is treated an arbitrary parameter that is not based on any measurable real-world attribute of an agent. Even though this may improve the adaptability of the rationality parameter, it limits the real-world applicability of such models in predicting the outcome of interactions among strategic players with non-optimal rationality.
Similarly, there has been recent interest in the effect of topology on the bounded rationality of players in a network and vice versa. For instance, it has been shown that certain topologies such as scale-free topology and core–periphery topology facilitate more rational interactions compared to other topologies. Kasthurirathna et al. [17] have shown that scale-free topologies emerge based on the premise that the degree of nodes infer the rationality values and the rationality of a node is a defined as a function of degree. Roman and Brede [45] have shown that, under the same assumptions, core–periphery topologies best facilitate more rational interactions compared to other topologies. Gunewardena et al. [46] further extended this approach to infer the rationality of nodes based on incoming information flows.
The underlying assumption of topology-based or information flow-based rationality is that the information availability at a node that is used to make more rational decisions can be inferred by the centrality of a node or the cumulative directed incoming information flow towards a node. In both of these scenarios, the cognitive capacity of nodes and the time available to compute the optimal decisions are assumed to be homogeneous.
2.2. Modelling Bounded Rationality Distributions
Several recent studies have considered how a rationality distribution could be modelled with respect to a given network topology [17,19,45,47]. The number of neighbours that an agent in a population has, which in network analysis is commonly referred to as the degree of a node, may indicate the amount of social interactions that the agent may have within the population of concern. However, there may be other factors that affect the level of social interaction, which are known as the ‘tie strength’ attributes. Examples of such attributes include the volume of information exchanged or even the frequency of interactions between a given pair of players. Moreover, there can be either a linear or a non-linear correlation between the social interaction an agent has and the agent’s bounded rationality. Recent studies have attempted to model such correlations [17,19] by quantifying the bounded rationality of an agent based on its weighted degree (or degree, in the case of an unweighted network), as shown in Equation (1):
Here, is the bounded rationality of an agent i and r is referred to as the ‘network rationality parameter’, which is a property of the network or the population that captures the sensitivity of the topological features to the rationality of an agent.
The average value of all rationality parameters can be defined as the average rationality of a given population, , where N is the number of people in the population. This average rationality of a given population is proportional to the network rationality parameter r. This is due to the fact that any deviation in r causes a corresponding shift in the bounded rationality value of an agent i in the population. Furthermore, represents the weight of the link connecting an agent i with each neighbour j, where k is the number of neighbours that an agent i has. Accordingly, an agent may operate completely randomly either if the network rationality parameter is set to or if the degree of an agent is zero. On the other hand, interactions may reach Nash equilibrium if the network rationality parameter or the (weighted) degrees of respective nodes become very large.
2.3. Prisoner’s Dilemma Game
The prisoner’s dilemma game [48] is one of the games most commonly used in networked game theory to model social interactions. In this work, we use the prisoner’s dilemma game to simulate the network game model and compute equilibrium solutions, although other games such as Stag Hunt could be equally appropriate. Ultimately, though, Nash equilibrium and QRE can be reached using any of the well known games, and it is thus immaterial which game is used in the simulation experiments.
The prisoner’s dilemma game payoff matrix denoted in Figure 1 is used in this work for modeling social interactions among neighboring players. In the prisoner’s dilemma game, the payoffs satisfy the inequality conditions .
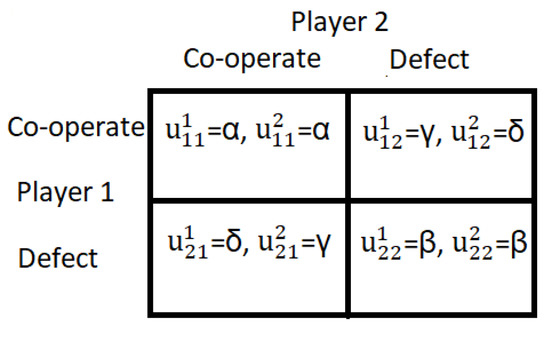
Figure 1.
Payoff matrix of the two-player prisoner’s dilemma game where .
2.4. Topologies That Optimise System Rationality
Having discussed the extensive background necessary to set up the premise of this work, we can now elaborate the specific problem that we aim to address, that is, the identification of topologies which optimise the topology-dependent system rationality even when the average rationality of the system, which is independent of topology, is constrained. The ‘system rationality’ of a population of players is a concept which alludes to the level of rational decision making behavior in a population where strategic games operate in comparison to the optimal rationality assumed in Nash equilibrium. In networked systems with bounded rationality distributions, ‘system rationality’ is a concept distinct from the average rationality of the networked system, and alludes to the fact that two networked systems with the same average rationality may have different ‘system rationalities’ based on where the more rational actors are placed in the network topology.
Recent work by Kasthurirathna et al. [17] quantified the ‘system rationality’ of a networked system as the negative average of the Jensen–Shannon divergence between the Nash equilibria and the Quantal Response Equilibria (QRE) of all games played in a single iteration of a networked game. The rationale for this definition was that the more a population diverges from Nash equilibria, the more irrational it is on average. Therefore, perfect system rationality is indicated by a value of zero and the more negative the system rationality value is, the more irrational the system becomes. Kasthururathna et al. [17] demonstrated that when a population of random networks with the same and constrained average rationality goes through an evolutionary process where interactions with higher ‘system rationality’ are preferentially selected, scale-free networks emerge as a result. Therefore, they postulated that evolutionary pressure to increase the ‘system rationality’ may have been a reason why scale-free networks emerged in socio-ecological systems.
It is important to note that while scale-free networks emerge from random networks when evolutionary pressure is applied to optimise system rationality, this does not imply that scale-free topology is the optimal topology to maximise system rationality. Roman and Brede [45] argued that core–periphery (or hub-and-spoke) network structures [49] are optimal for system rationality maximisation. Meanwhile, Law et al. [18] have argued that the public utility of a networked system depends on the placement of the players, and that scale-freeness and disassortativity in networks are positively correlated with public utility. However, their observation was in reference to public utility, not system rationality, and although these could be correlated, they are distinct concepts. Therefore, it is clear that a principled approach is necessary to identify optimal network topologies which maximise system rationality, particularly when the average rationality of the network is constrained. Furthermore, it is important to recognise that a placement protocol (for example, a procedure which places players employing a particular game-theoretic strategy at hubs or more central nodes and players employing another strategy at more peripheral nodes in the corresponding network) which optimises system rationality can be identified even when the topology itself is constrained. Essentially, we need to construct a dual-objective optimisation problem whereby one objective is to optimise the topology for maximum system rationality while the other is to find the placement strategy for that topology which further optimises system rationality. This is the approach followed in this paper to address the question of optimising system rationality.
The existing works on this topic are predominantly based on the presumption that the degree of nodes is positively correlated with node rationality [17,19]. It is based on this premise that scale-free and core–periphery network topologies have been argued to maximize system rationality and public utility, respectively. Extending from this body of work, we argue here that it is the (dis)assortative mixing of node rationality that plays a prominent role in determining system rationality, not necessarily the placement of the nodes with higher rationality.
In order to support this argument, we observe how the assortative mixing of the bounded rationality of players affects the system rationality. Thereby, we show that it is immaterial whether the ‘smartest’ or more rational players are assigned to the hubs (as in Kasthurirathna et al. [17] and Roman and Brede [45]) or the least rational players, as long as the node rationality-based scalar disassortativity of the network is maximised. We show that if topologies can be rewired, then networks with the highest disassortativity may optimise the system rationality; thus, the results obtained by Roman and Brede [45] in terms of core–periphery configurations represent a special case of this. Our results clearly demonstrate the intricacies of the relationship between network topology, topological placement of boundedly rational players, and system rationality. We demonstrate that a hub-and-spoke topology (or any topology which maximises disassortativity) is not guaranteed to result in the maximisation of system rationality if the placement of players is not one which maximises scalar disassortativity.
3. Definitions
Here, we present the technical definitions of concepts which are used in our experiments.
3.1. The Quantal Response Equilibrium
The logit function provided in Equation (2) can be used to compute the Quantal Response equilibrium [50,51]:
Here, is the probability of player i adopting the strategy j, is the expected utility of an agent i in choosing strategy j provided that other agents adopt their respective strategies according to the probability distribution , the parameter represents the total number of strategies that player i can choose from, and the value of the rationality parameter may vary from zero to positive infinity.
In a two-player prisoner’s dilemma game, we can apply the QRE model to derive Equations (3) and (4) from Equation (2) to represent the probabilities based on which the two agents may adopt cooperation as their strategy based on their mixed strategy quantal response equilibrium.
In this work, without loss of generality, we choose the following utility values for the Prisoner’s dilemma game: , , , .
That is, (note that these values satisfy the constraint , as mentioned earlier).
Here, and represent the probabilities which agent 1 and 2 may use to cooperate, respectively. Clearly, the respective probabilities of defection are and . Furthermore, and denote the rationality values of players 1 and 2, respectively. In this work, these values are derived as defined in Equation (1). The resulting probability distribution represents the QRE for the particular pair of agents engaging in a strategic interaction.
The Nash equilibrium for this game is when both players defect, where , and , .
3.2. The Jensen–Shannon Divergence
The Kullback–Leibler (KL) divergence [52], otherwise referred to as the relative entropy, is commonly used to measure the divergence between two probability distributions. Given two probability distributions P and Q, their Kullback–Leibler (KL) divergence is provided by
where and represent the two probability distributions of concern, respectively. It should be noted that the KL divergence is an asymmetric measure which has directionality, and the divergence from P to Q is thus not equal to the divergence from Q to P.
A symmetric measure that is derived using the directional KL divergence is the Jensen–Shannon Divergence [53]. Equation (8) defines Jensen–Shannon Divergence. Here, is the probability distribution derived by averaging the two probability distributions P and Q.
In this work, we use the Jensen–Shannon divergence to quantify the divergence of a QRE-based equilibrium from the equivalent Nash equilibrium of a given interaction. Thus, the negative of the Jensen–Shannon divergence is used in the calculation of ‘system rationality’, provided that the higher the divergence from Nash equilibria, the lower the system rationality. Jensen–Shannon divergence has been applied in previous works for the same purpose [17,45].
3.3. System Rationality
We employ the average Jensen–Shannon divergence between the Quantal Response and Nash equilibria to quantify the system rationality [17]. The justification for this is the premise that the more self-interested and rational the agents are, the less the divergence from the corresponding Nash equilibrium. The average is obtained by averaging across all links, as each link represents a pair of players between whom a Nash equilibrium and a Quantal Response Equilibrium can both be computed. Thus, in order to obtain a singular population-specific ‘system rationality’ value for a network of players that interact based on a given topology, the averaged value of the Jensen–Shannon divergence values of all interactions over all the links of the network is measured. The system rationality is provided by Equation (9), which is inversely proportional to the averaged divergence of the interactions from the corresponding Nash equilibria. In Equation (9), denotes the probability distribution corresponding to the Nash equilibrium at link k, denotes the probability distribution of the quantal response equilibrium at link k, and M denotes the number of links in the given network.
3.4. Average Rationality
The average rationality of a network is the average of the rationality parameters of all nodes in the population. The average rationality is independent of topology or mixing patterns, and depends only on the bounded rationality distribution.
The system rationality, which is the average Jensen–Shannon divergence as defined by Equation (9), is different from the average rationality . The quantity denotes the average of the heterogeneous rationality values assigned to each agent. However, two populations with the same may have different system rationality values, as it is possible to have more than one topology with the same degree distribution, and the rationality parameter of each node in this work is a function of its degree.
3.5. Assortativity and Scalar Assortativity
Assortativity measures the tendency of nodes to connect with other nodes that are similar to them based on a particular attribute of a given network. Degree assortativity, which is commonly referred to as the assortativity of a network, is the Pearson correlation [54,55,56] between the expected degree distribution and the joint degree distribution in a given network. The expected degree distribution is the probability distribution of traversing the links of the network and finding nodes with degree k at the end of the links. On the other hand, the joint degree distribution represents the probability distribution of a link connecting a node with degree j and a node with degree k. The normalized Pearson coefficient of and provides us with the assortativity coefficient for an undirected network. Assortativity has been widely studied in networks from several domains, including social networks and biological networks [56,57].
The degree assortativity coefficient is denoted by
where and are defined as mentioned above and and are respectively the expected value or mean and the standard deviation of the excess degree distribution . If a network has optimal assortativity, that is, all nodes mix with other nodes with exactly the same degree, then . If the network has zero assortativity, that is, if , then node degree has no correlation with the mixing of nodes and degree-based mixing is thus entirely random. If a network is perfectly disassortative (), this implies that all nodes are linked to other nodes with extremely different degrees. A good example of a perfectly disassortative network is a star network. In general, complex networks with star ‘motifs’ in them, such as core–periphery networks [45], are highly (although not perfectly) disassortative.
In addition, assortativity can be quantified based on any particular scalar attribute of the node. For instance, in a social network the assortativity can be measured using scalar attributes such as age, income, etc. Assortativity measured based on a scalar attribute, which is referred to as‘scalar-assortativity’, is provided by [55]:
where and are the fraction of each type of end of a link that is attached to node of type j and node of type k. For undirected networks, where there is no specific ‘source’ or ‘target’ node, ; likewise, is the proportion of links which have a node of type j as the source and a node of type k as the target. Again, in undirected networks .
Both degree and scalar assortativity can be used to gain insight into network structure that may not be apparent in the degree distribution.
In this work, we use the bounded rationality parameter of each player as the scalar attribute in order to compute the node rationality-based scalar assortativity of a network. This enables us to observe how the assortative mixing of bounded rationality affects the system rationality of a networked population of players.
4. Methodology
In this work, we used Erdős–Rényi random networks [2] of nodes and links, assigning bounded rationality parameter values based on the distribution functions described in the next subsection. The size of the networks was comparable to similar simulations in previous work [17,45], however, the results, as we explain, are independent of the network size. We fixed both the minimum degree and the number of connected components of the network as one, ensuring that there were no isolated nodes and the network was fully connected. The choice of Erdős–Rényi random networks is deliberate, as we wanted to begin the simulation with a completely random topology from which the evolution of particular features such as scale-freeness, could be studied. Furthermore, the optimisation methods we employed, which are described in the following subsections, are based on rewiring, and random networks provide the most freedom to undertake preferential rewiring based on the properties that we wished to study.
Our simulations used undirected networks and all of thegames were pairwise symmetric two-player prisoner’s dilemma games. Scalar assortativity in this work is always calculated based on node rationality parameters as the ‘scalar’ value.
Bounded Rationality Distributions
In this work, we use two distinct approaches for modelling the rationality values of players in a network: (1) assigning rationality values in such a way that they are positively correlated with the node degree; (2) assigning rationality values in such a way that they are negatively correlated with the node degree. Using these two approaches, we observed the effect of assortative mixing patterns of node rationality on system rationality.
Case 1: Node Rationality assigned to be positively correlated with Node Degree
where is the degree of node i.
Case 2: Node Rationality assigned to be negatively correlated with Node Degree
where is the degree of node i.
In our experiments, the quantity r which denotes the network rationality parameter was set to . This value was selected in order to obtain a broad distribution of rationality values based on experimental results conducted using the same payoff values of the prisoner’s dilemma game as reported in our previous work [17].
Based on each of the functions provided in Equations (12) and (13), the bounded rationality of each node was computed in the corresponding random network. Then, under each rationality model, pairs of links were iteratively selected randomly and rewired to check whether the resulting interactions improved the system rationality of the network. In each iteration, if the system rationality improved after the rewiring process then the new pair of links was preserved. If rewiring did not improve the system rationality, it was reverted and the previous pair of links was re-established. This method of optimizing the system rationality was inspired by simulated annealing optimization technique [58] as well as the Xulvi–Brunet–Sokolov algorithm [59] for changing assortative mixing by rewiring, and has previously been used to observe the topological evolution when system rationality is incrementally improved [17]. We opted for this type of iterative optimization technique because it allowed us to incrementally improve the system rationality while observing the evolving topological properties of the corresponding network.
After each iteration, the bounded rationality of each node was recalculated based on the functions provided in Equations (12) or (13), depending on the scenario being tested. This process was repeated for 2000 iterations until the system rationality values were stabilized, and each intermediate network was stored to measure their network properties.
The scale-free exponent [2,3], scale-free correlation [2,3], scalar assortativity, and system rationality of each intermediate network were computed at each iteration for the scenarios where the node rationality was assigned to be positively (Equation (12)) and negatively (Equation (13)) correlated with the node degree. The evolution of the scale-free exponent and scale-free correlation can provide an indication of the evolution of the topology throughout the rewiring process used to improve the system rationality. In addition, system rationality and scalar assortavitity based on the node rationality were computed in each intermediate network. The variation of scalar assortativity and system rationality signifies the effect of the assortative mixing of node rationality on the system rationality. These network properties of the intermediate networks were averaged over 20 such repeated experiments for each iteration in order to normalize the the effect of randomness in rewiring the links to incrementally improve system rationality. The resulting values were plotted against the number of rewiring iterations in order to observe how the evolution of the network topology affected the scale-free exponent, scale-free correlation, system rationality, and scalar assortativity. In the following section, we present the results obtained from the simulations described above.
5. Results
Figure 2 demonstrates the evolution of system rationality over multiple iterations of rewiring where the rewiring is based on preferential mixing of node rationality parameters, as mentioned in Section 4. The system rationality increases and stabiliizes over time. The evolution of the system rationality follows a similar trend irrespective of whether the node rationality is positively or negatively correlated with the node degree. This figure illustrates that when preferential rewiring occurs in terms of node rationality parameters, the system rationality increases as a result.
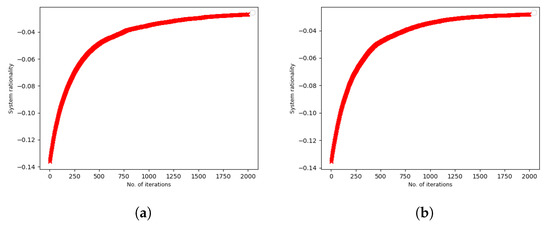
Figure 2.
System rationality against the number of iterations of network rewiring. The system rationality increases and stabilizes over 2000 iterations of rewiring when preferential rewiring based on node-rationality occurs. This happens whether the node rationality is (a) positively or (b) negatively correlated with the degree. Therefore, preferential rewiring based on the node rationality parameter results in increased system rationality.
Similarly, Figure 3 demonstrates the evolution of the scale-free correlation coefficient, which measures the ‘scale-freeness’ of the network, over multiple iterations of rewiring where the rewiring is based on preferential mixing of node rationality parameters, as mentioned in Section 4. Note that the scale-free correlation coefficient is distinct from the scale-free exponent. The former denotes the level of fitness of the degree distribution of a network to an ideal power-law degree distribution, whereas the later denotes the exponent of that power-law degree distribution. It can be observed that the scale-free correlation coefficient (‘scale-freeness’) increases with iterations, and again this is true whether the node rationality is positively or negatively correlated with the node degree. This figure illustrates that when preferential rewiring occurs in terms of node rationality parameters, the scale-freeness of the network increases as a result.
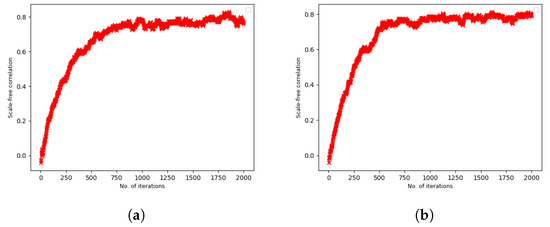
Figure 3.
Scale-free correlation against the number of iterations of rewiring. The figures indicate that the scale-freeness of the topology increases over 2000 iterations of rewiring when preferential re-wiring based on node-rationality occurs. This happens whether the node rationality is (a) positively or (b) negatively correlated with the degree. Therefore, preferential rewiring based on the node rationality parameter results in increased scale-freeness.
Together, Figure 2 and Figure 3 re-affirm the results obtained by Kasthurirathne and Piraveenan [17], who argued that when the system rationality of a networked system increases, scale-freeness emerges from initially random topologies. Here, we undertook preferential re-writing of initially random topologies based on node rationality parameters, which increased both system rationality and scale-freeness. Therefore, as the system rationality increased, scale-free topologies evolved from random topologies. Note that the average rationality of the system remained constant, as rewiring does not change the average degree of the system; thus, both the total of the rationality values (which are computed from the node degrees) and the size of the network remained unchanged. Therefore, the emergence of scale-freeness corresponds to the increase in system rationality and not to the average rationality.
Figure 4 traces the power-law exponent of the evolving networks when preferential rewiring based on node rationality parameters is undertaken. Obviously, at the start of simulation the networks are randomly connected and scale-free correlation is near zero, as shown in Figure 3; in this case, the scale-free exponent is meaningless. As rewiring progresses, the power-law exponent reaches the value of 1. The resulting topology is indicative of a core–periphery topology, as the power-law-exponent observed here is similar to that of a core–periphery topology [60].
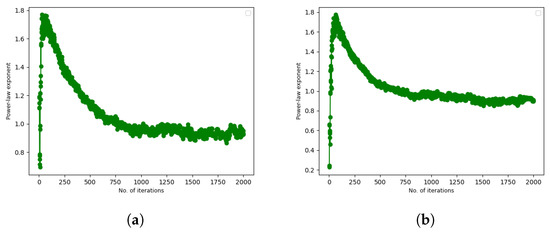
Figure 4.
Power-law exponent against the number of iterations of rewiring. The figures indicate that the power-law exponent reaches 1, indicative of a core-periphery topology emerging, over 2000 iterations of preferential rewiring based on node rationality. This happens whether the node rationality is (a) positively or (b) negatively correlated with the degree.
Another feature of all these results is that the observed trends depend only on node rationality-based preferential mixing. In this work, node rationality is derived from node degree; two seperate scenarios are considered, namely, those expressed by Equations (12) and (13) in Section 4, which are that the node rationality is (a) positively and (b) negatively, correlated with the node degree. However, the results indicate that the way in whichnode rationality is derived has no bearing on the evolution of system rationality and topological parameters, which are rather related to node rationality-based preferential mixing. In other words, regardless of the node in which rationality is computed, node rationality-based preferential rewiring of random networks results in (i) increased system rationality (ii) the evolution of scale-freeness.
Figure 5 shows the evolution of node rationality-based scalar assortativity when node rationality-based preferential mixing is undertaken. Unsurprisingly, it can be seen that the node rationality-based scalar disassortativity increases. This is expected, as node rationality-based scalar assortativity is able to precisely measure node rationality-based preferential mixing, essentially replicating the Xulvi–Brunet–Sokolov algorithm [59] (except that here scalar assortativity based on a particular scalar, the node rationality parameter, is being optimised rather than degree-based assortativity or disassortativity). Nevertheless, it is important to note that these results hold whether the node rationality is positively or negatively correlated to the node degree. This indicates that irrespective of whether the nodes with higher rationality are placed as hubs or leaf nodes initially, preferential re-writing based on node rationality results in optimisation of scalar disassortativity.
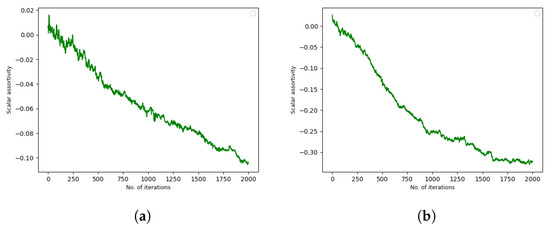
Figure 5.
Node rationality-based scalar-assortativity against the number of iterations of node rationality-based preferential rewiring. The scalar disassortativity increases over 2000 iterations whether (a) node rationality is positively correlated with node degree or (b) node rationality is negatively correlated with node degree.
Finally, Figure 6 depicts the evolution of system rationality against scalar assortativity, both quantifiable metrics of the network, when node rationality-based preferential rewiring is undertaken iteratively. Quantities of both axes in this figure were obtained from intermediate networks in the iterative experiments above averaged over 20 random network topologies, as mentioned in Section 4. As such, this figure combines results from Figure 2 and Figure 5. As expected based on those figures, this figure shows that there is a clear correlation between scalar assortativity and system rationality. As scalar assortativity (which is in the X axis in Figure 6) moves from disassortativity to non-assortativity, system rationality decreases. In terms of the rewiring experiments described above, this means that as preferential rewiring occurs, scalar assortativity moves from non-assortativity to disassortativity and system rationality increases. Again, we may observe that the way in which node rationality is derived from node degree, that is, whether they positively correlated or negatively correlated, has no qualitative bearing on the results.
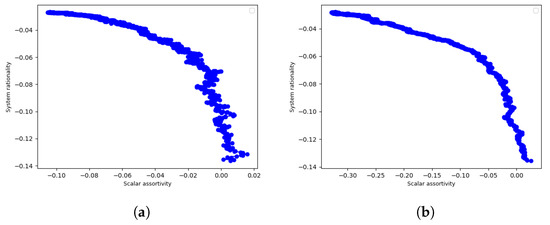
Figure 6.
System rationality against node rationality-based scalar assortativity, derived from the intermediate networks obtained when the random topology is rewired to improve the system rationality over 2000 iterations. It can be seen that system rationality is positively correlated with scalar disassortativity whether (a) node rationality is positively correlated with node degree or (b) node rationality is negatively correlated with node degree.
6. Discussion
It has been demonstrated that networks evolve to be scale-free networks when system rationality improves [17]; however, it has previously been argued that scale-free networks do not necessarily optimise system rationality, and hub-and-spoke networks of equal size typically have higher system rationality than scale-free networks [45]. Hub-and-Spoke networks have been observed to have high level of degree disassortativity [55,61]. Based on this premise, in this study we studied the correlation between node rationality-based scalar assortativity and system rationality. Our main conclusion is that when preferential rewiring based on node rationality occurs, it results in the optimisation of system rationality. Indeed, the Hub-and-Spoke network structure observed by Roman and Brede [45] could be said to be a special case of this phenomenon: Hub-and-Spokes strutures, due to their topology, have a high level of preferential mixing between high-rationality nodes and low-rationality nodes, and thus have high system rationality. It is important to note here that by “preferential mixing” we mean preferential mixing between high-rationality nodes and low-rationality nodes (nearly ideal disassortative mixing), though it is immaterial whether the high rationality nodes are hubs or peripheral nodes. Therefore, we use the phrase “preferential mixing” as simply the opposite of random (non-preferential) mixing. The main result here is that such preferential rewiring from initially random networks results in the evolution of higher system rationality.
By undertaking preferential rewiring based on node rationality, we found that scale-free networks evolve from random networks, as previously observed by Kasthurirathna and Piraveenan [17]. In addition, we found that the scale-free exponent evolves to be around , resulting in network structures similar to core–periphery networks [62]. Again, such core–periphery networks are highly disassortative in nature [55,61], providing further credence to the observation that disassortativity (both degree disassortativity and scalar disassortativity based on node rationality) aids the increase in system rationality. Nevertheless, our results indicate that system rationality may not be optimized based on topology alone, and that disassortative mixing of players based on individual rationality of players may be a decisive factor as well. From these results, it can be argued that it is the node rationality-based scalar-assortativity that drives system rationality, while network topology may play a role if it facilitates more disassortative mixing of bounded node rationality, as certain topologies (such as star, Hub-and-Spoke, and Core–Periphery structures) facilitate scalar disassortative mixing compared to random topologies.
It is interesting to ponder, in a socio-ecological sense, why system rationality might be correlated with scalar disassortativity (measured in terms of node rationality parameter values), as the results in this work show. This implies that when relatively ‘rational’ (‘smarter’) people preferentially make connections with relatively less rational people, it has the effect of increasing the system rationality. In other words, if one cannot increase the average rationality of a population, then it pays to have a social structure in which the more rational people are connected to the less rational people, rather than the relatively more rational people being in one section of the social structure and the less rational people in another. Segregation in terms of rationality results in the social system behaving as if it is overall less rational, while more rational people being in contact with less rational people results in the social system behaving as if it is overall more rational, even when the average rationality, or the rationality distribution, does not change. This intuitively makes perfect sense, as in any social system it is advantageous to have the available expertise, skill, ability, IQ, etc., distributed across the system, allowing those who have these qualities in lesser amounts to benefit from their neighbours who have relatively more of them. Such a system has an evolutionary advantage over systems that do not display this feature. We can note that this evolution of scalar disassortativity (in terms of rationality) seems to go hand-in-hand with the topological evolution of scale-freeness, which essentially increases the topological heterogeneity of the network, allowing agents/players/people who are at the hubs of the network to play more decisive roles. Thus, the interdependent evolution of scale-freeness and rationality-based disassortativity in a social network effectively seems to ensure that the social network is able to display more rationality at the systemic level even while the available levels of rationality (the average rationality) of the population remains unchanged. This is, essentially, a recipe for ‘better performance’ from a social system with fixed resources by improving both structure (topology) and placement.
The scope of the present work has been limited to identifying the basic topology types and mixing patterns which optimise system rationality, and there are several ways in which this work could be developed further. For example, it would be interesting to study scenarios in which node rationality distribution itself evolves. People or agents usually have the capability to learn and improve, and this learning may improve knowledge; alternatively it could improve rationality itself, that is, the ability to make good decisions. Indeed, people may possess various levels of ability to improve their own rationality, and this could be modelled by a separate ‘rationality improvement’ parameter that governs the ability of a node to improve its rationality over time. If nodes could do this it would open up a new set of research questions, including the optimal placement of nodes which have the highest ability to improve their rationality over time and the sensitivity of system rationality to improving levels of average rationality. For example, it would be interesting to analyse whether the system rationality improves linearly, exponentially, or logarithmically with the average rationality of the system, as well as the role played in answering these questions by the placement of nodes which have higher ability to improve their rationality. Similarly, a principled in-depth analysis of the influence of the scale-free exponents of scale-free networks on system rationality could be undertaken. Another branch of future research might look at other network types, such as small-world networks, and the factors that influence system rationality in those structures. In the present work, we have consciously focused on scale-free networks, as they evolve from random networks when optimised for system rationality and small world networks have not been shown to evolve from random structures in a similar way. Nevertheless, analysis of small-world and hierarchical networks may show other interesting features about the dependency of system rationality on network topology.
Incremental research undertaking further analysis of various parameters used in the present work and their influence on the results is possible as well. In particular, the game dynamics could be further analysed to identify trends in the payoffs and probabilities of particular strategies being played. In the present work, our focus has been on system rationality; the calculation of strategy probabilities was used primarily to compute the Jensen–Shannon divergence between Nash equilibria and quantal response equilibria. The values of the strategy probabilities or payoffs and their trajectories were not analysed as such. Due to the continuous rewiring in our experiments, it is evident that the payoffs of individual nodes change with time; thus, further analysis of game dynamics could potentially identify interesting correlations between topology and payoffs when system rationality is optimised. The individual evolution of QRE probabilities for each possible strategy at each pair of nodes and the correlation between this and the topological placement of nodes would be of interest in terms of game dynamics. Therefore, while the present work addresses a well-defined niche, this work could be expanded in a number of ways in the future.
Author Contributions
Conceptualization, M.P.; Formal analysis, D.K.; Investigation, D.K. and P.R.; Methodology, D.K., P.R. and M.P.; Software, D.K. and P.R.; Supervision, D.K. and M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Osborne, M.J. An Introduction to Game Theory; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Binmore, K. Playing for Real: A Text on Game Theory; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Kuhn, H.; Arrow, K.; Tucker, A. Contributions to the Theory of Games; Number v. 2 in Annals of Mathematics Studies; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Fudenberg, D.; Tirole, J. Game Theory; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Nowak, M.A.; Bonhoeffer, S.; May, R.M. Spatial games and the maintenance of cooperation. Proc. Natl. Acad. Sci. USA 1994, 91, 4877–4881. [Google Scholar] [CrossRef]
- Chen, X.; Wang, L. Promotion of cooperation induced by appropriate payoff aspirations in a small-world networked game. Phys. Rev. E 2008, 77, 017103. [Google Scholar] [CrossRef]
- Rong, Z.; Li, X.; Wang, X. Roles of mixing patterns in cooperation on a scale-free networked game. Phys. Rev. E 2007, 76, 027101. [Google Scholar] [CrossRef]
- Galeotti, A.; Goyal, S.; Jackson, M.O.; Vega-Redondo, F.; Yariv, L. Network games. Rev. Econ. Stud. 2010, 77, 218–244. [Google Scholar] [CrossRef]
- Simon, H.A. Models of Bounded Rationality, Volume 1: Economic Analysis and Public Policy; MIT Press Books: Cambridge, MA, USA, 1984; Volume 1. [Google Scholar]
- Simon, H.A. Bounded rationality. In Utility and Probability; Springer: Berlin/Heidelberg, Germany, 1990; pp. 15–18. [Google Scholar]
- Simon, H.A. Bounded rationality and organizational learning. Organ. Sci. 1991, 2, 125–134. [Google Scholar] [CrossRef]
- Simon, H.A. Models of Bounded Rationality: Empirically Grounded Economic Reason; MIT Press: Cambridge, MA, USA, 1997; Volume 3. [Google Scholar]
- Kasthurirathna, D.; Piraveenan, M. Emergence of scale-free characteristics in socio-ecological systems with bounded rationality. Sci. Rep. 2015, 5, 10448. [Google Scholar] [CrossRef]
- Law, S.Y.; Kasthurirathna, D.; Piraveenan, M. Placement matters in making good decisions sooner: The influence of topology in reaching public utility thresholds. In Proceedings of the 2019 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Vancouver, BC, Canada, 27–30 August 2019; pp. 787–795. [Google Scholar]
- Kasthurirathna, D.; Piraveenan, M.; Uddin, S. Modeling networked systems using the topologically distributed bounded rationality framework. Complexity 2016, 21, 123–137. [Google Scholar] [CrossRef]
- Schneeweiβ, C. Hierarchical structures in organisations: A conceptual framework. Eur. J. Oper. Res. 1995, 86, 4–31. [Google Scholar] [CrossRef]
- Meuleman, L. Public Management and the Metagovernance of Hierarchies, Networks and Markets: The Feasibility of Designing and Managing Governance Style Combinations; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Hop, L.; Post, G. A design typology of inter-organisational networks: A tool for network development in practice. In Recent Essentials in Innovation Management and Research; Springer: Berlin/Heidelberg, Germany, 1995; pp. 9–22. [Google Scholar]
- Moore, D.R. Project Management: Designing Effective Organisational Structures in Construction; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Amiripalli, S.S.; Bobba, V. Research on network design and analysis of TGO topology. Int. J. Netw. Virtual Organ. 2018, 19, 72–86. [Google Scholar] [CrossRef]
- Kant, L.; Young, K.; Younis, O.; Shallcross, D.; Sinkar, K.; Mcauley, A.; Manousakis, K.; Chang, K.; Graff, C. Network science based approaches to design and analyze MANETs for military applications. IEEE Commun. Mag. 2008, 46, 55–61. [Google Scholar] [CrossRef]
- Lai, C.M.; Tseng, M.L. Designing a reliable hierarchical military logistic network using an improved simplified swarm optimization. Comput. Ind. Eng. 2022, 169, 108153. [Google Scholar] [CrossRef]
- Paparone, C.R.; Anderson, R.A.; McDaniel, R.R., Jr. Where military professionalism meets complexity science. Armed Forces Soc. 2008, 34, 433–449. [Google Scholar] [CrossRef]
- Shneidman, J.; Parkes, D.C. Rationality and self-interest in peer to peer networks. In Proceedings of the International Workshop on Peer-to-Peer Systems; Springer: Berlin/Heidelberg, Germany, 2003; pp. 139–148. [Google Scholar]
- Ripeanu, M.; Foster, I.; Iamnitchi, A. Mapping the gnutella network: Properties of large-scale peer-to-peer systems and implications for system design. arXiv 2002, arXiv:cs/0209028. [Google Scholar]
- Lambton-Howard, D.; Simpson, E.; Quimby, K.; Kharrufa, A.; Hoi Ming Ng, H.; Foster, E.; Olivier, P. Blending into everyday life: Designing a social media-based peer support system. In Proceedings of the 2021 CHI Conference on Human Factors in Computing Systems, Yokohama, Japan, 8–13 May 2021; pp. 1–14. [Google Scholar]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Rong, Z.; Wu, Z.X. Effect of the degree correlation in public goods game on scale-free networks. EPL 2009, 87, 30001. [Google Scholar] [CrossRef]
- Santos, F.C.; Rodrigues, J.; Pacheco, J. Graph topology plays a determinant role in the evolution of cooperation. Proc. R. Soc. B Biol. Sci. 2006, 273, 51–55. [Google Scholar] [CrossRef]
- Kasthurirathna, D.; Piraveenan, M.; Uddin, S. Evolutionary stable strategies in networked games: The influence of topology. J. Artif. Intell. Soft Comput. Res. 2015, 5, 83–95. [Google Scholar] [CrossRef][Green Version]
- Kasthurirathna, D.; Piraveenan, M.; Harré, M. Influence of topology in the evolution of coordination in complex networks under information diffusion constraints. Eur. Phys. J. B 2014, 87, 1–15. [Google Scholar] [CrossRef]
- Myerson, R.B. Nash equilibrium and the history of economic theory. J. Econ. Lit. 1999, 37, 1067–1082. [Google Scholar] [CrossRef]
- Conlisk, J. Why bounded rationality? J. Econ. Lit. 1996, 34, 669–700. [Google Scholar]
- McKelvey, R.D.; Palfrey, T.R. Quantal response equilibria for normal form games. Games Econ. Behav. 1995, 10, 6–38. [Google Scholar] [CrossRef]
- Goeree, J.K.; Holt, C.A.; Palfrey, T.R. Quantal response equilibria. In Behavioural and Experimental Economics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 234–242. [Google Scholar]
- Wolpert, D.H. Information Theory—The Bridge Connecting Bounded Rational Game Theory and Statistical Physics. In Complex Engineered Systems; Springer: Berlin/Heidelberg, Germany, 2006; pp. 262–290. [Google Scholar]
- Camerer, C.F.; Ho, T.H.; Chong, J.K. A cognitive hierarchy model of games. Q. J. Econ. 2004, 119, 861–898. [Google Scholar] [CrossRef]
- Rogers, B.W.; Palfrey, T.R.; Camerer, C.F. Heterogeneous quantal response equilibrium and cognitive hierarchies. J. Econ. Theory 2009, 144, 1440–1467. [Google Scholar] [CrossRef]
- Golman, R. Homogeneity bias in models of discrete choice with bounded rationality. J. Econ. Behav. Organ. 2012, 82, 1–11. [Google Scholar] [CrossRef]
- Roman, S.; Brede, M. Topology-dependent rationality and quantal response equilibria in structured populations. Phys. Rev. E 2017, 95, 052310. [Google Scholar] [CrossRef]
- Gunawardana, L.; Ratnayake, P.; Piraveenan, M.; Kasthurirathna, D. Information Theoretic Approach for Modeling Bounded Rationality in Networked Games. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 2100–2107. [Google Scholar]
- Roman, S. Dynamic and Game Theoretic Modelling of Societal Growth, Structure and Collapse. Ph.D. Thesis, University of Southampton, Southampton, UK, 2018. [Google Scholar]
- Axelrod, R. Effective choice in the prisoner’s dilemma. J. Confl. Resolut. 1980, 24, 3–25. [Google Scholar] [CrossRef]
- Rombach, M.P.; Porter, M.A.; Fowler, J.H.; Mucha, P.J. Core-periphery structure in networks. SIAM J. Appl. Math. 2014, 74, 167–190. [Google Scholar] [CrossRef]
- Goeree, J.K.; Holt, C.A.; Palfrey, T.R. Quantal Response Equilibrium. In The New Palgrave Dictionary of Economics; Palgrave Macmillan: Basingstoke, UK, 2008. [Google Scholar]
- Zhang, B. Quantal response methods for equilibrium selection in normal form games. J. Math. Econ. 2016, 64, 113–123. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Entropy, relative entropy and mutual information. Elem. Inf. Theory 1991, 1, 12–49. [Google Scholar]
- Menéndez, M.; Pardo, J.; Pardo, L.; Pardo, M. The jensen-shannon divergence. J. Frankl. Inst. 1997, 334, 307–318. [Google Scholar] [CrossRef]
- Newman, M.E. Assortative mixing in networks. Phys. Rev. Lett. 2002, 89, 208701. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E. Mixing patterns in networks. Phys. Rev. E 2003, 67, 026126. [Google Scholar] [CrossRef]
- Piraveenan, M.; Prokopenko, M.; Zomaya, A. Assortative mixing in directed biological networks. IEEE/ACM Trans. Comput. Biol. Bioinform. 2010, 9, 66–78. [Google Scholar] [CrossRef]
- Liu, S.; Hu, X.; Wang, S.H.; Zhang, Y.D.; Fang, X.; Jiang, C. Mixing Patterns in Social Trust Networks: A Social Identity Theory Perspective. IEEE Trans. Comput. Soc. Syst. 2020, 8, 1249–1261. [Google Scholar] [CrossRef]
- Van Laarhoven, P.J.; Aarts, E.H. Simulated annealing. In Simulated Annealing: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 1987; pp. 7–15. [Google Scholar]
- Xulvi-Brunet, R.; Sokolov, I.M. Reshuffling scale-free networks: From random to assortative. Phys. Rev. E 2004, 70, 066102. [Google Scholar] [CrossRef]
- Perera, S.S.; Bell, M.G.; Piraveenan, M.; Kasthurirathna, D.; Parhi, M. Topological structure of manufacturing industry supply chain networks. Complexity 2018, 2018, 3924361. [Google Scholar] [CrossRef]
- Newman, M.E.J. Models of the Small World. J. Stat. Phys. 2000, 101, 819–841. [Google Scholar] [CrossRef]
- Perera, S.; Kasthurirathna, D.; Bell, M.; Bliemer, M. Topological rationality of supply chain networks. Int. J. Prod. Res. 2020, 58, 3126–3149. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).