Distributed H_∞ and H₂ Time-Varying Formation Tracking Control for Linear Multi-Agent Systems with Directed Topologies

Abstract

In this paper, the H_∞ and H₂ time-varying formation tracking problems for multi-agent systems with directed topologies in the presence of external disturbances are investigated. The followers need to achieve the desired time-varying formation during movement and simultaneously track the state trajectory generated by the leader. First, a distributed consensus protocol based on the local state information of neighbors of the agents for solving H_∞ and H₂ time-varying formation tracking problems are proposed without utilizing global information about the entire agents. The conditions to achieve H_∞ and H₂ time-varying formation tracking in the presence of external disturbances are suggested respectively. Then, to determine the parameters of the designed protocol which satisfy suitable conditions, algorithms for H_∞ and H₂ time-varying formation tracking in the form of pseudo-code are presented, respectively. Furthermore, the proofs of the proposed theorems are derived by utilizing algebraic graph theory and Lyapunov analysis theory tools to demonstrate the closed-loop stability of the system in the presence of external disturbances. Finally, the usefulness and effectiveness of the approaches proposed are demonstrated by numerical simulation examples.

1. Introduction

Distributed cooperative control of multi-agent systems (MASs) has drawn significant attention from both scientific research and engineering application communities due to its broad applications in formation of unmanned aerial vehicles (UAVs) [1,2], satellites [3], multiple mobile robots [4,5,6], multiple autonomous underwater vehicles (AUVs) [7,8] and so on. Formation control strategies have been extensively studied in the past few decades [9,10]. According to the basic idea of the control scheme, traditional formation control approaches can be roughly divided into leader–follower based [11], behavior based [12], and virtual structure based [13]. With the development of technology, traditional strategies have been unable to meet the needs of practical applications due to their disadvantages [14,15]. That is, these strategies have their weakness in terms of distributed form, mathematical model and theoretical stability analysis.

Benefiting from the development of algebraic graph theory, consensus-based control strategies, which have experienced rapid growth in recent years and showed more significant advantages than the above traditional approaches, have been applied to deal with formation control problems. The pioneering research work in the area of consensus was performed by Olfati-Saber and Murray, who first proposed the protocols based on the information exchange of local neighbors for multiple agents to achieve consensus [16]. Then, Ren et al. [17,18,19] proposed a necessary criterion that extended first-order consensus systems to second-order systems and argued that the above traditional approaches can be unified in consensus problems. They also utilized their principles to solve various formation control problems.

In reality, many systems, including UAVs and mobile robotic systems, are modeled as second-order systems [19]. Formation control based on first-order and second-order systems has formed a relatively well-developed theoretical system. However, in some practical applications, the dynamics of swarm systems can only be described by more complex high-order models, such as swarm systems of a multi-joint robotic manipulator. So far, many results on formation control of high-order systems have emerged [20,21,22,23], including time-varying systems, fixed-time, switching topologies and time delays, for example. In addition to time-varying formation control that achieves the desired formation, there is a requirement for the desired formation to track a certain trajectory in some practical applications. Hence, the formation tracking issues that have one or multiple leaders appear. This means that the states of a group of followers track the state trajectory of leaders while forming expected formations via various topologies which are affected by communication structure graphs. Various types of formation tracking control problems are studied by utilizing different control theory tools [24,25,26]. Dong et al. [24] investigated time-varying formation tracking issues of second-order swarm systems which applied to quadrotor formation flying. Wang et al. [25] studied the formation tacking problems of a multi-UAV system with a leader which has dynamic input based on the sliding mode control theory.

It is worth emphasizing that how to achieve formation control of multi-agent systems with a certain performance that is guaranteed is meaningful. Time-varying formation control under optimal/suboptimal performance conditions is an area that requires further attention. There are mainly two kinds of optimal/suboptimal formation control strategies. The first one is based on the consensus theory and $H_{\infty }$ control theory, and the other method is based on the guaranteed cost performance method or the linear quadratic regulator (LQR) method to study the formation or consensus actualization problem [27]. Based on the consensus theory and $H_{\infty }$ control theory, the robust $H_{\infty }$ consensus control and consensus tracking protocols were proposed to solve disturbance attenuation of swarm systems [28,29,30,31,32,33]. As for the second strategy, there are many kinds of research to apply guaranteed cost control methods to study time-varying delays or consensus tracking problems [34,35,36,37]. Note that many aforementioned works were focused on consensus tracking problems or fixed formation tracking issues of multi-agent systems. However, the consensus tracking problems can be unified in the framework of time-varying formation tracking if the formation reference functions are set to zero by the stability analysis theory. In the practical, complex application of a swarm system, external disturbances are inevitable. External disturbances to followers can affect the effectiveness of formation tracking control and even lead to failure of formation tasks. Therefore, it is worthwhile to handle the disturbances by utilizing an effective control strategy. In terms of previous research, robust $H_{\infty }$ methods are feasible to solve the external disturbances [28,29,30,31,32,33]. Wang et al. [33] investigated the $H_{\infty }$ consensus control and $H_2$ robust control synthesised with transient performance problems of multi-agent systems under an undirected communication topology. Cheng et al. [31] studied time-varying formation (TVF) and trajectory tracking $H_{\infty }$ control problem of swarm systems with communication delays and external disturbances.

It can be seen from the literature mentioned above that the $H_{\infty }$ norm represents the robustness of a swarm system to the worst case of external disturbances and has been well studied. However, the $H_2$ norm represents the disturbance rejection performance of a swarm system to the bounded external disturbances which still needs further research. Motivated by the aforementioned facts, we find that the disturbance rejection problems of time-varying formation tracking of linear multi-agent systems with directed communication topology graphs have not yet been studied. Thus, to sufficiently analyze the disturbance rejection performance, both the $H_{\infty }$ and $H_2$ time-varying formation tracking control problems of linear multi-agent systems with directed communication topology graphs that exist in a spinning tree are studied in this paper. We proposed distributed time-varying formation control protocols which utilized the information of local neighbors for $H_{\infty }$ and $H_2$ time-varying formation tracking issues, respectively. In addition, corresponding algorithms were presented to construct the parameters of the protocols to achieve the formation tracking of multi-agent systems. Compared with the previous research, our contribution is mainly focused on the following three aspects. First, the $H_{\infty }$ and $H_2$ time-varying formation tracking performance can be achieved. The $H_{\infty }$ and $H_2$ consensus problems can be a special case of time-varying formation tracking [38,39]. Dong et al. [24,40] proposed the protocols to deal with the time-varying formation tracking issues without considering external disturbances. Second, considering a more general directed topology, the Laplacian matrix is not positive (or semi-) definite where the similarity transformation cannot be feasible. The communication topology is more relaxed. Therefore, the condition for reaching time-varying formation tracking is analyzed by designing an appropriate Lyapunov function. The feasibility analysis and stability analysis of time-varying formation tracking problems are more straightforward and simplified. Third, the algorithms were designed to acquire the parameters of $H_{\infty }$ and $H_2$ time-varying formation tracking problems by solving the feasible solution of the low-dimensional linear matrix inequalities (LMIs) which greatly reduced the computational complexity. Table 1 summarizes the typical previous research in comparison with the current work.

Table 1. Summary of typical previous research in comparison with the current work.

Approaches	Contents
Literature [31]	The time-varying formation and trajectory tracking problem with communication delays and external disturbances was studied. The directed communication topology of the system comprises a spanning tree. It considered the influences of communication delays and external disturbances but did not involve $H_2$ time-varying formation tracking.
Literature [38,39]	The $H_{\infty }$ and $H_2$ consensus problems with directed communication graphs are investigated. The $H_{\infty }$ and $H_2$ consensus problems can be a special case of time-varying formation tracking problems. The communication topology was strongly connected, which is more relaxed than the generally directed communication topology of the current work.
Literature [41]	The time-varying formation robust tracking problems for high-order linear multiagent systems with a leader of unknown control input in the presence of heterogeneous parameter uncertainties and external disturbances were studied. The communication topology among followers was undirected which needed more constraints.
Literature [24,40]	The time-varying formation tracking problems are addressed without external disturbances. The formation tracking cannot be accomplished by followers due to external disturbances.
Current work	The $H_{\infty }$ and $H_2$ time-varying formation tracking problems for multi-agent systems with directed topologies in the presence of external disturbances are investigated. The communication topology of the system is generally directed which is more relaxed for application. The algorithms for determining the parameters of the designed protocol are more straightforward and simplify the analysis.

The rest of this paper is organized as follows. Section 2 provides some notations and results on algebraic graph theory and gives the problem descriptions. The $H_{\infty }$ and $H_2$ time-varying formation tracking control problems of the multi-agent systems are considered and the close-loop stability of the system is proven in Section 3. In Section 4, numerical simulation examples are given to demonstrate theoretical results. The conclusions and future work are presented in Section 5.

2. Preliminaries and Problem Descriptions

2.1. Notations

The notations used in this paper are defined as follows. Let ${ℝ}^n$ be the $n$ dimensional Euclidean space, ${ℝ}^{n\times m}$ be the set of $n\times m$ real matrices, $I_n$ be the identity matrix of order $n$ and $1_n$ be the $n$ dimensional column vector with all entries being one, respectively. A^T denotes the transpose of the matrix $A\in {ℝ}^{n\times n}$. let λ(A) be the eigenvalues of a matrix $A$, $\mathrm{Re}(a)$ be the real part of the complex number $a$ and $rank(A)$ be the rank of the matrix $A$, respectively. Denote by ${ℒ}_2^r\left[0,\infty \right)$ the space of $r$ dimensional square-integrable vector functions over $\left[0,\infty \right)$. Let $\Vert \cdot \Vert$ represent the $L_2$ norm of the corresponding vector or function. Moreover, $X>Y$($X\ge Y$) denotes that the matrix $X-Y$ is positive (or semi-) definite for real symmetric matrices $X$ and $Y$. The Kronecker product of matrix $A$ and matrix $B$ is represented by $A\otimes B$. Finally, the matrix $A\in {ℝ}^{n\times n}$ is called a Hurwitz matrix or stable matrix if and only if the real parts of all of its eigenvalues $\lambda (A)$ are less than zero.

2.2. Basic Graph Theory

The graph $\mathcal{G}=(\mathcal{V},ℰ)$ is a pair $(\mathcal{V},ℰ)$, where $\mathcal{V}=\left\{v_1,\cdots ,v_N\right\}$ is a nonempty finite set of $N$ nodes and $ℰ\subseteq \mathcal{V}\times \mathcal{V}$ is a set of edges. Elements of the $ℰ$ are denoted as $(v_i,v_j)$ which represents the flow of information from node $v_i$ to node $v_j$, that is, the node $v_j$ receives information from the node $v_i$. There are no self-loops and no multiple edges between the same pairs of nodes, which means $(v_i,v_i)\notin ℰ$. Let $A={[a_{ij}]}_{N\times N}$ be the adjacency or connectivity matrix of the graph $\mathcal{G}=(\mathcal{V},ℰ)$ with weights $a_{ij}=1$ if $(v_j,v_i)\in ℰ$ and $a_{ij}=0$ otherwise. The interaction between the nodes themselves is not considered, that is, the diagonal elements of the adjacency matrix satisfy $a_{ii}=0$. The set of neighbors of a node $v_i$ is defined as $N_i=\left\{v_j|(v_j,v_i)\in ℰ\right\}$, which means the set of nodes with edges incoming to the node $v_i$. The diagonal in-degree matrix of the graph $\mathcal{G}=(\mathcal{V},ℰ)$ is represented by $D=diag(d_1,\cdots ,d_N)$ where $d_i={\displaystyle \sum _j{a}_{ij}}$ is the in-degree of node $v_i$, i.e., the sum of the row $i$ of the adjacency matrix $A={[a_{ij}]}_{N\times N}$. Denote by $L=D-A$ the Laplacian matrix with all row sums equal to zero.

Lemma 1

[42]. The eigenvalues $L$ have positive real parts if $L\in {ℝ}^{n\times n}$ is a nonsingular M-matrix, i.e., $\mathrm{Re}(\lambda (L))>0$.

Lemma 2

[43]. For a non-singular M-matrix $L\in {ℝ}^{n\times n}$, there exists a symmetric positive definite matrix $Q\in {ℝ}^{n\times n}$ such that

$${(L-\frac{1}{2}\alpha I)}^{T}Q+Q(L-\frac{1}{2}\alpha I)>0$$

where $0<\alpha <2\min \left\{\mathrm{Re}(\lambda (L))\right\}$.

2.3. Problem Descriptions

Consider a multi-agent system of $N+1$ agents, which consists of a leader and $N$ followers. Let $E=\left\{N+1\right\}$ and $F=\left\{1,2,\cdots ,N\right\}$ be the sets of leader and followers, respectively. The dynamics of each agent of $N$ followers are described by

$${\dot{x}}_i(t)=A{x}_i(t)+B{u}_i(t)+D{\omega }_i(t),i\in F,$$

(1)

where $x_i(t)\in {ℝ}^n$ is the state of the i-th follower agent and $u_i(t)\in {ℝ}^m$ is the associated control input for all t ≥ 0. $A\in {ℝ}^{n\times n}$, $B\in {ℝ}^{n\times m}$ and $D\in {ℝ}^{n\times m}$ are constant matrices with $rank(B)=m$ and $(A,B)$ is stabilizable. ${\omega }_i(t)\in {ℒ}_2^n\left[0,\infty \right)$ are external unknown disturbances.

The dynamic of the leader is considered as follows

$${\dot{x}}_{N+1}(t)=A{x}_{N+1}(t)+B{u}_{N+1}(t),$$

(2)

where $x_{N+1}(t)\in {ℝ}^n$ and $u_{N+1}(t)\in {ℝ}^m$ are the state and associated control input, respectively.

Assumption 1.

All followers in the swarm system are aware of the leader’s input$u_{N+1}(t)$.

Remark 1.

The leader’s input is known to all followers which is equivalent to the case of$u_{N+1}(t)=0$. For simplicity of the analysis, let$u_{N+1}(t)=0$, i.e., the leader’s dynamics be described as${\dot{x}}_{N+1}(t)=A{x}_{N+1}(t)$.

Assumption 2.

The system matrix B is a column full-rank matrix, i.e., it satisfies$rank(B)=m$.

Remark 2.

IfAssumption 2holds, then there exists a non-singular matrix $\tilde{B}={\left[{\tilde{B}}_1^T,{\tilde{B}}_2^T\right]}^T\in {ℝ}^{n\times n}$ satisfying${\tilde{B}}_{1}B=I_m$, ${\tilde{B}}_{2}B=0$, where${\tilde{B}}_1\in {ℝ}^{m\times n}$, ${\tilde{B}}_2\in {ℝ}^{(n-m)\times n}$.

Assumption 3.

Suppose the swarm system consisting of a leader and$N$followers contains a spanning tree with the leader as the root node. That is, there exists a directed path from the leader node to each follower node.

Remark 3.

Under the conditions ofAssumption 1, the Laplacian matrix$L$of the graph$\mathcal{G}$consisting of a leader and$N$followers can be partitioned in the following form

$$L=\left[\begin{array}{cc}{L}_1& L_2\\ 0_{1\times N}& 0_{1\times 1}\end{array}\right],$$

where$L_1\in {ℝ}^{n\times n}$denotes the topological relationship between followers and$L_2\in {ℝ}^{n\times 1}$denotes the topological relationship between the leader and the followers. The desired formation of followers is specified by$h(t)={\left[h_1^T(t),h_2^T(t),\cdots ,h_N^T(t)\right]}^T$, where$h_i(t)\in {ℝ}^n$is the desired formation function of the agent$i$. $h_i(t)$is the predefined desired time-varying state formation of the i-th follower.

Lemma 3

[44]. If the directed communication topology of the swarm system satisfies the condition of Assumption 3, then

(1) 

All the eigenvalues of the matrix$L_1$have positive real parts;

(2) 

Each entry of the$-L_1^{-1}{L}_2$is nonnegative, and each row of the$-L_1^{-1}{L}_2$has a sum equal to one.

Remark 4.

From Assumption 3, we can obtain that the communication topological matrix $L_1$ between followers is a non-singular M-matrix.

Definition 1.

The multi-agent system is said to achieve time-varying formation tracking with a leader if for any given bound initial states$x_i(0)\in {ℝ}^n$for all$i\in F$, such that

$$\underset{t\to \infty }{\lim }\left(x_i(t)-h_i(t)-x_{N+1}(t)\right)=0,\forall i\in F,$$

(3)

In this paper, to achieve time-varying formation tracking control of the swarm system, we introduce a distributed time-varying formation control protocol which is given as follows

$$\{\begin{array}{l}{u}_i=cK{\delta }_i+v_i\\ \begin{array}{l}{\delta }_i={\displaystyle \sum _{j=1}^N{a}_{ij}\left[(x_i-h_i)-(x_j-h_j)\right]+a_{i,N+1}\left[(x_i-h_i)-x_{N+1}\right]}\\ v_i={\tilde{B}}_1\left(-A{h}_i+{\dot{h}}_i\right)\end{array}\end{array},i\in F,$$

(4)

where $K\in {ℝ}^{m\times n}$ denotes the constant gain matrix to be designed. $v_i\in {ℝ}^m$ is given by $v_i={\tilde{B}}_1\left(-A{h}_i+{\dot{h}}_i\right)$ which is the time-varying formation tracking compensational signal for extending the time-varying state formation set. $h_i\in {ℝ}^m$ is the desired time-varying formation of the followers of the swarm system for all $i\in F$. $c\in R_{>0}$ denotes the coupling strength that is a positive constant to be selected. $A={[a_{ij}]}_{N+1}$ is the adjacency matrix associated with the directed communication topology graph $\mathcal{G}$. ${\tilde{B}}_1\in {ℝ}^{m\times n}$ is the matrix that satisfies the conditions in Remark 2.

$$\begin{gathered} \mathrm{Let}\epsilon ={\left[{\epsilon }_1^T,{\epsilon }_2^T,\cdots ,{\epsilon }_N^T\right]}^T, x={\left[x_1^T,x_2^T,\cdots ,x_N^T\right]}^T,\omega ={\left[{\omega }_1^T,{\omega }_2^T,\cdots ,{\omega }_N^T\right]}^T \mathrm{and} \\ \delta ={\left[{\delta }_1^T,{\delta }_2^T,\cdots ,{\delta }_N^T\right]}^T. \mathrm{Let} {\epsilon }_i(t)=x_i(t)-h_i(t)-x_{N+1}(t) \end{gathered}$$

where $i\in F$, we can obtain

$$\epsilon (t)=x(t)-h(t)-1_n\otimes x_{N+1}(t),$$

(5)

For simplicity of expression, we omit time $t$. From (4), one can obtain

$$\delta =(L_1\otimes I_n)(x-h)+(L_2\otimes I_n)x_{N+1},$$

(6)

From Lemma 3, it follows that $L_1^{-1}{L}_2=-1_n$ and plugging this in (6) yields

$$(L_1^{-1}\otimes I_n)\delta =(x-h)-1_n\otimes x_{N+1},$$

(7)

Combining (5) and (7), one has

$$\delta =(L_1\otimes I_n)\epsilon ,$$

(8)

If time-varying formation tracking is achieved asymptotically by the followers, then it implies from (3) that

$$\underset{t\to \infty }{\lim }{\epsilon }_i(t)=0,$$

(9)

Therefore, the multi-agent system (1) achieves the formation tracking by applying the distributed time-varying formation control protocol (4), if for any given bound initial states $x_i(0)\in {ℝ}^n$ for all $i\in F$, $\underset{t\to \infty }{\lim }{\epsilon }_i(t)=0$ holds.

The major objective of this paper focuses on making all followers acquire the desired time-varying formation when tracking the state trajectory of the leader and reject external disturbances simultaneously. The following section is the main contribution of this article which considers the $H_{\infty }$ and $H_2$ time-varying formation tracking problems, designs distributed formation tracking protocols and algorithms for guaranteed $H_{\infty }$ and $H_2$ performance index such that swarm system (1) can achieve the formation tracking with external disturbances.

For ease of understanding. We plot a sketch for the proposed control structure which is shown in Figure 1.

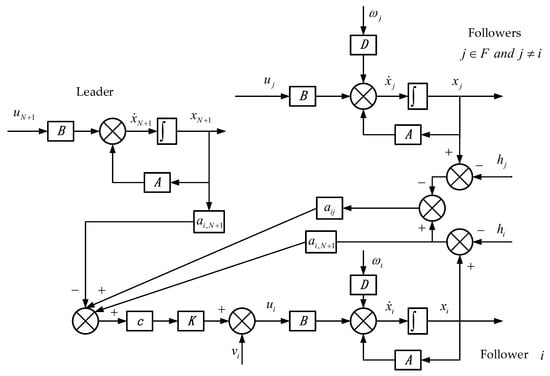
Figure 1. The sketch for the proposed control structure.

3. Methodology

3.1. $H_{\infty }$ Time-Varying Formation Tracking Algorithm

It is often difficult for a multi-agent system to achieve time-varying formation tracking when there are external disturbances. Therefore, it is necessary to design a suitable distributed protocol (4) for the multi-agent system, so that the multi-agent system can achieve formation tracking when there is no external disturbance. Furthermore, the system should be equipped with a good ability to suppress external disturbances when there are external disturbances. Thus, it needs a criterion to evaluate the desirable disturbances rejection performance of the multi-agent system. To this end, define the time-varying formation tracking performance variables of the swarm system as

$$z_i=\frac{1}{N}{\displaystyle \sum _{j=1}^{N}C\left((x_i-h_i)-(x_j-h_j)\right)},i=1,2,\cdots ,N,$$

(10)

where $C\in {ℝ}^{q_1\times n}$ is a given constant matrix.

Let $z={\left[z_1^T,z_2^T,\cdots ,z_N^T\right]}^T$, it follows from (5) that

$$z=(H\otimes C)\epsilon ,$$

(11)

where $H=I_N-\frac{1}{N}{I}_N{I}_N^T=\left[\begin{array}{cccc}1-\frac{1}{N}& -\frac{1}{N}& \cdots & -\frac{1}{N}\\ -\frac{1}{N}& 1-\frac{1}{N}& \cdots & -\frac{1}{N}\\ ⋮& ⋮& \ddots & ⋮\\ -\frac{1}{N}& -\frac{1}{N}& \cdots & 1-\frac{1}{N}\end{array}\right]$.

Lemma 4

([16]). For an undirected graph $G$ with $N$ nodes, the following conditions hold:

(1) 

Laplacian matrix$L$of the undirected graph$G$has at least one 0 eigenvalue and$1_N$is the associated eigenvector that satisfies$L{1}_N=0$.

(2) 

Zero is a simple eigenvalue of$L$and all the remaining$N-1$eigenvalues are positive, if the undirected graph$G$is connected.

From Lemma 4, it can be shown that 0 is the single eigenvalue of the matrix $H$, $1_N$ is the associated eigenvector and the algebraic multiplicity of eigenvalue 1 of the matrix $H$ is $N-1$.

Definition 2.

The multi-agent system (1) is said to accomplish the$H_{\infty }$time-varying formation tracking for any given disturbance attenuation coefficient$\gamma >0$, if the following conditions are satisfied:

(1) 

The multi-agent system (1) with$\omega (t)=0$can accomplish formation tracking in the sense of$\underset{t\to \infty }{\lim }\left((x_i(t)-h_i(t))-(x_j(t)-h_j(t))\right)=0$, $\forall i,j=1,2,\cdots ,N$, for any given initial state conditions$x_i(0)$.

(2) 

When$\omega (t)\ne 0$, under the zero-initial conditions, the formation tracking performance index satisfies:

$$J={\displaystyle {\int }_0^{\infty }\left(z^T(t)z(t)-{\gamma }^2{\omega }^T(t)\omega (t)\right)}dt<0$$

Next, the theorem for the multi-agent system (1) achieving time-varying formation tracking in the presence of external disturbances is given as follows.

Theorem 1.

Suppose the swarm system satisfiesAssumptions 1–3. The multi-agent system can achieve the$H_{\infty }$time-varying formation tracking utilizing the distributed formation tracking protocol (4) whose parameters are designed by (1)–(4) as followed for given disturbance attenuation coefficient$\gamma >0$, in the presence of external disturbances, if the desired time-varying formation specified by$h(t)$satisfies the following formation feasible condition (5):

(1) 

Computing${\tilde{B}}_1$and${\tilde{B}}_2$and based onRemark 2.

(2) 

FromLemma 2and$0<\alpha <2\min \left\{\mathrm{Re}(\lambda (L_1))\right\}$, solving the following linear matrix inequality$Q{L}_1+L_1^{T}Q>\alpha Q$for a positive definite matrix$Q>0$.

(3) 

For chosen$\tau >0$, solving the following linear matrix inequality for a positive definite matrix$P>0$:

$$\left[\begin{array}{ccc}PA+A^{T}P-\tau PB{B}^{T}P& C^T& PD\\ C& -\frac{{\phi }_2}{\varphi }{I}_n& 0\\ D^{T}P& 0& -\frac{{\gamma }^2}{{\phi }_1}{I}_n\end{array}\right]<0,$$

(12)

where$\varphi =\max \left\{\lambda (H^{T}H)\right\}$, ${\phi }_1=\max \left\{\lambda (Q)\right\}$, ${\phi }_2=\min \left\{\lambda (Q)\right\}$.

(4) 

Selecting the coupling strength parameter as$c>\frac{\tau }{\alpha }$and let the constant gain matrix be$K=-B^{T}P$.

(5) 

The following formation feasible condition

$${\tilde{B}}_2(A{h}_i-{\dot{h}}_i)=0, i\in F$$

(13)

Next, an algorithm shown in Algorithm 1 is proposed to construct the parameters of distributed control protocol (4) for achieving $H_{\infty }$ time-varying formation tracking.

Algorithm 1 Procedures to design parameters for $H_{\infty }$ time-varying formation tracking
1:	for each agent $i\in F$ then
2:	Design a directed communication topology that satisfies Assumptions 1–3;
3:	Fix the desired formation function $h_i(t), i\in F$ for followers;
4:	Computing ${\tilde{B}}_1$ and ${\tilde{B}}_2$ based on Remark 2;
5:	if the formation feasible condition (13) is satisfied then
6:	From Lemma 2 and $0<\alpha <2\min \left\{\mathrm{Re}(\lambda (L_1))\right\}$, solving the linear matrix   inequality $Q{L}_1+L_1^{T}Q>\alpha Q$ for a positive definite matrix $Q>0$;
7:	Compute parameters by $\varphi =\max \left\{\lambda (H^{T}H)\right\}$, ${\phi }_1=\max \left\{\lambda (Q)\right\}$, ${\phi }_2=\min \left\{\lambda (Q)\right\}$;
8:	Choose $\tau >0$, solving the following linear matrix inequality (12) for a positive   definite matrix $P>0$;
9:	Selecting the coupling strength parameter as $c>\frac{\tau }{\alpha }$ and computing the   constant gain matrix $K$ by $K=-B^{T}P$;
10:	Construct the distributed control protocol given in (4);
11:	else
12:	Back to Step 3;
13:	end if
14:	end for

Proof of Theorem 1.

From the definition of $\epsilon (t)$, one gets that ${\epsilon }_i(t)=x_i(t)-h_i(t)-x_{N+1}(t)$. Substituting (1) and (2) into the time derivative of the ${\epsilon }_i(t)$, the closed-loop dynamics of the multi-agent system can be transformed into

$${\dot{\epsilon }}_i=A{x}_i+B{u}_i+D{\omega }_i-{\dot{h}}_i-A{x}_{N+1}$$

(14)

The time $t$ is omitted for notational simplicity. From (4), one can obtain

$${\dot{\epsilon }}_i=A{\epsilon }_i+cBK{\delta }_i+D{\omega }_i+B{v}_i-{\dot{h}}_i+A{h}_i$$

(15)

First, analyze $B{v}_i-{\dot{h}}_i+A{h}_i$ in (15). Let ${\xi }_i=B{v}_i-{\dot{h}}_i+A{h}_i$. It holds from the definition of $v_i={\tilde{B}}_1\left(-A{h}_i+{\dot{h}}_i\right)$ in (4) that

$${\xi }_i=B{\tilde{B}}_1\left(-A{h}_i+{\dot{h}}_i\right)-{\dot{h}}_i+A{h}_i$$

(16)

From Remark 2, $\tilde{B}$ is a non-singular matrix. Multiply both sides of (16) by $\tilde{B}$, one can obtain

$$\tilde{B}{\xi }_i=\tilde{B}B{\tilde{B}}_1\left(-A{h}_i+{\dot{h}}_i\right)-\tilde{B}{\dot{h}}_i+\tilde{B}A{h}_i=\left[\begin{array}{c}0\\ {\tilde{B}}_2(A{h}_i-{\dot{h}}_i)\end{array}\right]$$

(17)

If formation feasible condition (13) holds, one has ${\xi }_i=0$. Therefore, (15) can be written in the following simplified form:

$${\dot{\epsilon }}_i=A{\epsilon }_i+cBK{\delta }_i+D{\omega }_i$$

(18)

From the definition of the $\delta$ in (8), (18) can be written in the following compact form by utilizing the Kronecker product:

$$\dot{\epsilon }=\left[(I_N\otimes A)+(L_1\otimes cBK)\right]\epsilon +(I_N\otimes D)\omega$$

(19)

Consider the following Lyapunov function candidate:

$$V(t)={\epsilon }^T(t)(Q\otimes P)\epsilon (t)$$

The time derivative of the above Lyapunov function $V(t)$ along the trajectory of (19) can be obtained as

$$\dot{V}=2{\epsilon }^T(Q\otimes P)\dot{\epsilon }=2{\epsilon }^T(Q\otimes P)\left[(I_N\otimes A)+(L_1\otimes cBK)\right]\epsilon +2{\epsilon }^T(Q\otimes P)(I_N\otimes D)\omega$$

(20)

Substituting $K=-B^{T}P$ into (20) yields

$$\dot{V}={\epsilon }^T\left[Q\otimes (PA+A^{T}P)\right]\epsilon +{\epsilon }^T\left[(Q{L}_1+L_1^{T}Q)\otimes (-cPB{B}^{T}P)\right]\epsilon +2{\omega }^T(Q\otimes D^{T}P)\epsilon$$

(21)

Since $Q{L}_1+L_1^{T}Q>\alpha Q$ holds, one can obtain from (21) that

$$\dot{V}={\epsilon }^T[Q\otimes (PA+A^{T}P-c\alpha PB{B}^{T}P)]\epsilon +2{\omega }^T(Q\otimes D^{T}P)\epsilon$$

(22)

Utilizing the Schur complement lemma, the linear matrix inequality (12) holds, if and only if the following matrix inequality holds:

$$PA+A^{T}P-\tau PB{B}^{T}P+\frac{\varphi }{{\phi }_2}{C}^{T}C+\frac{{\phi }_1}{{\gamma }^2}PD{D}^{T}P<0$$

(23)

That is to say, (12) and (23) are equivalent.

For the case of $\omega (t)\equiv 0$, it follows from (23) that

$$\dot{V}={\epsilon }^T\left[Q\otimes (PA+A^{T}P-c\alpha PB{B}^{T}P)\right]\epsilon <0$$

One can obtain $\underset{t\to \infty }{\lim }{\epsilon }_i(t)=0$. Therefore, (3) holds which indicates the $H_{\infty }$ time-varying formation tracking of multi-agent systems is achieved. Thus, condition (1) of Definition 2 is satisfied.

Next, analyze the $H_{\infty }$ performance of the formation tracking of multi-agent system with external disturbances $\omega (t)\ne 0$. Similarly, substituting $\varphi =\max \left\{\lambda (H^{T}H)\right\}$ and ${\phi }_2{I}_N\le Q\le {\phi }_1{I}_N$, one can obtain from (11) that

$$z^{T}z={\epsilon }^T\left[(H^{T}H)\otimes (C^{T}C)\right]\epsilon \le \frac{\varphi }{{\phi }_2}{\epsilon }^T\left[Q\otimes (C^{T}C)\right]\epsilon$$

(24)

Noting that the following inequality holds

$${\gamma }^2{\omega }^T\omega ={\gamma }^2{\omega }^T(I_N\otimes I_n)\omega$$

(25)

By conditions (23)–(25), one has

$$\begin{array}{ll}\dot{V}\le & {\epsilon }^T\left[Q\otimes (PA+A^{T}P-c\alpha PB{B}^{T}P)\right]\epsilon +2{\omega }^T(Q\otimes D^{T}P)\epsilon +\frac{\varphi }{{\phi }_2}{\epsilon }^T\left[Q\otimes (C^{T}C)\right]\epsilon \\ & -z^{T}z+{\gamma }^2{\omega }^T\omega -{\gamma }^2{\omega }^T(I_N\otimes I_n)\omega ={\left[\begin{array}{c}\epsilon \\ \omega \end{array}\right]}^T\mathsf{\Theta }\left[\begin{array}{c}\epsilon \\ \omega \end{array}\right]-z^{T}z+{\gamma }^2{\omega }^T\omega \end{array}$$

(26)

where $\mathsf{\Theta }=\left[\begin{array}{cc}Q\otimes (PA+A^{T}P-c\alpha PB{B}^{T}P+\frac{\varphi }{{\phi }_2}{C}^{T}C)& Q\otimes PD\\ Q\otimes D^{T}P& -{\gamma }^2(I_N\otimes I_n)\end{array}\right]$.

According to the Schur complement lemma and $-{\gamma }^2(I_N\otimes I_n)<0$, $\mathsf{\Theta }<0$ holds, if and only if the following inequality holds

$$Q\otimes (PA+A^{T}P-c\alpha PB{B}^{T}P+\frac{\varphi }{{\phi }_2}{C}^{T}C)+\frac{1}{{\gamma }^2}{Q}^2\otimes PD{D}^{T}P<0$$

(27)

Then, analyze the inequality (27). One has

$$\begin{array}{l}Q\otimes (PA+A^{T}P-c\alpha PB{B}^{T}P+\frac{\varphi }{{\phi }_2}{C}^{T}C)+\frac{1}{{\gamma }^2}{Q}^2\otimes PD{D}^{T}P\\ \le Q\otimes (PA+A^{T}P-c\alpha PB{B}^{T}P+\frac{\varphi }{{\phi }_2}{C}^{T}C)+\frac{{\phi }_1}{{\gamma }^2}Q\otimes PD{D}^{T}P\\ \le Q\otimes (PA+A^{T}P-\tau PB{B}^{T}P+\frac{\varphi }{{\phi }_2}{C}^{T}C+\frac{{\phi }_1}{{\gamma }^2}PD{D}^{T}P)\end{array}$$

(28)

Then, invoking (23) gives that

$$Q\otimes (PA+A^{T}P-\tau PB{B}^{T}P+\frac{\varphi }{{\phi }_2}{C}^{T}C+\frac{{\phi }_1}{{\gamma }^2}PD{D}^{T}P)<0$$

Thus, (27) holds. It follows that

$$\dot{V}+z^{T}z-{\gamma }^2{\omega }^T\omega <0$$

(29)

Recalling that $V(0)=0$, one has

$$\begin{array}{ll}J& ={\displaystyle {\int }_0^{\infty }\left(z^T(t)z(t)-{\gamma }^2{\omega }^T(t)\omega (t)\right)}dt={\displaystyle {\int }_0^{\infty }\left(z^T(t)z(t)-{\gamma }^2{\omega }^T(t)\omega (t)+\dot{V}\right)}dt-V(\infty )+V(0)\\ & <{\displaystyle {\int }_0^{\infty }\left(z^T(t)z(t)-{\gamma }^2{\omega }^T(t)\omega (t)+\dot{V}\right)}dt<0\end{array}$$

Thus, condition (2) of Definition 2 is satisfied. Therefore, the $H_{\infty }$ formation tracking problem with external disturbances is solved.

In summary, the multi-agent system can achieve $H_{\infty }$ formation tracking. This concludes the proof.    □

Remark 5.

As mentioned in [40], time-varying formation tracking problems for linear multi-agent systems with multiple leaders were investigated. It provided a useful theoretical reference for the research of $H_{\infty }$ formation tracking in this paper. It is clear that consensus and consensus tracking problems are the special case of formation control problems, so there is a certain similarity of analysis to some extent. The time-varying formation tracking problems in this paper can be transformed into the consensus tracking problems if the conditions of the $h(t)\equiv 0$ and $v(t)\equiv 0$ are satisfied. Compared with the results derived in [38], where the communication topology is supposed to be strongly connected, the communication topology between the agents in this paper is described as a more general directed topology, which greatly relaxes the constraints of the topological networks.

3.2. $H_2$ Time-Varying Formation Tracking Algorithm

In this section, the $H_2$ time-varying formation tracking problem of multi-agent system (1) is discussed. It is obvious that $H_{\infty }$ performance index indicates the robustness of the multi-agent system to the worst case with external disturbances. However, the disturbance rejection performance of the multi-agent system with bounded external disturbances is shown by $H_2$ performance index. For a comprehensive analysis of the formation tracking problem, the $H_2$ time-varying formation tracking problem needs to be discussed. So, this section will analyze the conditions of $H_2$ formation tracking problem and provide an algorithm for solving parameters of distributed protocol.

To evaluate the effectiveness of the algorithm, the $H_2$ time-varying formation tracking problem under a distributed protocol (4) is defined as follows.

Definition 3.

The multi-agent system is said to achieve$H_2$time-varying formation tracking if the following conditions are satisfied:

(1) 

The following error dynamical system is stable when$\omega (t)\equiv 0$.

$$\{\begin{array}{l}\dot{\epsilon }=\left[(I_N\otimes A)+(L_1\otimes BK)\right]\epsilon +(I_N\otimes D)\omega \hfill \\ z=(H\otimes C)\epsilon \hfill \end{array}$$

(30)

(2) 

For the case of$\omega (t)\ne 0$. When the initial conditions are zero, in other words, $\epsilon (0)=0$and the external disturbances are excited by a pulse signal, that means$\omega (t)={\omega }_0\delta (t)$. The $H_2$performance index$J_2$is defined as the following equation that satisfies$J_2<\beta$.

$$J_2=\underset{\begin{array}{c}\omega (t)={\omega }_0\delta (t)\\ \Vert {\omega }_0\Vert \le 1\end{array}}{\sup }{\Vert z\Vert }_2$$

(31)

The following theorem proposes a sufficient condition for the multi-agent system to achieve the H₂ time-varying formation tracking.

Theorem 2.

Suppose the swarm system satisfiesAssumptions 1–3. The multi-agent system can achieve the$H_2$time-varying formation tracking utilizing the distributed formation tracking protocol (4) whose parameters are designed by (1)–(5) for a given performance coefficient$\beta >0$in the presence of external disturbances, if the desired time-varying formation specified by$h(t)$satisfies the following formation feasible condition (6):

(1) 

Computing${\tilde{B}}_1$and${\tilde{B}}_2$based onRemark 2.

(2) 

FromLemma 2and$0<\alpha <2\min \left\{\mathrm{Re}(\lambda (L_1))\right\}$, solving the following linear matrix inequality$Q{L}_1+L_1^{T}Q>\alpha Q$for a positive definite matrix$Q>0$.

(3) 

For chosen$\tau >0$, solving the following linear matrix inequality for a positive definite matrix$P>0$.

$$\left[\begin{array}{cc}PA+A^{T}P-\tau PB{B}^{T}P& C^T\\ C& -\frac{{\phi }_2}{\varphi }{I}_n\end{array}\right]<0,$$

(32)

where$\varphi =\max \left\{\lambda (H^{T}H)\right\}$, ${\phi }_1=\max \left\{\lambda (Q)\right\}$and${\phi }_2=\min \left\{\lambda (Q)\right\}$.

(4) 

For a given performance coefficient$\beta >0$, solving the following linear matrix inequality for a positive definite matrix$W>0$.

$$\left[\begin{array}{cc}-W& D^T\\ D& -\frac{1}{{\phi }_1}{P}^{-1}\end{array}\right]<0$$

(33)

$$trace(W)<\frac{{\beta }^2}{N}$$

(34)

(5) 

Selecting the coupling strength parameter as$c>\frac{\tau }{\alpha }$and let the constant gain matrix be$K=-B^{T}P$.

(6) 

The following formation feasible condition

$${\tilde{B}}_2(A{h}_i-{\dot{h}}_i)=0,i\in F$$

(35)

Below, we present an algorithm shown in Algorithm 2 to construct the parameters of distributed control protocol (4) for achieving $H_2$ time-varying formation tracking.

Algorithm 2 Procedures to design parameters for $H_2$ time-varying formation tracking
1:	for each agent $i\in F$ then
2:	Design a directed communication topology that satisfies Assumptions 1–3;
3:	Fix the desired formation function $h_i(t), i\in F$ for followers;
4:	Computing ${\tilde{B}}_1$ and ${\tilde{B}}_2$ based on Remark 2;
5:	if the formation feasible condition (35) is satisfied then
6:	From Lemma 2 and $0<\alpha <2\min \left\{\mathrm{Re}(\lambda (L_1))\right\}$, solving the linear matrix   inequality $Q{L}_1+L_1^{T}Q>\alpha Q$ for a positive definite matrix $Q>0$;
7:	Compute parameters by $\varphi =\max \left\{\lambda (H^{T}H)\right\}$,${\phi }_1=\max \left\{\lambda (Q)\right\}$, ${\phi }_2=\min \left\{\lambda (Q)\right\}$;
8:	Choose $\tau >0$, solving the following linear matrix inequality (32) for a positive   definite matrix $P>0$;
9:	For a given performance coefficient $\beta >0$, solving the following linear matrix   inequality (33) and (34) for a positive definite matrix $W>0$;
10:	Selecting the coupling strength parameter as $c>\frac{\tau }{\alpha }$ and computing the   constant gain matrix $K$ by $K=-B^{T}P$;
11:	Construct the distributed control protocol given in (4);
12:	else
13:	Back to Step 3;
14:	end if
15:	end for

Proof of Theorem 2.

By Schur complement lemma, the above inequality (32) implies that

$$PA+A^{T}P-\tau PB{B}^{T}P+\frac{\varphi }{{\phi }_2}{C}^{T}C<0$$

(36)

Considering the same Lyapunov function candidate as in the previous section

$$V_2={\epsilon }^T(Q\otimes P)\epsilon$$

(37)

By following the similar proof steps in Theorem 1, one can obtain the time derivative of the Lyapunov function along the trajectory of (19) as

$${\dot{V}}_2={\epsilon }^T\left[Q\otimes (PA+A^{T}P-c\alpha PB{B}^{T}P)\right]\epsilon +2{\omega }^T(Q\otimes D^{T}P)\epsilon$$

(38)

By comparing the conditions of Theorem 1 and Theorem 2, it is clear that condition (1) of Definition 3 is satisfied.

Next, demonstrate the $H_2$ performance index of the multi-agent system under the condition of $\epsilon (0)=0$ and $\omega (t)={\omega }_0\delta (t)$.

From (38), one has

$${\dot{V}}_2={\epsilon }^T\left[Q\otimes (PA+A^{T}P-c\alpha PB{B}^{T}P)\right]\epsilon +2{\omega }^T(Q\otimes D^{T}P)\epsilon -z^{T}z$$

(39)

Noting that the equations $\epsilon (0)=0$ and $\omega (t)={\omega }_0\delta (t)$ are equivalent to $\epsilon (0)=(I_N\otimes D){\omega }_0$ and $\omega (t)=0$, respectively. One can obtain from (36) that

$${\dot{V}}_2+z^{T}z<0$$

(40)

Considering inequality (40), it follows over the infinite horizon that

$${\Vert z\Vert }_2^2<{\omega }_0^T\left[Q\otimes (D^{T}PD)\right]{\omega }_0$$

(41)

Invoking ${\phi }_1=\max \left\{\lambda (Q)\right\}$ yields

$${\Vert z\Vert }_2^2<{\omega }_0^T\left[I_N\otimes ({\phi }_1{D}^{T}PD)\right]{\omega }_0$$

(42)

Furthermore, considering inequality (33) and (34), one can obtain

$${\Vert z\Vert }_2^2<{\beta }^2{\omega }_0^T{\omega }_0$$

(43)

Since $\Vert {\omega }_0\Vert \le 1$, one has

$${\Vert z\Vert }_2^2<{\beta }^2$$

(44)

Therefore, $H_2$ time-varying formation tracking of the multi-agent system is achieved. The proof is completed. □

Remark 6.

The formation tracking problems in this paper can be transformed into a consensus tracking problem, if$h(t)\equiv 0$and$v(t)\equiv 0$. That is to say, consensus control and consensus tracking control of the multi-agent system are special cases of formation tracking problems, i.e., [38]. Moreover, the communication topology graph is directed, which is more relaxed. Therefore, the theorems and algorithms are useful for practical applications. The properly designed Lyapunov functions and the property of the Laplacian matrix$L$play a significant role in the proof of theorems of this paper.

4. Simulation Results and Discussions

In this section, numerical simulation examples are provided to demonstrate the usefulness and effectiveness of the theoretical results presented in the previous section. For simplicity of description, considering a higher-order multi-agent system consisting of a leader and five followers whose directed communication topology is shown in Figure 2a, where the weights of connected communication edges are zero or one.

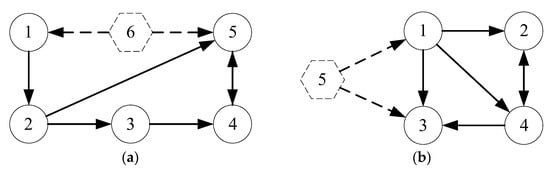
Figure 2. The directed communication topology. (a) The directed communication topology of leader and five followers in example 1 and example 2; (b) The directed communication topology of one leader and four followers in example 3.

The dynamics of all agents are described as follows with $x_i(t)={\left[x_{i1}(t),x_{i2}(t),x_{i3}(t)\right]}^T$.

$$\{\begin{array}{l}{\dot{x}}_{N+1}(t)=A{x}_{N+1}(t)\hfill \\ {\dot{x}}_i(t)=A{x}_i(t)+B{u}_i(t)+D{\omega }_i(t),i\in F\hfill \end{array}$$

where $A=\left[\begin{array}{ccc}0& 1& 1\\ 1& 2& 1\\ -2& -6& -3\end{array}\right]$, $B=\left[\begin{array}{cc}0& 1\\ -1& 0\\ 0& 0\end{array}\right]$, $D=\left[\begin{array}{c}0.1\\ 0\\ 0.05\end{array}\right]$.

For simplicity of computation, let $v_i(t)=0$ and $C=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]$.

The time-varying formation functions of followers are defined as follows:

$$h_i(t)=\left[\begin{array}{c}5\sin (t+\frac{2(i-1)\pi }{5})\\ -5\cos (t+\frac{2(i-1)\pi }{5})\\ 10\cos (t+\frac{2(i-1)\pi }{5})\end{array}\right],i\in F$$

The time-varying formation functions indicate that the five followers’ state trajectories will form a pentagon and keep rotation around the leader continuously. Let ${\tilde{B}}_1=\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\end{array}\right]$ and ${\tilde{B}}_2=\left[\begin{array}{ccc}0& 0& 1\end{array}\right]$ according to Remark 2. It is clear that the above time-varying formation functions satisfy the formation feasibility condition (13) of Theorem 1 and condition (35) of Theorem 2.

4.1. Example 1. Considering the $H_{\infty }$ Formation Tracking Problem

The external disturbances are defined as follows:

$$\omega (t)={\left[\begin{array}{ccccc}1\overline{\omega }(t)& 0.8\overline{\omega }(t)& 2\overline{\omega }(t)& 1.2\overline{\omega }(t)& 0.6\overline{\omega }(t)\end{array}\right]}^T$$

where $\overline{\omega }(t)=\{\begin{array}{l}2,0\le t\le 4\hfill \\ 0, \mathrm{others}\hfill \end{array}$.

From the Laplacian matrix of communication topology, one can obtain that $\alpha =1.5$.

Thus, by utilizing Algorithm 1, solving the linear matrix inequality $Q{L}_1+L_1^{T}Q>\alpha Q$ for a feasible solution matrix $Q$ as follows:

$$Q=\left[\begin{array}{ccccc}6.6454& 0.2163& -0.5117& 0.2636& 0.0616\\ 0.2163& 1.7912& -0.6913& 0.2257& 0.0839\\ -0.5117& -0.6913& 1.6255& -0.7196& -0.5824\\ 0.2636& 0.2257& -0.7196& 0.5528& -0.1130\\ 0.0616& 0.0839& -0.5824& -0.1130& 1.0184\end{array}\right]$$

Then, one can obtain that $\varphi =1$, ${\phi }_1=6.7371$ and ${\phi }_2=0.028$.

Choose the $H_{\infty }$ performance index $\gamma =1$.

Let $\tau =5.2$. Solving the linear matrix inequality (12) by utilizing Algorithm 1 and the LMI toolbox of MATLAB gives a feasible solution matrix $P$ as follows:

$$P=\left[\begin{array}{ccc}7.5137& 0.8096& 1.1743\\ 0.8096& 4.4455& 0.5502\\ 1.1743& 0.5502& 1.6952\end{array}\right]$$

Thus, the constant feedback gain matrix of (4) is provided as

$$K=\left[\begin{array}{ccc}0.8096& 4.4455& 0.5502\\ -7.5137& -0.8096& -1.1743\end{array}\right]$$

Therefore, the coupling strength parameter can be chosen as $c>3.6$. According to Theorem 1 and Algorithm 1, the multi-agent system can achieve the $H_{\infty }$ formation tracking with the feedback gain matrix $K$ and $H_{\infty }$ performance index $\gamma =1$, if the coupling strength $c>3.6$. For the case of external disturbances $\omega (t)\equiv 0$. The snapshots of the time-varying formation tracking states at moments $t=5 \mathrm{s}$ and $t=10 \mathrm{s}$ are shown in Figure 3. It indicates that the state trajectories of the multi-agent system achieve a pentagon formation and the point corresponding to the leader state trajectory lies in the center of the pentagon formation. Furthermore, for the case of zero initial conditions and external disturbances $\omega (t)\ne 0$, the trajectories of performance variables $z_i$, $i=1,2,\cdots ,5$ are shown in Figure 4. The results show that the multi-agent system has a good disturbance rejection performance with external disturbances. When there is no external disturbance, the performance variables are equal to zero. It is clear that the multi-agent system can achieve the $H_{\infty }$ time-varying formation tracking in the presence of disturbances by utilizing the distributed protocol (4).

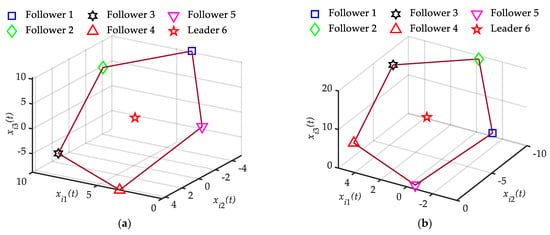
Figure 3. State snapshots of all the agents without external disturbances and the convex combination of five followers at different times. (a) t = 5 s; (b) t = 10 s.

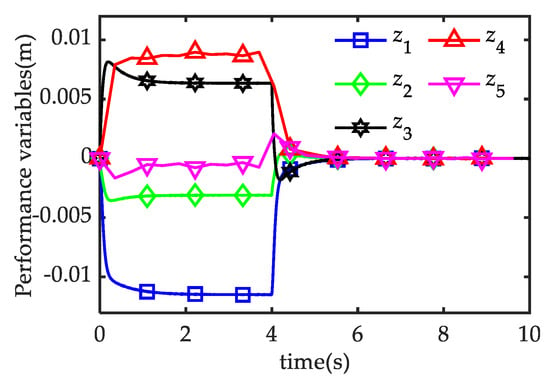
Figure 4. The trajectories of performance variables.

4.2. Example 2. Considering the $H_2$ Formation Tracking Problem

In this section, the $H_2$ time-varying formation tracking problem will be taken into consideration. The dynamics of agents and communication topology graph are the same as in Example 1. To demonstrate the effectiveness of the algorithm, the Gauss white noise with zero mean is chosen as external disturbances.

Choosing $H_2$ performance index $\beta =2$. By utilizing Algorithm 2, the constant feedback gain matrix can be solved as

$$K=\left[\begin{array}{ccc}0.2813& 4.6890& -0.8661\\ -4.2427& -0.2813& 0.3558\end{array}\right]$$

Then, according to Theorem 2 and Algorithm 2, the distributed protocol (4) can solve the $H_2$ time-varying formation tracking with performance index $\beta =2$ and the above chosen $K$ by choosing the coupling strength $c>7.4$. For the case of external disturbances $\omega (t)\equiv 0$. The snapshots of the time-varying formation tracking states at moments $t=5 \mathrm{s}$ are shown in Figure 5a. It is clear that the states of the five followers form a pentagon while rotating around the states of the leader, and the states of the leader are time-varying and lie in the center of the pentagon. The trajectories of state errors $x_i-h_i$, $i=1,2,\cdots ,5$ which are the differences between the states of followers and formation reference functions are shown in Figure 5b–d. From Figure 5b–d, one can see that the trajectories of state errors $x_i-h_i$ overlap with the trajectory of the leader. Therefore, the desired $H_2$ time-varying formation tracking with the leader is achieved.

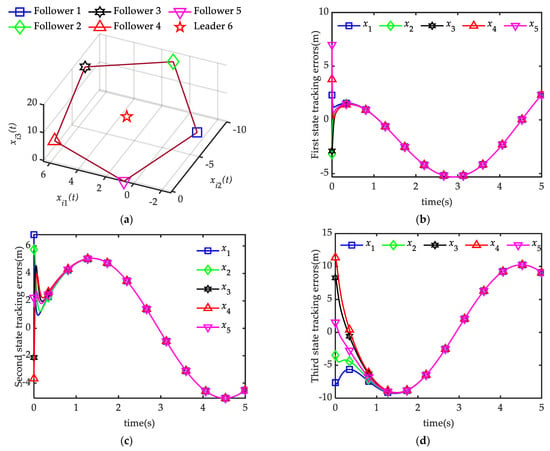
Figure 5. States snapshot of all the agents when $t=5 \mathrm{s}$ and state errors $x_i-h_i$, $i=1,2,\cdots ,5$ of five followers without external disturbances. (a) States snapshot of all the agents when $t=5 \mathrm{s}$; (b) First state errors $x_{i1}-h_{i1}$, $i=1,2,\cdots ,5$; (c) Second state errors $x_{i2}-h_{i2}$, $i=1,2,\cdots ,5$; (d) Third state errors $x_{i3}-h_{i3}$, $i=1,2,\cdots ,5$.

For the case of zero initial conditions and external disturbances of Gauss white noise with zero means, the snapshots of the time-varying formation tracking states at moments $t=5 \mathrm{s}$ are shown in Figure 6a. From Figure 6a, one can see that in the case of external disturbances, the states of five followers reach a pentagon shape and the state of the leader is located in the center of the formed pentagon while rotating. The state tracking errors $x_i-h_i-x_{N+1}$, $i=1,2,\cdots ,5$ of three orders of five followers are shown in Figure 6b–d. It can be seen that the state tracking errors stabilize within a small range. Therefore, the desired $H_2$ time-varying formation tracking with external disturbances is achieved.

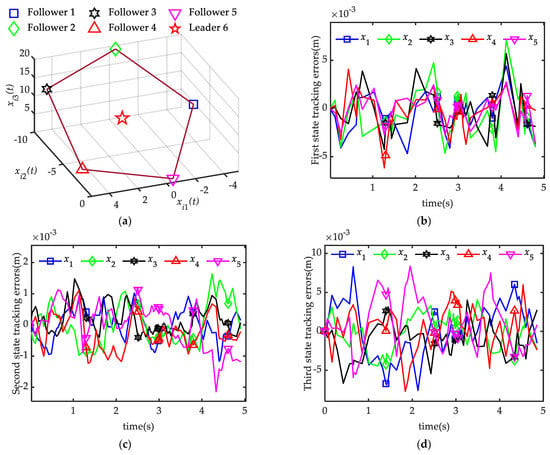
Figure 6. States snapshot of all the agents when $t=5 \mathrm{s}$ and state tracking errors $x_i-h_i-x_{N+1}$, $i=1,2,\cdots ,5$ of five followers with Gauss white noise disturbance. (a) States snapshot of all the agents when $t=5 \mathrm{s}$; (b) First state tracking errors $x_{i1}-h_{i1}-x_{N+1,1}$, $i=1,2,\cdots ,5$; (c) Second state tracking errors $x_{i2}-h_{i2}-x_{N+1,2}$, $i=1,2,\cdots ,5$; (d) Third state tracking errors $x_{i3}-h_{i3}-x_{N+1,3}$, $i=1,2,\cdots ,5$.

From Example 1 and Example 2, one can see that five followers achieve the expected time-varying formation around the leader using the proposed approach with or without external disturbance in this paper. The robustness of the multi-agent formation system to the worst case of external disturbances can be solved by $H_{\infty }$ time-varying formation tracking theorem and algorithm. Meanwhile, the robust disturbance attenuation performance of the multi-agent formation system to the bounded external disturbances can be guaranteed by $H_2$ time-varying formation tracking theorem and algorithm. Therefore, the algorithms can be used to solve the formation robust formation tracking problems with external disturbances under the conditions discussed in this paper. In practical applications, external disturbances caused by environmental changes are inevitable, so the research in this paper has important practical significance.

4.3. Example 3. Comparison of the Previous Approach and Current Approach

Consider a higher-order multi-agent system consisting of a leader and four followers. The directed communication topology of the system is shown in Figure 2b where the weights of connected communication edges are zero or one. The agent labeled by 5 is the leader and the agents labeled 1–4 represent the four followers. The multi-agent system needs to accomplish a quadrilateral shape and the leader is located in the center of the formed parallelogram while moving. The desired formation is described as

$$h_i(t)=\left[\begin{array}{c}5\sin (t+\frac{2(i-1)\pi }{5})\\ -5\cos (t+\frac{2(i-1)\pi }{5})\\ 10\cos (t+\frac{2(i-1)\pi }{5})\end{array}\right],i\in F$$

In order to further illustrate the effectiveness of the approaches proposed, the time-varying formation tracking protocol in [24] is provided as a comparison, where the gain matrix is designed as $K=\left[\begin{array}{ccc}1.0053& 3.9625& 0.5575\\ -1.2320& -1.0053& -0.3637\end{array}\right]$, and the external disturbances are defined as $\omega (t)={\left[\begin{array}{cccc}2& 3& 2& 3\end{array}\right]}^T$.

Figure 7 shows the formation tracking position trajectories and the position snapshots during the movement of four followers and one leader using the approach in this paper and previous work [24], respectively. The trajectories of the leader are denoted by the blue solid line. The four followers are represented by the square, diamond, hexagram, and upward-point triangle. Figure 7a shows that the followers achieve the desired circular formation and the leader is located in the center of the formation. Figure 7b shows that the leader is not located in the center of time-varying formation due to external disturbances.

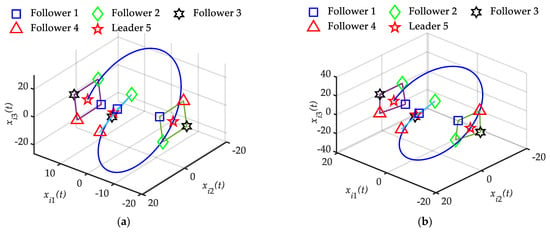
Figure 7. Formation tracking position trajectories and snapshots at different time instants of four followers and one leader. (a) Current approach; (b) Previous Approach [24].

In order to compare the tracking errors of different approaches, we calculate the two norm of error vectors of followers at different times. Figure 8 depicts the variation curve of two norm of the time-varying formation state tracking errors of four followers.

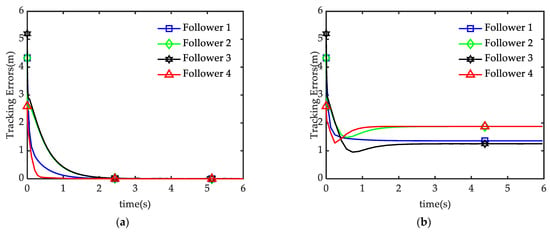
Figure 8. Variation curves of the time-varying formation tracking errors of four followers. (a) Current approach; (b) Previous Approach [24].

From Figure 7 and Figure 8, one can see that the four followers accomplish the desired quadrilateral formation and the leader is located in the center of the formed formation by using the approach in this paper. However, formation tracking cannot be accomplished using the approach in [24] due to external disturbances. Therefore, the proposed approach shows good performance while external disturbances exist.

5. Conclusions and Future Work

This paper studied $H_{\infty }$ and $H_2$ time-varying formation tracking control problems and proposed a distributed control protocol whose parameters can be determined by the proposed algorithms based only on the relative state information of neighboring agents.

(1)

Using local information about the state of neighbors of agents, the distributed $H_{\infty }$ and $H_2$ time-varying formation tracking protocol was presented. Some feasible sufficient conditions are provided to realize $H_{\infty }$ and $H_2$ time-varying formation tracking control of multi-agent systems. Algorithms and theorems are presented to design the parameters of distributed control protocol.

(2)

Theoretical basis of the proposed scheme was established by utilizing tools from Lyapunov stability analysis and algebraic graph theory and the control parameters were chosen via solving a linear matrix inequality. Followers can form and maintain the desired formation and achieve the trajectory tracking of the leader.

(3)

Numerical simulations of the proposed theorems and algorithms are carried out. The results show that theorems and algorithms can design the protocols which can be utilized to achieve formation tracking with guaranteed $H_{\infty }$ and $H_2$ performance index.

In future scope, the presented scheme may be extended to distributed output feedback control protocol for achieving $H_{\infty }$ and $H_2$ time-varying formation tracking of multiple leaders under communication delays with switching topology. Another important future research direction is to consider the $H_{\infty }$ and $H_2$ formation tracking with nonlinear dynamics. The theoretical results of this paper will be further experimentally verified on practical physical systems such as mobile robots.