1. Introduction
The Mean-Shift Outlier Model (MSOM) [
1] and Variance Inflation Outlier Model (VIOM) [
2] are the widely employed models in outlier accommodation in the literature. MSOM and VIOM are used not only for outlier accommodation but also for the detection of spatial outliers in the general spatial model as in the case of [
3,
4] in geodesy. Cook et al. [
1] noted that MSOM assumes that there is a shift in average of at least one of the responses, whereas [
2,
5,
6] described MSOM as case deletion for single observation that allows for a shift in the mean of the observations in question.
Outliers are those observations with large studentized residuals when the method of maximum likelihood (ML) or the ordinary least squares (OLS) are used in fitting the models. In the MSOM, the OLS are formulated with a dummy variable that assigns 1 for outlier and 0 otherwise. Insolia et al. [
7] noted that outliers detected through MSOM are assigned the weight 0 and hence, removed from the model, while the VIOM assumes that outliers result from inflation in the error variances [
2].
Cook [
2] also noted that the MSOM is a fixed effect model and VIOM is viewed as random effect version generated with certain variance. Beckman et al. [
8] highlighted that observations with inflated variance do not necessarily correspond to observation with large studentized residuals. Where the two correspond, however, then MSOM and VIOM agree with respect to the outlying models. According to [
8], employment of either MSOM or VIOM for accommodation depends on the relevance of the outlier; when it is assumed that the outlier contains vital information about the parameter in the model, VIOM is adopted, otherwise the MSOM is adopted.
The VIOM outliers are retained in the model in a weighted fit with the weight of each observation being inversely proportional to the variance of its random effect. Similar to the VIOM is the Variance Shift Outlier Model (VSOM). Gumedze [
9] adopted the term VSOM to focus on detecting the outliers and subsequently accommodate them in the model as shift in variance. Cook and Weisberg [
2] estimated the parameters of the fitted VSOM using the ML. Zimmerman [
10] suggested that the ML are biased due to “loss in degrees of freedom” from estimating the regression parameters.
A variant of the ML, which addressed the problem of loss in degree of freedom, Residual (Restricted) Maximum Likelihood (REML), is earlier adopted by [
5] to estimate parameters in VSOM, where [
6,
9,
11] employed VSOM as a robust outlier detection method. The VSOM is used to detect observations with inflated variance to isolate them for further investigation with earlier applications that include [
12,
13].
VSOM has advantage of downweighting outliers in the analysis, where weighting is automatically determined as part of estimation procedure [
9]. In some recent applications, Zhang et al. [
14] adopted MSOM for detection and accommodation of outliers in meta regression in a similar way [
11] adopted VSOM in meta-analysis. In the same vein, Insolia et al. [
7] claimed that VSOM achieves higher accuracy than MSOM due to accommodating outlier.
Gumedze [
9] proposed Likelihood Ratio (LR) test for determining whether an observation has inflated variance. Dai et al. [
3] employed MSOM and VIOM for outlier detection and accommodation in spatial statistics using the ML in line with [
15,
16,
17]. However, the ML is biased in estimating the regression parameters as noted by [
5,
10].
Insolia et al. [
7] relaxed the assumptions of constant variance through a parametric outlier model with parameterization that allows for two distinct groups of outliers that affect both the mean-shift and variance shift in the model. They stated that the parametrization is a mixed linear model that contain both fixed effect and random effect. They observed that combining mean-shift and variance shift could lead to over-parametrization. They further noticed that the VIOM is a generalization of the MSOM, since they are both functions of the studentized residuals.
Dai et al. [
3] adopted VIOM in spatial outlier detection and accommodation. However, they used the ML that is deficient of loss in degrees of freedom in their estimation. In addition, they accommodated the spatial outliers as a group instead of a fashion that will capture the spatial contiguity of the outlier as a block. These motivated us to accommodate the outliers with the proposed spatial variance shift outlier model (SVSOM) using the REML. Spatial outliers are accommodated based on spatial weights that contain neighborhood information, in the dependent variable and residuals of the spatial observations.
The variance shift outlier model (VSOM) is introduced in the classical regression model with the main aim of detecting observations with inflated variance and isolate them for further investigation. The attractive features of VSOM is the downweighting of those observations instead of deleting them, with the weights determined automatically as part of the estimation procedure. It is now evident that spatial outlier contains vital information about the outlier observation and also has an adverse effect on the computed values of various estimates.
Local instability, for example, can be discovered by identifying spatial outliers, which can lead to the discovery of unexpected, fascinating and implicit knowledge. In a variety of application, such as traffic control, satellite image analysis, weather forecasting and medical diagnostics, spatial outliers may disclose relevant occurrences [
18,
19]. In this regard, the formulation of VSOM in the spatial regression model to handle these issues has become pertinent.
In this article, the Variance Shift Outlier Model in the spatial representation using the Restricted Maximum Likelihood (REML) is formulated in the general spatial regression model (GSM). We call this model the spatial variance shift outlier model (SVSOM). The REML is used to estimate the variance components of the model where weights are incorporated based on the detected outliers in the model. A bootstrap method is used to generate the sampling distribution of the squared spatial studentized residuals so as to confirm the outlyingness of the detected outliers.
The rest of the paper is organized as follows:
Section 2 reviews the classical form of the variance shift outlier model.
Section 3 presents the proposed spatial variance shift outlier model and its representations.
Section 4 demonstrates the accommodation of the detected outliers using the weights based on the detected outliers.
Section 5 presents the simulation process and its results, and
Section 6 demonstrates the performance of the SVSOM using real life data. Finally,
Section 7 presents the conclusion of the article.
2. Variance Shift Outlier Model in the Classical Regression Model
The Variance Shift Outlier Model (VSOM) is a mixed effect model with a defined random effect that focuses on detecting outliers and then accommodating them into the model under the assumption that there is a shift in the variance of the outlier observations.
Consider the classical regression model:
where
y is an
vector of the response variable,
X is an
matrix of independent variable,
is
vector of regression parameters, and
is an
vector of the error terms, which is multivariate normally distributed (MVN). Define a dummy variable
, which is an
vector, with value 1 for position indexed by
i and 0 otherwise. Furthermore, define,
, an unknown random coefficient such that
, where
is the measure of inflation in the variance,
,
. The VSOM in linear regression model is given by
where
. The variance of any
ith observation is given by
. All observations with inflated variance would have variance shift from
to
. The Residual Maximum Likelihood (REML) by [
5] is used to estimate the coefficients of the model in Equation (2). Thompson [
5] and Gumedze [
9] have shown that the REML estimates of the variance components are given by
and
where
,
,
is the
ith diagonal term of the matrix
and
k is the number of regression parameters.
3. The Proposed VSOM in Spatial Regression Model (SVSOM)
The general spatial model (GSM) [
3,
15,
16] is a regression model that contains spatial autoregression in the dependent variable and the residual terms. Special cases of the spatial regression models are the spatial autoregressive-regressive model (SAR) and the spatial error autoregression model (SEM) that are deduced from the general spatial regression model when the coefficient of spatial autocorrelation in the residual term is zero, and the coefficient of spatial autoregression in the dependent variable is zero, respectively. The general spatial model is given in Equation (5).
Equation (5) can be re-written as
where
y is an
vector of response variable,
X is an
matrix of independent variables,
,
,
,
is the vector of random residual terms,
is the coefficient of spatial autocorrelation in the dependent variable
, and
is the coefficient of spatial autocorrelation in the residual term.
and
are
spatial weight square matrices. From Equation (6), we have
;
.
We adopt the VSOM in linear regression and formulate it to spatial regression model. We call the model as Spatial VSOM (SVSOM) and is given by
where
is an
vector with value 1 for position indexed by
i and 0 otherwise.
, and
is the weight measure that determines inflation in the variance,
. The expression in Equation (7) is similar to the variance-weight formulation of [
3].
We pre-multiplying Equation (7) by
B to obtain a generalized least squares (GLS) form
where
,
. Similarly,
is a diagonal matrix with the
ith diagonal element of value
, where
is the inflation in variance of
.
The model in Equation (9) is taken as the null model, which is equivalent to Equation (8) when
. This is because, in the null model, the index variable,
is
. Hence, it is the GLS form of the GSM.
The parameter estimate of the null model (9) is as follows
where
,
,
.
and
are the iteratively obtained ML estimates of
and
, respectively. The variance estimate for the null model is
, with
, and
.
As per [
9], the estimations for
and
can be obtained using mixed model equations for model (7) as given by
By using the REML method, the estimates of
and
are given by
and
where
and
is such that
.
is a variance component estimate, which is obtained using REML instead of ML. The variance component estimation for the SVSOM is obtained using the REML log likelihood function
as follows.
where
.
We adopt the method of [
5] for obtaining the estimate of the variance components in the classical regression model and extend this to the proposed SVSOM model. The idea is to first develop method of identifying influential observations for spatial regression and then define
and
using measures that encompass spatial information as follows
and
where
and
are the spatial studentized prediction residuals and residuals variance under null model, respectively,
and
is the spatial leverage of the
ith observation. The representations in Equations (12) and (13) use the same criteria of classifying suspicious observations in classical regression model, where [
9] employed
as in Equations (3) and (4).
Here, we propose using the spatial studentized prediction residual, , which is given by , where , is the ith column of matrix . The is the spatial studentized prediction residual that contains information on the spatial neighbourhood in both the dependent variable and residual term. The is the REML estimator of , which is smaller than the ML estimator by , as defined in Equation (9).
3.1. Identification of Inflation in Variance
In order to identify observations with inflated variance, index plot of the
are plotted. Accordingly, the largest
and
are obtained to determine observations with inflated variance with the aid of Equations (12) and (13). The log-likelihood,
, is calculated for each of the
ith observation. Observation with largest log-likelihood value has inflated variance and hence a potential outlier [
5]. In order to determine if the
ith observation has inflated variance or not, refs. [
6,
9,
11] test the hypothesis
using the likelihood ratio test,
as in the case of [
6,
9,
11], where
and
.
The residual log-likelihood function under null and alternative hypotheses are given by
and
respectively. The
follows the
distribution [
3,
4,
6,
11,
20] with degrees of freedom equals to the difference between model parameters in the two hypotheses. Gumedze et al. [
6] noted that the standard asymptotic theory does not hold due to the fact that the null hypothesis lies on the boundary of the parameter space. They adopted the parametric bootstrap to obtain the sampling distribution of the likelihood ratio test. The
is a monotonically increasing function of
and hence the hypothesis (14) can be tested directly based on
instead, as noted by [
9,
11].
3.2. Proposed Asymptotic Distribution of the
In line with [
6], a bootstrap method is adopted in generating the sampling distribution of the squared spatial studentized residuals (
) to confirm the outlyingness of the detected spatial outliers.
The sampling distribution of the is obtained from the following steps:
The GSM in Equation (9) is fitted to obtain , , and .
Using the estimated
,
,
and
X, generate a new set of dependent variable,
, such that
with
With the newly generated , fit Equation (9) and get the squared spatial studentized residuals (). Compute )% percentile of the for any suitable .
Repeat step 3 10,000 times to generate the empirical distribution of the and save in a vector .
Calculate the median of the vector in step 4 as a threshold for .
Declare any ith observation whose exceeds the threshold as an outlier.
Any observation declared as outlier based on the detection method and confirmed by the asymptotic , calls for a revised model for each of the outlying observations.
5. Simulation Experiment
In this section, we report a simulation study that is designed to investigate the performance of SVSOM model compared to GSM model. The spatial regression model in Equation (5) is simulated for a spatial grid, , (row standardized Queen’s contiguity spatial weights), and fixed throughout the simulation study for , and , . (vector of ones), , and the error term is , where is varied at 0.01, 0.10 and 1.00.
The simulation is run under five different contaminations: contamination on the dependent variable, y; contamination on the residual term, ; contamination on the dependent variable and the residual term; contamination on the independent variable, x, and the residual term; and contamination on y, and the x variable. The contamination on the dependent variable, y, is chosen such that they lie within the two extremes of the values (minimum and maximum).
They are only different from their neighbourhood values according to the first law of geography: “everything is related to everything else, but near things are more related than distant things” [
22]. The contamination in the dependent variable,
y, are location (1, 10) (with serial number 10) = 30 for
and 90 for
, location (10, 10) (with serial number 200) = 140 for
and 240 for
. The contamination in the residuals is assigned to location (1, 6) (with serial number 6) = 5 and location (14, 6) (with serial number 286) = −4.
The contamination in the x variable is assigned on the at the location (2, 6) (with serial number 26) = 15 and location (14, 6) (with serial number 286) = 10. The same locations are used for combination of contaminations. Furthermore, the same contamination locations and values are maintained for the residuals () and x variable. The simulation is run 5000 times for each of the combination of contamination source for different values of and .
As per [
7], the metric employed to measure the performance of the GSM and SVSOM in the presence of contamination is the Means Squared Error (MSE) of
(
).
where
k is the number of parameters in the model,
N is the number of times the simulation is run,
. On the other hand, the false positive rate (
) and true positive rate (
) for each of the 5000 runs for the different sources of contamination are calculated and averaged.
The simulation results for the
,
and
are summarised in
Table 1,
. Throughout the simulation study, the
for the SVSOM have maintained low values as compared to the GSM. The SVSOM consistently performs better than the GSM in estimating the true parameters of the model,
and
(see
Figure 1 and
Figure 2), for the fixed values of
and
. It is interesting to observe that the
’s are consistently closer to the true value, i.e.,
irrespective of the values of
,
and the contamination scenarios.
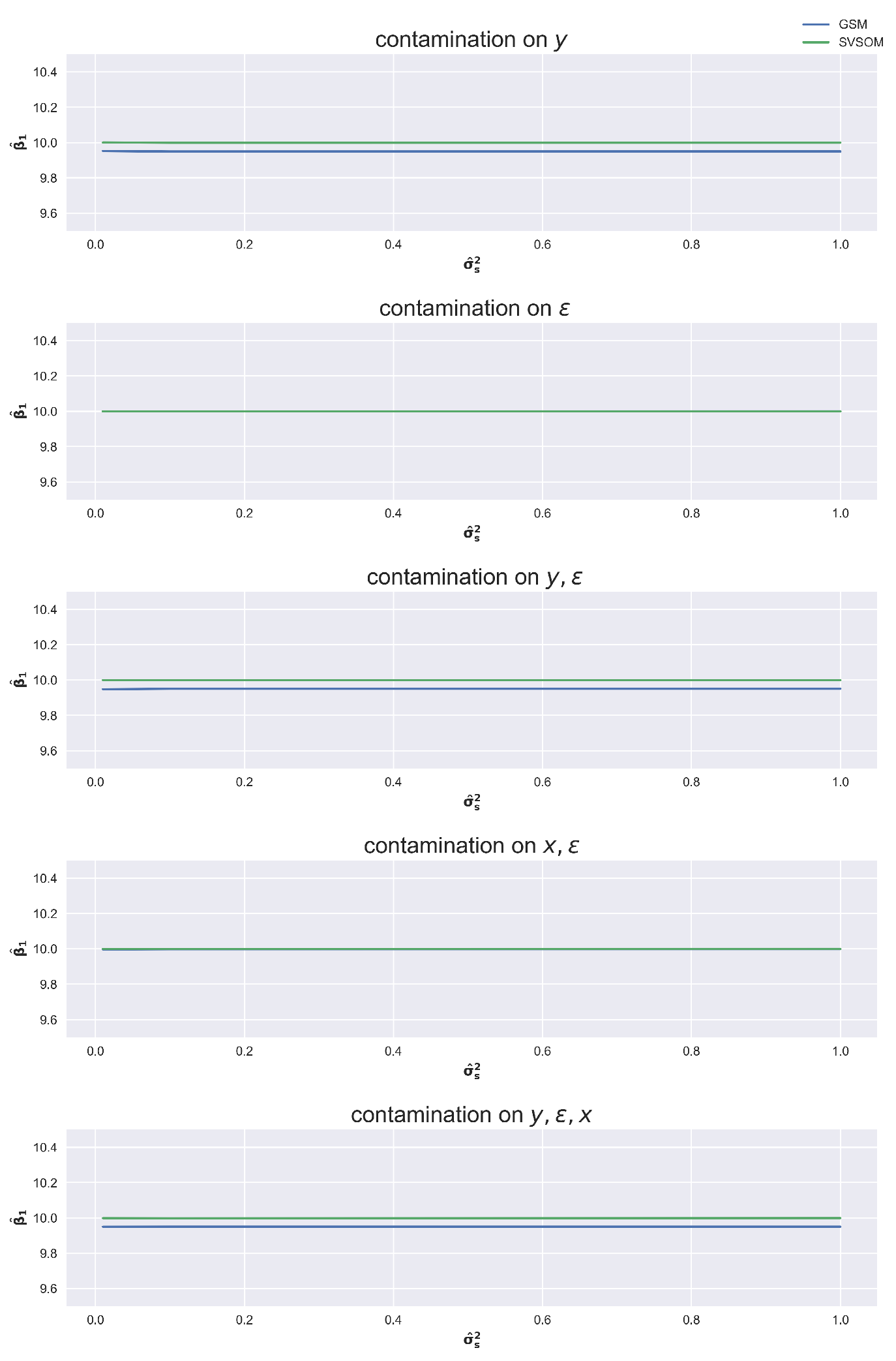
Figure 1 shows the graph of
against the variance,
when
,
, for contamination on
y, contamination on
, contamination on
y and
, contamination on
x and
and contamination on
y,
and
x for the GSM (blue line) and SVSOM (green line). The true value of the parameter,
, is 10, and the SVSOM has almost perfectly estimated it in all cases of contamination as depicted by the graph. Though the GSM almost coincides with the SVSOM when contamination is on the
and on the
x and
, the contamination that involves
y has a larger impact on the GSM fit. This graph further reveals that the contamination that does not involve
y over range of variances do not have much impact on both the GSM and SVSOM.
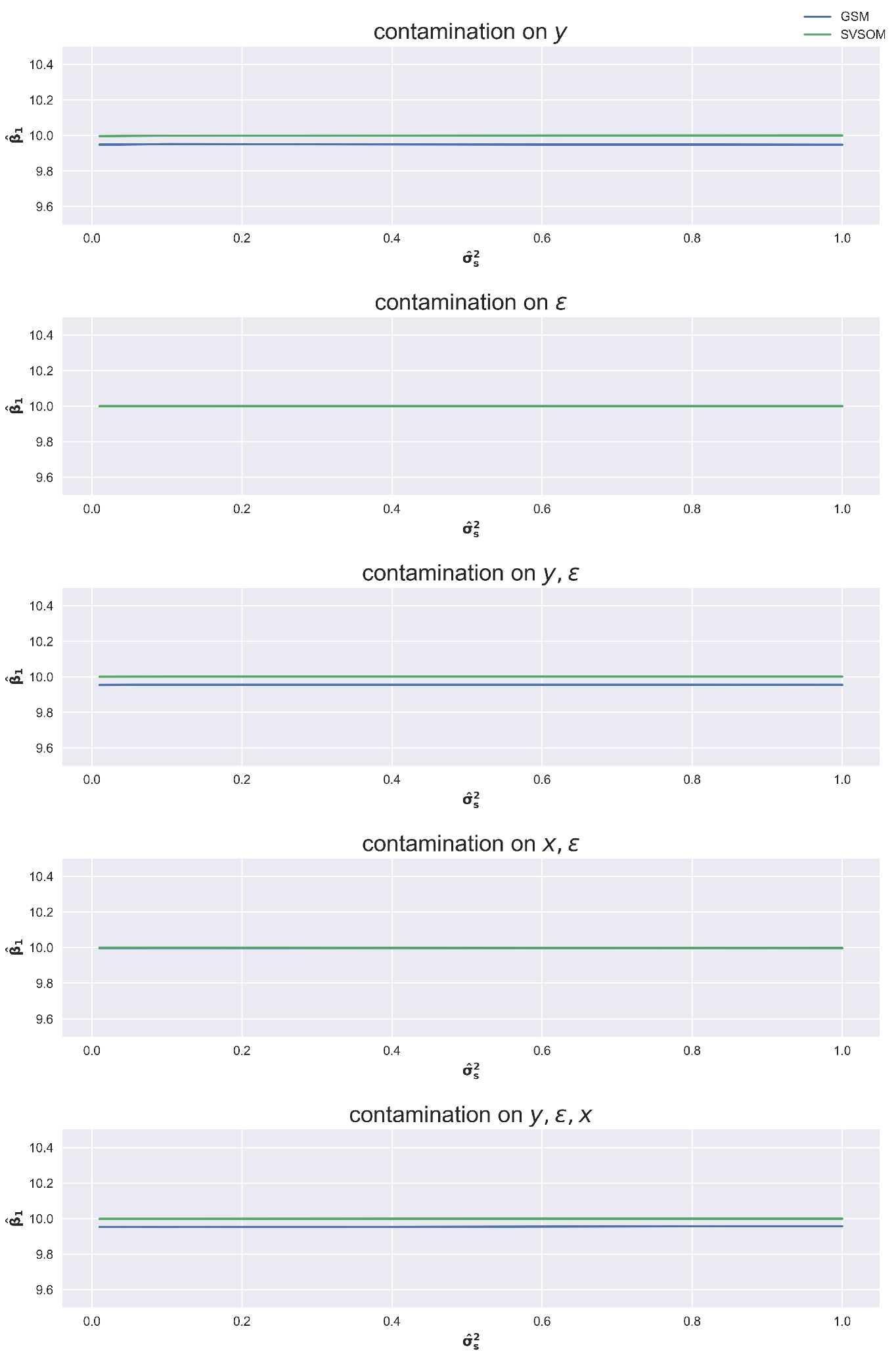
Similar results are obtained when
is plotted against the variance,
when
,
as displayed by
Figure 2. This further confirms the effectiveness of the SVSOM in handling the effect of influential observations compared to the GSM.
Table 1 depicts the values for the fits under different conditions of contamination, variances and the coefficient of spatial autocorrelation in the dependent variables and the residuals. The mean square error (MSE), which is a measure of quality of the method of estimation is also included in
Table 1. The MSE of the SVSOM are always much smaller in all cases of contamination than the GSM, which further supports the efficiency of the SVSOM.
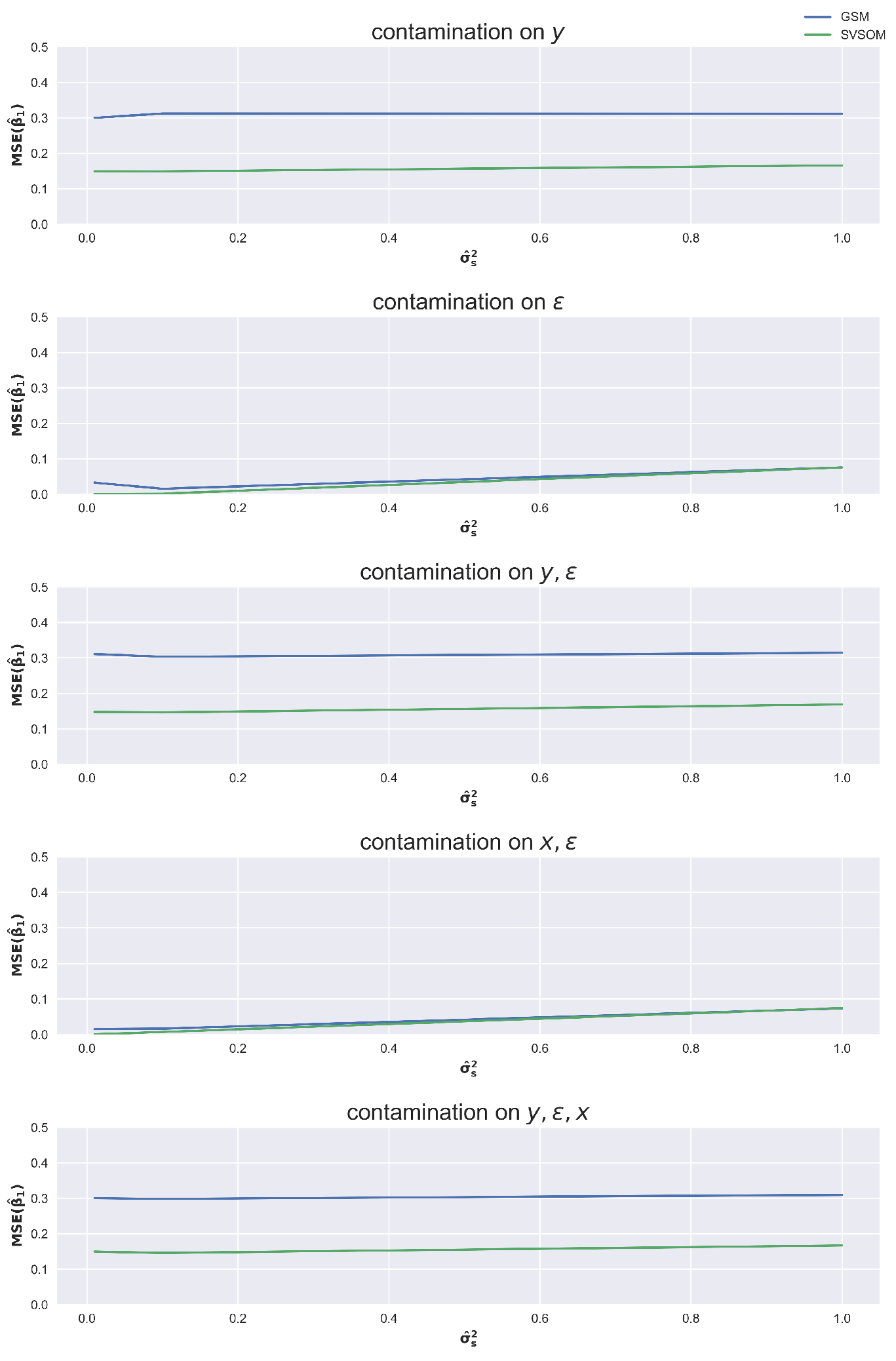
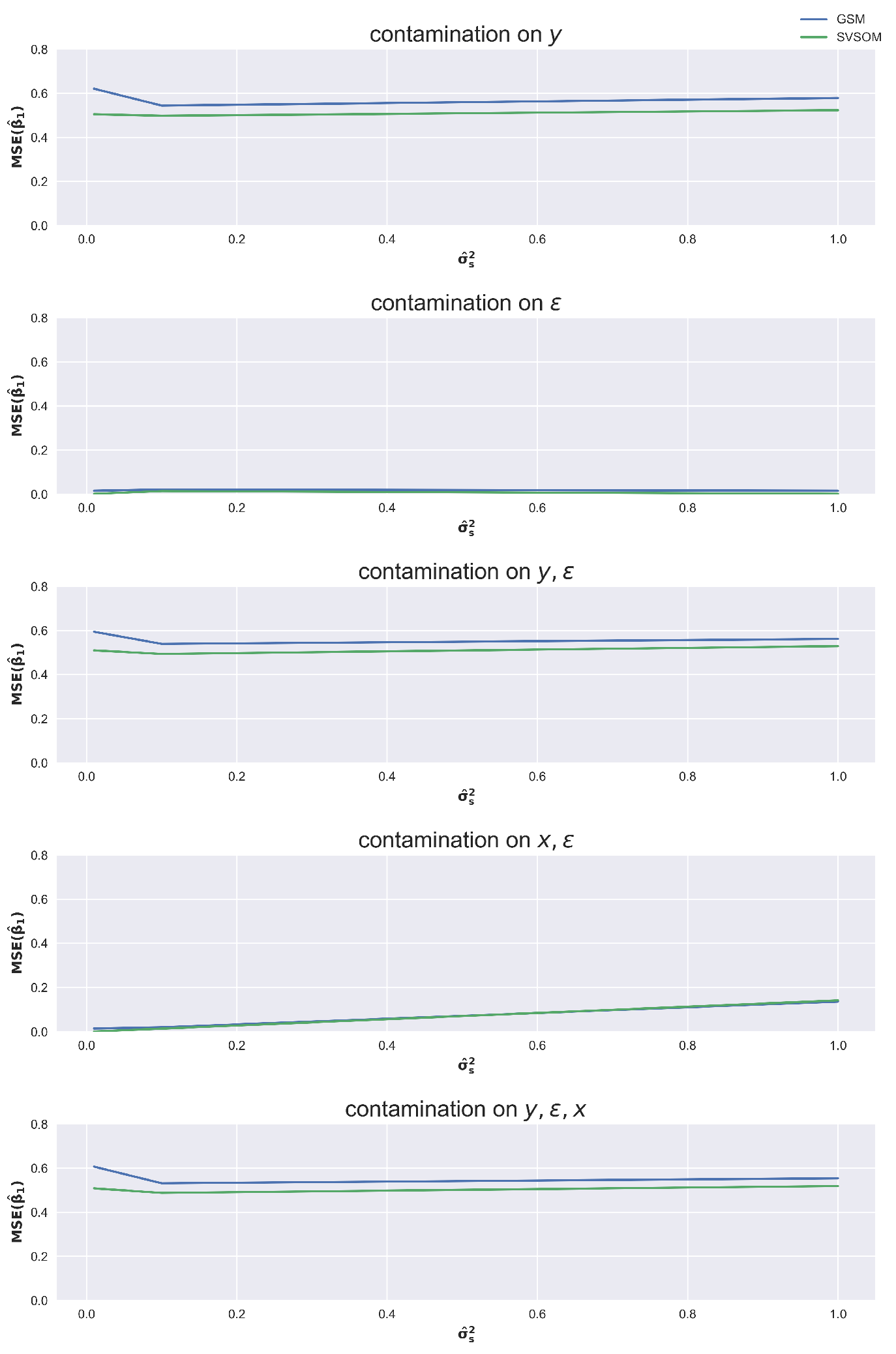
The lower coefficients of spatial autocorrelation,
and
, have produced smaller
in both GSM and SVSOM fits than the larger coefficients,
and
as can be observed from
Figure 3 and
Figure 4.
Contamination in the residual term, , has little or no influence on the parameter estimation in the SVSOM, where it stands at value very close to zero in all cases, for both lower and larger coefficients of spatial autocorrelations. Similar performance is observed in GSM, but with slightly larger MSE value and deviation from the true parameters.
Contamination in y or combinations that include y has/have greater influence on both the GSM and SVSOM fits. This is revealed by the values. However, in all forms of the outliers, the SVSOM outperforms the GSM.
Though the for the large coefficients of spatial autocorrelation, (0.7, 0.8), is large compared to that of smaller coefficients of spatial autocorrelation, the values of the estimated remain consistently very close to the true parameter value of . The values of the are slightly greater than one for , , .
The performance of our proposed method is investigated further by the power of test whereby it measures the rate of correctly classifying an observation in classification models. In common statistical terminology, it is referred to as probability of not making a type II error. The false positive rate, on the other, is the probability of committing a type I error.
In order to determine the power of the test, we record the number of times the SVSOM correctly classifies the clean observation in a 5000 runs of Monte Carlo simulation. Similarly, the false positive (also known as swamping) is obtained by recording the number of times the null hypothesis that the classified observation is wrongly rejected in favour of alternative in the 5000 runs of the simulation.
The power of the tests for the SVSOM is tabulated in
Table 2 for the contamination on
y,
,
y and
;
x and
; and
y,
and
x. The GSM is used only for estimation of parameters, while the SVSOM does both parameter estimation and classification. Thus, the power test for the SVSOM is presented in
Table 2.
The results of the power of the test statistics and false positive rate clearly demonstrated the robustness of the SVSOM as suggested by the following observations with respect to the various contamination or their combinations.
Due to the fact that contamination on the dependent variable, y, has influence on the model fit, the SVSOM accurately picks and classifies the outliers.
As demonstrated by the results of the simulation study, an outlier in the residual term does not mask other locations and hence yields a large power statistic according to the contamination criteria. Due to the robustness of the SVSOM, the effect of the contamination is neutralized, and a better estimate of the true parameter is always obtained.
Contamination in x and does not have much influence on the fit as demonstrated by the simulation study. The power statistics illustrate that the combination masked other locations as outliers and, hence, reduced the power.
Contamination on the y and yields results similar to those of contamination on y. Though some contaminated locations and masked locations are picked as outliers as a result of contamination on , contamination on the y variable is almost always picked due to the influence on the fitted model.
Similar to contamination on y and , contamination on y, and x masks other locations; hence, the lower power.
Worth nothing is that the false positive rate in all cases is very low (less than 0.05). The robustness of SVSOM is demonstrated in its performance in the simulated results.
6. Numerical Example
In this section, an artificial spatial data set and COVID-19 data set in the counties of Georgia state, USA are used to evaluate the performance of the SVSOM compared to the GSM. These datasets are also used to demonstrate the importance of the proposed method instead of using the classical regression approach, i.e., the ordinary least squares (OLS), when analysing data having spatial dependence. Empirical distribution of are generated for both datasets.
6.1. Artificial Data
In the artificial data, simulated data set discussed in the simulation study is used to fit the SVSOM to detect observations with inflated variance for investigation as outliers. We use the data for . and , with contamination on the dependent variable, y. We wish to fit the model in Equation (5), , .
The GSM estimates of the parameters are:
and
. The corresponding estimates for the SVSOM are
,
, with
and
.
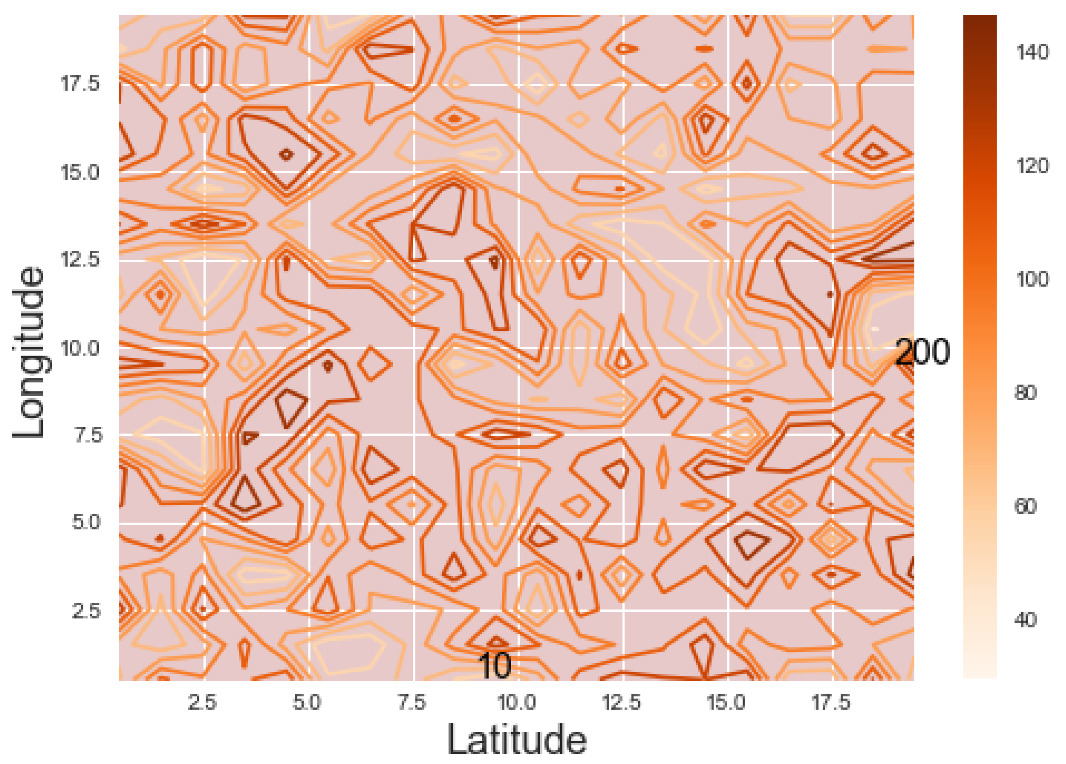
Figure 5 shows the contour map of the simulated data indicating the contaminated locations.
The SVSOM correctly classified only the contaminated locations as outliers (serial number 10, location (1, 10) and 200 (location (10, 10)).
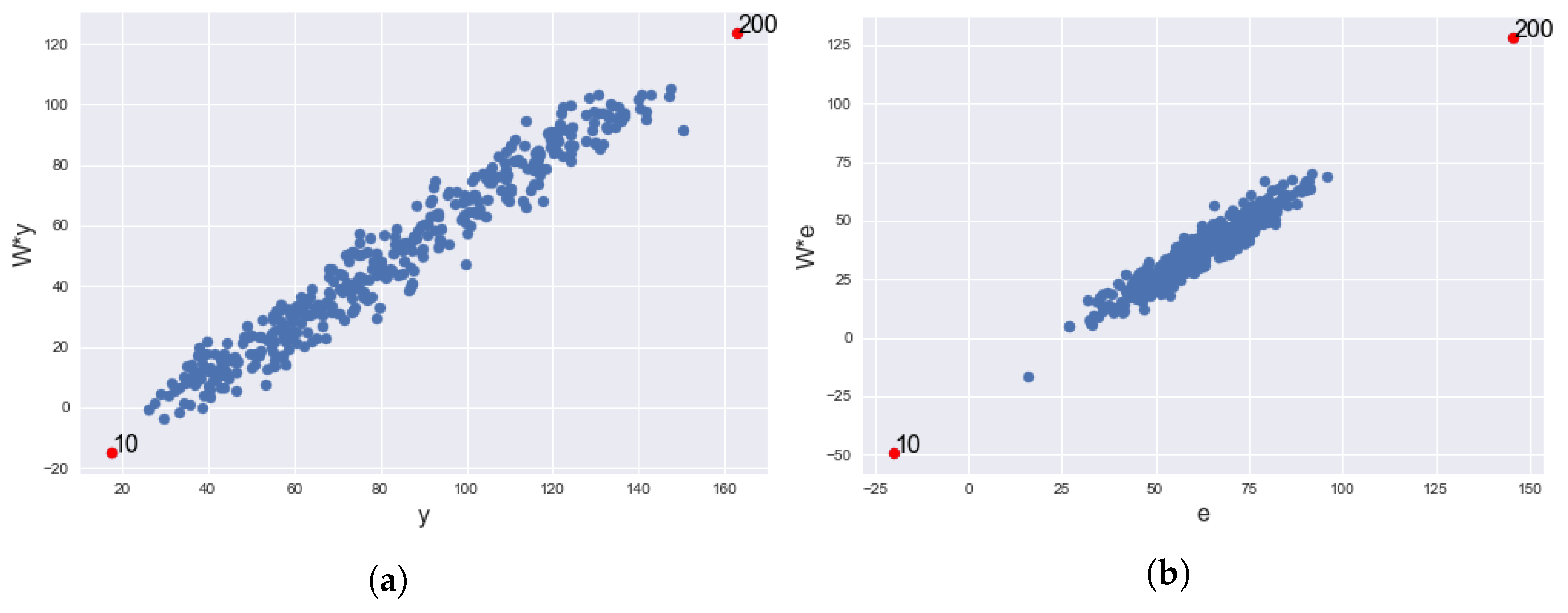
Figure 6 shows the scatter plot of the dependent variable against its average neighbourhood values and that of the autocorrelated residual against its average neighbourhood residuals, depicting spatial dependence in both the dependent variable and the autocorrelated residuals. Common to both of the graphs is that the contaminated locations (10 and 200) stand out away from their neighbourhood values in the dependent variable (
Figure 6a) and the residuals (
Figure 6b).
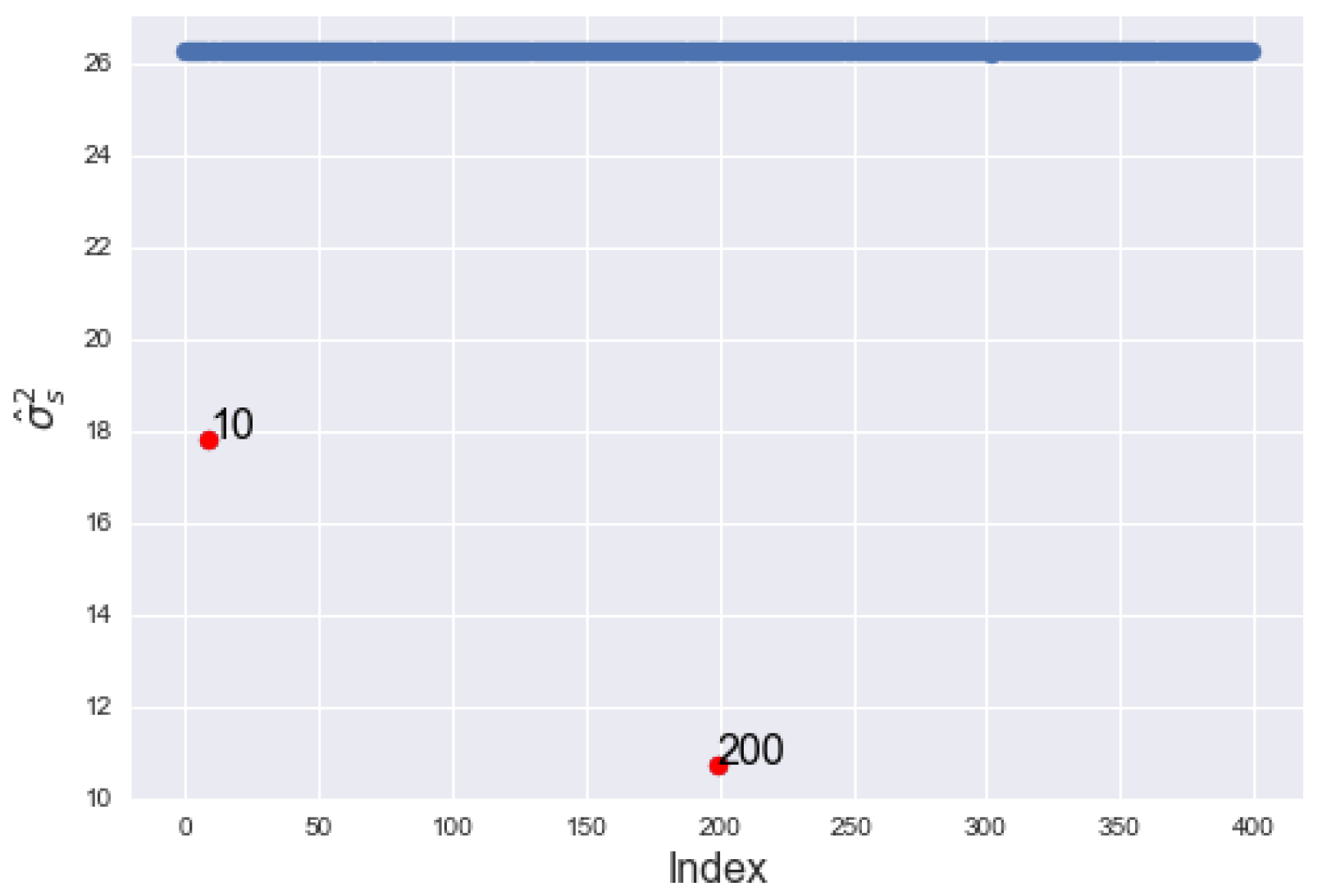
Figure 7 shows the index plot of the simulated data for
and
with contamination at location (1, 10) (serial no. 10) = 30 and location (10, 10) (serial no. 200) = 140, with red dots. It is noticeable from the graph that the two contaminated locations have the largest
(
Figure 7a) and
(
Figure 7b) with the lowest variance,
(
Figure 8). The dash-dot red line in
Figure 7a of index plot of
indicates the threshold, which is obtained based on the asymptotic distribution discussed in
Section 3.2.
Since the results of the fitted SVSOM revealed that the observations with serial number 10 and 200 (location (1, 10) and location (10, 10)) have inflated variances, they should be retained in the model by down weighting them, using estimated and .
It is important to note that fitting the ordinary least squares (OLS) to the artificial data yields and . The OLS estimates are much affected by spatial dependence because the values of and are quite far from the true values ( and ). Consequently, a misleading conclusion is obtained from the classical regression approach.
The VSOM in the classical regression could not detect the outliers since they are not global outliers but local. This clearly reveals the weakness of the OLS in addressing the problem of spatial dependence and the need for the incorporation of the spatial contiguity while fitting the spatial regression model. The GSM yields the estimates
and
. The SVSOM yields
,
,
and
. Thus, the revised model for the outliers are as follows:
where
and
,
and
.
As confirmed in the simulation results, where the SVSOM produces estimates very close to the true parameters than the GSM, the SVSOM estimate: and , are much closer to the value of true parameters, and . On the other hand, estimates for the GSM and , which are not so close to the true values. This is an assurance on the side of the SVSOM for estimation accuracy in addition to accommodation of the spatial outliers.
6.2. Georgia State COVID-19 Data
The Georgia State COVID-19 data is obtained from as at 30 June 2020 (
http://dph.georgia.gov/COVID-19-daily-status-report). The health ranking are from (
http://www.countyheathrankings.org). The dependent variable is the case-rate per 100,000 of COVID-19 cases. The independent variables are population of black race in the county
, population of Asians
, population of Hispanic
, population of people that are 65 years and above
, population of female in the county
and life expectancy
.
The Akaike Information Criteria (AIC) for the SAR, SEM and GSM indicate that the SAR has the lowest AIC of 2192. Hence, the data fitted for SAR. The results of the parameter estimation for the OLS, SAR (a variation of GSM) and SVSOM fit for the Georgia COVID-19 data are presented in
Table 3. The table also presented the inflation in the variances of the suspected outlier counties flagged by the RSDP that call for revised model in the SVSOM. It is interesting to observe the effect of spatial dependence on the OLS estimates.
Similar to the artificial data, the OLS gives the worst results evident by having standard error of estimates, which are much larger than the GSM and SVSOM. On the other hand, the results in
Table 3 clearly shows that the SVSOM possesses the least values of standard errors in comparison with other estimators. Relying on the classical regression will produce less efficient estimates and inaccurate predictions. Hence, it is important to use the SVSOM get better inferences.
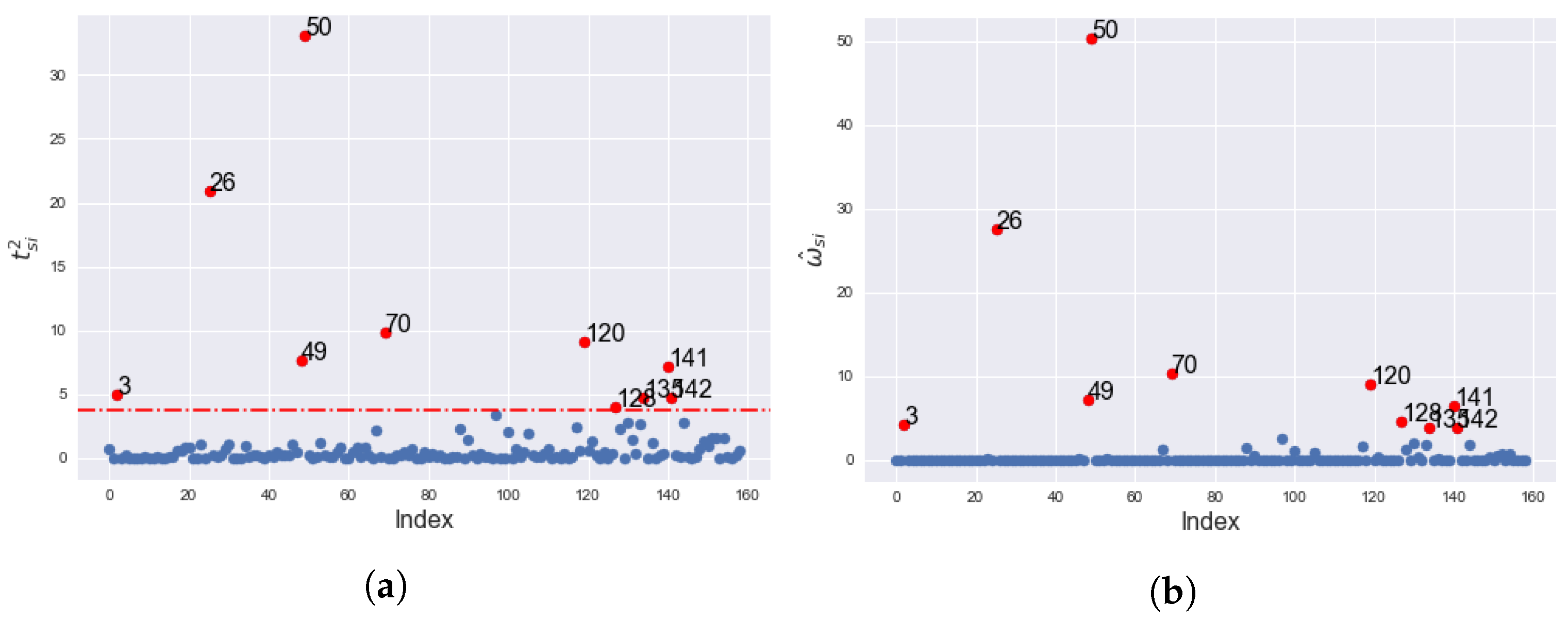
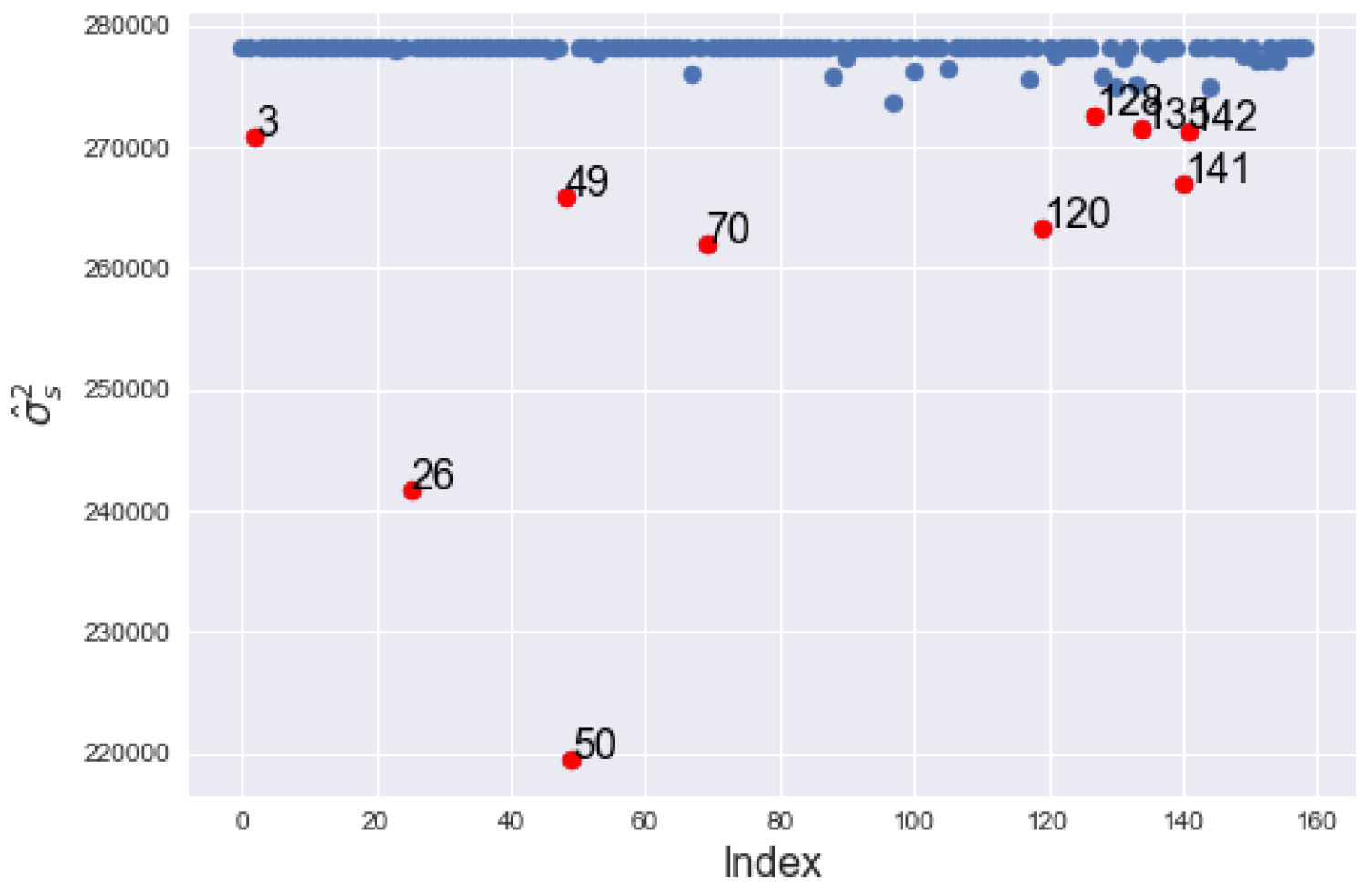
The index plot of the squared spatial studentized residuals in
Figure 9a shows the counties detected as outliers, having large
. Similarly, the index plot of the
in
Figure 9b shows the classified counties with the largest weights and, hence, inflation in the variance. The RSDP correctly classified counties with serial number 3, 26, 49, 50, 70, 120, 128, 135, 141 and 142, respectively.
Figure 9a shows the serial numbers of the counties with inflated variance that are greater than the threshold value of 3.73. Similarly,
Figure 9b and
Figure 10 show the indices of locations with largest weight (
) and that with inflation in variance (
), respectively.
Figure 11 shows the choropleth map for the cases in the counties and that of their corresponding squared spatial studentized residuals. County with serial number 50 (Echols) is the only county that is globally extreme to the cases of COVID-19 in Georgia, while all other detected counties are local to their neighbourhood. Though
Figure 11a depicts some dissimilarity between classified counties with their neighbourhood,
Figure 11b displays a clearer view, where the detected counties differ with their neighbourhood.
The SVSOM for accommodating the spatial outliers in the Georgia COVID-19 data is given by Equation (18).
Let the set of locations with largest
in the fitted model of Georgia COVID19 data be
, for all
and
,
and
The model in Equation (18) is the fitted SVSOM. Each ith elements in the flagged set, would have a revised model with the variance inflation effect for each of its element as defined in Equations (19) and (20).