Study on a Strong and Weak n-Connected Total Perfect k-Dominating set in Fuzzy Graphs

Abstract

In this paper, the concept of a strong $n$-Connected Total Perfect $k$-connected total perfect $k$-dominating set and a weak $n$-connected total perfect $k$-dominating set in fuzzy graphs is introduced. In the current work, the triple-connected total perfect dominating set is modified to an $n$-connected total perfect $k$-dominating set $n_{ctpkD}$(G) and number $\gamma n_{ctpD}\left(G\right).$ New definitions are compared with old ones. Strong and weak $n$-connected total perfect $k$-dominating set and number of fuzzy graphs are obtained. The results of those fuzzy sets are discussed with the definitions of spanning fuzzy graphs, strong and weak arcs, dominating sets, perfect dominating sets, generalization of triple-connected total perfect dominating sets of fuzzy graphs, complete, connected, bipartite, cut node, tree, bridge and some other new notions of fuzzy graphs which are analyzed with a strong and weak $n_{ctpkD}$(G) set of fuzzy graphs. The order and size of the strong and weak $n_{ctpkD}\left(\mathrm{G}\right)$ fuzzy set are studied. Additionally, a few related theorems and statements are analyzed.

1. Introduction

Fuzzy set theory is a recently developed mathematical framework that seeks to represent the issue of uncertainty in day-to-day challenges. Science and innovation today are described by intricate processes and occurrences for which comprehensive information is not always available. Different types of numerical models with aspects of uncertainty have been developed for such situations. Numerous models rely on the growth of the conventional set hypothesis, particularly fuzzy sets. Zadeh [1] proposed the concept of fuzzy sets as a method of conveying uncertainty and fuzziness. Since then, several disciplines have been researching the topic of fuzzy sets. Additionally, research into fuzzy logic has expanded exponentially in both mathematics as well as its applications [2,3,4].

The crisp graph’s generalization is a fuzzy graph. Throughout this method, it is typical that a lot of the characteristics of a fuzzy graph approach those of a crisp graph while deviating widely in other areas. The initial definition of a fuzzy graph was proposed by Kauffman [5] in 1973, and it was based on fuzzy relations that Zadeh [1] had introduced. Rosenfeld [6] introduced the idea of fuzzy graphs in 1975 based on Kauffman’s approach. He added a new, more thorough description of fuzzy graphs and established numerous findings using fuzzy graphs as an analogue to graph theory. Operations on fuzzy graphs were first introduced by Moderson and Nair [7], but Sunitha and Vijayakumar [8] expanded on this idea. The concept of fuzzy graph complement was described in ref. [7], and various fuzzy graph operations were explored in ref. [8].

In his article on fuzzy graphs [9], Bhattacharya lays out the connectivity notions between fuzzy cut nodes and fuzzy bridges. Arcs in the fuzzy graph were categorized by Mathew and Sunitha [10] based on their strength. Fuzzy graphs can be used to shed light on a wide range of problems. Fuzzy graphs are a relatively new concept, yet they have already found numerous uses in a variety of industries. In graph theory, the idea of dominance has been extensively researched. Numerous literary pieces have been written about various graph domination problems. More than 1200 publications linked to the domination of graphs are listed in a book [11] on the subject, and thousands of articles were published after the book’s release. A massive effort has been put forward in recent years in the study of fuzzy graph dominance. This generates a wealth of connected literature. To the best of the author’s knowledge, some effort has been made to systematically summarize the many kinds of domination in distinct fuzzy graphs. Up-to-date analysis of fuzzy graph dominance is provided in this article. The dominance problem is one of the most researched topics in graph theory due to the vast range of applications it offers and the accessibility of many of its forms. In the 1850s, a chess problem gave rise to a study of dominating sets in graphs. The majority of the dominating set has additional properties such as: being an independent set, inducing a connected subgraph or inducing a clique. These properties were reflected in their names as an adjective: independent domination, connected domination and clique domination in graph theory, respectively [12]. The types of domination in fuzzy graphs that have been researched primarily fall under the category of vertex domination. The idea of domination in fuzzy graphs utilizing effective edges was first suggested by Somasundaram [13]. They established some dominating properties for crisp graphs in ref. [14] that also apply to fuzzy graphs. In the same publication, they also established the terms independent dominance, total dominance, independent dominance number and total dominance number of fuzzy graphs. The impact of removing a vertex on its domination number was also researched [14]. Manjusha et al. [15] described total domination in fuzzy graphs using strong arcs. They also investigated high dominance in fuzzy graphs. Manjusha and Sunitha [16] defined strong domination in fuzzy graphs. Most instances of domination in fuzzy graphs may be connected back to the work of Nagoorgani et al. [17,18,19]. Bhutani and Rosenfeld [20] investigated strong arcs in fuzzy graphs. Senthilraj [21] defined a study on the double, triple and $n$-tuple domination of fuzzy graphs. Shanga et al. [22] modified algorithms for the minimum $m$-connected $k$-tuple dominating set problem. Nagoorgani and Gowri [23] studied fuzzy $k$-domination using a strong arc. Bharathi [24] introduced a note on $k$-domination in fuzzy graphs. Chaluvaraju et al. [25] studied perfect $k$-domination in graphs. Elavarasan and Gunasekar [26,27] introduced triple-connected total perfect domination and $n$-connected total perfect $k$-domination in fuzzy graphs. Natrajan and Ayyaswamy [28] introduced strong (weak) domination in fuzzy graphs. Revathi et al. [29,30,31] published some results regarding the perfect dominating set, triple-connected perfect and strong and weak triple-connected perfect dominating set in fuzzy graphs. Sarala et al. [32,33] published some results for this new parameter and introduced a strong (weak) triple-connected domination number of fuzzy graphs. In the present study, our standard results on the triple-connected total perfect domination of fuzzy graphs expand upon those developed by Kathavarayan et al. [34].

2. Preliminaries

This section provides the basic definitions of fuzzy graph theory. It should be noted that many concepts for fuzzy graphs are borrowed from regular graph theory. Important connections with recent literature in regard to fuzzy set theory [35], graph theory [36] and fuzzy graphs [37] may be viewed by the readers.

The membership function σ of a base set V specifies the fuzzy set of that set, where σ ∶ V → [0, 1] determines the degree to which u belongs to σ each u ∈ V. If there exists a set of membership functions σ: V → [0, 1] and μ: V × V → [0, 1] such that μ(u, v) ≤ σ(u)˄σ(v) for every u, v ∈ V, then G = (σ, μ) is referred to as a fuzzy graph. If $\tau$(u) ≤ $\sigma$(u) where u ∈ V and $\rho \left(u,v\right)\le \mu \left(u,v\right)$ for every u, v ∈ V, then H = ( τ , ρ ) is defined to be a fuzzy subgraph of G. The fuzzy graph H is considered a spanning fuzzy subgraph of G if $\tau$(u) = $\sigma$(u) where u ∈ V and $\rho \left(u,v\right)\le \mu \left(u,v\right)$ for every u, v ∈ V. An arc (u, v) is referred to as a strong edge if ${\mu }^{\infty }$(u, v) ≤ (u, v) for every u, v ∈ V. Since ${\mu }^{\infty }$(u, v) is the strongest path strength, the node u is a strong neighbor to v; otherwise, it is referred to as a weak arc. If (u, v) = 0 for all v ≠ u, v ∈ V, the vertex u is considered isolated in G. d_N(v) = ${\displaystyle \sum }_{\left(u\in N_s\left(v\right)\right)}\sigma \left(u\right)$, δ_N(G) = min{d_N(u): u ∈ V(G)} and ∆$N$(G) = max{d_N(u): u ∈ V(G)}. Order $n$ =${\displaystyle \sum }_{\left(u\in V\right)}\sigma \left(u\right)$ and Size q = ${\displaystyle \sum }_{\left(\left(u,v\right)\in E\right)}\mu \left(u,v\right)$. G is referred to as complete if µ(u, v) = σ(u)˄σ(v) for all u, v ∈ V. It is described by K_σ. G is divided into two parts: V₁ and V₂. The bipartition (V₁,V₂) is referred to as a complete bipartite $K$_(m,n) of G if all nodes in V₁(V₂) are strong neighbors in V₂(V₁). The fuzzy node connectedness $n$(G) of a connected G has the lowest strong weight of all fuzzy node cuts of G. Similarly, the fuzzy arc connectedness $m$(G) of a connected G has the lowest strong weight of all fuzzy edge cuts of G. If (u, v) is a strong edge, then for any vertex u, v ∈ V of G, the vertex u dominates the node v. P_D is considered a perfect dominating set of G if all vertex v ∉ P_D of V is absolutely dominated by a vertex of P_D. The fuzzy graph C_pD is said to be connected to P_D if it is connected to a subgraph and induced by the P_D of G. The fuzzy set T_pD is referred to as the total P_D of G if all vertex of G dominate at least one vertex of T_pD(G). The set C_tpD in a fuzzy graph G is said to be connected to T_pD if it has a connected subgraph induced by T_pD(G). A C_tpD of G is referred to as a minimal C_tpD(G) if for every node C_tpD − {v} ∉ C_tpD(G). γ_ctp(G) = min{ctp(G)} and Γ_ctp(G) = max{ C_tpD(G)}. Tc(G) stands for triple-connected fuzzy graph where three vertices are connected and located on the G path Tc. T_ctpD is said to be triple-connected to T_pD if it has a triple-connected subgraph, which is induced by C_tpD(G). If $m_1$(G)$\ge n$, then $G=\left(\sigma ,\mu \right)$ is defined to be $n$-connected for $n\in \left(0,\infty \right)$. That is, if no fuzzy node cut with strong weights less than $n$ exists. If $m$(G)$\ge n$, then $G=\left(\sigma ,\mu \right)$ is referred to as $n$-edge connected for $n\in \left(0,\infty \right)$. That is, if no fuzzy arc cut with strong weights less than $n$ exists. Examples of these notions are provided in Figure 1.

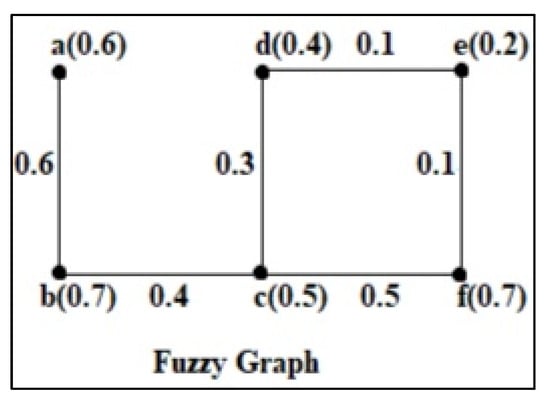
Figure 1. Fuzzy graph.

Here, {b} and {c} are two 1-fuzzy vertex cuts with 0.6 and 0.5 strong weights, respectively. The 2-fuzzy vertex cuts {b,c} and {d,f} have strong weights of 1 and 0.2, respectively. The all-fuzzy node cut in G has a minimum strongest weight of 0.1; therefore, $m_1$(G) = 0.1. Thus, for any $n$, G is $n$-connected such that $n\in \left(0,0.1\right]$. If the intensity of connectedness between some set of nodes in G is reduced when an arc $\left(x,y\right)\in {\mu }^{*}$ is removed, it is defined as a fuzzy bridge. If removing a vertex $v\in {\sigma }^{*}$ decreases the intensity of connectivity between another set of nodes, it is referred to be a fuzzy cut node of G. A connected G = ($\sigma ,\mu$) is referred to as a fuzzy tree if it is a fuzzy spanning subgraph F $=\left(\sigma ,v\right)$, in which for any arcs $\left(x,y\right)$ $\notin$ F, then there is a path: $x\to y\in$ F with a strength greater than $\mu \left(x,y\right)$. If there is Tctp with µ(u, v) = σ(u)˄σ(v) and d_N(u) ≥ d_N(v) for all u,v ∈ V and the fuzzy subgraph induced by <Tctp>, which is strongly triple connected, then the subgraph of G is called a strong triple connected total perfect dominating set. There exists a minimum fuzzy cardinality taken from the strong triple-connected total perfect dominating set, which is said to be a strong domination number G. If there is Tctp with µ(u, v) = σ(u)˄σ(v) and d_N(u) ≤ d_N(v) for all u,v ∈ V and the fuzzy subgraph induced by <Tctp>, which is weakly triple connected, then the subgraph of G is called a weak triple-connected total perfect dominating set. There exists a minimum fuzzy cardinality taken from the weak triple-connected total perfect dominating set, which is said to be a weak domination number G. If a dominating set induces a connected subgraph C_s, it is referred to as a connected dominating set C_D. K_D is referred to as a $n$-connected dominating set n_cD if a C_D induces a $n$-connected subgraph of G. n_ctpD is said to be $n$-connected to T_pD if it has a $n$-connected subgraph induced by C_tpD(G). The $n$-connected total perfect dominant number of G is indicated by $n_{ctp}\left(G\right)$., which is the minimum fuzzy cardinality calculated over all $n_{ctp}\left(G\right)$. A set D⊆ V of a fuzzy graph G = (V, σ, μ) is a fuzzy $k$-dominating set of G if for every node u ∊ V-D there exist at least $k$ strong arcs (u,v) for v ∊ D. The minimum fuzzy cardinality of a fuzzy $k$-dominating set in G is called the fuzzy $k$-dominating number γ_kD of G. If for every node v not in a subset P of V which dominated by absolutely $k$ nodes of P, then P is called a perfect $k$-dominating set of G. It is identified by P_kD. The minimum cardinality of a perfect $k$-dominating set of G is the perfect $k$-domination number γ_PkD(G). A connected total perfect $k$- dominating set is said to be $n$-connected total perfect $k$-dominating set if the induced subgraph $⟨ctpkD\left(G\right)⟩$ is $n$-connected, denoted by $n_{ctpkD}$(G). The smallest number of vertices in the $n$-connected total perfect $k$-dominating set of G is called its number, denoted by $\gamma n_{ctpD}\left(G\right)$.

3. Main Results

Strong and weak $n$-connected total perfect $k$-dominating sets and the number of fuzzy graphs are discussed in this section.

3.1. Strong $n$-Connected Total Perfect $k$-Domination

Definition 1.

If there is an$n$-connected total perfect$k$-dominating set of a fuzzy graph G with µ(u, v) = σ(u)˄σ(v), d_N(u) ≥ d_N(v) for all u,v ∈ V and the fuzzy subgraph induced by <$n_{ctpkD}$(G)>, which is strongly $n$-connected, then the subgraph of G is called a strong $n$-connected total perfect $k$-dominating set. It is denoted by ${\hat{\mathrm{S}}}_{nk}D\left(G\right)$.

Definition 2.

The minimum fuzzy cardinality taken over all the strong$n$-connected total perfect$k$-dominating set is said to be a strong$n$-connected total perfect$k$-dominating number. Denoted by$\gamma {\hat{\mathrm{S}}}_{nk}D\left(G\right)$.

Here, an example is provided to the above definitions, as shown in Figure 2.

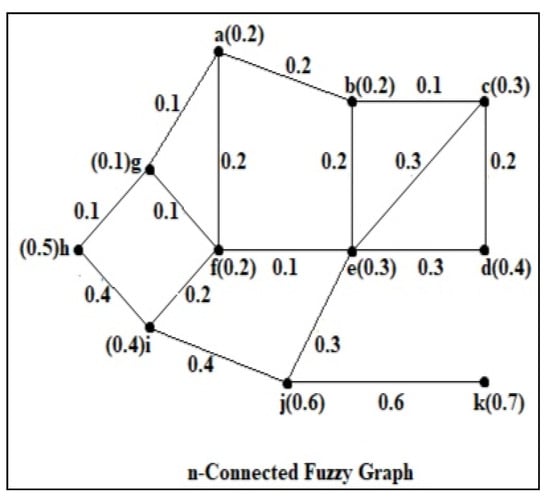
Figure 2. An 11-connected fuzzy graph.

Here, $d_N\left(k\right)=0.6$, $d_N\left(j\right)=\left\{0.7+0.4+0.3\right\}=1.4$, $d_N\left(i\right)=\left\{0.6+0.5+0.2\right\}=1.3$, $d_N\left(h\right)=\left\{0.4+0.1\right\}=0.5$, $d_N\left(g\right)=\left\{0.5+0.2+0.2\right\}=0.9$, $d_N\left(f\right)=\left\{0.4+0.2+0.1\right\}=0.7$, $d_N\left(e\right)=\left\{0.6+0.4+0.3+0.2\right\}=1.3$, $d_N\left(d\right)=0.3$, $d_N\left(c\right)=0.3$, $d_N\left(b\right)=\left\{0.3+0.2\right\}=0.5$, $d_N\left(a\right)=\left\{0.2+0.2+0.1\right\}=0.5$. The order of this $n$-connected fuzzy graph is 3.9, and the size is 3.8.

Now $\{d_N\left(e\right)>d_N\left(j\right)>d_N\left(i\right)>d_N\left(f\right)\}$ and µ (u, v) = σ(u)˄σ(v), for all u,v ∈ V.

Hence, ${\hat{\mathrm{S}}}_{nk}D\left(G\right)=\left\{e,j,i,f\right\}$ and $\gamma {\hat{\mathrm{S}}}_{nk}D\left(G\right)=\left\{0.3+0.6+0.4+0.2\right\}=1.5$.

Proposition 1.

For a strong$n$-connected total perfect$k$-dominating set with$n$nodes and$k$dominating sets,$O\left(G\right)-\gamma {\hat{\mathrm{S}}}_{nk}D={\displaystyle \sum }{d}_N\left(V-D\right)$.

Theorem 1.

If there is a${\hat{\mathrm{S}}}_{nk}D\left(G\right)$with a maximum neighborhood degree$\Delta$, order$n$and size q, then$n-{\Delta }_N\left({\hat{\mathrm{S}}}_{nk}D\right)\ge \gamma {\hat{\mathrm{S}}}_{nk}D\left(G\right)\ge \left|n-q\right|$.

Proof. 

Case 1. Let G be a fuzzy graph with a strong $n$-connected total perfect $k$-dominating set. It is known that the difference between order $n$ of any fuzzy graph and the strong $n$-connected total perfect $k$-dominating number is the total number of cardinalities of the remaining nodes. Additionally, the difference between the order and size of ${\hat{\mathrm{S}}}_{nk}D$ is less than the $\gamma {\hat{\mathrm{S}}}_{nk}D\left(G\right)$. Hence, $\left|n-q\right|\le \gamma {\hat{\mathrm{S}}}_{nk}D\left(G\right)$.

Case 2. Consider the strong $n$-connected total perfect $k$-dominating number of fuzzy graph G, the maximum neighborhood of ${\hat{\mathrm{S}}}_{nk}D\left(G\right),$ which is taken over all the strong $n$-connected total perfect $k$-dominating set and from proposition 1, $\gamma {\hat{\mathrm{S}}}_{nk}D\left(G\right)\le n-{\Delta }_N\left({\hat{\mathrm{S}}}_{nk}D\right)$. From case 1 and case 2, $\left|n-q\right|\le \gamma {\hat{\mathrm{S}}}_{nk}D\left(G\right)\le n-{\Delta }_N\left({\hat{\mathrm{S}}}_{nk}D\right)$. □

Theorem 2.

If there is a${\hat{\mathrm{S}}}_{nk}D$set in a fuzzy graph G, the (i) connected total perfect$k$-dominating set exists, (ii) the total perfect$k$-dominating set exists and (iii) the perfect$k$-dominating set exists.

Proof. 

Let G be a strong $n$-connected total perfect $k$-dominating set of a fuzzy graph with µ(u, v) = σ(u)˄σ(v), d_N(u) ≥ d_N(v) for all u,v ∈ V and the fuzzy subgraph induced by the connected total perfect $k$-dominating set, total perfect $k$-dominating set and perfect $k$-dominating set which are strongly $n$-connected to the subgraph of G. □

Note that the converse of theorem 2 need not be true.

Corollary 1.

The complement of the${\hat{\mathrm{S}}}_{nk}D$set in a fuzzy graph G need not be${\hat{\mathrm{S}}}_{nk}D\left(G\right)$.

Corollary 2.

If there exists a spanning fuzzy subgraph H of the${\hat{\mathrm{S}}}_{nk}D$set in a fuzzy graph G, then the fuzzy set${\hat{\mathrm{S}}}_{nk}D\left(H\right)$is also${\hat{\mathrm{S}}}_{nk}D\left(G\right)$.

Corollary 3.

For the strong$n$-connected fuzzy graph without isolated nodes,$\gamma {\hat{\mathrm{S}}}_{nk}D\left(G\right)\le \frac{nk}{3}$.

Theorem 3.

If G is a constant$d_N\left(n_1\right), d_N\left(n_2\right),d_N\left(n_3\right),\dots , d_N\left(n_k\right)$in the${\hat{\mathrm{S}}}_{nk}D$set, without isolated nodes and the minimal${\hat{\mathrm{S}}}_{nk}D$set, then$V-{\hat{\mathrm{S}}}_{nk}D$is a strongly$n$-connected total perfect$k$-dominating set.

Proof. 

Consider a minimal ${\hat{\mathrm{S}}}_{nk}D$ set of fuzzy graph G and $n_k$ is any node in ${\hat{\mathrm{S}}}_{nk}D\left(G\right)$, then there exists a node $n_k\in d_N\left(n_k\right)$ of ${\hat{\mathrm{S}}}_{nk}D\left(G\right)$. Here, $n_k$ must be dominated by exactly one node in ${\hat{\mathrm{S}}}_{nk}D-\left\{n_k\right\}$ which is a ${\hat{\mathrm{S}}}_{nk}D$ set of fuzzy graph G. There are no isolated nodes and every node in ${\hat{\mathrm{S}}}_{nk}D$ must be strongly dominated by at least one node in $V-{\hat{\mathrm{S}}}_{nk}D,$ which is a ${\hat{\mathrm{S}}}_{nk}D$ set of fuzzy graph G. □

3.2. Weak $n$-Connected Total Perfect $k$-Domination

Definition 3.

If there is an$n$-connected total perfect$k$-dominating set of a fuzzy graph G with µ (u, v) < σ(u)˄σ(v), d_N(u)$<$d_N(v) for all u,v ∈ V and the fuzzy subgraph induced by <$n_{ctpkD}$(G)>, which is weakly $n$-connected, then the subgraph of G is called a weak $n$-connected total perfect $k$-dominating set. It is denoted by ${\hat{\mathrm{W}}}_{nk}D\left(G\right)$.

Definition 4.

The minimum fuzzy cardinality taken over all the weak$n$-connected total perfect$k$-dominating set is said to be a weak$n$-connected total perfect$k$-dominating number. Denoted by$\gamma {\hat{\mathrm{W}}}_{nk}D\left(G\right)$.

Here, an example is provided to the above definitions, as shown in Figure 3.

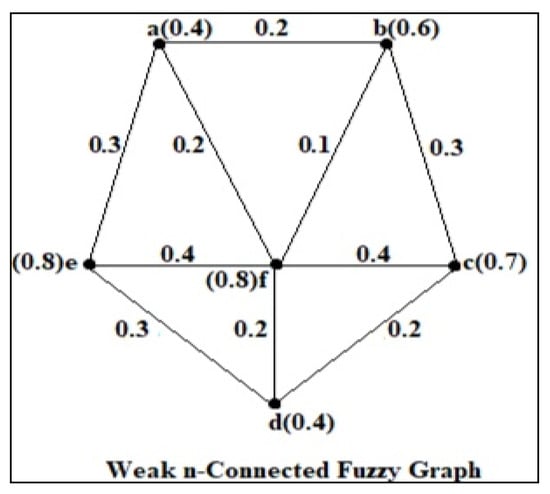
Figure 3. A weak 6-connected fuzzy graph.

Here, $d_N\left(a\right)=0.8$, $d_N\left(b\right)=0.7$, $d_N\left(c\right)=\left\{0.8+0.6\right\}=1.4$, $d_N\left(d\right)=0.8$, $d_N\left(e\right)=\left\{0.8+0.4+0.4\right\}=1.6$, $d_N\left(f\right)=\left\{0.8+0.7\right\}=1.5$. The order of this weak $n$-connected fuzzy graph is 3.7, and the size is 2.6.

Now $\{d_N\left(c\right)<d_N\left(f\right)<d_N\left(e\right)\}$ and µ(u, v) < σ(u)˄σ(v), for all u,v ∈ V.

Hence, ${\hat{\mathrm{W}}}_{nk}D\left(G\right)=\left\{c,f,e\right\}$ and $\gamma {\hat{\mathrm{W}}}_{nk}D\left(G\right)=\left\{0.8+0.8+0.7\right\}=2.3$.

Proposition 2.

For a weak$n$-connected total perfect$k$-dominating set with$n$nodes and$k$dominating sets,$O\left(G\right)-\gamma {\hat{\mathrm{W}}}_{nk}D={\displaystyle \sum }{d}_N\left(V-D\right)$.

Theorem 4.

If there is a${\hat{\mathrm{W}}}_{nk}D\left(G\right)$with a minimum neighborhood degree$\delta$, order$n$and size q, then$n-q\le \gamma {\hat{\mathrm{W}}}_{nk}D\left(G\right)\le n-{\delta }_N\left({\hat{\mathrm{W}}}_{nk}D\right)$.

Proof. 

Case 1. Let G be a fuzzy graph with a weak $n$-connected total perfect $k$-dominating set. It is known that the difference between order $n$ of any fuzzy graph and the weak $n$-connected total perfect $k$-dominating number is the total number of cardinalities of the remaining nodes. Additionally, the difference between the order and size of ${\hat{\mathrm{W}}}_{nk}D$ is less than the $\gamma {\hat{\mathrm{W}}}_{nk}D\left(G\right)$. Hence, $n-q\le \gamma {\hat{\mathrm{W}}}_{nk}D\left(G\right)$.

Case 2. Consider the weak $n$-connected total perfect $k$-dominating number of fuzzy graph G, the minimum neighborhood of ${\hat{\mathrm{W}}}_{nk}D\left(G\right),$ which is taken over all the weak $n$-connected total perfect $k$-dominating set and from proposition 1, $\gamma {\hat{\mathrm{W}}}_{nk}D\left(G\right)\le n-{\Delta }_N\left({\hat{\mathrm{W}}}_{nk}D\right)$. □

Corollary 4.

The complement of the${\hat{\mathrm{W}}}_{nk}D$set in a fuzzy graph G need not be${\hat{\mathrm{W}}}_{nk}D\left(G\right)$.

Corollary 5.

If there exists a spanning fuzzy subgraph H of the${\hat{\mathrm{W}}}_{nk}D$set in a fuzzy graph G, then the fuzzy set${\hat{\mathrm{W}}}_{nk}D\left(H\right)$is also${\hat{\mathrm{W}}}_{nk}D\left(G\right)$.

Corollary 6.

For the weak$n$-connected fuzzy graph without isolated nodes,$\gamma {\hat{\mathrm{W}}}_{nk}D\left(G\right)\le \frac{nk}{3}$.

Theorem 5.

If there is a${\hat{\mathrm{W}}}_{nk}D$set in a fuzzy graph G, the (i) connected total perfect$k$-dominating set exists, (ii) the total perfect$k$-dominating set exists and (iii) the perfect$k$-dominating set exists.

Proof. 

Consider the weak $n$-connected total perfect $k$-dominating set of a fuzzy graph G with µ(u, v) < σ(u)˄σ(v), d_N(u) $<$ d_N(v) for all u,v ∈ V and the fuzzy subgraph induced by the connected total perfect $k$-dominating set, the total perfect $k$-dominating set and the perfect $k$-dominating set which is weakly $n$-connected to the subgraph of G. □

Theorem 6.

Let G be a minimal${\hat{\mathrm{W}}}_{nk}D\left(G\right)$, then for every$n_k\in {\hat{\mathrm{W}}}_{nk}D\left(G\right)$, one of the following axioms holds:

(i) no nodes in${\hat{\mathrm{W}}}_{nk}D\left(G\right)$weakly dominates$n_k$;

(ii) there exists a node$n_k\in V-{\hat{\mathrm{W}}}_{nk}D\left(G\right)$such that$n_k$is the only node in${\hat{\mathrm{W}}}_{nk}D\left(G\right),$which weakly dominates$n_k$.

Proposition 3.

If there are two fuzzy sets${\hat{\mathrm{S}}}_{nk}D\left(G\right)$and${\hat{\mathrm{W}}}_{nk}D\left(G\right)$, which are the minimal dominating sets if and only if for every$n_k\in {\hat{\mathrm{S}}}_{nk}D\left(G\right) or {\hat{\mathrm{W}}}_{nk}D\left(G\right),$then one of the following axioms holds: (i)$d_N\left(n_k\right){\displaystyle \cap } {\hat{\mathrm{S}}}_{nk}D or {\hat{\mathrm{W}}}_{nk}D=\varnothing$;

(ii) there is a node$n_k\in {\hat{\mathrm{S}}}_{nk}D\left(G\right) or {\hat{\mathrm{W}}}_{nk}D\left(G\right)$such that$d_N\left(n_k\right){\displaystyle \cap } {\hat{\mathrm{S}}}_{nk}D or {\hat{\mathrm{W}}}_{nk}D=\left\{n_k\right\}$.

Remark 1.

Let${\hat{\mathrm{S}}}_{nk}D\left(G\right)$be a minimal dominating set, then the$V-{\hat{\mathrm{S}}}_{nk}D$set need not be${\hat{\mathrm{W}}}_{nk}D\left(G\right).$

Remark 2.

Two fuzzy sets,${\hat{\mathrm{S}}}_{nk}D\left(G\right)$and${\hat{\mathrm{W}}}_{nk}D\left(G\right),$do not exist for all fuzzy graphs.

4. Conclusions

This research study investigated some new notions such as the triple-connected total perfect $k$-dominating set, the $n$-connected total perfect $k$-dominating set, the strong $n$-connected total perfect $k$-dominating set ${\hat{\mathrm{S}}}_{nk}D\left(G\right)$ and the weak $n$-connected total perfect $k$-dominating set ${\hat{\mathrm{W}}}_{nk}D\left(G\right)$ in fuzzy graphs. Here, two cases were discussed, one was a triple-connected total perfect $k$-dominating set and the other was a strong (weak) $n$-connected total perfect $k$-dominating set in a fuzzy graph. Additionally, the dominating number of such a dominating set was discussed with examples and some existing theorems were compared with these new definitions. Some limitations must be considered when interpreting the results. First, the results may not be able to be generalized to all types of fuzzy graphs. Second, only a simple fuzzy graph was considered. Future research on this study could consider practical applications. Additionally, the results of $n$-connected total perfect domination will be extern to the various types of fuzzy graphs such as picture fuzzy graphs, bipolar fuzzy graphs, intuitionistic fuzzy graphs and interval-valued fuzzy graphs.