The Discrete Fractional Variable-Order Tinkerbell Map: Chaos, 0–1 Test, and Entropy
Abstract
:1. Introduction
2. Fractional Variable-Order Discrete-Time of the Tinkerbell Map
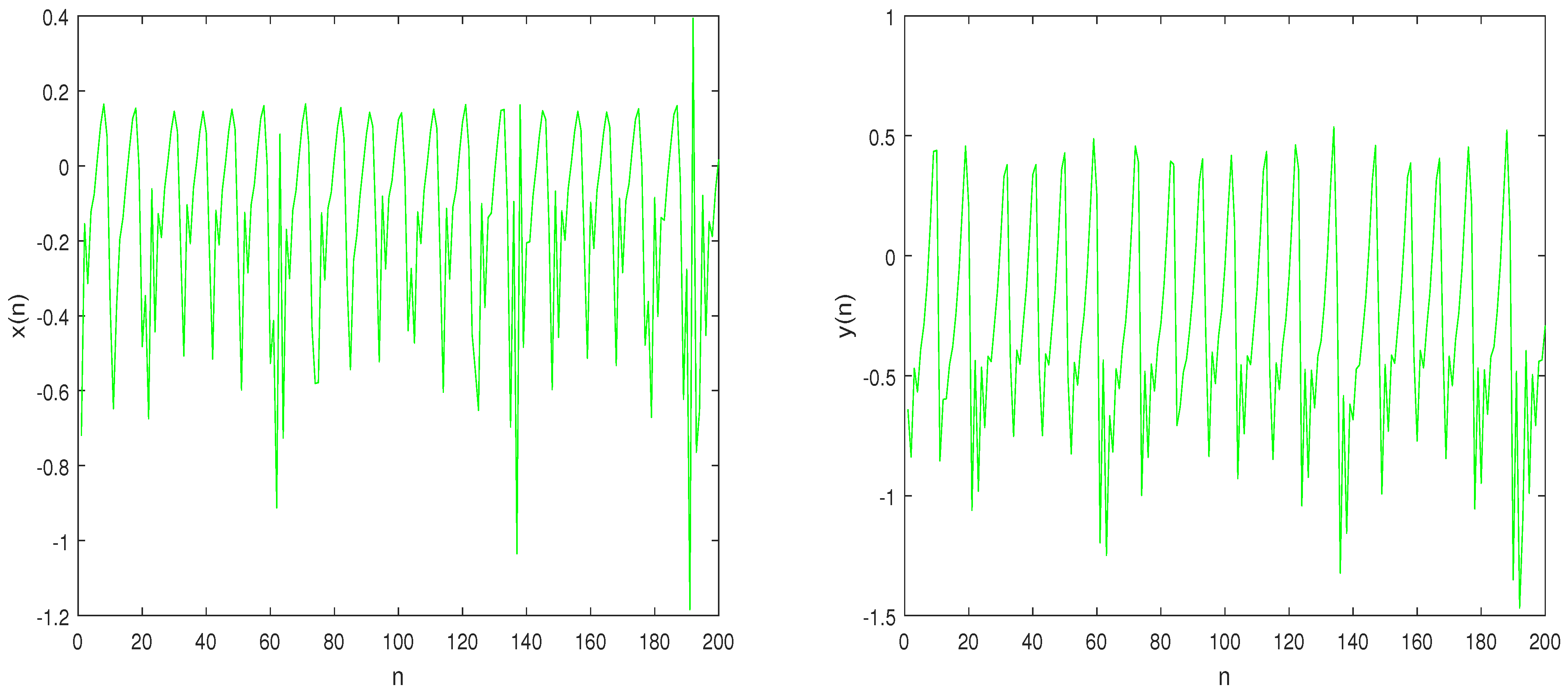
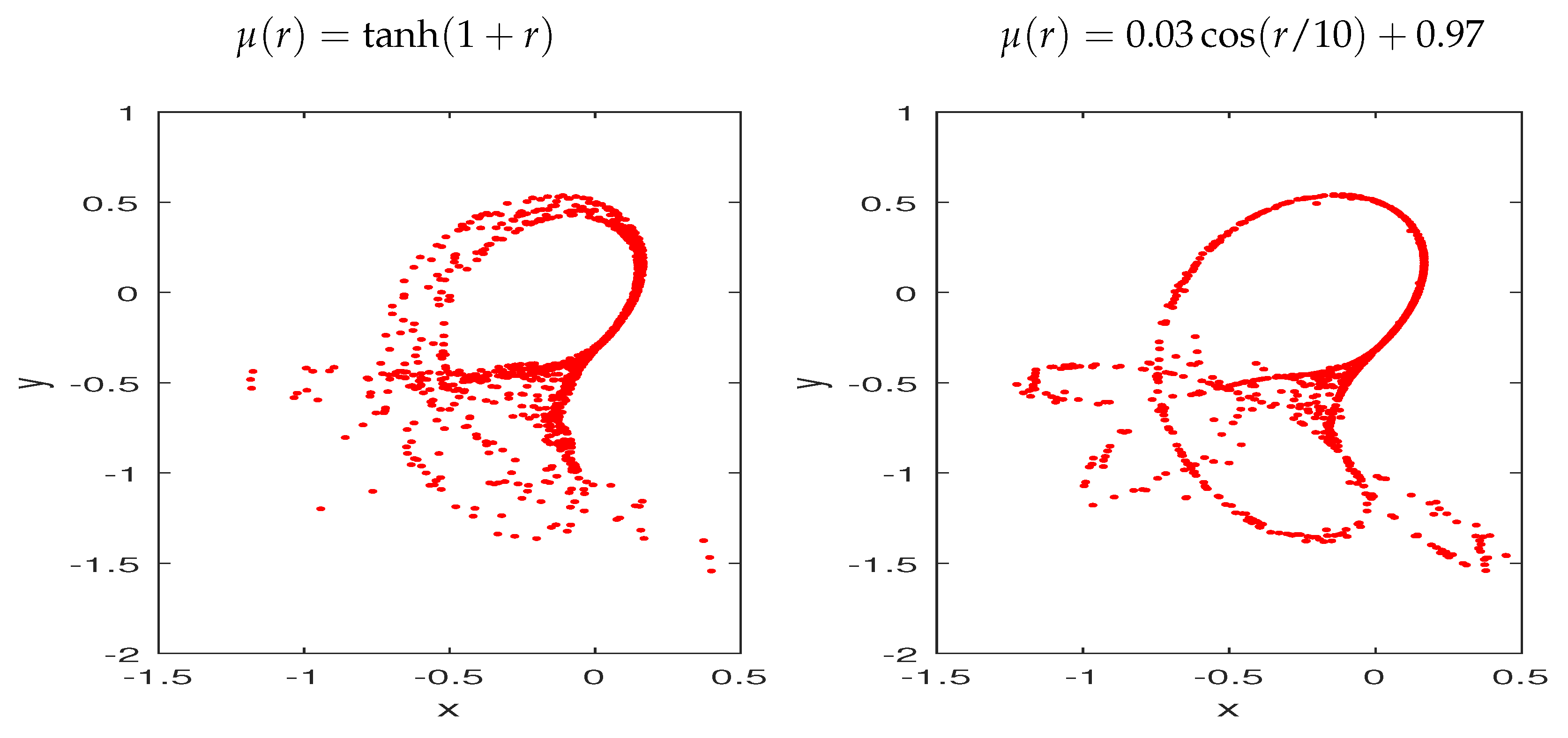
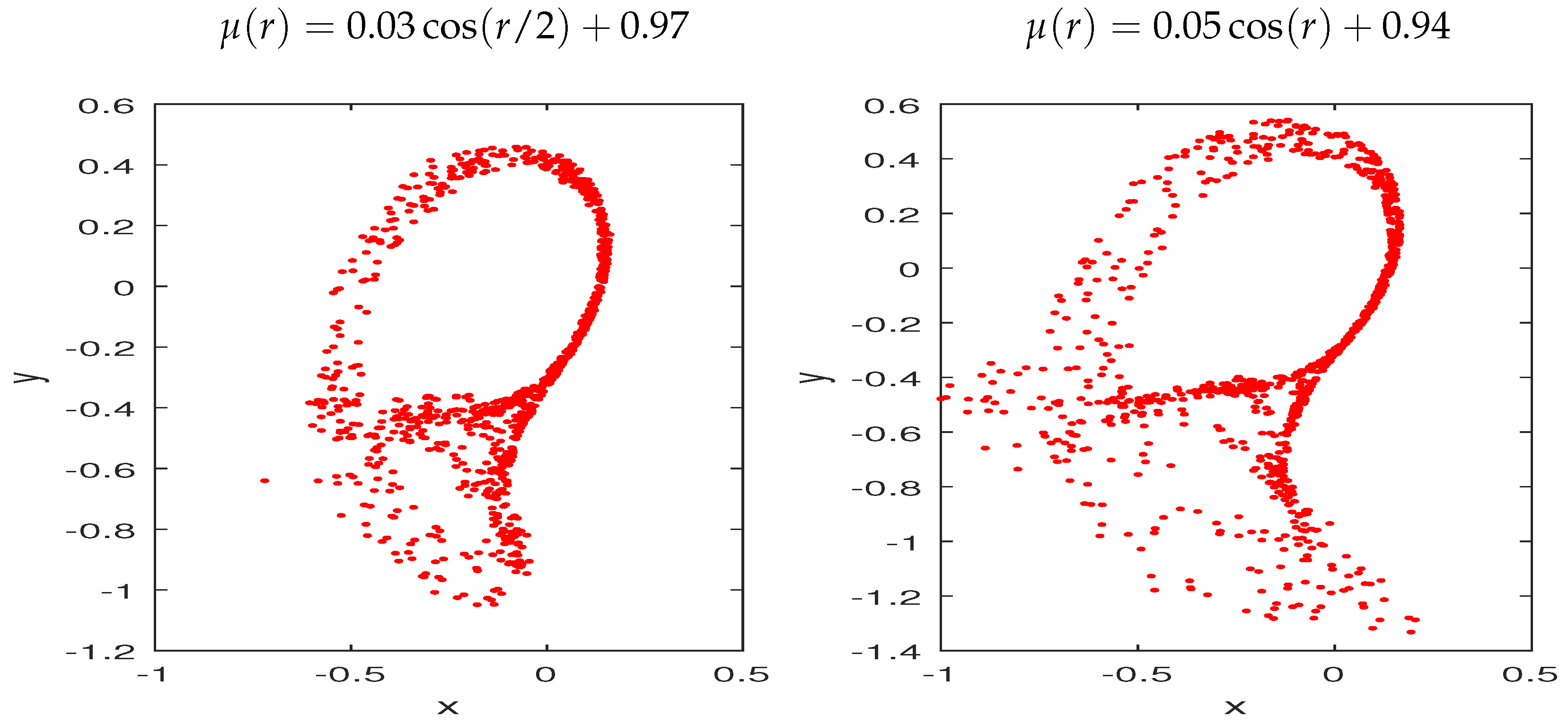
3. Dynamics of the Tinkerbell Map with the Fractional Variable-Order
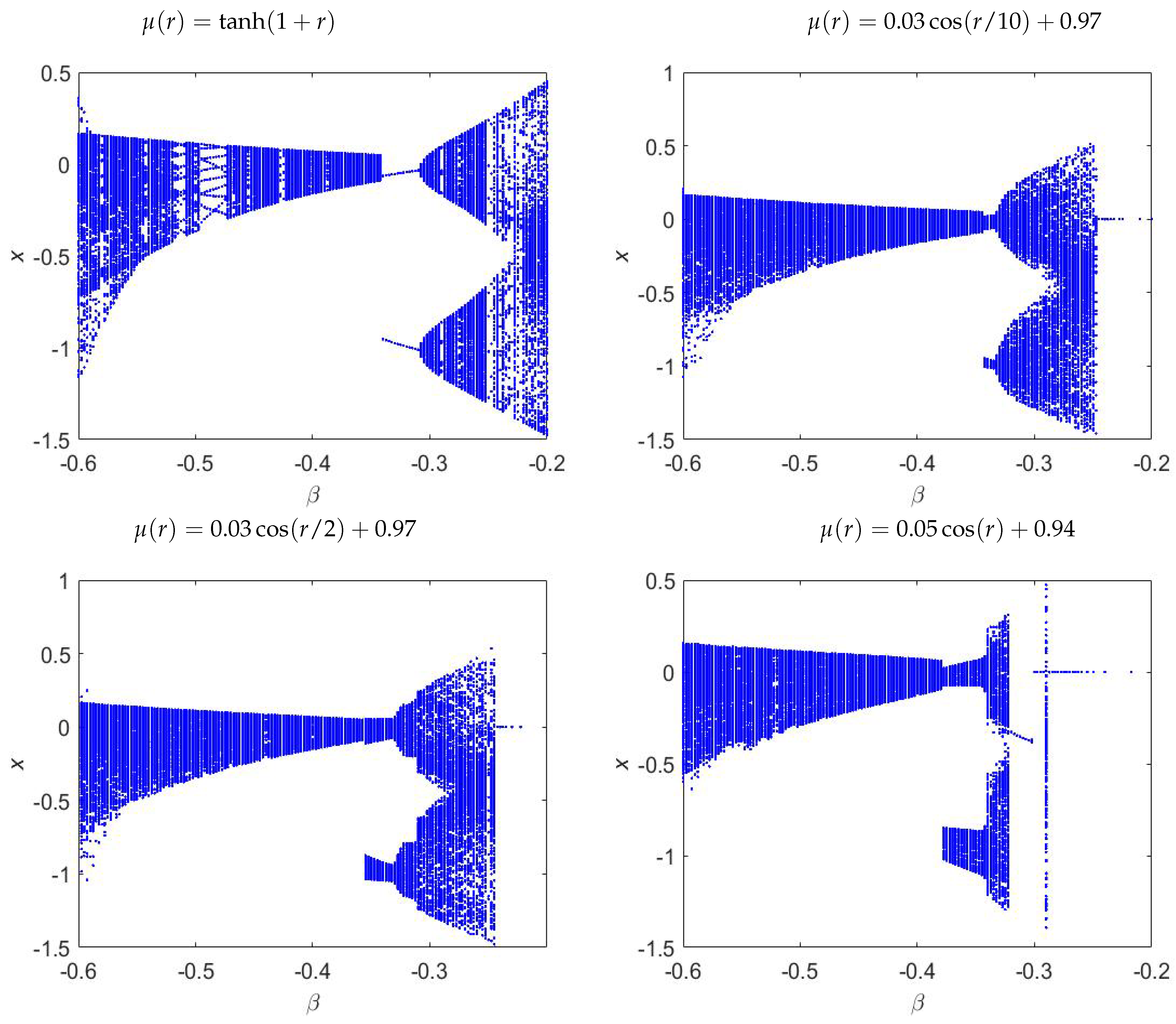
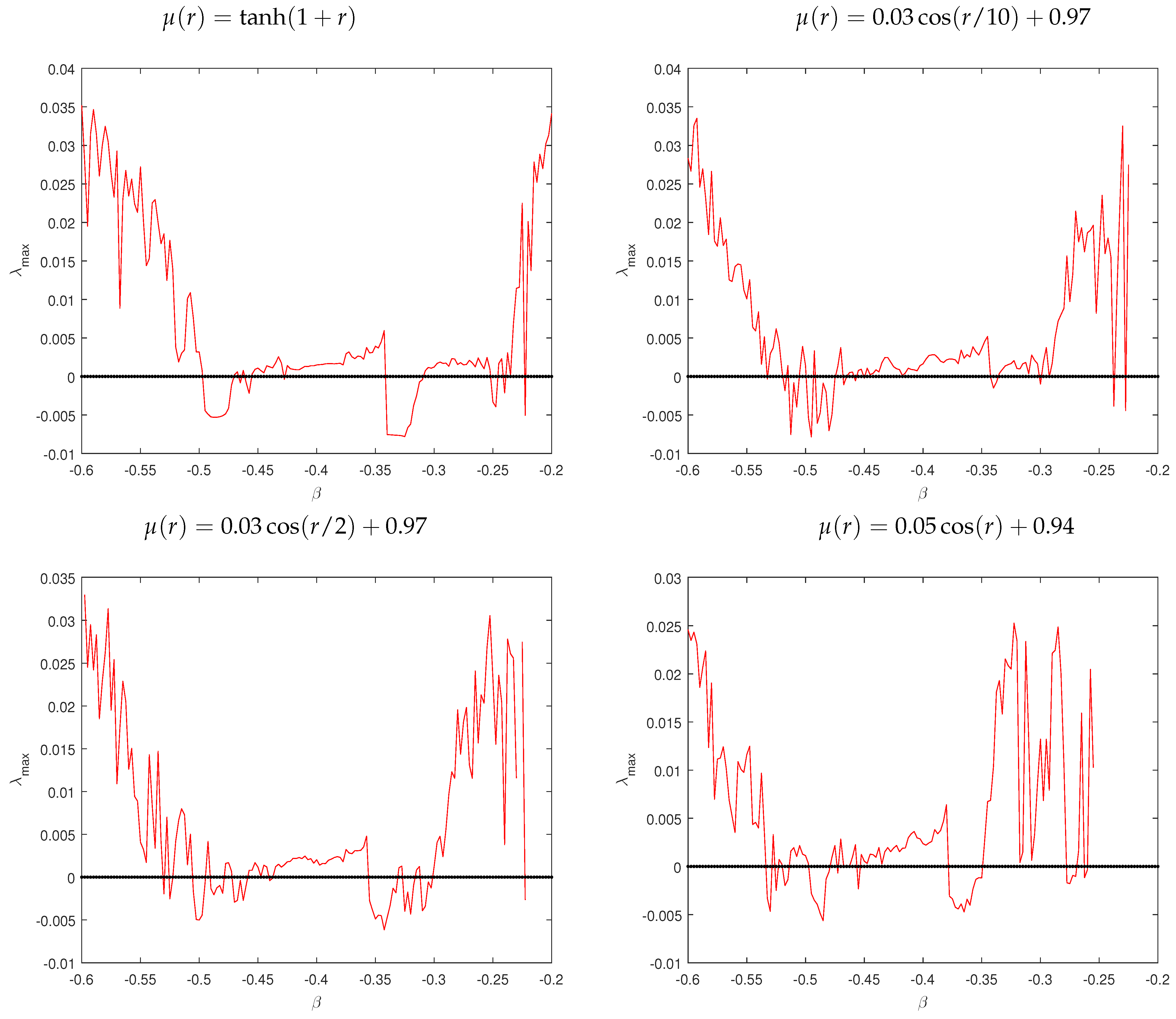
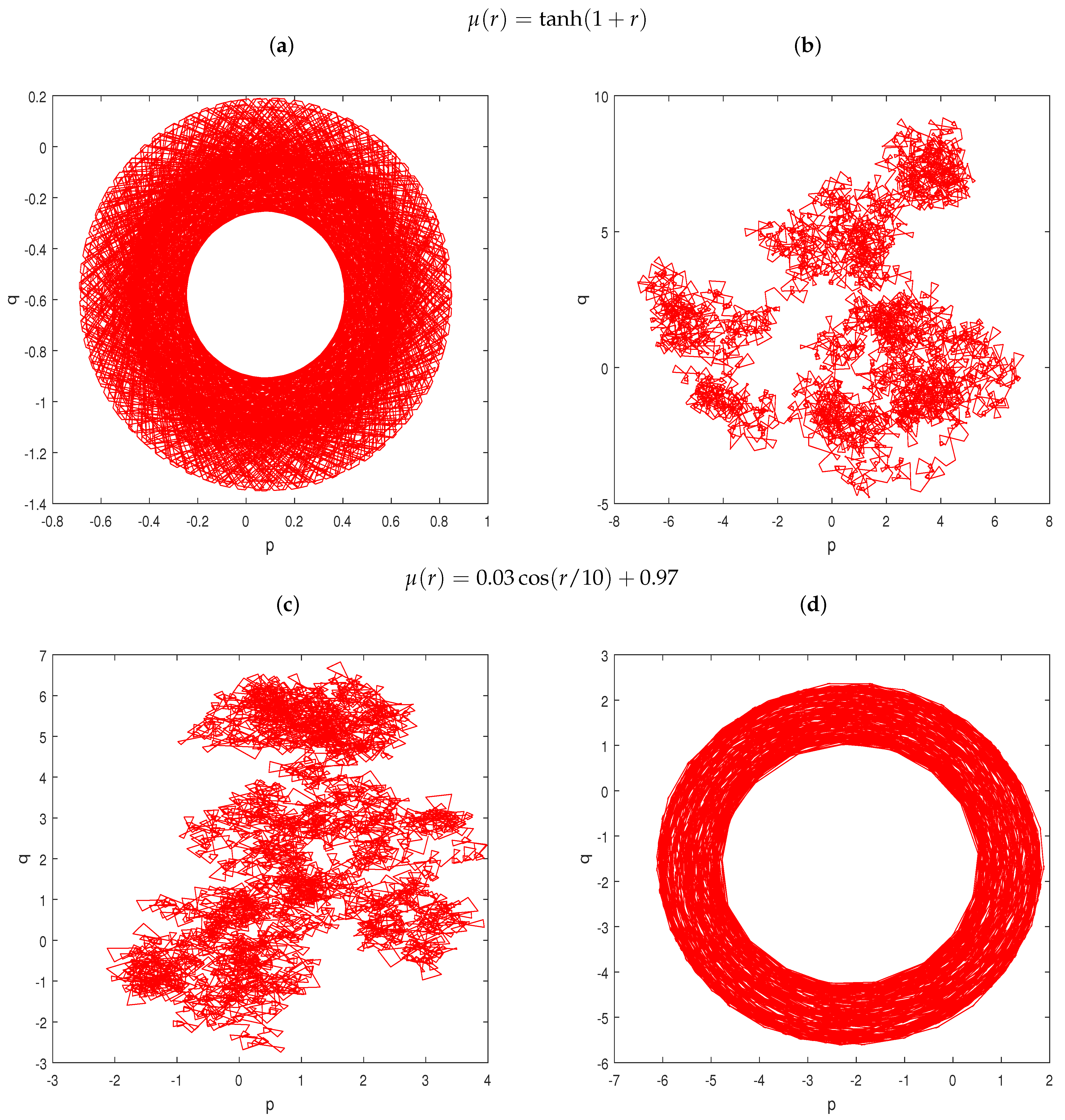
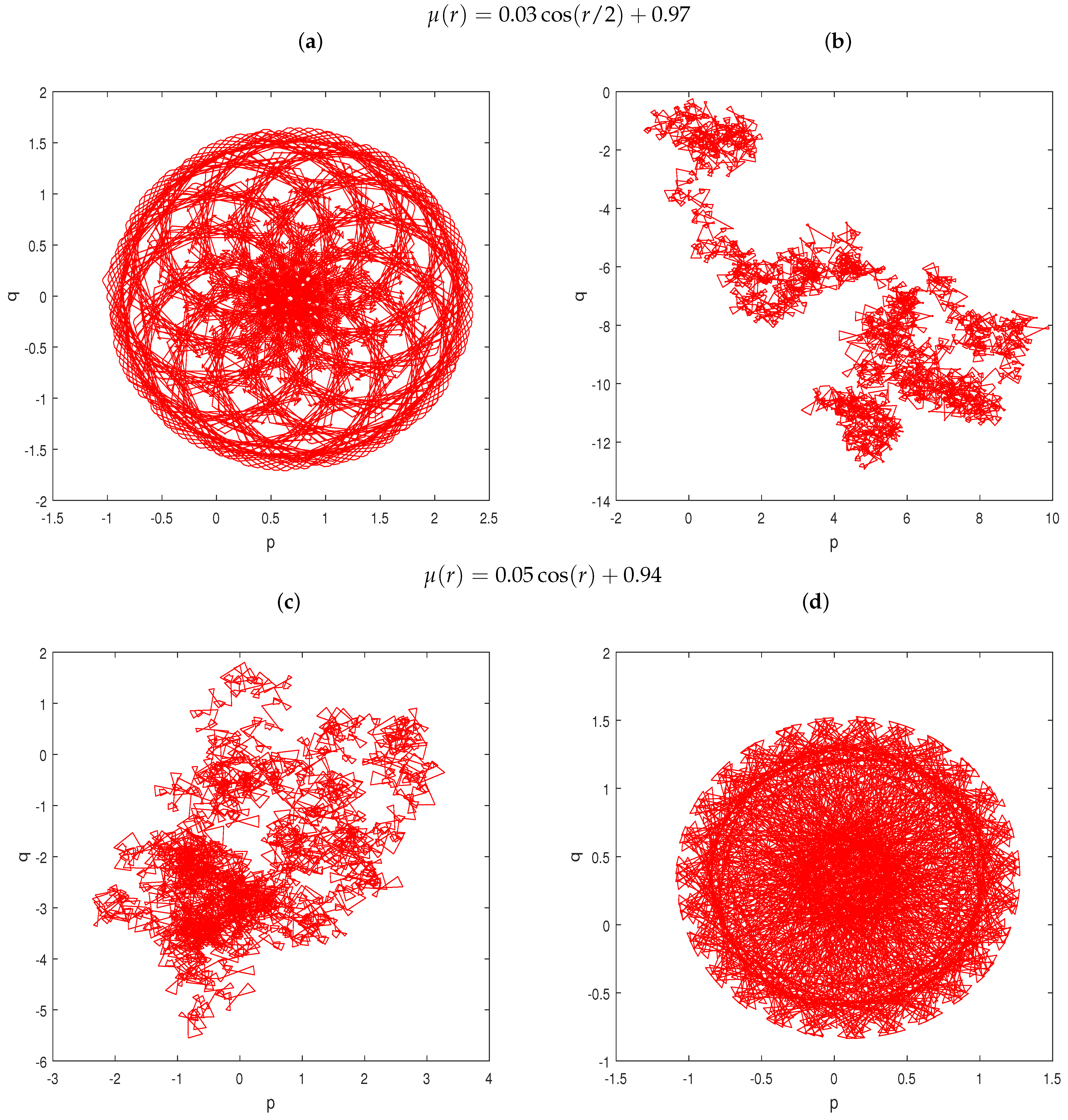
3.1. Bifurcation and Largest Lyapunov Exponents (LLE)
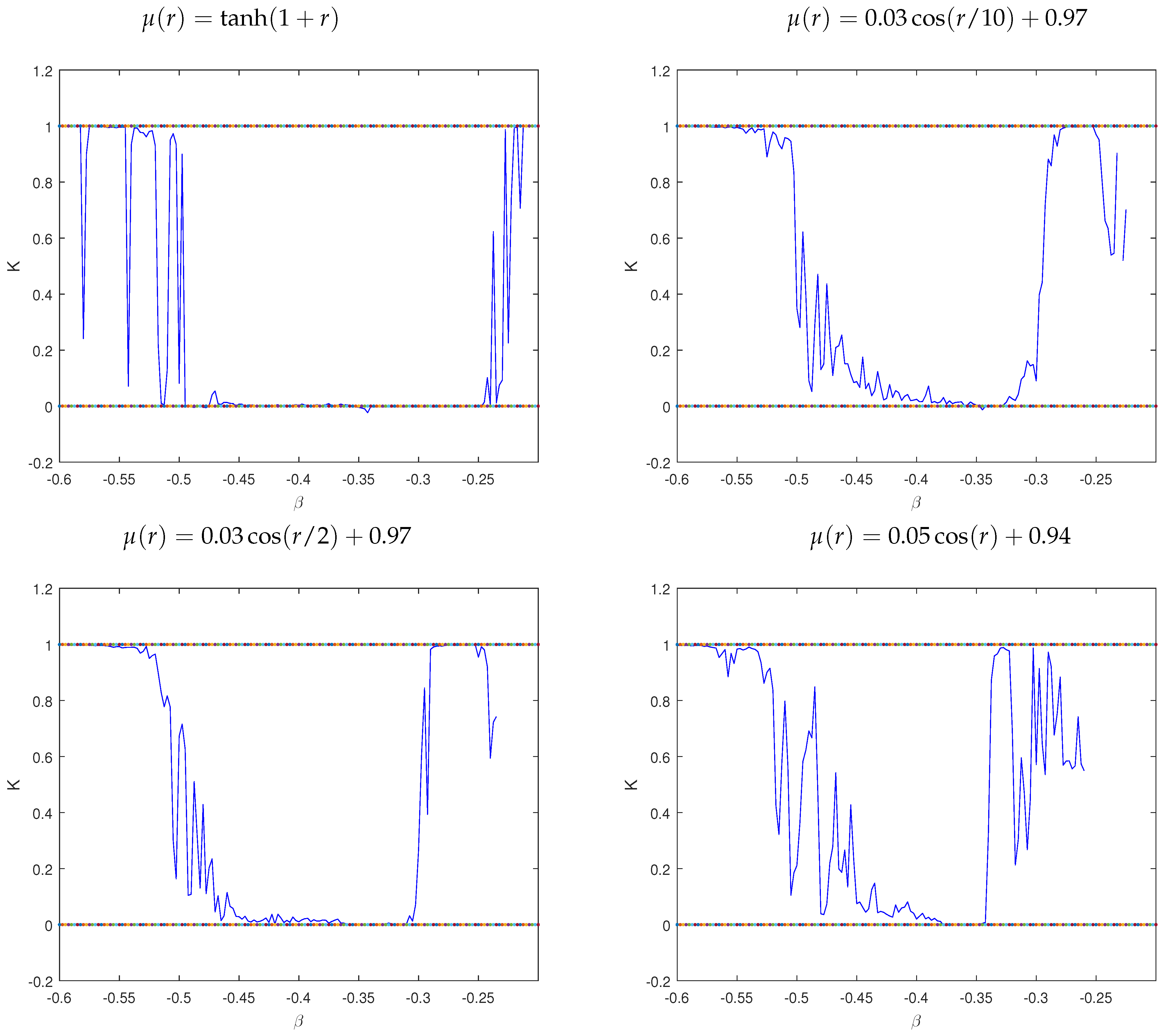
3.2. The 0–1 Test
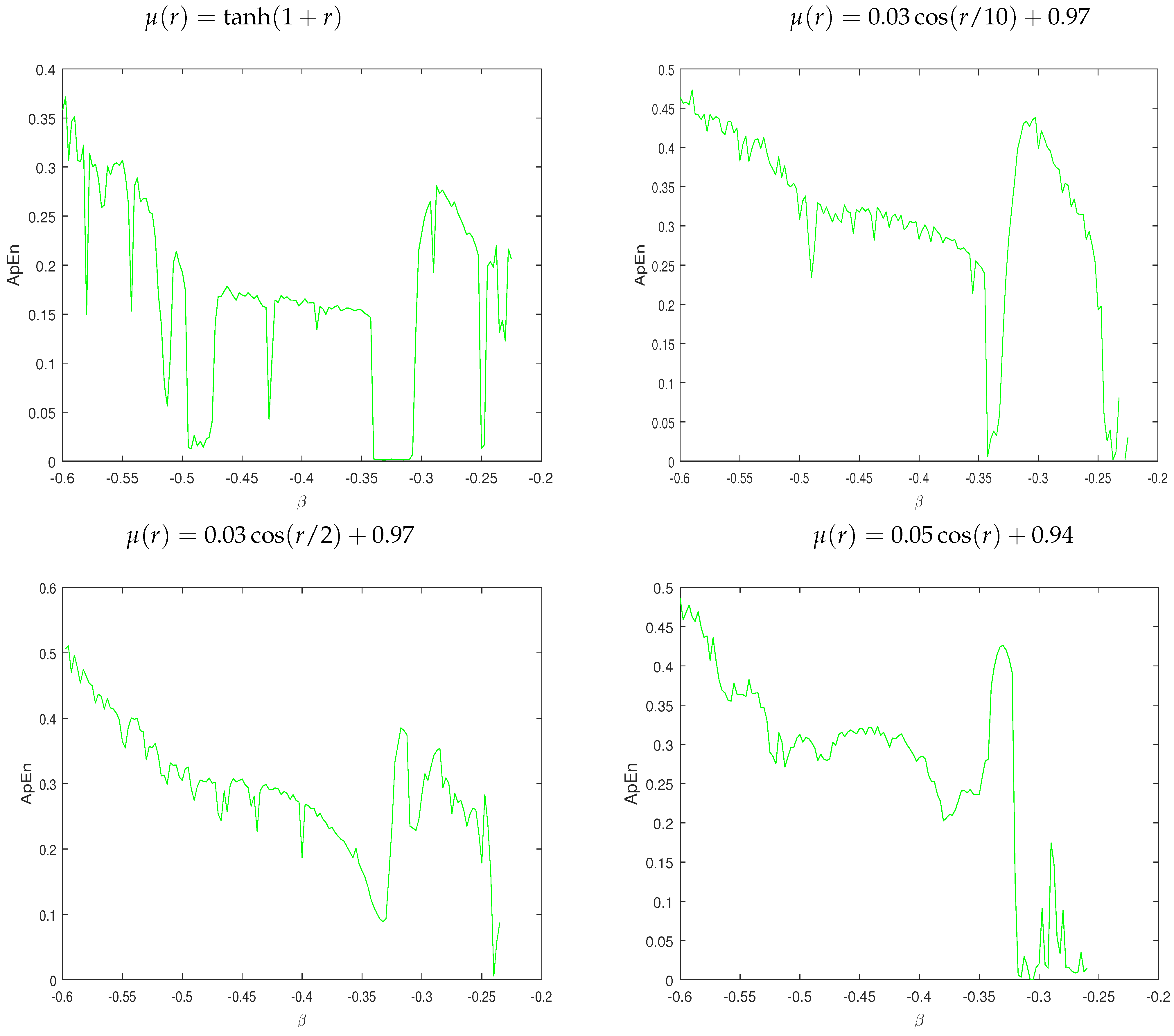
3.3. The Approximate Entropy
4. Conclusions and Future Works
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vaidyanatham, S. Global chaos synchronisation of identical Li-Wu chaotic systems via sliding mode control. Int. J. Model. Identif. Control 2014, 22, 170–177. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- May, R. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Itoh, M.; Yang, T.; Chua, L.O. Conditions for impulsive synchronization of chaotic and hyperchaotic systems. Int. J. Bifurc. Chaos 2001, 11, 551–560. [Google Scholar] [CrossRef]
- Stefanski, K. Modelling chaos and hyperchaos with 3D maps. Chaos Solit. Fractals 1998, 9, 83–93. [Google Scholar] [CrossRef]
- Hénon, M. A two-dimensional mapping with a strange attractor. Commun. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Lozi, R. Un atracteur étrange du type attracteur de Hénon. J. Phys. Colloq. 1978, 39, 9–10. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Hioual, A.; Ouannas, A. On fractional variable-order neural network with time varying external inputs. Innov. J. Math. 2022, 1, 52–65. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional DiffErential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Montesinos-García, J.J.; Martínez -Guerra, R. A numerical estimation of the fractional-order liouvillian systems and its application to secure communications. Int. J. Syst. Sci. 2019, 50, 791–806. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional calculus in bioengineering. Begell House Redd. 2006, 2. [Google Scholar]
- Wang, L.; Song, Q. Pricing policies for dual-channel supply chain with green investment and sales effort under uncertain demand. Math. Comput. Simul. 2020, 171, 79–93. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientifc: Singapore, 2000. [Google Scholar]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Pham, V. The Discrete Fractional Duffing System: Chaos, 0–1 Test, Co Complexity, Entropy and Control. Chaos 2020, 30, 083131. [Google Scholar] [CrossRef] [PubMed]
- Ouannas, A.; Khennaoui, A.A.; Odibat, Z.; Pham, V.T.; Grassi, G. On the dynamics, control and synchronization of fractional-order Ikeda map. Chaos Solitons Fractals 2019, 123, 108–115. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, W.; Chen, Y.Q. Variable-order fractional differential operators in anomalous diffusion modeling. Phys. A Stat Mech. Appl. 2009, 388, 4586–4592. [Google Scholar] [CrossRef]
- Coimbra, C.F.M. Mechanics with variable-order differential operators. Ann. Phys. 2003, 12, 692–703. [Google Scholar] [CrossRef]
- Samko, S.G.; Ross, B. Integration and differentiation to a variable fractional order. Integral Transform. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Yousefi, F.S.; Ordokhani, Y.; Yousefi, S. Numerical solution of variable order fractional differential equations by using shifted Legendre cardinal functions and Ritz method. Eng. Comput. 2020, 38, 1–8. [Google Scholar] [CrossRef]
- Pedro, H.T.C.; Kobayashi, M.H.; Pereira, J.M.C.; Coimbra, C.F.M. Variable order modeling of difusive-convective efects on the oscillatory fow past a sphere. J. Vib. Control 2008, 14, 1569–1672. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, Y.Q.; Chen, W. Random-order fractional differential equation models. Signal Process 2011, 91, 525–530. [Google Scholar] [CrossRef]
- Obembe, A.D.; Hossain, M.E.; Abu-Khamsin, S.A. Variable-order derivative time fractional difusion model for heterogeneous porous media. J. Petrol. Sci. Eng. 2017, 152, 391–405. [Google Scholar] [CrossRef]
- Soon, C.M.; Coimbra, C.F.M.; Kobayashi, M.H. The variable viscoelasticity oscillator. Ann. Phys. 2005, 14, 378–389. [Google Scholar] [CrossRef]
- Ingman, D.; Suzdalnitsky, J.; Zeifman, M. Constitutive dynamic-order model for nonlinear contact phenomena. J. Appl. Mech. 2000, 67, 383–390. [Google Scholar] [CrossRef]
- Ma, S.; Xu, Y.; Yue, W. Numerical solutions of a variable-order fractional financial system. J. Appl. Math. 2012, 2012, 417942. [Google Scholar] [CrossRef]
- Khan, A.; Alshahri, H.M.; Gómez-Aguilar, J.F.; Khan, Z.A.; Fernández-Anaya, G. A predator–prey model involving variable-order fractional differential equations with Mittag-Leffler kernel. Adv. Differ. Equ. 2021, 1, 1–18. [Google Scholar]
- Wu, G.C.; Deng, Z.G.; Beleanu, D.; Zeng, D.Q. New variable-order fractional chaotic systems for fast image encryption. Chaos 2019, 29, 083103. [Google Scholar] [CrossRef]
- Aulbach, B.; Colonius, F. Six Lectures on Dynamical Systems; World Scientific: Singapore, 1996. [Google Scholar]
- Nusse, H.; Yorke, J. Dynamics: Numerical Explorations; Springer: New York, NY, USA, 1997. [Google Scholar]
- Davidchack, R.; Lai, Y.; Klebanoff, A.; Bollt, E. Towards complete detection of unstable periodic orbits in chaotic systems. Phys. Lett. A 2001, 287, 99–104. [Google Scholar] [CrossRef]
- Mcsharry, P.; Ruffino, P. Asymptotic angular stability in non-linear systems: Rotation numbers and winding numbers. Dyn. Syst. 2003, 18, 191–200. [Google Scholar] [CrossRef]
- Yuan, S.; Jiang, T.; Jing, Z. Bifurcation and chaos in the tinkerbell map. Int. J. Bifurc. Chaos 2011, 21, 3137–3156. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Bendoukha, S.; Vo, T.; Pham, V.; Huynh, V. The fractional form of the Tinkerbell map is chaotic. Appl. Sci. 2018, 8, 2640. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef] [Green Version]
- Atici, F.; Eloe, P.W. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. 2009, 3, 1–12. [Google Scholar] [CrossRef]
- Chen, F.; Luo, X.; Zhou, Y. Existence results for nonlinear fractional difference equation. Adv. Differ. Equ. 2011, 2011, 713201. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Jacobian matrix algorithm for Lyapunov exponents of the discrete fractional maps. Commun. Nonlinear. Sci. Numer. Simulat. 2015, 22, 95–100. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. A new test for chaos in deterministic systems. Proc. Math. Phys. Eng. Sci. 2004, 460, 603–611. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bensid Ahmed, S.; Ouannas, A.; Al Horani, M.; Grassi, G. The Discrete Fractional Variable-Order Tinkerbell Map: Chaos, 0–1 Test, and Entropy. Mathematics 2022, 10, 3173. https://doi.org/10.3390/math10173173
Bensid Ahmed S, Ouannas A, Al Horani M, Grassi G. The Discrete Fractional Variable-Order Tinkerbell Map: Chaos, 0–1 Test, and Entropy. Mathematics. 2022; 10(17):3173. https://doi.org/10.3390/math10173173
Chicago/Turabian StyleBensid Ahmed, Souad, Adel Ouannas, Mohammed Al Horani, and Giuseppe Grassi. 2022. "The Discrete Fractional Variable-Order Tinkerbell Map: Chaos, 0–1 Test, and Entropy" Mathematics 10, no. 17: 3173. https://doi.org/10.3390/math10173173
APA StyleBensid Ahmed, S., Ouannas, A., Al Horani, M., & Grassi, G. (2022). The Discrete Fractional Variable-Order Tinkerbell Map: Chaos, 0–1 Test, and Entropy. Mathematics, 10(17), 3173. https://doi.org/10.3390/math10173173



