Insight into Dynamic of Mono and Hybrid Nanofluids Subject to Binary Chemical Reaction, Activation Energy, and Magnetic Field through the Porous Surfaces
Abstract
:1. Introduction
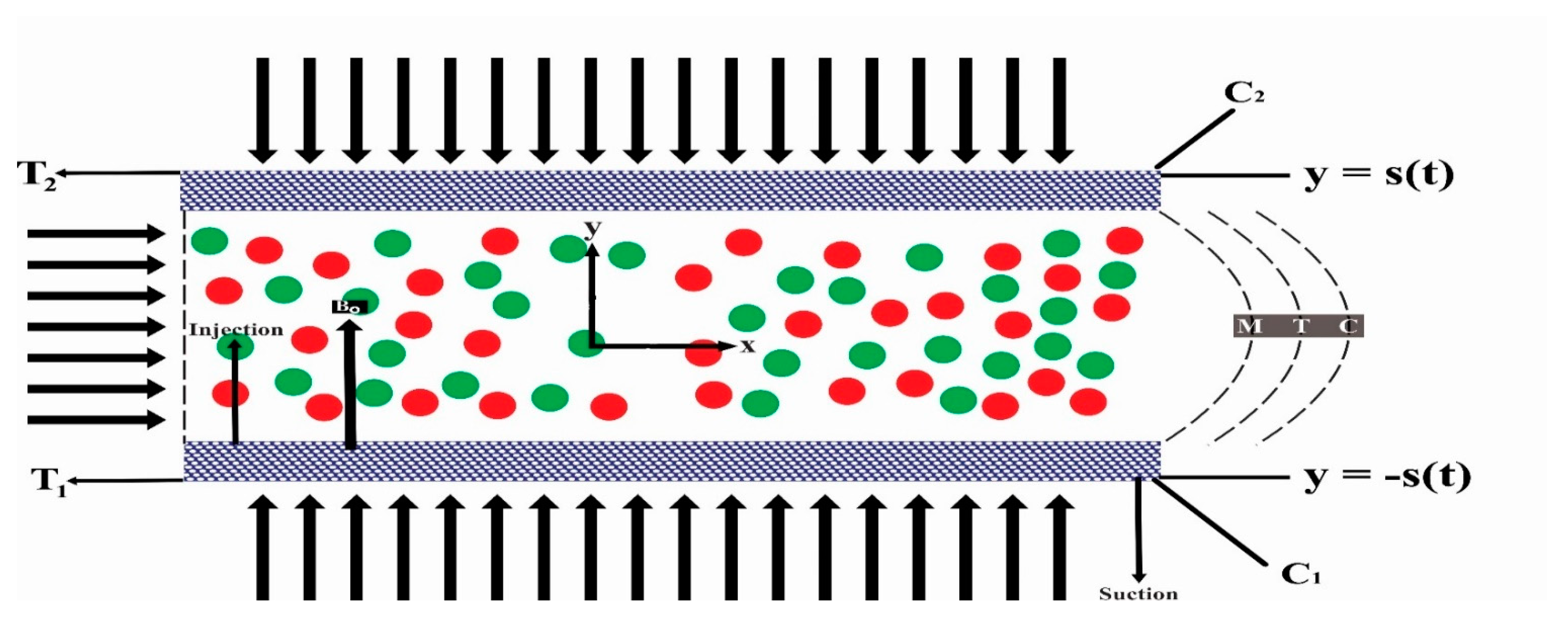
2. Mathematical Formulation
3. Solution Procedure
3.1. Practical and Engineering Interests
3.1.1. Skin Friction Coefficients
3.1.2. Nusselt Numbers
3.1.3. Sherwood Number
3.1.4. Numerical Solution and Modeling for Thermophysical Properties of (HNfd)
4. Solution of the Problem
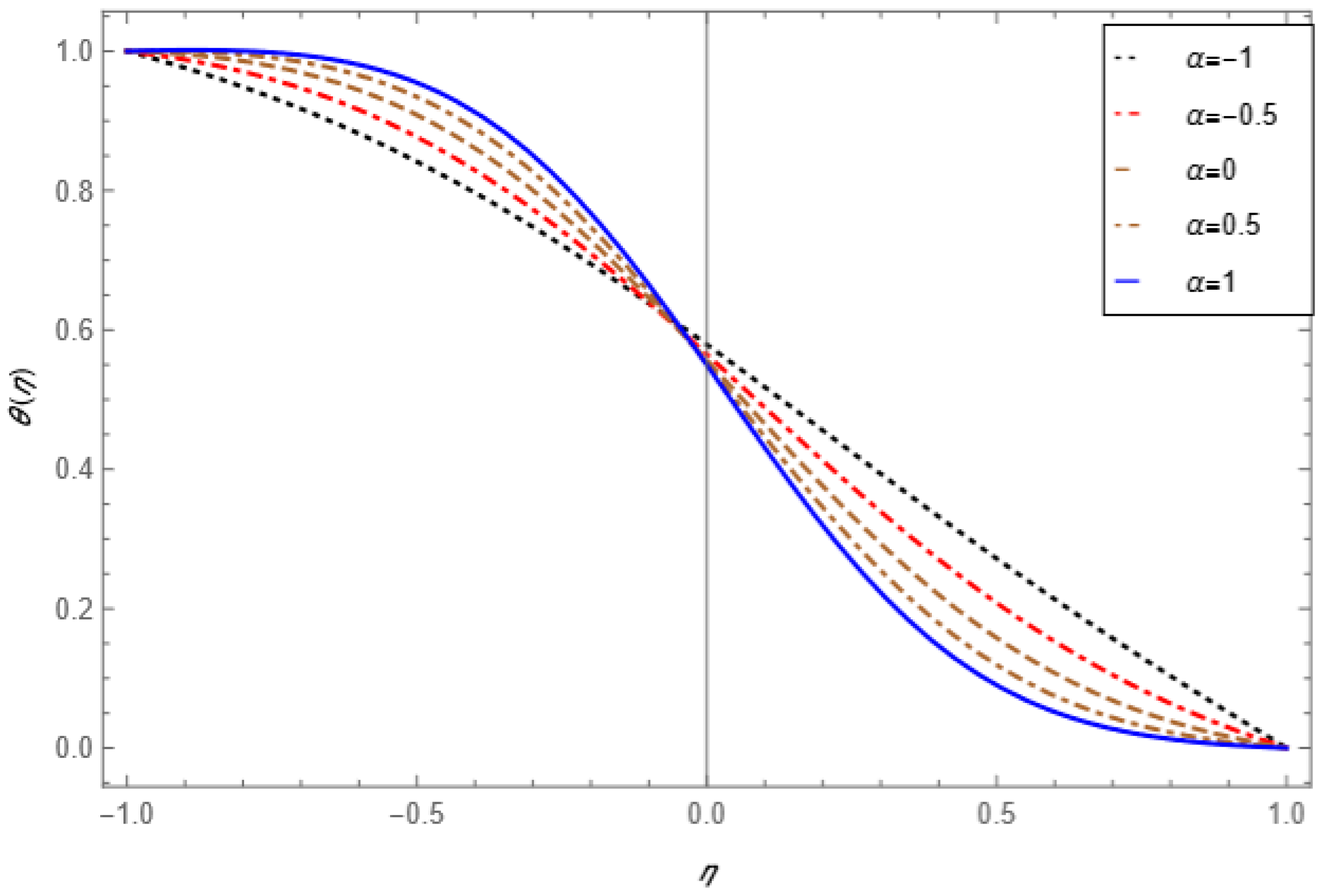
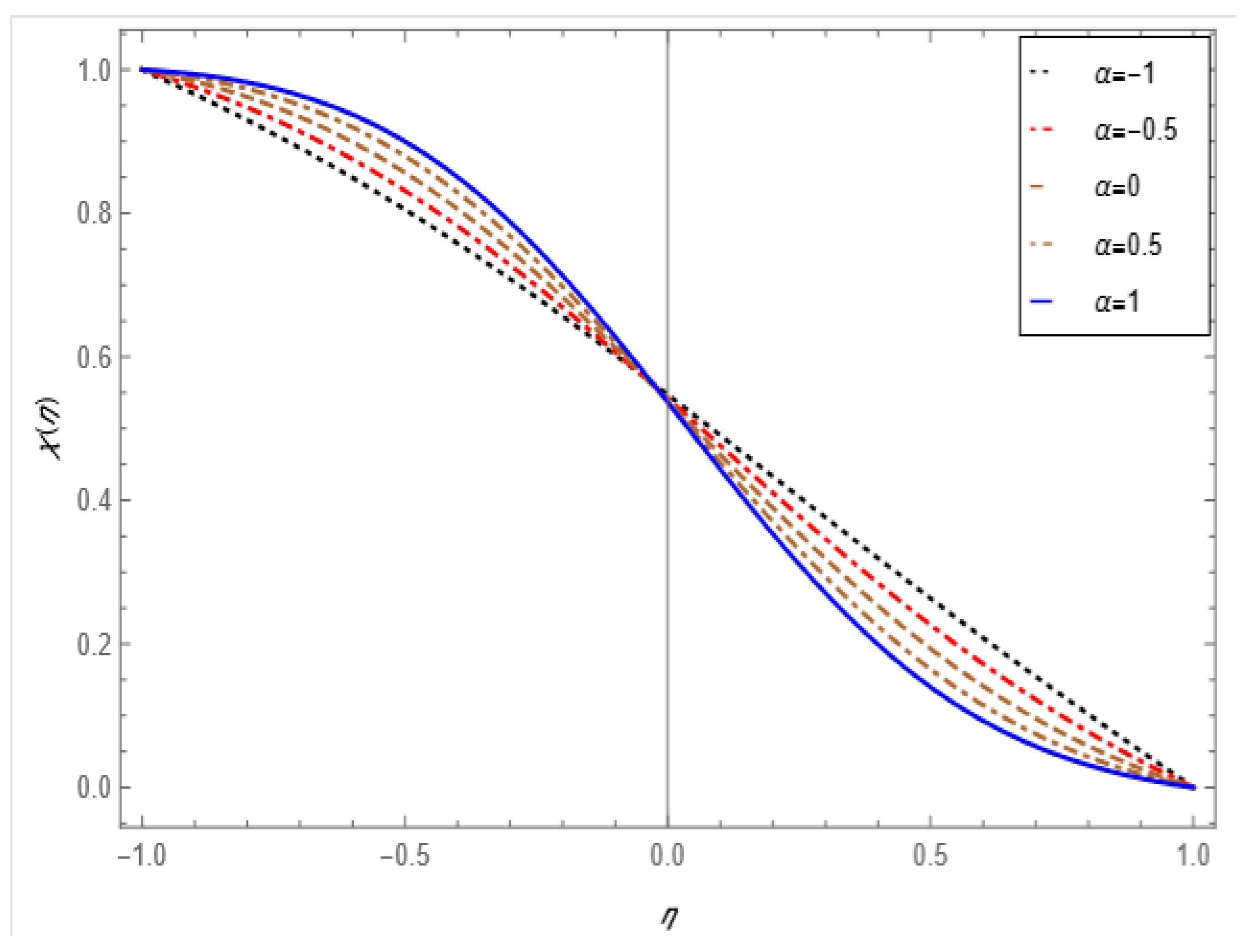
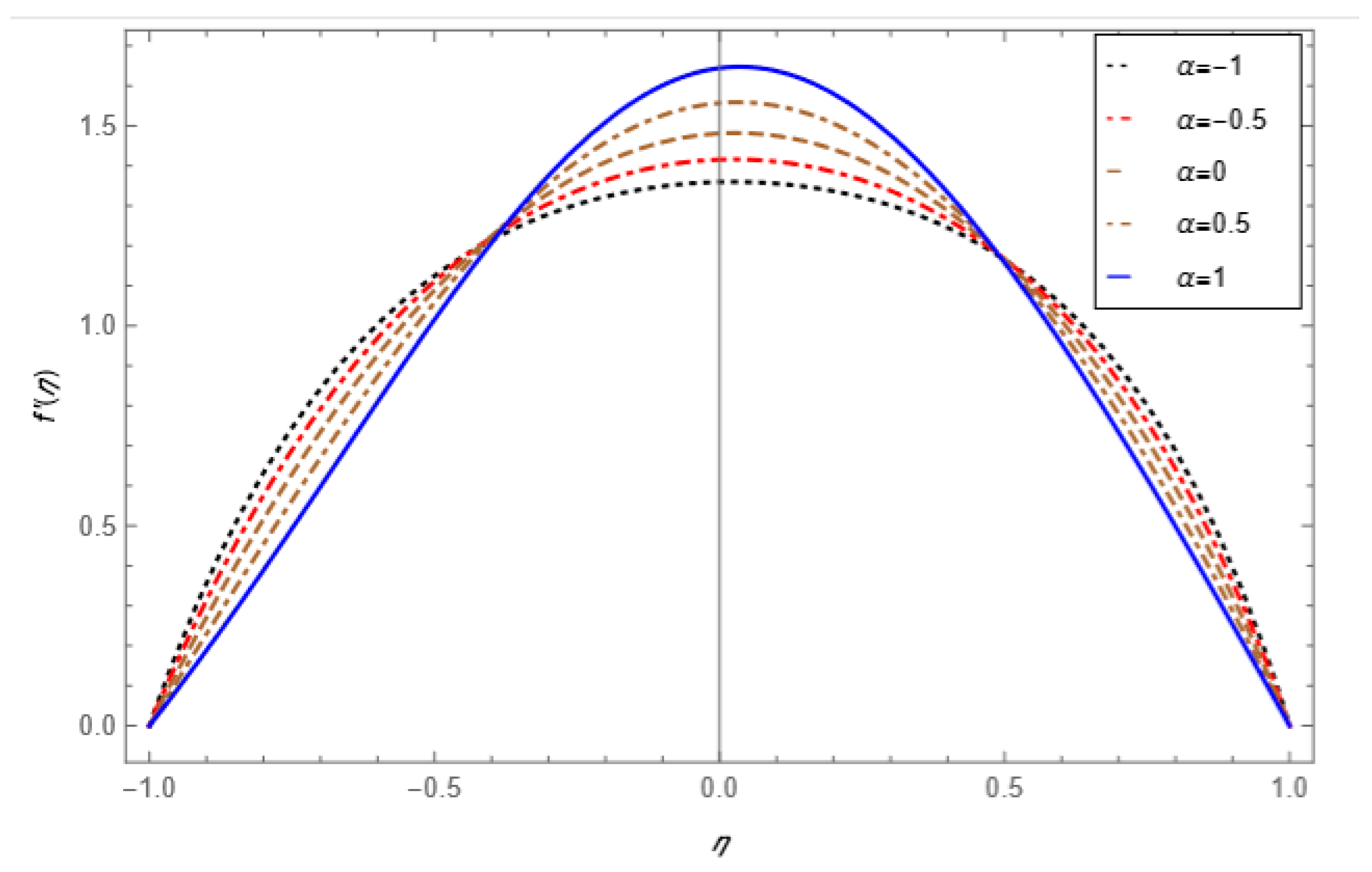
5. Result and Discussion
6. Numerical Stability
7. Conclusions
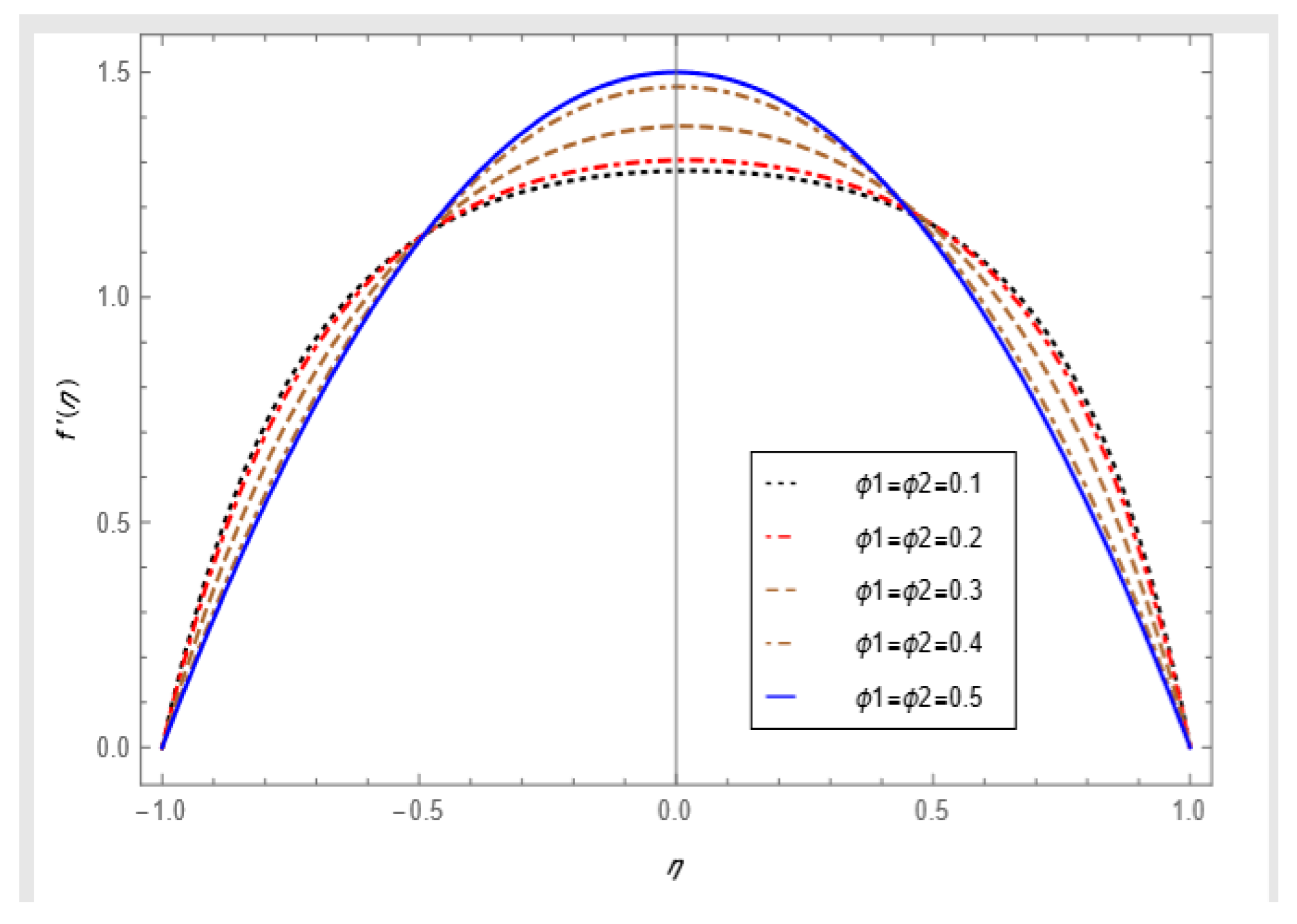
- The skin friction coefficient increases at both porous walls with the increase in the permeable Reynolds number, and a similar trend is observed for the nanoparticles volume fraction.
- The Nusselt number shows significant results under the effect of the hybrid nanofluid flow.
- The Prandtl number has a significant role in the heat transfer system for every type of hybrid nanofluid flow.
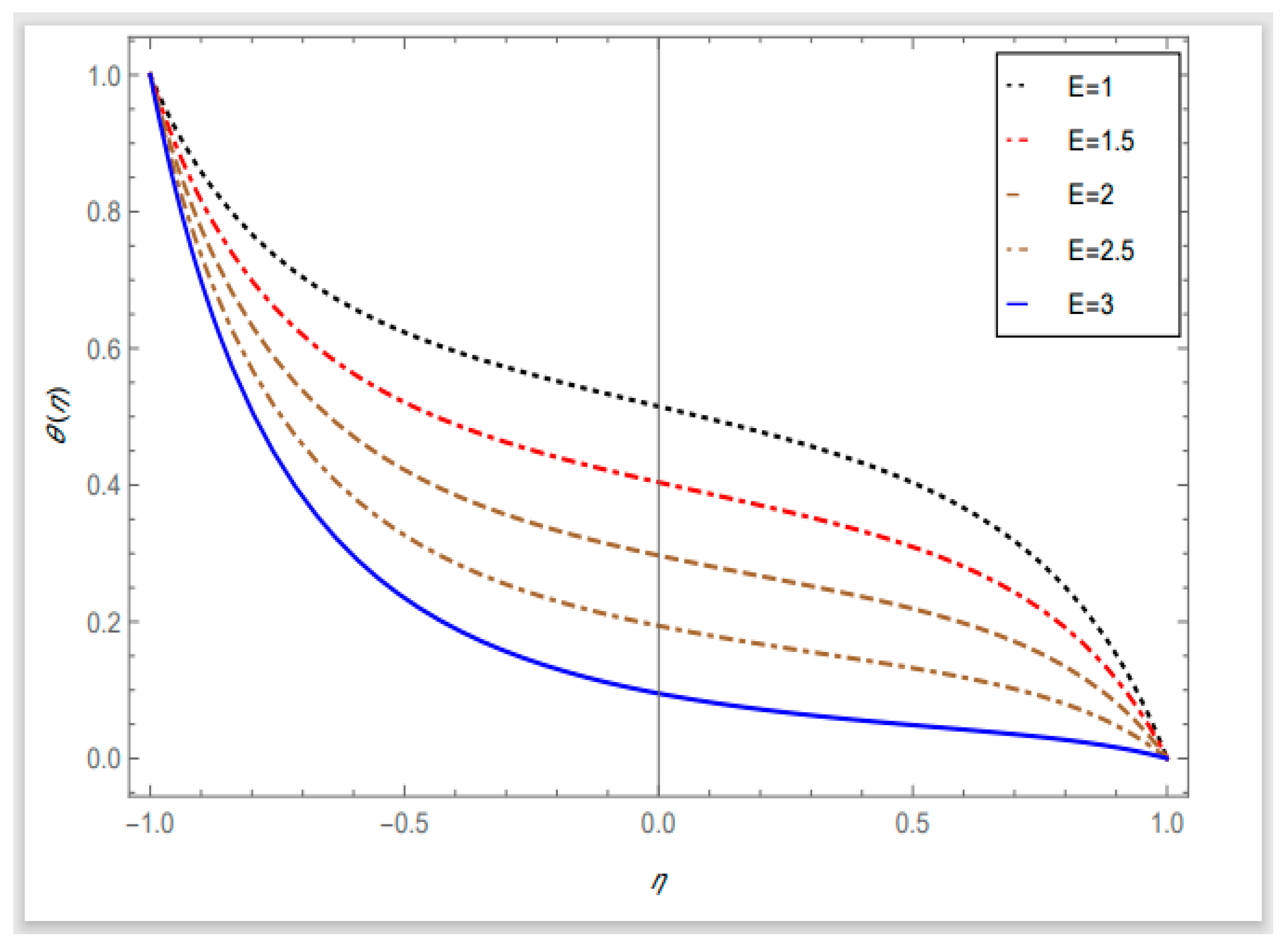
- When the dimensionless activation energy parameter has higher values, the rate of the mass transfer rises.
- The measurements of the dimensionless exothermic/endothermic parameter and the dimensionless reaction rate parameter are increased; the flow of heat transfer improves progressively.
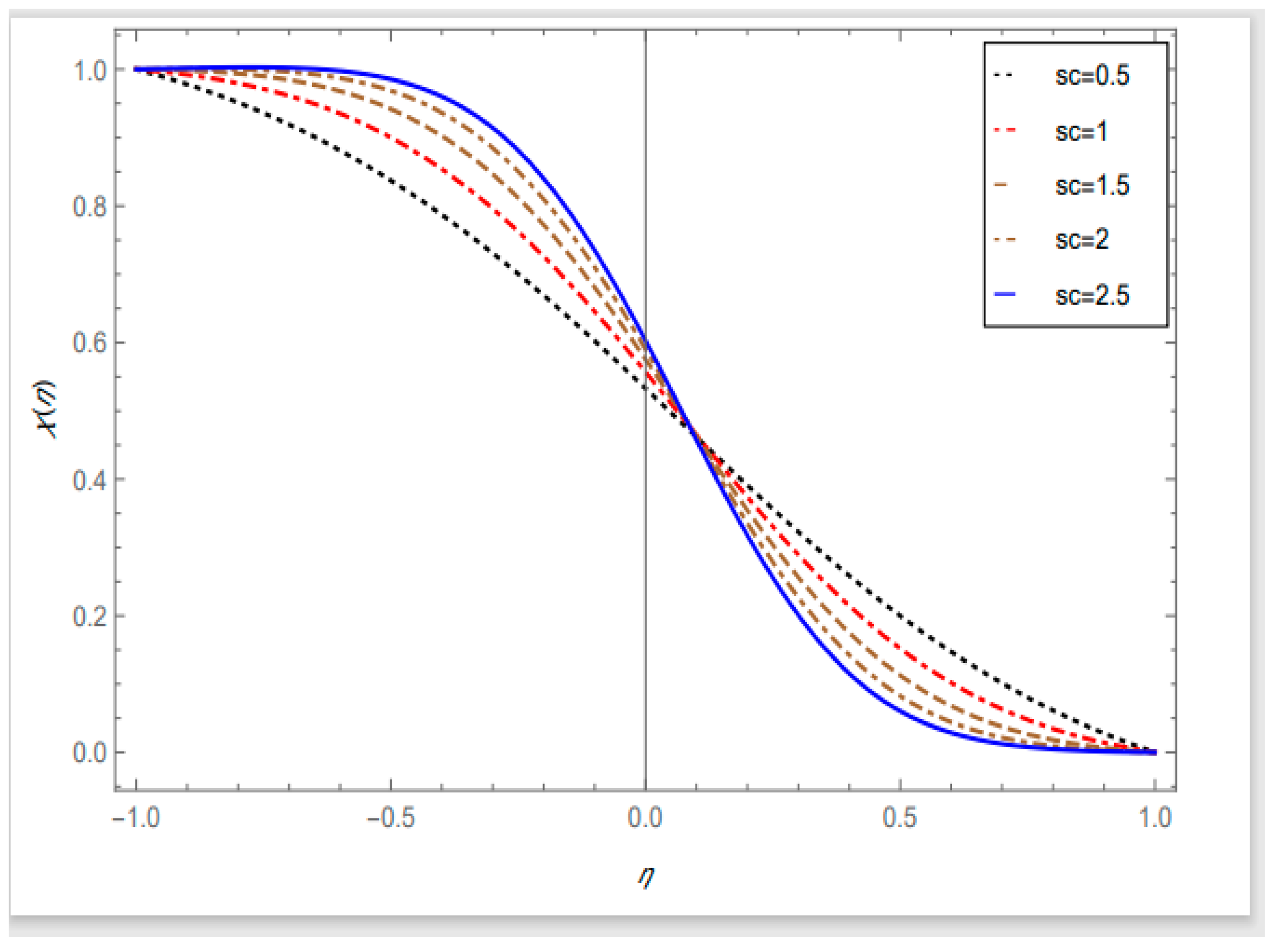
- As the values of the Schmidt number rise, the mass transfer flow improves on the lower porous surfaces.
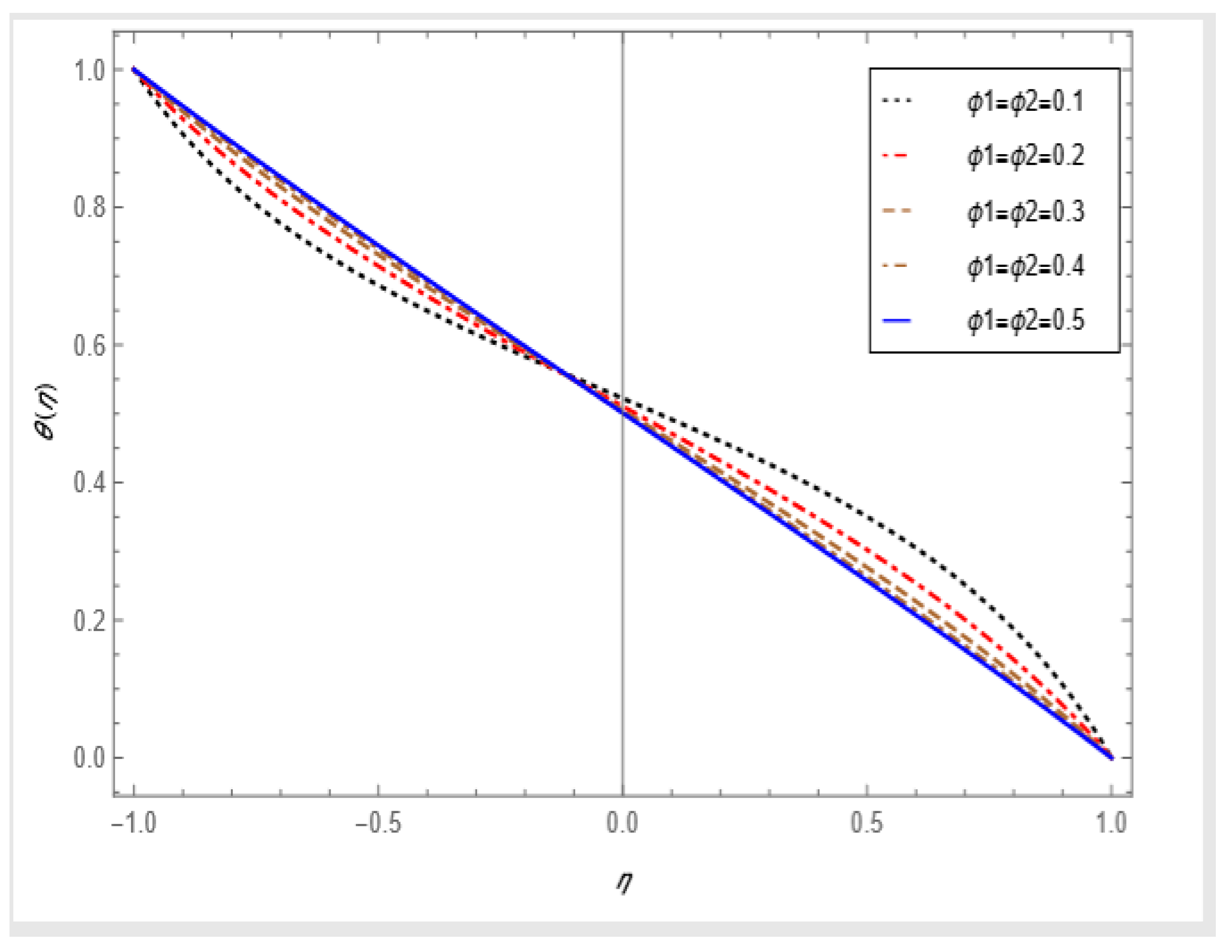
- For the injection cases, the hybrid nanoparticles have a significant effect on the temperature as well as the radial velocity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| u, v | Velocity components |
| Sc | Schmidt number |
| T | Temperature |
| Hybrid nanofluids specific heat | |
| Expansion ratio | |
| E | Dimensionless activation energy Parameter |
| Activation energy | |
| Lower plate concentration | |
| Upper plate temperature | |
| Magnetic field strength | |
| Nanoparticles volume fraction | |
| Water density (base fluid) | |
| Density for nanoparticles 1st and 2nd | |
| Thermal conductivity | |
| , | Thermal conductivity for nanoparticles 1st and 2nd |
| M | Magnetic field |
| Boltzmann constant | |
| Exothermic/endothermic coefficient | |
| Prandtl number | |
| n | Dimensionless parameter |
| Reynolds number | |
| N | Size |
| Dimensionless exothermic/endothermic Parameter | |
| Dimensionless reaction rate | |
| T1 | Lower plate temperature |
| C2 | Upper plate concentration |
| Temperature difference parameter | |
| x, y | Space coordinate |
| Hybrid nanofluids density | |
| Hybrid nanofluid’s thermal conductivity | |
| Water dynamic velocity | |
| Base fluid | |
| Thermal diffusivity hybrid Nanofluid | |
| N | Similarity variable |
| D | Diffusion coefficient |
References
- Sreedevi, P.; Reddy, P.S.; Chamkha, A. Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. SN Appl. Sci. 2020, 2, 1222. [Google Scholar] [CrossRef]
- Roy, N.C.; Pop, I. Heat and mass transfer of a hybrid nanofluid flow with binary chemical reaction over a permeable shrinking surface. Chin. J. Phys. 2021, 76, 283–298. [Google Scholar] [CrossRef]
- Xu, H. Modelling unsteady mixed convection of a nanofluid suspended with multiple kinds of nanoparticles between two rotating disks by generalized hybrid model. Int. Commun. Heat Mass Transf. 2019, 108, 104275. [Google Scholar] [CrossRef]
- Kapen, P.T.; Ketchate, C.G.N.; Fokwa, D.; Tchuen, G. Linear stability analysis of (Cu-Al2O3)/water hybrid nanofluid flow in porous media in presence of hydromagnetic, small suction and injection effects. Alex. Eng. J. 2021, 60, 1525–1536. [Google Scholar] [CrossRef]
- Maskeen, M.M.; Zeeshan, A.; Mehmood, O.U.; Hassan, M. Heat transfer enhancement in hydromagnetic alumina–copper/water hybrid nanofluid flow over a stretching cylinder. J. Therm. Anal. 2019, 138, 1127–1136. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Devi, S.P.A. Numerical investigation of three-dimensional hybrid Cu–Al2O3/Water nanofluids flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 2016, 94, 490–496. [Google Scholar] [CrossRef]
- Sahoo, R.R.; Kumar, V. Development of a new correlation to determine the viscosity of ternary hybrid nanofluids. Int. Commun. Heat Mass Transf. 2020, 111, 104451. [Google Scholar] [CrossRef]
- Aladdin, N.A.L.; Bachok, N.; Pop, I. Cu-Al2O3/water hybrid nanofluids flow over a permeable moving surface in presence of hydromagnetic and suction effects. Alex. Eng. J. 2020, 59, 657–666. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow and heat transfer over a nonlinear permeable stretching/shrinking surface. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3110–3127. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Heat transfer enhancement with Ag–CuO/water hybrid nanofluids. Results Phys. 2017, 7, 2317–2324. [Google Scholar] [CrossRef]
- Das, P.K. A review based on the effect and mechanism of thermal conductivity of normal nanofluids and hybrid nanofluids. J. Mol. Liq. 2017, 240, 420–446. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD flow and heat transfer of hybrid nanofluids over a permeable moving surface in the presence of thermal radiation. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 858–879. [Google Scholar] [CrossRef]
- Devi, S.U.; Devi, S.P.A. Heat transfer enhancement of CuAl2O3/water hybrid nanofluids flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Chahregh, H.S.; Dinarvand, S. TiO2–Ag/blood hybrid nanofluids flow through an artery with applications of drug delivery and blood circulation in the respiratory system. Int. J. Numer. Methods Heat Fluid Flow 2020, 11, 4775–4796. [Google Scholar] [CrossRef]
- Dinarvand, S.; Nademi Rostami MDinarvand, R.; Pop, I. Improvement of drug delivery micro-circulatory system with a novel pattern of CuO-Cu/blood hybrid nanofluids flow towards a porous stretching sheet. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4408–4429. [Google Scholar] [CrossRef]
- Shahsavar, A.; Talebizadeh Sardari, P.; Toghraie, D. Free convection heat transfer and entropy generation analysis of water-Fe3O4/CNT hybrid nanofluids in a concentric annulus. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 915–934. [Google Scholar] [CrossRef]
- Ahamed, N.; Asirvatham, L.G.; Wong, W.S. Entropy generation analysis of graphene–alumina hybrid nanofluid in multiport mini-channel heat exchanger coupled with thermoelectric cooler. Int. J. Heat Mass Transf. 2016, 103, 1084–1097. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Dogonchi, A.S.; Ganji, D.D. Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluids in a rotating system among two surfaces in the presence of thermal radiation and Joule heating. AIP Adv. 2019, 9, 025103. [Google Scholar] [CrossRef] [Green Version]
- Bhattad, A.; Sarkar, J.; Ghosh, P. Discrete phase numerical model and experimental study of hybrid nanofluid heat transfer and pressure drop in plate heat exchanger. Int. Commun. Heat Mass Transf. 2018, 91, 262–273. [Google Scholar] [CrossRef]
- Hussien, A.A.; Abdullah, M.Z.; Yusop, N.M.; Al-Nimr, M.A.; Atieh, M.A.; Mehrali, M. Experiment on forced convective heat transfer enhancement using MWCNTs/GNPs hybrid nanofluid and monotube. Int. J. Heat Mass Transf. 2017, 115, 1121–1131. [Google Scholar] [CrossRef]
- Soltani, O.; Akbari, M. Effects of temperature and particles concentration on the dynamic viscosity of MgO-MWCNT/ethylene glycol hybrid nanofluids: Experimental study. Phys. E 2016, 84, 564–570. [Google Scholar] [CrossRef]
- Abdelmalek, Z.; Qureshi, M.Z.A.; Bilal, S.; Raza, Q.; Sherif, E.-S.M. A case study on morphological aspects of distinct magnetized 3D hybrid nanoparticles on fluid flow between two orthogonal rotating disks: An application of thermal energy systems. Case Stud. Therm. Eng. 2020, 23, 100744. [Google Scholar] [CrossRef]
- Singh, K.; Kumar, M. Influence of Chemical Reaction on Heat and Mass Transfer Flow of a Micropolar Fluid over a Permeable Channel with Radiation and Heat Generation. J. Thermodyn. 2016, 2016, 8307980. [Google Scholar] [CrossRef] [Green Version]
- Ojjela, O.; Kumar, N.N. Unsteady Heat and Mass Transfer of Chemically Reacting Micropolar Fluid in a Porous Channel with Hall and Ion Slip Currents. Int. Sch. Res. Not. 2014, 2014, 646957. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roy, N.C.; Pop, I. Analytical investigation of transient free convection and heat transfer of a hybrid nanofluid between two vertical parallel plates. Phys. Fluids 2022, 34, 072005. [Google Scholar] [CrossRef]
- Jyothi, A.M.; Kumar, R.S.V.; Madhukesh, J.K.; Prasannakumara, B.C.; Ramesh, G.K. Squeezing flow of Casson hybrid nanofluid between parallel plates with a heat source or sink and thermophoretic particle deposition. Heat Transf. 2021, 50, 7139–7156. [Google Scholar] [CrossRef]
- Santhi, M.; Rao, K.V.S.; Reddy, P.S.; Sreedevi, P. Heat and mass transfer characteristics of radiative hybrid nanofluid flow over a stretching sheet with chemical reaction. Heat Transf. 2020, 50, 2929–2949. [Google Scholar] [CrossRef]
- Bilal, M.; Gul, T.; Alsubie, A.; Ali, I. Axisymmetric hybrid nanofluid flow with heat and mass transfer amongst the two gyrating plates. ZAMM-J. Appl. Math. Mech. Z. Für Angew. Math. Und Mech. 2021, 101, e202000146. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Madhukesh, J.K.; Prasannakumara, B.C.; Roopa, G.S. Significance of aluminium alloys particle flow through a parallel plates with activation energy and chemical reaction. J. Therm. Anal. 2021, 147, 6971–6981. [Google Scholar] [CrossRef]
- Shanmugapriya, M.; Sundareswaran, R.; Kumar, P.S. Heat and Mass Transfer Enhancement of MHD Hybrid Nanofluid Flow in the Presence of Activation Energy. Int. J. Chem. Eng. 2021, 2021, 9473226. [Google Scholar] [CrossRef]
- Shah, N.A.; Wakif, A.; El-Zahar, E.R.; Ahmad, S.; Yook, S.-J. Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG), (40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud. Therm. Eng. 2022, 35, 102046. [Google Scholar] [CrossRef]
- Ali, B.; Naqvi, R.A.; Ali, L.; Abdal, S.; Hussain, S. A comparative description on time-dependent rotating magnetic transport of a water base liquid H2O with hybrid nano-materials Al2O3-Cu and Al2O3-TiO2 over an extending sheet using Buongiorno model: Finite element approach. Chin. J. Phys. 2021, 70, 125–139. [Google Scholar] [CrossRef]
- Ali, B.; Khan, S.A.; Hussein, A.K.; Thumma, T.; Hussain, S. Hybrid nanofluids: Significance of gravity modulation, heat source/ sink, and magnetohydrodynamic on dynamics of micropolar fluid over an inclined surface via finite element simulation. Appl. Math. Comput. 2021, 419, 126878. [Google Scholar] [CrossRef]
- Sajjan, K.; Shah, N.A.; Ahammad, N.A.; Raju, C.S.K.; Kumar, M.D.; Weera, W. Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. AIMS Mathematics 2022, 7, 18416–18449. [Google Scholar] [CrossRef]
- Bestman, A.R. Natural convection boundary layer with suction and mass transfer in a porous medium. Int. J. Energy Res. 1990, 14, 389–396. [Google Scholar] [CrossRef]
- Khan, N.S.; Kumam, P.; Thounthong, P. Second law analysis with effects of Arrhenius activation energy and binary chemical reaction on nanofluids flow. Sci. Rep. 2020, 10, 1226. [Google Scholar] [CrossRef] [Green Version]
- Jayadevamurthy, P.G.R.; Rangaswamy, N.K.; Prasanna kumara, B.C.; Nisar, K.S. Emphasis on unsteady dynamics of bioconvective hybrid nanofluids flow over an upward–downward moving rotating disk. Numer. Methods Partial. Differ. Equ. 2020, 5, 1–22. [Google Scholar] [CrossRef]
- Reddy, M.G.; Naveen, K.R.; Prasanna, K.B.; Rudraswamy, N.G.; Kumar, K.G. Magnetohydrodynamic flow and heat transfer of a hybrid nanofluids over a rotating disk by considering Arrhenius energy. Commun. Theor. Phys. 2021, 73, 045002. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. Buoyancy effects on the MHD nanofluids flow past a vertical surface with chemical Reaction and activation energy. Int. J. Heat Mass Transf. 2017, 108, 1340–1346. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Michaelides, E.E. Study of Arrhenius activation energy on the thermo-bioconvection nanofluid flow over a Riga plate. J. Anal. Calorim. 2020, 143, 2029–2038. [Google Scholar] [CrossRef]
- Kasaeian, A.; Daneshazarian, R.; Mahian, O.; Kolsi, L.; Chamkha, A.J.; Wongwises, S.; Pop, I. Nanofluid flow and heat transfer in porous media: A review of the latest developments. Int. J. Heat Mass Transf. 2017, 107, 778–791. [Google Scholar] [CrossRef]
- Singh, J.; Mahabaleshwar, U.S.; Bognár, G. Mass Transpiration in Nonlinear MHD Flow Due to Porous Stretching Sheet. Sci. Rep. 2019, 9, 18484. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Subhani, M.; Nadeem, S. Numerical investigation into unsteady magnetohydrodynamics flow of micropolar hybrid nanofluid in porous medium. Phys. Scr. 2019, 94, 105–120. [Google Scholar] [CrossRef]
- Al-Zamily, A.M.J. Analysis of natural convection and entropy generation in a cavity filled with multi-layers of porous medium and nanofluids with a heat generation. Int. J. Heat Mass Transf. 2017, 106, 1218–1231. [Google Scholar] [CrossRef]
- Dzulkifli, N.F.; Bachok, N.; Yacob, N.A.; Arifin, N.; Rosali, H. Unsteady Stagnation-Point Flow and Heat Transfer Over a Permeable Exponential Stretching/Shrinking Sheet in Nanofluid with Slip Velocity Effect: A Stability Analysis. Appl. Sci. 2018, 8, 2172. [Google Scholar] [CrossRef] [Green Version]
- Younis, O.; Alizadeh, M.; Hussein, A.K.; Ali, B.; Biswal, U.; Malekshah, E.H. MHD Natural Convection and Radiation over a Flame in a Partially Heated Semicircular Cavity Filled with a Nanofluid. Mathematics 2022, 10, 1347. [Google Scholar] [CrossRef]
- Lou, Q.; Ali, B.; Rehman, S.U.; Habib, D.; Abdal, S.; Shah, N.A.; Chung, J.D. Micropolar Dusty Fluid: Coriolis Force Effects on Dynamics of MHD Rotating Fluid When Lorentz Force Is Significant. Mathematics 2022, 10, 2630. [Google Scholar] [CrossRef]
- Ashraf, M.Z.; Rehman, S.U.; Farid, S.; Hussein, A.K.; Ali, B.; Shah, N.A.; Weera, W. Insight into Significance of Bioconvection on MHD Tangent Hyperbolic Nanofluid Flow of Irregular Thickness across a Slender Elastic Surface. Mathematics 2022, 10, 2592. [Google Scholar] [CrossRef]
- Mehryan, S.; Sheremet, M.A.; Soltani, M.; Izadi, M. Natural convection of magnetic hybrid nanofluid inside a double-porous medium using two-equation energy model. J. Mol. Liq. 2019, 277, 959–970. [Google Scholar] [CrossRef]
- Mallikarjuna, B.; Rashad, A.M.; Chamkha, A.J.; Raju, S.H. Chemical reaction effects on MHD convective heat and mass transfer flow past a rotating vertical cone embedded in a variable porosity regime. Afr. Mat. 2015, 27, 645–665. [Google Scholar] [CrossRef]
- Fetecau, C.; Shah, N.A.; Vieru, D. General Solutions for Hydromagnetic Free Convection Flow over an Infinite Plate with Newtonian Heating, Mass Diffusion and Chemical Reaction. Commun. Theor. Phys. 2017, 68, 768. [Google Scholar] [CrossRef]
- Dawar, A.; Wakif, A.; Thumma, T.; Shah, N.A. Towards a new MHD non-homogeneous convective nanofluid flow model for simulating a rotating inclined thin layer of sodium alginate-based Iron oxide exposed to incident solar energy. Int. Commun. Heat Mass Transf. 2021, 130, 105800. [Google Scholar] [CrossRef]
- Sabu, A.; Wakif, A.; Areekara, S.; Mathew, A.; Shah, N.A. Significance of nanoparticles’ shape and thermo-hydrodynamic slip constraints on MHD alumina-water nanoliquid flows over a rotating heated disk: The passive control approach. Int. Commun. Heat Mass Transf. 2021, 129, 105711. [Google Scholar] [CrossRef]
- Saba, F.; Ahmed, N.; Khan, U.; Waheed, A.; Rafiq, M.; Mohyud-Din, S.T. Thermophysical Analysis of Water Based (Cu–Al2O3) Hybrid Nanofluid in an Asymmetric Channel with Dilating/Squeezing Walls Considering Different Shapes of Nanoparticles. Appl. Sci. 2018, 8, 1549. [Google Scholar] [CrossRef] [Green Version]
- Sheikholeslami, M.; Ganji, D.D. Nanofluid flow and heat transfer between parallel plates considering Brownian motion using DTM. Comput. Methods Appl. Mech. Eng. 2014, 283, 651–663. [Google Scholar] [CrossRef]
- Majdalani, J.; Zhou, C.; Dawson, C.A. Two dimensional viscous flows between slowly expanding or contracting walls with weak permeability. J. Biomech. 2002, 35, 1399–1403. [Google Scholar] [CrossRef]
- Ahmad, S.; Farooq, M.; Mir, N.A.; Anjum, A.; Javed, M. Magneto-hydrodynamic flow of squeezed fluid with binary chemical reaction and activation energy. J. Cent. South Univ. 2019, 26, 1362–1373. [Google Scholar] [CrossRef]

| Properties | Hybrid Nanofluid |
|---|---|
| Density () | = + − (1 − − ) |
| Viscosity () | |
| Heat Capacity | ()() |
| Thermal Conductivity () | = Where = |
| Title | ||||||
|---|---|---|---|---|---|---|
| kg | 997.1 | 4250 | 8933 | 3970 | 6320 | 10,500 |
| (J k). | 4180 | 686.2 | 385 | 765 | 531.5 | 235 |
| 0.6013 | 8.9538 | 401 | 40 | 76.5 | 429 |
| 1 | 1 | 0.01 | 0.01 | 1 | 3.1951 | 3.1951 |
| 1.2 | 3.3435 | 3.3435 | ||||
| 1.4 | 3.4983 | 3.4983 | ||||
| 1 | 2.0561 | 2.0561 | ||||
| 3 | 2.0954 | 2.0954 | ||||
| 5 | 2.1342 | 2.1342 | ||||
| 0.01 | ||||||
| 0.03 | ||||||
| 0.05 | ||||||
| 0.03 | ||||||
| 0.06 | ||||||
| 0.09 | ||||||
| 0.1 | ||||||
| 0.5 | ||||||
| 0.9 |
| 1 | 1 | 0.01 | 0.01 | 1 | 0.5 | 1 | 0.1 | 0.1 | ||
| 1.2 | ||||||||||
| 1.4 | ||||||||||
| 1 | ||||||||||
| 3 | ||||||||||
| 5 | ||||||||||
| 0.01 | ||||||||||
| 0.03 | ||||||||||
| 0.05 | ||||||||||
| 0.03 | ||||||||||
| 0.06 | ||||||||||
| 0.09 | ||||||||||
| 0.1 | 1 | |||||||||
| 0.5 | ||||||||||
| 0.9 | ||||||||||
| 0.2 | ||||||||||
| 0.5 | ||||||||||
| 0.8 | ||||||||||
| 0.35 | ||||||||||
| 0.70 | ||||||||||
| 0.95 | ||||||||||
| 0.15 | ||||||||||
| 0.20 | ||||||||||
| 0.25 | 1 | |||||||||
| 0.20 | ||||||||||
| 0.50 | ||||||||||
| 0.80 |
| 5.0 | 6.2 | ||
| 5.5 | |||
| 6.2 | |||
| 1.3 | |||
| 1.5 | |||
| 1.7 |
| 0.01 = 1% | 0.05680 | 0.05725 | 0.05703 | 0.05680 | 0.05532 | |||
| 0.03 = 3% | 0.07621 | 0.07712 | 0.07651 | 0.07585 | 0.07158 | |||
| 0.05 = 5% | 0.09524 | 0.09616 | 0.09520 | 0.09415 | 0.08734 | |||
| 0.07 = 7% | 0.11368 | 0.11440 | 0.11310 | 0.11172 | 0.01025 | |||
| 0.09 = 9% | 0.13152 | 0.13187 | 0.13023 | 0.12858 | 0.11733 |
| AHMAD et al. [57] | Present Results | ||
|---|---|---|---|
| 1.1 | 2 | 1.17039 | 1.17040 |
| 1.2 | 1.27024 | 1.27025 | |
| 1.4 | 1.36100 | 1.36101 | |
| 1.6 | 1.41025 | 1.41026 | |
| 1.1 | 2 | 1.17039 | 1.17040 |
| 1.5 | 1.10472 | 1.10474 | |
| 1 | 1.01015 | 1.01017 | |
| 0.5 | 0.82109 | 0.82110 |
| f(−1) | f′(−1) | f″(−1) | |
|---|---|---|---|
| −1 | −1 | 0 | |
| −0.9 | |||
| −0.8 | |||
| −0.7 | |||
| −0.6 | |||
| −0.5 | |||
| −0.4 | |||
| −0.3 | |||
| −0.2 | |||
| −0.1 | |||
| 0 | |||
| 0.1 | |||
| 0.2 | |||
| 0.3 | |||
| 0.4 | |||
| 0.5 | |||
| 0.6 | |||
| 0.7 | |||
| 0.8 | |||
| 0.9 | |||
| 1 | 1 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, Q.; Qureshi, M.Z.A.; Khan, B.A.; Kadhim Hussein, A.; Ali, B.; Shah, N.A.; Chung, J.D. Insight into Dynamic of Mono and Hybrid Nanofluids Subject to Binary Chemical Reaction, Activation Energy, and Magnetic Field through the Porous Surfaces. Mathematics 2022, 10, 3013. https://doi.org/10.3390/math10163013
Raza Q, Qureshi MZA, Khan BA, Kadhim Hussein A, Ali B, Shah NA, Chung JD. Insight into Dynamic of Mono and Hybrid Nanofluids Subject to Binary Chemical Reaction, Activation Energy, and Magnetic Field through the Porous Surfaces. Mathematics. 2022; 10(16):3013. https://doi.org/10.3390/math10163013
Chicago/Turabian StyleRaza, Qadeer, M. Zubair Akbar Qureshi, Behzad Ali Khan, Ahmed Kadhim Hussein, Bagh Ali, Nehad Ali Shah, and Jae Dong Chung. 2022. "Insight into Dynamic of Mono and Hybrid Nanofluids Subject to Binary Chemical Reaction, Activation Energy, and Magnetic Field through the Porous Surfaces" Mathematics 10, no. 16: 3013. https://doi.org/10.3390/math10163013
APA StyleRaza, Q., Qureshi, M. Z. A., Khan, B. A., Kadhim Hussein, A., Ali, B., Shah, N. A., & Chung, J. D. (2022). Insight into Dynamic of Mono and Hybrid Nanofluids Subject to Binary Chemical Reaction, Activation Energy, and Magnetic Field through the Porous Surfaces. Mathematics, 10(16), 3013. https://doi.org/10.3390/math10163013







