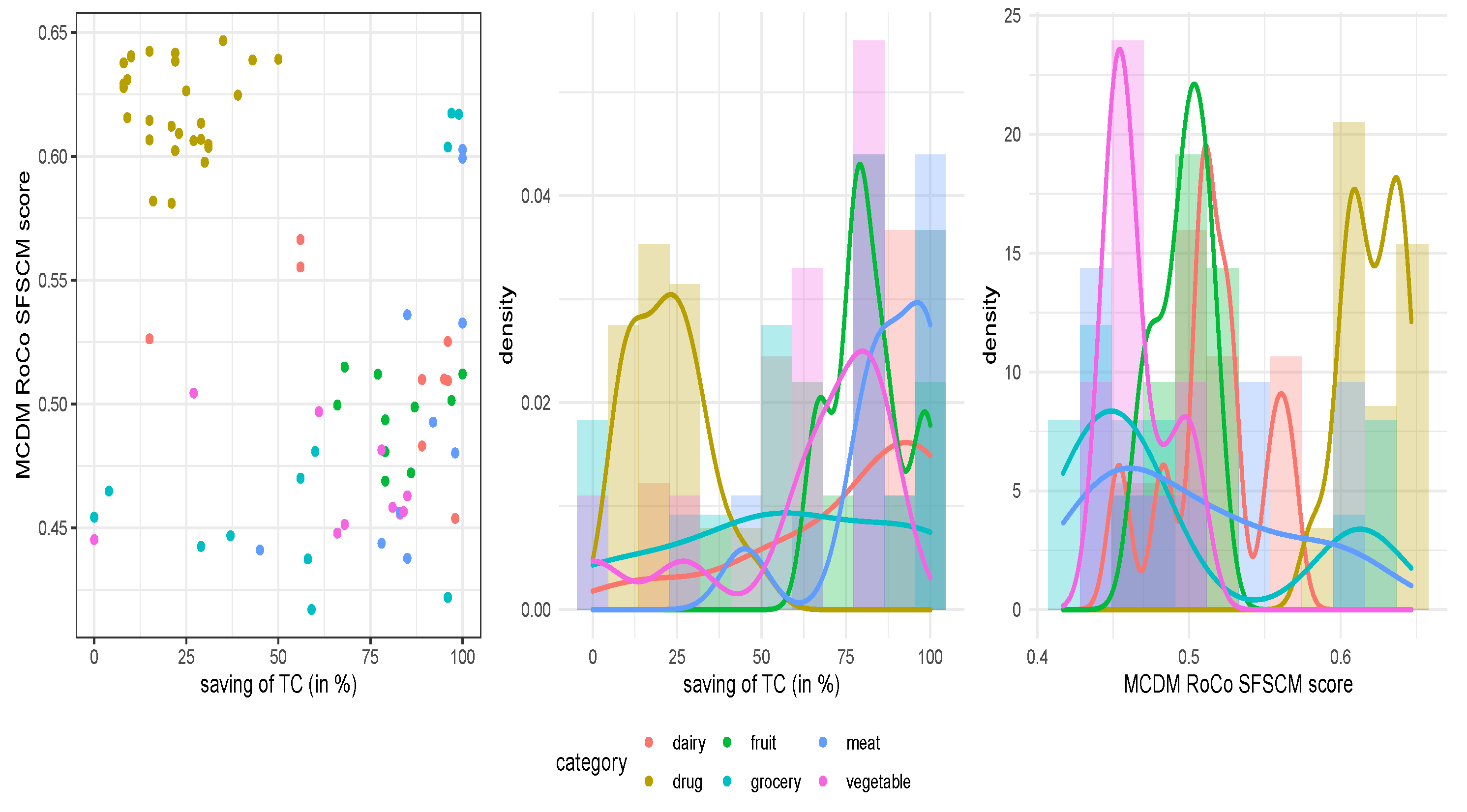
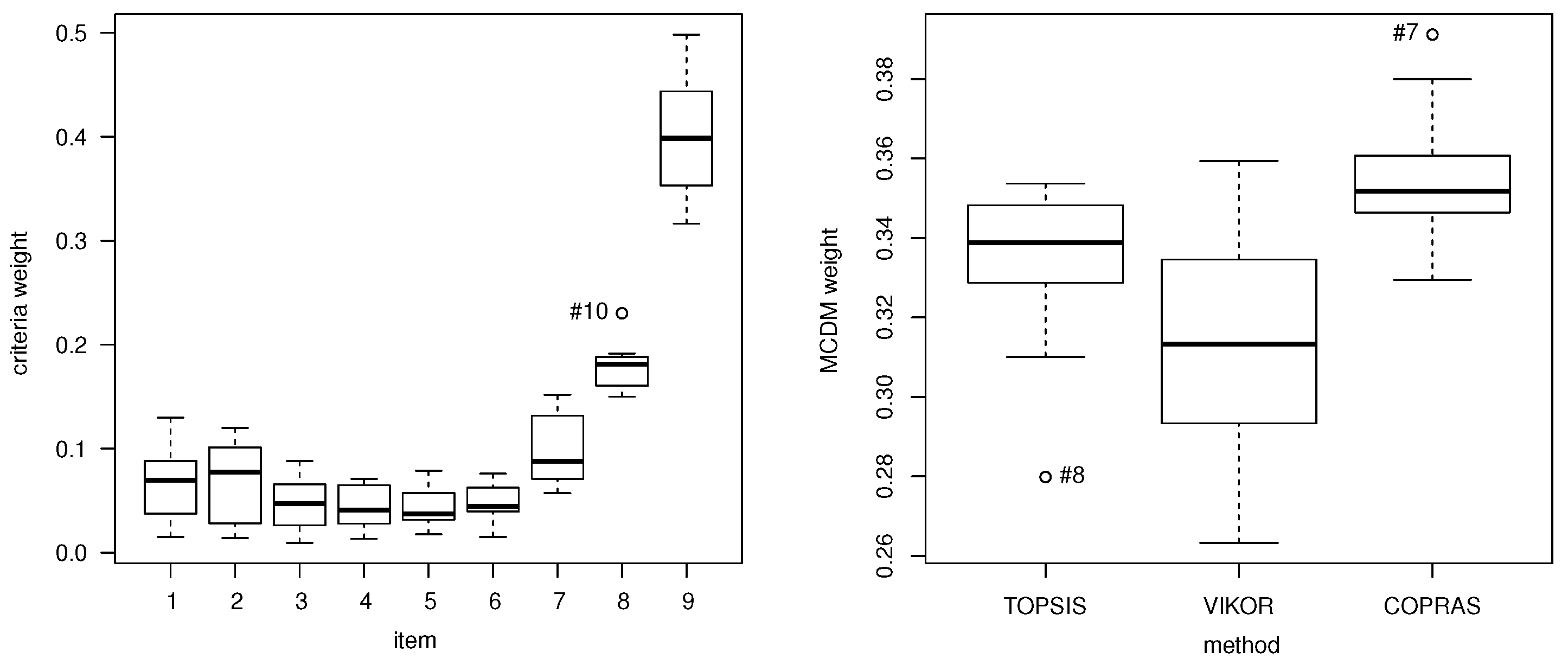
In this section, we provide the abbreviations, introduction, literature study, contribution, and objective of the study, as well as the description of the next sections.
1.2. Introductory Aspects
The supply chain is a framework of people and industries/organizations who are elaborating a product (good) or service to deliver it to a client. Links on this chain start with the producers of the raw materials and finish when the final product is delivered to the consumer.
Supply chain management is a key aspect and it must be optimized at low costs to obtain an efficient production cycle. Organizations try to enhance their supply chains to reduce their costs and to be more competitive.
Supply management in industry can be improved through efficient inventory policies that allows us to optimize an assortment of goods to meet customer demand [
1]. However, each company, as in the case of pharmacies and FNS, has its own peculiarities. Such peculiarities must be studied and modeled using appropriate methodologies that optimize supply management, making it necessary to consider performance measures, such as cost savings [
2,
3]. Several studies, summarized in [
4], indicated that optimizing inventory management can enable cost savings in supply chains for the service industry. The possible savings from inventory management vary according to the performance achieved by each organization, depending on its internal strategy [
5]. In particular, on the one hand, pharmacies require the supply of medicines and pharmaceutical products. On the other hand, FNS prepares a daily menu where the components or raw materials required to make up the menu constitute an assortment of inventory to be demanded by groups of people in closed regimes, such as hospitals, institutions, schools, and universities.
It is common in healthcare to classify products that make up the inventory according to factors as employment, expiration, treatment, prices, and storage. These factors are relevant to determining the parameters related to order, storage, and shortage penalty costs, according to the category at which the product belongs and whose supply we want to optimize [
6]. From another perspective, the inventory cost savings from may vary depending on the product category whose cost is optimized [
7]. Blockchain might save billions for healthcare by stating the chain of custody in supply management [
8].
1.3. State of the Art
Although FNS and pharmacies have shown growth in developing countries, there is little literature related to the supply chain of these services in the public area. The scarce research is limited to gastronomy, healthcare, hospital, and tourism services [
9,
10]. In [
11], a proposal for sustainable and home healthcare logistics, as a response to the COVID-19 pandemic [
12,
13], was designed. In [
14], two-level programming for the home healthcare supply chain considering outsourcing was established. In [
15,
16,
17,
18,
19], stochastic inventory models, by assuming traditional cost parameters and a random DPUT to minimize the TC of the inventory, were formulated. Particularly, the work presented in [
17] considered time dependence for the DPUT of drugs modeled through conditional statistical distributions with respect to explanatory variables (covariates) and an ARMA structure.
The ARMA models are highly flexible, with its parameters being estimated and interpreted in a simple way, in addition to allowing us to directly carry our forecasting [
20]. However, the usual ARMA structures assume linearity and Gaussian/normal distributed errors, making such structures limited. When non-Gaussianity is identified in the underlying data distribution, for example in intermittent DPUT [
21], practitioners often transform the data for reaching Gaussianity. Nevertheless, when transforming the data, interpretation problems of the obtained information arise, besides undesirable statistical properties.
GLM [
22] are used to handle these problems in a more general statistical framework. GLM are more flexible than Gaussian regression and assume any distribution belonging to the exponential family, as the binomial, gamma, and normal distributions, among others [
22]. Note that the Gaussian regression is a special case of GLM when the normal distribution is assumed. GLM assume a distribution for the response (explained or dependent) variable instead of the model error and permit us to describe non-linear and linear settings linking the covariates to the model structure by a suitable function.
If time dependency and non-Gaussianity are present, the DPUT can be modeled by GARMA models [
17], which are a GLM extension of ARMA models that modify the data mean through a link function. Note also that, although the GARMA models state a temporal dependency on the DPUT, if this is not considered, the parameters associated with the ARMA structure can be set as zero and a usual GLM is obtained. Therefore, the GLM are a particular case of the GARMA models. Thus, once the underlying distribution has been assumed, the GARMA parameters may be estimated utilizing the ML method [
23,
24]. Similarly, a zero-inflated distribution can be stated to model an intermittent DPUT [
21], that is, demand values equal to zero.
Once the random structure of demand has been modeled, it can be forecasted using probabilistic scenarios into an SP approach to find optimal supply costs [
25]. To optimize the model, a two-stage SP approach can be utilized following the works presented in [
19,
26]. In its first stage, a purchase decision related to when and how much to acquire is made, without knowing the values that the DPUT can take. Then, forecasting the probabilistic scenarios of the DPUT for a product/service, the decision of the second stage is made by calculating stocks at hand and expected shortages [
17]. Note that, at any stage, there is a finite number of states that are described by multidimensional variables [
27].
Although the forecasting of supply in hospital pharmacies and FNS is carried out generally in one period, the two-stage SP models are more helpful in determining optimal costs in that case as well [
28]. In [
17,
19], two-stage SP approaches were considered to lead to significant cost savings in inventory management.
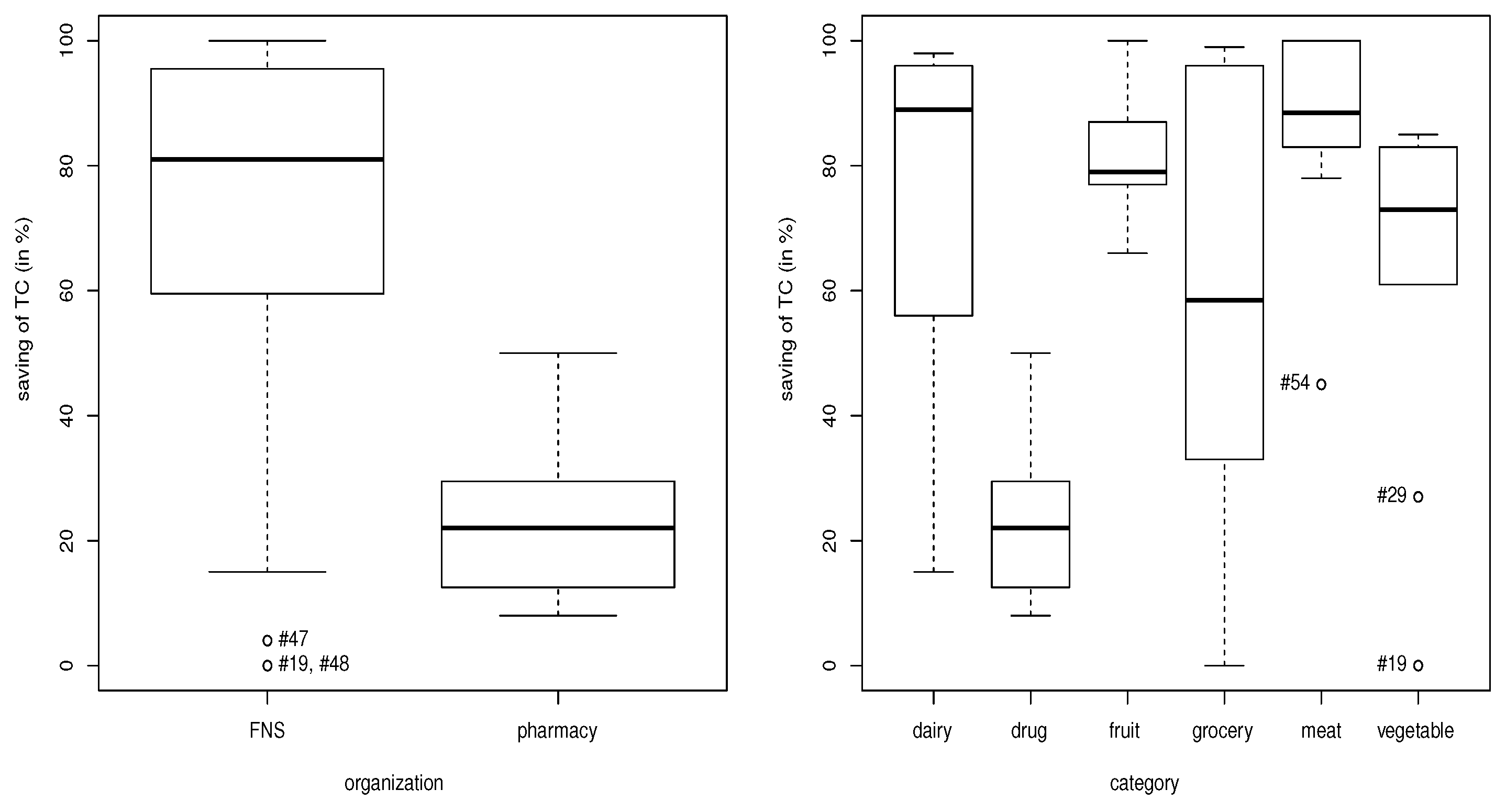
These savings are related to the supply chain management of pharmacies and FNS by means of success factors that were identified. However, in spite of the importance of inventory management based on the supply chain that minimizes costs in pharmacies and FNS, there is a lack of performance measures that quantify the cost saving [
2].
The correct operation of the supply chain involves, among others, to suppliers, dealers, and final service to arrive on time with the product or service to the user; see [
29] for the case of pharmacies and FNS. Several studies [
2,
29,
30,
31] indicated that there are saving opportunities in the supply chain related to success factors for its management, such as: (i) purchasing products and raw materials agreed between technical and supply staff [
2,
9]; (ii) successful partnership with a group purchasing organization [
30,
32]; and (iii) existence of supply data management technology, which are synchronized and integrated with the purchase system [
31].
Problems involving multiple alternatives and criteria through a structured framework can be applied by using a stochastic MCDM model. This type of models are a growing research field with different approaches being developed to explore the underlying epistemic uncertainty in ranking alternatives and weighting criteria for measuring performance, such as indicated in [
33,
34,
35,
36].
Note that the cost savings achieved through inventory policies in service industries (such as pharmacies and FNS) and supply chain success factors could occur simultaneously or in both directions [
37]. Then, the factors previously mentioned in (i)–(iii), as determinants of the performance of a stochastic inventory model (saving effect), can also be considered as an inverse relationship. Thus, inefficiency in saving performance (cause) is a determinant of the inability of grouped purchases, poor coordination between technical-supply staff, and lack of investment in data management platforms (effect). Then, the relationship between cost savings obtained by using a stochastic inventory model and its determinant factors may be modeled under a statistical regression context as mentioned in the following paragraph [
38].
A temporal correlation between the errors can exist, as they may be influenced by the mentioned success factors. Then, we must consider this correlation because ignoring it can lead to biased and inefficient estimators of the corresponding regression coefficients [
39,
40]. One can hypothesize relationships between the success factors at different levels. At the lowest level of the response variable, we have cost savings per product. At an intermediate level, we have those products belonging to certain categories. Then, at a higher hierarchical level, we have the organization analyzed (pharmacy or FNS). Therefore, we know that, like in single-level regression models, endogeneity is a concern to be also considered in multilevel models [
41].
In multilevel models [
42], there are several assumptions involving random components at multiple levels. In this kind of models, any moderate correlation between a covariate and a random component might cause significant bias in the estimated coefficients and variance components [
41]. This estimation framework is known as SUR [
39]. Furthermore, the multilevel models could include variables that simultaneously appear on the left and right sides of equations. This simultaneity can be rectified by employing each equation through a 2SLS estimation method. When this method is used with the SUR, the system of equations is simultaneously estimated utilizing the 3SLS method [
39].
Note that the SUR estimators are biased if the covariates are correlated with the errors. This can be circumvented by 2SLS, W2SLS, or 3SLS estimation with instrumental variables. These variables for each simultaneous equation can be either different or identical for all equations. In some cases, such variables may be of dummy type and then we can use the Wald estimator, also called the grouping estimator. This estimator weights the proportion between the number of times that the instrumental variable takes the zero value and the number of times it takes the one value in the sample [
43]. The instrumental variable technique has also been extended to the GLM framework [
44]. To face this challenge in a simpler way, a multilevel hierarchical structure was proposed in [
42] by using a GMSM method.
The GMSM method addresses endogeneity in multilevel models without the need for external instrumental variables, handling this difficulty in a simpler way. The GMSM method employs both between and within variations of the exogenous variables, but only assumes the within variation of the variables to be endogenous [
45].
1.4. Contribution, Objectives, and Organization of the Article
Despite the advances made in determining success factors for managing supply chains of pharmacies and FNS, these advances are still scarce. For example, in [
46], a multi-criteria framework was stated considering profit, environmental pollution, consumer health level, and brand equity for a competitive pharmaceutical supply chain, whereas the work presented in [
47] utilized a data-driven method mixed with a knowledge-driven MCDM method to reduce the dependence of judges. In another application of MCDM presented in [
48], a framework developed based on five different criteria using design, manufacture, service, maintenance, scrap, and recycling for an environmentally friendly reliability-based optimization method.
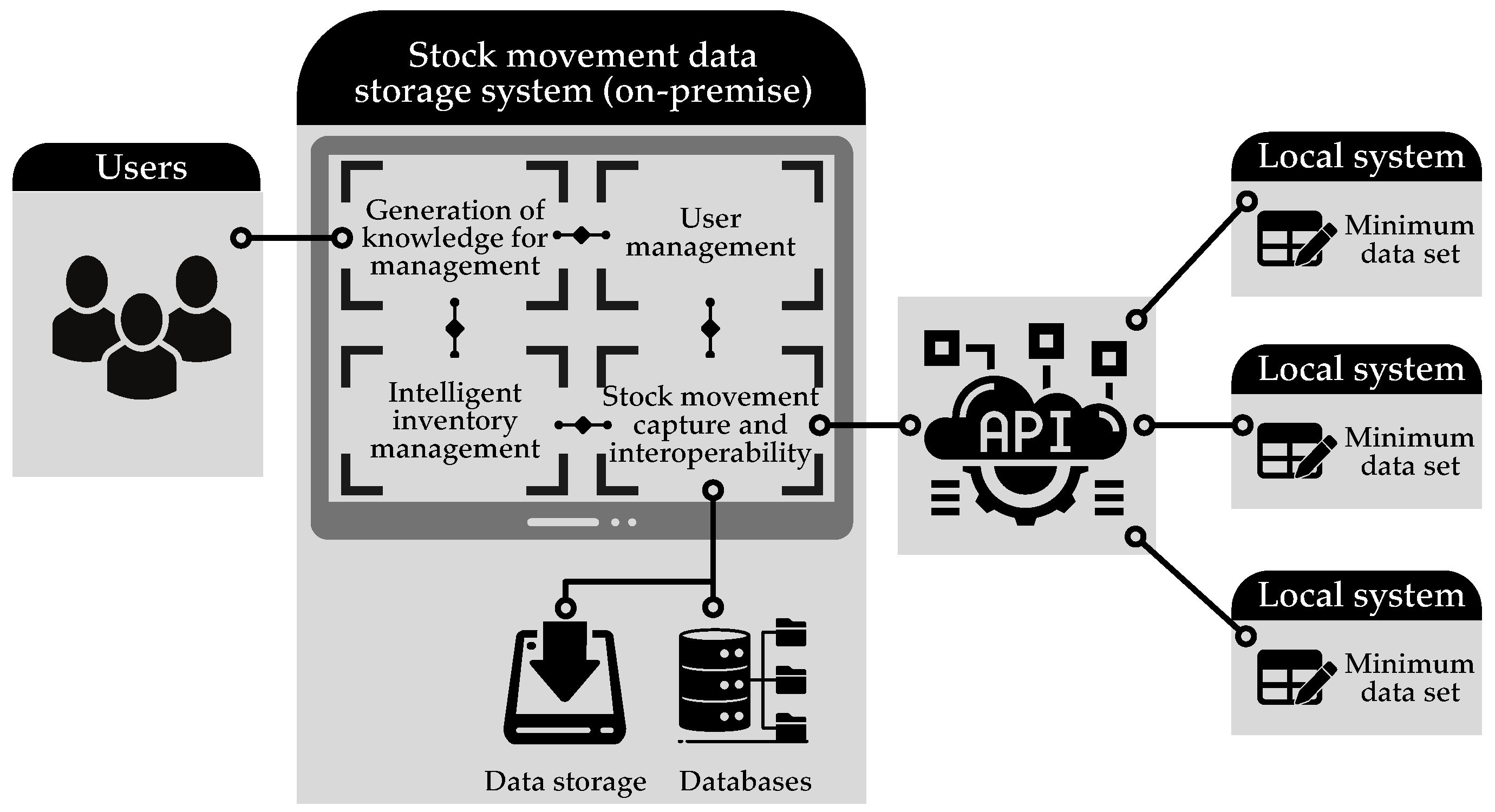
According to our literature review, to the best of our knowledge, there is a gap in the related state of the art due to no previous studies defined a score that measures the mentioned success factors. To fill this gap, the present study contributes to the MCDM literature by addressing various issues that are associated with establishing relationships between inventory cost savings and success factors in the supply chain, which we apply to pharmacy and FNS industries. Our study includes how to robustly establish an indicator of success factors in supply chain management of these industries, and how to deal with the relationships of inventory cost savings n multilevel products, categories, and organizations. In addition, we consider the possible endogeneity of this relationship with the help of a computer application that registers the factors of interest in the supply system. Determining success factors for managing supply chains is a relevant aspect for the companies. Then, modeling the relationship between inventory cost savings and supply chain success factors is a route for stating such a determination. This is particularly important in pharmacies and FNS, where the advances made on this topic are still scarce.
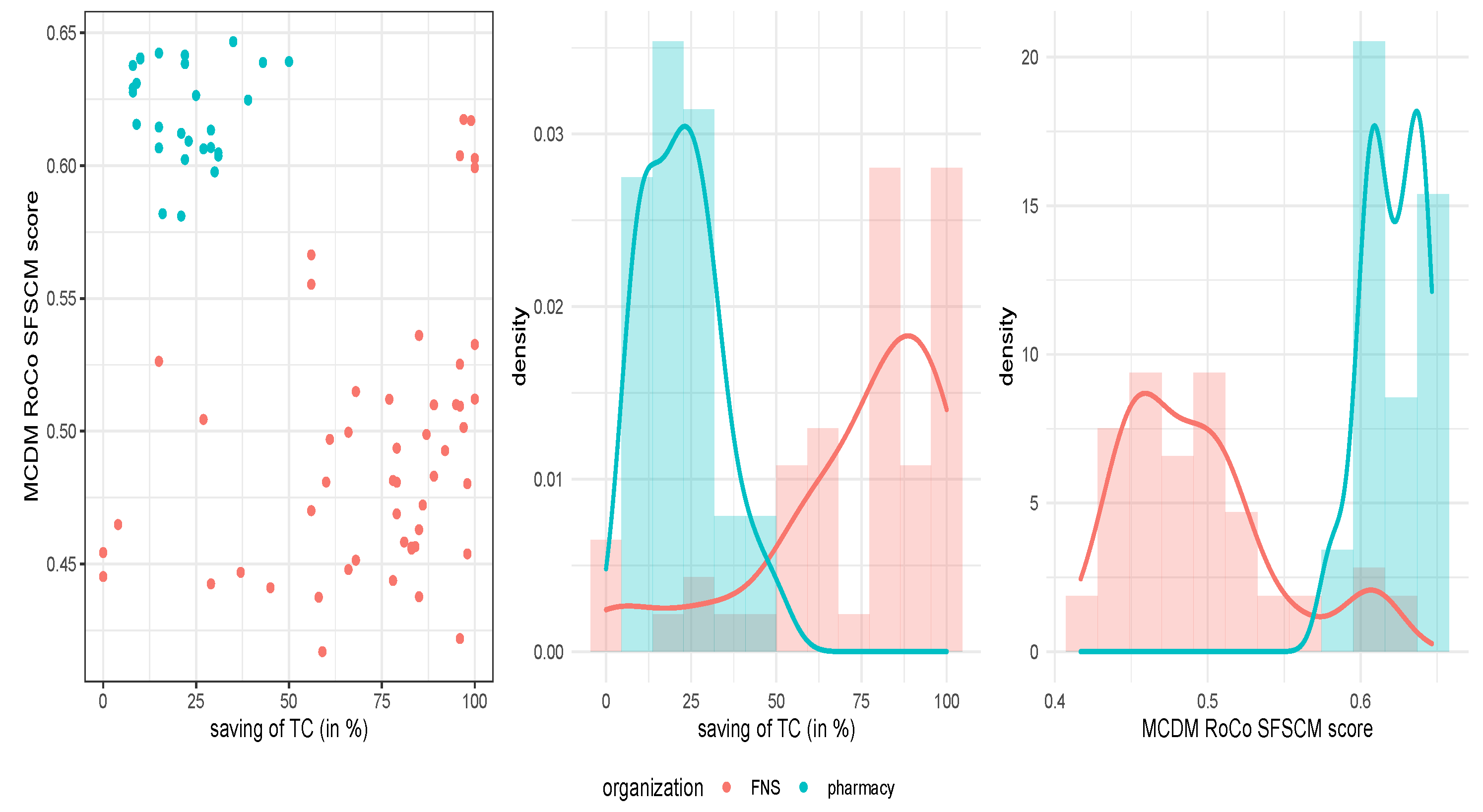
A novel RoCo MCDM model is proposed to obtain a score of the supply chain success factors, such as a group purchasing organization, economies of scale, and the existence of supply data management technology, which are synchronized and integrated with the purchase system. The structure of the proposed model considers non-linear SP, solved by a differential evolution algorithm—specifically with a genetic algorithm [
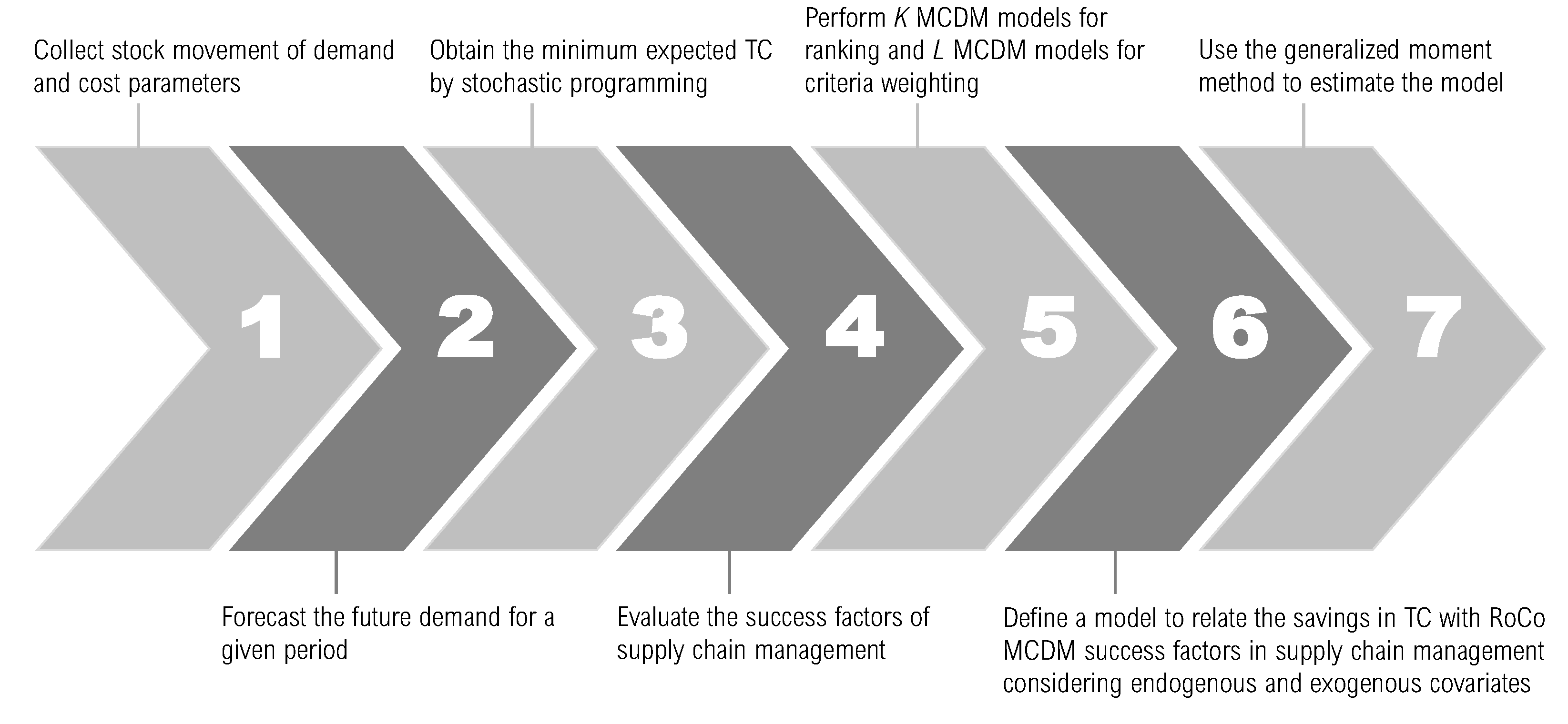
49], and a multilevel setting between savings obtained for pharmacies/FNS products and success factor scores according to the products studied. To deal with the endogeneity bias of the relationships proposed, internal instrumental variables are used by a GMSM method. We believe that the results to be obtained will directly benefit the function of supply chain managers. We conjecture it since a method to obtain a robust indicator will be able to measure success factors for the supply chains they manage. Moreover, our results will allow the managers to understand how these factors influence the organization and product categories on the inventory cost savings. Therefore, the novelty of our proposal is in defining a score that permits us to measure the mentioned success factors in a simple way, in meeting together all three elements (RoCo multi-criteria, non-linear programming, and time-dependent demand) to state a new model, and in applying it to pharmacies and FNS. In summary, the objective of the present investigation is to formulate a novel stochastic inventory model that minimizes the inventories TC in pharmacies and FNS industries. We compare these TC with true TC to establish savings and relate them to supply chain success factors in such industries.
The rest of the paper is organized as follows.
Section 2 describes the empirical and methodological design to study the mentioned relationships. In
Section 3, the results of applying this methodology are reported in a case study. Finally, in
Section 4, we carry out a discussion of our findings summarized in conclusions along with their scope, learning of managerial utility, limitations, and ideas for future research.