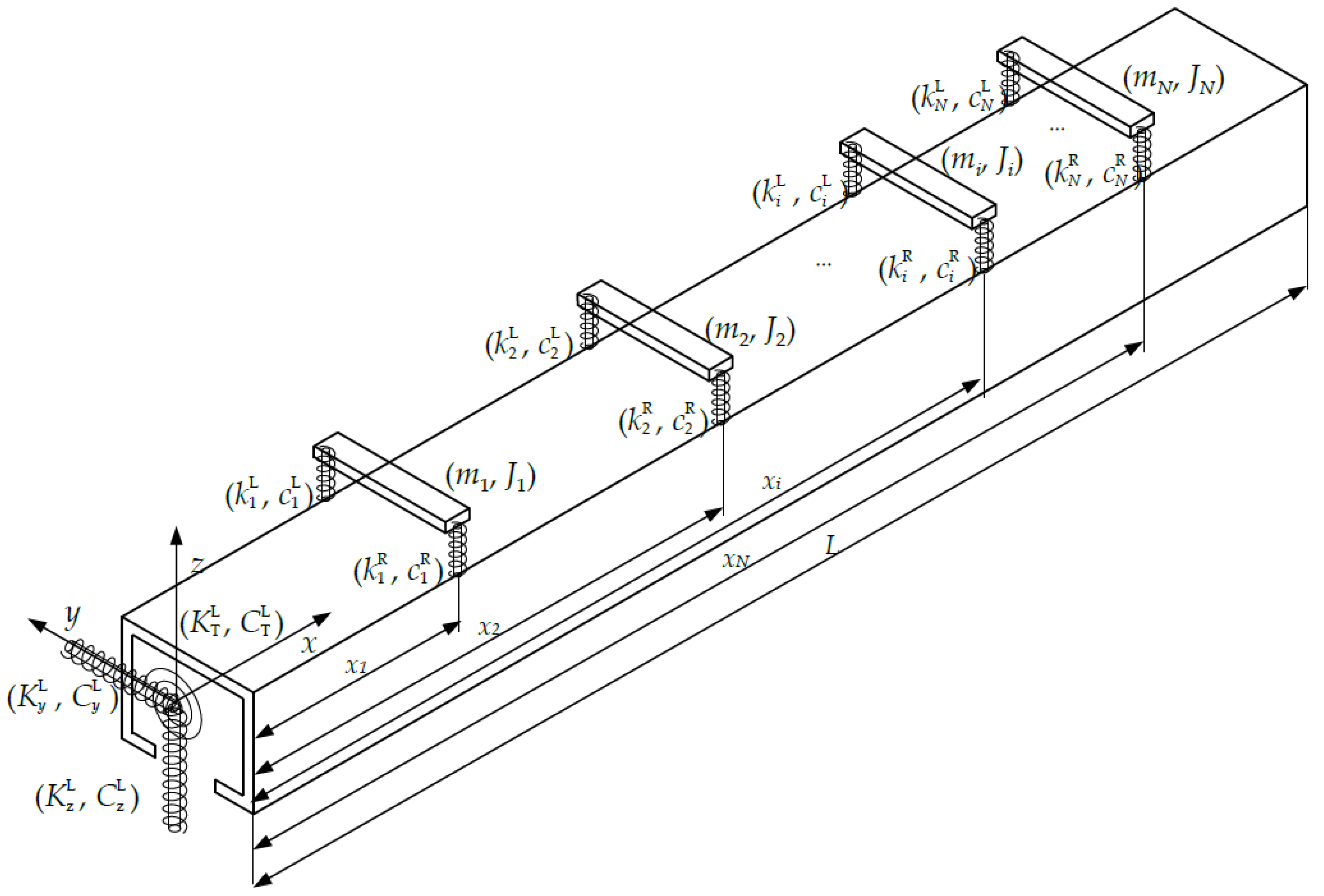
On the Forced Vibration of Bending-Torsional-Warping Coupled Thin-Walled Beams Carrying Arbitrary Number of 3-DoF Spring-Damper-Mass Subsystems
Abstract
:1. Introduction
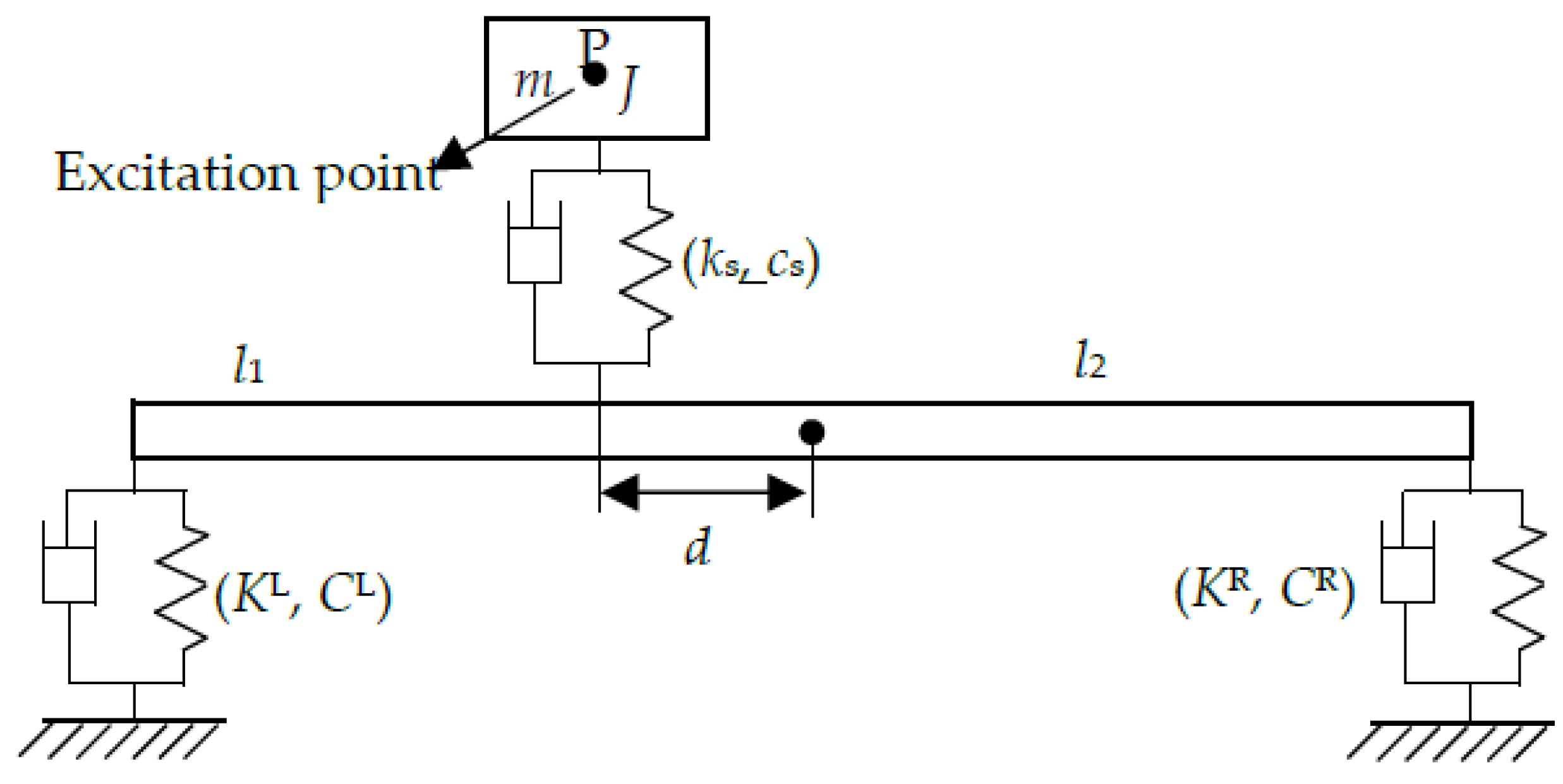
2. Derivation of the Frequency Response Function
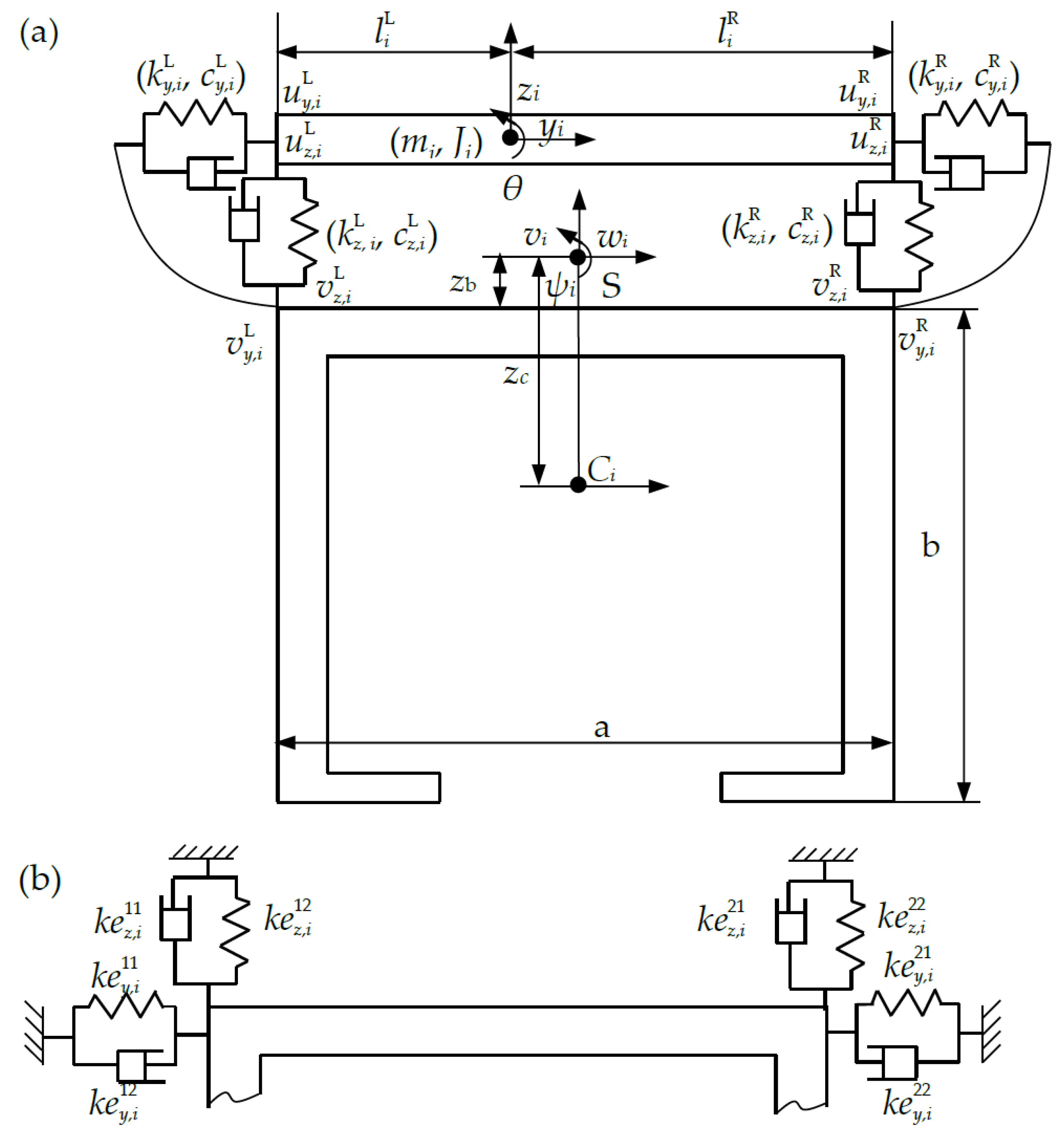
2.1. Dynamic Condensation of the Three-DOF SDM Subsystems
2.2. The Frequency Response Function for the Thin-Walled Beam System
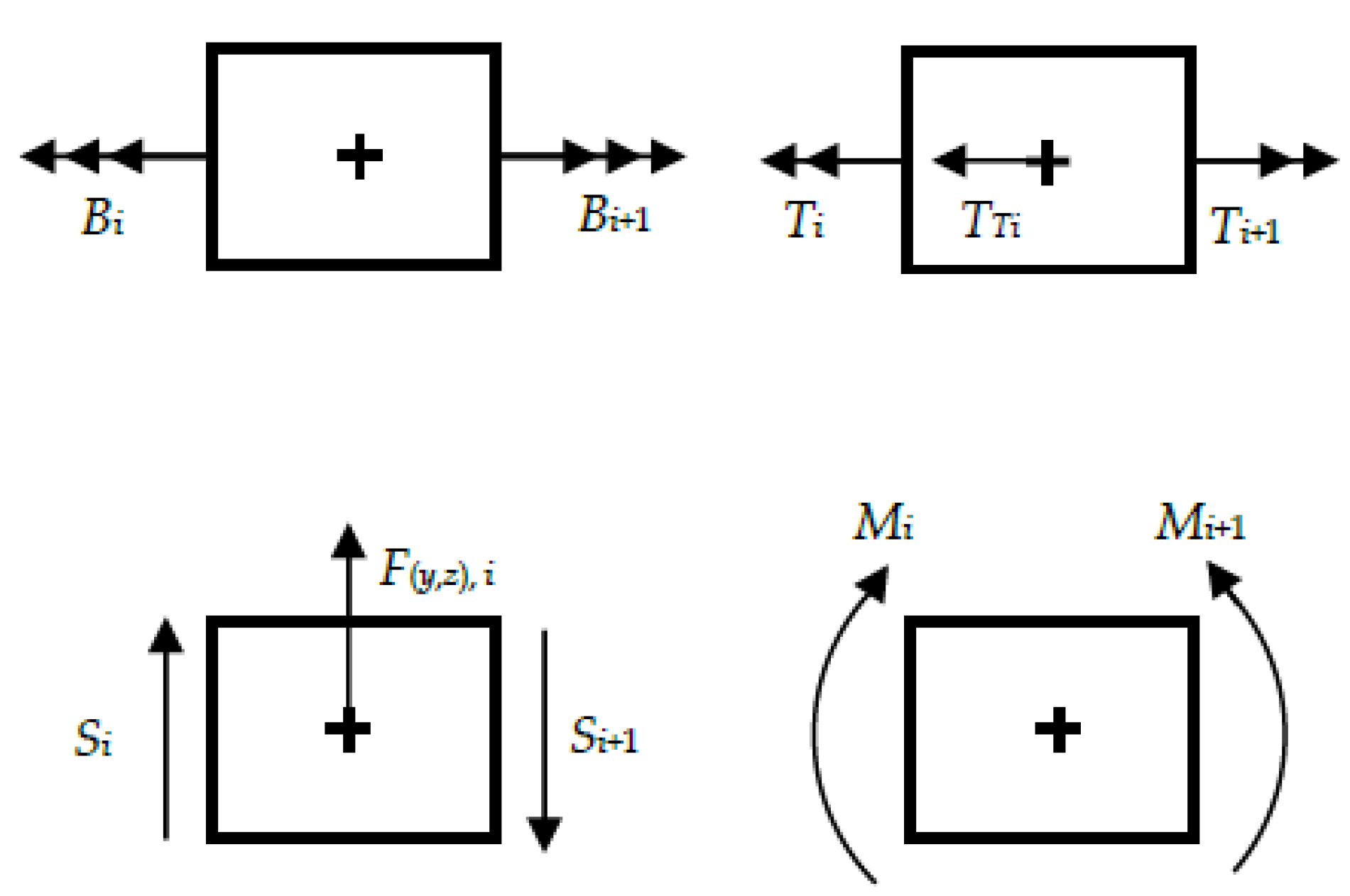
2.2.1. Force Excitation at the Ends
2.2.2. Force Excitation at an Arbitrary Position of the Thin-Walled Beam
2.2.3. Force Excitation at the Subsystem
3. Validation of the Proposed Method
4. Parameter Study and Discussion
4.1. Effect of Subsystem Parameters on Vibration Transmission of the Thin-Walled Beam
4.2. Effect of Parameters on the Vibration Isolation Characteristic of the Thin-Walled Beams Systems
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C. The Derivations of BL and BR
Appendix D. The Expressions of the Derivative Matrices Tw, Tψ and Tv
Appendix E
References
- Narayanan, S.; Mallik, A.K. Free vibration of thin walled open section beams with constrained damping treatment. J. Sound Vib. 1981, 74, 429–439. [Google Scholar] [CrossRef]
- Bank, L.C.; Kao, C.H. Dynamic response of thin-walled composite material Timoshenko beams. J. Energy Resour. Technol. 1990, 112, 149–154. [Google Scholar] [CrossRef]
- Rao, S.S.; Jin, H. Analysis of coupled bending-torsional vibration of beams in the presence of uncertainties. J. Vib. Acoust. 2014, 136, 051004. [Google Scholar] [CrossRef]
- Li, J.; Shen, R.; Hua, H.; Jin, X. Coupled bending and torsional vibration of axially loaded thin-walled Timoshenko beams. Int. J. Mech. Sci. 2004, 46, 299–320. [Google Scholar] [CrossRef]
- Jun, L.; Rongying, S.; Hongxing, H.; Xianding, J. Coupled bending and torsional vibration of axially loaded Bernoulli–Euler beams including warping effects. Appl. Acoust. 2004, 65, 153–170. [Google Scholar] [CrossRef]
- Li, J.; Hua, H.; Shen, R.; Jin, X. Stochastic vibration of axially loaded monosymmetric Timoshenko thin-walled beam. J. Sound Vib. 2004, 274, 915–938. [Google Scholar] [CrossRef]
- Lezgy-Nazargah, M.; Vidal, P.; Polit, O. A quasi-3D finite element model for the analysis of thin-walled beams under axial–flexural–torsional loads. Thin-Walled Struct. 2021, 164, 107811. [Google Scholar] [CrossRef]
- Jrad, W.; Mohri, F.; Robin, G.; Daya, E.M.; Al-Hajjar, J. Analytical and finite element solutions of free and forced vibration of unrestrained and braced thin-walled beams. J. Vib. Control 2020, 26, 255–276. [Google Scholar] [CrossRef]
- Chen, H.H.; Hsiao, K.M. Coupled axial-torsional vibration of thin-walled Z-section beam induced by boundary conditions. Thin-Walled Struct. 2007, 45, 573–583. [Google Scholar] [CrossRef]
- Prokić, A. On triply coupled vibrations of thin-walled beams with arbitrary cross-section. J. Sound Vib. 2005, 279, 723–737. [Google Scholar] [CrossRef]
- Prokić, A. On fivefold coupled vibrations of Timoshenko thin-walled beams. Eng. Struct. 2006, 28, 54–62. [Google Scholar] [CrossRef]
- Chen, H.H.; Hsiao, K.M. Quadruply coupled linear free vibrations of thin-walled beams with a generic open section. Eng. Struct. 2008, 30, 1319–1334. [Google Scholar] [CrossRef]
- Kim, N.I.; Seo, K.J.; Kim, M.Y. Free vibration and spatial stability of non-symmetric thin-walled curved beams with variable curvatures. Int. J. Solids Struct. 2003, 40, 3107–3128. [Google Scholar] [CrossRef]
- Kim, N.I.; Kim, M.Y. Spatial free vibration of shear deformable circular curved beams with non-symmetric thin-walled sections. J. Sound Vib. 2004, 276, 245–271. [Google Scholar] [CrossRef]
- Xu, X.; Carrera, E.; Augello, R.; Daneshkhah, E.; Yang, H. Benchmarks for higher-order modes evaluation in the free vibration response of open thin-walled beams due to the cross-sectional deformations. Thin-Walled Struct. 2021, 166, 107965. [Google Scholar] [CrossRef]
- Wu, J.S.; Chou, H.M. Free vibration analysis of a cantilever beam carrying any number of elastically mounted point masses with the analytical-and-numerical-combined method. J. Sound Vib. 1998, 213, 317–332. [Google Scholar] [CrossRef]
- Wu, J.S.; Chang, B.H. Free vibration of axial-loaded multi-step Timoshenko beam carrying arbitrary concentrated elements using continuous-mass transfer matrix method. Eur. J. Mech. A/Solids 2013, 38, 20–37. [Google Scholar] [CrossRef]
- Liu, X.; Sun, C.; Banerjee, J.R.; Dan, H.C.; Chang, L. An exact dynamic stiffness method for multibody systems consisting of beams and rigid-bodies. Mech. Syst. Signal Processing 2021, 150, 107264. [Google Scholar] [CrossRef]
- Bambill, D.V.; Rossit, C.A. Forced vibrations of a beam elastically restrained against rotation and carrying a spring–mass system. Ocean Eng. 2002, 29, 605–626. [Google Scholar] [CrossRef]
- Lin, H.Y.; Tsai, Y.C. Free vibration analysis of a uniform multi-span beam carrying multiple spring–mass systems. J. Sound Vib. 2007, 302, 442–456. [Google Scholar] [CrossRef]
- Wu, J.S.; Hsu, T.F. Free vibration analyses of simply supported beams carrying multiple point masses and spring-mass systems with mass of each helical spring considered. Int. J. Mech. Sci. 2007, 49, 834–852. [Google Scholar] [CrossRef]
- Yesilce, Y.; Demirdag, O. Effect of axial force on free vibration of Timoshenko multi-span beam carrying multiple spring-mass systems. Int. J. Mech. Sci. 2008, 50, 995–1003. [Google Scholar] [CrossRef]
- Banerjee, J.R. Free vibration of beams carrying spring-mass systems− A dynamic stiffness approach. Comput. Struct. 2012, 104, 21–26. [Google Scholar] [CrossRef]
- Wu, J.J. Free vibration analysis of beams carrying a number of two-degree-of-freedom spring-damper-mass systems. Finite Elem. Anal. Des. 2004, 40, 363–381. [Google Scholar] [CrossRef]
- Wu, J.J. Use of equivalent-damper method for free vibration analysis of a beam carrying multiple two degree-of-freedom spring–damper–mass systems. J. Sound Vib. 2005, 281, 275–293. [Google Scholar] [CrossRef]
- Wu, J.J. Use of effective stiffness matrix for the free vibration analyses of a non-uniform cantilever beam carrying multiple two degree-of-freedom spring–damper–mass systems. Comput. Struct. 2003, 81, 2319–2330. [Google Scholar] [CrossRef]
- El-Sayed, T.A.; El-Mongy, H.H. Application of variational iteration method to free vibration analysis of a tapered beam mounted on two-degree of freedom subsystems. Appl. Math. Model. 2018, 58, 349–364. [Google Scholar] [CrossRef]
- Mei, C. A Wave-Based Analytical Solution to Free Vibrations in a Combined Euler–Bernoulli Beam/Frame and a Two-Degree-of-Freedom Spring–Mass System. J. Vib. Acoust. 2018, 140, 061001. [Google Scholar] [CrossRef]
- Chen, G.; Zeng, X.; Liu, X.; Rui, X. Transfer matrix method for the free and forced vibration analyses of multi-step Timoshenko beams coupled with rigid bodies on springs. Appl. Math. Model. 2020, 87, 152–170. [Google Scholar] [CrossRef]
- Wu, J.S.; Chen, D.W. Dynamic analysis of a uniform cantilever beam carrying a number of elastically mounted point masses with dampers. J. Sound Vib. 2000, 229, 549–578. [Google Scholar] [CrossRef]
- Muscolino, G.; Benfratello, S.; Sidoti, A. Dynamics analysis of distributed parameter system subjected to a moving oscillator with random mass, velocity and acceleration. Probabilistic Eng. Mech. 2002, 17, 63–72. [Google Scholar] [CrossRef]
- Barry, O.; Oguamanam, D.C.D.; Zu, J.W. On the dynamic analysis of a beam carrying multiple mass-spring-mass-damper system. Shock Vib. 2014, 2014, 485630. [Google Scholar] [CrossRef]
- Bukhari, M.A.; Barry, O.R. Nonlinear Vibrations Analysis of Overhead Power Lines: A Beam With Mass–Spring–Damper–Mass Systems. J. Vib. Acoust. 2018, 140, 031004. [Google Scholar] [CrossRef]
- Gupta, S.K.; Malla, A.L.; Barry, O.R. Nonlinear vibration analysis of vortex-induced vibrations in overhead power lines with nonlinear vibration absorbers. Nonlinear Dyn. 2021, 103, 27–47. [Google Scholar] [CrossRef]
- Aasi, A.; Aghaei, S.M.; Panchapakesan, B. Experimental Investigation of Natural Frequency and Forced Vibration of Euler-Bernoulli Beam under Displacement of Concentrated Mass and Load. Int. J. Aerosp. Mech. Eng. 2022, 16, 103–107. [Google Scholar]
- Chen, J.; Dong, D.; Yan, B.; Hua, C. An Analytical Study on Forced Vibration of Beams Carrying a Number of Two Degrees-of-Freedom Spring–Damper–Mass Subsystems. J. Vib. Acoust. 2016, 138, 061011. [Google Scholar] [CrossRef]
- Mei, C. Free and Forced Wave Vibration Analysis of a Timoshenko Beam/Frame Carrying a Two Degrees-of-Freedom Spring-Mass System. J. Vib. Acoust. 2021, 143, 061008. [Google Scholar] [CrossRef]
- Oguamanam, D.C.D. Free vibration of beams with finite mass rigid tip load and flexural–torsional coupling. Int. J. Mech. Sci. 2003, 45, 963–979. [Google Scholar] [CrossRef]
- Gökdağ, H.; Kopmaz, O. Coupled bending and torsional vibration of a beam with in-span and tip attachments. J. Sound Vib. 2005, 287, 591–610. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Z.; Fan, B. Coupled bending and torsional vibration characteristics analysis of inhomogeneous wind turbine tower with variable cross section under elastic constraint. Appl. Math. Model. 2021, 93, 188–205. [Google Scholar] [CrossRef]
- Wu, J.; Titurus, B. Damping augmentation of a rotating beam-tendon system via internally placed spring-damper elements. J. Sound Vib. 2021, 510, 116315. [Google Scholar] [CrossRef]
- Hoffmeyer, D.; Høgsberg, J. Calibration and balancing of multiple tuned mass absorbers for damping of coupled bending-torsion beam vibrations. J. Vib. Acoust. 2020, 142, 044501. [Google Scholar] [CrossRef]
- Burlon, A.; Failla, G.; Arena, F. Coupled bending–torsional frequency response of beams with attachments: Exact solutions including warping effects. Acta Mech. 2018, 229, 2445–2475. [Google Scholar] [CrossRef]
- Burlon, A.; Failla, G.; Arena, F. Coupled bending and torsional free vibrations of beams with in-span supports and attached masses. Eur. J. Mech. A/Solids 2017, 66, 387–411. [Google Scholar] [CrossRef]
- Burlon, A.; Failla, G.; Arena, F. Exact stochastic analysis of coupled bending-torsion beams with in-span supports and masses. Probabilistic Eng. Mech. 2018, 54, 53–64. [Google Scholar] [CrossRef]
- Burlon, A.; Failla, G.; Arena, F. Exact frequency response of two-node coupled bending-torsional beam element with attachments. Appl. Math. Model. 2018, 63, 508–537. [Google Scholar] [CrossRef]
- Burlon, A.; Failla, G. Flexural wave propagation in locally-resonant beams with uncoupled/coupled bending-torsion beam-like resonators. Int. J. Mech. Sci. 2022, 215, 106925. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, S.; Li, F.; Zhu, Y. Coupled bending and torsional vibrations of non-uniform thin-walled beams by the transfer differential transform method and experiments. Thin-Walled Struct. 2018, 127, 373–388. [Google Scholar] [CrossRef]
- Zhong, H.; Liu, Z.; Qin, H.; Liu, Y. Static analysis of thin-walled space frame structures with arbitrary closed cross-sections using transfer matrix method. Thin-Walled Struct. 2018, 123, 255–269. [Google Scholar] [CrossRef]
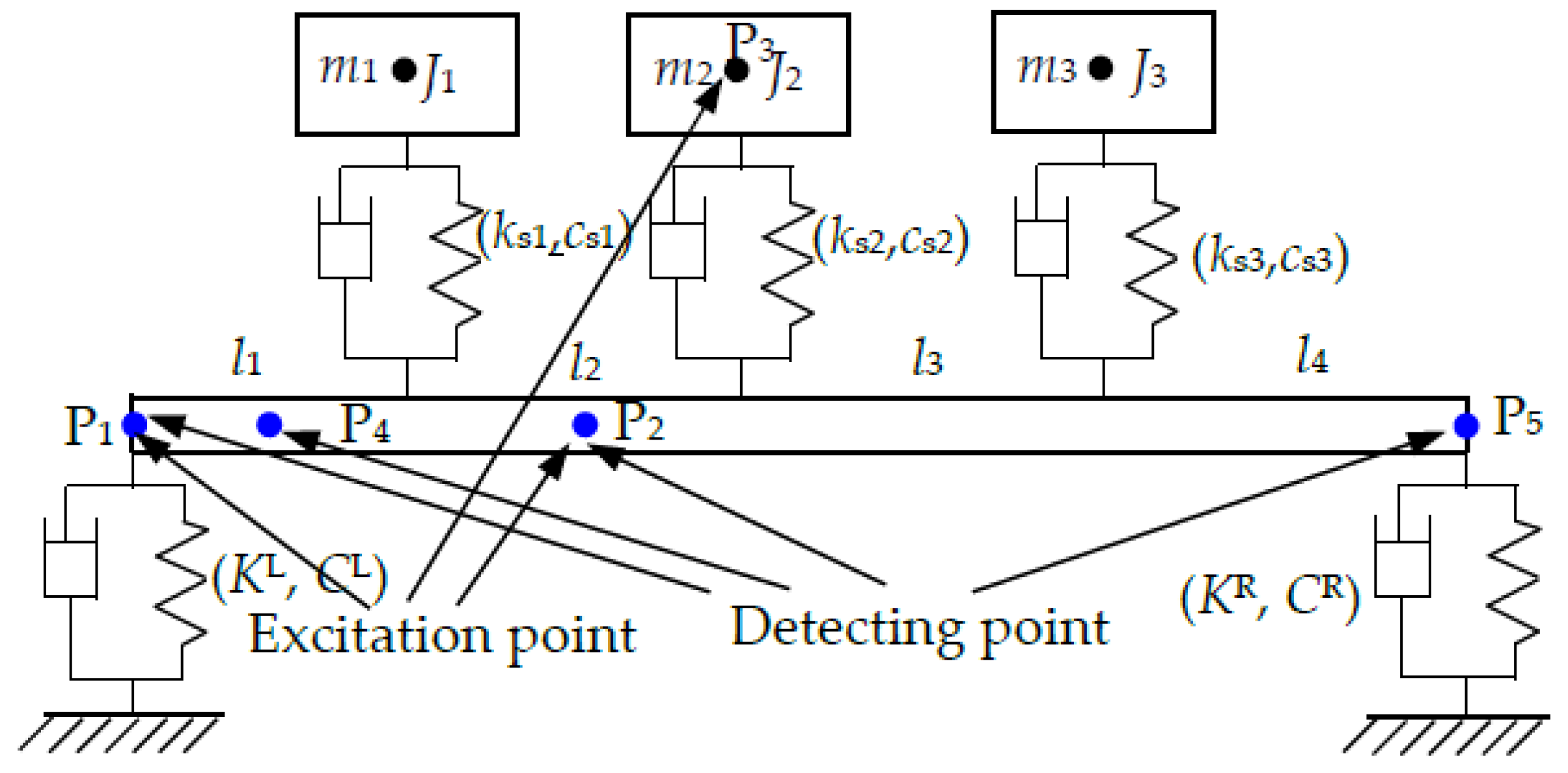
 FR at P1 with the presented method, ○ FR at P1 with FEM,
FR at P1 with the presented method, ○ FR at P1 with FEM,  FR at P2 with the presented method, ○ FR at P2 with FEM,
FR at P2 with the presented method, ○ FR at P2 with FEM,  FR at P4 with the presented method, ○ FR at P4 with FEM,
FR at P4 with the presented method, ○ FR at P4 with FEM,  FR at P5 with the presented method, and ○ FR at P5 with FEM). (a) Force is applied at P1; (b) Force is applied at P2; (c) Force is applied at P3.
FR at P5 with the presented method, and ○ FR at P5 with FEM). (a) Force is applied at P1; (b) Force is applied at P2; (c) Force is applied at P3.
 FR at P1 with the presented method, ○ FR at P1 with FEM,
FR at P1 with the presented method, ○ FR at P1 with FEM,  FR at P2 with the presented method, ○ FR at P2 with FEM,
FR at P2 with the presented method, ○ FR at P2 with FEM,  FR at P4 with the presented method, ○ FR at P4 with FEM,
FR at P4 with the presented method, ○ FR at P4 with FEM,  FR at P5 with the presented method, and ○ FR at P5 with FEM). (a) Force is applied at P1; (b) Force is applied at P2; (c) Force is applied at P3.
FR at P5 with the presented method, and ○ FR at P5 with FEM). (a) Force is applied at P1; (b) Force is applied at P2; (c) Force is applied at P3.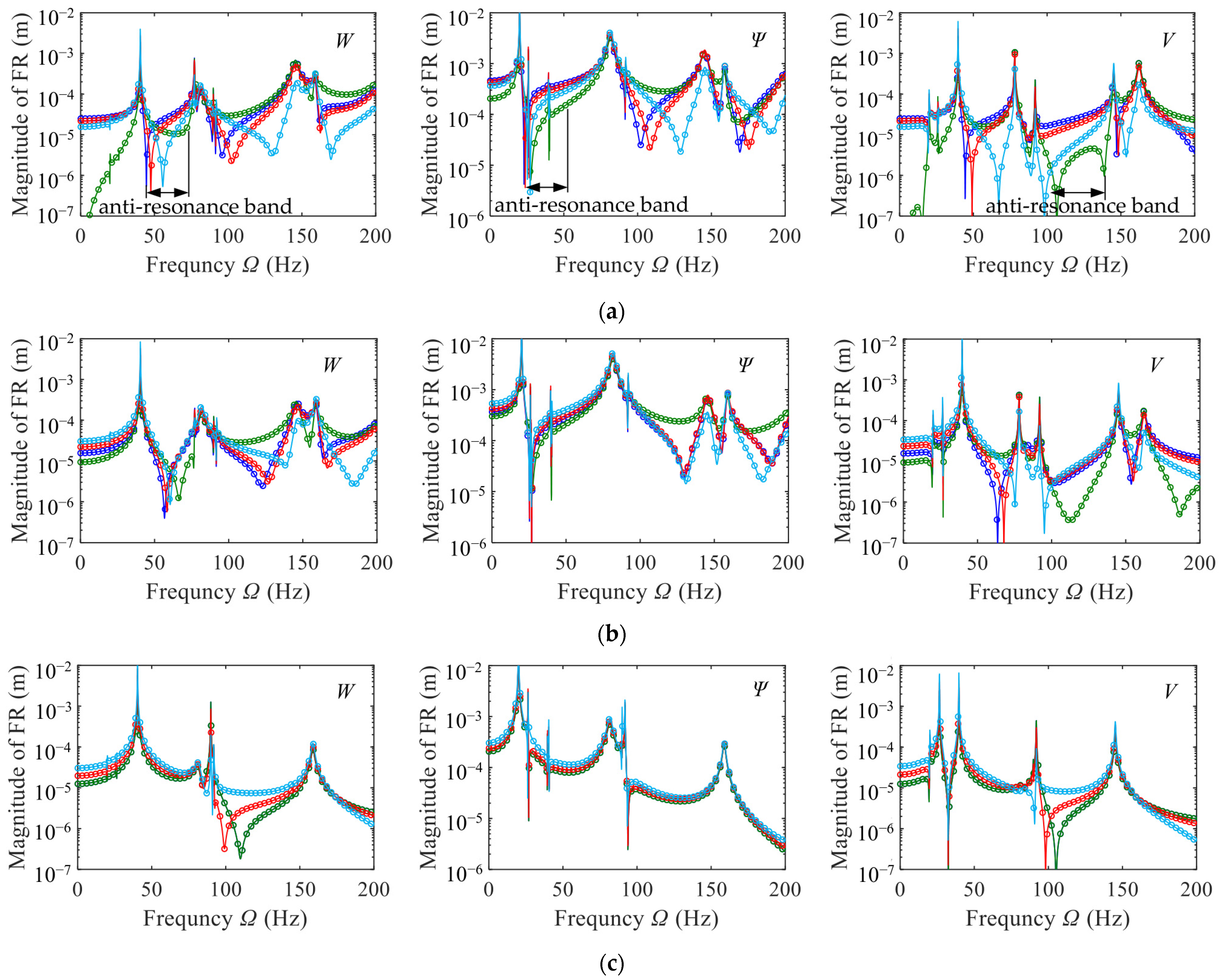
 FR at P1,
FR at P1,  FR at P2,
FR at P2,  FR at P4,
FR at P4,  FR at P5).
FR at P5).
 FR at P1,
FR at P1,  FR at P2,
FR at P2,  FR at P4,
FR at P4,  FR at P5).
FR at P5).
 W (with symmetrical systems),
W (with symmetrical systems),  W (with asymmetrical systems),
W (with asymmetrical systems),  Ψ (with symmetrical systems)
Ψ (with symmetrical systems)  Ψ (with asymmetrical systems)
Ψ (with asymmetrical systems)  V (with symmetrical systems),
V (with symmetrical systems),  V (with asymmetrical systems)). (a) Force is applied in W direction; (b) Force is applied in Ψ direction; (c) Force is applied in V direction.
V (with asymmetrical systems)). (a) Force is applied in W direction; (b) Force is applied in Ψ direction; (c) Force is applied in V direction.
 W (with symmetrical systems),
W (with symmetrical systems),  W (with asymmetrical systems),
W (with asymmetrical systems),  Ψ (with symmetrical systems)
Ψ (with symmetrical systems)  Ψ (with asymmetrical systems)
Ψ (with asymmetrical systems)  V (with symmetrical systems),
V (with symmetrical systems),  V (with asymmetrical systems)). (a) Force is applied in W direction; (b) Force is applied in Ψ direction; (c) Force is applied in V direction.
V (with asymmetrical systems)). (a) Force is applied in W direction; (b) Force is applied in Ψ direction; (c) Force is applied in V direction.
 ksi = 3333.33/2 kN/m,
ksi = 3333.33/2 kN/m,  ksi = 3333.33 kN/m,
ksi = 3333.33 kN/m,  ksi = 3333.33 × 2 kN/m,
ksi = 3333.33 × 2 kN/m,  ksi =3333.33 × 4 kN/m).
ksi =3333.33 × 4 kN/m).
 ksi = 3333.33/2 kN/m,
ksi = 3333.33/2 kN/m,  ksi = 3333.33 kN/m,
ksi = 3333.33 kN/m,  ksi = 3333.33 × 2 kN/m,
ksi = 3333.33 × 2 kN/m,  ksi =3333.33 × 4 kN/m).
ksi =3333.33 × 4 kN/m).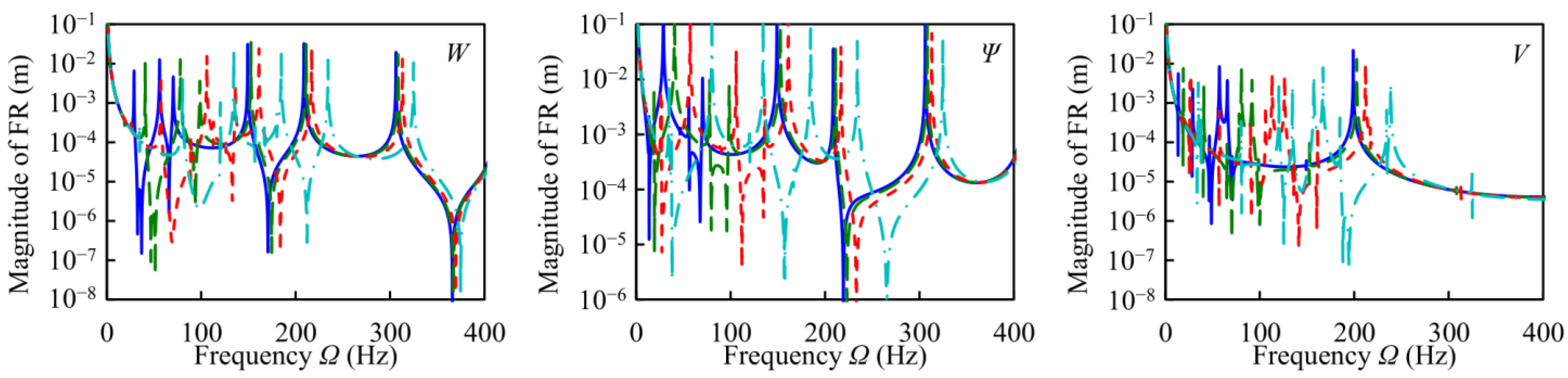
 csi = 66.67/2 N∙s/m,
csi = 66.67/2 N∙s/m,  csi =66.67 N∙s/m,
csi =66.67 N∙s/m,  csi =66.67 × 2 N∙s/m,
csi =66.67 × 2 N∙s/m,  csi = 66.67 × 4 N∙s/m).
csi = 66.67 × 4 N∙s/m).
 csi = 66.67/2 N∙s/m,
csi = 66.67/2 N∙s/m,  csi =66.67 N∙s/m,
csi =66.67 N∙s/m,  csi =66.67 × 2 N∙s/m,
csi =66.67 × 2 N∙s/m,  csi = 66.67 × 4 N∙s/m).
csi = 66.67 × 4 N∙s/m).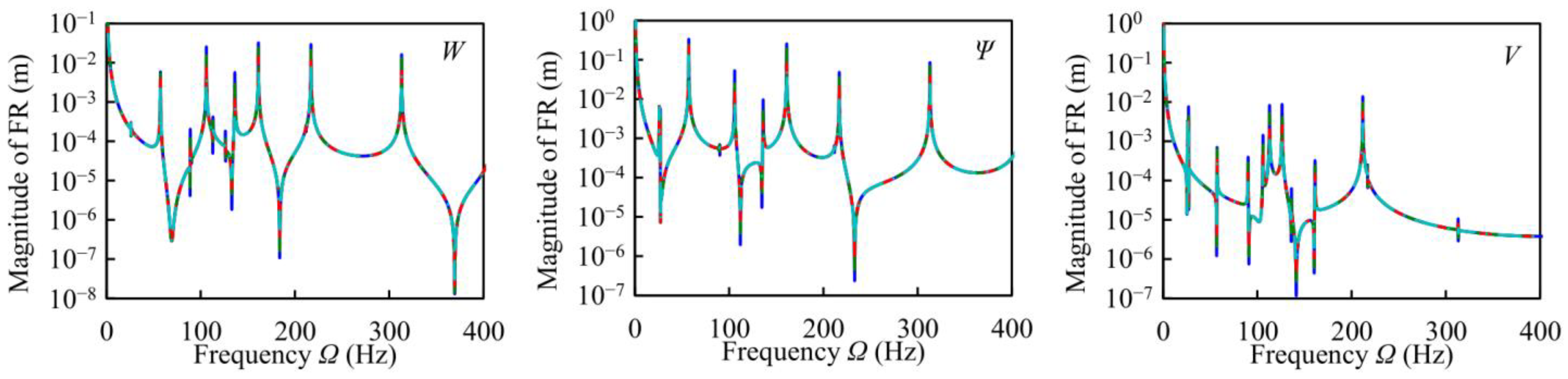
 mi = 266.67/2 kg,
mi = 266.67/2 kg,  mi = 266.67 kg,
mi = 266.67 kg,  mi = 266.67 × 2 kg,
mi = 266.67 × 2 kg,  mi = 266.67 × 4 kg).
mi = 266.67 × 4 kg).
 mi = 266.67/2 kg,
mi = 266.67/2 kg,  mi = 266.67 kg,
mi = 266.67 kg,  mi = 266.67 × 2 kg,
mi = 266.67 × 2 kg,  mi = 266.67 × 4 kg).
mi = 266.67 × 4 kg).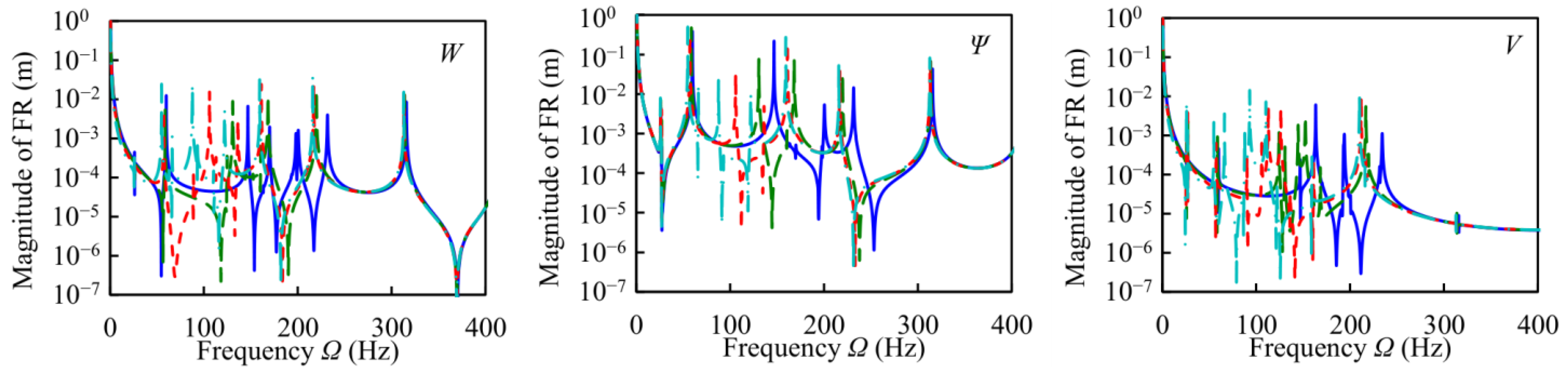
 Ji = 53.33/2 kg∙m2,
Ji = 53.33/2 kg∙m2,  Ji = 53.33 kg∙m2,
Ji = 53.33 kg∙m2,  Ji = 53.33 × 2 kg∙m2,
Ji = 53.33 × 2 kg∙m2,  Ji = 53.33 × 4 kg∙m2).
Ji = 53.33 × 4 kg∙m2).
 Ji = 53.33/2 kg∙m2,
Ji = 53.33/2 kg∙m2,  Ji = 53.33 kg∙m2,
Ji = 53.33 kg∙m2,  Ji = 53.33 × 2 kg∙m2,
Ji = 53.33 × 2 kg∙m2,  Ji = 53.33 × 4 kg∙m2).
Ji = 53.33 × 4 kg∙m2).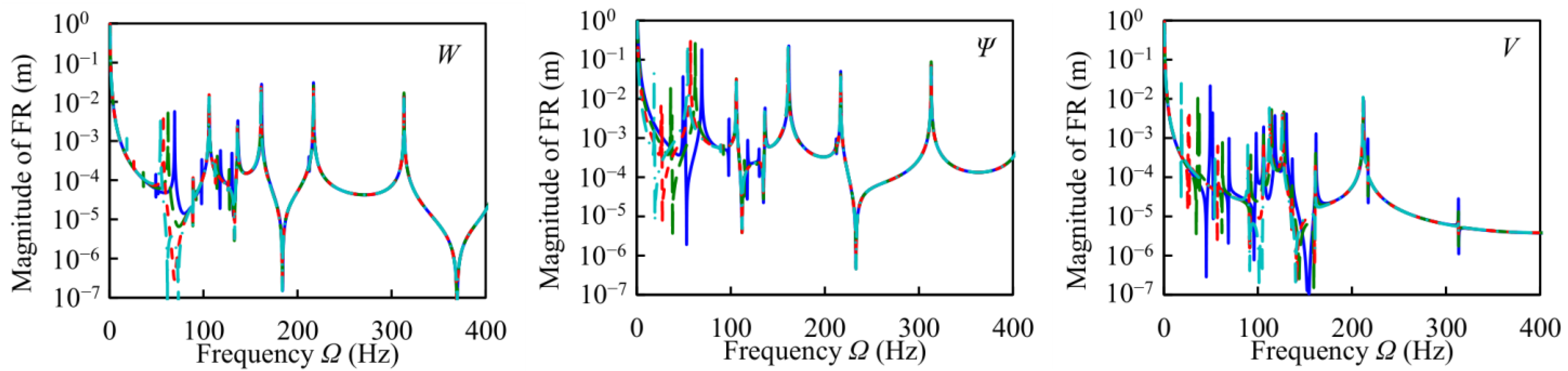
 ks = 40,000/100 kN/m,
ks = 40,000/100 kN/m,  ks = 40,000/10 kN/m,
ks = 40,000/10 kN/m,  ks = 40,000 kN/m,
ks = 40,000 kN/m,  ks = 40,000 × 10 kN/m).
ks = 40,000 × 10 kN/m).
 ks = 40,000/100 kN/m,
ks = 40,000/100 kN/m,  ks = 40,000/10 kN/m,
ks = 40,000/10 kN/m,  ks = 40,000 kN/m,
ks = 40,000 kN/m,  ks = 40,000 × 10 kN/m).
ks = 40,000 × 10 kN/m).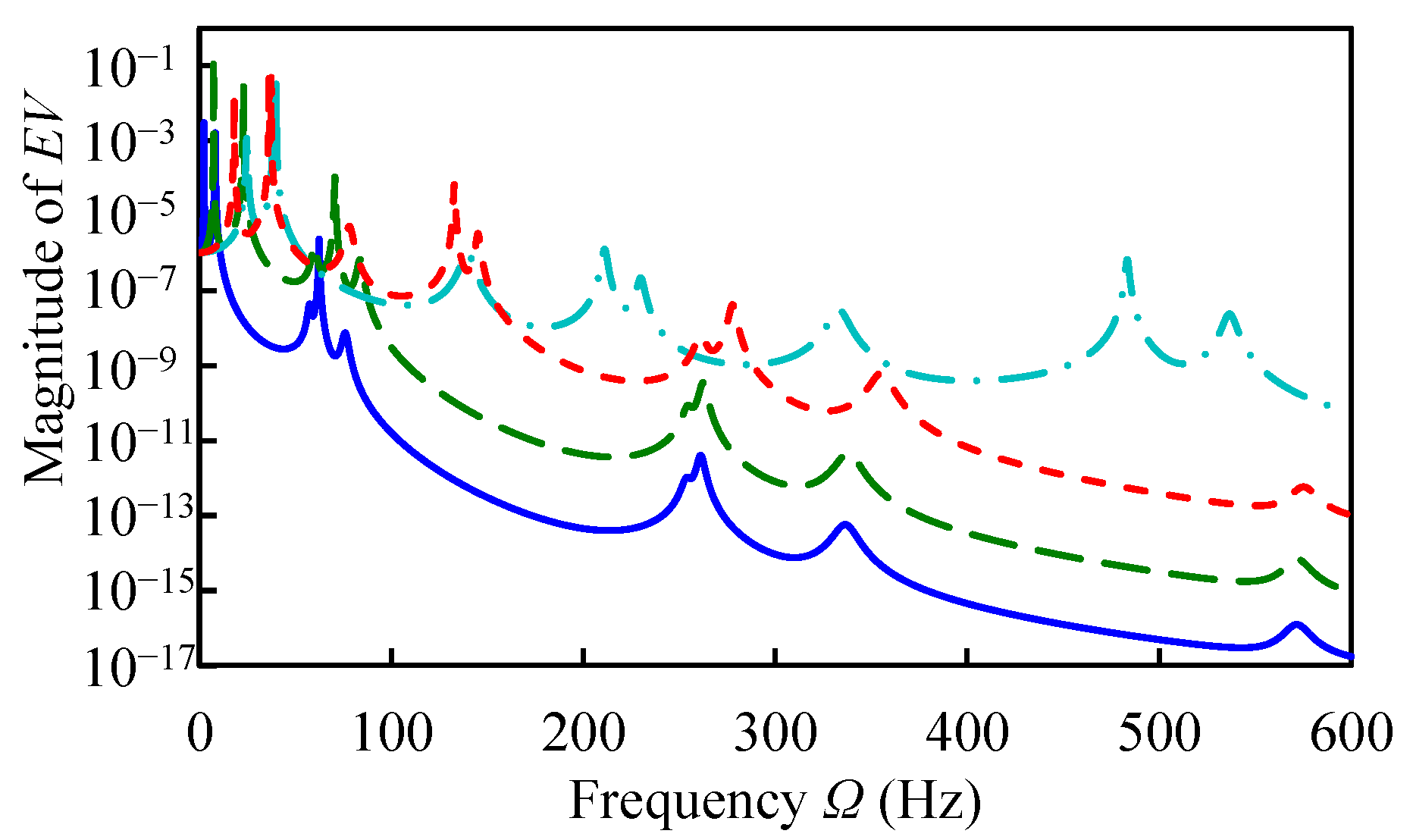
 cs = 100/10 N∙s/m,
cs = 100/10 N∙s/m,  cs = 100 N∙s/m kN/m,
cs = 100 N∙s/m kN/m,  cs = 100 × 10 N∙s/m,
cs = 100 × 10 N∙s/m,  ks = 100 × 100 N∙s/m).
ks = 100 × 100 N∙s/m).
 cs = 100/10 N∙s/m,
cs = 100/10 N∙s/m,  cs = 100 N∙s/m kN/m,
cs = 100 N∙s/m kN/m,  cs = 100 × 10 N∙s/m,
cs = 100 × 10 N∙s/m,  ks = 100 × 100 N∙s/m).
ks = 100 × 100 N∙s/m).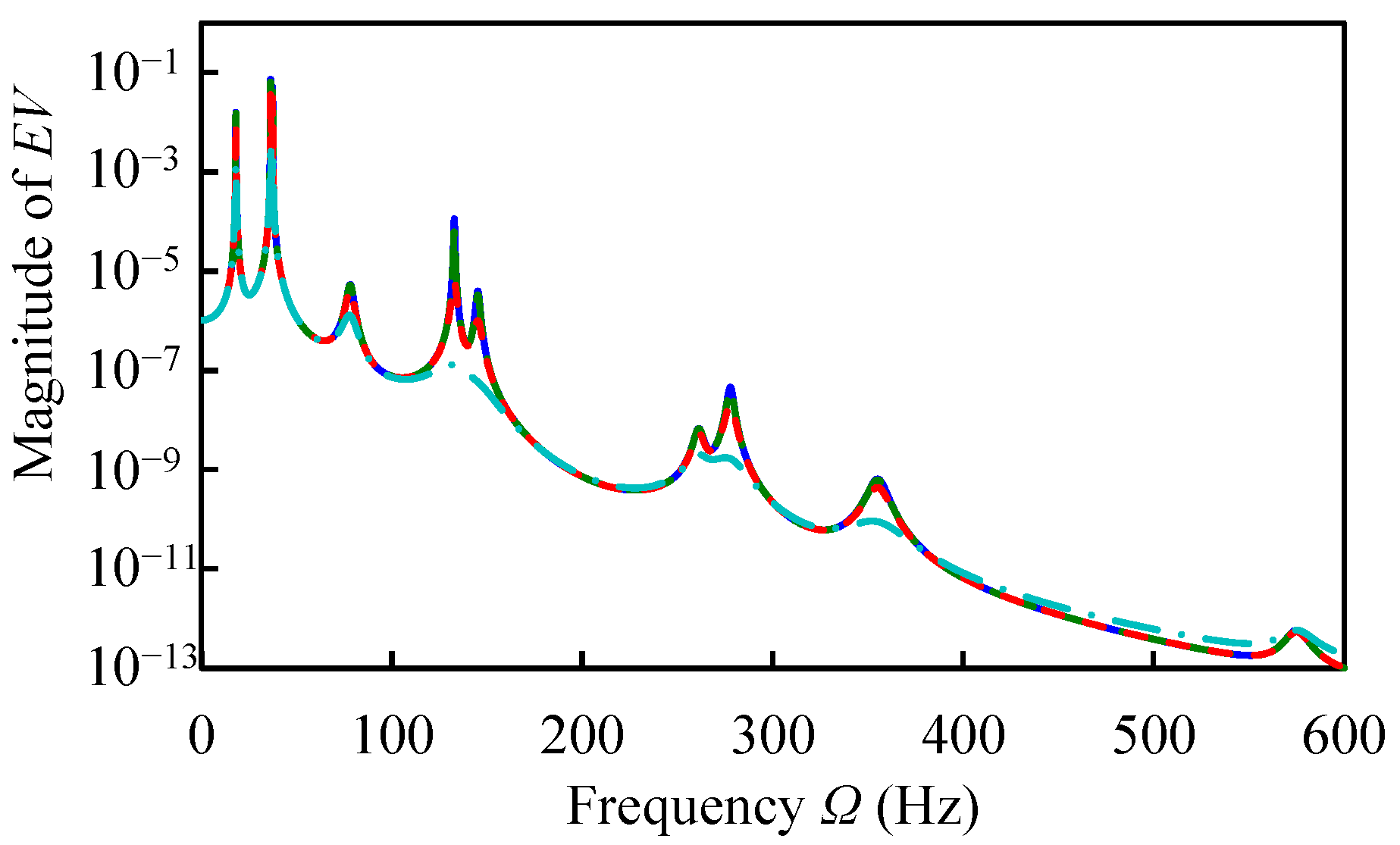
 d = 0 m,
d = 0 m,  d = 0.3 m,
d = 0.3 m,  d = 0.6 m,
d = 0.6 m,  d = 0.9 m).
d = 0.9 m).
 d = 0 m,
d = 0 m,  d = 0.3 m,
d = 0.3 m,  d = 0.6 m,
d = 0.6 m,  d = 0.9 m).
d = 0.9 m).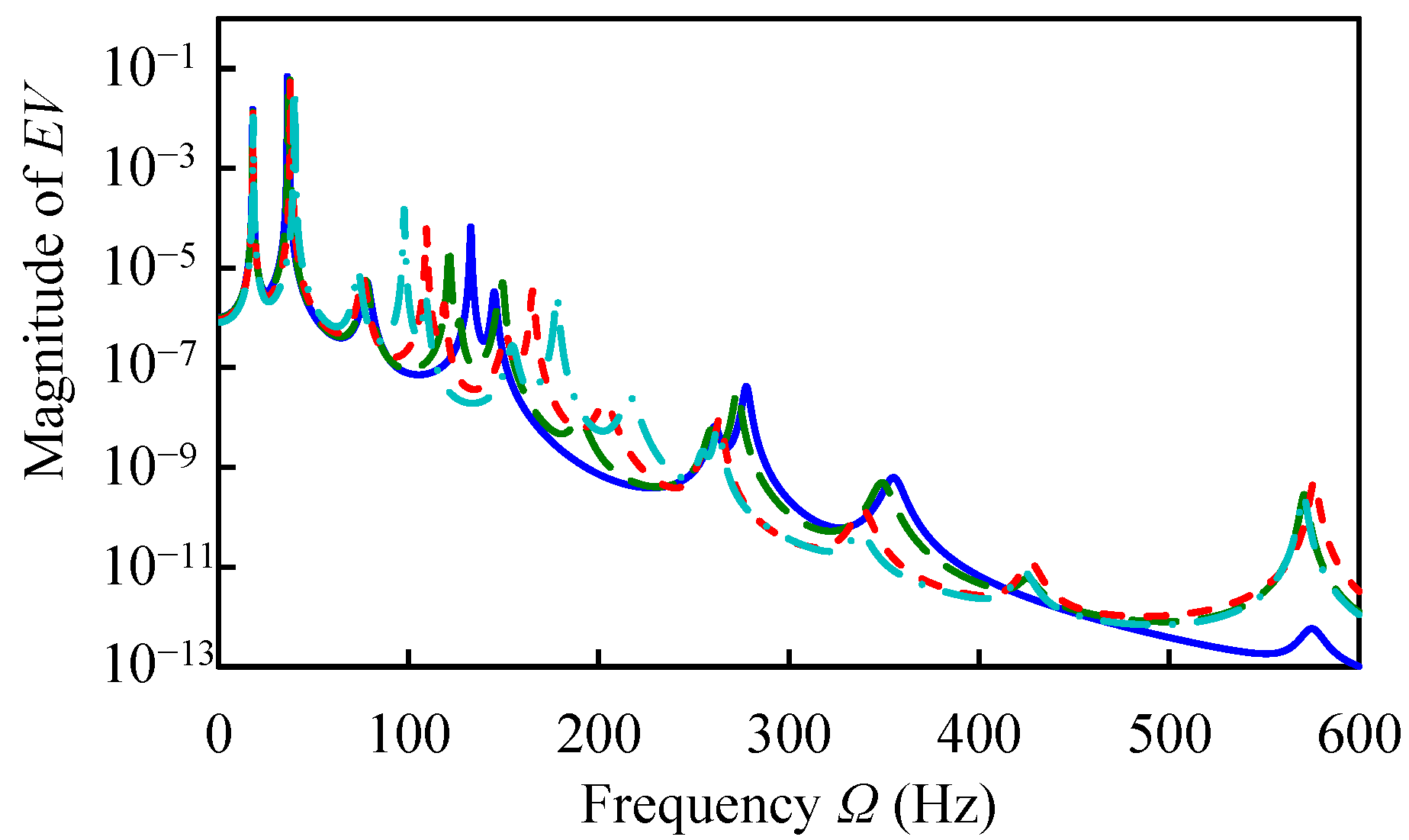
 K/100,
K/100,  K/10,
K/10,  K,
K,  K×10, K = (Ky, Kz, KT)).
K×10, K = (Ky, Kz, KT)).
 K/100,
K/100,  K/10,
K/10,  K,
K,  K×10, K = (Ky, Kz, KT)).
K×10, K = (Ky, Kz, KT)).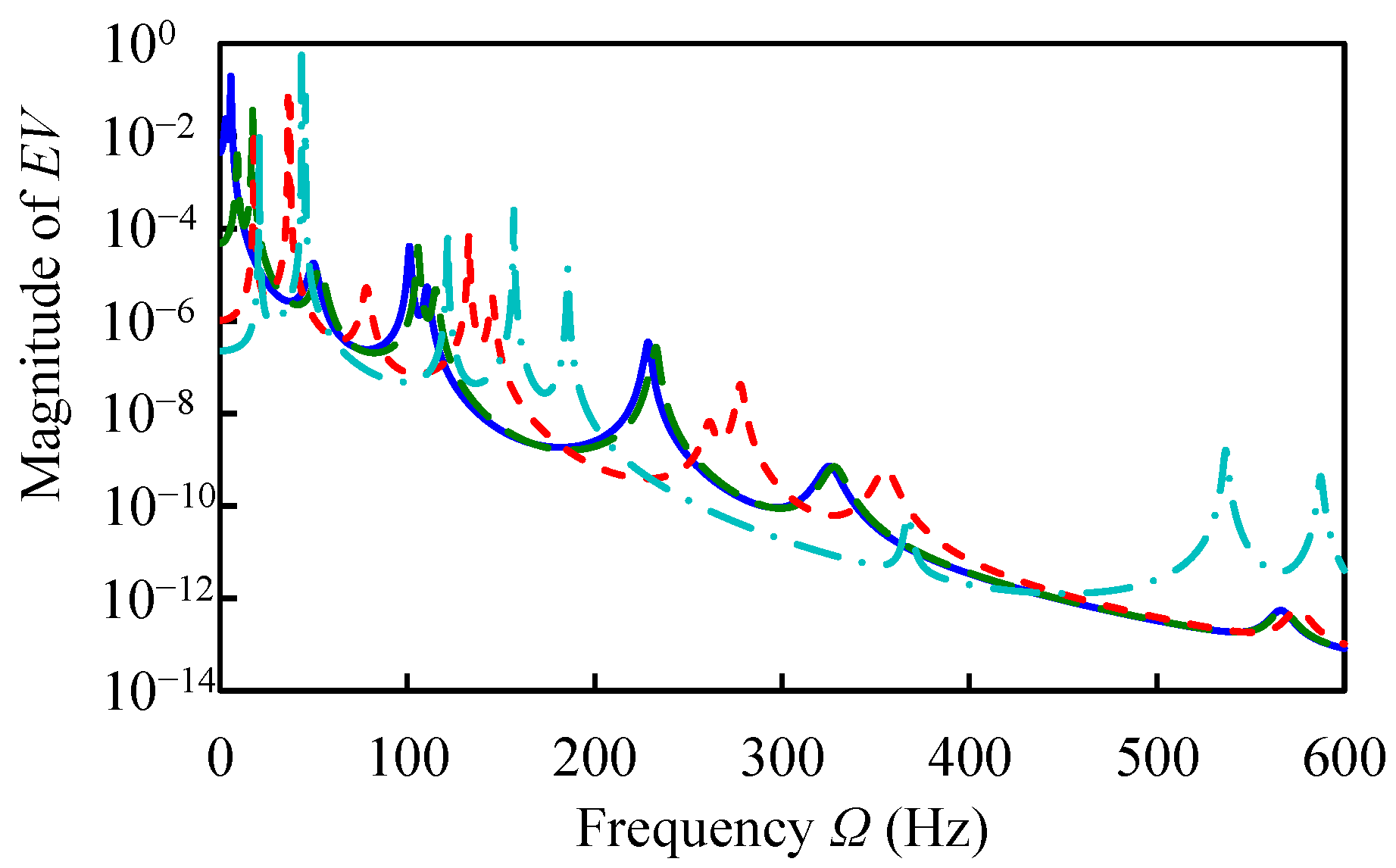
 C/10,
C/10,  C,
C,  C × 10,
C × 10,  C × 100, C= (Cy, Cz, CT)).
C × 100, C= (Cy, Cz, CT)).
 C/10,
C/10,  C,
C,  C × 10,
C × 10,  C × 100, C= (Cy, Cz, CT)).
C × 100, C= (Cy, Cz, CT)).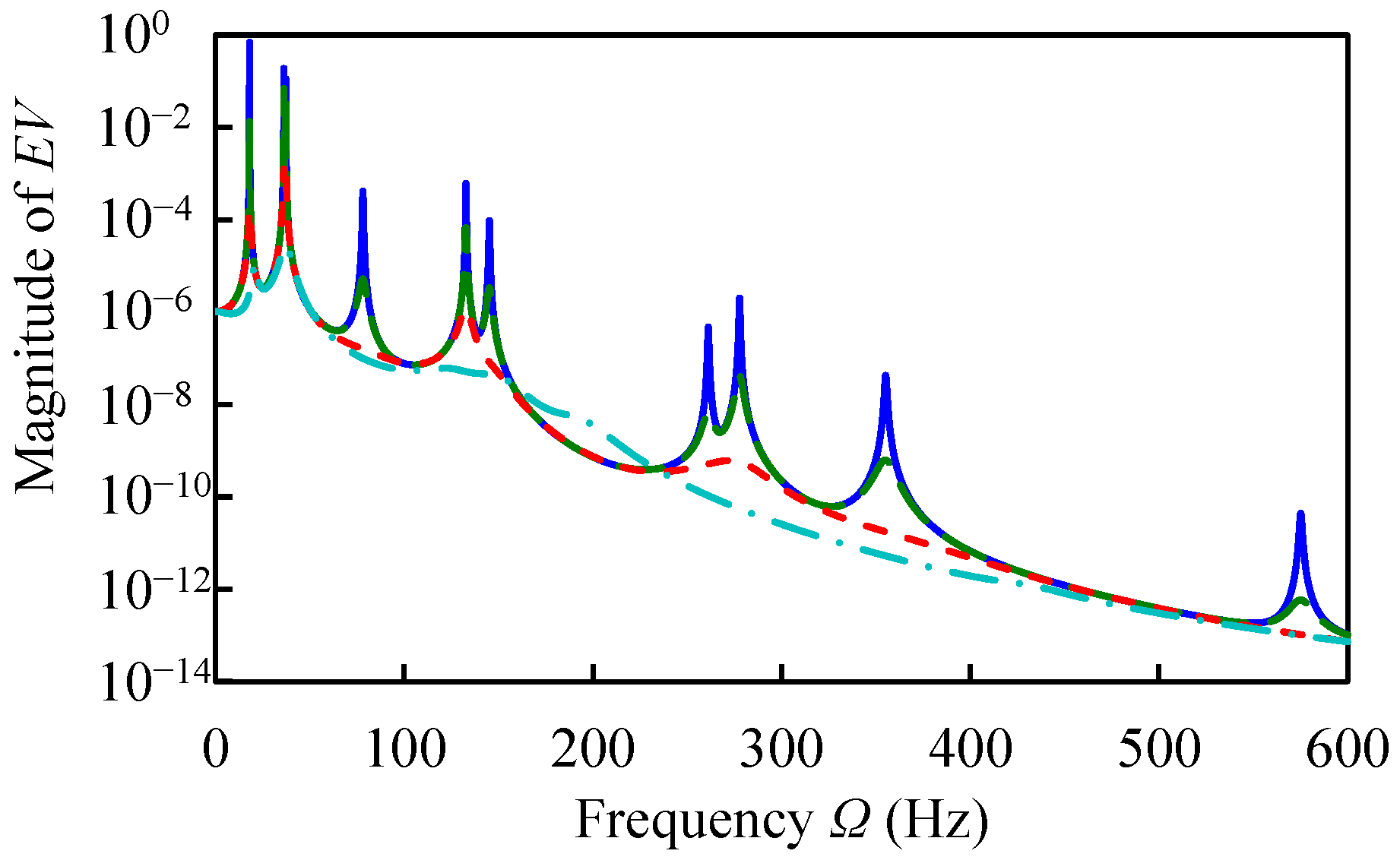
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Liu, X. On the Forced Vibration of Bending-Torsional-Warping Coupled Thin-Walled Beams Carrying Arbitrary Number of 3-DoF Spring-Damper-Mass Subsystems. Mathematics 2022, 10, 2849. https://doi.org/10.3390/math10162849
Chen J, Liu X. On the Forced Vibration of Bending-Torsional-Warping Coupled Thin-Walled Beams Carrying Arbitrary Number of 3-DoF Spring-Damper-Mass Subsystems. Mathematics. 2022; 10(16):2849. https://doi.org/10.3390/math10162849
Chicago/Turabian StyleChen, Jun, and Xiang Liu. 2022. "On the Forced Vibration of Bending-Torsional-Warping Coupled Thin-Walled Beams Carrying Arbitrary Number of 3-DoF Spring-Damper-Mass Subsystems" Mathematics 10, no. 16: 2849. https://doi.org/10.3390/math10162849
APA StyleChen, J., & Liu, X. (2022). On the Forced Vibration of Bending-Torsional-Warping Coupled Thin-Walled Beams Carrying Arbitrary Number of 3-DoF Spring-Damper-Mass Subsystems. Mathematics, 10(16), 2849. https://doi.org/10.3390/math10162849






