System of Generalized Variational Inclusions Involving Cayley Operators and XOR-Operation in q-Uniformly Smooth Banach Spaces
Abstract
:1. Introduction
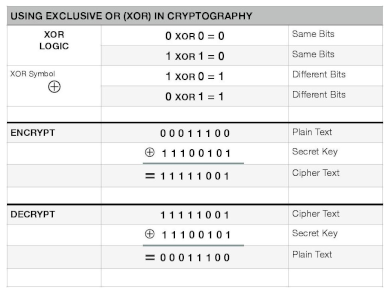
2. Basic Tools
- (i)
- is called OR-operation,
- (ii)
- is called AND-operation,
- (iii)
- is called the XOR-operation,
- (iv)
- is called the XNOR-operation.
- (i)
- ,
- (ii)
- if , then ,
- (iii)
- , if ,
- (iv)
- if , then if and only if ,
- (v)
- ,
- (vi)
- ,
- (vii)
- , then .
- (i)
- A is called ξ-order non-extended mapping if there exists a constant such that
- (ii)
- A is called a comparison mapping if , then and , for all ,
- (iii)
- A is called strongly comparison mapping, if A is comparison mapping and if and only if , for all .
- (i)
- M is called weak-comparison mapping if , and if , then there existssuch that , for all ,
- (ii)
- M is called -weak-non-ordinary difference mapping with respect to A if it is a weak comparison and for each there exist and and such that
- (iii)
- M is called ρ-order different weak-comparison mapping with respect to A, if there exists and for all there exist such that
- (iv)
- A weak-comparison mapping M is called -weak ANODD if it is an -weak-non-ordinary difference mapping and ρ-order different weak-comparison mapping associated with A, and
- (i)
- B is said to be accretive if
- (ii)
- B is said to be strongly accretive if there exists a constant such that
- (iii)
- N is said to be accretive if for all ,
3. Problem Structure and Iterative Scheme
4. Example
- (i)
- Then for any , we havethat is, is Lipschitz continuous in the first argument with constant . it is easy to show that is Lipschitz continuous in the second argument with constant .In the same manner one can show that is Lipschitz continuous in both the arguments with constants and , respectively.
- (ii)
- Suppose that are the multi-valued mappings defined as:Now,Clearly, is D-Lipschitz continuous with constant . Similarly, it can be shown that is D-Lipschitz continuous with constant .
- Let be the single-valued mappings such that
Clearly, A is Lipschitz continuous mapping with constant and B is Lipschitz continuous mapping with constant . In addition, A is ξ-ordered non-extended mapping with constant , and B is strongly accretive with constant . - (iii)
- Let be the multi-valued mappings such thatFor , it is clear that M is -weak ANODD mapping with , and N is B-accretive mapping.
- (iv)
- In view of the above calculations, we obtain the resolvent operators and such thatwhere and .The resolvent operator satisfies the condition (1) that isThe resolvent operator satisfies the condition (3) for ; that is
- (v)
- Using the values of and calculated in step (v), we obtain the generalized Cayley operators as:We calculate and below:It is easy to check that the generalized Cayley operator satisfies condition (2) and the generalized Cayley operator satisfies condition (4) with the above calculated and , respectively.
- (vi)
- Thus, all the conditions of Theorem 2 are satisfied and the system of generalized variational inclusions involving Cayley operators and an XOR-operation admits a solution . Consequently, the sequences and converge strongly to and v, respectively.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hartman, P.; Stampacchia, G. On some non-linear elliptic differential-functional equations. Acta Math. 1966, 115, 271–310. [Google Scholar] [CrossRef]
- Ahmad, R.; Siddiqi, A.H. Mixed variational-like inclusions and Jη-proximal operator equations in Banach spaces. J. Math. Anal. Appl. 2007, 327, 515–524. [Google Scholar] [CrossRef] [Green Version]
- An, N.T.; Dong, P.D.; Qin, X. Robust feature selection via nonconvex sparsity-based methods. J. Nonlinear Var. Anal. 2021, 5, 59–77. [Google Scholar]
- Ceng, L.C. A subgradient-extragradient method for bilevel equilibrium problems with the constraints of variational inclusion systems and fixed point problems. Commun. Optim. Theory 2021, 2021, 4. [Google Scholar]
- Ceng, L.C. On a viscosity iterative algorithm for variational inclusion problems and the fixed point problem of countably many nonexpansive mappings. Appl. Set-Valued Anal. Optim. 2021, 3, 203–214. [Google Scholar]
- Cubiotti, P.; Yao, J.C. On the Cauchy problem for a class of differential inclusions with applications. Appl. Anal. 2020, 99, 2543–2554. [Google Scholar] [CrossRef]
- Glowinski, R.; Lions, J.L.; Trémolières, R. Numerical Analysis of Variational Inequalities; North-Holland: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Liu, L.; Cho, S.Y.; Yao, Y.C. Convergence analysis of an inertial Tseng’s extragradient algorithm for solving pseudomonotone variational inequalities and applications. J. Nonlinear Var. Anal. 2021, 5, 627–644. [Google Scholar]
- Liu, L.; Yao, J.C. Iterative methods for solving variational inequality problems with a double-hierarchical structure in Hilbert spaces. Optimization 2022. [Google Scholar] [CrossRef]
- Olona, M.A.; Alakoya, T.O.; Owolabi, A.O.E.; Mewomo, O.T. Inertial algorithm for solving equilibrium, variational inclusion and fixed point problems for an infinite family of strict pseudocontractive mappings. J. Nonlinear Funct. Anal. 2021, 2021, 10. [Google Scholar]
- Shehu, Y.; Izuchukwu, C.; Qin, X.; Yao, J.C. Strongly convergent inertial extragradient type methods for equilibrium problems. Appl. Anal. 2021. [Google Scholar] [CrossRef]
- Yao, Y.; Postolache, M.; Yao, J.C. Strong convergence of an extragradient algorithm for variational inequality and fixed point problems. Sci. Bull. Ser. A 2020, 82, 3–12. [Google Scholar]
- Zong, C.; Tang, Y. Dual three-operator splitting algorithms for solving composite monotone inclusion with applications to convex minimization. J. Appl. Numer. Optim. 2021, 3, 533–554. [Google Scholar]
- Pang, J.S. Asymmetric variational inequality problems over product sets: Applications and iterative methods. Math. Program. 1988, 31, 206–219. [Google Scholar] [CrossRef]
- Cohen, G.; Chaplais, F. Nested monotony for variational inequalities over product of spaces and convergence of iterative algorithms. J. Optim. Theory Appl. 1988, 59, 369–390. [Google Scholar] [CrossRef] [Green Version]
- Ansari, Q.H.; Yao, J.C. A fixed point theorem and its applications to a system of variational inequalities. Bull. Aust. Math. Soc. 1999, 59, 433–442. [Google Scholar] [CrossRef] [Green Version]
- Ceng, L.C.; Petruse, A.; Qin, X.; Yao, J.C. A modified inertial subgradient extragradient method for solving pseudomonotone variational inequalities and common fixed point problems. Fixed Point Theory 2020, 21, 93–108. [Google Scholar] [CrossRef]
- Fang, Y.P.; Huang, N.J.; Thompson, H. A new system of variational inclusions with (H,η)-monotone operators in Hilbert spaces. Comput. Math. Appl. 2005, 49, 365–374. [Google Scholar] [CrossRef] [Green Version]
- Yan, W.; Fang, Y.P.; Huang, N.J. A new system of set-valued variational inclusions with H-monotone operators. Math. Inequal. Appl. 2005, 8, 537–546. [Google Scholar] [CrossRef]
- Qiu, Y.Q.; Liu, L.Y. A new system of generalized quasi-variational-like inclusions in Hilbert spaces. Comput. Math. Appl. 2010, 59, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Ali, I.; Ahmad, R.; Wen, C.F. Cayley inclusion problem involving XOR-operation. Mathematics 2019, 7, 302. [Google Scholar] [CrossRef] [Green Version]
- Helmberg, G. Introduction to Spectral Theory in Hilbert Space: The Cayley Transform; North-Holland Series in Applied Mathematics and Mechanics; Courier Dover Publications: Mineola, NY, USA, 1969; Volume 6. [Google Scholar]
- Rather, Z.A.; Ahmad, R.; Wen, C.F. Variational-like inequality problem involving generalized Cayley operator. Axioms 2021, 10, 133. [Google Scholar] [CrossRef]
- Xu, H.K. Inequalities in Banach spaces with applications. Nonlinear Anal. Theory Methods Appl. 1991, 16, 1127–1138. [Google Scholar] [CrossRef]
- Li, H.G. A nonlinear inclusion problem involving (α,λ)-NODM set-valued mappings in ordered Hilbert space. Appl. Math Lett. 2012, 25, 1384–1388. [Google Scholar] [CrossRef]
- Li, H.G.; Li, L.P.; Jin, M.M. A class of nonlinear mixed ordered inclusion problems for ordered (αA,λ)-ANODM set-valued mappings with strong comparison mapping A. Fixed Point Theory Appl. 2014, 2014, 79. [Google Scholar] [CrossRef] [Green Version]
- Li, H.G.; Pan, X.B.; Deng, Z.Y.; Wang, C.Y. Solving frameworks involving (γG,λ)-weak-GRD set-valued mappings in positive Hilbert spaces. Fixed Point Theory Appl. 2014, 2014, 146. [Google Scholar] [CrossRef] [Green Version]
- Li, H.G.; Qiu, D.; Zou, Y. Characterizations of weak-ANODD set-valued mappings with applications to approximate solution of GNMOQV inclusions involving ⊕ operator in ordered Banach spaces. Fixed Point Theory Appl. 2013, 2013, 241. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.P.; Huang, N.J. H-accretive operator and resolvent operator technique for variational inclusions in Banach spaces. Appl. Math. Lett. 2004, 17, 647–653. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, R.; Ali, I.; Rahaman, M.; Ishtyak, M.; Yao, J.C. Cayley inclusion problem with its corresponding generalized resolvent equation problem in uniformly smooth Banach spaces. Appl. Anal. 2020, 101, 1354–1368. [Google Scholar] [CrossRef]
- Lan, H.Y.; Kim, J.H.; Cho, Y.J. On a new system of nonlinear A-monotone multivalued variational inclusions. J. Math. Anal. Appl. 2007, 327, 481–493. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iqbal, J.; Rajpoot, A.K.; Islam, M.; Ahmad, R.; Wang, Y. System of Generalized Variational Inclusions Involving Cayley Operators and XOR-Operation in q-Uniformly Smooth Banach Spaces. Mathematics 2022, 10, 2837. https://doi.org/10.3390/math10162837
Iqbal J, Rajpoot AK, Islam M, Ahmad R, Wang Y. System of Generalized Variational Inclusions Involving Cayley Operators and XOR-Operation in q-Uniformly Smooth Banach Spaces. Mathematics. 2022; 10(16):2837. https://doi.org/10.3390/math10162837
Chicago/Turabian StyleIqbal, Javid, Arvind Kumar Rajpoot, Monirul Islam, Rais Ahmad, and Yuanheng Wang. 2022. "System of Generalized Variational Inclusions Involving Cayley Operators and XOR-Operation in q-Uniformly Smooth Banach Spaces" Mathematics 10, no. 16: 2837. https://doi.org/10.3390/math10162837
APA StyleIqbal, J., Rajpoot, A. K., Islam, M., Ahmad, R., & Wang, Y. (2022). System of Generalized Variational Inclusions Involving Cayley Operators and XOR-Operation in q-Uniformly Smooth Banach Spaces. Mathematics, 10(16), 2837. https://doi.org/10.3390/math10162837






