System of Generalized Variational Inclusions Involving Cayley Operators and XOR-Operation in q-Uniformly Smooth Banach Spaces

Abstract

In this paper, we consider and study a system of generalized variational inclusions involving Cayley operators and an XOR-operation in q-uniformly smooth Banach spaces. To obtain the solution of the system of generalized variational inclusions involving Cayley operators and an XOR-operation, we use some properties of Cayley operators as well as an XOR-operation. We also discuss the convergence criterion. In support of our main result, we provide an example.

1. Introduction

In the early 1960s, Hartman and Stampacchia [1] introduced the concept of variational inequalities, which later proved to be a powerful tool for solving many problems of mathematics and other technologies. Variational inclusions which are generalized forms of variational inequalities have been broadly studied by several authors to deal with the problems occurring in mechanics, economics, financial modelling, structural analysis, oceanography, image restoration and applied sciences. For more details on variational inequalities (inclusions), see [2,3,4,5,6,7,8,9,10,11,12,13] and references therein. A system of variational inclusions was considered and studied by Pang [14], Cohen and Chaplais [15], Ansari and Yao [16], Ceng et al. [17], Fang et al. [18], Yan et al. [19], Qiu and Liu [20] and many others.

In mathematics, a set of simultaneuous inequalities, also known as a system of inequalities or an inequality system, is a finite set of inequalities for which a common solution is obtained.

In 1846, Cayley originally described the Cayley transform, which is a mapping between skew-symmetric matrices and special orthogonal matrices. The nice applications of the Cayley transform can be found in real analysis, complex analysis and quaternionic analysis, see for example [21,22,23].

A Boolean logic operation called the XOR-operation is widely used in cryptography as well as generating parity bits for error checking and fault tolerance. XOR compares two input bits and generates one output bit. It is a simple logic; that is, if the bits are the same, the result is zero, and if the bits are different, the result is one. It is well known that the XOR-operation is commutative and associative.

The applications of the XOR-operation can be found in memory-optimized doubly linked lists, swapping, XOR ciphers, comparing two values, gray codes, generating pseudo-random numbers, implementation of multi-layer perception in neural network, etc. A way to use XOR in cryptography is shown below.

Motivated by the above discussion, in this paper, we consider and study a system of generalized variational inclusions involving Cayley operators and an XOR-operation in q-uniformly smooth Banach spaces. An existence and convergence result is established, and for illustration an example is provided.

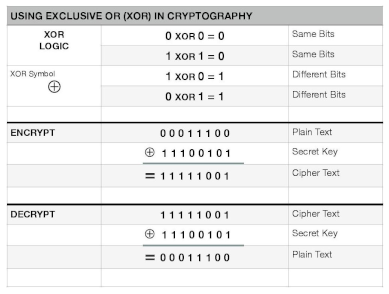
2. Basic Tools

Throughout the paper, unless otherwise specified, we assume $\tilde{E}$ to be a real ordered Banach space with its norm $\parallel ·\parallel$. Let ${\tilde{E}}^{*}$ be the topological dual of $\tilde{E}$, $\langle ·,·\rangle$ be the duality pairing between $\tilde{E}$ and ${\tilde{E}}^{*}$, $2^{\tilde{E}}$ be the family of non-empty subsets of $\tilde{E}$ and $C\left(\tilde{E}\right)$ be the family of compact subsets of $\tilde{E}$. Suppose $D(·,·)$ is the Hausdorff metric on $C\left(\tilde{E}\right)$. Let $\tilde{C}\subset \tilde{E}$ be a cone and ≤ be the partial ordering induced by cone $\tilde{C}$.

The generalized duality mapping $J_q:\tilde{E}\to 2^{{\tilde{E}}^{*}}$ is defined by

$$J_q\left(x\right)=\left\{f\in {\tilde{E}}^{*}:\langle x,f\rangle ={\parallel x\parallel }^q\mathrm{and}\parallel f\parallel ={\parallel x\parallel }^{q-1}\right\},forallx\in \tilde{E},$$

where $q>1$ is a constant. It is well known that for $q=2$, the generalized duality mapping coincides with the normalized duality mapping.

The modulus of smoothness of $\tilde{E}$ is the function ${\rho }_{\tilde{E}}:[0,+\infty )\to [0,+\infty )$ such that

$${\rho }_{\tilde{E}}\left(t\right)=sup\left\{\frac{\parallel x+y\parallel +\parallel x-y\parallel }{2}-1:\parallel x\parallel \le 1,\parallel y\parallel \le t\right\}.$$

A Banach space is called uniformly smooth if

$$\underset{t\to 0}{lim}\frac{{\rho }_{\tilde{E}}\left(t\right)}{t}=0,$$

and q-uniformly smooth if there exists a constant $k>0$ such that

$${\rho }_{\tilde{E}}\left(t\right)\le k{t}^q,q>1.$$

The following result of Xu [24] is important to prove our main result.

Lemma 1.

Let $\tilde{E}$ be a real uniformly smooth Banach space. Then $\tilde{E}$ is q-uniformly smooth if and only if there exists a constant $k_q>0$ such that for all $x,y\in \tilde{E}$,

$${\parallel x+y\parallel }^q\le {\parallel x\parallel }^q+q\langle y,J_q\left(x\right)\rangle +k_q{\parallel y\parallel }^q.$$

Definition 1.

A mapping $A:\tilde{E}\to \tilde{E}$ is called Lipschitz continuous, if there exists a constant ${\lambda }_A>0$ such that

$$\parallel A\left(x\right)-A\left(y\right)\parallel \le {\lambda }_A\parallel x-y\parallel ,forallx,y\in \tilde{E}.$$

Definition 2.

Let $\tilde{S}:\tilde{E}\to C\left(\tilde{E}\right)$ be a multi-valued mapping, then $\tilde{S}$ is called D-Lipschitz continuous if there exists a constant ${\lambda }_{D_{\tilde{S}}}>0$ such that

$$D(\tilde{S}\left(x\right),\tilde{S}\left(y\right))\le {\lambda }_{D_{\tilde{S}}}\parallel x-y\parallel ,forallx,y\in \tilde{E}.$$

The following concepts and results can be found in [25,26,27,28].

Definition 3.

For arbitrary elements $x,y\in \tilde{E}$, if $x\le y(\mathrm{or}y\le x)$ holds, then x and y are said to be comparable to each other (denoted by $x\prec y$).

Definition 4.

For arbitrary elements $x,y\in \tilde{E}$, let $\mathrm{lub}\{x,y\}$ and $\mathrm{glb}\{x,y\}$ for the set $\{x,y\}$ exist, where $\mathrm{lub}$ means the least upper bound and $\mathrm{glb}$ means the greatest lower bound for the set $\{x,y\}$. Then some binary operations are mentioned below:

(i) 

$x\vee y=\mathrm{lub}\{x,y\},where\vee$ is called OR-operation,

(ii) 

$x\wedge y=\mathrm{glb}\{x,y\},where\wedge$ is called AND-operation,

(iii) 

$x\oplus y=(x-y)\vee (y-x),where\oplus$ is called the XOR-operation,

(iv) 

$x\odot y=(x-y)\wedge (y-x),where\odot$ is called the XNOR-operation.

Proposition 1.

Let ⊕ be an XOR-operation and ⊙ be an XNOR-operation. Then the following are true.

(i) 

$x\odot x=0,x\odot y=y\odot x=-(x\oplus y)=-(y\oplus x)$,

(ii) 

if $x\prec 0$, then $-x\oplus 0\le x\le x\oplus 0$,

(iii) 

$0\le x\oplus y$, if $x\prec y$,

(iv) 

if $x\prec y$, then $x\oplus y=0$ if and only if $x=y$,

(v) 

$\parallel 0\oplus 0\parallel =\parallel 0\parallel =0$,

(vi) 

$\parallel x\oplus y\parallel \le \parallel x-y\parallel$,

(vii) 

$x\prec y$, then $\parallel x\oplus y\parallel =\parallel x-y\parallel$.

Definition 5.

Let $A:\tilde{E}\to \tilde{E}$ be a single-valued mapping. Then

(i) 

A is called ξ-order non-extended mapping if there exists a constant $\xi >0$ such that

$$\xi (x\oplus y)\le A\left(x\right)\oplus A\left(y\right),forallx,y\in \tilde{E},$$

(ii) 

A is called a comparison mapping if $x\prec y$, then $A\left(x\right)\prec A\left(y\right),x\prec A\left(x\right)$ and $y\prec A\left(y\right)$, for all $x,y\in \tilde{E}$,

(iii) 

A is called strongly comparison mapping, if A is comparison mapping and $A\left(x\right)\prec A\left(y\right)$ if and only if $x\prec y$, for all $x,y\in \tilde{E}$.

Definition 6.

Let $A:\tilde{E}\to \tilde{E}$ be a single-valued mapping and $M:\tilde{E}\to 2^{\tilde{E}}$ be a multi-valued mapping. Then

(i) 

M is called weak-comparison mapping if $t_x\in M\left(x\right),x\prec t_x$, and if $x\prec y$, then there exists

$t_y\in M\left(y\right)$ such that $t_x\prec t_y$, for all $x,y\in \tilde{E}$,

(ii) 

M is called ${\alpha }_A$-weak-non-ordinary difference mapping with respect to A if it is a weak comparison and for each $x,y\in \tilde{E},$ there exist ${\alpha }_A>0$ and $t_x\in M\left(A\left(x\right)\right)$ and $t_y\in M\left(A\left(y\right)\right)$ such that

$$\left(t_x\oplus t_y\right)\oplus {\alpha }_A\left(A\left(x\right)\oplus A\left(y\right)\right)=0,$$

(iii) 

M is called ρ-order different weak-comparison mapping with respect to A, if there exists $\rho >0$ and for all $x,y\in \tilde{E},$ there exist $t_x\in M\left(A\left(x\right)\right),t_y\in M\left(A\left(y\right)\right)$ such that

$$\rho \left(t_x-t_y\right)\prec x-y,$$

(iv) 

A weak-comparison mapping M is called $({\alpha }_A,\rho )$-weak ANODD if it is an ${\alpha }_A$-weak-non-ordinary difference mapping and ρ-order different weak-comparison mapping associated with A, and $\left[A+\rho M\right]\left(\tilde{E}\right)=\tilde{E}.$

Definition 7.

Let A be ξ-ordered non-extended mapping and M is ${\alpha }_A$-non-ordinary difference mapping with respect to A. The resolvent operator $R_{A,\rho }^M:\tilde{E}\to \tilde{E}$ associated with A and M is defined by

$$R_{A,\rho }^M\left(x\right)={\left[A+\rho M\right]}^{-1}\left(x\right),forallx\in \tilde{E},\rho >0.$$

Lemma 2.

Let $M:\tilde{E}\to 2^{\tilde{E}}$ be an ordered $({\alpha }_A,\rho )$-weak ANODD mapping and $A:\tilde{E}\to \tilde{E}$ be a ξ-ordered non-extended mapping with respect to A. Then for ${\alpha }_A>\frac{1}{\rho }$, the following relation holds:

$$\begin{array}{c}\hfill R_{A,\rho }^M\left(x\right)\oplus R_{A,\rho }^M\left(y\right)\le \frac{1}{\xi ({\alpha }_A\rho -1)}(x\oplus y),forallx,y\in \tilde{E}.\end{array}$$

(1)

Definition 8.

The generalized Cayley operator $C_{A,\rho }^M:\tilde{E}\to \tilde{E}$ is defined as:

$$C_{A,\rho }^M\left(x\right)=\left[2R_{A,\rho }^M-A\right]\left(x\right),forallx\in \tilde{E}.$$

Proposition 2.

The generalized Cayley operator is Lipschitz continuous provided $x\prec y,A$ is ${\lambda }_A$-Lipschitz continuous, $C_{A,\rho }^M\left(x\right)\prec C_{A,\rho }^M\left(y\right),A\left(x\right)\prec A\left(y\right)$, for all $x,y\in \tilde{E}$.

Proof. 

For all $x,y\in \tilde{E}$, using Lemma 2, we evaluate

$$\begin{array}{cc}\hfill \parallel C_{A,\rho }^M\left(x\right)\oplus C_{A,\rho }^M\left(y\right)\parallel & =∥\left[2R_{A,\rho }^M\left(x\right)-A\left(x\right)\right]\oplus \left[2R_{A,\rho }^M\left(x\right)-A\left(y\right)\right]∥\hfill \\ \hfill & =2\parallel R_{A,\rho }^M\left(x\right)\oplus R_{A,\rho }^M\left(y\right)\parallel +\parallel A\left(x\right)\oplus A\left(y\right)\parallel \hfill \\ \hfill & \le 2·\frac{1}{\xi ({\alpha }_A\rho -1)}\parallel x\oplus y\parallel +\parallel A\left(x\right)\oplus A\left(y\right)\parallel .\hfill \end{array}$$

Since $x\prec y,C_{A,\rho }^M\left(x\right)\prec C_{A,\rho }^M\left(y\right),A\left(x\right)\prec A\left(y\right)$ by (1) of Proposition 1 and using Lipschitz continuity of A, we obtain

$$\parallel C_{A,\rho }^M\left(x\right)-C_{A,\rho }^M\left(y\right)\parallel \le \left[\frac{2}{\xi ({\alpha }_A\rho -1)}+{\lambda }_A\right]\parallel x-y\parallel ,$$

that is

$$\begin{array}{c}\hfill \parallel C_{A,\rho }^M\left(x\right)-C_{A,\rho }^M\left(y\right)\parallel \le {\lambda }_{C_1}\parallel x-y\parallel ,\end{array}$$

(2)

where ${\lambda }_{C_1}=\frac{2+{\lambda }_A\xi ({\alpha }_A\rho -1)}{\xi ({\alpha }_A\rho -1)}$. □

Definition 9.

Let $B:\tilde{E}\to \tilde{E}$ be a single-valued mapping and $N:\tilde{E}\to 2^{\tilde{E}}$ be a multi-valued mapping. Then

(i) 

B is said to be accretive if

$$\langle B\left(x\right)-B\left(y\right),J_q(x-y)\rangle \ge 0,forallx,y\in \tilde{E},$$

(ii) 

B is said to be strongly accretive if there exists a constant $r>0$ such that

$$\langle B\left(x\right)-B\left(y\right),J_q(x-y)\rangle \ge r{\parallel x-y\parallel }^q,forallx,y\in \tilde{E},$$

(iii) 

N is said to be accretive if for all $x,y\in \tilde{E}$,

$$\langle u-v,J_q(x-y)\rangle \ge 0,forallu\in N\left(x\right),v\in N\left(y\right).$$

Definition 10.

A multi-valued mapping $N:\tilde{E}\to 2^{\tilde{E}}$ is called B-accretive, if N is accretive and $[B+\nu N]\left(\tilde{E}\right)=\tilde{E},forall\nu >0.$

Definition 11.

Let N be a B-accretive multi-valued mapping. The resolvent operator $R_{A,\rho }^M:\tilde{E}\to \tilde{E}$ associated with B and N is defined as:

$$R_{B,\nu }^N\left(x\right)={[B+\nu N]}^{-1}\left(x\right),forallx\in \tilde{E},\nu >0.$$

Theorem 1.

([29]). Let $B:\tilde{E}\to \tilde{E}$ be a strongly accretive mapping with constant r and $N:\tilde{E}\to 2^{\tilde{E}}$ be B-accretive multi-valued mapping. Then the resolvent operator $R_{B,\nu }^N:\tilde{E}\to \tilde{E}$ is Lipschitz continuous with constant $\frac{1}{r}$, that is,

$$\begin{array}{c}\hfill \parallel R_{B,\nu }^N\left(x\right)-R_{B,\nu }^N\left(y\right)\parallel \le \frac{1}{r}\parallel x-y\parallel ,forallx,y\in \tilde{E}.\end{array}$$

(3)

Definition 12.

The generalized Cayley operator $C_{B,\nu }^N$ is defined as:

$$C_{B,\nu }^N\left(x\right)=[2R_{B,\nu }^N-B]\left(x\right),forallx\in \tilde{E}\mathrm{and}\nu >0.$$

Proposition 3

([30]). The generalized Cayley operator is Lipschitz continuous, that is

$$\begin{array}{c}\hfill \parallel C_{B,\nu }^N\left(x\right)-C_{B,\nu }^N\left(y\right)\parallel \le {\lambda }_{C_2}\parallel x-y\parallel ,with{\lambda }_{C_2}=\left(\frac{2+{\lambda }_{B}r}{r}\right),\end{array}$$

(4)

where the mapping $B:\tilde{E}\to \tilde{E}$ is Lipschitz continuous with constant ${\lambda }_B$.

3. Problem Structure and Iterative Scheme

Let $\tilde{E}$ be an ordered real Banach space. Let $f_1,f_2:\tilde{E}\times \tilde{E}\to \tilde{E}$ and $A,B:\tilde{E}\to \tilde{E}$ be single-valued mappings. Let $M,N:\tilde{E}\to 2^{\tilde{E}}$ and $\tilde{S},\tilde{T}:\tilde{E}\to C\left(\tilde{E}\right)$ be multi-valued mappings. Let for $\rho ,\nu >0,C_{A,\rho }^M,C_{B,\nu }^N:\tilde{E}\to \tilde{E}$ be generalized Cayley operators. We consider the following problem.

Find $x,y\in \tilde{E},u\in \tilde{S}\left(x\right),v\in \tilde{T}\left(y\right)$ such that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill 0& \in f_1\left(x-C_{A,\rho }^M\left(x\right),v\right)\oplus M\left(x\right),\hfill \\ \hfill 0& \in f_2\left(u,y-C_{B,\nu }^N\left(y\right)\right)+N\left(y\right).\hfill \end{array}\end{array}$$

(5)

Problem (5) is called a system of generalized variational inclusions involving Cayley operators and an XOR-operation.

For suitable choices of operators involved in the system of generalized variational inclusions involving Cayley operators and an XOR-operation (5), one can find problems studied in [19,31].

The following Lemma ensures the equivalence between a system of generalized variational inclusions involving Cayley operators and an XOR-operation (5) and a set of fixed point equations.

Lemma 3.

$x,y\in \tilde{E},u\in \tilde{S}\left(x\right),v\in \tilde{T}\left(y\right)$ constitute the solution for the system of generalized variational inclusions involving Cayley operators and an XOR-operation (5), if and only if the following equations are satisfied:

$$\begin{array}{cc}\hfill x& =R_{A,\rho }^M\left[A\left(x\right)\oplus \rho f_1(x-C_{A,\rho }^M\left(x\right),v)\right],\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill y& =R_{B,\nu }^N\left[B\left(y\right)-\nu f_2(u,y-C_{B,\nu }^N\left(y\right)\right)].\hfill \end{array}$$

(7)

Proof. 

Proof is easy and depends on the definition of the resolvent operators $R_{A,\rho }^M$ and $R_{B,\nu }^N$. □

Applying Lemma 3, we suggest the following iterative scheme for solving a system of generalized variational inclusions involving Cayley operators and an XOR-operation (5).

Iterative Scheme 3.1.

For any given$x_0,y_0\in \tilde{E}$, choose$u_0\in \tilde{S}\left(x_0\right),v_0\in \tilde{T}\left(y_0\right)$ and compute the sequences$\left\{x_n\right\},\left\{y_n\right\},\left\{u_n\right\}$and$\left\{v_n\right\}$by the following scheme:

$$\begin{array}{cc}\hfill x_{n+1}& =(1-{\alpha }_n)x_n+{\alpha }_n{R}_{A,\rho }^M\left[A\left(x_n\right)\oplus \rho f_1(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right],\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill y_{n+1}& =(1-{\beta }_n)y_n+{\beta }_n{R}_{B,\nu }^N\left[B\left(y_n\right)-\nu f_2(u_n,y_n-C_{B,\nu }^N\left(y_n\right)\right].\hfill \end{array}$$

(9)

Let $u_{n+1}\in \tilde{S}\left(x_{n+1}\right)$ and $v_{n+1}\in \tilde{T}\left(y_{n+1}\right)$ such that

$$\begin{array}{cc}\hfill \parallel u_n-u_{n+1}\parallel & \le \tilde{D}\left(\tilde{S}\left(x_n\right),\tilde{S}\left(x_{n+1}\right)\right),\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \parallel v_n-v_{n+1}\parallel & \le \tilde{D}\left(\tilde{T}\left(y_n\right),\tilde{T}\left(y_{n+1}\right)\right),\hfill \end{array}$$

(11)

where $0\le {\alpha }_n,{\beta }_n\le 1;\rho ,\nu >0$ are constants and $n=0,1,2,\cdots$.

Theorem 2.

Let $\tilde{E}$ be a real ordered q-uniformly smooth Banach space. Let $f_1,f_2:\tilde{E}\times \tilde{E}\to \tilde{E}$ be single-valued mappings such that $f_1$ is Lipschitz continuous in both the arguments with constants ${\lambda }_{f_1}^1$ and ${\lambda }_{f_1}^2$, respectively; $f_2$ is Lipschitz continuous in both the arguments with constants ${\lambda }_{f_2}^1$ and ${\lambda }_{f_2}^2$, respectively. Let $\tilde{S},\tilde{T}:\tilde{E}\to C\left(\tilde{E}\right)$ be multi-valued mappings such that $\tilde{S}$ is D-Lipschitz continuous with constant ${\lambda }_{D_{\tilde{S}}}$ and $\tilde{T}$ is D-Lipschitz continuous with constant ${\lambda }_{D_{\tilde{T}}}$. Let $A,B:\tilde{E}\to \tilde{E}$ be single-valued mappings such that A is ξ-ordered non-extended mapping and Lipschitz continuous with constant ${\lambda }_A,B$ is strongly accretive with constant $r>0$ and Lipshcitz continuous with constant ${\lambda }_B$. Let $M,N:\tilde{E}\to 2^{\tilde{E}}$ be multi-valued mappings such that M is $({\alpha }_A,\rho )$-weak ANODD mapping and N is B-accretive mapping. Let $R_{A,\rho }^M,R_{B,\nu }^N:\tilde{E}\to \tilde{E}$ be the resolvent operators such that $R_{A,\rho }^M$ satisfy the condition (1) and $R_{B,\nu }^N$ satisfy the condition (3). Suppose $C_{A,\rho }^M,C_{B,\nu }^N:\tilde{E}\to \tilde{E}$ be the generalized Cayley operators such that $C_{A,\rho }^M$ satisfy the condition (2), $C_{B,\nu }^N$ satisfy the condition (4). Let $x_n\prec x_{n+1},n=0,1,2,\cdots ,C_{A,\rho }^M\left(x\right)\prec C_{A,\rho }^M\left(y\right),A\left(x\right)\prec A\left(y\right)$, for all $x,y\in \tilde{E}$. Suppose that the following conditions are satisfied:

$$\begin{array}{cc}\hfill 0& <(1-{\alpha }_n)+{\alpha }_n{\lambda }_A{P}_1\left(\theta \right)+{\alpha }_n{P}_1\left(\theta \right)\rho \left({\lambda }_{f_1}^1\sqrt[q]{1-(q-k_q){\lambda }_{C_1}^q}\right)+{\beta }_n{P}_2\left(\theta \right)\nu {\lambda }_{f_2}^1{\lambda }_{D_{\tilde{S}}}<1,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill 0& <(1-{\beta }_n)+{\beta }_n{\lambda }_B{P}_2\left(\theta \right)+{\beta }_n{P}_2\left(\theta \right)\nu \left({\lambda }_{f_2}^2\sqrt[q]{1-(q-k_q){\lambda }_{C_2}^q}\right)+{\alpha }_n{P}_1\left(\theta \right)\rho {\lambda }_{f_1}^2{\lambda }_{D_{\tilde{T}}}<1.\hfill \end{array}$$

(13)

where $P_1\left(\theta \right)=\frac{1}{\xi ({\alpha }_A\rho -1)},{\alpha }_A>\frac{1}{\rho }$ and $P_2\left(\theta \right)=\frac{1}{r}$. Then the system of generalized variational inclusions involving Cayley operators and an XOR-operation (5) admits a solution $(x,y,u,v)$, and the sequences $\left\{x_n\right\},\left\{y_n\right\},\left\{u_n\right\}$ and $\left\{v_n\right\}$ generated by scheme 3.1 strongly converge to $x,y,u$ and v, respectively.

Proof. 

Using (8) of scheme 3.1 and (iii) of Proposition 1, we have

$$\begin{array}{cc}\hfill 0\le x_{n+1}\oplus x_n& =\left[(1-{\alpha }_n)x_n+{\alpha }_n{R}_{A,\rho }^M\left[A\left(x_n\right)\oplus \rho f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)\right]\right]\hfill \\ \hfill & \oplus \left[(1-{\alpha }_n)x_{n-1}+{\alpha }_n{R}_{A,\rho }^M\left[A\left(x_{n-1}\right)\oplus \rho f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\right]\right]\hfill \\ \hfill & =(1-{\alpha }_n)(x_n\oplus x_{n-1})+{\alpha }_n\left[R_{A,\rho }^M\left[A\left(x_n\right)\oplus \rho f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)\right]\right.\hfill \\ \hfill & \oplus R_{A,\rho }^M\left.\left[A\left(x_{n-1}\right)\oplus \rho f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\right]\right].\hfill \end{array}$$

(14)

Using Lemma 2 and commutativity of ⊕ operation, (14) becomes

$$\begin{array}{cc}\hfill 0\le x_{n+1}\oplus x_n& \le (1-{\alpha }_n)(x_n\oplus x_{n-1})+{\alpha }_n{P}_1\left(\theta \right)[\left(A\left(x_n\right)\oplus \rho f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)\right)\hfill \\ \hfill & \oplus \left(A\left(x_{n-1}\right)\oplus \rho f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\right)]\hfill \\ \hfill & =(1-{\alpha }_n)(x_n\oplus x_{n-1})+{\alpha }_n{P}_1\left(\theta \right)[A\left(x_n\right)\oplus A\left(x_{n-1}\right)\oplus \rho \left(f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)\right.\hfill \\ \hfill & \left.\oplus f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\right)].\hfill \end{array}$$

(15)

Using $\left(vi\right)$ of Proposition 1, from (15), we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}\oplus x_n\parallel & \le (1-{\alpha }_n)\parallel x_n\oplus x_{n-1}\parallel +{\alpha }_n{P}_1\left(\theta \right)\parallel A\left(x_n\right)\oplus A\left(x_{n-1}\right)\hfill \\ \hfill & \oplus \rho \left(f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)\oplus f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\right)\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\parallel x_n\oplus x_{n-1}\parallel +{\alpha }_n{P}_1\left(\theta \right)\parallel A\left(x_n\right)\oplus A\left(x_{n-1}\right)\parallel \hfill \\ \hfill & +{\alpha }_n{P}_1\left(\theta \right)\rho \parallel f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)\oplus f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\parallel x_n\oplus x_{n-1}\parallel +{\alpha }_n{P}_1\left(\theta \right)\parallel A\left(x_n\right)-A\left(x_{n-1}\right)\parallel \hfill \\ \hfill & +{\alpha }_n{P}_1\left(\theta \right)\rho \parallel f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)-f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\parallel .\hfill \end{array}$$

(16)

As $x_n\prec x_{n+1}$ for all n, using $\left(vii\right)$ of Proposition 1 and Lipschitz continuity of A, from (16), we obtain

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x_n\parallel & \le (1-{\alpha }_n)\parallel x_n-x_{n-1}\parallel +{\alpha }_n{P}_1\left(\theta \right){\lambda }_A\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & +{\alpha }_n{P}_1\left(\theta \right)\rho \parallel f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)-f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\parallel .\hfill \end{array}$$

(17)

Using Lipschitz continuity of $f_1$ in both the arguments, D-Lipschitz continuity of $\tilde{T}$ and Lipschitz continuity of the generalized Cayley operator $C_{A,\rho }^M$, we have

$$\begin{array}{cc}\hfill & \parallel f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)-f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\parallel \hfill \\ \hfill & =\parallel f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)-f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_{n-1}\right)\hfill \\ \hfill & +f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_{n-1}\right)-f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\parallel \hfill \\ \hfill & \le \parallel f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)-f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_{n-1}\right)\parallel \hfill \\ \hfill & +\parallel f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_{n-1}\right)-f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\parallel \hfill \\ \hfill & \le {\lambda }_{f_1}^2\parallel v_n-v_{n-1}\parallel +{\lambda }_{f_1}^1\parallel \left(x_n-C_{A,\rho }^M\left(x_n\right)\right)-\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right)\right)\parallel \hfill \\ \hfill & ={\lambda }_{f_1}^2\parallel v_n-v_{n-1}\parallel +{\lambda }_{f_1}^1\parallel x_n-x_{n-1}-\left(C_{A,\rho }^M\left(x_n\right)-C_{A,\rho }^M\left(x_{n-1}\right)\right)\parallel \hfill \\ \hfill & \le {\lambda }_{f_1}^{2}D\left(\tilde{T}\left(y_n\right),\tilde{T}\left(y_{n-1}\right)\right)+{\lambda }_{f_1}^1\parallel x_n-x_{n-1}-C_{A,\rho }^M\left(x_n\right)-C_{A,\rho }^M\left(x_{n-1}\right)\parallel \hfill \\ \hfill & \le {\lambda }_{f_1}^2{\lambda }_{D_{\tilde{T}}}\parallel y_n-y_{n-1}\parallel +{\lambda }_{f_1}^1\parallel x_n-x_{n-1}-\left(C_{A,\rho }^M\left(x_n\right)-C_{A,\rho }^M\left(x_{n-1}\right)\right)\parallel .\hfill \end{array}$$

(18)

Applying Lemma 1, we obtain

$$\begin{array}{cc}\hfill & \parallel x_n-x_{n-1}-\left(C_{A,\rho }^M\left(x_n\right)-C_{A,\rho }^M\left(x_{n-1}\right)\right){\parallel }^q\hfill \\ \hfill & \le \parallel x_n-x_{n-1}{\parallel }^q-q\langle C_{A,\rho }^M\left(x_n\right)-C_{A,\rho }^M\left(x_{n-1}\right),J_q(x_n-x_{n-1})\rangle \hfill \\ \hfill & +k_q\parallel C_{A,\rho }^M\left(x_n\right)-C_{A,\rho }^M\left(x_{n-1}\right)\parallel \hfill \\ \hfill & =\parallel x_n-x_{n-1}{\parallel }^q-(q-k_q){\parallel C_{A,\rho }^M\left(x_n\right)-C_{A,\rho }^M\left(x_{n-1}\right)\parallel }^q\hfill \\ \hfill & \le \parallel x_n-x_{n-1}{\parallel }^q-(q-k_q){\lambda }_{C_1}^q{\parallel x_n-x_{n-1}\parallel }^q\hfill \\ \hfill & =\left(1-(q-k_q){\lambda }_{C_1}^q\right){\parallel x_n-x_{n-1}\parallel }^q.\hfill \end{array}$$

We have

$$\begin{array}{c}\hfill \parallel x_n-x_{n-1}-\left(C_{A,\rho }^M\left(x_n\right)-C_{A,\rho }^M\left(x_{n-1}\right)\right)\parallel \le \sqrt[q]{1-(q-k_q){\lambda }_{C_1}^q}\parallel x_n-x_{n-1}\parallel ,\end{array}$$

(19)

where ${\lambda }_{C_1}=\frac{2+{\lambda }_A\xi ({\alpha }_A\rho -1)}{\xi ({\alpha }_A\rho -1)}$.

Using (19), (18) becomes

$$\begin{array}{cc}\hfill & \parallel f_1\left(x_n-C_{A,\rho }^M\left(x_n\right),v_n\right)-f_1\left(x_{n-1}-C_{A,\rho }^M\left(x_{n-1}\right),v_{n-1}\right)\parallel \hfill \\ \hfill & \le {\lambda }_{f_1}^2{\lambda }_{D_{\tilde{T}}}\parallel y_n-y_{n-1}\parallel +\left({\lambda }_{f_1}^1\sqrt[q]{1-(q-k_q){\lambda }_{C_1}^q}\right)\parallel x_n-x_{n-1}\parallel .\hfill \end{array}$$

(20)

Combining (17) and (20), we obtain

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x_n\parallel & \le (1-{\alpha }_n)\parallel x_n-x_{n-1}\parallel +{\alpha }_n{P}_1\left(\theta \right){\lambda }_A\parallel x_n-x_{n-1}\parallel +{\alpha }_n{P}_1\left(\theta \right)\rho {\lambda }_{f_1}^2{\lambda }_{D_{\tilde{T}}}\parallel y_n-y_{n-1}\parallel \hfill \\ \hfill & +{\alpha }_n{P}_1\left(\theta \right)\rho \left({\lambda }_{f_1}^1\sqrt[q]{1-(q-k_q){\lambda }_{C_1}^q}\right)\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & =\left[(1-{\alpha }_n)+{\alpha }_n{P}_1\left(\theta \right){\lambda }_A+{\alpha }_n{P}_1\left(\theta \right)\rho \left({\lambda }_{f_1}^1\sqrt[q]{1-(q-k_q){\lambda }_{C_1}^q}\right)\right]\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & +{\alpha }_n{P}_1\left(\theta \right)\rho {\lambda }_{f_1}^2{\lambda }_{D_{\tilde{T}}}\parallel y_n-y_{n-1}\parallel .\hfill \end{array}$$

(21)

Applying (9) of scheme 3.1, Theorem 1 and Lipschitz continuity of B, we obtain

$$\begin{array}{cc}\hfill \parallel y_n-y_{n+1}\parallel & =\parallel \left[(1-{\beta }_n)y_n+{\beta }_n{R}_{B,\nu }^N[B\left(y_n\right)-\nu f_2\left(u_n,y_n-C_{B,\nu }^N\left(y_n\right)\right)]\right]\hfill \\ \hfill & -\left[(1-{\beta }_n)y_{n-1}+{\beta }_n{R}_{B,\nu }^N[B\left(y_{n-1}\right)-\nu f_2\left(u_{n-1},y_{n-1}-C_{B,\nu }^N\left(y_{n-1}\right)\right)]\right]\parallel \hfill \\ \hfill & =(1-{\beta }_n)\parallel y_n-y_{n-1}\parallel +{\beta }_n\parallel R_{B,\nu }^N\left[B\left(y_n\right)-\nu f_2\left(u_n,y_n-C_{B,\nu }^N\left(y_n\right)\right)\right]\hfill \\ \hfill & -R_{B,\nu }^N\left[B\left(y_{n-1}\right)-\nu f_2\left(u_{n-1},y_{n-1}-C_{B,\nu }^N\left(y_{n-1}\right)\right)\right]\parallel \hfill \\ \hfill & \le (1-{\beta }_n)\parallel y_n-y_{n-1}\parallel +{\beta }_n{P}_2\left(\theta \right)\parallel B\left(y_n\right)-B\left(y_{n-1}\right)-\nu \left(f_2\left(u_n,y_n-C_{B,\nu }^N\left(y_n\right)\right)\right.\hfill \\ \hfill & \left.-f_2\left(u_{n-1},y_{n-1}-C_{B,\nu }^N\left(y_{n-1}\right)\right)\right)\parallel \hfill \\ \hfill & \le (1-{\beta }_n)\parallel y_n-y_{n-1}\parallel +{\beta }_n{P}_2\left(\theta \right)\parallel B\left(y_n\right)-B\left(y_{n-1}\right)\parallel +{\beta }_n{P}_2\left(\theta \right)\nu \parallel f_2\left(u_n,y_n-C_{B,\nu }^N\left(y_n\right)\right)\hfill \\ \hfill & -f_2\left(u_{n-1},y_{n-1}-C_{B,\nu }^N\left(y_{n-1}\right)\right)\parallel \hfill \\ \hfill & \le (1-{\beta }_n)\parallel y_n-y_{n-1}\parallel +{\beta }_n{P}_2\left(\theta \right){\lambda }_B\parallel y_n-y_{n-1}\parallel \hfill \\ \hfill & +{\beta }_n{P}_2\left(\theta \right)\nu \parallel f_2\left(u_n,y_n-C_{B,\nu }^N\left(y_n\right)\right)-f_2\left(u_{n-1},y_{n-1}-C_{B,\nu }^N\left(y_{n-1}\right)\right)\parallel ,\hfill \end{array}$$

(22)

where $P_2\left(\theta \right)=\frac{1}{r}$.

Using Lipschitz continuity of $f_2$ in both the arguments, D-Lipschitz continuity of $\tilde{S}$ and Lipschitz continuity of the generalized Cayley operator $C_{B,\nu }^N$, we have

$$\begin{array}{cc}\hfill & \parallel f_2\left(u_n,y_n-C_{B,\nu }^N\left(y_n\right)\right)-f_2\left(u_{n-1},y_{n-1}-C_{B,\nu }^N\left(y_{n-1}\right)\right)\parallel \hfill \\ \hfill & =\parallel f_2\left(u_n,y_n-C_{B,\nu }^N\left(y_n\right)\right)-f_2\left(u_{n-1},y_n-C_{B,\nu }^N\left(y_n\right)\right)\hfill \\ \hfill & +f_2\left(u_{n-1},y_n-C_{B,\nu }^N\left(y_n\right)\right)-f_2\left(u_{n-1},y_{n-1}-C_{B,\nu }^N\left(y_{n-1}\right)\right)\parallel \hfill \\ \hfill & \le \parallel f_2\left(u_n,y_n-C_{B,\nu }^N\left(y_n\right)\right)-f_2\left(u_{n-1},y_n-C_{B,\nu }^N\left(y_n\right)\right)\parallel \hfill \\ \hfill & +\parallel f_2\left(u_{n-1},y_n-C_{B,\nu }^N\left(y_n\right)\right)-f_2\left(u_{n-1},y_{n-1}-C_{B,\nu }^N\left(y_{n-1}\right)\right)\parallel \hfill \\ \hfill & \le {\lambda }_{f_2}^1\parallel u_n-u_{n-1}\parallel +{\lambda }_{f_2}^2\parallel y_n-y_{n-1}-\left(C_{B,\nu }^N\left(y_n\right)-C_{B,\nu }^N\left(y_{n-1}\right)\right)\parallel \hfill \\ \hfill & \le {\lambda }_{f_2}^{1}D\left(\tilde{S}\left(x_n\right),\tilde{S}\left(x_{n-1}\right)\right)+{\lambda }_{f_2}^2\parallel y_n-y_{n-1}-\left(C_{B,\nu }^N\left(y_n\right)-C_{B,\nu }^N\left(y_{n-1}\right)\right)\parallel \hfill \\ \hfill & \le {\lambda }_{f_2}^1{\lambda }_{D_{\tilde{S}}}\parallel x_n-x_{n-1}\parallel +{\lambda }_{f_2}^2\parallel y_n-y_{n-1}-\left(C_{B,\nu }^N\left(y_n\right)-C_{B,\nu }^N\left(y_{n-1}\right)\right)\parallel .\hfill \end{array}$$

(23)

Applying the same technique as used for (19), we have

$$\begin{array}{c}\hfill \parallel y_n-y_{n-1}-\left(C_{B,\nu }^N\left(y_n\right)-C_{B,\nu }^N\left(y_{n-1}\right)\right)\parallel \le \sqrt[q]{1-(q-k_q){\lambda }_{C_2}^q}\parallel y_n-y_{n-1}\parallel ,\end{array}$$

(24)

where ${\lambda }_{C_2}=\frac{2+{\lambda }_{B}r}{r}$.

Combining (24) with (23), we have

$$\begin{array}{cc}\hfill & \parallel f_2\left(u_n,y_n-C_{B,\nu }^N\left(y_n\right)\right)-f_2\left(u_{n-1},y_{n-1}-C_{B,\nu }^N\left(y_{n-1}\right)\right)\parallel \hfill \\ \hfill & \le {\lambda }_{f_2}^1{\lambda }_{D_{\tilde{S}}}\parallel x_n-x_{n-1}\parallel +\left({\lambda }_{f_2}^2\sqrt[q]{1-(q-k_q){\lambda }_{C_2}^q}\right)\parallel y_n-y_{n-1}\parallel .\hfill \end{array}$$

(25)

Using (25) , (22) becomes

$$\begin{array}{cc}\hfill \parallel y_{n+1}-y_n\parallel & \le (1-{\beta }_n)\parallel y_n-y_{n-1}\parallel +{\beta }_n{P}_2\left(\theta \right){\lambda }_B\parallel y_n-y_{n-1}\parallel +{\beta }_n{P}_2\left(\theta \right)\nu {\lambda }_{f_2}^1{\lambda }_{D_{\tilde{S}}}\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & +{\beta }_n{P}_2\left(\theta \right)\nu \left({\lambda }_{f_2}^2\sqrt[q]{1-(q-k_q){\lambda }_{C_2}^q}\right)\parallel y_n-y_{n-1}\parallel \hfill \\ \hfill & =\left[(1-{\beta }_n)+{\beta }_n{P}_2\left(\theta \right){\lambda }_B+{\beta }_n{P}_2\left(\theta \right)\nu \left({\lambda }_{f_2}^2\sqrt[q]{1-(q-k_q){\lambda }_{C_2}^q}\right)\right]\parallel y_n-y_{n-1}\parallel \hfill \\ \hfill & +{\beta }_n{P}_2\left(\theta \right)\nu {\lambda }_{f_2}^1{\lambda }_{D_{\tilde{S}}}\parallel x_n-x_{n-1}\parallel .\hfill \end{array}$$

(26)

Adding (21) and (22), we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x_n\parallel +\parallel y_{n+1}-y_n\parallel & \le [(1-{\alpha }_n)+{\alpha }_n{\lambda }_A{P}_1\left(\theta \right)+{\alpha }_n{P}_1\left(\theta \right)\rho \left({\lambda }_{f_1}^1\sqrt[q]{1-(q-k_q){\lambda }_{C_1}^q}\right)\hfill \\ \hfill & +{\beta }_n{P}_2\left(\theta \right)\nu {\lambda }_{f_2}^1{\lambda }_{D_{\tilde{S}}}]\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & +[(1-{\beta }_n)+{\beta }_n{P}_2\left(\theta \right){\lambda }_B+{\beta }_n{P}_2\left(\theta \right)\nu \left({\lambda }_{f_2}^2\sqrt[q]{1-(q-k_q){\lambda }_{C_2}^q}\right)\hfill \\ \hfill & +{\alpha }_n{P}_1\left(\theta \right){\lambda }_{f_1}^2{\lambda }_{D_{\tilde{T}}}\rho ]\parallel y_n-y_{n-1}\parallel ,\hfill \\ \hfill & \le \xi \left(\theta \right)\left[\parallel x_n-x_{n-1}\parallel +\parallel y_n-y_{n-1}\parallel \right],\hfill \end{array}$$

(27)

where

$$\begin{array}{cc}\hfill \xi \left(\theta \right)=max\left\{\right[& (1-{\alpha }_n)+{\alpha }_n{\lambda }_A{P}_1\left(\theta \right)+{\alpha }_n{P}_1\left(\theta \right)\rho \left({\lambda }_{f_1}^1\sqrt[q]{1-(q-k_q){\lambda }_{C_1}^q}\right)+{\beta }_n{P}_1\left(\theta \right)\nu {\lambda }_{f_2}^1{\lambda }_{D_{\tilde{S}}}],\hfill \\ \hfill & \left[(1-{\beta }_n)+{\beta }_n{P}_2\left(\theta \right){\lambda }_B+{\beta }_n{P}_2\left(\theta \right)\nu \left({\lambda }_{f_2}^2\sqrt[q]{1-(q-k_q){\lambda }_{C_2}^q}\right)+{\alpha }_n{P}_2\left(\theta \right)\rho {\lambda }_{f_1}^2{\lambda }_{D_{\tilde{T}}}\right]\}.\hfill \end{array}$$

By conditions (12) and (14), it is clear that $\xi \left(\theta \right)<1$, and consequently (27) implies that $\left\{x_n\right\}$ and $\left\{y_n\right\}$ are both Cauchy sequences. Thus, there exists $x,y\in \tilde{E}$ such that $x_n\to x$ and $y_n\to y$, as $n\to \infty$. From (10) and (11) of scheme 3.1 and the D-Lipschitz continuity of $\tilde{S}$ and $\tilde{T}$, it follows that $\left\{u_n\right\}$ and $\left\{v_n\right\}$ are also Cauchy sequences in $\tilde{E}$. Thus, there exists $u,v\in \tilde{E}$ such that $u_n\to u$ and $v_n\to v$, as $n\to \infty$. It is also easy to show that $u\in \tilde{S}\left(x\right),v\in \tilde{T}\left(y\right)$, see [2]. By the continuity of all the operators involved in a system of generalized variational inclusions involving Cayley operators and an XOR-operation (5) and from Lemma 3, we conclude that

$$\begin{array}{cc}\hfill x& =R_{A,\rho }^M\left[A\left(x\right)\oplus \rho f_1\left(x-C_{A,\rho }^M\left(x\right),v\right)\right],\hfill \\ \hfill y& =R_{B,\nu }^N\left[B\left(x\right)-\nu f_2\left(u,y-C_{B,\nu }^N\left(y\right)\right)\right].\hfill \end{array}$$

Thus, the result follows. □

4. Example

In support of Theorem 2, we provide the following example.

Example 1.

Let $\tilde{E}=\mathbb{R}$ with the usual norm. Let $f_1,f_2:\tilde{E}\times \tilde{E}\to \tilde{E}$ be single-valued mappings such that

$$\begin{array}{c}\hfill f_1(x,y)=\frac{x}{9}+\frac{y}{11},\\ \hfill f_2(x,y)=\frac{x}{13}+\frac{y}{17}.\end{array}$$

(i) 

Then for any $x_1,x_2,y\in \tilde{E}$, we have

$$\begin{array}{cc}\hfill \parallel f_1(x_1,y)-f_1(x_2,y)\parallel & =∥\frac{x_1}{9}+\frac{y}{11}-\frac{x_2}{9}-\frac{y}{11}∥\hfill \\ \hfill & =\frac{1}{9}\parallel x_1-x_2\parallel \hfill \\ \hfill & \le \frac{1}{7}\parallel x_1-x_2\parallel ,\hfill \end{array}$$

that is, $f_1$ is Lipschitz continuous in the first argument with constant ${\lambda }_{f_1}^1=\frac{1}{7}$. it is easy to show that $f_1$ is Lipschitz continuous in the second argument with constant ${\lambda }_{f_1}^2=\frac{1}{9}$.In the same manner one can show that $f_2$ is Lipschitz continuous in both the arguments with constants ${\lambda }_{f_2}^1=\frac{1}{11}$ and ${\lambda }_{f_2}^2=\frac{1}{15}$, respectively.

(ii) 

Suppose that $\tilde{S},\tilde{T}:\tilde{E}\to C\left(\tilde{E}\right)$ are the multi-valued mappings defined as:

$$\begin{array}{c}\hfill \tilde{S}\left(x\right)=\left\{\frac{x}{9}\right\},\\ \hfill \tilde{T}\left(x\right)=\left\{\frac{x}{11}\right\}.\end{array}$$

Now,

$$\begin{array}{cc}\hfill D\left(\tilde{S}\left(x\right),Also\tilde{S}\left(y\right)\right)& \le max\left\{∥\frac{x}{9}-\frac{y}{9}∥,∥\frac{y}{9}-\frac{x}{9}∥\right\}\hfill \\ \hfill & =\frac{1}{9}max\left\{\parallel x-y\parallel ,\parallel y-x\parallel \right\}\hfill \\ \hfill & \le \frac{1}{5}\parallel x-y\parallel .\hfill \end{array}$$

Clearly, $\tilde{S}$ is D-Lipschitz continuous with constant ${\lambda }_{D_{\tilde{S}}}=\frac{1}{5}$. Similarly, it can be shown that $\tilde{T}$ is D-Lipschitz continuous with constant ${\lambda }_{D_{\tilde{T}}}=\frac{1}{7}$.

• Let $A,B:\tilde{E}\to \tilde{E}$ be the single-valued mappings such that

  $$\begin{array}{c}\hfill A\left(x\right)=\frac{x}{3}\\ \hfill andB\left(x\right)=\frac{x}{2}.\end{array}$$

Clearly, A is Lipschitz continuous mapping with constant ${\lambda }_A=\frac{2}{3}$ and B is Lipschitz continuous mapping with constant ${\lambda }_B=\frac{2}{3}$. In addition, A is ξ-ordered non-extended mapping with constant $\xi =\frac{1}{3}$, and B is strongly accretive with constant $r=1$.

(iii) 

Let $M,N:\tilde{E}\to 2^{\tilde{E}}$ be the multi-valued mappings such that

$$\begin{array}{cc}\hfill M\left(x\right)& =\left\{4x\right\},\hfill \\ \hfill N\left(x\right)& =\left\{x\right\}.\hfill \end{array}$$

For $\rho =3$, it is clear that M is $({\alpha }_A,\rho )$-weak ANODD mapping with ${\alpha }_A=4$, and N is B-accretive mapping.

(iv) 

In view of the above calculations, we obtain the resolvent operators $R_{A,\rho }^M$ and $R_{B,\nu }^N$ such that

$$\begin{array}{cc}\hfill R_{A,\rho }^M\left(x\right)& ={\left[A+\rho M\right]}^{-1}\left(x\right)=\frac{3}{37}xand\hfill \\ \hfill R_{B,\nu }^N\left(x\right)& ={\left[B+\nu N\right]}^{-1}\left(x\right)=\frac{2}{3}x,\hfill \end{array}$$

where $\rho =3$ and $\nu =1$.

The resolvent operator $R_{A,\rho }^M$ satisfies the condition (1) that is

$$\begin{array}{cc}\hfill R_{A,\rho }^M\left(x\right)+R_{A,\rho }^M\left(y\right)& =\frac{3}{3}7x\oplus \frac{3}{37}y\hfill \\ \hfill & =\frac{3}{37}(x\oplus y)\hfill \\ \hfill & \le \frac{5}{37}(x\oplus y).\hfill \end{array}$$

The resolvent operator $R_{B,\nu }^N$ satisfies the condition (3) for $r=1$; that is

$$\begin{array}{cc}\hfill \parallel R_{B,\nu }^N\left(x\right)-R_{B,\nu }^N\left(y\right)\parallel & =∥\frac{2}{3}x-\frac{2}{3}y∥\hfill \\ \hfill & \le \parallel x-y\parallel .\hfill \end{array}$$

(v) 

Using the values of $R_{A,\rho }^M$ and $R_{B,\nu }^N$ calculated in step (v), we obtain the generalized Cayley operators as:

$$\begin{array}{cc}\hfill C_{A,\rho }^M\left(x\right)& =\frac{-19}{111}xand\hfill \\ \hfill C_{B,\nu }^N\left(x\right)& =\frac{5}{6}x,wherex\in \mathbb{R}.\hfill \end{array}$$

We calculate ${\lambda }_{C_1}$ and ${\lambda }_{C_2}$ below:

$$\begin{array}{cc}\hfill {\lambda }_{C_1}& =\frac{2+{\lambda }_A\xi ({\alpha }_A\rho -1)}{\xi (\alpha \rho -1)}=\frac{40}{33}and\hfill \\ \hfill {\lambda }_{C_2}& =\frac{2+{\lambda }_{B}r}{r}=\frac{8}{3}.\hfill \end{array}$$

It is easy to check that the generalized Cayley operator $C_{A,\rho }^M$ satisfies condition (2) and the generalized Cayley operator $C_{B,\nu }^N$ satisfies condition (4) with the above calculated ${\lambda }_{C_1}$ and ${\lambda }_{C_2}$, respectively.

(vi) 

For $P_1\left(\theta \right)=\frac{3}{11},P_2\left(\theta \right)=1,q=3,k_q=3,{\alpha }_n=\frac{3}{4}$ and ${\beta }_n=\frac{1}{3}$, the conditions (12) and (13) of Theorem 2 are fulfilled.

Thus, all the conditions of Theorem 2 are satisfied and the system of generalized variational inclusions involving Cayley operators and an XOR-operation admits a solution $(x,y,u,v)$. Consequently, the sequences $\left\{x_n\right\},\left\{y_n\right\},\left\{u_n\right\}$ and $\left\{v_n\right\}$ converge strongly to $x,y,u$ and v, respectively.

5. Conclusions

This study is focussed on a system of generalized variational inclusions involving Cayley operators and an XOR-operation in q-uniformly smooth Banach spaces. It is well known that variational inclusions, Cayley operators as well as an XOR-operation have applications in all modern sciences and technologies. That is why we have considered and studied a system of generalized variational inclusions involving Cayley operators and an XOR-operation. An existence and convergence result is proved for the system of generalized variational inclusions involving Cayley operators and an XOR-operation in q-uniformly smooth Banach spaces. An example is provided for illustration.