Inference for a Progressive-Stress Model Based on Ordered Ranked Set Sampling under Type-II Censoring

Abstract

The progressive-stress accelerated life test is discussed under the ordered ranked set sampling procedure. It is assumed that the lifetime of an item under use stress is exponentially distributed and the law of inverse power is considered as the relationship between the scale parameter and the applied stress. The involved parameters are estimated using the Bayesian technique, under symmetric and asymmetric loss functions, based on ordered ranked set samples and simple random samples subject to type-II censoring. Real and simulated data sets are used to illustrate the theoretical results presented in this paper. Finally, a simulation study followed by numerical calculations is performed to evaluate the Bayesian estimation performance based on the two sampling types.

1. Introduction

With the continuous advancement in manufacturing technologies, lifetime testing experiments, and reliability engineering studies, modern products are produced and developed to work under normal operating conditions without failure for a lengthy interval of time. Therefore, manufacturers find it hard to provide enough details about the failure times for their products when implementing conventional life research experiments. Therefore, accelerated life tests (ALTs) are implemented to acquire enough details for a highly reliable products in short times, as well as to determine the relationship between different stress variables and product lifetimes. In such experiments, products are tested under stresses that are more extreme than those under normal conditions. The details obtained from the experiment under accelerated conditions are often used to estimate the product’s performance under normal conditions. The widely used ways by which stress can be used are constant-stress, step-stress, and progressive-stress. Many authors discussed progressive-stress ALTs considering that the used stress is described as a linearly increasing function of time. For more details on ALTs, see, for example, [1,2,3,4,5,6,7,8,9].

In 1952, McIntyre [10] suggested the ranked set sampling to obtain a more effective approach for calculating mean pasture yield. Takahashi and Wakimoto [11] improved and built a theoretical basis for this approach when calculating the population mean. It may be used to optimize the cost efficiency of choosing sample units for a test or a study. It is often recommended when the operation of measuring sample units is very difficult or costly, but the ordering of sample units could be inexpensive and easy. It is applied in many fields such as biological, agricultural, ecological, medical, engineering, and social studies, see, for example, [12]. The importance of ranked set sampling and its applications in many of the previously mentioned areas motivate us to consider it in our study.

To obtain a ranked set sample (RSS) of size n from the given population, the following steps could be applied:

• Select from the given population $n^2$ units and split them into n simple random samples (SRSs), all of the size n.
• For each sample, rank the units without practical measurement. Different methods may be used to obtain this ranking such as personal professional judgment, expert opinion, available helpful information, or any other information.
• In all of the ordered samples, one and only one unit is measured.
• A sample is selected for actual quantification as follows: In the first sample, the smallest unit, say $Y_{11}$, is measured and the remaining units are not measured. In the second sample, only the second smallest unit, say $Y_{22}$, is measured. This technique continues in the same style until the largest unit, say $Y_{nn}$, of the last sample, is measured.
• The process mentioned above is called a one-cycle RSS of size n and the obtained data are indicated by ${\mathrm{Y}}_{RSS}=\{Y_{11},Y_{22},\dots ,Y_{nn}\}$. Notice that $Y_{11},Y_{22},\dots ,Y_{nn}$ are independent and non-identically distributed (INID) random variables.
• Repeat the above step ℏ cycles to obtain an RSS of size $\hslash n$. The obtained data are indicated by ${\mathrm{Y}}_{(\hslash )RSS}=\{Y_{1,11},Y_{1,22},\dots ,Y_{1,nn},\dots \dots ,Y_{\hslash ,11},Y_{\hslash ,22},\dots ,Y_{\hslash ,nn}\}$.

Based on the concept of order statistics from INID random variables, Balakrishnan and Li [13] suggested the ordered RSS (ORSS) which can be obtained by arranging the RSS, $\{Y_{11},Y_{22},\dots ,Y_{nn}\}$, in increasing order of magnitude. They proved that the ORSS is very much more efficient than SRS.

Some authors have studied the prediction and estimation problems based on the ORSS of different distributions. Li and Balakrishnan [14], based on ORSSs, developed the best linear unbiased estimators of parameters of a simple linear regression model for normal data. Salehi et al. [15] discussed the distribution-free prediction intervals for future order statistics and record values based on ORSS. Mohie El-Din et al. [16] and Kotb and Raqab [17] studied Bayesian estimation of the model parameters for Pareto and Rayleigh distributions as well as two-sample Bayesian prediction of the unobserved data based on SRS and ORSS under type-II censoring scheme. Kotb and Raqab [18], and Kotb and Mohie El-Din [19] discussed estimation of the model parameters considering step-stress ALT data from exponential and Rayleigh distributions based on SRS and ORSS under type-I censoring scheme.

In this article, based on type-II censored SRS and ORSS, we discuss the Bayesian estimation, using symmetric and asymmetric loss functions (LFs), based on progressive-stress ALT data from an exponential distribution (ED).

The remaining parts of the article are regulated as follows: Section 2 describes the ORSS under the progressive-stress model. The Bayesian estimation based on ORSS and SRS under type-II censoring is investigated in Section 3 and Section 4, respectively. Section 5 presents illustrative examples. Simulation studies followed by conclusions are given in Section 6 and Section 7, respectively.

2. Model Description

Due to the simplicity and ease of mathematical manipulations, the ED is considered one of the distributions most used in reliability studies and lifetime testing experiments, as it provides simple, excellent, and closed-form solutions to several problems. As one of its applications in electrical and mechanical engineering, the ED has been used to describe the lifetimes of electric circuits and semiconductors.

Presume that the random variable Y represents the lifetime of a unit under normal use conditions and subject to ED with scale parameter $\delta >0$. Then the cumulative distribution function (CDF) and probability density function (PDF) of Y are given, respectively, by

$$G\left(y\right)=1-\exp \left[-\frac{y}{\delta }\right],y>0,$$

(1)

$$g\left(y\right)=\frac{1}{\delta }\exp \left[-\frac{y}{\delta }\right],y>0.$$

(2)

2.1. Cumulative Exposure Model

The cumulative exposure model (CEM) links the distribution under accelerated stress to that under normal stress. If the applied stress $\mathcal{V}$ is a function of time, $\mathcal{V}=\mathcal{V}\left(y\right)$, and affects the scale parameter $\delta$ of the underlying distribution, then $\delta$ becomes a function of time, $\delta \left(y\right)=\delta \left(\mathcal{V}\right(y\left)\right)$. Hence, the CEM, $\varpi \left(y\right)$, can be written as (see [2]),

$$\varpi \left(y\right)={\int }_0^y\frac{\mathrm{d}u}{\delta \left(\mathcal{V}\right(u\left)\right)}.$$

(3)

The CDF under progressive-stress is given by

$$F\left(y\right)=G\left(\varpi \right(y\left)\right),$$

(4)

where $G(.)$ is the supposed CDF with scale parameter equal to 1.

2.2. Basic Assumptions

• Under normal use stress, the lifetime of a unit is subject to ED with CDF (1).
• The law of inverse power regulates the relationship between the applied stress $\mathcal{V}$ and the scale parameter $\delta$ in CDF (1), i.e.

  $${\displaystyle \delta \left(y\right)=\delta \left(\mathcal{V}\left(y\right)\right)=\frac{1}{\alpha {\left[\mathcal{V}\left(y\right)\right]}^{\gamma }},}$$

  where $\alpha$ and $\gamma$ are two positive parameters to be estimated.
• The stress $\mathcal{V}\left(y\right)$ is a linear increasing function of time y, i.e.,

  $$\mathcal{V}\left(y\right)=ky,k>0.$$
• During the testing process, the N units to be tested are split into $\mathfrak{D}$($>1$) groups, each consisting of n units and operating under progressive-stress. Thus,

  $${\mathcal{V}}_j\left(y\right)=k_{j}y,j=1,\dots ,\mathfrak{D},k_1<k_2<\dots <k_{\mathfrak{D}}.$$
• For $j=1,\dots ,\mathfrak{D}$, the n failure times in group j, denoted by $Y_{j,1}$, $Y_{j,2}$, ⋯, $Y_{j,n}$ (with realizations $y_{j,1}$, $y_{j,2}$, ⋯, $y_{j,n}$) are statistically independent random variables.
• Under any stress level, the unit failure mechanisms are the same.

Using Assumptions 2 and 4, CEM (3) can be rewritten as follows:

$${\varpi }_j\left(y\right)=\frac{\alpha k_j^{\gamma }{y}^{\gamma +1}}{\gamma +1},j=1,\dots ,\mathfrak{D}.$$

(5)

From (1), CDF (4) under progressive-stress for a unit in group $j,j=1,\dots ,\mathfrak{D},$ is given by

$$F_j\left(y\right)=1-\exp \left[{\displaystyle -\frac{\alpha k_j^{\gamma }}{\gamma +1}{y}^{\gamma +1}}\right],y>0,(\alpha ,\gamma )>0.$$

(6)

Notice that CDF (6) is the CDF of a Weibull distribution with scale parameter ${\displaystyle \left(\frac{\gamma +1}{\alpha k_j^{\gamma }}\right)}$ and shape parameter $(\gamma +1)$.

The PDF corresponding to (6) is given by

$$f_j\left(y\right)=\alpha k_j^{\gamma }{y}^{\gamma }\exp \left[{\displaystyle -\frac{\alpha k_j^{\gamma }}{\gamma +1}{y}^{\gamma +1}}\right],y>0.$$

(7)

2.3. RSS under Progressive-Stress ALT

To obtain an RSS of size N under progressive-stress ALT with $\mathfrak{D}$($>1$) levels of stress, the following algorithm can be followed:

• Choose fixed values of N, $\mathfrak{D}$, and n, such that $\mathfrak{D}\times n=N$.
• Select, from the given population, $\mathfrak{D}{n}^2$ units and split them into $\mathfrak{D}n$ SRSs, all of the size n.
• Set $i=1$.
• As shown previously in Section 1, the N units to be tested are split into $\mathfrak{D}$($>1$) groups, each consisting of an SRS of size n units and operating under progressive-stress with stress level ${\mathcal{V}}_j\left(y\right),j=1,\dots ,\mathfrak{D}$.
• Order, without practical measurement, the selected SRS of size n units presented in each group.
• One and only one unit is measured in the j-th ordered SRS, $j=1,\dots ,\mathfrak{D}$.
• In group j, the i-th smallest unit, say $Y_{j,ii},j=1,\dots ,\mathfrak{D}$, is measured.
• Set $i=i+1$. If $i=n+1$, then stop the above procedure and go to Step 10. Otherwise, in group j the $(i+1)$-th smallest unit, say $Y_{j,i+1i+1},j=1,\dots ,\mathfrak{D}$, is measured.
• Repeat Steps 4–8.
• By this manner we obtain an RSS of size N under progressive-stress ALT, see Figure 1.
  

  Figure 1. A ranked set sampling procedure under progressive-stress ALT with $\mathfrak{D}$($>1$) levels of stress.
• The procedure given above is named one-cycle RSS of size N under progressive-stress ALT and the data obtained in this manner are indicated by

  $$\begin{array}{cccc}{\mathbf{Y}}_{RSS}=\{Y_{1,11},& Y_{2,11}& \dots ,& Y_{\mathfrak{D},11},\\ Y_{1,22},& Y_{2,22},& \dots ,& Y_{\mathfrak{D},22},\\ ⋮& ⋮& ⋮& ⋮\\ Y_{1,nn},& Y_{2,nn},& \dots ,& Y_{\mathfrak{D},nn}\}.\end{array}$$
  Notice that, for example, $Y_{2,33}$, means the third smallest unit in the third sample presented in the second group. Moreover, the elements of the RSS are INID.
• Repeat Steps 2–9, ℏ cycles to obtain an RSS of size $\hslash N$ and the obtained data are indicated by

  $$\begin{array}{cc}& {\mathbf{Y}}_{(\hslash )RSS}=\hfill \\ & \{\{Y_{1,1,11},Y_{1,2,11},\dots ,Y_{1,\mathfrak{D},11}\},\{Y_{1,1,22},Y_{1,2,22},\dots ,Y_{1,\mathfrak{D},22}\},\dots ,\{Y_{1,1,nn},Y_{1,2,nn},\dots ,Y_{1,\mathfrak{D},nn}\},\hfill \\ & ⋮⋮⋮\hfill \\ & \{Y_{\hslash ,1,11},Y_{\hslash ,2,11},\dots ,Y_{\hslash ,\mathfrak{D},11}\},\{Y_{\hslash ,1,22},Y_{\hslash ,2,22},\dots ,Y_{\hslash ,\mathfrak{D},22}\},\dots ,\{Y_{\hslash ,1,nn},Y_{\hslash ,2,nn},\dots ,Y_{\hslash ,\mathfrak{D},nn}\}\}.\hfill \end{array}$$

Suppose that ${\mathbf{Y}}_{RSS}$ is a one-cycle RSS from a population under progressive-stress ALT with CDF (6) and PDF (7). Then, the CDF and PDF of $Y_{j,rr},j=1,\dots ,\mathfrak{D}$, indicated by $F_{j,r:n}$ and $f_{j,r:n}$, are in fact the CDF and PDF of the r-th order statistic of group j. They take the following forms (see [20,21]),

$$\begin{array}{c}\hfill F_{j,r:n}\left(y\right)=\sum _{l=r}^n\left(\genfrac{}{}{0pt}{}{n}{l}\right){\left[F_j\left(y\right)\right]}^l{[1-F_j\left(y\right)]}^{n-l},\end{array}$$

(8)

$$\begin{array}{c}\hfill f_{j,r:n}\left(y\right)=r\left(\genfrac{}{}{0pt}{}{n}{r}\right){\left[F_j\left(y\right)\right]}^{r-1}{[1-F_j\left(y\right)]}^{n-r}{f}_j\left(y\right),\end{array}$$

(9)

where $F_j\left(y\right)$ and $f_j\left(y\right)$ are given by (6) and (7), respectively.

PDF (9) and CDF (8) can be rewritten as

$$\begin{array}{c}\hfill f_{j,r:n}\left(y\right)=\sum _{l=0}^{r-1}{b}_{l,r}\left(n\right){[1-F_j\left(y\right)]}^{n+l-r}{f}_j\left(y\right),\end{array}$$

(10)

$$\begin{array}{c}\hfill F_{j,r:n}\left(y\right)=1-\sum _{l=1}^r{b}_{l,r}^{*}\left(n\right){[1-F_j\left(y\right)]}^{n+l-r},\end{array}$$

(11)

where

$$\left.\begin{array}{cc}\hfill b_{l,r}\left(n\right)& ={(-1)}^{l}r\left(\genfrac{}{}{0pt}{}{r-1}{l}\right)\left(\genfrac{}{}{0pt}{}{n}{r}\right),\hfill \\ \hfill b_{l,r}^{*}\left(n\right)& {\displaystyle =\frac{b_{l-1,r}\left(n\right)}{n+l-r}.}\hfill \end{array}\right\}$$

(12)

3. Bayes Estimation Based on ORSS under Progressive-Stress ALT

Censoring has a significant role in reliability and lifetime experiments where the experimenters are unable to monitor the lifetimes of all experiment units. Moreover, it is important in saving time and cost, which are considered practical aspects for the experimenters. Types-I and -II censoring are two generally applied censoring schemes. In this section, we investigate the Bayes estimation of the model parameters based on the ORSS (one-cycle and ℏ-cycle) and SRS when the observed failure data are type-II censored under progressive-stress ALT, considering the symmetric (squared error (SE)) and asymmetric (general entropy (GE) and linear-exponential (LINEX)) loss functions (LFs).

Under progressive-stress ALT, the type-II censored ordered one-cycle RSS can be obtained as follows: After assigning the RSS for group j, $\{Y_{j,11},Y_{j,22},\dots ,Y_{j,nn}\}$, $j=1,\dots ,\mathfrak{D}$, assign the first m order statistics in it, say $\{T_{j,1}\le T_{j,2}\le \dots \le T_{j,m}\}$, where, for example, $T_{j,1}=\min (Y_{j,11},Y_{j,22},\dots ,Y_{j,nn})$. The data obtained from this operation are called type-II one-cycle ORSS and are denoted by ${\mathbf{T}}_{ORSS}=\{\{T_{1,1}\le T_{1,2}\le \dots \le T_{1,m}\},\dots \dots ,\{T_{\mathfrak{D},1}\le T_{\mathfrak{D},2}\le \dots \le T_{\mathfrak{D},m}\}\}.$ Based on an idea due to Balakrishnan [22] for order statistics from INID random variables, the likelihood function for one-cycle ORSS under type-II censoring is then given by

$$\begin{array}{cc}\hfill \mathbb{L}(\alpha ,\gamma ;\mathbf{T}=\mathbf{t})\propto & \prod _{j=1}^{\mathfrak{D}}\left[\sum _{S\left[j\right]}\prod _{r=1}^m{f}_{j,i_{j,r}}\left(t_{j,r}\right)\prod _{r=m+1}^n[1-F_{j,i_{j,r}}\left(t_{j,m}\right)]\right],\hfill \end{array}$$

(13)

where $\mathbf{t}=({\mathbf{t}}_1,\dots ,{\mathbf{t}}_{\mathfrak{D}})$, ${\mathbf{t}}_j=(t_{j,1},\dots ,t_{j,m}),j=1,\dots ,\mathfrak{D}$, and ${\sum }_{S\left[j\right]}$ indicates the summation over all $n!$ permutations $(i_{j,1},i_{j,2},...,i_{j,n})$ of $(1,2,...,n)$. From (13), we can rewrite the likelihood function as follows

$$\begin{array}{cc}\hfill \mathbb{L}(\alpha ,\gamma ;\mathbf{t})\propto & \prod _{j=1}^{\mathfrak{D}}\mathrm{Per}{\mathsf{\Omega }}_{\mathbf{j}},\hfill \end{array}$$

(14)

where $\mathrm{Per}{\mathsf{\Omega }}_{\mathbf{j}}={\sum }_{S\left[j\right]}{\prod }_{r=1}^n{a}_{r,i_{j,r}}$ indicates the permanency of a square real matrix ${\mathsf{\Omega }}_{\mathbf{j}}=\left(a_{i,r}\right)$ of size $n\times n$,

$${\mathsf{\Omega }}_{\mathbf{j}}=\left(\begin{array}{ccccc}\hfill f_{j,1}\left(t_{j,1}\right)& f_{j,2}\left(t_{j,1}\right)& \dots \hfill & f_{j,n}\left(t_{j,1}\right)& \\ \hfill ⋮& ⋮& \ddots \hfill & ⋮& \\ \hfill f_{j,1}\left(t_{j,m}\right)& f_{j,2}\left(t_{j,m}\right)& \dots \hfill & f_{j,n}\left(t_{j,m}\right)& \\ \hfill 1-F_{j,1}\left(t_{j,m}\right)& 1-F_{j,2}\left(t_{j,m}\right)& \dots \hfill & 1-F_{j,n}\left(t_{j,m}\right)\end{array}\right)\begin{array}{c}\\ \\ \\ \}(n-m)\mathrm{rows}.\end{array}$$

By substituting PDF (10) and CDF (11) in (13), the likelihood function can take the following form:

$$\begin{array}{cc}\hfill \mathbb{L}(\alpha ,\gamma ;\mathbf{t})\propto & \prod _{j=1}^{\mathfrak{D}}\left[\sum _{S\left[j\right]}\right(\prod _{r=1}^m\sum _{l=0}^{i_{j,r}-1}{b}_{l,i_{j,r}}\left(n\right){[1-F_j\left(t_{j,r}\right)]}^{n+l-i_{j,r}}{f}_j\left(t_{j,r}\right)\hfill \\ \hfill & .\prod _{r=m+1}^n\sum _{l=1}^{i_{j,r}}{b}_{l,i_{j,r}}^{*}\left(n\right){[1-F_j\left(t_{j,m}\right)]}^{n+l-i_{j,r}}\left)\right].\hfill \end{array}$$

(15)

Based on CDF (6) and PDF (7) and using the following relations

$$\left.\begin{array}{cc}\hfill \prod _{r=1}^m\sum _{l=0}^{i_{j,r}-1}{\mathbf{Y}}_l\left(i_{j,r}\right)& =\sum _{{\xi }_{j,1}=0}^{i_{j,1}-1}\sum _{{\xi }_{j,2}=0}^{i_{j,2}-1}\dots \sum _{{\xi }_{j,m}=0}^{i_{j,m}-1}\prod _{r=1}^m{\mathbf{Y}}_{{\xi }_{j,r}}\left(i_{j,r}\right),\hfill \\ \hfill \prod _{r=m+1}^n\sum _{l=1}^{i_{j,r}}{\mathbf{Y}}_l^{*}\left(i_{j,r}\right)& =\sum _{{\eta }_{j,m+1}=1}^{i_{j,m+1}}\sum _{{\eta }_{j,m+2}=1}^{i_{j,m+2}}\dots \sum _{{\eta }_{j,n}=1}^{i_{j,n}}\prod _{r=m+1}^n{\mathbf{Y}}_{{\eta }_{j,r}}^{*}\left(i_{j,r}\right),\hfill \end{array}\right\}$$

(16)

the likelihood function takes the following form

$$\begin{array}{cc}\hfill \mathbb{L}(\alpha ,\gamma ;\mathbf{t})\propto & \prod _{j=1}^{\mathfrak{D}}\left[\sum _{S\left[j\right]}\sum _{{\mathit{\xi }}_j,{\mathit{\eta }}_j}^{m,n}\left(A_{{\mathit{\xi }}_j,{\mathit{\eta }}_j}\left({\mathit{i}}_j\right)\left[\prod _{r=1}^m\alpha k_j^{\gamma }{t}_{j,r}^{\gamma }\right]\exp \left[-\frac{\alpha k_j^{\gamma }}{\gamma +1}{\mathsf{\Psi }}_{{\mathit{\xi }}_j,{\mathit{\eta }}_j}\left({\mathbf{t}}_j\right)\right]\right)\right],\hfill \end{array}$$

(17)

where ${\mathit{i}}_j=(i_{j,1},\dots ,i_{j,m},i_{j,m+1},\dots ,i_{j,n})$, ${\mathbf{\xi }}_j=({\xi }_{j,1},\dots ,{\xi }_{j,m})$, ${\mathbf{\eta }}_j=({\eta }_{j,m+1},\dots ,{\eta }_{j,n})$, $j=1,\dots ,\mathfrak{D}$, and

$$\begin{array}{c}\hfill \sum _{{\xi }_j,{\eta }_j}^{m,n}=\sum _{{\xi }_{j,1}=0}^{i_{j,1}-1}\sum _{{\xi }_{j,2}=0}^{i_{j,2}-1}\dots \sum _{{\xi }_{j,m}=0}^{i_{j,m}-1}·\sum _{{\eta }_{j,m+1}=1}^{i_{j,m+1}}\sum _{{\eta }_{j,m+2}=1}^{i_{j,m+2}}\dots \sum _{{\eta }_{j,n}=1}^{i_{j,n}},\end{array}$$

(18)

$$\begin{array}{c}\hfill A_{{\mathbf{\xi }}_j,{\mathbf{\eta }}_j}\left({\mathit{i}}_j\right)=\left[\prod _{r=1}^m{b}_{{\xi }_{j,r},i_{j,r}}\left(n\right)\right]\left[\prod _{r=m+1}^n{b}_{{\eta }_{j,r},i_{j,r}}^{*}\left(n\right)\right],\end{array}$$

(19)

$$\begin{array}{c}\hfill {\mathsf{\Psi }}_{{\mathbf{\xi }}_j,{\mathbf{\eta }}_j}\left({\mathbf{t}}_j\right)=\left[\sum _{r=1}^m(n+{\xi }_{j,r}-i_{j,r}+1)t_{j,r}^{\gamma +1}\right]+\left[\sum _{r=m+1}^n(n+{\eta }_{j,r}-i_{j,r})t_{j,m}^{\gamma +1}\right].\end{array}$$

(20)

Using the relations given in (16), the likelihood function can be rewritten as

$$\begin{array}{cc}\hfill \mathbb{L}(\alpha ,\gamma ;\mathbf{t})\propto & \sum _{{\mathit{S}}^{*},{\mathbf{\xi }}^{*},{\mathbf{\eta }}^{*}}^{\mathfrak{D},m,n}\left(\left[\prod _{j=1}^{\mathfrak{D}}{A}_{{\mathbf{\xi }}_j,{\mathbf{\eta }}_j}\left({\mathit{i}}_j\right)\right]\left[\prod _{j=1}^{\mathfrak{D}}\prod _{r=1}^m\alpha k_j^{\gamma }{t}_{j,r}^{\gamma }\right]\exp \left[-\sum _{j=1}^{\mathfrak{D}}\frac{\alpha k_j^{\gamma }}{\gamma +1}{\mathsf{\Psi }}_{{\mathbf{\xi }}_j,{\mathbf{\eta }}_j}\left({\mathbf{t}}_j\right)\right]\right),\hfill \end{array}$$

(21)

where ${\mathit{S}}^{*}=(S\left[1\right],\dots ,S\left[\mathfrak{D}\right])$, ${\mathbf{\xi }}^{*}=({\mathbf{\xi }}_1,\dots ,{\mathbf{\xi }}_{\mathfrak{D}})$, ${\mathbf{\xi }}_j=({\xi }_{j,1},\dots ,{\xi }_{j,m})$, ${\mathbf{\eta }}^{*}=({\mathbf{\eta }}_1,\dots ,{\mathbf{\eta }}_{\mathfrak{D}})$, ${\eta }_j=({\eta }_{j,m+1},\dots ,{\eta }_{j,n})$, $j=1,\dots ,\mathfrak{D}$, and

$$\begin{array}{c}\hfill \sum _{{\mathit{S}}^{*},{\mathbf{\xi }}^{*},{\mathbf{\eta }}^{*}}^{\mathfrak{D},m,n}=\prod _{j=1}^{\mathfrak{D}}\sum _{S\left[j\right]}\sum _{{\mathbf{\xi }}_j,{\mathbf{\eta }}_j}^{m,n}=\sum _{S\left[1\right]}\sum _{{\mathbf{\xi }}_1,{\mathbf{\eta }}_1}^{m,n}\dots \sum _{S\left[\mathfrak{D}\right]}\sum _{{\xi }_{\mathfrak{D}},{\eta }_{\mathfrak{D}}}^{m,n},\end{array}$$

(22)

where ${\sum }_{{\xi }_j,{\eta }_j}^{m,n}$ is given by (18).

For ℏ-cycle ORSS, the likelihood function under type-II censoring is then given by

$$\begin{array}{cc}\hfill \mathbb{L}(\alpha ,\gamma ;\mathbf{t})\propto & \prod _{q=1}^{\hslash }\left[\sum _{{\mathit{S}}_q^{*},{\xi }_q^{*},{\eta }_q^{*}}^{\mathfrak{D},m,n}\right(\left[\prod _{j=1}^{\mathfrak{D}}{A}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathit{i}}_{q,j}\right)\right]\left[\prod _{j=1}^{\mathfrak{D}}\prod _{r=1}^m\alpha k_j^{\gamma }{t}_{q,j,r}^{\gamma }\right]\hfill \\ \hfill & ·\exp \left[-\sum _{j=1}^{\mathfrak{D}}\frac{\alpha k_j^{\gamma }}{\gamma +1}{\mathsf{\Psi }}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathbf{t}}_{q,j}\right)\right]\left)\right].\hfill \end{array}$$

(23)

Using the relations given in (16), the likelihood function can be rewritten as

$$\begin{array}{cc}\hfill \mathbb{L}(\alpha ,\gamma ;\mathbf{t})\propto & \sum _{{\mathit{S}}^{**},{\mathbf{\xi }}^{**},{\mathbf{\eta }}^{**}}^{\mathfrak{D},m,n}(\left[\prod _{q=1}^{\hslash }\prod _{j=1}^{\mathfrak{D}}{A}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathit{i}}_{q,j}\right)\right]{\alpha }^{\hslash \mathfrak{D}m}{\mathsf{\Lambda }}^{\gamma }\hfill \\ \hfill & ·\exp \left[-\sum _{q=1}^{\hslash }\sum _{j=1}^{\mathfrak{D}}\frac{\alpha k_j^{\gamma }}{\gamma +1}{\mathsf{\Psi }}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathbf{t}}_{q,j}\right)\right]),\hfill \end{array}$$

(24)

where

$$\begin{array}{c}\hfill \mathsf{\Lambda }=\prod _{q=1}^{\hslash }\prod _{j=1}^{\mathfrak{D}}\prod _{r=1}^m{k}_j{t}_{q,j,r},\end{array}$$

(25)

$$\begin{array}{c}\hfill \sum _{{\mathit{S}}^{**},{\xi }^{**},{\eta }^{**}}^{\mathfrak{D},m,n}=\prod _{q=1}^{\hslash }\sum _{{\mathit{S}}_q^{*},{\xi }_q^{*},{\eta }_q^{*}}^{\mathfrak{D},m,n}=\sum _{{\mathit{S}}_1^{*},{\xi }_1^{*},{\eta }_1^{*}}^{\mathfrak{D},m,n}\dots \sum _{{\mathit{S}}_{\hslash }^{*},{\xi }_{\hslash }^{*},{\eta }_{\hslash }^{*}}^{\mathfrak{D},m,n},\end{array}$$

(26)

$$\begin{array}{c}\hfill \sum _{{\mathit{S}}_q^{*},{\xi }_q^{*},{\eta }_q^{*}}^{\mathfrak{D},m,n}=\sum _{S[q,1]}\sum _{{\xi }_{q,1},{\eta }_{q,1}}^{m,n}\dots \sum _{S[\mathfrak{q},\mathfrak{D}]}\sum _{{\xi }_{q,\mathfrak{D}},{\eta }_{q,\mathfrak{D}}}^{m,n},\end{array}$$

(27)

$$\begin{array}{c}\hfill \sum _{{\xi }_{q,j},{\eta }_{q,j}}^{m,n}=\sum _{{\xi }_{q,j,1}=0}^{i_{q,j,1}-1}\sum _{{\xi }_{q,j,2}=0}^{i_{q,j,2}-1}\dots \sum _{{\xi }_{q,j,m}=0}^{i_{q,j,m}-1}.\sum _{{\eta }_{q,j,m+1}=1}^{i_{q,j,m+1}}\sum _{{\eta }_{q,j,m+2}=1}^{i_{q,j,m+2}}\dots \sum _{{\eta }_{q,j,n}=1}^{i_{q,j,n}},\end{array}$$

(28)

and ${\mathit{i}}_{q,j}=(i_{q,j,1},\dots ,i_{q,j,m},i_{q,j,m+1},\dots ,i_{q,j,n})$, $q=1,\dots ,\hslash$, $j=1,\dots ,\mathfrak{D}$, ${\mathit{S}}^{**}=({\mathit{S}}_1^{*},\dots ,{\mathit{S}}_{\hslash }^{*})$, ${\mathit{S}}_q^{*}=(S[q,1],\dots ,S[q,\mathfrak{D}])$, ${\xi }^{**}=({\xi }_1^{*},\dots ,{\xi }_{\hslash }^{*})$, ${\xi }_q^{*}=({\xi }_{q,1},\dots ,{\xi }_{q,\mathfrak{D}})$, ${\xi }_{q,j}=({\xi }_{q,j,1},\dots ,{\xi }_{q,j,m})$, ${\eta }^{**}=({\eta }_1^{*},\dots ,{\eta }_{\hslash }^{*})$, ${\eta }_q^{*}=({\eta }_{q,1},\dots ,{\eta }_{q,\mathfrak{D}})$, ${\eta }_{q,j}=({\eta }_{q,j,m+1},\dots ,{\eta }_{q,j,n})$.

3.1. Prior and Posterior Distributions

Since the parameters $\alpha$ and $\gamma$ are combined in a new scale parameter of CDF (6), it is appropriate to choose $\alpha$ and $\gamma$ to be dependent. Waller and Waterman [23] clarified that in Bayesian reliability analysis the gamma distribution family can be used as priors. Therefore, the gamma prior density could be sufficient to cover the prior experience of the tester/experimenter. Hence, we assume that $\alpha$ and $\gamma$ each have a gamma distribution. That is, the joint prior density of $\alpha$ and $\gamma$ can be written as

$$\pi (\alpha ,\gamma )={\pi }_1\left(\alpha \right){\pi }_2\left(\gamma \right|\alpha ),$$

(29)

where

$${\pi }_1\left(\alpha \right)=\frac{a_2^{a_1}}{\mathsf{\Gamma }\left(a_1\right)}{\alpha }^{a_1-1}\exp \left[-a_2\alpha \right],\alpha >0,(a_1,a_2)>0,$$

(30)

$${\pi }_2\left(\gamma \right|\alpha )=\frac{{\alpha }^{a_3}}{\mathsf{\Gamma }\left(a_3\right)}{\gamma }^{a_3-1}\exp \left[-\alpha \gamma \right],\gamma >0,a_3>0.$$

(31)

Using (30) and (31), joint prior density (29) becomes

$$\pi (\alpha ,\gamma )=\frac{a_2^{a_1}}{\mathsf{\Gamma }\left(a_1\right)\mathsf{\Gamma }\left(a_3\right)}{\alpha }^{a_1+a_3-1}{\gamma }^{a_3-1}\exp \left[-(a_2+\gamma )\alpha \right],\alpha ,\gamma >0,(a_1,a_2,a_3)>0.$$

(32)

From (24) and (32), the joint posterior density function of $\alpha$ and $\gamma$ can take the next form

$${\pi }^{*}(\alpha ,\gamma |\mathrm{t})={\Im }^{-1}\sum _{{\mathit{S}}^{**},{\xi }^{**},{\eta }^{**}}^{\mathfrak{D},m,n}\left(\left[\prod _{q=1}^{\hslash }\prod _{j=1}^{\mathfrak{D}}{A}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathit{i}}_{q,j}\right)\right]{\mathsf{\Lambda }}^{\gamma }{\alpha }^{\mu -1}{\gamma }^{a_3-1}\exp \left[-\alpha {\mathcal{B}}_{{\xi }^{**},{\eta }^{**}}\left(\gamma \right)\right]\right),$$

(33)

where

$$\begin{array}{cc}\hfill \mu & =a_1+a_3+\hslash \mathfrak{D}m,\hfill \end{array}$$

(34)

$${\mathcal{B}}_{{\xi }^{**},{\eta }^{**}}\left(\gamma \right)=a_2+\gamma +\sum _{q=1}^{\hslash }\sum _{j=1}^{\mathfrak{D}}\frac{k_j^{\gamma }}{\gamma +1}{\mathsf{\Psi }}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathbf{t}}_{q,j}\right),$$

(35)

$$\begin{array}{cc}\hfill \Im & =\sum _{{\mathit{S}}^{**},{\xi }^{**},{\eta }^{**}}^{\mathfrak{D},m,n}\left(\left[\prod _{q=1}^{\hslash }\prod _{j=1}^{\mathfrak{D}}{A}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathit{i}}_{q,j}\right)\right]\mathsf{\Gamma }\left(\mu \right){\int }_0^{\infty }{\gamma }^{a_3-1}{\mathsf{\Lambda }}^{\gamma }{\left[{\mathcal{B}}_{{\xi }^{**},{\eta }^{**}}\left(\gamma \right)\right]}^{-\mu }\mathrm{d}\gamma \right).\hfill \end{array}$$

3.2. Bayes Estimation Based on Symmetric and Asymmetric LFs

In Bayesian estimation procedures, the symmetric SE LF is one of the very common LFs which could be used to estimate unknown parameters. However, its development is driven by its good mathematical properties, not by its applicability to the description of a true loss structure. On the other hand, asymmetric LFs may be appropriate in many situations in which overestimation or underestimation of the model parameters may occur. Overestimation may be more severe than underestimation, or conversely. For example, in estimating the mean reliable operating life of the components of an aircraft or a spaceship, overestimation is often more severe than underestimation.

Different asymmetric LFs are suggested in the literature, such as the GE and LINEX LFs. The estimators of the model parameters under asymmetric LFs show their superiority over the estimators obtained under symmetric LFs. The Bayes estimation of the underlying parameters based on symmetric and asymmetric LFs is discussed by several authors, see, for example, [8,24,25,26,27].

The BEs of $\alpha$ and $\gamma$, based on symmetric and asymmetric LFs are obtained as follows:

• The SE LF is defined as follows

  $$\mathcal{L}(\widehat{\mathsf{\Theta }},\mathsf{\Theta })\propto {\left(\widehat{\mathsf{\Theta }}-\mathsf{\Theta }\right)}^2,$$

  where $\widehat{\mathsf{\Theta }}$ indicates the estimate of $\mathsf{\Theta }$.
  The BEs of $\alpha$ and $\gamma$, based on the SE LF, are given by

  $${\widehat{\alpha }}_S=E\left[\alpha \right|\mathbf{t}]={\Im }^{-1}\mathsf{\Gamma }(\mu +1)\sum _{{\mathit{S}}^{**},{\xi }^{**},{\eta }^{**}}^{\mathfrak{D},m,n}\left({\mathcal{I}}_{{\xi }^{**},{\eta }^{**}}\prod _{q=1}^{\hslash }\prod _{j=1}^{\mathfrak{D}}{A}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathit{i}}_{q,j}\right)\right),$$

  (36)

  $${\widehat{\gamma }}_S=E\left[\gamma \right|\mathrm{t}]={\Im }^{-1}\mathsf{\Gamma }\left(\mu \right)\sum _{{\mathit{S}}^{**},{\xi }^{**},{\eta }^{**}}^{\mathfrak{D},m,n}\left({\mathcal{I}}_{{\xi }^{**},{\eta }^{**}}^{*}\prod _{q=1}^{\hslash }\prod _{j=1}^{\mathfrak{D}}{A}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathit{i}}_{q,j}\right)\right),$$

  (37)

  where

  $$\begin{array}{cc}\hfill {\mathcal{I}}_{{\xi }^{**},{\eta }^{**}}& ={\int }_0^{\infty }{\gamma }^{a_3-1}{\mathsf{\Lambda }}^{\gamma }{\left[{\mathcal{B}}_{{\xi }^{**},{\eta }^{**}}\left(\gamma \right)\right]}^{-\mu -1}\mathrm{d}\gamma ,\hfill \\ \hfill {\mathcal{I}}_{{\xi }^{**},{\eta }^{**}}^{*}& ={\int }_0^{\infty }{\gamma }^{a_3}{\mathsf{\Lambda }}^{\gamma }{\left[{\mathcal{B}}_{{\xi }^{**},{\eta }^{**}}\left(\gamma \right)\right]}^{-\mu }\mathrm{d}\gamma .\hfill \end{array}$$
• The LINEX LF is defined as follows:

  $$\mathcal{L}\left(\delta \right)\propto e^{\rho \delta }-\rho \delta -1,\rho \ne 0,$$

  where $\delta =\widehat{\mathsf{\Theta }}-\mathsf{\Theta }$.
  The BE of $\mathsf{\Theta }$, based on the LINEX LF, is given by

  $$\begin{array}{c}\hfill {\widehat{\mathsf{\Theta }}}_L=\frac{-1}{\rho }\log \left[E\left(e^{-\rho \mathsf{\Theta }}\right|\mathrm{t})\right].\end{array}$$

  (38)
  From (33) and (38), the BEs of $\alpha$ and $\gamma$, based on the LINEX LF, are then given, respectively, by

  $${\widehat{\alpha }}_L=\frac{-1}{\rho }\log \left[{\Im }^{-1}\mathsf{\Gamma }\left(\mu \right)\sum _{{\mathit{S}}^{**},{\xi }^{**},{\eta }^{**}}^{\mathfrak{D},m,n}\left({\mathcal{R}}_{{\xi }^{**},{\eta }^{**}}\prod _{q=1}^{\hslash }\prod _{j=1}^{\mathfrak{D}}{A}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathit{i}}_{q,j}\right)\right)\right],$$

  (39)

  $${\widehat{\gamma }}_L=\frac{-1}{\rho }\log \left[{\Im }^{-1}\mathsf{\Gamma }\left(\mu \right)\sum _{{\mathit{S}}^{**},{\xi }^{**},{\eta }^{**}}^{\mathfrak{D},m,n}\left({\mathcal{R}}_{{\xi }^{**},{\eta }^{**}}^{*}\prod _{q=1}^{\hslash }\prod _{j=1}^{\mathfrak{D}}{A}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathit{i}}_{q,j}\right)\right)\right],$$

  (40)

  where

  $$\begin{array}{cc}\hfill {\mathcal{R}}_{{\xi }^{**},{\eta }^{**}}& ={\int }_0^{\infty }{\gamma }^{a_3-1}{\mathsf{\Lambda }}^{\gamma }{[\rho +{\mathcal{B}}_{{\xi }^{**},{\eta }^{**}}\left(\gamma \right)]}^{-\mu }\mathrm{d}\gamma ,\hfill \\ \hfill {\mathcal{R}}_{{\xi }^{**},{\eta }^{**}}^{*}& ={\int }_0^{\infty }{e}^{-\rho \gamma }{\gamma }^{a_3-1}{\mathsf{\Lambda }}^{\gamma }{\left[{\mathcal{B}}_{{\xi }^{**},{\eta }^{**}}\left(\gamma \right)\right]}^{-\mu }\mathrm{d}\gamma .\hfill \end{array}$$
• The GE LF is defined as follows:

  $$\mathcal{L}({\widehat{\mathsf{\Theta }}}_G,\mathsf{\Theta })\propto {\left(\frac{{\widehat{\mathsf{\Theta }}}_G}{\mathsf{\Theta }}\right)}^{\upsilon }-\upsilon \log \left[\frac{{\widehat{\mathsf{\Theta }}}_G}{\mathsf{\Theta }}\right]-1,\upsilon \ne 0.$$
  The BE of $\mathsf{\Theta }$, based on the GE LF, is given by

  $$\begin{array}{c}\hfill {\widehat{\mathsf{\Theta }}}_G={\left[E\left({\mathsf{\Theta }}^{-\upsilon }\right)\right]}^{\frac{-1}{\upsilon }}.\end{array}$$

  (41)
  From (33) and (41), the BEs of $\alpha$ and $\gamma$, based on the GE LF, are then given, respectively, by

  $${\widehat{\alpha }}_G={\left[{\Im }^{-1}\mathsf{\Gamma }(\mu -\upsilon )\sum _{{\mathit{S}}^{**},{\xi }^{**},{\eta }^{**}}^{\mathfrak{D},m,n}\left({\mathcal{K}}_{{\xi }^{**},{\eta }^{**}}\prod _{q=1}^{\hslash }\prod _{j=1}^{\mathfrak{D}}{A}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathit{i}}_{q,j}\right)\right)\right]}^{\frac{-1}{\upsilon }},$$

  (42)

  $${\widehat{\gamma }}_G={\left[{\Im }^{-1}\mathsf{\Gamma }\left(\mu \right)\sum _{{\mathit{S}}^{**},{\xi }^{**},{\eta }^{**}}^{\mathfrak{D},m,n}\left({\mathcal{K}}_{{\xi }^{**},{\eta }^{**}}^{*}\prod _{q=1}^{\hslash }\prod _{j=1}^{\mathfrak{D}}{A}_{{\xi }_{q,j},{\eta }_{q,j}}\left({\mathit{i}}_{q,j}\right)\right)\right]}^{\frac{-1}{\upsilon }},$$

  (43)

  where

  $$\begin{array}{cc}\hfill {\mathcal{K}}_{{\xi }^{**},{\eta }^{**}}& ={\int }_0^{\infty }{\gamma }^{a_3-1}{\mathsf{\Lambda }}^{\gamma }{\left[{\mathcal{B}}_{{\xi }^{**},{\eta }^{**}}\left(\gamma \right)\right]}^{-\mu +\upsilon }\mathrm{d}\gamma ,\hfill \\ \hfill {\mathcal{K}}_{{\xi }^{**},{\eta }^{**}}^{*}& ={\int }_0^{\infty }{\gamma }^{a_3-\upsilon -1}{\mathsf{\Lambda }}^{\gamma }{\left[{\mathcal{B}}_{{\xi }^{**},{\eta }^{**}}\left(\gamma \right)\right]}^{-\mu }\mathrm{d}\gamma .\hfill \end{array}$$

4. Bayes Estimation Based on SRS under Progressive-Stress ALT

Suppose that ${\mathrm{Z}}_{SRS}=\{Z_{q,1,1},Z_{q,1,2},\dots ,Z_{q,1,m},\dots \dots ,Z_{q,\mathfrak{D},1},Z_{q,\mathfrak{D},2},\dots ,Z_{q,\mathfrak{D},m}\}$, $q=1,\dots ,\hslash$, is a type-II censored ℏ-cycle SRS under progressive-stress ALT from a population with CDF (6) and PDF (7). Then, the likelihood function is given by

$$\begin{array}{cc}\hfill \mathfrak{L}(\alpha ,\gamma ;\mathrm{Z})\propto & \prod _{q=1}^{\hslash }\left[\prod _{j=1}^{\mathfrak{D}}{\left[1-F_j\left(z_{q,j,m}\right)\right]}^{n-m}\prod _{r=1}^m{f}_j\left(z_{q,j,r}\right)\right]\hfill \\ \hfill & ={\alpha }^{\hslash \mathfrak{D}m}{\mathsf{\Delta }}^{\gamma }\exp \left[-\alpha \sum _{q=1}^{\hslash }\sum _{j=1}^{\mathfrak{D}}\frac{k_j^{\gamma }}{\gamma +1}\left((n-m)z_{q,j,m}^{\gamma +1}+\sum _{r=1}^m{z}_{q,j,r}^{\gamma +1}\right)\right],\hfill \end{array}$$

(44)

where

$$\begin{array}{c}\hfill \mathsf{\Delta }=\prod _{q=1}^{\hslash }\prod _{j=1}^{\mathfrak{D}}\prod _{r=1}^m{k}_j{z}_{q,j,r}.\end{array}$$

(45)

From (32) and (44), the joint posterior density function of $\alpha$ and $\gamma$ can take the next form

$$\begin{array}{cc}\hfill {\pi }^{**}(\alpha ,\gamma ;\mathrm{z})& ={\wp }^{-1}{\alpha }^{\mu -1}{\gamma }^{a_3-1}{\mathsf{\Delta }}^{\gamma }\exp \left[-\alpha {\mathsf{\Psi }}^{*}\left(\gamma \right)\right],\hfill \end{array}$$

(46)

where

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}^{*}\left(\gamma \right)& =a_2+\gamma +\sum _{q=1}^{\hslash }\sum _{j=1}^{\mathfrak{D}}\frac{k_j^{\gamma }}{\gamma +1}\left((n-m)z_{q,j,m}^{\gamma +1}+\sum _{r=1}^m{z}_{q,j,r}^{\gamma +1}\right),\hfill \\ \hfill \wp & =\mathsf{\Gamma }\left(\mu \right){\int }_0^{\infty }{\gamma }^{a_3-1}{\mathsf{\Delta }}^{\gamma }{\left[{\mathsf{\Psi }}^{*}\left(\gamma \right)\right]}^{-\mu }\mathrm{d}\gamma .\hfill \end{array}$$

(47)

The BEs of $\alpha$ and $\gamma$, based on the SE LF, are given, respectively, by

$${\widehat{\alpha }}_S={\wp }^{-1}\mathsf{\Gamma }(\mu +1){\int }_0^{\infty }{\gamma }^{a_3-1}{\mathsf{\Delta }}^{\gamma }{\left[{\mathsf{\Psi }}^{*}\left(\gamma \right)\right]}^{-\mu -1}\mathrm{d}\gamma ,$$

(48)

$${\widehat{\gamma }}_S={\wp }^{-1}\mathsf{\Gamma }\left(\mu \right){\int }_0^{\infty }{\gamma }^{a_3}{\mathsf{\Delta }}^{\gamma }{\left[{\mathsf{\Psi }}^{*}\left(\gamma \right)\right]}^{-\mu }\mathrm{d}\gamma .$$

(49)

From (38) and (46), the BEs of $\alpha$ and $\gamma$, based on the LINEX LF, are given, respectively, by

$${\widehat{\alpha }}_L=\frac{-1}{\rho }\log \left[{\wp }^{-1}\mathsf{\Gamma }\left(\mu \right){\int }_0^{\infty }{\gamma }^{a_3-1}{\mathsf{\Delta }}^{\gamma }{[\rho +{\mathsf{\Psi }}^{*}\left(\gamma \right)]}^{-\mu }\mathrm{d}\gamma \right],$$

(50)

$${\widehat{\gamma }}_L=\frac{-1}{\rho }\log \left[{\wp }^{-1}\mathsf{\Gamma }\left(\mu \right){\int }_0^{\infty }{e}^{-\rho \gamma }{\gamma }^{a_3-1}{\mathsf{\Delta }}^{\gamma }{\left[{\mathsf{\Psi }}^{*}\left(\gamma \right)\right]}^{-\mu }\mathrm{d}\gamma \right].$$

(51)

From (41) and (46), the BEs of $\alpha$ and $\gamma$, based on the GE LF, are then given, respectively, by

$${\widehat{\alpha }}_G={\left[{\wp }^{-1}\mathsf{\Gamma }(\mu -\upsilon ){\int }_0^{\infty }{\gamma }^{a_3-1}{\mathsf{\Delta }}^{\gamma }{\left[{\mathsf{\Psi }}^{*}\left(\gamma \right)\right]}^{-\mu +\upsilon }\mathrm{d}\gamma \right]}^{\frac{-1}{\upsilon }},$$

(52)

$${\widehat{\gamma }}_G={\left[{\wp }^{-1}\mathsf{\Gamma }\left(\mu \right){\int }_0^{\infty }{\gamma }^{a_3-\upsilon -1}{\mathsf{\Delta }}^{\gamma }{\left[{\mathsf{\Psi }}^{*}\left(\gamma \right)\right]}^{-\mu }\mathrm{d}\gamma \right]}^{\frac{-1}{\upsilon }}.$$

(53)

5. Illustrative Examples

In this section, we present a simulated data set as well as a real data set to illustrate the theoretical results presented in the previous sections.

5.1. Example 1: Simulated Data Set

In this subsection, considering $\mathfrak{D}=2$ (two stress levels), we explain the Bayesian estimation procedures based on data generated from CDF (6). Using (30) and (31), we generate the population parameter values $\alpha =1.25132$ and $\gamma =0.640139$ based on the hyperparameter values $a_1=1.5,a_2=1.2$, and $a_3=0.8$. To obtain a one-cycle RSS of size $N(=12)$, generate $n(=6)$ SRSs of sizes $N(=12)$ and each SRS is split into two groups of sizes $n(=6)$, see the 4th column of Table 1. The first and second groups in each SRS are generated from CDF (6) with two stress levels $k_1=1$ and $k_2=3$, respectively. Apply the procedure of RSS (as shown in Section 2.3) to these SRSs to obtain a one-cycle RSS, then order it to obtain the ORSS; see the last two columns of Table 1. The type-II censoring is applied to the values of the ORSS, presented in the last column of Table 1, by choosing the first m values of them. Through the estimation procedure, the values of m have been chosen to be 4, 5, and 6 as shown in Table 2. Similarly, a second cycle type-II censored ORSS can be obtained as shown above.

Table 1. The generated SRSs, RSSs, and ORSSs (one-cycle and two-cycle).

q	SN	j	SRSs						RSS		ORSS
									$\mathit{j}=\mathbf{1}$	$\mathit{j}=\mathbf{2}$	$\mathit{j}=\mathbf{1}$	$\mathit{j}=\mathbf{2}$
1	1	1	0.62869	0.74550	0.82769	1.08925	1.63549	1.79960	0.62869	0.09945	0.50097	0.09945
		2	0.09945	0.16651	0.52975	0.61511	0.92148	0.97780
	2	1	0.40466	0.50097	0.72384	0.91502	0.94297	1.27080	0.50097	0.61819	0.62869	0.41101
		2	0.21357	0.61819	0.61872	0.64643	0.68302	0.69081
	3	1	0.39613	0.79211	1.09190	1.70029	1.92951	2.37244	1.09190	0.41101	0.72207	0.61819
		2	0.28536	0.33472	0.41101	0.67774	0.73224	0.98121
	4	1	0.43194	0.67499	0.70694	0.72207	1.04718	1.26674	0.72207	0.80841	0.93115	0.80841
		2	0.32619	0.54256	0.71499	0.80841	0.83007	1.15576
	5	1	0.46377	0.58722	0.61592	0.70572	1.22801	1.44783	1.22801	0.98634	1.09190	0.95547
		2	0.38004	0.66307	0.73080	0.77100	0.98634	1.38750
	6	1	0.46640	0.49247	0.58259	0.83341	0.88019	0.93115	0.93115	0.95547	1.22801	0.98634
		2	0.30466	0.40847	0.44639	0.61364	0.79324	0.95547
2	1	1	0.26317	0.26711	0.42187	0.61205	0.89934	0.98977	0.26317	0.13934	0.26317	0.13934
		2	0.13934	0.4649	0.49377	0.64862	0.88906	1.04488
	2	1	0.16719	0.28359	0.46341	1.04667	1.30399	1.33791	0.28359	0.51493	0.28359	0.37922
		2	0.36814	0.51493	0.58078	0.7535	1.48766	1.6172
	3	1	0.15701	0.51006	0.53069	0.62174	0.88069	1.65156	0.53069	0.37922	0.53069	0.51493
		2	0.13544	0.23631	0.37922	0.43267	0.61472	0.62408
	4	1	0.61671	0.87544	0.95792	1.56069	2.31227	3.95962	1.56069	0.74195	1.56069	0.74195
		2	0.31827	0.36938	0.49496	0.74195	1.23981	1.29935
	5	1	0.95442	1.07906	1.24972	1.26945	1.6566	1.65672	1.6566	0.83244	1.6566	0.78234
		2	0.06583	0.08971	0.14998	0.29278	0.83244	1.48854
	6	1	0.64908	0.8308	1.01052	1.25373	1.79936	1.96924	1.96924	0.78234	1.96924	0.83244
		2	0.29669	0.53363	0.55488	0.60676	0.67346	0.78234

SN: Sample number.

Table 2. BEs of $\alpha$ and $\gamma$ based on SRSs and ORSSs (one-cycle and two-cycle) presented in Table 1.

	N				ORSS		SRS
ℏ	$\mathfrak{D}$	n	m	LF	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\gamma }}$	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\gamma }}$
1	12	6	4	SE	1.19442	0.63133	1.39331	0.77371
	2			LINEX ($\rho =-0.001$)	1.19445	0.63138	1.39341	0.77382
				LINEX ($\rho =1.5$)	1.14613	0.56557	1.26324	0.63400
				GE ($\upsilon =-0.5$)	1.18028	0.58805	1.35829	0.69382
				GE ($\upsilon =0.01$)	1.16577	0.53000	1.32233	0.58870
			5	SE	1.30263	0.65708	1.23552	0.68187
				LINEX ($\rho =-0.001$)	1.30266	0.65711	1.23558	0.68195
				LINEX ($\rho =1.5$)	1.26098	0.60309	1.14889	0.57587
				GE ($\upsilon =-0.5$)	1.29155	0.62430	1.21004	0.61441
				GE ($\upsilon =0.01$)	1.28021	0.58224	1.18388	0.52447
			6	SE	1.48150	0.75641	1.36555	0.88405
				LINEX ($\rho =-0.001$)	1.48153	0.75644	1.36562	0.88415
				LINEX ($\rho =1.5$)	1.43968	0.70689	1.27071	0.75846
				GE ($\upsilon =-0.5$)	1.47175	0.73171	1.34032	0.82468
				GE ($\upsilon =0.01$)	1.46179	0.70260	1.31440	0.74889
2	12	6	4	SE	1.14352	0.50813	1.62675	0.62591
	2			LINEX ($\rho =-0.001$)	1.14353	0.50815	1.62684	0.62595
				LINEX ($\rho =1.5$)	1.11806	0.47308	1.51537	0.56128
				GE ($\upsilon =-0.5$)	1.1359	0.48054	1.60185	0.58361
				GE ($\upsilon =0.01$)	1.12809	0.44466	1.57634	0.52839
			5	SE	1.29955	0.62316	1.48251	0.56388
				LINEX ($\rho =-0.001$)	1.29956	0.62318	1.48256	0.56392
				LINEX ($\rho =1.5$)	1.27721	0.59201	1.41085	0.51413
				GE ($\upsilon =-0.5$)	1.2937	0.60459	1.46539	0.52812
				GE ($\upsilon =0.01$)	1.28772	0.58311	1.44787	0.48148
			6	SE	1.45755	0.75294	1.68111	0.70429
				LINEX ($\rho =-0.001$)	1.45756	0.75296	1.68117	0.70433
				LINEX ($\rho =1.5$)	1.43624	0.72383	1.60402	0.65408
				GE ($\upsilon =-0.5$)	1.45259	0.73922	1.66492	0.67711
				GE ($\upsilon =0.01$)	1.44752	0.72443	1.64835	0.6449

Based on the generated SRS (say, the first sample) and ORSS (one-cycle and two-cycle) under progressive-stress ALT given in Table 1, Table 2 presents the BEs of $\alpha$ and $\gamma$, based on SE, LINEX, and GE LFs.

5.2. Example 2: Real Data Set

The theoretical results obtained in Section 3 and Section 4 are clarified here with a real data set that was considered in Zhu [28]. The data set is presented in Table 3 which is obtained from ramp-voltage experiments of miniature light bulbs under two various voltage ramp-rates, $k_1=0.010$ V/h and $k_2=0.015$ V/h, beginning from 2V at each group. Table 3 presents, in the second row, the lifetimes of 62 miniature light bulbs experimented under ramp-rate 0.010 V/h, while, in the third row, it presents the lifetimes of 61 miniature light bulbs experimented under ramp-rate 0.015 V/h. Before going further, we examine the validity of Weibull distribution with CDF (6) to fit the real data presented in Table 3 by applying the Kolmogorov–Smirnov (K-S) test statistic and its associated p-value for each stress level. The results are displayed in Table 4 in which we can observe that CDF (6) fits well the given real data, for each stress level, because all the p-values are larger than 0.05. Graphically, this is accomplished by plotting the empirical CDF of the real data set for each stress level versus the CDF of Weibull distribution (6), see Figure 2.

Table 3. Lifetime data from ramp-voltage tests.

Stress Level	Data Set
0.010 v/h	$13.57,19.92,23.30,27.81,31.16,31.56,34.00,46.26,46.41,50.60,56.76,56.85,60.13,65.00,$
	$65.86,66.20,66.40,66.80,66.93,68.25,70.23,72.33,72.60,75.43,75.85,76.20,77.78,79.13,$
	$80.65,82.65,90.33,14.51,15.61,15.85,17.73,19.65,21.05,21.20,24.21,24.85,31.18,35.08,$
	$42.06,47.88,54.21,54.55,55.85,56.43,58.86,60.60,62.48,62.81,63.41,63.76,64.18,66.15,$
	$66.41,69.91,71.73,72.46,73.78,78.91$
0.015 v/h	$19.30,23.28,23.50,26.50,27.42,28.32,28.62,30.62,34.42,35.30,35.48,38.30,40.52,43.83,$
	$43.00,43.00,43.12,44.43,45.32,47.58,47.65,49.65,51.42,51.27,53.25,54.25,55.47,56.83,$
	$56.17,8.85,11.31,11.83,14.50,14.83,17.73,19.35,25.50,26.15,27.45,27.61,28.05,30.96,$
	$31.00,34.81,36.03,43.08,45.63,46.03,46.33,49.62,49.86,50.66,50.93,51.03,51.73,51.95,$
	$52.36,54.78,55.58,55.83,57.13$

Table 4. MLEs of the parameters, K-S statistic, and p-value.

Parameters	Stress	K-S	p-Value
$\widehat{\alpha }=0.174566,\widehat{\gamma }=2.24909$	0.010 v/h	0.155999	0.09782
	0.015 v/h	0.114285	0.40304

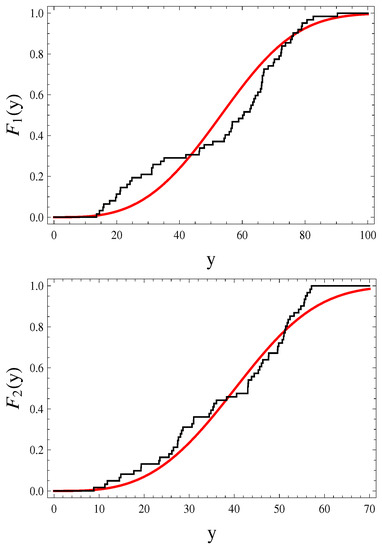
Figure 2. Empirical CDF (black line) versus CDF of Weibull distribution (red line) for the data given in Table 3, under two stress levels.

To obtain a one-cycle RSS of size N (=10) under progressive-stress, select n (=5) SRSs each of the size N (=10). Each SRS consists of two groups, ($\mathfrak{D}=2$, two stress levels). The first (second) group consists of five observations drawn from the data given in Table 3 under the first (second) level of stress 0.010 v/h (0.015 v/h). Apply the procedure of RSS (as shown in Section 2.3) to these SRSs to obtain a one-cycle RSS, then order it to obtain the ORSS; see the last two columns of Table 5. The type-II censoring is applied to the ORSS presented in the last column of Table 5 by choosing the first m values of them. The values of m were chosen to be 3, 4, and 5, as shown in Table 6. Similarly, a second cycle type-II censored ORSS can be obtained from the remaining data of Table 3, as shown above.

Table 5. The real SRSs and ORSSs (one-cycle and two-cycle).

q	SN	j	SRSs					RSS		ORSS
								$\mathit{j}=\mathbf{1}$	$\mathit{j}=\mathbf{2}$	$\mathit{j}=\mathbf{1}$	$\mathbf{j}=\mathbf{2}$
1	1	1	24.85	27.81	55.85	66.20	78.91	24.85	11.83	24.85	11.83
		2	11.83	27.61	44.43	53.25	56.83
	2	1	21.05	46.41	64.18	72.60	82.65	46.41	30.96	46.41	30.96
		2	28.32	30.96	34.42	51.27	55.47
	3	1	17.73	23.30	63.41	65.00	79.13	63.41	46.33	62.48	34.81
		2	28.05	43.12	46.33	49.62	55.58
	4	1	31.56	50.60	60.60	62.48	66.40	62.48	34.81	63.41	46.33
		2	19.35	23.28	28.62	34.81	50.93
	5	1	15.61	19.65	66.15	72.33	72.46	72.46	55.83	72.46	55.83
		2	14.83	45.32	45.63	49.65	55.83
2	1	1	31.18	69.91	70.23	75.43	75.85	31.18	14.50	31.18	14.50
		2	14.50	19.30	23.50	40.52	43.00
	2	1	14.51	34.00	35.08	42.06	62.81	34.00	46.03	34.00	43.08
		2	17.73	46.03	49.86	50.66	56.17
	3	1	46.26	56.76	65.86	66.41	71.73	65.86	43.08	58.86	46.03
		2	26.15	30.62	43.08	43.83	47.65
	4	1	19.92	56.43	56.85	58.86	66.8	58.86	47.58	65.86	47.58
		2	27.45	31.00	35.48	47.58	51.03
	5	1	24.21	54.21	54.55	76.2	77.78	77.78	54.78	77.78	54.78
		2	26.50	27.42	35.30	43.00	54.78

SN: Sample number.

Table 6. BEs of $\alpha$ and $\gamma$ based on SRSs and ORSSs (one-cycle and two-cycle) presented in Table 5.

	N				ORSS		SRS
ℏ	$\mathfrak{D}$	n	m	LF	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\gamma }}$	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\gamma }}$
1	10	5	3	SE	0.12591	1.68406	0.09161	1.23444
	2			LINEX ($\rho =-0.001$)	0.12592	1.68431	0.09161	1.23469
				LINEX ($\rho =1.5$)	0.12011	1.33048	0.08777	0.91307
				GE ($\upsilon =-0.5$)	0.11171	1.5928	0.07952	1.10254
				GE ($\upsilon =0.01$)	0.09778	1.44981	0.06815	0.86598
			4	SE	0.17546	2.01879	0.09695	1.3575
				LINEX ($\rho =-0.001$)	0.17547	2.01871	0.09695	1.35772
				LINEX ($\rho =1.5$)	0.16803	1.71085	0.09411	1.06122
				GE ($\upsilon =-0.5$)	0.16186	1.96036	0.08806	1.25643
				GE ($\upsilon =0.01$)	0.14832	1.88987	0.07938	1.09084
			5	SE	0.20307	2.21734	0.12568	1.62539
				LINEX ($\rho =-0.001$)	0.20307	2.21752	0.12569	1.6256
				LINEX ($\rho =1.5$)	0.19614	1.95872	0.1223	1.3404
				GE ($\upsilon =-0.5$)	0.19198	2.17464	0.11721	1.55272
				GE ($\upsilon =0.01$)	0.18090	2.12809	0.10878	1.45607
2	10	5	3	SE	0.10999	1.73465	0.07486	1.20759
	2			LINEX ($\rho =-0.001$)	0.11000	1.73479	0.07486	1.20773
				LINEX ($\rho =1.5$)	0.10745	1.52792	0.0734	1.01138
				GE ($\upsilon =-0.5$)	0.10287	1.68979	0.06905	1.13773
				GE ($\upsilon =0.01$)	0.09587	1.63851	0.06339	1.03148
			4	SE	0.16507	2.11737	0.09216	1.42944
				LINEX ($\rho =-0.001$)	0.16507	2.1175	0.09216	1.43042
				LINEX ($\rho =1.5$)	0.16115	1.92929	0.09069	1.25041
				GE ($\upsilon =-0.5$)	0.15751	2.08536	0.08722	1.38069
				GE ($\upsilon =0.01$)	0.15001	2.05147	0.08235	1.32208
			5	SE	0.19862	2.35293	0.13497	1.76468
				LINEX ($\rho =-0.001$)	0.19862	2.35306	0.13497	1.7648
				LINEX ($\rho =1.5$)	0.19469	2.18854	0.13263	1.58997
				GE ($\upsilon =-0.5$)	0.1922	2.32822	0.12945	1.7281
				GE ($\upsilon =0.01$)	0.18579	2.30243	0.12396	1.68899

Using (30) and (31), the hyperparameter values were chosen to be $a_1=0.50,$$a_2=2.87$ and $a_3=0.39$ to generate population parameter values $\widehat{\alpha }=0.174566$ and $\widehat{\gamma }=2.24909$. Based on an SRS (say, the first sample) and ORSSs (one-cycle and two-cycle) given in Table 5, Table 6 presents the BEs of $\alpha$ and $\gamma$, based on SE, LINEX, and GE LFs.

6. Simulation Study

In this section, the techniques of ORSS and SRS under type-II censoring are compared via a Monte Carlo simulation study. Moreover, the BEs of $\alpha$ and $\gamma$, based on symmetric and asymmetric LFs, are obtained and compared. Monte Carlo simulation can be performed as follows:

• Select the hyperparameter values $a_1=1.5,a_2=1.2$, and $a_3=0.8$ to generate the population parameter values $\alpha =1.25132$ and $\gamma =0.640139$, using (30) and (31). The hyperparameter values were chosen to satisfy the following conditions of unbiasedness, see Al-Hussaini and Abdel-Hamid [4] and Abdel-Hamid [29],

  $$E\left[\widehat{\alpha }\right]=\frac{a_1}{a_2}=\alpha ,$$

  $$E\left[\widehat{\gamma }\right]=\frac{a_3}{\alpha }=\gamma ,$$

  where E stands for the expectation.
• Consider $\mathfrak{D}=2$ (two stress levels), generate $n(=4,5,6)$ SRSs all of the size $N(=2n)$ and each SRS is split into two groups each of the same size. The first and second groups in each SRS are generated using CDF (6) with two stress levels $k_1=1$ and $k_2=3$, respectively.
• Apply the procedure of RSS (as shown in Section 2.3) to the SRSs obtained in Step 2 to obtain a one-cycle RSS, then order it to obtain the ORSS.
• Apply the technique of type-II censoring to the values of the ORSS, obtained in Step 3, by choosing the first m values of them.
• To obtain ℏ-cycle type-II censored ORSS, repeat Steps 2–4 ℏ times.
• The BEs, under SE, LINEX, and GE LFs, of the parameters $\alpha$ and $\gamma$ are calculated based on the SRSs and ORSSs under type-II censoring.
• Repeat the above steps 1000 times.
• Determine the estimates mean, mean squared errors (MSEs), and relative absolute biases (RABs) of $\widehat{\delta }$ over 1000 iterations according to the following relations:

  $$\begin{array}{c}\hfill \overline{\widehat{\delta }}=\frac{1}{1000}\sum _{i=1}^{1000}{\widehat{\delta }}_i,\mathrm{MSE}\left(\widehat{\delta }\right)=\frac{1}{1000}\sum _{i=1}^{1000}{({\widehat{\delta }}_i-\delta )}^2,\mathrm{RAB}\left(\widehat{\delta }\right)=\frac{1}{1000}\sum _{i=1}^{1000}\frac{|{\widehat{\delta }}_i-\delta |}{\delta },\end{array}$$

  where $\widehat{\delta }$ is an estimate of $\delta$.
• Determine the estimates mean of the parameters $\alpha$ and $\gamma$ with their RABs and MSEs as shown in Step 8.
• Determine the mean of the RABs (MRAB) and the mean of the MSEs (MMSE) as follows:

  $$\begin{array}{c}\hfill \mathrm{MRAB}=\frac{\mathrm{RAB}\left(\widehat{\alpha }\right)+\mathrm{RAB}\left(\widehat{\gamma }\right)}{2},\mathrm{MMSE}=\frac{\mathrm{MSE}\left(\widehat{\alpha }\right)+\mathrm{MSE}\left(\widehat{\gamma }\right)}{2}.\end{array}$$

The numerical results are presented in Table A1, Table A2 and Table A3.

Simulation Results

The numerical results shown in Table A1, Table A2 and Table A3 assure that the estimates under the ORSS procedure are more efficient than those obtained under the SRS procedure. This can be clarified by the following points through which we can observe:

• For fixed n and m, the MSEs, RABs, MMSEs, and MRABs of the estimates under the ORSS procedure are less than those obtained under the SRS procedure as the number of cycles (ℏ) increases.
• For fixed n and m, and ℏ, the ORSS procedure is better than the SRS procedure through fewer values of the MSEs, RABs, MMSEs, and MRABs of the estimates.
• The BEs under LINEX LF (at $\rho =1.5$) are better than those under SE and GE LFs because they have the lowest values of MSEs, RABs, MMSEs, and MRABs.
• For fixed ℏ and n, by increasing m, the MSEs, RABs, MMSEs, and MRABs decrease.
• For fixed ℏ and m$(=60\%,80\%$, and $100\%$ of the sample size), by increasing n, the MSEs, RABs, MMSEs, and MRABs decrease.

The above results are true except in rare states, this may be due to fluctuations in the data.

Remark 1.

Using historical samples and the empirical Bayes technique, the hyperparameters can be estimated if they are unknown; for example, see [30]. As an alternative, the hierarchical Bayes method could be used, which makes use of a suitable prior for the hyperparameters, see [31].

Remark 2.

During the simulation study, we checked some distributions as prior ones, such as log-normal and logistic distributions but we did not obtain good results. When we considered the gamma as a prior distribution we obtained good results. This is considered evidence that specific distributions should be used as prior ones under some given conditions, see [4].

Remark 3.

The integrals presented in Equations (36), (37), (39), (40), (42), (43) and (48)–(53) are obtained numerically using the command "NIntegrate" included in Mathematica software.

7. Conclusions

The ORSS technique has attracted more attention in the last few years due to the fact that estimates under ORSSs are more efficient than those under SRSs. In this paper, we discussed the technique of ORSS under progressive-stress ALTs when the lifetime of a unit under use stress follows the exponential distribution. Under type-II censoring and based on symmetric and asymmetric LFs, the BEs of the considered parameters are studied based on ORSS and SRS. Real and simulated data sets were used to illustrate the theoretical results presented in this paper. Finally, a simulation study followed by numerical calculations was performed to evaluate the performance of BEs under ORSS and SRS. The numerical results assure that the ORSS is more efficient than the SRS as a sampling technique.