Abstract
In this work, we present a numerical algorithm to solve the inverse problem of volumetric sources from measurements on the boundary of a non-homogeneous conductive medium, which is made of conductive layers with constant conductivity in each layer. This inverse problem is ill-posed since there is more than one source that can generate the same measurement. Furthermore, the ill-posedness is due to the fact that small variations (or errors) in the measurement (input data) can produce substantial variations in the identified source location. We propose two steps to solve this inverse problem in some classes of sources: we first recover the harmonic part of the volumetric source, and, in a second step, we compute the non-harmonic part of the source. For the reconstruction of the harmonic part of the source, we follow a variational approach based on the reformulation of the inverse problem as a distributed control problem, for which the cost function incorporates a penalized term with the input data on the boundary. This cost function is minimized by a conjugate gradient algorithm in combination with a finite element discretization. We recover the non-harmonic component of the source using a priori information and an iterative algorithm for some particular classes of sources. To validate the numerical methodology, we develop synthetic examples both in circular (simple) and irregular (complex) regions. The numerical results show that the proposed methodology allows to recover the complete source and produce stable and accurate numerical solutions.
Keywords:
inverse problem; harmonic sources; control theory; conjugate gradient method; finite element method MSC:
31A25; 65N20; 65M32; 65N21
1. Introduction
Currently, there is a great interest in research on non-destructive (non-invasive) methods for the detection of sources or unknown characteristic(s) of a system from partial information on the mentioned system [1,2]. Examples of this are medical tomography, industrial process tomography, inverse geophysics, inverse electroencephalography, and inverse electrocardiography [3,4,5,6,7,8,9].
In medical tomography, the objective is to identify a bioelectric source from one or more external manifestation effects produced by that source and measured by means of an electronic device. Non-invasive techniques include magnetic resonance and radio-isotope imaging, which provide functional images of blood flow and metabolism, essential for diagnosing and investigating the brain, heart, liver, kidney, bones, and other organs of the human body. One non-invasive technique for the reconstruction of brain or cardiac electrical activity from electrical potentials measured outside the brain, using electroencephalograms (EEG), and the heart, using electrocardiograms (ECG), is the so-called electrical source imaging, which consists of “reconstructing” the brain or heart activity from potentials measured outside the brain or heart. This method is used in electrocardiography or electroencephalography to determine the location of current sources in the body or brain from voltage measurements; it is also used for diagnosis and therapeutic guidance regarding epilepsy and abnormalities in the conduction of the heart. These last two methods for source identification from measurements at the boundary of a conductive medium are known as the electrocardiographic inverse problem and electroencephalographic inverse problem (we will abbreviate the latter as EIP). In particular, the EIP consists of finding bioelectric sources (which are generated by the electrochemical activity of large conglomerates of neurons that act simultaneously) in the brain from the EEG measured on the scalp. One of the advantages of the EEG is that the information it provides is captured in real-time, in a simple way, and it is non-invasive as well as inexpensive. On the other hand, the EIP is an ill-posed problem because there is a diversity of sources that produce the same measurement, and it is impossible to univocally determine the source that generated the EEG; that is, there is more than one source that can produce or generate the same EEG [10,11]. The ill-posedness of this problem is also associated with numerical instability, i.e., small variations in the EEG can produce substantial variations in the location of the source [5]. In general, sources cannot be determined except for their harmonic component [12,13]. In [13,14], a stable algorithm is presented to identify the harmonic component of the source from noisy data, when the head is modelled by concentric circles or concentric spheres. To find the non-harmonic component of the source, it is necessary to have a priori information, which can be determined from mathematical or physiological considerations [10,12,15,16]. In particular, in [16] the fact that the unknown source belongs to a class of piecewise constant functions is considered a priori information, and the uniqueness of the solution to the inverse problem is proved. Furthermore, the authors presented a stable method to identify an approximate solution within this class of sources when the data includes measurements errors. The method was illustrated in simple geometries.
In this work, a methodology is proposed to recover the complete source in a stable form, in circular and irregular geometries. We employ a variational formulation and distributed control techniques to obtain a numerical method which allows us to find solutions to the inverse source identification problem in a stable way. In the first step, the numerical method allows us to obtain harmonic sources in the interior of a non-homogeneous region (made of two or three conductive layers with constant and positive conductivity in each layer) from noisy measurements on the exterior boundary. The methodology combines conjugate gradient iterations (CG) to find the optimal control and finite element approximations (FE) for the elliptical problems that appear in each iteration of the CG. This methodology has already been used by other authors to solve inverse and control problems in other contexts (see [17,18,19]). The second step consists of recovering the non-harmonic component of the source, taking into account a priori information. We apply the mentioned methodology to 2D synthetic examples, defined in a simple circular domain and in irregular complex regions. The proposed algorithm may be applied and implemented for the identification of 3D bioelectric sources in the brain from the EEG measured on the scalp, which is the object of future study.
The organization of this work is as follows. Section 2 introduces a mathematical model from where the operational statement of the inverse source problem is established. In Section 3, the variational formulation of the inverse problem is presented as a control problem. Additionally, the derivative of the cost function is presented, and the optimality conditions of the minimization problem are established. In Section 4, the CG algorithm is presented in detail, as well as the discretization of the elliptical problems using FE. We also include the analytical solutions to the forward and inverse problems in a circular geometry when the region is made of two and three conducting layers. In Section 5, some numerical results are presented to recover harmonic functions defined in the interior region. These examples are developed in a circular and irregular two-dimensional region made of two or three conductive layers. Section 6 presents three examples for which we compute the non-harmonic component of the complete source, besides its harmonic component and the complete source using a priori information. Finally, in Section 7, some conclusions are established.
2. Mathematical Model
2.1. Mathematical Model for a Region with Two Conductive Layers
Let us consider the following boundary value problem defined in a region (see Figure 1a):
where represents the Laplace operator, is the boundary of , is the exterior boundary of , and also of , i.e., , denotes the normal derivative of on with respect to the unit normal vector , exterior to for , f denotes the source, , , 2, where u is the electric potential in generated by f, which is the solution to problems (1)–(5). From now on, the measurement on generated by f will be denoted by . This electrostatic model has been widely used for the study and analysis of the EIP in [5,11,13,14,20,21,22,23,24], among others. For the EIP, this model can be deduced from Maxwell’s equations and from some experimental results, where f represents the bioelectric source located in the brain , and the measurement V is the EEG on the scalp . The boundary conditions (3) and (4) are the transmission conditions, and the boundary condition (5) indicates that air conductivity (i.e., of ) is zero [25,26,27,28].
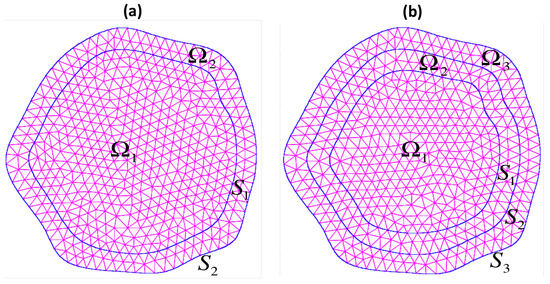
Figure 1.
(a) Irregular region compound by two coupled homogeneous conductive media and , where and . (b) Irregular region compound by three coupled homogeneous conductive media , and , where , is the interior boundary of , and .
From the Green’s formulas, f satisfies the following compatibility condition:
When there are superficial sources, they are defined on and the boundary condition, corresponding to the flux on the boundary , changes. For example, in inverse electroencephalography, these superficial currents correspond to bioelectrical cortical sources [29,30].
In this work, only volumetric (distributed) sources defined in region are considered, so we neglect the activity of superficial sources. We will call problems (1)–(5) the volumetric boundary problem (VBP). We consider the following definitions concerning the forward and inverse problems:
Definition 1.
Given a function f defined in , the forward problem (FP) consists of finding the measurement , where u is the solution to the VBP.
Definition 2.
Given a function V defined on , the inverse problem (IP) consists of finding a source f defined on such that the solution u to the FP corresponding to f satisfies that .
2.2. Mathematical Model for a Region with Three Conductive Layers
In this case, (see Figure 1b) with different positive constant conductivities , , and , respectively, and the VBP is given by:
where the notation is the same as before, but now . For the numerical solution to problems (7)–(14), we use the FE, since it is a very robust method which can be applied to the VBP, defined in both simple and irregular regions; also, it is well adapted to variational formulations.
2.3. Operational Formulation of the Inverse Problem
Let , , , and be the spaces of square integrable functions defined in , on and in , respectively. We denote by , , and the corresponding Sobolev spaces of the functions in and , respectively, whose first generalized derivatives are also square integrable functions. We denote by , the subspaces of , which contain the traces of the functions in . Finally, , , denotes the (closed) subspaces of harmonic functions in . We will use the subscript ⊥ for any of the previous spaces to denote the space of functions that are orthogonal to the constants with respect to the corresponding scalar product. More precisely, if W is any of the previous spaces, then , where is the scalar product of W.
2.3.1. Weak Solution to VBP
Definition 3.
Given , which satisfies condition (6), a function is called a weak solution to problems (1)–(5), or to problems (7)–(14), if it satisfies
where , , with or 3, and or (see [31]).
The compatibility condition (6) is necessary and sufficient for the existence and uniqueness of the weak solutions u to the VBP. Formally, we have the following:
Theorem 1.
The condition is necessary and sufficient for the existence of the weak solution u to the VBP. In this case, there is a unique weak solution u that satisfies and
where constant C does not depend on f (see [31]).
2.3.2. Operational Formulation
Consider the spaces , , , and with them the continuous operator , defined by , where u is the weak solution to (15) given f. Notice that the composition of T with the compact trace operator defines the compact operator , given by . Then
Therefore, the inverse problem in Definition 2 can be expressed as follows:
The following theorems are proved in [13]:
Theorem 2.
, where is the subspace of harmonic functions of .
Theorem 3.
is dense in .
Theorem 2 indicates that the inverse problem has no unique solution, except in the subspace of harmonic functions orthogonal to the constants . Theorem 3 indicates that does not always hold exactly, but there are approximate solutions such that for each , where n is a natural number.
From the numerical point of view, the main drawback is that the operator A is a compact operator, so when it is restricted to harmonic functions, , its inverse is injective but not continuous, and small errors or perturbations over measurements V will produce substantial variations in the process of identifying the source f. Therefore, the inverse problem is ill-posed in the sense of Hadamard. It is well known that, in general terms, identification problems are ill-posed [2].
3. Variational Formulation of the Inverse Problem: The Optimization Model
As a first step, we will consider the inverse source identification problem restricted to the subspace of the harmonic functions, which are orthogonal to the constants. To handle numerical instability, we take advantage of the density property of Theorem 3 and formulate an optimization model whose minimum is an approximate solution. To handle numerical instability, we will use the Tikhonov regularization. The density property of Theorem 3 allows us to find an approximate solution to the inverse problem by minimizing a quadratic functional, which will be presented in the following Section. This quadratic functional is equivalent to the Tikhonov functional.
3.1. Control Approach of the Inverse Problem: The Cost Functional
A control problem, related to the inverse source identification problem, where the control f acts on region , is the following:
Findthat minimizes the following cost functional
and that satisfies the constraint.
The constraint may not be exactly satisfied. However, from the computational point of view, it is enough to obtain good approximate solutions. Taking advantage of the density result (Theorem 3), we can achieve one of these approximate solutions by adding to (18) a penalized norm of the difference , obtaining the new quadratic functional:
where k is the penalty parameter. Therefore, we can approximate the exact controllability problem (18) by the following one (of the approximation by penalty type):
Standard continuity and strong convexity arguments guarantee that (20) has a unique minimum (see, for instance [17]), characterized by
where denotes the differential of the quadratic functional .
3.2. Tikhonov Regularization: The L-Curve Method for the Regularization Parameter
Minimizing functional (19) is equivalent to minimizing the following Tikhonov functional:
with regularization parameter . Thus, we can apply results from Tikhonov regularization for choosing this parameter. Considering the case with noisy measurements , let be an approximation of f where is the operator associated to the Tikhonov regularization strategy. For the sake of clarity and completeness, we include the following theorems here ([32]):
Theorem 4.
is boundedly invertible, and is the unique solution to the normal equation . Furthermore, .
Theorem 5.
Any choice such that and ensures that
when . In this case, is called admissible and obviously
There are different methods for determining a suitable regularization parameter , which should balance the two terms of the functional . Two of them are the discrepancy principle and the L-curve method. The name L-curve comes from the shape of the curve and is a log-log plot of the norm of a regularized solution versus the norm of the corresponding residual norm. More geometrical and analytical details can be found in ([33]).
3.3. Functional Derivative of the Tikhonov Functional
Theorem 6.
The derivative of the Tikhonov functional is given by
where is given, and w is the solution to the adjoint problem:
Notice that , in (31), is the solution to the state Equations (7)–(14) and here.
Proof.
where is the residual term. We have considered that A is linear, , where u is the solution to the state Equations (7)–(14), and , where is the solution to the following perturbed problem:
Applying Green’s formulas to the adjoint problems (24)–(31) and to the above perturbed problems (33)–(40), we obtain:
Since on , we obtain that implying that (32) becomes
Now, is the solution in to problems (33)–(40); then, by Theorem 1, there is a constant , such that . Thus, , as in , which means that as in . Therefore, the derivative of functional (21) is given by
where, as mentioned before, w is calculated in two steps:
- (1)
- Given , solve the state Equations (7)–(14) to obtain .
- (2)
- Then, solve the adjoint problems(24)–(31) to obtain w.
□
Optimality Conditions
Considering that , let be the unique solution to the control problem (20), and denote by and the solutions to (7)–(14) and (24)–(31), respectively. It follows, from the previous Subsection, that the solution to the control problem is characterized, along with and , by the following relationships (optimality system):
These relationships suggest an iterative fixed-point approach to solve the control problem. In the next Section, we show that this solution can be achieved using a conjugate gradient algorithm operating in space . This methodology has been used in other works to solve inverse problems in elliptic differential equations in similar or different contexts (see, for example, [18,19,30,34]).
4. Conjugate Gradient Algorithm
The controllability problem (20) is a well-posed minimization problem in the control space , a real Hilbert space for the inner product . Therefore, the solution to (20) can be achieved by the conjugate gradient algorithm given in the Algorithm 1. For it we consider the following elliptic problems:
Remark 1.
In the Algorithm 1, the expression for (in Step 2) is the exact solution to the one-dimensional minimization problem
at each iteration. It is also possible to solve this one-dimensional program numerically, but most likely, it will be less efficient.
| Algorithm 1. Conjugate Gradient |
|
Remark 2.
Notice that , , and belong to , so their integrals must be zero. To numerically enforce this property at every iteration, each of these functions, denoted by v, is replaced by with
where μ denotes the Lebesgue measure in , or 3. Then, it is clear that
Of course, the above algorithm is easily adaptable to the case of two coupled regions or extended to the case of models with more layers, when each layer has constant conductivity.
4.1. Discretization of Elliptic Problems by Finite Element Method
The computational implementation of the Algorithm 1 requires solving two elliptic problems at the initialization step, namely problems (45) and (46), as well as problems (47) and (48) at each iteration. The numerical solution to these problems is standard and can be achieved by any approximation method. We advocate using a finite element approximation since it is well-suited to the fact that we are dealing with a variational formulation of the inverse problem [35].
Then, to describe the numerical approximation procedure, we consider the following elliptic model problem:
where is a bounded region in ( 2, or 3) with sufficiently smooth boundary , and is constant in . This problem has a unique solution in if f and satisfy the compatibility condition . The variational formulation of this boundary value problem is:
Find such that
The corresponding variational formulation of the elliptic problems (7)–(14), in case of three coupled regions, with on , is given by (15) and is discretized in a similar way.
To approximate , we consider a finite element triangulation of , where h is the length of the largest edge of . That is, region is approximated by a polyhedral region (see Figure 1). Then, is approximated by the discrete space
where denotes the space of continuous functions defined on ; is the set of polynomials of degree less than or equal to one. Then, the variational problem can be approximated by the following discrete variational formulation:Find such that and
In this formulation, and are, respectively, piecewise linear approximations of f in and on . The first two integrals in (52) may be calculated using the trapezoidal rule on each triangle , since .
The various discrete linear elliptic problems occurring in (45)–(48) are all associated with the same matrix, differing only by their right-hand sides. This matrix is sparse, symmetric and positive semidefinite, then singular. However, the corresponding linear system can be solved by a sparse Cholesky solver after fixing to zero the value of the unknown function at one node of the mesh. In the end, we subtract the mean value of the numerical solution (as indicated above, in Remark 2).
4.2. Analytic Solution to Forward and Inverse Problems in a Circular Domain
For the special case when the domain is circular, we can compute an analytic solution to the forward and inverse problem using the Fourier series method. The numerical results obtained with this method are used to validate the algorithm proposed above.
For instance, when and is a circular domain of radius , is a circular annular domain with interior radius and exterior radius , and is a circular annular domain with interior radius and exterior radius , a harmonic source has the following representation with circular harmonics:
where and , , are its Fourier coefficients.
When the domain is coupled by three concentric circles centered at the origin, we seek solutions to the VBP as follows:
where , , , and , for , 2, are coefficients to be determined.
Assuming that these series converge in an norm, for , 2, 3, function in (54) is biharmonic in , and functions defined in (55) and (56) are harmonic in and , respectively. The Fourier coefficients in (54)–(56) are computed from the boundary conditions (10)–(14): , , , , , , , , , , , ,
where
Evaluating (56) on , the solution to the forward problem is
where and , with , for all k. On the other hand, given an exact measurement where and are the Fourier coefficients of V, the solution to the inverse problem with noiseless data V is
where and .
We can proceed similarly when the domain is coupled by two concentric circles centered in the origin , with being a circular domain centered in the origin of radius , a circular annular domain centered in the origin with interior radius and exterior radius . If the source f is given by (53), then the solution to the VBP is given by (54) and (55), but now with the Fourier coefficients obtained from conditions (3)–(5): , , , , , , , , where Therefore, the solution to the forward problem is given by
where and . Additionally, given an exact measurement , where and are the Fourier coefficients of V, the solution to the inverse problem with noiseless data V is given by (53), where for each k
5. Numerical Results for Harmonic Sources
In this Section, we present numerical results when the volumetric source to be identified is harmonic. The examples presented in this section are designed to test the numerical algorithm introduced in Section 4. Numerical examples for the general case (non-harmonic) will be presented in the next section.
For each example, we generate synthetic data V in either a simple domain or an irregular domain made of either two or three layers. To generate this data, we solve the state equation to obtain the exact potential u from a known harmonic source , and then we get (forward problem). Then, we solve the inverse problem with the numerical algorithm using V as input data to the control problem (20). The numerical recovered source will be denoted by , where h is the mesh size, n is the number of conjugate gradient iterations (cg. iters.) to achieve the desired accuracy (given by tolerance ), and is the regularization parameter obtained by the L-curve criterion. Similarly, the numerical potential obtained with this numerical source is denoted by .
Noisy data with are generated, adding to noiseless data V ‘white noise’ with mean and standard deviation . Using the function of MATLAB, we define the random vector
with length the number of mesh nodes on the exterior boundary . The corresponding approximate solutions are denoted by and . Of course, is the regularization parameter that depends on the level of noise (see Section 2.2).
From now on, we will use the following notation for the relative errors:
For the computational implementation, the elliptic subproblems, at each step of the Algorithm 1, are solved using FE with linear triangular elements, so we generate an initial mesh called with mesh size , where indicates the number of nodes (vertices) and denotes the number of elements (triangles). Successive regular refinements will be denoted by for .
Example 1.
We present a case with a simple circular domain made of two and three layers and a harmonic source. We consider a circular region Ω, which is made of either two or three circular layers. For the first case, is determined by two concentric circles with circumferences and of radii and , and constant conductivities and , respectively. For the second case, is determined by three concentric circles with circumferences , , and of radii , , and , and constant conductivities , , and , respectively. In both cases, for the harmonic source in these examples, we choose the exact function with , which in Cartesian coordinates is , . For the second case, the exact potential can be computed with Formulas (54)–(56), and its value on the exterior boundary V is generated by (57). Observe that only the second mode survives in the expansion of each Fourier series. After computing the Fourier coefficients and transforming them to Cartesian coordinates, we obtain (for the case of the domain Ω with three layers):
where the values of the coefficients , , , , , are obtained using the expressions given in Section 4.2, and the values of parameters , , , , and are given above in this Section.
Similar solutions in , in , and V on are obtained for the case of the domain with two layers.
- Case with exact data. We assume that measurement V on is noiseless. The solution to the inverse problem is achieved with the regularization parameter and tolerance (for the stopping criterion of the Algorithm 1). Table 1 shows that the relative errors decrease with each refinement of the coarse mesh . These results show numerical convergence regarding the finite element discretization. Additionally, the accuracy of the solution in this case is very good for both the two and three coupled circular regions.
 Table 1. Convergence of the numerical results obtained with two refinements of mesh , for source .
Table 1. Convergence of the numerical results obtained with two refinements of mesh , for source .
- Case with noisy data. Here, we consider noisy data on with three different noise levels . The coarsest mesh is the same as before, and the numerical solutions are achieved with tolerance to stop the conjugate gradient iterations and with the regularization parameters shown in Table 2. This Table shows that the method to find the numerical solutions to the ill-posed inverse problem is stable. Actually, and are bounded by the perturbation when . Additionally, when noise vanishes, the numerical solution converges to the one obtained with noiseless data.
 Table 2. Numerical results with noisy input data , and source .
Table 2. Numerical results with noisy input data , and source .
To better illustrate, below we include several figures which show plots of numerical results for the case of three circular coupled media and . The corresponding figures for two circular coupled media are qualitatively similar and are not included.
Figure 2 shows a plot of noisy data along with exact data V and the numerical external potential obtained with the recovered source . Figure 3 and Figure 4 show plots of the numerical source and the numerical potential , respectively.
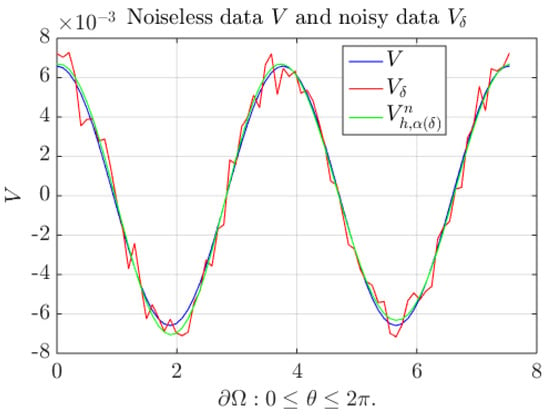
Figure 2.
Plots of V (blue), (red), and the recovered potential (green) on , with . Case of three circular coupled media.
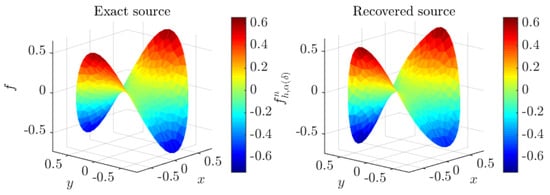
Figure 3.
Exact source f and its corresponding approximate solution at iteration when , obtained with mesh . Case of three circular coupled media.
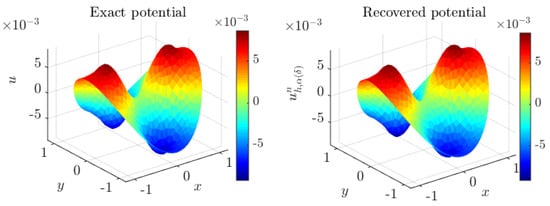
Figure 4.
Exact potential u and its corresponding numerical solution at iteration when , obtained with mesh . Case of three circular coupled media.
Example 2.
We present here a case with a simple circular domain made of two and three layers and a harmonic source. For this example, we consider the harmonic source , , or, in polar coordinates, , . This function does not have a finite Fourier expansion, so it is approximated by a truncated series with N terms. The Fourier coefficients and , , are obtained numerically using the function quad2d of MATLAB. We choose , since for this value . Hereafter (in this example), we will call the exact source and will denote it as f. The exact solution u to the state Equations (7)–(14) is obtained with the first terms of series (54)–(56) for the domain with three circular coupled media. Similarly, exact data V are generated with the first terms of series (57). Synthetic data and the exact potential for the case when the domain is compound of two coupled media are obtained in the same way.
- Case with exact data. Notice that data V are not really exact, but they are an accurate approximation on . The solution to the inverse problem is achieved with the regularization parameter and tolerance for the case of two conductive layers and for three conductive layers, as shown in Table 3. This Table shows that the numerical solutions are still accurate and convergent with respect to h.
 Table 3. Numerical results show convergence regarding two refinements of mesh for .
Table 3. Numerical results show convergence regarding two refinements of mesh for .
- Case with noisy data. Table 4 shows numerical results for different levels of noise for perturbed data and a discretization obtained with mesh . Again, the numerical results show the stability of the numerical method, and the relative errors are all bounded above by perturbation when .
 Table 4. Numerical results with noisy input data for and .
Table 4. Numerical results with noisy input data for and .
Again, below we include Figure 5, Figure 6 and Figure 7 to compare the numerical solutions with the exact ones only for the case of the three circular coupled domain and when .
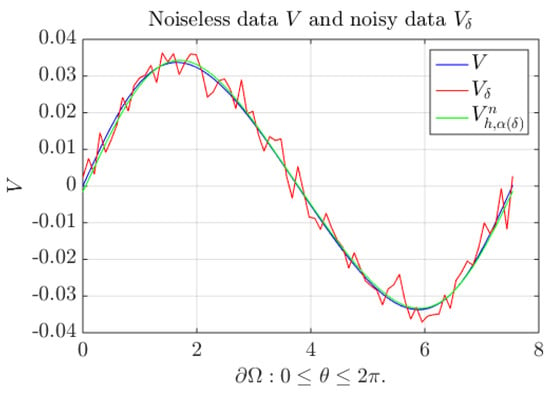
Figure 5.
Plots of V (blue), (red), and recovered potential (green) on , with . Case of three circular coupled media.
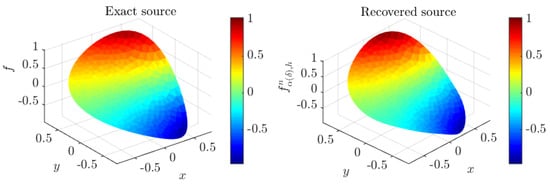
Figure 6.
Exact source f and its corresponding approximate solution at iteration when , obtained with mesh . Case of three circular coupled media.
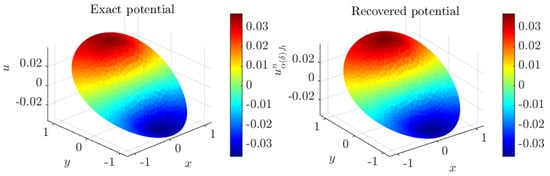
Figure 7.
Exact potential u and its corresponding approximate solution at iteration when , obtained with mesh . Case of three circular coupled media.
Example 3.
Solution to the inverse problem in an irregular region. In this example, we consider the irregular regions shown in Figure 1. For the region with two coupled media , the conductivities are and , while for the region with three coupled media , we chose the conductivities as , , and . The exact harmonic source is given by
where , . As before, μ denotes the Lebesgue measure on .
Again, with this source, we generate synthetic data , where u is the solution to the forward problems (1)–(5) for the case of two coupled media, or (7)–(14) for the case of three coupled media. Now, we are able to compute only the numerical solutions, so we compute the solution for each case, using the FEM with a very fine mesh to obtain an accurate solution. We employ the fine meshes and for two coupled media and three coupled media, respectively. These meshes are obtained after three successive regular refinements of the triangular meshes and shown in Figure 1.
- Case of noiseless data. We consider V, generated on , as mentioned in the previous paragraph. Again, for both cases (two and three coupled media), the regularization parameter employed is , and the tolerance to stop the conjugate gradient iteration is . The numerical results in Table 5 show that the relative errors decrease at each refinement. This indicates that the initial starting mesh for both cases is good enough to get accurate numerical solutions.
 Table 5. Numerical results show convergence regarding two refinements of mesh for the source given by (66).
Table 5. Numerical results show convergence regarding two refinements of mesh for the source given by (66).
- Case with noisy data. Table 6 shows the results for the case of noisy data for different values of using mesh . Again, the numerical results show that the proposed method solves the inverse ill-posed problem in a stable way. This time, all relative errors are bounded above by RE(,V) only for and , but not for . Observe that, for the case , the value of is below the values , , obtained with noiseless data . Then, the discretization error dominates over the error due to the perturbation in the data when the noise is small (). Remember that, in this example, V is not exact, but obtained by discretization with a very fine mesh.
 Table 6. Numerical results with noisy input data for and source given by (66).
Table 6. Numerical results with noisy input data for and source given by (66).
Below, we show Figure 8, Figure 9 and Figure 10 with plots of exact (synthetic solutions) and numerical solutions. Again, we show figures for only three coupled media. For two coupled media, the figures are qualitatively similar, and the most significant difference is the magnitude of the electric potential, which for this case, is about twice the one for three coupled media.
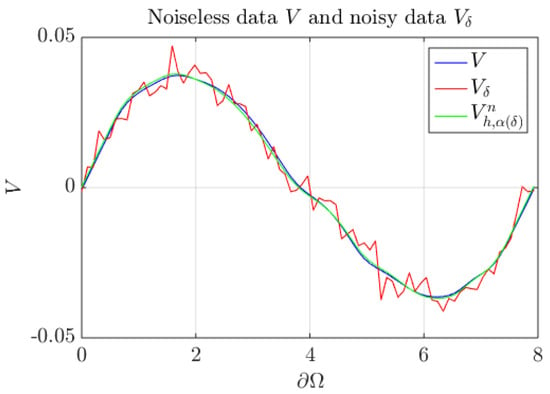
Figure 8.
Plots of V (blue), (red), and the recovered potential (green) on , with . Case of three irregular coupled media.
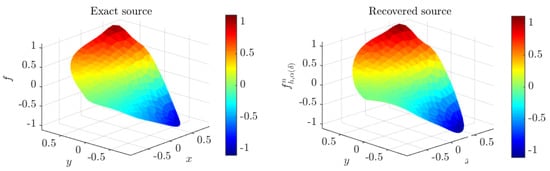
Figure 9.
Exact source f and its corresponding approximate solution at iteration when , obtained with mesh . Case of three irregular coupled media.
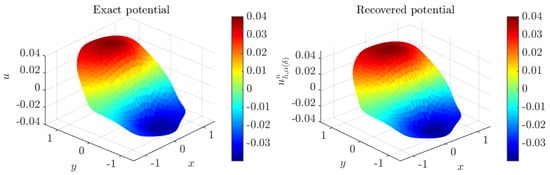
Figure 10.
Exact potential u and its corresponding approximate solution at iteration when , obtained with mesh . Case of three irregular coupled media.
In summary, we have found that the numerical method to solve the inverse problem for the identification of harmonic sources is stable and produces accurate solutions for all cases in the previous three examples. We obtain convergence of the numerical results to the exact solutions when input data V are exact, i.e., noiseless data, for both simple and complex domains with two and three coupled media. For noisy input data, the stability of the method is demonstrated numerically since the relative errors of the numerical solutions are bounded above by the relative error of noisy input data (taking into account the size of the mesh in which the numerical experiments were done), except when the discretization error exceeds the level of noise added to the input data.
6. Identification of Non-Harmonic Sources
We know that a general source is the direct sum of two sources; one of them is a harmonic function and the other one belongs to , i.e.,
In previous sections, we have dealt with the computation of the harmonic part , which can be recovered from measurements on the exterior boundary . We emphasize that
In this section, we are concerned with the non-harmonic component , which can be identified using a priori information. We present a preliminary study of the problem in this Section. We also consider the case when region is made of two homogeneous media for simplicity. Below, we include three examples. Some related results can be found in [12,16]. When the sources depend on a finite number of parameters, we can apply traditional methods used to find them. However, we are interested in applying a priori information and the harmonic function recovered from the measurements to determine the parameters as an alternative for more complex sources.
Example 4.
Case when the general source is harmonic in a subdomain ω of . Let ω be a subdomain of with (see Figure 11). In this example, we are concerned with the class of sources in that are harmonic in the subdomain ω and vanish in the complement . Of course, must satisfy compatibility condition (6). We denote this particular class of harmonic sources by , which is a uniqueness class, i.e., two different functions of this class produce different measurements. Then, from (67), with , we obtain:
We are interested in computing from measurements V on . Since it is the subtraction of two harmonic sources, in and in , we can apply the algorithm designed to compute harmonic sources in three and two coupled regions to obtain the unique sources and , respectively. More precisely, we apply the Algorithm 2.
| Algorithm 2. To identify the non-harmonic component |
|
We choose and , and the exact harmonic source defined as in (66), but now with slightly modified:
where . Again, we compute the synthetic measurement from the discrete solution to (1)–(5), computed with the FEM using a very fine mesh , like the one used in Example 3 of the previous Section. Additionally, the referent discrete sources and are computed with Algorithm 2 using this fine mesh.
Table 7 shows numerical results for noiseless data V and noisy data . The values shown in that table are obtained with the coarsest triangular mesh with discretization parameter . These results show that the numerical solutions are obtained in an stable way. We observe that all relative errors decrease when the noise of the input data decreases. Observe that the relative errors associated with the numerical calculation of are bounded above by for and , but not for , because in this case, the discretization error dominates.

Table 7.
Numerical results with synthetic data obtained with the source given by (69) using mesh . The tolerance to stop the conjugate gradient iteration for both cases is .
Figure 11a shows the two coupled domain and the subdomain . Figure 11b shows the synthetic noisy measurement , generated by (61) with , and the numerical potentials , , produced by the computed sources and , respectively.
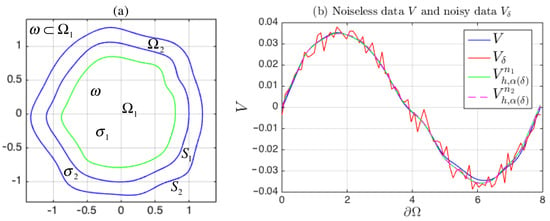
Figure 11.
(a) Irregular region with two coupled media and subdomain . The boundary of is shown in green line, and the boundaries of and , denoted by and , are shown in blue line. (b) Plots of V (blue), (red), and the recovered potentials (green) and (magenta) on , with .
Figure 12, Figure 13 and Figure 14 show the recovered sources, , , and , respectively. They are compared with to the exact solution and the computed sources , , obtained from noiseless data V.
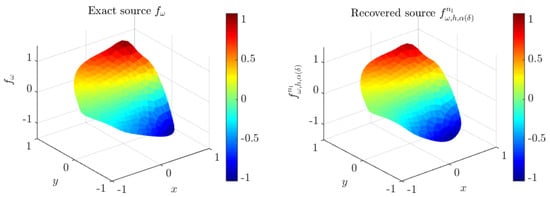
Figure 12.
Exact source and its corresponding approximate solution at iteration in region when , obtained with mesh .
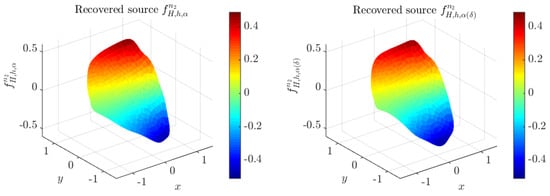
Figure 13.
Recovered sources and at iteration in region when , obtained with mesh .
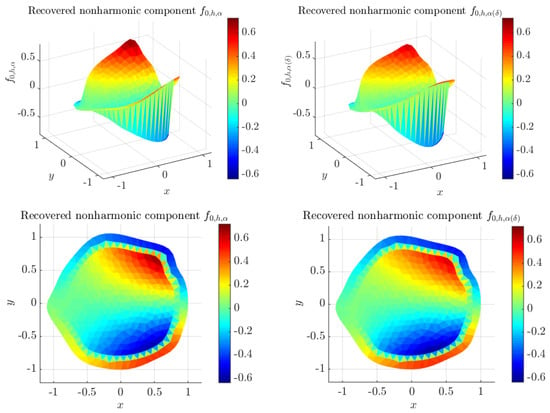
Figure 14.
Recovered sources and at iteration in region when , obtained with mesh .
Example 5.
Case of a particular class of piecewise constant sources. Let be a class of piecewise sources that take two constant values and known in , such that f takes the value in a subset and in . We consider the subclass of sources such that the sets are closed circles contained in with , where all circles ω have the same radius. Let be the center and the radius of ω. Then, each is of the form
where is the indicator function of ω. Since must be orthogonal to the constants, we obtain
Then, and , and can also be written as
The set is a class of uniqueness to identify the source of the VBP (1)–(5) from a measurement V on (see Theorem 5.1 in [16]). To solve the inverse problem in a two coupled region (circular or complex) with conductivities and , we applied the Algorithm 3.
| Algorithm 3. To identify a source |
|
For circular regions, a similar algorithm is given in [16].
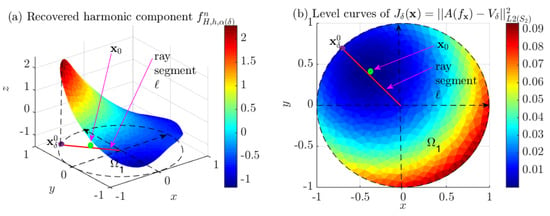
Figure 15.
Case of two circular coupled region : (a) recovered harmonic component (in region ) corresponding to the exact complete source , for , obtained with Algorithm 1, which applies the finite element using a triangular mesh with a mesh size , for Method 3 presented above. (b) Level curves of the functional , where , for , and is the point in which the minimum is reached, for the Iterative Method 3.1 presented above. Similar Figures are obtained for the case of two irregular coupled regions and are not included.
We apply this algorithm with stopping parameter and two fixed step sizes and 0.01 to identify the source in for the two coupled domains shown in Figure 16a, with conductivities , for , , respectively, where the exact set has center and radius . The synthetic data are generated from the exact source (72) with , , and .
Table 8 shows numerical results from noisy data using a triangular mesh with . Remember that the only free parameter to completely determine is the center of . These results show that the algorithm approximates the exact source from noisy data in a stable way, since the errors and are bounded above by for and , except for , where the discretization error dominates. Additionally, observe that similar numerical results are obtained for the step size , used to apply the Iterative Method 3.1.
Figure 16b shows the noisy measurement , generated by (61) with , along with the numerical potential generated by the recovered source obtained with Algorithm 3 and iterations of the Iterative Method 3.1. The exact and the numerical recovered sources are shown in Figure 17.
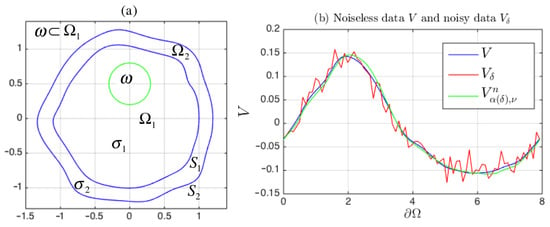
Figure 16.
(a) Irregular two coupled region with the circular subdomain . The boundary of is shown in green line, and the boundaries of and , denoted by and , are shown in blue line. (b) Exact and noisy data on , V (blue) and (red), along with the recovered potential (green), for .
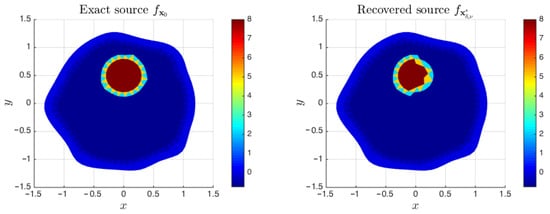
Figure 17.
Exact source and the numerical solution obtained at iteration with the Iterative Method 3.1 using mesh . Case with .

Table 8.
Numerical results obtained from noisy input data in the region shown in Figure 16a. The tolerance to stop the conjugate gradient iteration for both cases is and exact source given by (72), using mesh .
Table 8.
Numerical results obtained from noisy input data in the region shown in Figure 16a. The tolerance to stop the conjugate gradient iteration for both cases is and exact source given by (72), using mesh .
| Using Algorithm 3 with and Step Size . | ||||
|---|---|---|---|---|
| 0 | 0.01 | 0.05 | 0.1 | |
| 0 | 1.7704 | 8.7372 | 1.8427 | |
| n (cg. iters.) | 2 | 2 | 2 | 2 |
| (−0.1356, 1.0604) | (−0.1356, 1.0604) | (−0.1356, 1.0604) | (−0.1356, 1.0604) | |
| (−0.9761, 0.7628) | (−0.9761, 0.7628) | (−0.9761, 0.7628) | (−0.9761, 0.7628) | |
| (number of iters.) | 12 | 12 | 12 | 11 |
| (−0.0627, 0.4900) | (−0.0627, 0.4900) | (−0.0627, 0.4900) | (−0.0658, 0.5148) | |
| 4.6883 | 4.8781 | 7.7204 | 1.5390 | |
| 6.3493 | 6.3493 | 6.3493 | 6.7525 | |
| Using Algorithm 3 with and Step Size . | ||||
| 0 | 0.01 | 0.05 | 0.1 | |
| 0 | 1.6687 | 8.9383 | 1.4726 | |
| n (cg. iters.) | 2 | 2 | 2 | 2 |
| (−0.1356, 1.0604) | (−0.1356, 1.0604) | (−0.1356, 1.0604) | (−0.1356, 1.0604) | |
| (−0.9761, 0.7628) | (−0.9761, 0.7628) | (−0.9761, 0.7628) | (−0.9761, 0.7628) | |
| (number of iters.) | 28 | 28 | 28 | 28 |
| (−0.0633, 0.4949) | (−0.0633, 0.4949) | (−0.0633, 0.4949) | (−0.0633, 0.4949) | |
| 4.6883 | 4.8676 | 8.3866 | 1.1955 | |
| 6.3538 | 6.3538 | 6.3538 | 6.3538 | |
Example 6.
Comparison with the method given in [16] for circular regions. In this example, we will compare the results obtained by applying Algorithm 3 with those obtained by applying the method introduced in [16] for the case of two coupled circular regions Ω and circular subdomains , similar to the one shown in Figure 18a.
We employ the same parameter values and and the exact source defined by (72) with , , and . This time, the closed circle ω has a center at and the same radius .
The method in [16] employs circular harmonics (a Fourier series technique) to solve both the FP and the IP using relations (53)–(60) in Section 4.2 (in the case of two coupled circular regions ). Therefore, to numerically recover the complete source in the circular geometry, the steps in Algorithm 3 can be simplified. For instance, in Step 1 of Algorithm 3, we may generate the harmonic component , the solution u to the VBP, and the synthetic data V, employing the first harmonics of each of the corresponding Fourier series, using polar coordinates. Then, these functions are not exact but accurate approximations. On the other hand, for the case of noisy data , the number of Fourier terms to compute the harmonic component of the approximate source, denoted by , depends on the level of noise (see Reference [16]). For this example and the noise levels , , and , the number of Fourier terms are , 2, 3, respectively. In Step 2 of Algorithm 3, the MATLAB fmincon routine may be employed to compute the point where takes its maximum on (minimum of ), where only four iterations are needed (see Figure 19a). Finally, in Step 3 of Algorithm 3, again the MATLAB fmincon routine may be employed to find the minimum point of the functional expressed in polar coordinates (i.e., the Iterative Method 3.1 is ignored). Figure 19b shows the functional expressed in Cartesian coordinates for different points . The starting point in this minimization is denoted by , and the minimum point is denoted by , where is the number of iterations conducted by fmincon. Similar figures are obtained for the recovered harmonic component and when Algorithm 3 is applied (see Figure 15a,b).
We emphasize that the numerical results obtained with the simplifications described in the previous paragraph are compared with the numerical results obtained without any simplification in the steps of Algorithm 3. Table 9 shows the numerical results obtained with both methods for the case of noisy data using a triangular mesh with . The step size when the Iterative Method 3.1 is used is .

Table 9.
Numerical results with noisy input data for the two coupled circular region shown in Figure 18a. The tolerance to stop the conjugate gradient iteration for both cases is , with the exact source given by (72), mesh .
Therefore, as expected, the numerical results in Table 9 show that both Algorithm 3 and the method proposed in [16] are stable regarding noise in the input data. Additionally, the numerical results are very similar for both methods with the given discretization parameters.
Figure 18b shows the noisy data for , generated by (61), along with the computed potential obtained from the recovered source at iteration of the Iterative Method 3.1. This figure also shows the potential obtained from the recovered source with the method proposed in [16] at iteration . Figure 20 shows the recovered source obtained with Algorithm 3. Finally, Figure 21 shows the recovered source obtained with the method proposed in [16]. These two last Figures show that the numerical results obtained with both methods are indistinguishable.
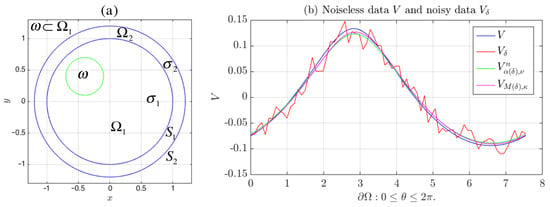
Figure 18.
(a) Circular two coupled region with conductivities and , , and the circular subset . (b) Plots of V (blue), (red) and the two recovered potentials (green) and (magenta) on . Case with .
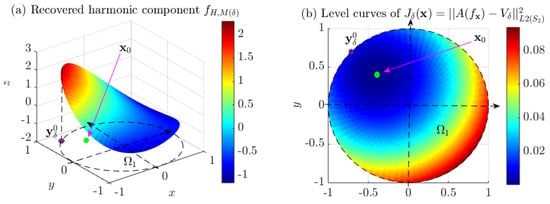
Figure 19.
Case of two circular coupled region . (a) Recovered harmonic component (in region ) corresponding to the exact complete source , for , obtained with the method given in [16]. (b) Level curves of the functional , where for and is the point in which the minimum is reached for the method presented in [16].
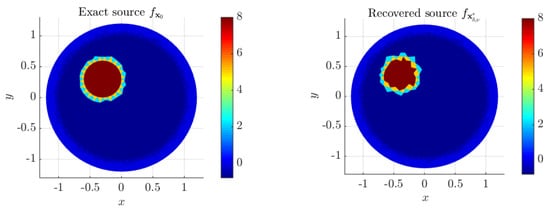
Figure 20.
Exact source and its approximate solution at iteration of the Iterative Method 3.1. Case for using mesh .
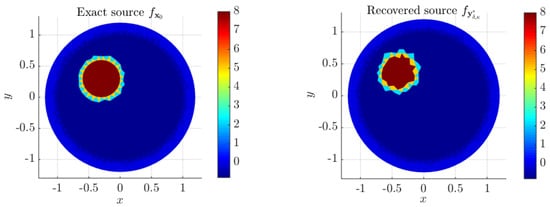
Figure 21.
Exact source and its approximate solution at iteration of the method given in [16]. Case for using mesh .
7. Conclusions
We present a stable numerical algorithm that allows us to compute interior volumetric sources from measurements on the boundary of a non-homogeneous conductive medium. The conductive medium may consist of two or three conductive layers, but the method can be easily extended for models with more layers.
On the other hand, finding the non-harmonic part requires a priori information to guarantee the uniqueness of the inverse problem, as well as additional numerical techniques to compute it, as shown in this work. To the best of our knowledge, nowadays there is not a general method to compute the non-harmonic part of the source, at least for the simple static model (7)–(14). The examples considered in Section 6, especially those for piecewise constant sources in a two-layered medium, elucidate some of the difficulties that arise when attempting to compute the non-harmonic part, so they may help to get a better insight into the problem. Meanwhile, we hope that these experiments also help to build up more general effective numerical techniques to recover either this kind of piecewise constant source or other types.
Author Contributions
Conceptualization, J.J.C.M., C.A.H.G., M.M.M.C., J.J.O.O. and L.H.J.V.; methodology, J.J.C.M., J.J.O.O. and L.H.J.V.; software, J.J.C.M.; validation, J.J.C.M. and J.J.O.O.; formal analysis, J.J.C.M., C.A.H.G., M.M.M.C., J.J.O.O. and L.H.J.V.; investigation, J.J.C.M., C.A.H.G., M.M.M.C., J.J.O.O. and L.H.J.V.; data curation, J.J.C.M. and J.J.O.O.; writing—original draft preparation, J.J.C.M., C.A.H.G., M.M.M.C., J.J.O.O. and L.H.J.V.; writing—review and editing, J.J.C.M., C.A.H.G., M.M.M.C., J.J.O.O. and L.H.J.V.; visualization, J.J.C.M., C.A.H.G., M.M.M.C., J.J.O.O. and L.H.J.V.; supervision, J.J.C.M. and J.J.O.O.; project administration, J.J.C.M. and J.J.O.O.; funding acquisition, J.J.C.M., C.A.H.G., M.M.M.C., J.J.O.O. and L.H.J.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Council of Science and Technology in Mexico (CONACYT), VIEP-BUAP, and PRODEP-SEP.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank VIEP-BUAP and PRODEP-SEP for the support provided. We thank the National Council of Science and Technology in Mexico (CONACYT) for the support provided through a retention project for the first author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kirsch, A. An Introduction to the Mathematical Theory of Inverse Problems, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Isakov, V. Inverse Source Problems; American Mathematical Society: Providence, RI, USA, 1990. [Google Scholar]
- Fraguela, A.; Oliveros, J.; Cervantes, L.; Morín, M.; Gómez, S. A non-iterative algorithm for electrical capacitance tomography. Rev. Mex. Fis. 2005, 51, 236–242. (In Spanish) [Google Scholar]
- Morín-Castillo, M.M.; Arriaga-Hernández, J.; Cuevas-Otahola, B.; Oliveros-Oliveros, J.J. Analysis of dipolar sources in the solution of the Electroencephalographic Inverse Problem. Mathematics 2022, 10, 1926. [Google Scholar] [CrossRef]
- Koptelov, Y.M.; Zakharov, E.V. Inverse problems in electroencephalography and their numerical solving. In Ill-posed Problems in Natural Sciences; De Gruyter: Berlin, Germany, 1992; pp. 543–552. [Google Scholar]
- Sundness, J.; Lines, G.T.; Cai, X.; Nielsen, B.F.; Mardal, K.A.; Toveito, A. Computing the Electrical Activity in the Heart; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Denisov, A.M. Elements of the Theory of Inverse Problems; De Gruyter: Berlin, Germany; Boston, MA, USA, 1999. [Google Scholar]
- Gockenbach, M.S. Linear Inverse Problems and Tikhonov Regularization; American Mathematical Soc.: Providence, RI, USA, 2016. [Google Scholar]
- Kalinin, A.; Potyagaylo, D.; Kalinin, V. Solving the inverse problem of electrocardiography on the endocardium using a single layer source. Front. Physiol. 2019, 10, 13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dassios, G.; Hadjiloizi, D. On the non-uniqueness of the inverse problem associated with electroencephalography. Inverse Prob. 2009, 25, 18. [Google Scholar] [CrossRef]
- Ueno, S.; Wakisako, H.; Matsuoka, S. Determination of the spatial distribution of abnormal EEG and MEG from current dipole in inhomogeneous volume conductor. IL Nuovo Cimento D 1983, 2, 558–566. [Google Scholar] [CrossRef]
- El Badia, A.; Ha Duong, T. Some remarks on the problem of source identification from boundary measurements. Inverse Prob. 1998, 14, 883–891. [Google Scholar] [CrossRef]
- Fraguela, A.; Morín, M.; Oliveros, J. Inverse electroencephalography for volumetric sources. Math. Comput. Simul. 2008, 78, 481–492. [Google Scholar]
- Oliveros, J.; Morín, M.; Conde, J.; Fraguela, A. A regularization strategy for the inverse problem of identification of bioelectrical sources for the case of concentric spheres. Far East J. Appl. Math. 2013, 77, 1–20. [Google Scholar]
- Amir, A. Uniqueness of the generators of brain evoked potential maps. IEEE Trans. Biomed. Eng. 1994, 41, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Fraguela Collar, A.F.; Oliveros, J.J.; Castillo, M.M.; Mones, J.J. Identification of piecewise constant sources in non-homogeneous media based on boundary measurements. Appl. Math. Model. 2015, 39, 7697–7717. [Google Scholar] [CrossRef]
- Glowinski, R.; Lions, J.L.; He, J.W. Exact and Approximate Controllability for Distributed Parameter Systems: A Numerical Approach; Cambridge University Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Rojas, B.I. Inverse Electroencephalographic Problem: Numerical study of the volumetric sources identification subproblem. Master’s Thesis, Universidad Autónoma Metropolitana, Ciudad de México, México, 2015. (In Spanish). [Google Scholar]
- Trinidad, G.Y. Variational Methods in Hilbert Spaces for the Identification of Bioelectric Sources. Master’s Thesis, Universidad Autónoma Metropolitana, Ciudad de México, México, 2018. (In Spanish). [Google Scholar]
- Pursiainen, S.; Sorrentino, A.; Campi, C.; Piana, M. Forward simulation and inverse dipole localization with the lowest order Raviart-Thomas elements for electroencephalography. Inverse Probl. 2011, 27, 17. [Google Scholar] [CrossRef] [Green Version]
- Clerc, M.; Leblond, J.; Marmorat, J.P.; Papadopoulo, T. Source localization using rational approximation on plane sections. Inverse Probl. 2012, 28, 24. [Google Scholar] [CrossRef]
- Dassios, G.; Fokas, A.S. Electro-magneto-encephalography for a three-shell model: Dipoles and beyond for the spherical geometry. Inverse Probl. 2009, 25, 20. [Google Scholar] [CrossRef]
- Fokas, A.S.; Hauk, O.; Michel, V. Electro-magneto-encephalography for the three-shell model: Numerical implementation via splines for distributed current in spherical geometry. Inverse Probl. 2012, 28, 035009. [Google Scholar] [CrossRef]
- Fokas, A.S.; Kurylev, Y. Electro-magneto-encephalography for the three-shell model: Minimal L2-norm in spherical geometry. Inverse Probl. 2012, 28, 11. [Google Scholar] [CrossRef]
- Nunez, P.L.; Srivivasan, R. Electric Field of the Brain, 2nd ed.; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Heller, L. Return current in encephalography. Variational principles. Biophys. J. 1990, 57, 601–606. [Google Scholar] [CrossRef] [Green Version]
- Plonsey, R.; Fleming, D.G. Bioelectric Phenomena; Mc Graw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Sarvas, J. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys. Med. Biol. 1987, 32, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Morín-Castillo, M.; Netzahualcoyotl-Bautista, C.; Conde-Mones, J.; Oliveros-Oliveros, J.; Santillán-Guzmán, A. Stable identification of sources associated with epileptic focus on the cerebral cortex. Rev. Mex. Ing. Bioméd. 2019, 40, 1–14. [Google Scholar]
- Conde, J.J.; Estrada, E.R.; Oliveros, J.J.; Hernández, C.A.; Morín, M.M. Stable identification of sources located on interface of non-homogeneous media. Mathematics 2021, 9, 23. [Google Scholar]
- Mikhailov, V.P. Partial Differential Equations; Mir Publishers: Moscow, Russia, 1978. [Google Scholar]
- Kress, R. Linear Integral Equations; Springer: Berlin, Germany, 1989. [Google Scholar]
- Hansen, P.C. The L-curve and its use in the numerical treatment of inverse problems. In Computational Inverse Problems in Electrocardiology; Johnston, P., Ed.; WIT Press: Southampton, UK, 2001; pp. 119–142. [Google Scholar]
- El Badia, A.; Ha Duong, T.; Moutazaim, F. Numerical solution for the identification of source terms from boundary measurements. Inverse Probl. Eng. 2000, 8, 345–364. [Google Scholar] [CrossRef]
- Brenner, S.C.; Scott, L.R. The Mathematical Theory of Finite Element Methods, 3rd ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).