1. Introduction
Face recognition has been used in various fields, such as personal identification [
1,
2] descriptions of gender and gestures [
3], victim identification, surveillance security systems, medical diagnosis, multimedia communication, and human–computer interfaces [
4,
5]. The face has different cues that help to uniquely identify an individual human. These cues have been widely utilized by authentication and verification algorithms to extract diverse discriminative features, achieving accurate identification [
4,
6]. The wide spectrum of facial features has enabled face recognition challenges to attract broad interest compared to other biometric systems, and it has become one of the most important topics of research [
7,
8,
9]. In addition, the robustness of the face localization and normalization processes are considered the core of an efficient feature extraction process [
10].
Even though many face recognition methods have been studied, system accuracy and processing time remain critical issues and need to be treated carefully. Generally, the results of well known methods do not provide the required accuracy with a fast execution time. Therefore, careful investigation of an accurate and fast face recognition method is required. Moreover, to the best of our knowledge, most of the existing works do not take into consideration the effect of noise in input images. Noise may appear mainly in non-cooperative applications, where the lighting conditions are beyond control.
In order to address the above-mentioned challenges, the present paper proposes a robust face recognition algorithm by using a kind of Hybrid Orthogonal Polynomials (HOPs), specifically, Squared Krawtchouk–Tchebichef polynomials (SKTP) [
11], and a fast overlapping block processing algorithm for feature extraction. These HOPs have been used widely in the literature on image and signal processing because of their powerful capabilities in feature extraction. In addition, the use of the fast algorithm for overlapping block processing [
12] provides the construction of auxiliary matrices, which virtually extends the original image and makes it possible to avoid time-consuming computation loops. The introduced solution reaps the benefits of adopting the SKTP model in multiple dimensions. The energy compaction and localization properties of the SKTP outperform the existing orthogonal polynomials (OPs) and other hybrid-form OPs, which helps to represent the images efficiently and reduces the computation cost of feature extraction. In addition, the extraction of moments from overlapped blocks increases the robustness of the features, which in turn increases the recognition rate. One of the main advantages of the proposed solution is its high robustness to noise in the input images. This is achieved by standard Gaussian smoothing implemented in a novel way: the Gaussian kernel is embedded into the moment calculation step, meaning that it does not increase the computation time.
1.1. Literature Review and Discussion
There are several well known classes of image feature extraction methods: deep learning methods, the eigenface and Fisher face methods, texture-based methods, and projection-based methods. This last approach “projects” facial images on a functional basis and uses these projection coefficients as features. The basis is usually formed by a set of orthogonal functions such as wavelets, harmonic functions or polynomials [
2]. The method we propose in this paper falls into this category.
Deep learning-based approaches have a high level of recognition accuracy; however, they require a large amount of data to perform better than other methods and provide an extreme level of computational complexity [
13,
14,
15,
16,
17]. In the OM-based methods, the features of faces can be computed effectively using Orthogonal Polynomials (OPs) [
11]. In recent works, OPs and their moments have been intensively used for image analysis, shape descriptors, and pattern recognition [
18]. In the moment domain, image components are represented in a transform domain, offering a powerful capability for analyzing them [
11]. Orthogonal moments (OMs) can be defined as scalar quantities that are utilized to characterize the function and capture its significant features. In addition, they are the coordinates of an image in the orthogonal polynomial function [
19,
20]. Furthermore, OMs have the ability to extract features from images that have different geometric invariants, such as translation, scaling, and rotation [
2].
Different types of moments are used in image processing systems. First, geometric moments have been introduced over other kinds of moments due to their explicit geometric meaning and simplicity [
21]. Zernike and Pseudo-Zernike moments are utilized to represent the image with minimal redundancy of information [
22], while fractional quaternion Zernike moments have been used for detection of color image copy–move forgery [
23] because fractional-order polynomials can represent functions better than integer-order polynomials [
2]. Fractional-order Zernike moments have been used efficiently in plant disease recognition [
24]. Legendre moments were used in [
25] to reduce block artifacts. For image analysis, Zernike and Legendre polynomials are used as kernel functions for Zernike and Legendre moments, respectively [
26]. In addition to the ability of Zernike moments to store information about images with minimum redundancy, they have the property of invariance. However, these moments require image coordinate transformations for discrete situations, as they are defined specifically in the continuous domain [
27].
Recently, discrete orthogonal moments have been adopted to overcome the computational cost of image analysis of continuous moments [
28]. Mukundan presented a set of moments to analyze the image using discrete Tchebichef polynomials [
29]. In addition, Tchebyshev moments have been implemented in watermarking algorithms and image encryption algorithms [
30]. For face recognition, an adaptively weighted patch of pseudo-Zernike moments has been used [
31]. Different OMs have been used in this field, such as higher-order OMs [
32], Fourier–Mellin moments [
33], rotation-invariant complex Zernike moments [
34], discrete Krawtchouk moments [
35], Tchebichef moments [
36], orthogonal exponent Fourier moments [
37], 2D orthogonal Gaussian–Hermite moments [
38], and 2D Krawtchouk moments [
21]. The 2D Krawtchouk OMs provided good results in conditions with noise, tilt, and changes in expression [
39]. In comparison with other moments, Gaussian–Hermite moments are considered very robust against noise [
28,
40]. Gaussian–Hermite moments can bne used as a set of useful features to capture the facial expression from face images [
39,
41]. Generally, the extraction methods of image features are classified into two groups: global features-based methods (termed Holistic approaches [
42]) and local features-based methods (termed Component-based methods [
42] or Block Processing-based methods). The former method captures the features from an entire image of a human face, while the local feature extraction method can extract features from certain areas of the face image, such as the eyes, mouth, and chin [
39]. There are various global feature extraction methods, such as Eigenfaces [
43], Fisher faces [
44], Linear Discriminant Analysis [
45], Discrete Cosine Transform [
46], Independent Component Analysis [
47], and others. The global features-based method has achieved superior performance when implemented with different imaging conditions [
48].
In block processing-based methods the extraction of image features can be performed locally using OMs, meaning that processing of the image blocks takes place after partitioning. Block processing is implemented in different applications of signal processing in which signals (images and videos) are partitioned into blocks. These blocks are converted to the transform domain in order to extract the features, which are stored in a memory location equivalent to the image block for processing in the next steps [
12]. In general, block processing-based methods perform better than holistic-based methods [
42]. Local Binary Patterns is one of local feature extraction methods, it is used to partition face image into sub-images where feature distribution is extracted and fused together [
49]. This method is a good descriptor to represent local structures [
50,
51]. A combination of global and local methods, that is called a Fusion (or hybrid) algorithm, is also adopted to achieve a desired face recognition with high accuracy [
39,
48].
Block processing that represents local feature extraction provides high accuracy at the expense of increased computation cost. Different types of transforms have been used for this purpose. Gabor transform [
52] has been used widely to extract the local features [
53,
54], alhough the extracted face features are particularly sensitive to noise. In addition, face recognition methods that use local feature are dependent on face localization and the registration model [
39]. In [
55], an algorithm for face recognition was proposed in which Krawtchouk polynomials with different values of parameters were used for noise-free and noisy environments. This algorithm can overcome the problem of numerical instability by utilizing symmetry properties across polynomials’ diagonals to address the effect of their parameter on feature extraction. The computation cost of this method is considered relatively high. Partitioning of the images using image block processing extracts the blocks of the images and processes them sequentially. This process is not sequential from the perspective of the memory, however, which is considered a key drawback in terms of computation performance and results in an essential gap between CPU speed and memory. Accessing the entire matrix in sequence maintains the spatial locality, although it causes more cache misses and replacements [
12]. Exclusion of further processes accelerates the extraction of local features; in other words, the extraction of local features from the image blocks by discrete transformation decreases computational complexity. This is called the fast overlapping block processing algorithm [
12].
1.2. Contributions
The main contributions of this paper are: (1) design of a robust face recognition method for multiple imaging conditions following the shape-invariant concept; (2) use of powerful hybrid OPs called SKTP to extract image features; (3) utilization of a fast-overlapping block processing algorithm for feature extraction in order to decrease computation time; and (4) application of an embedded filter to suppress noise and maintain the speed of feature extraction.
The rest of this paper is organized as follows:
Section 2 introduces the preliminaries of the fundamental OPs used to form the SKTP; in
Section 3, the methodology is presented;
Section 4 introduces and discusses the obtained results; finally, in
Section 5, the conclusions of this work are drawn.
3. Methodology
In this section, the feature extraction process and the recognition process for face recognition are described. The flowchart of the proposed face recognition method is shown in
Figure 1.
The feature extraction process is the main part of any recognition system. For the sake of accurate results, instead of using a global feature, local feature extraction is used to enable more efficient face recognition. Local features are considered more robust and leverage the recognition accuracy when compared to global features [
61,
62,
63]. Therefore, in order to increase the robustness of recognition accuracy, the face image is partitioned into blocks with a block size of
. The TP and KP are generated using the procedures in Appendices
Appendix A.1 and
Appendix A.2, respectively. Note that the KP is generated with a localization parameter
p. After obtaining the two matrices of KP and TP, the SKTP matrices (
/
) are generated using Equation (
2).
Most face recognition algorithms have concentrated on a collaborative scenario in a noise-free environment. In a noisy environment, the face recognition process is degraded and the face recognition accuracy is significantly affected. Thus, face image preprocessing is needed to reduce the noise effect without excessively increasing the computation cost. The use of embedded image kernels to reduce computation cost was proposed in [
64], and we adopt this idea here. In order to embed a smoothing kernel in the generated SKTP matrices (
/
), Toeplitz matrices (
/
) are generated [
65] using a Gaussian smoothing kernel:
where
determines the effective size of the kernel (most often
). Thus, (
/
) can be generated as follows [
65]:
where
m and
l are the lengths of the smoothing kernels
and
, respectively. To this end, the embedded SKTP matrices (
/
) can be formulated as follows [
64]:
After generating the SKTP matrices with embedded smoothing kernels, we are ready for the feature extraction step. However, the use of traditional methods to extract local features leads to a high computation cost [
66], as they extract the local features directly from the small blocks. Most applications utilize non-overlapped block processing to extract local features. However, overlapped block processing increases the recognition accuracy [
67,
68,
69]. Thus, in this paper, overlapped block processing is performed. It is well known that overlapped block processing increases the computation cost considerably. In order to overcome this problem, we utilize the fast overlapped block processing method presented in [
12]. The main concept of fast overlapped block processing (FOBP) is based on the creation of auxiliary matrices that extend the image and eliminate the need for a nested loop. The elimination of the nested loops greatly reduces the computation cost of the feature extraction process.
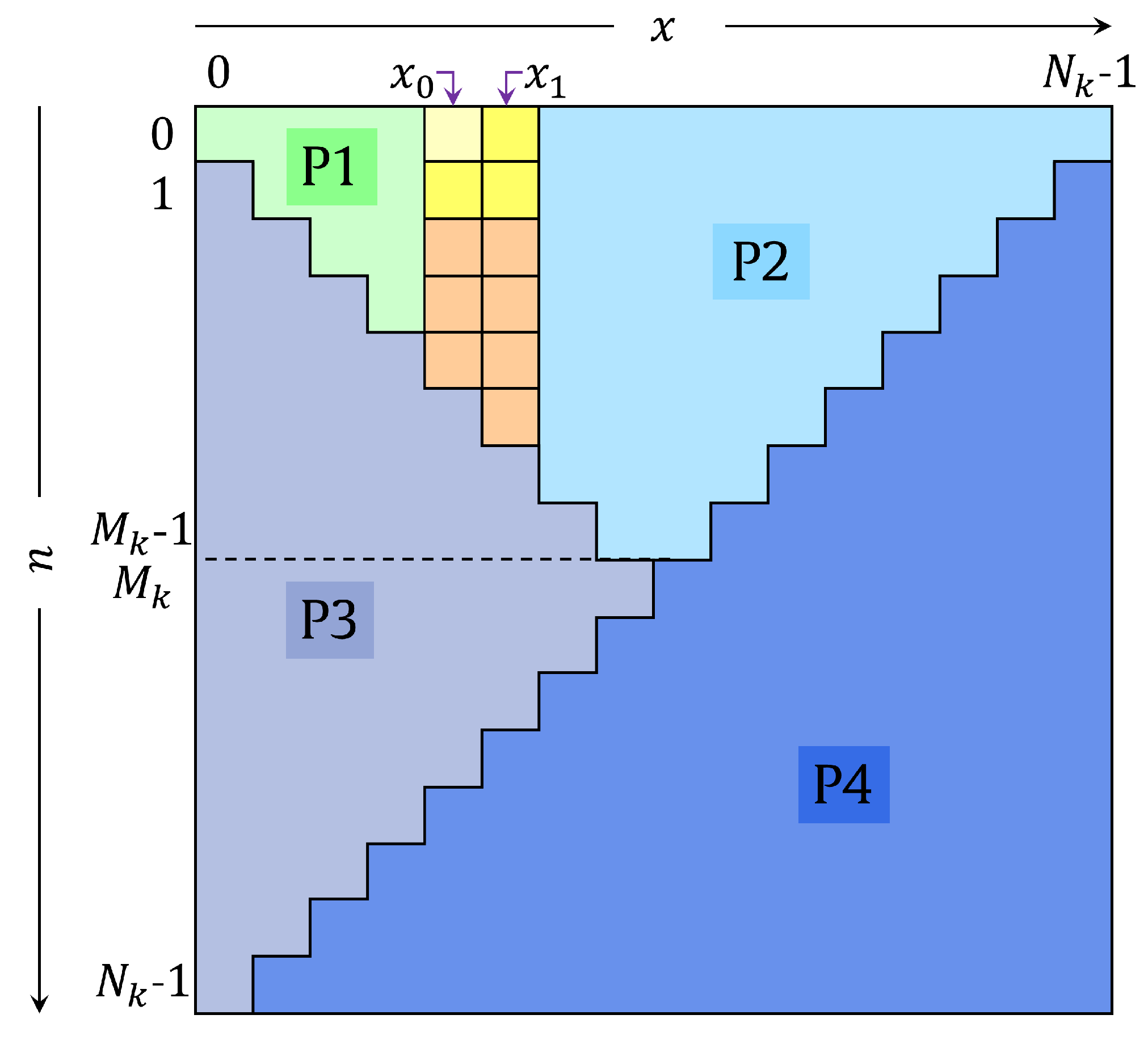
Suppose an image
has
rows and
columns. The image is partitioned into overlapped blocks with a size of
, with overlap size
in the
x-direction and
in the
y-direction such that the total blocks are equal to
. Suppose the matrix
represents the extended image version of
; it can be generated as follows [
12]:
where
and
are rectangular matrices with a size of
and
, respectively. For further elucidation, the matrix
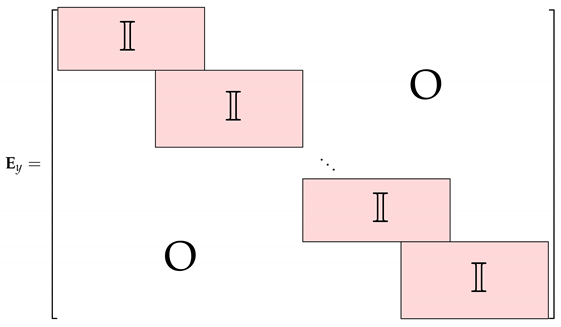
is provided by
where
represents the identity matrix, with a size of
. Now, the moments for the overlapped block can be computed as follows:
where
and
. To obtain the matrices
and
, they can be formulated as follows [
12]:
where ⊗ represents the Kronecker product and
represents the identity matrix. Because these matrices are independent of the image, they are computed first, stored, and utilized repeatedly [
12].
After generating the required matrices ( and ), the images are sent to the next stage for feature extraction and classification. Note that the extracted features are normalized.
After the normalized feature vector has been obtained, a label (ID) is applied to each input face image. The feature vector is considered as an input to the classifier. The classification itself is performed by a support vector machine (SVM) classifier. The SVM approach was chosen because of its ability to optimize the margin between two hyperplanes separating the classes [
70]. In addition, SVM is suitable for recognition, as it is more robust to signal fluctuation than nearest-neighbor classifiers [
71]. In this paper, LIB-SVM was applied [
72].
4. Experiments and Analysis
In this section, two different datasets are employed to evaluate the performance of the face recognition algorithm. The datasets used in the experiments are the ORL [
73] and FEI datasets [
74]. The ORL Face Database from AT&T [
73] is a well-known datset which has been used by many researchers for evaluation purposes. The ORL dataset includes 40 distinct classes (persons). Each class has ten images, which are acquired at different position and lighting conditions to form 400 images, and each image has a size of
[
75].
Figure 2 shows samples of the ORL face dataset.
For the ORL dataset, the block size in the
x and
y directions was set to 16 and 20, respectively. The overlap sizes in the
x and
y directions were set to {(0,0), (2,2), (4,4), (8,8)}. The size of the smoothing kernel was set to {3, 5, 7}. In addition, the test was performed with noise-free and noisy environments and with Gaussian and Salt and Pepper noise. The Gaussian noise was generated with the standard deviation 0.005, and 0.01, respectively. The Salt and Pepper noise was generated with densities 0.05 and 0.1.
Figure 3 depicts samples of images with different types of noise.
Table 1 summarizes the average results for 20 runs, and the detailed results of individual runs can be found in
Appendix B.
For SVM implementation, we used LIB-SVM [
72]. In the training phase, five-fold cross-validation was employed to obtain stable values of the SVM parameters.
First, an experiment was carried out for the proposed algorithm using two cases, with and without a smoothing kernel. This experiment was performed to highlight the effect of the smoothing kernel on the recognition accuracy. The experiment was performed for different overlap sizes of {(0,0), (2,2), (4,4)} and different environments (noise-free and noisy environments), as shown in
Table 2. Note that the results reported in
Table 2 represent the average results for 20 runs; the detailed results of individual runs can be found in
Appendix C. The results show that the recognition accuracy of the proposed algorithm is higher with a smoothing kernel than that without, with average recognition accuracy showing an improvement ratio of ∼0.5%.
Another experiment was performed to identify the best block overlap size and smoothing parameter
, which determines the kernel size (the kernel size was always taken as
to maintain more than 95% of the ideal Gaussian filter). The optimal
of course depends on the noise level and on the images themselves; in our case, we conclude that
is the best choice, providing the highest recognition performance (see
Table 1). As for the block overlap, it can be observed that while the differences are slight, the overlap (4,4) mostly yields the best results.
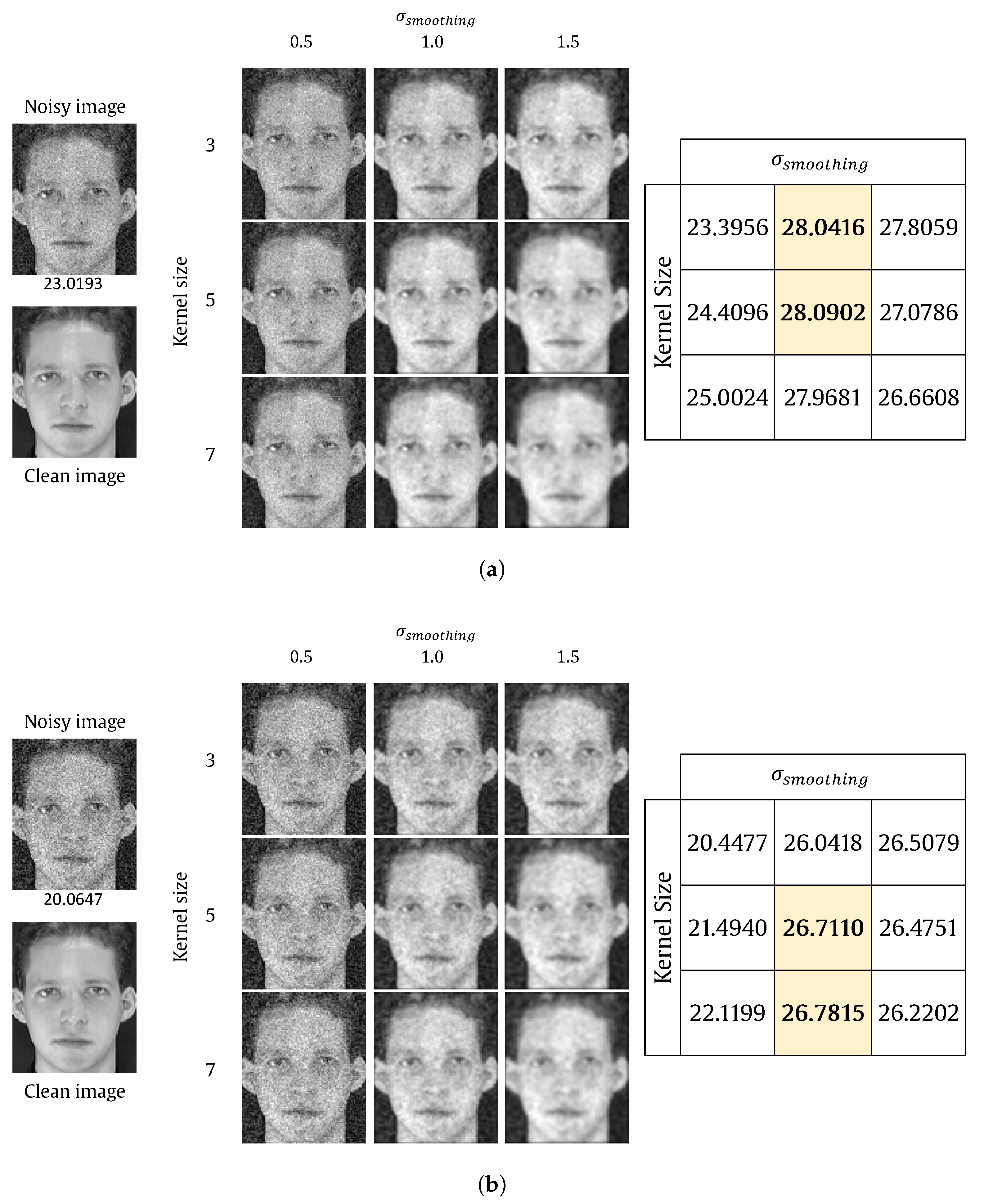
The effect of the smoothing kernel on the recognition rate can be shown through the following experiment. An image was selected from the ORL dataset and two Gassuain noise levels were applied to the image with standard deviations of 0.01 and 0.05. The noisy image was processed using the smoothing kernel with different kernel sizes and different smoothing parameters using SKTP. Then, the PSNR between the original image and the resulted image was measured. The results are shown in
Figure 4. It is clear that a kernel size of 5 and smoothing value of 1.0 is the best choice for both noise densities.
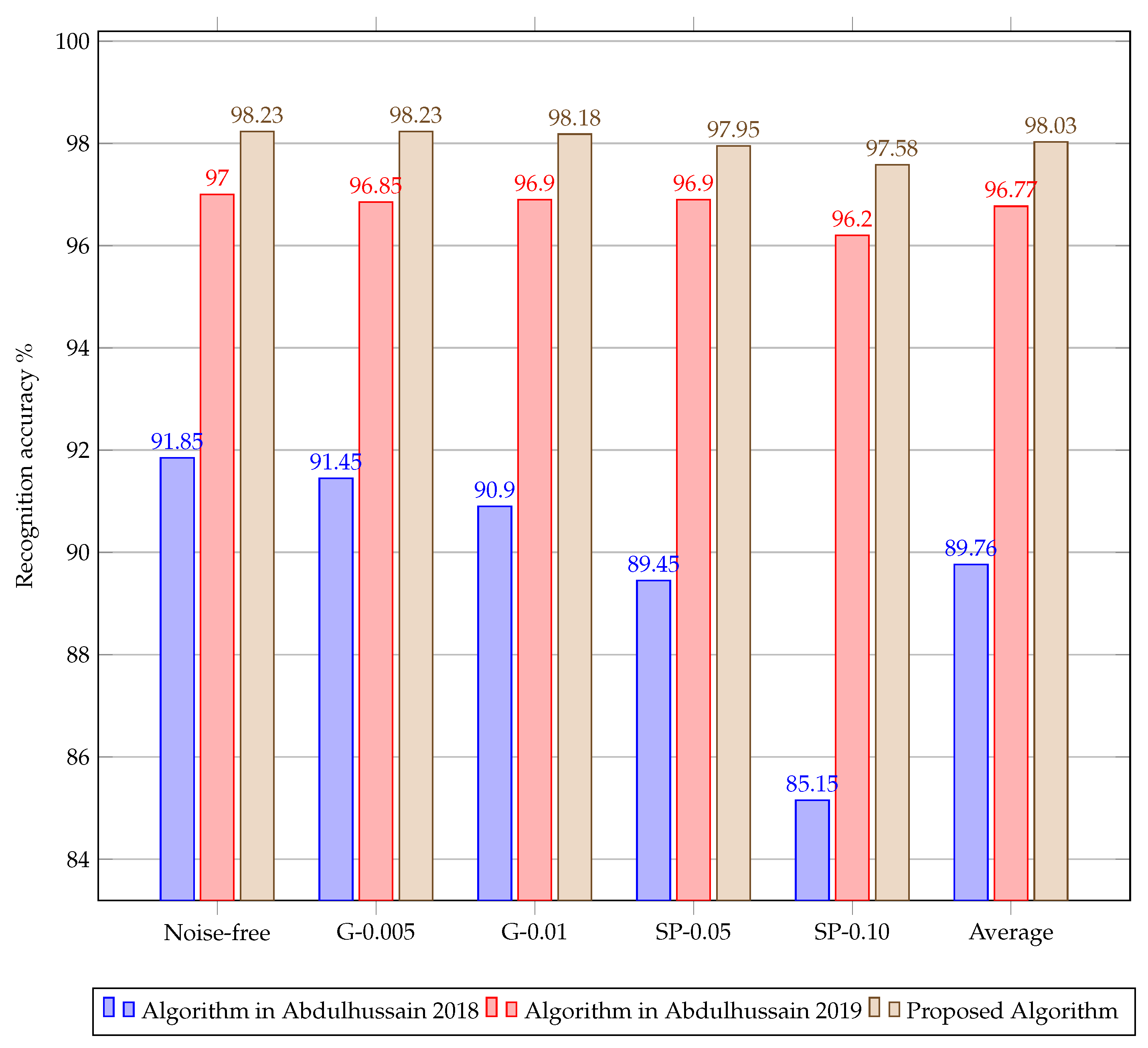
A comparison with existing algorithms which do not utilize block processing is shown in
Figure 5. The results with the proposed algorithm show higher accuracy than the existing algorithms presented in [
11,
55] in the presence of noise. Measured by average accuracy, the proposed algorithm shows an improvement of 1.29% and 8.44% compared to [
11,
55], respectively.
In order to show the promising performance of the proposed algorithm, a comparison was made with traditional methods in terms of computational cost as well. The experiment was performed for ten runs; the average computation time for each image is reported in
Table 3. The experiment was performed with a block size of 20, smoothing kernel sizes of 3, 5, and 7, and overlap sizes of (0,0), (2,2), and (4,4). It can be observed that the computation time using the proposed algorithm is less than that of the traditional methods, and the improvement ratio increases as the overlap size increases. This is obviously because the proposed algorithm performs the computation for the entire image only once, while the traditional methods repeat the computation in a loop over all blocks.
Finally, a comparison was performed between the proposed algorithm and existing algorithms in terms of recognition accuracy; the results are listed in
Table 4. It can be clearly observed that the proposed algorithm outperforms the existing algorithms in terms of recognition accuracy.
The second dataset is the FEI dataset [
74] which is a Brazilian facial dataset. The FEI dataset is composed of 100 faces, including males and females. In the experiment we included ten images for each person, with a size of
. The participants’ images have a neutral background, their age is between 19 and 40 years, and the dataset consists of faces with facial expressions and poses of various types.
Figure 6 shows samples of the FEI face dataset.
The experiment wass performed for three different image sizes: the original size (
pixels), downsampled by a factor of two, and downsampled by a factor of four. Various block overlaps were tested. The accuracy is reported both for noise-free and noisy environments. The noise was Gaussian with two variance values and Salt and Pepper with two density values as depicted in
Figure 7. The obtained results are reported in
Table 5. The results show that the best overlap size for this dataset is one sixth of the block size. For example, with a block size of
, the best overlap size is (8,8), for a block size of
, the best overlap size is (4,4), and for a block size of
, the best overlap size is (2,2). As these results were obtained from a large image database, it is highly probable that these conclusions are valid for other datasets of a similar kind.
In order to illustrate the efficiency of our fast block processing method, the proposed algorithm was compared to an algorithm that processes the blocks sequentially. The experiment was performed with an image size of
, a block size of
, and for different overlap sizes, as shown in
Table 6, where the runtime in seconds is provided. The results show that the proposed algorithm outperforms the traditional one for all overlap sizes (obviously, larger overlap sizes lead to a higher improvement). The average incease in speed is about 50 times, which is quite impressive.
Finally, we compared the proposed algorithm to eleven state-of-the-art face recognition algorithms. The recognition rates are shown in
Table 7. It can be observed that, at least on this database, the proposed algorithm outperforms all compared algorithms.