Abstract
In this work, we extend the topology-based framework and method for the quantification and classification of general resilient asynchronous complexity. We present the arbitrary resilient asynchronous complexity theorem, applied to decision tasks in an iterated delayed model which is based on a series of communicating objects, each of which mainly consists of the delayed algorithm. In order to do this, we first introduce two topological structures, delayed complex and reduced delayed complex, and build the topological computability model, and then investigate some properties of those structures and the computing power of that model. Our theorem states that the time complexity of any arbitrary resilient asynchronous algorithm is proportional to the level of a reduced delayed complex necessary to allow a simplicial map from a task’s input complex to its output complex. As an application, we use it to derive the bounds on time complexity to approximate agreement with processes.
Keywords:
distributed computation; asynchronous computation; combinatorial topology; computability; complexity; resilience; task-solvability MSC:
68Q05; 68Q22; 68W15; 68M14
1. Introduction
Since the in-depth applications of computers to all aspects of modern life, computers are progressively and mainly being used as coordination devices in asynchronous distributed systems. However, the proof of the FLP theorem [1], which says that the consensus task cannot be solved in an asynchronous message passing system even though only one process may fail by halting, implies that distributed computing is different from the standard Turing computing.
A distributed computing system consists of finitely many sequential processes communicating via shared-memory, message-passing and other mechanisms [2]. The communicating mechanisms include communication channels, synchronizing primitives and general services [3]. The processes are asynchronous, which may make the message and communication delay leading to a great effect in Information Exchange, such as a hyper hexa-cell interconnection network [4]. In addition, they may also fail by stopping, so it is indistinguishable whether an irresponsive process has failed or is only running slowly in a distributed system.
Fortunately, as a revolutionary development, a new framework of modeling and analysis based on classical algebraic topology was introduced by Herlihy and Shavit [5] for understanding and reasoning of computability problems in an asynchronous distributed system in 1993. In that work, they presented a topological characterization of the asynchronous computability of general tasks with crash failures in a share-memory model which is equivalent to a message-passing model showed by Attiya et al. [6]. Furthermore, they then extended to a complete characterization of wait-free solvability of distributed tasks in shared-memory systems, namely, a task is solvable if and only if its specification is topologically compatible in some sense [7,8]. Later, that technique was further generalized in three directions. The first direction is generalization to systems with arbitrary communication objects [9,10,11,12,13], to arbitrary resilience (rather than one or n failures) [9,14], to arbitrary synchrony [9,15], or to Byzantine failures [16,17]. The second direction is to explore the way for the classification of distributed tasks in asynchronous shared-memory systems: two tasks are reducible to each other if and only if they are equivalent in a topological manner [18,19,20,21]. The last is to explore of the complexity of decision tasks in some communicating model, that is to say, one can give the upper bounds and/or lower bounds [22,23,24], or just give a theoretical estimation of the cost of time or space and so on [25,26,27,28,29,30,31,32]. We feel the time is ripe to extend these techniques to arbitrary resilient asynchronous complexity.
This paper studies asynchronous shared memory solutions to the decision tasks in a distributed asynchronous system with processes. We focus on the iterated delayed model which is based on a delayed snapshot algorithm introduced by Saraph et al. in [33]. The model can guarantee that the scan operations of each process return a view that contain more than elements of sets of the participating processes’ inputs, where t means the number of crashing processes it tolerates by t () or fewer for that system.
Our contribution lies in three aspects. Firstly, we introduce a topological structure, N-fold delayed complex, which is a sub-complex of the -fold standard chromatic subdivision, where N is an arbitrary non-negative integer. Using it can give a precise description of the protocol complex of full-information protocol leading to the acquisition of computing power, which is a modification of the result showed by Saraph et al. [33]. Secondly, we introduce a novel computational model, the iterated delayed model, which has a particularly nice geometric representation and hence easily lends itself to topological analysis. Furthermore, by a new topological structure, the reduced complex is constructed from a delayed complex, and we will give a theoretical measure of computational complexity of an arbitrary resilient asynchronous model, which may lead some applications in practical applications. That is, the time (or round) complexity in that model is equal to the level of the chromatic subdivisions necessary to allow a simplicial map from a task’s input simplex corresponding to the worst case to its output complex. As an application, we derive the tight bound on the time to achieve an process approximate agreement in an iterated delayed model: on any input n-simplex I, where if and if .
2. Preliminaries
In this subsection, we give an overview of the basic definitions and concepts of combinatorial topology that we will use to formulate our model. The complete definitions on algebraic topology can be taken from the classical textbooks [34,35].
2.1. Basic Concepts of Combinatorial Topology
An (abstract) simplicial complex , or complex for short, is a finite set V together with a collection of subsets of V closed under containment, which means that, if , any subset of is also in . An element v of V is called a vertex and an element of is called a simplex, and is called a face of if . Subset of is called a sub-complex if itself is closed under containment. The dimension of simplex is defined as (here means the number of the vertices of ), denoted , and the dimension of is defined as the highest dimension among its simplexes. Call simplex a facet of if . Usually, use n-simplex (complex) as shorthand for an n-dimensional simplex (complex). By default, any complex in this paper is pure in the sense that any simplex is a face of a facet in that complex. In addition, call the complex generated by X if it is a collection of X and all its faces, where X is a simplex in .
To ease understanding, one can equivalently view simplicial complex through a geometric lens. Bijectively map the set of vertices of a k-simplex of to an arbitrary set of affinely independent points in a Euclidean space with an appropriate dimension. Then, there is natural convex hull spanned by . Call a geometric simplex or the geometric realization of , and call the vertex scheme of . Put all geometric simplexes together such that the collection is closed under containment and every pair of distinct simplexes has disjoint interiors if they have intersections, by which we can obtain a geometric simplicial complex corresponding to . For the details, one can follow Munkres [35]. Nevertheless, hereunder we still adopt the abstract simplex complex definition.
Let and be two simplexes of complex with no intersection; then, the join of them is with the vertex scheme being . The star of is the collection of simplexes of , denoted . See Figure 1; consider a complex consisting of all vertices , and all segments and all triangles ; the star of 0-simplex , consists of all simplexes of except the red dotted segments and its faces.
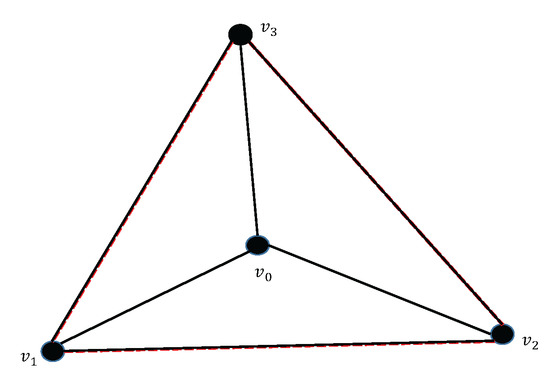
Figure 1.
The star of in complex .
Given two complexes and , a vertex map is a simplicial map if f carries each simplex of to a simplex of , and f is called non-collapsed if, for every simplex , there is , and f is called equivalent if there is a simplicial map such that and are all identity maps. A map is called a carrier map if and for any . In addition, f is said to be carried by if for any . is said to be a chromatic complex with colors C if there is a non-collapsed simplicial map from to ; call the coloring of . A map is said to be a color-preserving map if, for each vertex v of , there is , where and are the colorings of complexes and . In addition, a map is called a color-preserving simplicial map if it is both a color-preserving map and a simplicial map.
Suppose is a coloring of n-simplex X with colors ; call once standard chromatic subdivision of simplex X if any m-simplex of can be given by the form of satisfying the following conditions:
- there are vertices in total in ;
- for all , if , and either or ;
- for all , if , then ;
where is a face of X, and is equal to .
As showed in Figure 2, on the left side of this figure is a chromatic 2-simplex with colors , and in the middle of it is a once standard chromatic subdivision of , and on the right is a general chromatic subdivision of , since it is easy to check that it does not satisfy the second condition.
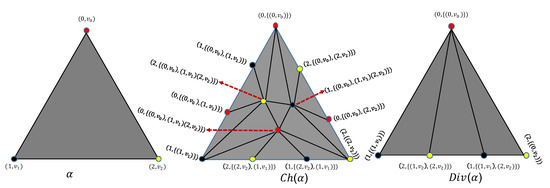
Figure 2.
Once standard chromatic and general chromatic subdivision of 2-simplex .
2.2. Distributed Computing Model
For the sake of the discussion, we first construct a series datatype for an arbitrary given datatype D. The datatype (k is a non-negative integer) can be defined inductively as follows:
- ;
- , where can be regarded as the location for some data, ⊥ means nothing but a placeholder, and is a pair.
Following the model by Moses and Rajsbaum [15], there are processes, up to t of which may fail by crashing. The processes execute a round-by-round protocol in an asynchronous manner. A decision task is a specification of eligible outputs with regard to the inputs, which intuitively models coordination problems. A protocol is a distributed program consisting of the processes. We say that a protocol solves a decision task if the outputs of any execution sequence (which consists of a series of round executions) conform with the specification of the task.
Our distributed computing model is based on the delayed object, denoted , a delayed algorithm proposed by Saraph et al. [33], and has been showed to be a useful building block for analysis of a t-resilient distributed asynchronous system; see Algorithm A1. Although Delporte et al. [36] showed that a t-resilient immediate snapshot is impossible, two snapshots each in delayed objects are wait-free immediate snapshots which can be implemented in a t-resilient asynchronous distributed system [37].
Intuitively, consists of three phases, the first and the third phases each are wait-free immediate snapshot (IS) operations, and the middle phase is a waiting operation. Before each process executes the second IS, it may need to wait until the view of some process contains at least pairs after the first IS. Formally, we can specify as an automata for -processes with at most t processes crashing and datatype D, denoted by . Here, we only take , since means the model is wait-free, and the complexity of that situation had been investigated by Hoest and shavit [30].
Our memory model is an iterated delayed model abbreviated as , in which each process communicates with the other processes only by delayed object , and every process accesses that object at most once in every round. It assumes an unbounded sequence of delayed objects , , ⋯ with initial datatype D, abbreviated as , , , ⋯, if the datatype is explicit in the context. This model has each participating process proceed in ascending order in the sequence.
Suppose , as in Algorithm 1, is a protocol in , and each process starts with a value coming from the datatype in that model, where m is a non-negative integer and D is some given datatype. Before communicating with other processes in round by object , process needs to check whether or not its local state can be decidable by a evaluated function , and a decision map , where is called the output datatype. If is , the process can decide and execute a decision operation; otherwise, do nothing. In addition, is taken as the signal that records whether or not a process has output before the current round, and it admits only two possible values 0 and 1, where means the process does not have an output before the current round; otherwise, it means it already has an output. If and , the process can make a decision but has no output; then, it decides and outputs ; Otherwise, it needs to access the object to accumulate information and then it accesses the next round with object .
| Algorithm 1: An execution of a protocol for process in |
| (1) input value; (2) ; (3) ; (4) forever do (5) ; (6) if and (7) then output and ; (8) ; (9) od; |
2.3. Topological Task Specification
In this subsection, we set some notions to make our statement straightforward. Let be the set of input values and the set of output values; then, any local state of the process can be regarded as a pair such that , and , where m is a non-negative integer.
The input configurations for processes with input are a chromatic n-complex, in which each k-simplex, , has form , —likewise for output configurations except . Formally, a topological specification of a decision task with processes is a triple , where and are input n-complex and output n-complex, respectively, and is a name (color)-preserving carrier map [17,38].
3. The Topological Description of
This section introduces a topological structure, k-fold delayed complex, which can be showed a sub-complex of times standard chromatic subdivision, and investigate their properties. By this, we give a characterization of computing power of , which is a modification of the results showed by Saraph et al. in [33].
3.1. Delayed Complexes
Suppose is a chromatic n-simplex with the coloring map and the colors , and is the chromatic n-complex generated by . and mean the geometric realization and the number of vertices of , respectively.
Definition 1.
A -partition of a given finite set S is a partition such that , for any , and if , where means some "priority" to the property .
Lemma 1.
There is a one-to-one correspondence between the set of the facets of and the collection of all -partitions of the set .
Proof of Lemma 1.
Suppose is a -partition of C. Let be the containment in the complex , that is, if for any simplexes , . Consider set ; there must be a subset of V with , such that, for any two elements , there are if for , and if for . In fact, it only needs to take the subset of , in which each simplex satisfies . By Kozlov [39], can span a facet of .
On the contrary, let be a facet of , by the definition of standard chromatic subdivision of . There is naturally a partition of the colorings set C under the containment in the set . □
By this lemma, any facet of a standard chromatic subdivision of a chromatic n-simplex can be represented by a -partition of its colors, which provides a simple way to describe a sub-complex structure of the standard chromatic subdivision. Suppose X is any facet of standard chromatic subdivision corresponding to a -partition .
Definition 2.
A n-simplex is said to be a -extended of the facet X in , denoted by , if it can be given as follows:
Call the collection the -extended of X, denoted by . Furthermore, call the -neighborhood of X, denoted by .
It is not hard to see that the -extended is symmetrical, that is, if X is a -extended of Y, Y is also a -extended of X. In addition, a -extended of a facet is usually not unique unless the cardinal number of the first component in its -partition is equal to one.
The -neighborhood describes a combinatorial adjacent relation of two facets in , which is not a neighborhood in the usual sense in topology or geometry. In general, a neighborhood of a facet in the triangulation of an n-manifold is equal to the union of facets in itself and its collar, which is indeed not its -neighborhood. Seeing Figure 3, let X be the black fields, the collection of all the facets of the star of in , the green areas are the -extended of X, and the -neighborhood is the collection of all the 2-simplexes colored black and green.
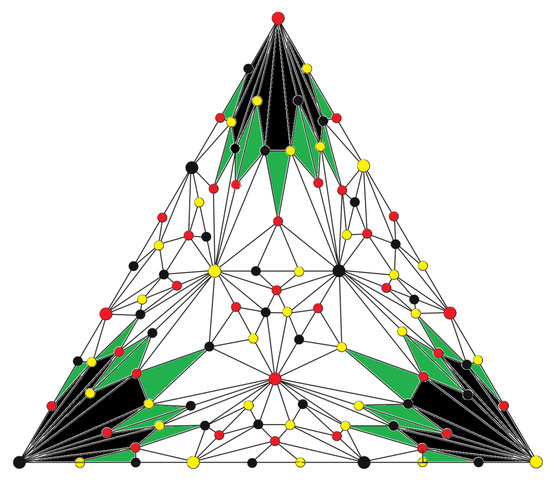
Figure 3.
-extended and -neighborhood.
Lemma 2.
Suppose α is a facet of ; then, a -extended is also a facet in .
Proof of Lemma 2.
This is a direct result of the Definition 2 and the Lemma 1. □
For general discussion, let be any pure chromatic n-complex with the coloring map and colors , and let be the collection of the facets of , , where t is an integer and . The -neighborhood of is equal to . Set .
Definition 3.
A subcomplex, denoted , of is called the delayed complex about complex if , where is the complex generated by simplex α. Inductively, the k-fold delayed complex about complex can be defined as .
Example 1.
Consider an execution in delayed object with an input 2-simplex = , where the colors red, black and yellow are corresponding to , and , and is the input value of the process , seeing the left side of Figure 4. Each 2-simplex colored black in the middle and the right of Figure 4 corresponds to a possible execution for and , respectively. Comparing Figure 3 and the middle of Figure 4, it can be seen that each black 2-simplex in the middle of Figure 4 is a 2-simplex of .

Figure 4.
Execution for three processes with input simplex .
It is not hard to see that any two vertices can be linked by a path (a sequence of 1-simplexes) in , that is to say, it is 0-connected. In fact, by the similar arguments as Theorem 5 and Theorem 6 in [33], we can also show that is -connected, which means that any continuous map f from -sphere to the geometric realization of can be extended to a continuous map from t-disk to . Here, we do not re-show those topology properties of delayed complexes any more, while we focus on the relation between executions in a delayed object and delayed complex. Saraph et al. introduced a sub-complex of , denoted by , which is in fact the complementary of the star of in . In addition, they implied that there is one-to-one correspondence between a simplex in and an execution of that object, which is actually inaccurate. There actually exists some simplex in that does not correspond to any execution of object . The next results present some properties of -extended and -neighborhood of the complex , by which will give an accurate geometric description of object .
Lemma 3.
Suppose is any facet of with the -partition ; then, there exists an integer m such that and for any , any and any , where and .
Proof of Lemma 3.
Let , ; then, for any vertex , there are and . Take a simplex, denoted , from with the maximal dimension, and it is obvious that is unique. In addition, then there exists a -partition of , denoted .
We claim that is the front of components of . If not, must be a successive truncation in the interior of , for is a face of . Hence, there exists at least one component in but not in , such that, for any element in with vertex , there is , where is any element of an arbitrary component of with vertex . Therefore, . Note that ; then, , and then . Since but , there is ; then, , which is an obvious contradiction. It follows that there is always for any . Next, it needs to show that is a satisfied integer.
In fact, it has showed that for any element in any component with . Hence, it only needs to show that for any element . If it is not true, there is a vertex such that there exists a vertex with . Since , there must be a simplex with . Note that , and it follows that ; then, . By the construction of , there is . Note that and , hence , which is a contradiction. □
If we take as an input n-simplex in an execution of , it is obvious that corresponds to an impossible execution. Any process executing the second IS does not need to wait after the first IS leading to , which contradicts with Lemma 3. The next lemma implies that, if a facet is in -extended of the , it corresponds to an impossible execution of object .
Lemma 4.
Suppose α is an arbitrary facet of , and is any facet in with -partition . Then, there exists an integer q such that, for any integer and any element , there is either and for any vertex , or , and there exists at least one vertex with , where is a vertex of .
Proof of Lemma 4.
Assume the -partition of is . If , there is only one element in , and then the -partition of can be represented as by Definition 2. Otherwise, , and the -partition of is , where is an arbitrary element of .
Set . Let be a simplex of with the maximal dimension; then, -partition of is the previous components of by the same argument of the proof of Lemma 3, denoted , . Since , there is .
If , then , and there is only one element in . Suppose it is ; then, -partition of is . By Lemma 3, for any non-negative integer j, if , then and , where . Otherwise, , and there is for the choice of , where is a vertex of but not for , and . By Definition 2, , then , with , which implies that it only changes of the vertex of into of the vertex of with , where is any vertex of with . It follows that and at least one vertex with for any , any component with , and any element , where is a vertex of .
If , then or .
For the former case, the -partition of is . By Lemma 3, for any , there are and , where is an arbitrary element of and is a vertex of . Hence, , where ; then, , , , ⋯, . Note that the transformation from to is only changing into , which contains only one element, where is a vertex of . Let ; then, for any and any , or . It follows that or , and , where is a vertex of and is any element of .
For the latter case, the -partition of is ; then, either for and , or for . For the former situation, let , and, for the latter situation, let . By the similar arguments as the situation , it can always obtain that, for any and any , there are and , where is the value of the corresponding vertex of in , and is an arbitrary element of . □
Through the discussion above, we can obtain the following result directly.
Corollary 1.
Suppose α is an n-simplex of with the -partition ; then, there is a non-negative integer q such that, for any and any , there exists one vertex with and .
3.2. The Characterization of
In the previous section, we have given the concepts of the k-fold delayed complex and -neighborhood, and then discussed about their properties. In this section, we will characterize from a topological point of view.
Suppose is an execution in a protocol with a given input n-simplex ; we say a simplex X is reachable by execution if it can take as a possible return after executing .
Lemma 5.
Suppose is the delayed algorithm in Algorithm A1 and an input n-simplex, then the protocol complex is equivalent to delayed complex .
Proof of Lemma 5.
We only need to show that there is a one-to-one correspondence between the facets of and the facets of .
Suppose is an arbitrary facet in ; then, there exists an execution in such that is reachable. Every process in just accesses object once. That is, the process runs the first IS (denoted by IS), waits or not, and then runs the second IS (denoted by IS). Hence, it can model as a composite of and , each of which having a wait-free IS. Following Kozlov [39], every IS can be modeled as an ordered partition along the processes’ running, such that processes in the same component run concurrently, and processes in run after the processes in for . It follows that there are ordered partitions for and , denoted and , respectively. Assuming is a return after executing IS, then is a face of for any , and for and , and for , where . Likewise, for a return except after executing IS. Let and ; then, is a facet in . In the next, it only needs to show that is not a facet in a -neighborhood of an arbitrary facet of .
By steps 5 and step 6 in a delayed algorithm in Algorithm A1, we know that, if the number of elements of the view of a process is at most after finishing , it needs to wait until is . Assume is the largest integer such that all processes need to wait in , (here, means that all processes are wait-free). Then, any process in should wait until at least one process in has finished . Meanwhile, processes in do not need to wait and immediately run IS after IS, where , . It follows that, for any process in , it must appear in with . Assume is the view of after executing IS; then, . Let ; then, is an n-simplex in with for . Since is actual, the -partition of and , it follows that by Corollary 1. As a result, . Since is arbitrary, up to equivalence.
On the other hand, assume is an arbitrary facet of . We will construct an execution in object , such that is a reachable n-simplex for .
Since , there exists only one facet admitting form such that is a facet in , where is a face of for any . By Lemma 1, has a -partition under containment of the values of its vertices, denoted , such that, for any vertex , , if , and , and if , . Note that this partition corresponds to an execution IS, hence we can divide the first IS into a sequence of executions, denoted , such that processes run concurrently if they are in the same component , and processes in execute after processes in running for . It not hard to see that is a reachable n-simplex after executing . Likewise, the argument for the -partition of except a series of executions and is a reachable n-simplex after executing . Let . It only needs to show that is possible executing in object with input . Equivalently, it only needs to show that, for any vertex , if , does not appear in . That is, process does not execute immediately after running , and it needs to wait until “done” is .
Assume there exists a vertex in such that when . By Corollary 1, is an n-simplex of the -neighborhood of an facet in , , which is an obvious contradiction for . As a result, is indeed an execution in with input .
Let be the view of process after executing , then . It follows that is indeed a reachable n-simplex after executing . Since is arbitrary in , up to equivalence. By the upper arguments, is equivalent to . □
Corollary 2.
Suppose is an input n-simplex and a protocol with k rounds in which each executes a delayed algorithm in Algorithm A1; then, the protocol complex is equivalent to k-fold delayed complex .
Proof of Corollary 2.
Execution in P can be modeled as a sequence of executions, denoted by , in which each execution is an one round execution in delayed object , and each return of a process after executing is as an input in execution for . By Lemma 5 and Definition 3, we know that is equivalent to . □
4. Measure Complexity
In this section, we introduce some concepts about the measure of complexity of arbitrary resilient , and then we give a topological characterization of the complexity for that model.
4.1. Complexity of the Delayed Model
Suppose is a decision task and is a general algorithm solving T in . Let be an arbitrary execution of with a legal input simplex I (i.e., ), and the maximum number among the effective access to object for all participating processes in the execution with input I. Here, “effective” means the number of outputs is less than or equal to in an execution in a distributed system. In addition, from now on, once we refer to a protocol , it means that the protocol can aways solve some implied decision task.
Definition 4.
The time complexity of a protocol on a given input simplex I is the supremum of the set is any execution of the with input , denoted .
Remark 1.
Set if an input simplex is illegal, since the dimension of that input simplex is less than and this time any participating process could not make a decision or output.
Definition 5.
The time complexity of a protocol on a given input complex , denoted , is the supremum of the set .
Before we explore the complexity of a protocol in a delayed model, we introduce some properties of any execution in , which may be useful for the next discussing.
Lemma 6.
Any execution in object is finite.
Proof of Lemma 6.
Since any execution in can be modeled as an execution of two-round executions of wait-free IS, even though there is a barrier layer between the two-round IS, it does not contain other actions except for waiting. Note that any execution of IS is finite by Hoest [30], then any execution of two-round IS is also finite. Hence, is finite. □
Lemma 7.
Let ε be any execution of protocol for a task T in , then ε is finite.
Proof of Lemma 7.
Suppose there is no process stopping by crashing; then, contains at most starting actions and decision actions for there are at most processes and each of them has at most one initial state and one final state. Consider an integer which is the time complexity of ; then, can be modeled as an ordered executing sequence with at most one-round execution of delayed object , denoted , , ⋯, . Despite the fact that some processes may make a decision and output a value among those executions, there is no essential effect on the finiteness. By Lemma 6, each is finite. Note that is finite, hence is finite. □
4.2. Reduced Delayed Complex
Suppose is a pure chromatic n-complex with coloring map and colors . Let X be an m-simplex in and the complex generated by X; then, there is a facet in such that , and . Let be any partition of the set of vertices of X with , such that , .
Definition 6.
Call a reduced delayed complex of X about if
each simplex has form , where , and ;
there exists one simplex in such that is a face of X.
Furthermore, call a reduced delayed complex of about C if .
Remark 2.
- C and T can not be empty-set at the same time.
- If , then is a sub-complex of .
- is also a pure chromatic m-complex with the same set of colors as X.
- Suppose is a partition of ; then, there must be and .
- Suppose Y is another simplex in with a partition , and assume . If and , then , and vice versa; if and , then , and vice versa.
- In fact, it needs only to consider all the facets of complex to construct the reduced delayed complex ; that is, .
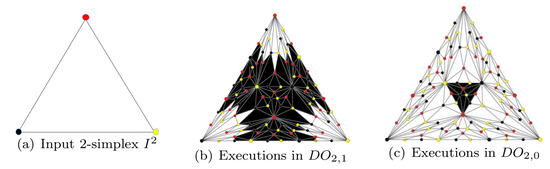
Example 2.
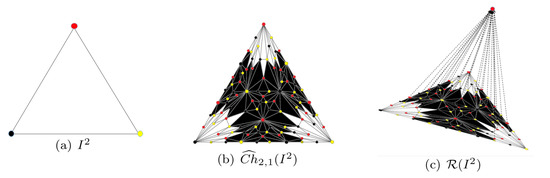
Let be a chromatic 2-simplex with coloring map χ, where , and , seeing the left in Figure 5. Suppose and ; then, is a collection of and all the vertices coloring black and yellow in the black area of the middle figure in Figure 5. Reduced delayed complex can be obtained by pulling all vertices coloring red in the black area of the middle figure in Figure 5 over the flat and then pasting them together as just one vertex, seeing the right in Figure 5.

Figure 5.
An intuitive procedure of 2-simplex to some reduced delayed complex.
Inductively, we can define a k-fold reduced delayed complex for n-complex , denoted . For , it is equal to . For , it can be given by the following procedure: the vertices of can be divided into two disjoint parts, denoted and with , respectively. Let ; then, for any element , there exists a partition of X such that , and . Hence,
Let be a sub-complex of complex , and , . Any simplex in has form , where , , is an n-simplex of , and . Here, represents a complex, in which each simplex is a face of a simplex with . It is not hard to show that is a pure sub-complex of the complex with dimension . By Definition 6, we can construct inductively.
Intuitively, each vertex of the reduced delayed complex with input simplex X records a local state, in which the process can decide and has no output. Without loss of generality, assume is a facet. For each process , it needs to check whether its initial state can decide by the predicted function before accessing . If it can decide and there is no output, then it will make a decision and give an output, and then the process may continue executing in the following round or just stop for crashing; anyway, it has nothing to do with output of the process . If it can not, it needs to accumulate more information by object , which does have an effect on its output. Putting all initial states in which each process can decide together as a set ; it not hard to see that can span a face of X. Since, for a process that is not in , it needs to access object to obtain more information to decide, each local state of a process with on output after executing object corresponds to a vertex in , where . By the Definition 6, indeed describes the one-round execution of . The next two lemmas show the general execution (i.e., there are many rounds in it) of .
Lemma 8.
Suppose is a protocol in with input n-complex . If the time complexity of about is k, then protocol complex is equivalent to a k-fold reduced delayed complex of , where k is non-negative integer.
Proof of Lemma 8.
Use induction to the complexity. Assume , it is obvious that ≅ . Note that , hence . Suppose the conclusion is established for any non-negative integer , which is less than k. Consider .
Let be any vertex in , and and the coloring map and assignment function for such that and . Note that whether the process can make a decision and output a value in its initial state before accessing object or not depends on the value of predicted function on . If is and does not output, is decidable and outputs before proceeding. Otherwise, process can not make a decision, and it needs to accumulate information by accessing object . It follows that divides into two disjoint parts, denoted and , respectively, such that and . Since , there is at least one vertex in such that , and then .
Consider an arbitrary facet , such that the time complexity of the protocol about X is k. By the former argument, there must exist a partition of , denoted by , such that and . Any execution of can be modeled as a composite of an ordered sequence of one-round executions, in which each participating process accesses object at most once in round r, and the returns of concurrent round can be as the inputs to the next round. By Lemma 5, each return after executing round 1 is a simplex in ; then, the time complexity of on each simplex in is at most . By hypothesis,
If for a vertex , the process has obtained an output before accessing object . Hence, it only needs to focus on the sub-complex of complex , and there is
Let be the collection of all simplexes with form , where , , and and can not be empty sets at the same time. Since and all are chromatic complexes and , is a chromatic complex. Likewise, is also a chromatic complex.
It follows that
Note that and Hence, . Since X is arbitrary facet in , there is
Therefore,
By Definition 6, there is
It follows that . □
Lemma 9.
Suppose is a pure chromatic n-complex with coloring map χ, and is a k-fold reduced delayed complex about , where k is a non-negative integer. Then, there exists a protocol in with time complexity k about complex , such that its protocol complex is equivalent to .
Proof of Lemma 9.
Assume we have obtained the predicted function and the decision map in the delayed system with processes, then we can construct a protocol in that model in the way shown as in Algorithm A1. By Lemma 8, the protocol complex is indeed equivalent to complex . Next, we mainly focus on constructing the predicted function and the decision map .
Consider an arbitrary facet X in n-complex . By Definition 6 and the fundamental configuration process of k-fold reduced delayed complex , there is a sequence of complexes, denoted , respectively, and two corresponding complex sequences, denoted and , respectively. Such that, for any , if , there are and , and, for any , there is .
Note that, for any , and are the subsets of . Define function
satisfying if , then , otherwise . Since for any , is well-defined. By the similar way, we can define a color-preserving simplicial map
such that, for any , if , then , otherwise , where x is a value in and ⊥ is just a placeholder. It is obvious that is also well-defined.
Note that is pure and X is arbitrary in complex , and let
Next, we only need to check that and are well-defined. Assume Y is another facet in complex and . By Definition 6 and the construction of and , there is
which implies that is well-defined. Therefore, is exactly a satisfied predicted function from to . In a similar way, it can also show that is well-defined and a satisfied decision map from to . □
4.3. Arbitrary Resilient Asynchronous Complexity Theorem
The strength and usefulness of of computation comes from the fact that each of its associated protocol complexes has a slightly nice, recursive structure. In fact, it turns out that any protocol complex of is equivalent to a reduced delayed complex which can be constructed by iterated chromatic subdivision of the input complex, and vice versa. This is the essence of our main theorem, which we state and prove in this section. The level of subdivision necessary for the existence of a simplicial map from the input to the output complex of a decision task that agrees with the task specification can be interpreted as a topological measure of the task’s time complexity.
Let be a decision task and k a non-negative integer. We say is a mappable reduced subdivision of the input complex and k is a mappable level of reduced subdivision if there exists a color-preserving simplicial map from to such that, for all , .
Theorem 1.
A decision task has a t-resilient solvable protocol in with worst case time complexity on legal inputs if and only if there is a mappable reduced subdivision with level on X.
Proof of Theorem 1.
Herlihy and Shavit in [40] imply that decision task T has a t-resilient solvable protocol in if and only if the following triangle is commutative, where is a color and carrier preserving simplicial map from to .
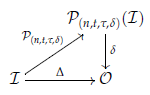
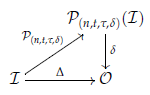
By Lemma 8, any protocol complex is equivalent to a k-fold reduced delayed complex . The protocol solves task T in with worst case time complexity on X. It follows that . Let k be equal to and a color-preserving isomorphism from to , and let . Then, is a color and carrier preserving simplicial map from to . It follows that is mappable.
On the other hand, any mappable reduced subdivision with level on X is equivalent to the protocol complex of a protocol in the delayed model with worst case complexity on legal input X by Lemma 9. Assume is a color-preserving simplicial map from to . If there is a color and carrier preserving simplicial map from to , by setting , then protocol can solve T in a delayed model with worst case time complexity on legal inputs . □
Remark 3.
When , is actually a wait-free non-standard iterated immediate snapshot model(NIIS) proposed by Hoest and Shavit [30]. As a corollary of Theorem 1, it can easily obtain the wait-free asynchronous complexity theorem.
5. Application
In this section, we will analyze the time complexity of the well-known Approximate Agreement task as an application of Theorem 1. An approximate agreement in a distributed system with processes can be specified as follows: each n-simplex has form , where each is in a finite set S of real numbers, and is the ID of the process. In addition, each n-simplex has the form , such that, for any , is also in S; and, for any , there is , where is the same predetermined number that is more than 0, and if .
For a wait-free model, Hoest et al. [30] have showed that the time complexity of approximate agreement is for if and if with any input simplex I. Here, we investigate the time complexity of approximate agreement in . Since any legal input simplex , there is always a facet such that is a face of , and they admit the same time complexity. Therefore, it only needs to consider all the facets in the input complex .
In order to make the next discussion brief, let for any chromatic simplex , and for a chromatic complex . In addition, let be the coloring map with the collection of all the IDs of the processes.
Theorem 2.
Suppose is a predetermined number and is an approximate agreement, then there is a protocol solving T in with time complexity on any input n-simplex I, where if and if .
Proof of Theorem 2.
Assume task T has protocol with the time complexity on input n-simplex . By Theorem 1, there is a color-preserving simplicial map
carried by , such that if acts on the sub-complex of the complex .
Relabel all of the vertices of by associating map in the following way. For each vertex , label v with while retaining its coloring. It is obvious that this labeling satisfies the task specification, since, for any n-simplex that contains v, the labeling must be in . Note that is a simplicial map from to ; then,
for any . Since and is chosen arbitrary, then
Consider an arbitrary n-simplex . By the Definition 6, -fold reduced delayed complex can be obtained from an l-fold reduced delayed complex . That is, can be divided into two disjoint sets of vertices and , such that and and each simplex of can be spanned by a subset of and a subset of . Hence, , where is the complex generated by in which each simplex in . By the similar argument of the proof of Theorem 6.1 [30], there is
where is the complexity on I, and if and if . Then,
Let , then
where if and if . Therefore, is a lower bound of the time complexity on simplex I.
On the other hand, suppose there is a color and carrier preserving simplicial map from k-fold reduced delayed complex to , such that if acts on the sub-complex of the complex for any input facet , where if and if . By Theorem 1, there is a protocol that solves approximate agreement T with the worst case time complexity on input n-simplex I, which implies that is also an upper bound of the time complexity on input I.
In fact, the existence of that map is equivalent to that there exists a labeling of the vertices of which agrees with the initial values of input complex with . By definition 6, we know that k-fold reduced delayed complex is recursive, hence we can label each vertex of at each fold as follows. Consider any facet I of ; for each fold , a vertex v is in if there exists a facet in taking v as one of its vertices, such that ; otherwise, v is in , where w is a vertex in . Assume it has relabelled all vertices of but with colors in . Before entering the next fold, it needs to relabel all vertices of but in . Consider any facet in . At first, relabel all vertices of as follows: If , label the new vertices with values , such that ; otherwise, label new vertices with , such that , where . It follows that for the su-bcomplex of . By this construction, we can see that, if , either or , where , which implies that, for any facet , is as a -fold reduced sub-complex of for if and if . □
Remark 4.
We only consider the input simplex which is a facet, since, for any legal input simplex α, there always exists a facet such that they have the same time complexity for it only needs to assign the processes that are in but not in with the same value as any value in .
6. Conclusions and Future Work
This paper modifies the description of a protocol complex of a delayed algorithm proposed by Saraph, Herlihy, and Gafni in [33], in which they thought the protocol complex was equivalent to . However, we give a precisely topological characterization of that algorithm and show that the protocol complex is equivalent to , which is a proper subset of complex , which implies there exists a simplex in complex corresponding to an impossible execution in .
Take as a black-box and then construct an iterated delayed model (), which turns out to be an arbitrary resilient algorithm in an asynchronous distributed system. Even though Delporte et al. [36] have showed that a t-resilient immediate snapshot is impossible in a t-resilient asynchronous distributed system by showing the equivalence of consensus (-set agreement) and a t-resilient immediate snapshot for (), there exist some tasks that admit weaker computing power than consensus and set agreement. In addition, each immediate snapshot in is actually a wait-free immediate snapshot from a local point of view, which turns out to be implemented in a t-resilient asynchronous distributed system [37] but not for a t-immediate snapshot. Hence, it makes sense for the construction of .
This paper gives a topological characterization of the time complexity of an arbitrary resilient distributed asynchronous model theoretically by the number of subdivisions of the worst input case. Although the topological structures are very complex and difficult to construct, it turns the dynamic analysis of that system into a static geometric structure analysis, which may lead to a great significance in practical applications. Using that characterization gives a time complexity of approximate agreement in t-resilient , in which it can obtain the time complexity of approximate agreement in a wait-free asynchronous model by taking , showed by Hoest et al. [30].
Unfortunately, any model involved in this paper refers to only a crashing failure model, which is an ideal failure model. Meanwhile, the most common failure model is the Byzantine failure model, in which the behavior of a byzantine process is out of control, leading to difficulty in analyzing its complexity in a distributed asynchronous system. In addition, in order to obtain the characterization of the complexity of the Byzantine failure model, it may be necessary to obtain more information during an execution, not just the initial states and terminal states. However, the main technique of our work is based on the method and framework proposed by Herlihy et al. [8,18,40,41], in which it is not necessary to care about the intermediate process during an execution but the initial states and terminal states.
In the future, we will construct a new geometric structure, the directed topological model, which is proposed mainly to be used to study concurrent computation [42], and from which it may catch up not only the initial states and terminal states but also almost all information during an execution. Investigating the topological characterization, such as the invariant of directed homotopy or directed homology, and then exploring the relationship between the computational complexity and those topological characterizations, may give us a feasible way to study Byzantine complexity.
Author Contributions
Conceptualization, Y.Y. and X.L.; Formal analysis, Y.Y., X.L., and F.L.; Methodology, Y.Y. and J.W.; Writing—original draft, Y.Y.; Writing—review and editing, X.L. and F.L. All authors have read and agreed to the published version of the manuscript.
Funding
The work is partially supported by the National Natural Science Foundation of China (Grant No. 12071051, 62072433), partially supported by National Natural Science Foundation of China 647 (Grant No. 11971144), and partially supported the Fundamental Research Funds for the Central Universities (Grant No. DUT21RC(3)102) and partially supported High-level Scientific Research Foundation of Hebei Province and the start-up research fund from BIMSA.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| Symbol | Corresponding Meaning |
| , | (abstract) simplicial complexes |
| (abstract) simplexes | |
| the set of vertices of simplex X/simplicial complexes | |
| the number of vertices (or elements) of simplex (or set) X | |
| the geometric realization of simplex X | |
| the complex generated by simplex X | |
| delayed object consists of processes with t-resilience | |
| invoking delayed object in r-th round execution | |
| the datatype generated by k-fold iterations with data D | |
| -extended of simplex X | |
| -neighborhood of simplex X | |
| k-fold delayed complex about n-simplicial complex | |
| k-fold reduced delayed complex about n-simplicial complex | |
| iterated delayed model |
Appendix A. Delayed Algorithm
| Algorithm A1: Delayed algorithm [33] |
(1) shared , , done; (2) done ← false; (3) immediate (4) ; (5) ; (6) if then (7) while (8) skip (9) immediate (10) ; (11) ; (12) ; (13) return ; |
References
- Fischer, M.J.; Lynch, N.A.; Paterson, M.S. Impossibility of distributed consensus with one faulty process. In Proceedings of the Second ACM SIGACT-SIGMOD Symposium on Principles of Database Systems, Atlanta, GA, USA, 21–23 March 1983; pp. 1–7. [Google Scholar]
- Lynch, N. Distributed Algorithms; Morgan Kaufmann: San Francisco, CA, USA, 1996. [Google Scholar]
- Herlihy, M. Wait-free synchronization. ACM Trans. Program. Lang. Syst. 1991, 13, 124–149. [Google Scholar] [CrossRef]
- Mahafzah, B.A.; Al-Zoubi, I. Broadcast communication operations for hyper hexa-cell interconnection network. Telecommun. Syst. 2018, 67, 73–93. [Google Scholar] [CrossRef]
- Herlihy, M.; Shavit, N. The asynchronous computability theorem for t-resilient tasks. In Proceedings of the Twenty-Fifth Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 16–18 May 1993; pp. 111–120. [Google Scholar]
- Attiya, H.; Amotz, B.N.; Dolev, D. Sharing memory robustly in message-passing systems. J. ACM 1995, 42, 124–142. [Google Scholar] [CrossRef]
- Herlihy, M.; Rajsbaum, S. Set consensus using arbitrary objects (preliminary version). In Proceedings of the Thirteenth Annual ACM Symposium on Principles of Distributed Computing, Los Angeles, CA, USA, 14–17 August 1994; pp. 324–333. [Google Scholar]
- Herlihy, M.; Rajsbaum, S. Algebraic spans (preliminary version). In Proceedings of the Fourteenth Annual ACM Symposium on Principles of Distributed Computing, Ottawa, ON, Canada, 20–23 August 1995; pp. 90–99. [Google Scholar]
- Herlihy, M.; Rajsbaum, S. The topology of distributed adversaries. Distrib. Comput. 2013, 26, 173–192. [Google Scholar] [CrossRef]
- Herlihy, M.; Rajsbaum, S.; Raynal, M.; Stainer, J. From wait-free to arbitrary concurrent solo executions in colorless distributed computing. Theor. Comput. Sci. 2017, 683, 1–21. [Google Scholar] [CrossRef]
- Herlihy, M.; Rajsbaum, S.; Tuttle, M.R. Unifying synchronous and asynchronous message-passing models. In Proceedings of the Seventeenth Annual ACM Symposium on Principles of Distributed Computing, PODC '98, Puerto Vallarta, Mexico, 28 June–2 July 1998; ACM: New York, NY, USA, 1998; pp. 133–142. [Google Scholar]
- Kuznetsov, P.; Rieutord, T.; He, Y. An asynchronous computability theorem for fair adversaries. CoRR 2020, abs/2004.08348. [Google Scholar]
- Yue, Y.G.; Lei, F.C.; Liu, X.W.; Wu, J. Asynchronous computability theorem in arbitrary solo models. Mathematics 2020, 5, 757. [Google Scholar] [CrossRef]
- Gafni, E.; Kuznetsov, P.; Manolescu, C. A generalized asynchronous computability theorem. In Proceedings of the ACM Symposium on Principles of Distributed Computing, PODC’14, Paris, France, 15–18 July 2014; pp. 222–231. [Google Scholar]
- Moses, Y.; Rajsbaum, S. Toward a topological characterization of asynchronous complexity. SIAM J. Comput. 2002, 31, 989–1021. [Google Scholar] [CrossRef]
- Nicolas, B.S.; Guerraoui, R.; Florian, H. Fast byzantine agreement. In Proceedings of the ACM Symposium on Principles of Distributed Computing, PODC’13, Montreal, QC, Canada, 22–24 July 2013; pp. 57–64. [Google Scholar]
- Mendes, H.; Tasson, C.; Herlihy, M. Distributed computability in byzantine asynchronous systems. CoRR 2013, abs/1302.6224. [Google Scholar]
- Herlihy, M.; Rajsbaum, S. The decidability of distributed decision tasks (extended abstract). In Proceedings of the Twenty-Ninth Annual ACM Symposium on the Theory of Computing, El Paso, TX, USA, 4–6 May 1997; pp. 589–598. [Google Scholar]
- Herlihy, M.; Rajsbaum, S. A classification of wait-free loop agreement tasks. Theor. Comput. Sci. 2003, 291, 55–77. [Google Scholar] [CrossRef]
- Liu, Y.W.; Xu, Z.W.; Pan, J.Z. Classifying rendezvous tasks of arbitrary dimension. Theor. Comput. Sci. 2009, 410, 2162–2173. [Google Scholar] [CrossRef][Green Version]
- Yue, Y.G.; Lei, F.C.; Wu, J. The evolution of non-degenerate and degenerate rendezvous tasks. Topol. Its Appl. 2019, 264, 187–200. [Google Scholar] [CrossRef]
- Biran., O.; Moran, S.; Zaks, S. Tight bounds on the round complexity of distributed 1-solvable tasks. Theor. Comput. Sci. 1995, 145, 271–290. [Google Scholar] [CrossRef][Green Version]
- Castañeda, A.; Rajsbaum, S. New combinatorial topology bounds for renaming: The lower bound. Distributed Comput. 2010, 22, 287–301. [Google Scholar] [CrossRef]
- Castañeda, A.; Rajsbaum, S. New combinatorial topology bounds for renaming: The upper bound. J. ACM 2012, 59, 3. [Google Scholar] [CrossRef]
- Abraham, I.; Dolev, D. Byzantine agreement with optimal early stopping, optimal resilience and polynomial complexity. In Proceedings of the Forty-Seventh Annual ACM on Symposium on Theory of Computing, Portland, OR, USA, 14–17 June 2015; pp. 605–614. [Google Scholar]
- Attiya, H.; Guerraoui, R.; Hendler, D.; Kuznetsov, P. The complexity of obstruction-free implementations. J. ACM 2009, 56, 24:1–24:33. [Google Scholar] [CrossRef]
- Galil, Z.; Mayer, A.J.; Yung, M. Resolving message complexity of byzantine agreement and beyond. In Proceedings of the 36th Annual Symposium on Foundations of Computer Science, Milwaukee, WN, USA, 23–25 October 1995; pp. 724–733. [Google Scholar]
- Georgiou, C.; Russell, A.; Shvartsman, A.A. The complexity of synchronous iterative do-all with crashes. Distributed Comput. 2004, 17, 47–63. [Google Scholar] [CrossRef]
- Helmi, M.; Higham, L.; Pacheco, E.; Woelfel, P. The space complexity of long-lived and one-shot timestamp implementations. J. ACM 2014, 61, 7. [Google Scholar] [CrossRef]
- Hoest, G.; Shavit, N. Toward a topological characterization of asynchronous complexity. SIAM J. Comput. 2006, 36, 457–497. [Google Scholar] [CrossRef]
- Chordia, S.; Rajamani, S.K.; Rajan, K.; Ramalingam, G.; Vaswani, K. Asynchronous Resilient Linearizability. In Distributed Computing, Proceedings of the 27th International Symposium, DISC 2013, Jerusalem, Israel, 14–18 October 2013; Lecture Notes in Computer Science; Afek, Y., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8205, pp. 164–178. [Google Scholar]
- Choudhury, A.; Patra, A. Optimally Resilient Asynchronous MPC with Linear Communication Complexit. In Proceedings of the 2015 International Conference on Distributed Computing and Networking, ICDCN 2015, Goa, India, 4–7 January 2015; Das, S.K., Krishnaswamy, D., Karkar, S., Korman, A., Kumar, M.J., Portmann, M., Sastry, S., Eds.; ACM: New York, NY, USA, 2015; p. 5. [Google Scholar]
- Vikram, S.; Herlihy, M.; Gafni, E. Asynchronous Computability Theorems for t-Resilient Systems. In Distributed Computing, Proceedings of the 30th International Symposium, DISC 2016, Paris, France, 27–29 September 2016; Lecture Notes in Computer Science; Cyril, G., David, I., Eds.; Springer: Berlin/Heidelberg, Germany; Volume 9888, pp. 428–441.
- Kozlov, D.N. Combinatorial Algebraic Topology; Algorithms and Computation in Mathematics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 21. [Google Scholar]
- Munkres, J.R. Elements of Algebraic Topology; Addision-Wesley: Reading, MA, USA, 1984. [Google Scholar]
- Delporte, C.; Fauconnier, H.; Rajsbaum, S.; Raynal, M. t-resilient immediate snapshot is impossible. In Structural Information and Communication Complexity, Proceedings of the 23rd International Colloquium, SIROCCO 2016, Helsinki, Finland, 19–21 July 2016; Revised Selected Papers; Lecture Notes in Computer Science; Jukka, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 177–191. [Google Scholar]
- Borowsky, E.; Gafni, E. A simple algorithmically reasoned characterization of wait-free computations (extended abstract). In Proceedings of the Sixteenth Annual ACM Symposium on Principles of Distributed Computing, Santa Barbara, CA, USA, 21–24 August 1997; pp. 189–198. [Google Scholar]
- Herlihy, M.; Rajsbaum, S. Concurrent computing and shellable complexes. In Proceedings of the Distributed Computing, 24th International Symposium, DISC 2010, Cambridge, MA, USA, 13–15 September 2010; pp. 109–123. [Google Scholar]
- Kozlov, D.N.; Shavit, N. Combinatorial topology of the standard chromatic subdivision and weak symmetry breaking for 6 processes. CoRR 2015, abs/1506.03944. [Google Scholar]
- Herlihy, M.; Shavit, N. The topological structure of asynchronous computability. J. ACM 1999, 46, 858–923. [Google Scholar] [CrossRef]
- Herlihy, M.; Kozlov, D.N.; Rajsbaum, S. Distributed Computing through Combinatorial Topology, 1st ed.; Morgan Kaufmann: San Francisco, CA, USA, 2013. [Google Scholar]
- Fajstrup, L.; Raußen, M.; Goubault, E. Algebraic topology and concurrency. Theor. Comput. Sci. 2006, 357, 241–278. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).