Corrigendum of a Theorem on New Upper Bounds for the α-Indices. Comment on Lenes et al. New Bounds for the α-Indices of Graphs. Mathematics 2020, 8, 1668
Abstract
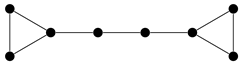
:The Statement, Counterexamples, and Corrigendum
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nikiforov, V. Merging the A- and Q- spectral theories. Appl. Anal. Discrete Math. 2017, 11, 81–107. [Google Scholar] [CrossRef] [Green Version]
- Lenes, E.; Mallea-Zepeda, E.; Rodríguez, J. New bounds for the α-indices of graphs. Mathematics 2020, 8, 1668. [Google Scholar] [CrossRef]
- Ellingham, M.; Zha, X. The spectral radius of graphs on surfaces. J. Comb. Theore Ser. B 2000, 78, 45–56. [Google Scholar] [CrossRef] [Green Version]
- Hong, Y.; Shu, J.-L.; Fang, K. A sharp bound of the spectral radius of graphs. J. Combin. Theory Ser. B 2001, 81, 177–183. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Zhou, B. On the α-spectral radius of graphs. Appl. Anal. Discrete Math. 2000, 14, 431–458. [Google Scholar] [CrossRef]
- Huang, X.; Lin, H.; Xue, J. The Nordhaus-Gaddum type inequalities of Aα-matrix. Appl. Math. Comput. 2000, 365, 124716. [Google Scholar]
- Liu, A.; Das, K.C.; Shu, J. On the eigenvalue of Aα-matrix of graphs. Discrete Math. 2020, 343, 111917. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.-J.; Kao, L.; Weng, C.-w. Corrigendum of a Theorem on New Upper Bounds for the α-Indices. Comment on Lenes et al. New Bounds for the α-Indices of Graphs. Mathematics 2020, 8, 1668. Mathematics 2022, 10, 2619. https://doi.org/10.3390/math10152619
Cheng Y-J, Kao L, Weng C-w. Corrigendum of a Theorem on New Upper Bounds for the α-Indices. Comment on Lenes et al. New Bounds for the α-Indices of Graphs. Mathematics 2020, 8, 1668. Mathematics. 2022; 10(15):2619. https://doi.org/10.3390/math10152619
Chicago/Turabian StyleCheng, Yen-Jen, Louis Kao, and Chih-wen Weng. 2022. "Corrigendum of a Theorem on New Upper Bounds for the α-Indices. Comment on Lenes et al. New Bounds for the α-Indices of Graphs. Mathematics 2020, 8, 1668" Mathematics 10, no. 15: 2619. https://doi.org/10.3390/math10152619
APA StyleCheng, Y.-J., Kao, L., & Weng, C.-w. (2022). Corrigendum of a Theorem on New Upper Bounds for the α-Indices. Comment on Lenes et al. New Bounds for the α-Indices of Graphs. Mathematics 2020, 8, 1668. Mathematics, 10(15), 2619. https://doi.org/10.3390/math10152619




