A Primal–Dual Fixed-Point Algorithm for TVL1 Wavelet Inpainting Based on Moreau Envelope
Abstract
1. Introduction
2. Background
2.1. Moreau Envelope
2.2. The PDFP2O Algorithm
3. The Proposed Model and Its Numerical Scheme
3.1. Wavelet Inpainting Variational Model Based on L1 Norm
3.2. Numerical Scheme for the Proposed Model
| Algorithm 1 The numerical scheme for the proposed model |
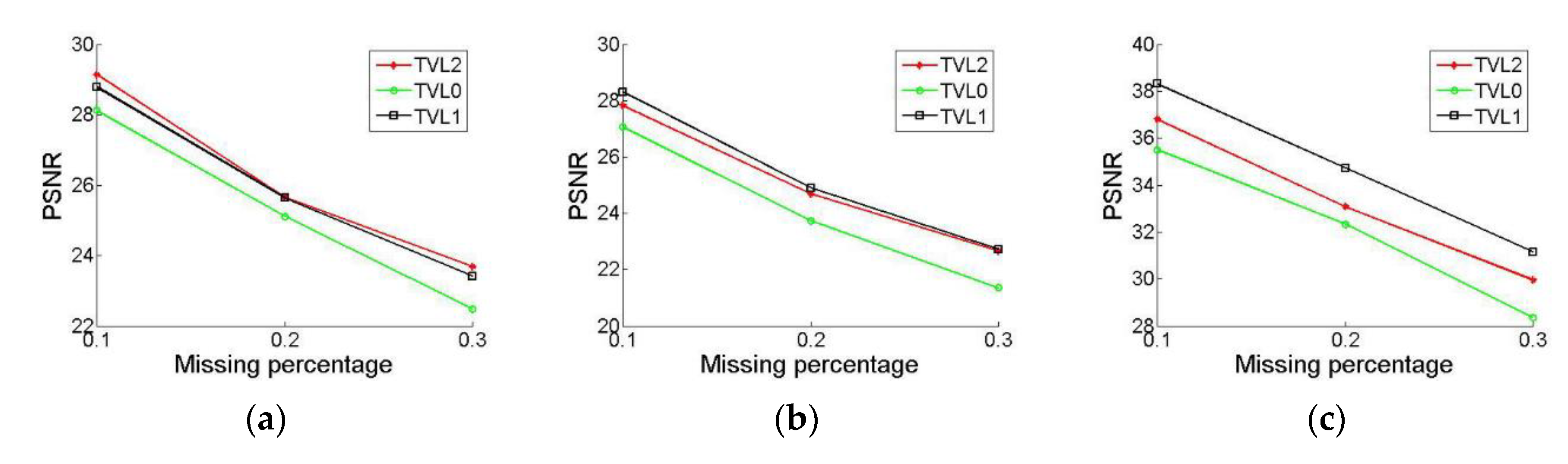
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yashtini, M.; Kang, S.H. A fast relaxed normal two split method and an effective weighted TV approach for Euler’s elastica image inpainting. SIAM J. Imaging Sci. 2016, 9, 1552–1581. [Google Scholar] [CrossRef]
- Ning, W.; Ma, S.; Li, J.; Zhang, Y.; Zhang, L. Multistage attention network for image inpainting. Pattern Recognit. 2020, 106, 107448. [Google Scholar]
- Chan, T.F.; Shen, J.; Zhou, H.M. Total variation wavelet inpainting. J. Math. Imag. Vis. 2006, 25, 107–125. [Google Scholar] [CrossRef]
- Ballester, C.; Bertalmio, M.; Caselles, V.; Sapiro, G.; Verdera, J. Filling-in by joint interpolation of vector fields and gray levels. IEEE Trans. Image Process. 2001, 10, 1200–1211. [Google Scholar] [CrossRef]
- Li, F.; Bao, Z.; Liu, R.H.; Zhang, G.X. Fast image inpainting and colorization by Chambolle’s dual method. J. Vis. Commun. Image R 2011, 22, 529–542. [Google Scholar] [CrossRef]
- Chan, T.F.; Shen, J. Mathematical models for local non-texture inpaintings. SIAM J. Appl. Math 2002, 62, 1019–1043. [Google Scholar]
- Cai, J.F.; Chan, R.H.; Shen, Z. A framelet-based image inpainting algorithm. Appl. Comput. Harm. Anal. 2008, 24, 131–149. [Google Scholar] [CrossRef]
- Chan, R.H.; Chan, T.F.; Shen, L.X.; Shen, Z. Wavelet algorithms for high-resolution image reconstruction. SIAM J. Sci. Comput. 2003, 24, 1408–1432. [Google Scholar] [CrossRef]
- Huang, Y.; Ng, M.K.; Wen, Y. Fast image restoration methods for impulse and Gaussian noises removal. IEEE Signal Process. Lett. 2009, 16, 457–460. [Google Scholar] [CrossRef]
- Fuchs, M.; Muller, J. A higher order TV-type variational problem related to the denoising and inpainting of images. Nonlinear Anal. 2017, 154, 122–147. [Google Scholar] [CrossRef]
- Bertalmio, M.; Sapiro, G.; Caselles, V.; Ballester, C. Image inpainting. In Proceedings of the ACM SIGGRAPH, New Orleans, LA, USA, 23–28 July 2000; pp. 417–424. [Google Scholar]
- Chan, T.F.; Shen, J. Nontexture inpainting by curvature-driven diffusions. J. Vis. Commun. Image R. 2001, 12, 436–449. [Google Scholar] [CrossRef]
- Chan, T.F.; Kang, S.H.; Shen, J. Euler’s elastic and curvature-based inpainting. SIAM J. Appl. Math. 2002, 63, 564–592. [Google Scholar]
- Ren, Z. Adaptive active contour model driven by fractional order fitting energy. Signal Process. 2015, 117, 138–150. [Google Scholar] [CrossRef]
- Arias, P.; Facciolo, G.; Caselles, V.; Sapiro, G. A variational framework for exemplar-based image inpainting. Int. J. Comput. Vis. 2011, 93, 319–347. [Google Scholar] [CrossRef]
- Peyré, G.; Bougleux, S.; Cohen, L. Non-local regularization of inverse problems. Inverse Probl. Imaging 2011, 5, 511–530. [Google Scholar] [CrossRef]
- Jiang, L.; Yin, H. Wavelet inpainting by fractional order total variation. Multidimens. Syst. Signal Process. 2018, 29, 299–320. [Google Scholar] [CrossRef]
- Yau, A.C.; Tai, X.; Ng, M.K. L0-norm and Total Variation for wavelet inpainting. In Proceedings of the 2nd International Conference on Scale Space & Variational Methods in Computer Vision, Berlin/Heidelberg, Germany, 1–5 June 2009. [Google Scholar]
- Zhang, H.Y.; Peng, Q.C.; Wu, Y.D. Wavelet inpainting based on p-Laplace operator. Acta Autom. Sin. 2007, 33, 546–549. [Google Scholar] [CrossRef]
- Chan, R.H.; Yang, J.F.; Yuan, X.M. Alternating direction method for image inpainting in wavelet domains. SIAM J. Imaging Sci. 2011, 4, 807–826. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Chan, T.F. Wavelet inpainting by Nonlocal total variation. Inverse Probl. Imaging 2010, 4, 191–210. [Google Scholar] [CrossRef]
- Wen, Y.W.; Chan, R.H.; Yip, A.M. A primal-dual method for total-variation-based wavelet domain inpainting. IEEE Trans. Image Process. 2012, 21, 106–114. [Google Scholar] [CrossRef]
- Durand, S.; Froment, J. Reconstruction of wavelet coefficients using total variation minimization. SIAM J. Sci. Comput. 2003, 24, 1754–1767. [Google Scholar] [CrossRef]
- Chan, T.F.; Zhou, H.M. Optimal Constructions of Wavelet Coefficients Using Total Variation Regularization in Image Compression; UCLA CAM Report 00-27; Department of Math. UCLA: Los Angeles, CA, USA, 2000. [Google Scholar]
- Wu, C.L.; Zhang, J.Y.; Tai, X.C. Augmented Lagrangian method for total variation restoration with non-quadratic fidelity. Inverse Probl. Imaging 2011, 5, 237–261. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The Split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Micchelli, C.A.; Shen, L.X.; Xu, Y.S. Proximity algorithms for image models: Denoising. Inverse Probl. 2011, 27, 045009. [Google Scholar] [CrossRef]
- Combettes, P.; Wajs, V.R. Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul. 2005, 4, 1168–1200. [Google Scholar] [CrossRef]
- Chen, P.J.; Huang, J.; Zhang, X. A primal-dual fixed point algorithm for convex separable minimization with applications to image restoration. Inverse Probl. 2013, 29, 025011. [Google Scholar] [CrossRef]
- Liu, X.; Tang, Y.; Yang, Y. Primal-dual algorithm to solve the constrained second-order total generalized variational model for image denoising. J. Electron. Imaging 2019, 28, 043017. [Google Scholar] [CrossRef]
- Aujol, J.F.; Gilboa, G.; Chan, T.F.; Osher, S. Structure-texture image decomposition-modeling, algorithms, and parameter selection. Int. J. Comput. Vision. 2006, 67, 111–136. [Google Scholar] [CrossRef]
- Yang, J.; Yin, W. An efficient TVL1 algorithm for deblurring multichannel images corrupted by impulsive noise. SIAM J. Sci. Comput. 2009, 31, 2842–2865. [Google Scholar] [CrossRef]
- Chen, F.; Shen, S.; Xu, F.; Zeng, X. The Moreau envelope approach for the L1/TV image denoising model. Inverse Probl. Imaging 2017, 8, 53–77. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Wets, R.J. Variational Analysis, 3rd ed.; Springer: New York, NY, USA, 2009; p. 21. [Google Scholar]







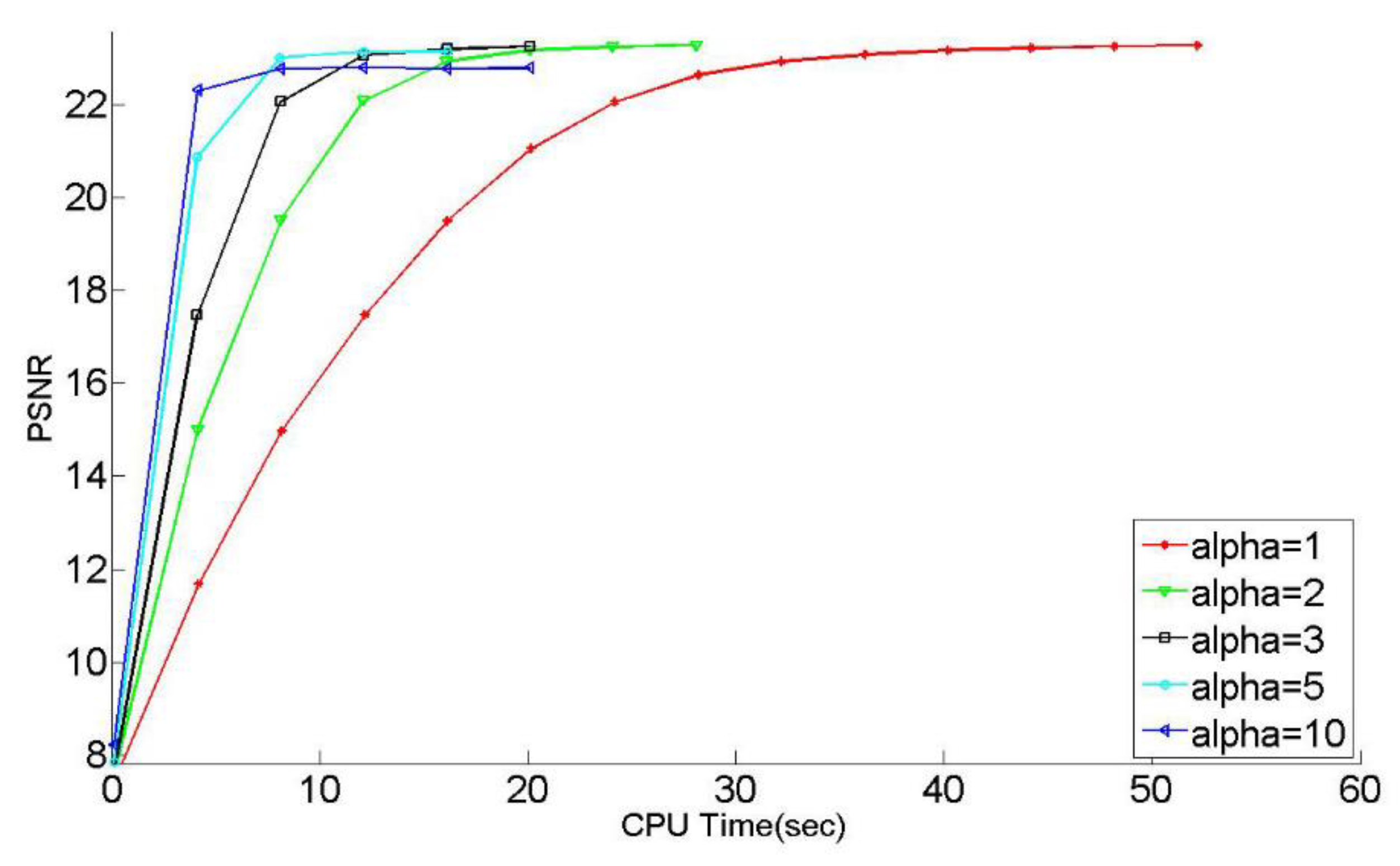
| α = 1 | α = 2 | α = 3 | α = 5 | α = 10 | |
|---|---|---|---|---|---|
| Lenna | 23.07 | 23.07 | 23.04 | 22.92 | 22.59 |
| Goldhill | 21.65 | 21.65 | 21.64 | 21.57 | 21.26 |
| Synthetic | 28.54 | 28.49 | 28.41 | 28.20 | 27.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Zhang, Q.; Yuan, Y. A Primal–Dual Fixed-Point Algorithm for TVL1 Wavelet Inpainting Based on Moreau Envelope. Mathematics 2022, 10, 2470. https://doi.org/10.3390/math10142470
Ren Z, Zhang Q, Yuan Y. A Primal–Dual Fixed-Point Algorithm for TVL1 Wavelet Inpainting Based on Moreau Envelope. Mathematics. 2022; 10(14):2470. https://doi.org/10.3390/math10142470
Chicago/Turabian StyleRen, Zemin, Qifeng Zhang, and Yuxing Yuan. 2022. "A Primal–Dual Fixed-Point Algorithm for TVL1 Wavelet Inpainting Based on Moreau Envelope" Mathematics 10, no. 14: 2470. https://doi.org/10.3390/math10142470
APA StyleRen, Z., Zhang, Q., & Yuan, Y. (2022). A Primal–Dual Fixed-Point Algorithm for TVL1 Wavelet Inpainting Based on Moreau Envelope. Mathematics, 10(14), 2470. https://doi.org/10.3390/math10142470





