Quantitative Mean Square Exponential Stability and Stabilization of Linear Itô Stochastic Markovian Jump Systems Driven by Both Brownian and Poisson Noises

Abstract

In this paper, quantitative mean square exponential stability and stabilization of Itô-type linear stochastic Markovian jump systems with Brownian and Poisson noises are investigated. First, the definition of quantitative mean square exponential stability, which takes into account the transient and steady behaviors of the system, is presented. Second, the relationship between general finite-time mean square stability, finite-time stochastic stability, and quantitative mean square exponential stability is proposed. Subsequently, some sufficient conditions for the existence of state feedback and observer-based controllers are derived, and an algorithm is offered to solve the matrix inequalities resulting from quantitative mean square exponential stabilization. Finally, the effectiveness of the proposed results is illustrated with the numerical example and the practical example.

1. Introduction

Exponential stability is a fundamental concept that has been discussed for a variety of system models, yielding considerable results. For instance, the authors of [1] dealt with the exponential stability of linear differential equations with impulsive effects. In [2], the issue of exponential stability of discrete-time impulsive systems was researched using the Razumikhin technique. Subsequently, the almost sure exponential stability was extended to nonlinear systems in [3]. In addition, other good results are available in [4,5,6,7,8]. However, in the current literature, the exponential stability has been analyzed mainly considering the steady-state behavior without considering the transient behavior. In fact, it is necessary for practical systems to have both stable performance and satisfactory transient characteristics. To deal with this problem, a new concept called quantitative mean square exponential stability (QMSES) for continuous-time stochastic systems is first proposed in [9], which considers both the transient behavior and steady performance of systems. On the basis of [9], the authors of [10] investigate this issue for discrete-time stochastic Markov jump systems (MJSs).

On the other hand, MJSs have attracted a great deal of attention in recent years. Essentially, MJSs are a class of dynamic hybrid system with multiple modes, which can be applied to manipulator systems [11], network control systems [12], motor systems [13], and so on. So far, a great number of achievements about MJSs have been obtained; see [14,15,16,17,18,19,20] and their references therein. As is well known, environment noise exists and cannot be neglected in many dynamical systems. Therefore, MJSs driven by Brownian motion or Poisson jumps have been developed gradually and achieved many related results. For example, in [21,22], the robust nonlinear control design problems driven by both external disturbances and Poisson noises were researched, respectively. Literature [23] discussed the problem of dissipative control for nonlinear systems with Wiener and Poisson noises. Later, finite-time annular domain stability was extended to such systems to be investigated by using differential Gronwall inequality approach in [24,25]. However, the above works do not include QMSES and quantitative mean square exponential stabilization (QMSE-stabilization) for continuous-time stochastic MJSs.

Inspired by the above discussion, both QMSES and QMSE-stabilization problems for Itô-type linear stochastic MJSs perturbed by Brownian and Poisson noises are investigated in this work. Owing to the fact that the model contains Poisson noise, it poses many challenges in terms of stability analysis and controller design. By applying the Itô–Levy formula, Gronwall’s inequality, the above challenges are overcome. The main contributions of this work can be summarized as follows: (i) Compared with the exponential mean square stability (EMSS) in [26], the QMSES not only focuses on the systematic steady-state behavior but also takes into account the systematic transient behavior, which is desired in the practical systems. (ii) In contrast to the reference [9], the system is not only suffering from the Wiener noises but also suffering from the discontinuous interferences, such as Poisson process, which is more prevalent in real systems. (iii) Some new stability criteria for QMSES, general finite-time mean square stability (GFTMSS) and finite-time stochastic stability (FTSS) are derived, and relationships between them are well established. (iv) Several new sufficient conditions for QMSE-stabilization are proposed. In addition, an algorithm is offered to find the relationship between the attenuation coefficient ${\psi }_{min}$ and attenuation rate $\phi$.

The organization of in the rest of the paper is as follows. In Section 2, we present some preliminaries and definitions, which are used to prove the main results. In Section 3, QMSES is studied and the relevant criterion is obtained. In Section 4, we implement the QMSE-stabilization problem by designing the state feedback controller (SFC) and observer-based controller (OBC). In Section 5, we present an algorithm to solve the corresponding matrix inequilities. Furthermore, two examples are offered to show the validity of the results in Section 6. Finally, our conclusions are provided in the last section.

Notations: $A^{\prime }$ denotes the transpose of matrix A; $A>0(A⩾0)$ indicates that A is a positive definite (positive semidefinite) matrix; $I_{n\times n}$ denotes n-order unit matrix; $\Pi$ represents the mathematical expectation; ${\lambda }_{MAX}\left(A\right)\left({\lambda }_{MIN}\left(A\right)\right)$ represents the largest eigenvalue (the smallest eigenvalue) of matrix A; The “w.r.t.” is short for “with respect to”.

2. Preliminaries

Consider the following Itô-type stochastic linear system described by

$$\left\{\begin{array}{ccc}d\mathcal{X}\left(t\right)\hfill & =& (A_1\left({\eta }_t\right)\mathcal{X}\left(t\right)+B_1\left({\eta }_t\right)\mathcal{U}\left(t\right))dt+(A_2\left({\eta }_t\right)\mathcal{X}\left(t\right)+B_2\left({\eta }_t\right)\mathcal{U}\left(t\right))d\mathcal{W}\left(t\right)\hfill \\ \hfill & & +(A_3\left({\eta }_t\right)\mathcal{X}\left(t\right)+B_3\left({\eta }_t\right)\mathcal{U}\left(t\right))dN\left(t\right),\hfill \\ \mathcal{Y}\left(t\right)\hfill & =& C\left({\eta }_t\right)\mathcal{X}\left(t\right)+D\left({\eta }_t\right)\mathcal{U}\left(t\right),\hfill \\ \mathcal{X}\left(0\right)\hfill & =& {\mathcal{X}}_0\in R^n,{\eta }_0\in \Omega ,\hfill \end{array}\right.$$

(1)

where $\mathcal{X}\left(t\right)$, $\mathcal{Y}\left(t\right)$, and $\mathcal{U}\left(t\right)$ are state, measurement output, and control input, respectively. ${\mathcal{X}}_0$ represents the initial state. $\mathcal{W}\left(t\right)$ and $N\left(t\right)$ indicate one-dimensional Brownian motion and Poisson process defined on a complete probability space ($\Omega$,$\mathcal{F}$,${\mathcal{F}}_t$, P) with a filter ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$, respectively. The Poisson jump intensity of $N\left(t\right)$ is $\lambda >0$. ${\eta }_t$ is a right-continuous Markov chain with transition rate matrix $\Xi ={\left[{\varphi }_{ij}\right]}_{n\times n}$, taking values in the finite set $\Omega =\{1,2,\cdots ,n\}$. Furthermore, we assume that ${\eta }_t$, $\mathcal{W}\left(t\right)$ and $N\left(t\right)$ are independent of each other and transition probability is as follows:

$$P\{{\eta }_{t+\Delta t}=j|{\eta }_t=i\}=\left\{\begin{array}{c}{\varphi }_{ij}\Delta t+o(\Delta t),i\ne j,\hfill \\ 1+{\varphi }_{ii}\Delta t+o(\Delta t),i=j,\hfill \end{array}\right.$$

where $\Delta t>0$, ${\varphi }_{ij}$ is the transition rate from i to j with ${\varphi }_{ij}>0,i\ne j$ and ${\varphi }_{ii}=-{\sum }_{i\ne j}{\varphi }_{ij}$. For ${\eta }_t=i$, $A_1\left({\eta }_t\right),B_1\left({\eta }_t\right),A_2\left({\eta }_t\right),B_2\left({\eta }_t\right),A_3\left({\eta }_t\right),B_3\left({\eta }_t\right),C\left({\eta }_t\right),D\left({\eta }_t\right)$ are constant matrices, denoted by $A_{1i}$, $B_{1i}$, $A_{2i}$, $B_{2i}$, $A_{3i}$, $B_{3i}$, $C_i$, $D_i$ for simplicity.

Next, a new definition of QMSES for the system (1) is presented.

Definition 1 ([9]).

For given constants $\psi \ge 1$ and $\phi >0$, the system (1) with $\mathcal{U}\left(t\right)\equiv 0$ is said to be QMSE-stable w.r.t. ($\psi ,\phi$), if for all ${\mathcal{X}}_0\in {\mathcal{R}}^n\backslash \left\{0\right\}$ and any ${\eta }_0\in \Omega$,

$$\begin{array}{c}{\Pi [\parallel \mathcal{X}\left(t\right)\parallel }^2|{\mathcal{X}}_0,{\eta }_0]<\psi \parallel {\mathcal{X}}_0{\parallel }^2{e}^{-\phi t},t\ge 0.\hfill \end{array}$$

(2)

Remark 1.

The definition of QMSES means the state trajectory of the system does not exceed the given upper bound $\psi \parallel {\mathcal{X}}_0{\parallel }^2{e}^{-\phi t}$. By definition 1, the system (1) has a satisfactory transient behavior when ψ is small and φ is large.

In the following, we will illustrate the superiority of QMSES. Compared with EMSS, QMSES considers both the transient behavior and steady performance of systems. A digital example is provided to demonstrate that EMSS probably does not ensure satisfactory transient as well as steady-state performances.

Example 1.

The two model parameters for the given system (1) are given below:

$$A_{11}=\left[\begin{array}{cc}-0.18& 0.55\\ 0& -0.01\end{array}\right],A_{12}=\left[\begin{array}{cc}1& -0.05\\ 0.02& 0.11\end{array}\right],A_{21}=\left[\begin{array}{cc}-0.1& 0.8\\ 0& -0.04\end{array}\right],$$

$$A_{22}=\left[\begin{array}{cc}0.2& -0.2\\ 0.04& 0.6\end{array}\right],A_{31}=\left[\begin{array}{cc}0.003& 0.004\\ 0.002& 0.006\end{array}\right],A_{32}=\left[\begin{array}{cc}0.001& 0.002\\ 0.003& 0.005\end{array}\right],$$

$x\left(0\right)={[-11]}^{\prime }$, $\lambda =0.001$, $\Pi =\left[\begin{array}{cc}-1.5& 1.5\\ 2& -2\end{array}\right]$. According to the Euler–Maruyama method, in Figure 1, the red line shows the state trajectory curve of $\Pi {\parallel \mathcal{X}\left(t\right)\parallel }^2$, and the green line shows 10 state trajectory curve of ${\parallel \mathcal{X}\left(t\right)\parallel }^2$. It can be observed that the free system is EMSS, but it is not QMSES for given (ψ, φ), such as (4, 2), due to its poor transient performance. In other words, for the given $(\psi ,\phi )$, an EMS-stable system is not necessarily QMSE-stable w.r.t. $(\psi ,\phi )$.

Then, the definitions of GFTMSS and FTSS are provided.

Definition 2 ([9]).

For given constants $\psi \ge 1$ and $T>0$, the system (1) with $\mathcal{U}\left(t\right)\equiv 0$ is said to GFTMS-stable w.r.t. ($\psi ,T$), if for all ${\mathcal{X}}_0\in {\mathcal{R}}^n\backslash \left\{0\right\}$ and any ${\eta }_0\in \Omega$,

$$\begin{array}{c}{\Pi [\parallel \mathcal{X}\left(t\right)\parallel }^2|{\mathcal{X}}_0,{\eta }_0]<\psi \parallel {\mathcal{X}}_0{\parallel }^2,\forall t\in [0,T].\hfill \end{array}$$

(3)

Definition 3 ([9]).

For given constants ${\mathcal{C}}_1$, ${\mathcal{C}}_2$, and $0<{\mathcal{C}}_1<{\mathcal{C}}_2$, $T>0$, the system (1) with $\mathcal{U}\left(t\right)\equiv 0$ is said to be FTS-stable w.r.t. (${\mathcal{C}}_1,{\mathcal{C}}_2,T$), if

$$\begin{array}{c}\parallel {\mathcal{X}}_0{\parallel }^2<{\mathcal{C}}_1\Rightarrow \Pi {\parallel \mathcal{X}\left(t\right)\parallel }^2<{\mathcal{C}}_2,0\le t\le T.\hfill \end{array}$$

(4)

Remark 2.

Definitions 1–3 all reflect the transient performance of the system (1). In other words, the state trajectory curve is controlled within the given upper bound on a given time period. In addition, according to the literature [9], the relationship between QMSES, GFTMSS, and FTSS is, when ${\mathcal{C}}_2=\psi {\mathcal{C}}_1$, as follows:

$$QMSE\text{-}stablew.r.t.(\psi ,\phi )\Rightarrow GFTMS\text{-}stablew.r.t.(\psi ,T)\Rightarrow FTS\text{-}stablew.r.t.({\mathcal{C}}_1,{\mathcal{C}}_2,T).$$

Remark 3.

For a given system (1), the sufficient conditions for QMSES, FTSS, and GFTMSS are presented, and the relationship of the stability criteria between FTSS, GFTMSS, and QMSES will be revealed in the following section.

With the basis of Definition 1, the QMSE-stabilization is defined below.

Definition 4.

The system (1) is said to be QMSE-stabilizable w.r.t ($\psi ,\phi$), if for given $\psi \ge 1$ and $\phi >0$, there exists a controller ${\mathcal{U}}^{*}\left(t\right)$ to make

$$\left\{\begin{array}{ccc}d\mathcal{X}\left(t\right)\hfill & =& (A_1\left({\eta }_t\right)\mathcal{X}\left(t\right)+B_1\left({\eta }_t\right){\mathcal{U}}^{*}\left(t\right))dt+(A_2\left({\eta }_t\right)\mathcal{X}\left(t\right)+B_2\left({\eta }_t\right){\mathcal{U}}^{*}\left(t\right))d\mathcal{W}\left(t\right)\hfill \\ \hfill & & +(A_3\left({\eta }_t\right)\mathcal{X}\left(t\right)+B_3\left({\eta }_t\right){\mathcal{U}}^{*}\left(t\right))dN\left(t\right),\hfill \\ \mathcal{X}\left(0\right)\hfill & =& {\mathcal{X}}_0\in R^n,\hfill \end{array}\right.$$

(5)

QMSE-stable w.r.t. ($\psi ,\phi$).

For deriving the main results of this work, the below lemmas will be used:

Lemma 1 ([22]).

Let $\mathcal{V}(t,\xi \left(t\right),i)\in C^2(R_{+},R^l,\mathcal{S};R_{+})$. Based on the following stochastic system

$$d\xi \left(t\right)=a(\xi \left(t\right),{\eta }_t)dt+b(\xi \left(t\right),{\eta }_t)d\mathcal{W}\left(t\right)+c(\xi \left(t\right),{\eta }_t)dN\left(t\right),$$

defining the infinitesimal operator $\mathfrak{L}\mathcal{V}$ as follows:

$$\begin{array}{cc}\hfill \mathfrak{L}\mathcal{V}(t,\xi ,i)=& \frac{\partial \mathcal{V}(t,\xi ,i)}{\partial t}+\frac{\partial \mathcal{V}(t,\xi ,i)}{\partial \xi }a(\xi ,i)+\frac{1}{2}{b}^{\prime }(\xi ,i)\frac{{\partial }^2\mathcal{V}(t,\xi ,i)}{\partial {\xi }^2}b(\xi ,i)\hfill \\ \hfill & +\lambda \left[\mathcal{V}\right((t,\xi ,i)+c(\xi ,i))-\mathcal{V}(t,\xi ,i\left)\right]+\sum _{j=1}^n{\varphi }_{ij}\mathcal{V}(t,\xi ,j).\hfill \end{array}$$

(6)

Lemma 2 ([27]).

(Gronwall inequality) Suppose $g\left(t\right)$ is a non-negative function which satisfies the condition

$$g\left(t\right)\le u+v{\int }_0^{t}g\left(s\right)ds,0\le t\le T$$

for the given constants $u,v\ge 0$; then, the below formula holds:

$$g\left(t\right)\le u{e}^{vt},0\le t\le T.$$

3. Quantitative Mean Square Exponential Stability

The stability criteria of QMSES, GFTMSS, and FTSS will be given in the following three theorems, respectively.

Theorem 1.

The system (1) ($\mathcal{U}\left(t\right)\equiv 0$) is QMSE-stable w.r.t. ($\phi ,\psi$) if for the given scalars $\phi >0$, $\psi \ge 1$, a positive scalar λ, there exists a group of symmetric matrices ${\mathcal{Q}}_i>0,i\in \Omega$ such that

$$\begin{array}{c}\hfill \underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{Q}}_i\right)\right\}/\underset{i\in \Omega }{MIN}\left\{{\lambda }_{MIN}\left({\mathcal{Q}}_i\right)\right\}<\psi ,\end{array}$$

(7)

$$\begin{array}{c}{A}_{1i}^{{}^{\prime }}{\mathcal{Q}}_i+{\mathcal{Q}}_i{A}_{1i}+A_{2i}^{{}^{\prime }}{\mathcal{Q}}_i{A}_{2i}+\lambda (A_{3i}^{{}^{\prime }}{\mathcal{Q}}_i+{\mathcal{Q}}_i{A}_{3i}+A_{3i}^{{}^{\prime }}{\mathcal{Q}}_i{A}_{3i})+{\displaystyle \sum _{j=1}^n}{\varphi }_{ij}{\mathcal{Q}}_j<-\phi {\mathcal{Q}}_i,\hfill \end{array}$$

(8)

hold.

Proof of Theorem 1.

For each ${\eta }_t=i,i\in \Omega$, we define $\mathcal{V}(t,\mathcal{X}\left(t\right),i)=e^{\phi t}{\mathcal{X}}^{\prime }\left(t\right){\mathcal{Q}}_i\mathcal{X}\left(t\right)$, where ${\mathcal{Q}}_i$ is the solution to be determined by solving (7) and (8). Applying Lemma 1 for $\mathcal{V}(t,\mathcal{X}(t),i)$, it follows

$$\begin{array}{cc}\hfill \mathfrak{L}\mathcal{V}(t,\mathcal{X}(t),i)=& e^{\phi t}{\mathcal{X}}^{\prime }\left(t\right)\{\phi {\mathcal{Q}}_i+A_{1i}^{{}^{\prime }}{\mathcal{Q}}_i+{\mathcal{Q}}_i{A}_{1i}+A_{2i}^{{}^{\prime }}{\mathcal{Q}}_i{A}_{2i}+\sum _{j=1}^n{\varphi }_{ij}{\mathcal{Q}}_j\hfill \\ \hfill & +\lambda (A_{3i}^{{}^{\prime }}{\mathcal{Q}}_i+{\mathcal{Q}}_i{A}_{3i}+A_{3i}^{{}^{\prime }}{\mathcal{Q}}_i{A}_{3i})\}\mathcal{X}\left(t\right).\hfill \end{array}$$

(9)

Combining (8) and (9), we can have

$$\mathfrak{L}\mathcal{V}(t,\mathcal{X}(t),i)<0$$

(10)

By first integrating from 0 to t and then taking mathematical expectation on the left and right sides of (10), we gain

$$\begin{array}{c}\hfill \Pi \mathcal{V}(t,\mathcal{X}\left(t\right),i)<\Pi \mathcal{V}(0,{\mathcal{X}}_0,{\eta }_0).\end{array}$$

(11)

Due to

$$\begin{array}{ccc}\Pi \mathcal{V}(t,\mathcal{X}(t),i)\hfill & =& \Pi \left[e^{\phi t}{\mathcal{X}}^{\prime }\left(t\right){\mathcal{Q}}_i\mathcal{X}\left(t\right)\right]\ge e^{\phi t}\underset{i\in \Omega }{MIN}\left\{{\lambda }_{MIN}\left({\mathcal{Q}}_i\right)\right\}\Pi {\parallel \mathcal{X}\left(t\right)\parallel }^2,\hfill \end{array}$$

$$\begin{array}{ccc}\Pi \mathcal{V}(0,{\mathcal{X}}_0,{\eta }_0)\hfill & =& \Pi [{\mathcal{X}}_0^{{}^{\prime }}{Q}_{{\eta }_0}{\mathcal{X}}_0]\le \underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{Q}}_i\right)\right\}\Pi {\parallel {\mathcal{X}}_0\parallel }^2.\hfill \end{array}$$

Then, (11) implies

$$\begin{array}{c}{\Pi \parallel \mathcal{X}\left(t\right)\parallel }^2<{\displaystyle \frac{\underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{Q}}_i\right)\right\}}{\underset{i\in \Omega }{MIN}\left\{{\lambda }_{MIN}\left({\mathcal{Q}}_i\right)\right\}}}{\parallel {\mathcal{X}}_0\parallel }^2{e}^{-\phi t}.\hfill \end{array}$$

(12)

According to (7) and (12), we can acquire ${\Pi \parallel \mathcal{X}\left(t\right)\parallel }^2<\psi {\parallel {\mathcal{X}}_0\parallel }^2{e}^{-\phi t}$, that is, the open-loop system (1) is QMSE-stable w.r.t. $(\phi ,\psi )$. This is the end of the proof.    □

Next, the sufficient condition for the GFTMSS w.r.t. $(\psi ,T)$ is provided.

Theorem 2.

The system (1) ($\mathcal{U}\left(t\right)\equiv 0$) is GFTMS-stable w.r.t. ($\psi ,T$) if for the given $\psi \ge 1$, $T>0$, there exists a group of symmetric matrices ${\mathcal{Q}}_i>0,i\in \Omega$ and a constant $m>0$ such that

$$\begin{array}{c}\hfill \underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{Q}}_i\right)\right\}/\underset{i\in \Omega }{MIN}\left\{{\lambda }_{MIN}\left({\mathcal{Q}}_i\right)\right\}<\psi e^{-mT},\end{array}$$

(13)

$$\begin{array}{c}{A}_{1i}^{{}^{\prime }}{\mathcal{Q}}_i+{\mathcal{Q}}_i{A}_{1i}+A_{2i}^{{}^{\prime }}{\mathcal{Q}}_i{A}_{2i}+\lambda (A_{3i}^{{}^{\prime }}{\mathcal{Q}}_i+{\mathcal{Q}}_i{A}_{3i}+A_{3i}^{{}^{\prime }}{\mathcal{Q}}_i{A}_{3i})+{\displaystyle \sum _{j=1}^n}{\varphi }_{ij}{\mathcal{Q}}_j<m{\mathcal{Q}}_i,\hfill \end{array}$$

(14)

hold.

Proof of Theorem 2.

For each ${\eta }_t=i,i\in \Omega$, we define $\mathcal{V}(t,\mathcal{X}\left(t\right),i)={\mathcal{X}}^{\prime }\left(t\right){\mathcal{Q}}_i\mathcal{X}\left(t\right)$, where ${\mathcal{Q}}_i$ is the solution to be determined by solving (13) and (14). By using Lemma 1 for $\mathcal{V}(t,\mathcal{X}(t),i)$, we can obtain

$$\begin{array}{cc}\hfill \mathfrak{L}\mathcal{V}(t,\mathcal{X}(t),i)=& {\mathcal{X}}^{\prime }\left(t\right)\{A_{1i}^{{}^{\prime }}{\mathcal{Q}}_i+{\mathcal{Q}}_i{A}_{1i}+A_{2i}^{{}^{\prime }}{\mathcal{Q}}_i{A}_{2i}+\sum _{j=1}^n{\varphi }_{ij}{\mathcal{Q}}_j+\lambda (A_{3i}^{{}^{\prime }}{\mathcal{Q}}_i+{\mathcal{Q}}_i{A}_{3i}\hfill \\ \hfill & +A_{3i}^{{}^{\prime }}{\mathcal{Q}}_i{A}_{3i}\left)\right\}\mathcal{X}\left(t\right).\hfill \end{array}$$

(15)

By (14) and (15), we can gain

$$\mathfrak{L}\mathcal{V}(t,\mathcal{X}(t),i)<m\mathcal{V}(t,\mathcal{X}(t),i).$$

(16)

By first integrating from 0 to t and then taking mathematical expectation on the left and right sides of (16), we can attain

$$\begin{array}{c}\hfill \Pi \mathcal{V}(t,\mathcal{X}\left(t\right),i)<\Pi \mathcal{V}(0,{\mathcal{X}}_0,{\eta }_0)+m{\int }_0^t\Pi \mathcal{V}(s,\mathcal{X}\left(s\right),{\eta }_s)ds.\end{array}$$

(17)

From Lemma 2, we know

$$\begin{array}{c}\hfill \Pi \mathcal{V}(t,\mathcal{X}\left(t\right),i)<e^{mT}\Pi \mathcal{V}(t,{\mathcal{X}}_0,{\eta }_0).\end{array}$$

(18)

Due to

$$\begin{array}{cc}\hfill & \Pi \mathcal{V}(t,\mathcal{X}\left(t\right),i)=\Pi \left[{\mathcal{X}}^{\prime }\left(t\right){\mathcal{Q}}_i\mathcal{X}\left(t\right)\right]\ge \underset{i\in \Omega }{MIN}\left\{{\lambda }_{MIN}\left({\mathcal{Q}}_i\right)\right\}\Pi {\parallel \mathcal{X}\left(t\right)\parallel }^2,\hfill \\ \hfill & \Pi \mathcal{V}(0,{\mathcal{X}}_0,{\eta }_0)=\Pi \left[{\mathcal{X}}_0^{{}^{\prime }}{Q}_{{\eta }_0}{\mathcal{X}}_0\right]\le \underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{Q}}_i\right)\right\}\Pi {\parallel {\mathcal{X}}_0\parallel }^2.\hfill \end{array}$$

Based on (18), we obtain

$$\begin{array}{c}{\Pi \parallel \mathcal{X}\left(t\right)\parallel }^2<{\displaystyle \frac{\underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{Q}}_i\right)\right\}}{\underset{i\in \Omega }{MIN}\left\{{\lambda }_{MIN}\left({\mathcal{Q}}_i\right)\right\}}}{\parallel {\mathcal{X}}_0\parallel }^2{e}^{mT}.\hfill \end{array}$$

(19)

According to (13) and (19), we can acquire ${\Pi \parallel \mathcal{X}\left(t\right)\parallel }^2<\psi {\parallel {\mathcal{X}}_0\parallel }^2$, that is, the open-loop system (1) is GFTMS-stable w.r.t. $(\psi ,T)$ when $t\in [0,T]$. This is the end of the proof.    □

In the next part, the sufficient conditions for FTSS will be presented.

Theorem 3.

The system (1) ($\mathcal{U}\left(t\right)\equiv 0$) is FTS-stable w.r.t. (${\mathcal{C}}_1,{\mathcal{C}}_2,T$) if for given ${\mathcal{C}}_1>0$, ${\mathcal{C}}_2>0$, and a positive scalar λ, there exists a group of symmetric matrices ${\mathcal{Q}}_i>0,i\in \Omega$ and a constant $m>0$ such that

$$\begin{array}{c}\hfill \underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{Q}}_i\right)\right\}/\underset{i\in \Omega }{MIN}\left\{{\lambda }_{MIN}\left({\mathcal{Q}}_i\right)\right\}<{\displaystyle \frac{{\mathcal{C}}_2}{{\mathcal{C}}_1}}{e}^{-mT},\end{array}$$

(20)

$$\begin{array}{c}{A}_{1i}^{{}^{\prime }}{\mathcal{Q}}_i+{\mathcal{Q}}_i{A}_{1i}+A_{2i}^{{}^{\prime }}{\mathcal{Q}}_i{A}_{2i}+\lambda (A_{3i}^{{}^{\prime }}{\mathcal{Q}}_i+{\mathcal{Q}}_i{A}_{3i}+A_{3i}^{{}^{\prime }}{\mathcal{Q}}_i{A}_{3i})+{\displaystyle \sum _{j=1}^n}{\varphi }_{ij}{\mathcal{Q}}_j<m{\mathcal{Q}}_i,\hfill \end{array}$$

(21)

hold.

Proof of Theorem 3.

For each ${\eta }_t=i,i\in \Omega$, we define $\mathcal{V}(t,\mathcal{X}\left(t\right),i)={\mathcal{X}}^{\prime }\left(t\right){\mathcal{Q}}_i\mathcal{X}\left(t\right)$ as in Theorem 2, where ${\mathcal{Q}}_i$ is the solution to be determined by solving (20) and (21). Applying the similar processing technique, we obtain

$$\begin{array}{c}{\Pi \parallel \mathcal{X}\left(t\right)\parallel }^2<{\displaystyle \frac{\underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{Q}}_i\right)\right\}}{\underset{i\in \Omega }{MIN}\left\{{\lambda }_{MIN}\left({\mathcal{Q}}_i\right)\right\}}}{\parallel {\mathcal{X}}_0\parallel }^2{e}^{mT}.\hfill \end{array}$$

(22)

Considering conditions $\Pi \parallel {\mathcal{X}}_0{\parallel }^2<{\mathcal{C}}_1$, (20), and (22), ${\Pi \parallel \mathcal{X}\left(t\right)\parallel }^2<{\mathcal{C}}_2$ is gained. Thus, the open-loop system (1) is FTS-stable w.r.t. (${\mathcal{C}}_1,{\mathcal{C}}_2,T$). The proof is completed here.    □

Remark 4.

From Theorems 1 and 2, we can see that (7) implies (13) when $m=0$, that is, (7) and (8) mean (13) and (14), this indicates the system (1) is GFTMS-stable w.r.t. $(\psi ,T)$. From Theorems 2 and 3, we obtain (13) implies (20) when ${\mathcal{C}}_1\psi -{\mathcal{C}}_2<0$, that is, (13) and (14) mean (20) and (21), this shows the system (1) is FTS-stable w.r.t. (${\mathcal{C}}_1,{\mathcal{C}}_2,T$).

4. Quantitative Mean Square Exponential Stabilization

4.1. Stabilization via SFC

The purpose of this part is to consider the SFC ${\mathcal{U}}^{*}\left(t\right)=K\left({\eta }_t\right)x\left(t\right)$ to make the closed-loop system (5) to achieve QMSE-stabilization, where $K\left({\eta }_t\right)$ is the controller gain. When ${\eta }_t=i$, $K\left({\eta }_t\right)$ is abbreviated to $K_i$. In the following theorem, the sufficient conditions for QMSE-stabilization in SFC case will be presented.

Theorem 4.

The system (5) is QMSE-stable w.r.t. ($\psi ,\phi$) if for given $\psi \ge 1$, $\phi >0$, there exists a group of symmetric matrices ${\mathcal{S}}_i>0$, matrices ${\mathcal{O}}_i$, and positive constants ${\delta }_1,{\delta }_2$ such that

$$\begin{array}{c}\hfill \left[\begin{array}{cccc}{\Gamma }_{i11}& {\mathcal{S}}_i{A}_{2i}^{{}^{\prime }}+{\mathcal{O}}_i^{{}^{\prime }}{B}_{2i}^{{}^{\prime }}& \sqrt{\lambda }{\mathcal{S}}_i{A}_{3i}^{{}^{\prime }}+\sqrt{\lambda }{\mathcal{O}}_i^{{}^{\prime }}{B}_{3i}^{{}^{\prime }}& {\Gamma }_{i14}\\ *& -{\mathcal{S}}_i& 0& 0\\ *& *& -{\mathcal{S}}_i& 0\\ *& *& *& -{\Gamma }_{i44}\end{array}\right]<0,\end{array}$$

(23)

$$\begin{array}{c}{\delta }_{2}I<{\mathcal{S}}_i<{\delta }_{1}I,{\delta }_1-\psi {\delta }_2<0,\hfill \end{array}$$

(24)

hold, where ${\Gamma }_{i11}={\mathcal{S}}_i{A}_{1i}^{{}^{\prime }}+{\mathcal{O}}_i^{{}^{\prime }}{B}_{1i}^{{}^{\prime }}+A_{1i}{\mathcal{S}}_i+B_{1i}{\mathcal{O}}_i+\lambda A_{3i}{\mathcal{S}}_i+\lambda B_{3i}{\mathcal{O}}_i+\lambda {\mathcal{S}}_i{A}_{3i}^{{}^{\prime }}+\lambda {\mathcal{O}}_i^{{}^{\prime }}{B}_{3i}^{{}^{\prime }}+\phi {\mathcal{S}}_i+{\varphi }_{ii}{\mathcal{S}}_i$, ${\Gamma }_{i14}=[\sqrt{{\varphi }_{i,1}}{\mathcal{S}}_i,\cdots ,\sqrt{{\varphi }_{i,i-1}}{\mathcal{S}}_i,\sqrt{{\varphi }_{i,i+1}}{\mathcal{S}}_i,\cdots ,\sqrt{{\varphi }_{i,n}}{\mathcal{S}}_i]$, ${\Gamma }_{i44}=diag\{{\mathcal{S}}_1,\cdots ,{\mathcal{S}}_{i-1},{\mathcal{S}}_{i+1},\cdots ,{\mathcal{S}}_n\}$. In this case, $K_i={\mathcal{O}}_i{\mathcal{S}}_i^{-1},i=1,2,\cdots ,n$.

Proof of Theorem 4.

Bringing ${\mathcal{U}}^{*}\left(t\right)=K_i\mathcal{X}\left(t\right)$ into the system (5), the system (5) can be changed to

$$\begin{array}{c}d\mathcal{X}\left(t\right)=(A_{1i}+B_{1i}{K}_i)\mathcal{X}\left(t\right)dt+(A_{2i}+B_{2i}{K}_i)\mathcal{X}\left(t\right)d\mathcal{W}\left(t\right)+(A_{3i}+B_{3i}{K}_i)\mathcal{X}\left(t\right)dN\left(t\right).\hfill \end{array}$$

(25)

In (23), letting ${\mathcal{S}}_i={\mathcal{Q}}_i^{-1}$, then ${\mathcal{O}}_i=K_i{\mathcal{Q}}_i^{-1}$, ${\Gamma }_{i14}=[\sqrt{{\varphi }_{i,1}}{\mathcal{Q}}_i^{-1},\cdots ,\sqrt{{\varphi }_{i,i-1}}{\mathcal{Q}}_i^{-1},\cdots ,\sqrt{{\varphi }_{i,n}}\times {\mathcal{Q}}_i^{-1}]$, ${\Gamma }_{i44}=diag\{{\mathcal{Q}}_1^{-1},\cdots ,{\mathcal{Q}}_{i-1}^{-1},{\mathcal{Q}}_{i+1}^{-1},\cdots ,{\mathcal{Q}}_n^{-1}\}$ and note that ${\Sigma }_{j=1,j\ne i}^n{\varphi }_{ij}{\mathcal{Q}}_i^{-1}{\mathcal{Q}}_j{\mathcal{Q}}_i^{-1}={\Gamma }_{i14}{\Gamma }_{i44}^{-1}{\Gamma }_{i14}^{{}^{\prime }}$. By using Schur Complement, from (23), we obtain

$$\begin{array}{c}{\mathcal{Q}}_i^{-1}{(A_{1i}+B_{1i}{K}_i)}^{\prime }+(A_{1i}+B_{1i}{K}_i){\mathcal{Q}}_i^{-1}+{\mathcal{Q}}_i^{-1}{(A_{2i}+B_{2i}{K}_i)}^{\prime }{\mathcal{Q}}_i(A_{2i}+B_{2i}{K}_i){\mathcal{Q}}_i^{-1}\hfill \\ +\lambda [(A_{3i}+B_{3i}{K}_i){\mathcal{Q}}_i^{-1}+{\mathcal{Q}}_i^{-1}{(A_{3i}+B_{3i}{K}_i)}^{\prime }+{\mathcal{Q}}_i^{-1}{(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{Q}}_i(A_{3i}+B_{3i}{K}_i){\mathcal{Q}}_i^{-1}]\hfill \\ +\sum _{j=1}^n{\varphi }_{ij}{\mathcal{Q}}_i^{-1}{\mathcal{Q}}_j{\mathcal{Q}}_i^{-1}<-\phi {\mathcal{Q}}_i^{-1}.\hfill \end{array}$$

(26)

Premultiplying and postmultiplying (26) by ${\mathcal{Q}}_i$, we have

$$\begin{array}{c}{(A_{1i}+B_{1i}{K}_i)}^{\prime }{\mathcal{Q}}_i+{\mathcal{Q}}_i(A_{1i}+B_{1i}{K}_i)+{(A_{2i}+B_{2i}{K}_i)}^{\prime }{\mathcal{Q}}_i(A_{2i}+B_{2i}{K}_i)+\lambda [{\mathcal{Q}}_i(A_{3i}+B_{3i}{K}_i)\hfill \\ +{(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{Q}}_i+{(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{Q}}_i(A_{3i}+B_{3i}{K}_i)]+\sum _{j=1}^n{\varphi }_{ij}{\mathcal{Q}}_j<-\phi {\mathcal{Q}}_i.\hfill \end{array}$$

(27)

Therefore, (23) is equivalent to (27). From Theorem 1, next, we only need to prove that inequality (7) holds. According to the inequality (24), it follows that

$$\begin{array}{c}{\displaystyle \frac{\underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{Q}}_i\right)\right\}}{\underset{i\in \Omega }{MIN}\left\{{\lambda }_{MIN}\left({\mathcal{Q}}_i\right)\right\}}}<{\displaystyle \frac{{\delta }_1}{{\delta }_2}}<\psi .\hfill \end{array}$$

That is, (7) is obtained. The proof is complete.    □

4.2. Stabilization via OBC

In the previous part, the SFC ${\mathcal{U}}^{*}\left(t\right)=K\left({\eta }_t\right)\mathcal{X}\left(t\right)$ has been considered to solve the QMSE-stabilization problem. However, the state of the system is always difficult to be measured in practical applications. Therefore, an OBC is proposed.

$$\left\{\begin{array}{ccc}d\hat{\mathcal{X}}\left(t\right)\hfill & =& [A_1\left({\eta }_t\right)\hat{\mathcal{X}}\left(t\right)+B_1({\eta }_t){\mathcal{U}}^{*}\left(t\right)\left(t\right)+L\left({\eta }_t\right)(\mathcal{Y}\left(t\right)-C\left({\eta }_t\right)\hat{\mathcal{X}}\left(t\right))]dt,\hfill \\ {\mathcal{U}}^{*}\left(t\right)\left(t\right)\hfill & =& K\left({\eta }_t\right)\hat{\mathcal{X}}\left(t\right),\hat{\mathcal{X}}\left(0\right)={\hat{\mathcal{X}}}_0,\hfill \end{array}\right.$$

(28)

where $\hat{\mathcal{X}}\left(t\right)\in R^n$ and $L\left({\eta }_t\right)$ are estimated state and estimated gain, respectively. When ${\eta }_t=i$, $L\left({\eta }_t\right)$ is abbreviated to $L_i$. Set $\mathcal{E}\left(t\right)=\mathcal{X}\left(t\right)-\hat{\mathcal{X}}\left(t\right)$, the system (5) is transformed into

$$\left\{\begin{array}{ccc}d\mathcal{X}\left(t\right)\hfill & =& [(A_{1i}+B_{1i}{K}_i)\mathcal{X}\left(t\right)-B_{1i}{K}_i\mathcal{E}\left(t\right)]dt+[(A_{2i}+B_{2i}{K}_i)\mathcal{X}\left(t\right)-B_{2i}{K}_i\mathcal{E}\left(t\right)]d\mathcal{W}\left(t\right)\hfill \\ \hfill & & +[(A_{3i}+B_{3i}{K}_i)\mathcal{X}\left(t\right)-B_{3i}{K}_i\mathcal{E}\left(t\right)]dN\left(t\right),\hfill \\ \mathcal{X}\left(0\right)\hfill & =& {\mathcal{X}}_0,\hfill \end{array}\right.$$

(29)

with

$$\left\{\begin{array}{ccc}d\mathcal{E}\left(t\right)\hfill & =& [-L_i{D}_i{K}_i\mathcal{X}\left(t\right)+(A_{1i}-L_i{C}_i+L_i{D}_i{K}_i)\mathcal{E}\left(t\right)]dt+[(A_{2i}+B_{2i}{K}_i)\mathcal{X}\left(t\right)\hfill \\ \hfill & & -B_{2i}{K}_i\mathcal{E}\left(t\right)]d\mathcal{W}\left(t\right)+[(A_{3i}+B_{3i}{K}_i)\mathcal{X}\left(t\right)-B_{3i}{K}_i\mathcal{E}\left(t\right)]dN\left(t\right),\hfill \\ \mathcal{E}\left(0\right)\hfill & =& {\mathcal{X}}_0-{\hat{\mathcal{X}}}_0.\hfill \end{array}\right.$$

(30)

In the practical system, the smaller the estimation error $\mathcal{E}\left(t\right)$, the better. We may assume that the error satisfies $\Pi \left[{\mathcal{E}}^{\prime }\left(t\right)\mathcal{E}\left(t\right)\right]<1$, for arbitrary $0\le t\le T$.

Next, the sufficient conditions for QMSE-stabilization in OBC case will be provided.

Theorem 5.

The system (29) is QMSE-stable w.r.t. ($\psi ,\phi$) if for given $\psi \ge 1$, $\phi >0$, there exist two groups of positive definition matrices ${\mathcal{H}}_i$, ${\mathcal{G}}_i$ and matrices ${\mathcal{M}}_i$, $i\in \Omega$, and positive constants ${\theta }_1,{\theta }_2,{\theta }_3$ such that

$$\begin{array}{c}\hfill \left[\begin{array}{cc}{\Gamma }_4& {\Gamma }_5\\ *& {\Gamma }_6\end{array}\right]<0,\end{array}$$

(31)

$$\begin{array}{c}{\theta }_{1}I<{\mathcal{G}}_i<{\theta }_{2}I,0<{\mathcal{H}}_i<{\theta }_{3}I,{\theta }_2+{\theta }_3<\psi {\theta }_1,\hfill \end{array}$$

(32)

hold, where ${\Gamma }_4={(A_{1i}+B_{1i}{K}_i)}^{\prime }{\mathcal{G}}_i+{\mathcal{G}}_i(A_{1i}+B_{1i}{K}_i)+{(A_{2i}+B_{2i}{K}_i)}^{\prime }{\mathcal{G}}_i(A_{2i}+B_{2i}{K}_i)+\lambda {\mathcal{G}}_i(A_{3i}+B_{3i}{K}_i)+\lambda {(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{G}}_i+\lambda {(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{G}}_i(A_{3i}+B_{3i}{K}_i)+{(A_{2i}+B_{2i}{K}_i)}^{\prime }\times {\mathcal{H}}_i(A_{2i}+B_{2i}{K}_i)+\lambda {(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{H}}_i(A_{3i}+B_{3i}{K}_i)+{\sum }_{j=1}^n{\varphi }_{ij}{\mathcal{G}}_j+\phi {\mathcal{G}}_i$, ${\Gamma }_5=-{\mathcal{G}}_i{B}_{1i}{K}_i-{(A_{2i}+B_{2i}{K}_i)}^{\prime }{\mathcal{G}}_i{B}_{2i}{K}_i-\lambda {\mathcal{G}}_i{B}_{3i}{K}_i-\lambda {(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{G}}_i{B}_{3i}{K}_i-K_i^{{}^{\prime }}{D}_i^{{}^{\prime }}{\mathcal{M}}_i^{{}^{\prime }}-{(A_{2i}+B_{2i}{K}_i)}^{\prime }{\mathcal{H}}_i{B}_{2i}{K}_i+\lambda {(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{H}}_i-\lambda {(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{H}}_i{B}_{3i}{K}_i$, ${\Gamma }_6=K_i^{{}^{\prime }}{B}_{2i}^{{}^{\prime }}{\mathcal{G}}_i{B}_{2i}{K}_i+\lambda K_i^{{}^{\prime }}{B}_{3i}^{{}^{\prime }}{\mathcal{G}}_i{B}_{3i}{K}_i+A_{1i}^{{}^{\prime }}{\mathcal{H}}_i-C_i^{{}^{\prime }}{\mathcal{M}}_i^{{}^{\prime }}+K_i^{{}^{\prime }}{D}_i^{{}^{\prime }}{\mathcal{M}}_i^{{}^{\prime }}+{\mathcal{H}}_i{A}_{1i}-{\mathcal{M}}_i{C}_i+{\mathcal{M}}_i{D}_i{K}_i+K_i^{{}^{\prime }}{B}_{2i}^{{}^{\prime }}{\mathcal{H}}_i{B}_{2i}{K}_i-\lambda {\mathcal{H}}_i{B}_{3i}{K}_i-\lambda K_i^{{}^{\prime }}{B}_{3i}^{{}^{\prime }}{\mathcal{H}}_i+\lambda K_i^{{}^{\prime }}{B}_{3i}^{{}^{\prime }}{\mathcal{H}}_i{B}_{3i}{K}_i+{\sum }_{j=1}^n{\varphi }_{ij}{\mathcal{H}}_j+\phi {\mathcal{H}}_i$. In this case, $L_i={\mathcal{H}}_i^{-1}{\mathcal{M}}_i$, $i=1,\cdots ,n$.

Proof of Theorem 5.

Set ${\tilde{\mathcal{Q}}}_i=diag\{{\mathcal{G}}_i,{\mathcal{H}}_i\}$ and $\mathcal{Z}\left(t\right)={[{\mathcal{X}}^{\prime }\left(t\right),{\mathcal{E}}^{\prime }\left(t\right)]}^{\prime }$, where ${\mathcal{G}}_i$ and ${\mathcal{H}}_i$ are the solutions to be determined by solving (31) and (32). Then, we define $\mathcal{V}(t,\mathcal{Z}\left(t\right),i)=e^{\phi t}{z}^{\prime }\left(t\right){\tilde{\mathcal{Q}}}_i\mathcal{Z}\left(t\right)$. For each ${\eta }_t=i,i\in \Omega$, we can attain

$$\begin{array}{c}\mathcal{V}(t,\mathcal{Z}\left(t\right),{\eta }_t=i)=e^{\phi t}{z}^{\prime }\left(t\right){\tilde{\mathcal{Q}}}_i\mathcal{Z}\left(t\right)=e^{\phi t}{\mathcal{X}}^{\prime }\left(t\right){\mathcal{G}}_i\mathcal{X}\left(t\right)+e^{\phi t}{\mathcal{E}}^{\prime }\left(t\right){\mathcal{H}}_i\mathcal{E}\left(t\right).\hfill \end{array}$$

(33)

Applying Lemma 1 for $\mathcal{V}(t,\mathcal{X}(t),i)$, we can obtain

$$\begin{array}{c}\mathfrak{L}\mathcal{V}(t,\mathcal{Z}\left(t\right),{\eta }_t=i)=e^{\phi t}{\left[\begin{array}{c}\mathcal{X}\left(t\right)\\ \mathcal{E}\left(t\right)\end{array}\right]}^{\prime }\left[\begin{array}{cc}{\Gamma }_4& {\Gamma }_5^{*}\\ *& {\Gamma }_6^{*}\end{array}\right]\left[\begin{array}{c}\mathcal{X}\left(t\right)\\ \mathcal{E}\left(t\right)\end{array}\right],\hfill \end{array}$$

(34)

where ${\Gamma }_5^{*}=-{\mathcal{G}}_i{B}_{1i}{K}_i-{(A_{2i}+B_{2i}{K}_i)}^{\prime }{\mathcal{G}}_i{B}_{2i}{K}_i-\lambda {\mathcal{G}}_i{B}_{3i}{K}_i-\lambda {(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{G}}_i{B}_{3i}{K}_i-K_i^{{}^{\prime }}{D}_i^{{}^{\prime }}\times L_i^{{}^{\prime }}{\mathcal{H}}_i-{(A_{2i}+B_{2i}{K}_i)}^{\prime }{\mathcal{H}}_i{B}_{2i}{K}_i+\lambda {(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{H}}_i-\lambda {(A_{3i}+B_{3i}{K}_i)}^{\prime }{\mathcal{H}}_i{B}_{3i}{K}_i$, ${\Gamma }_6^{*}=K_i^{{}^{\prime }}{B}_{2i}^{{}^{\prime }}{\mathcal{G}}_i\times B_{2i}{K}_i+\lambda K_i^{{}^{\prime }}{B}_{3i}^{{}^{\prime }}{\mathcal{G}}_i{B}_{3i}{K}_i+A_{1i}^{{}^{\prime }}{\mathcal{H}}_i-C_i^{{}^{\prime }}{L}_i^{{}^{\prime }}{\mathcal{H}}_i+K_i^{{}^{\prime }}{D}_i^{{}^{\prime }}{L}_i^{{}^{\prime }}{\mathcal{H}}_i+{\mathcal{H}}_i{A}_{1i}-{\mathcal{H}}_i{L}_i{C}_i+{\mathcal{H}}_i{L}_i{D}_i{K}_i+K_i^{{}^{\prime }}{B}_{2i}^{{}^{\prime }}{\mathcal{H}}_i{B}_{2i}{K}_i-\lambda {\mathcal{H}}_i{B}_{3i}{K}_i-\lambda K_i^{{}^{\prime }}{B}_{3i}^{{}^{\prime }}{\mathcal{H}}_i+\lambda K_i^{{}^{\prime }}{B}_{3i}^{{}^{\prime }}{\mathcal{H}}_i{B}_{3i}{K}_i+{\sum }_{j=1}^n{\varphi }_{ij}{\mathcal{H}}_j+\phi {\mathcal{H}}_i$.

Letting ${\mathcal{M}}_i={\mathcal{H}}_i{L}_i$, (31) implies

$$\begin{array}{c}\mathfrak{L}\mathcal{V}(t,\mathcal{Z}\left(t\right),{\eta }_t=i)<0.\hfill \end{array}$$

(35)

By first integrating from 0 to t and then taking mathematical expectation on the left and right sides of (35), we can attain

$$\begin{array}{c}\hfill \Pi \mathcal{V}(t,\mathcal{Z}\left(t\right),i)<\Pi \mathcal{V}(0,{\mathcal{X}}_0,{\eta }_0)\end{array}$$

(36)

Due to

$$\begin{array}{ccc}\Pi \mathcal{V}(t,\mathcal{Z}(t),i)\hfill & =& \Pi [e^{\phi t}{\mathcal{X}}^{\prime }\left(t\right){\mathcal{G}}_i\mathcal{X}\left(t\right)+e^{\phi t}{\mathcal{E}}^{\prime }\left(t\right){\mathcal{H}}_i\mathcal{E}\left(t\right)]\ge e^{\phi t}\underset{i\in \Omega }{MIN}\left\{{\lambda }_{MIN}\left({\mathcal{G}}_i\right)\right\}\Pi {\parallel \mathcal{X}\left(t\right)\parallel }^2,\hfill \end{array}$$

$$\begin{array}{ccc}\Pi \mathcal{V}(0,{\mathcal{Z}}_0,{\eta }_0)\hfill & =& \Pi [{\mathcal{X}}_0^{{}^{\prime }}{G}_{{\eta }_0}{\mathcal{X}}_0+{\mathcal{E}}_0^{{}^{\prime }}{H}_{{\eta }_0}{\mathcal{E}}_0]\hfill \\ \hfill & \le & [\underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{G}}_i\right)\right\}+\underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{H}}_i\right)\right\}]\Pi {\parallel {\mathcal{X}}_0\parallel }^2.\hfill \end{array}$$

Then, (36) implies

$$\begin{array}{c}{\Pi \parallel \mathcal{X}\left(t\right)\parallel }^2<{\displaystyle \frac{\underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{G}}_i\right)\right\}+\underset{i\in \Omega }{MAX}\left\{{\lambda }_{MAX}\left({\mathcal{H}}_i\right)\right\}}{\underset{i\in \Omega }{MIN}\left\{{\lambda }_{MIN}\left({\mathcal{G}}_i\right)\right\}}}{\parallel {\mathcal{X}}_0\parallel }^2{e}^{-\phi t}.\hfill \end{array}$$

(37)

According to (32) and (37), ${\Pi \parallel \mathcal{X}\left(t\right)\parallel }^2<\psi {\parallel {\mathcal{X}}_0\parallel }^2{e}^{-\phi t}$ is attained. Therefore, the system (29) is QMSE-stable w.r.t. ($\psi ,\phi$). The proof is completed here.    □

5. Numerical Algorithm

In order to solve the matrix inequalities in Theorem 4, we propose an algorithm in this section. The same algorithm can be adopted for solving the inequalities in Theorem 5. The specific idea is to find feasible solutions satisfying the inequalities (23) and (24) by linear searching, starting from $\phi =0$ and $\psi =1$. The detailed steps of the algorithm are provided in Algorithm 1.

Algorithm 1 2-mode case

Step 1: Take a group of ${\phi }_i(i=1,\cdots ,n)$ with step size $f_1$, a group of ${\psi }_j(j=1,\cdots ,n)$ with step size $f_2$, and a given large number l. Step 2: Start from $i=1$, $j=1$ and set ${\phi }_1=0$, ${\psi }_1=1$. Step 3: if (${\phi }_i,{\psi }_j$) makes (23) and (24) have solutions, save (${\phi }_i,{\psi }_j$) into ($\Phi \left(i\right),\Psi \left(j\right)$), and enter to Step 4; else if $\psi <l$, then set ${\psi }_j={\psi }_{j+1}$, $j=j+1$, and proceed to to Step 3; otherwise, go to Step 5. Step 4: Set ${\phi }_i={\phi }_{i+1}$, $i=i+1$, and back to Step 3. Step 5: Stop.

6. Numerical Examples

In the following part, we provide the numerical calculation example and the practical application example to display the validity of the results, respectively.

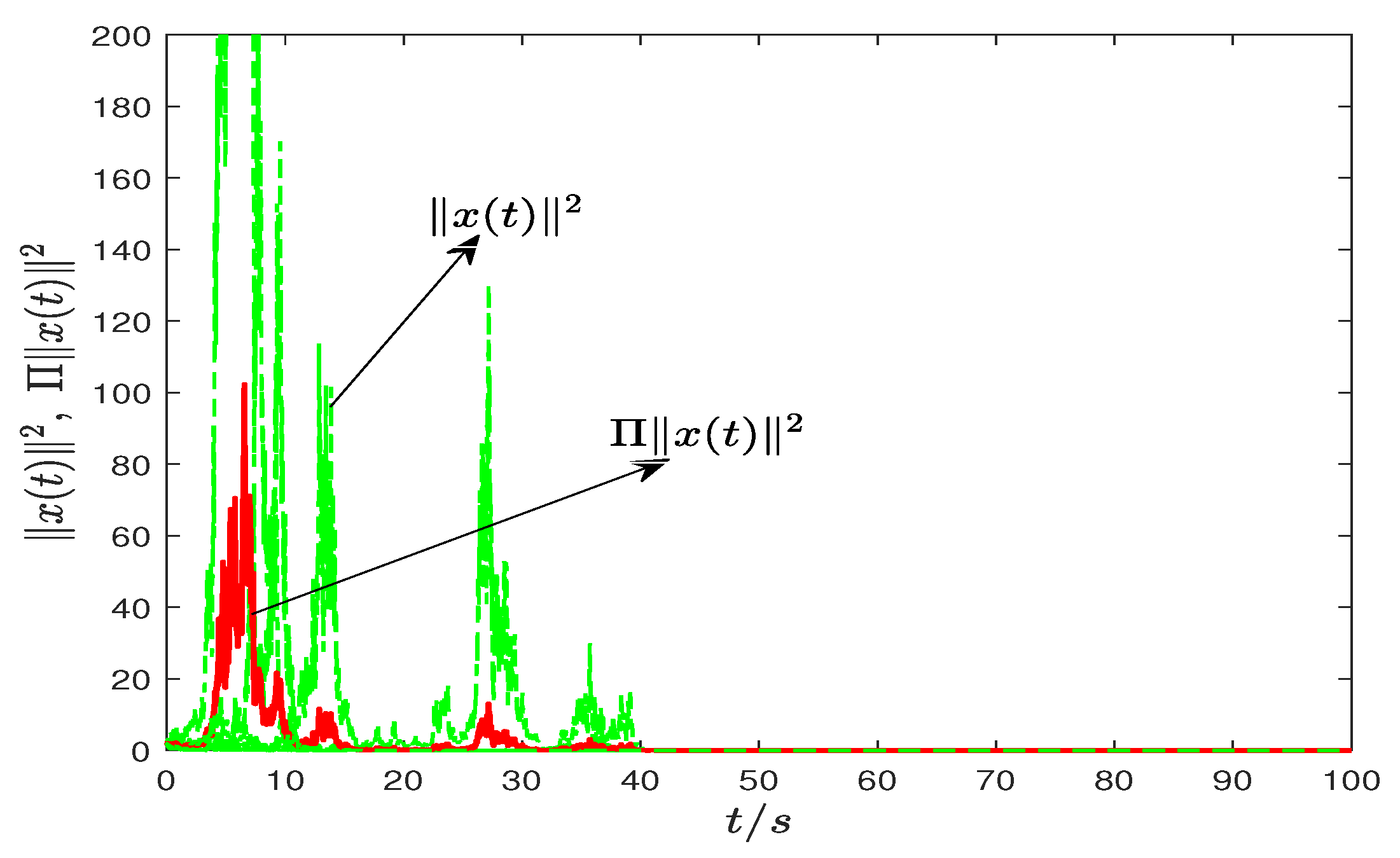
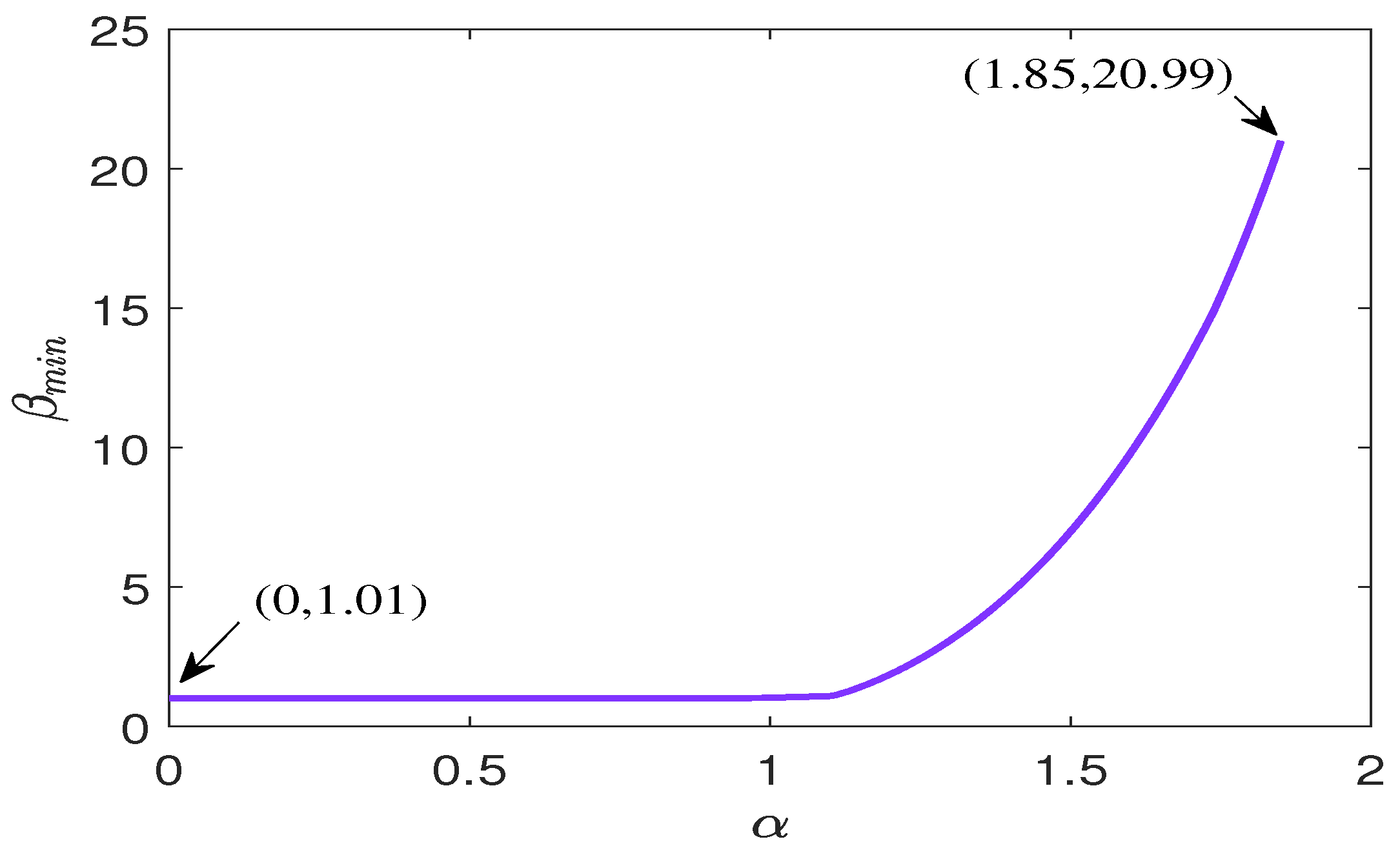
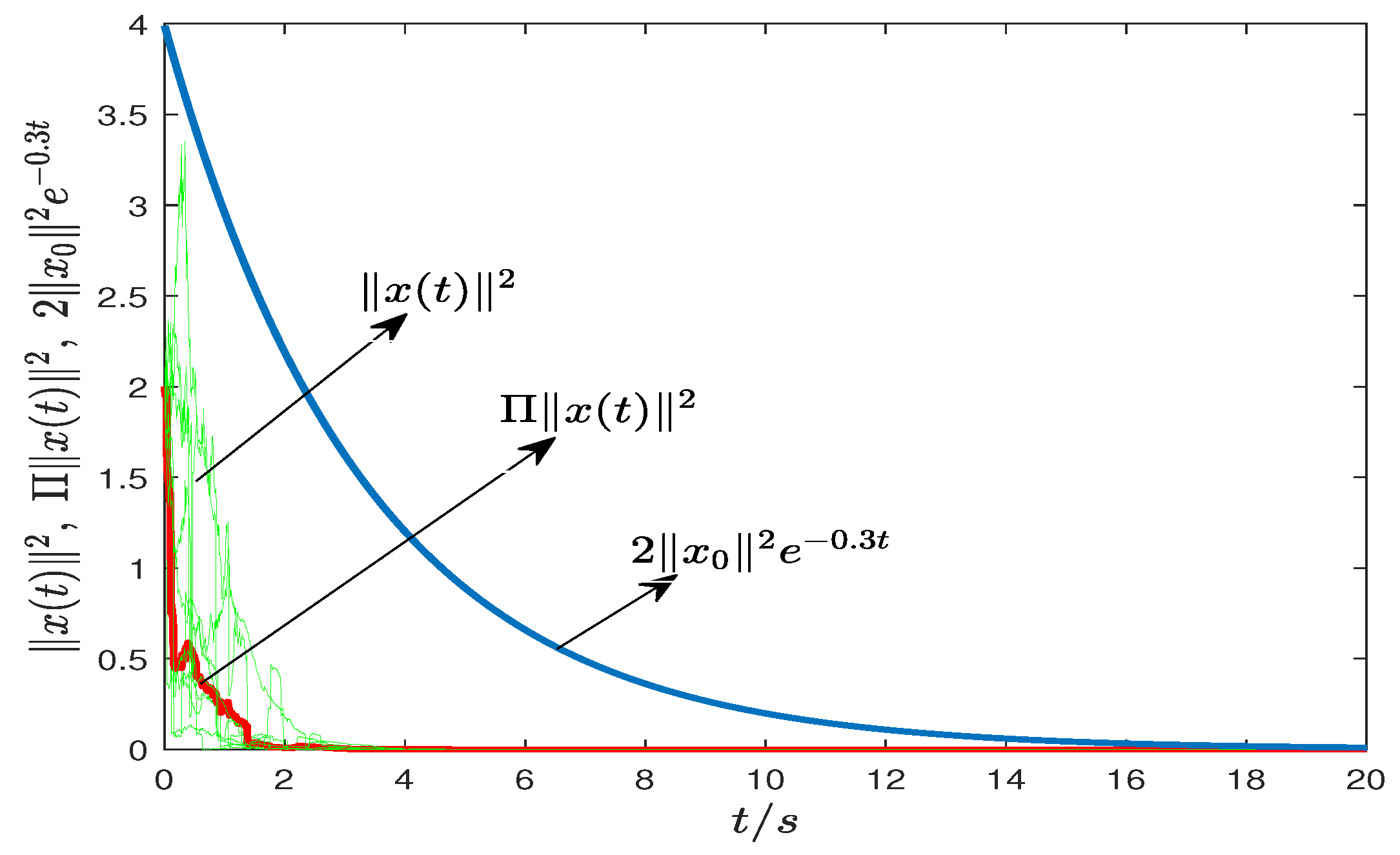
6.1. Example 1

The two model parameters for the given system (1) are given below:

• when $i=1$,

  $$\begin{array}{c}{A}_{11}=\left[\begin{array}{cc}-0.15& 1\\ 0& -0.06\end{array}\right],B_{11}=\left[\begin{array}{c}0.8\\ 0.6\end{array}\right],A_{21}=\left[\begin{array}{cc}0.3& -0.05\\ 0.01& 0.1\end{array}\right],B_{21}=\left[\begin{array}{c}0.3\\ 0.1\end{array}\right],\end{array}$$

  $$\begin{array}{c}{A}_{31}=\left[\begin{array}{cc}-0.1& 1\\ 0.5& -0.15\end{array}\right],B_{31}=\left[\begin{array}{c}0.6\\ 0.3\end{array}\right],C_1=\left[\begin{array}{cc}-0.1& -0.3\\ 0.2& -0.1\end{array}\right],D_1=\left[\begin{array}{c}0.5\\ 0.3\end{array}\right],\end{array}$$
• when $i=2$,

  $$\begin{array}{c}{A}_{12}=\left[\begin{array}{cc}-0.2& 1\\ 0& -0.04\end{array}\right],B_{12}=\left[\begin{array}{c}1\\ 0.5\end{array}\right],A_{22}=\left[\begin{array}{cc}0.2& -0.2\\ 0.04& 0.6\end{array}\right],B_{22}=\left[\begin{array}{c}0.2\\ 0.6\end{array}\right],\end{array}$$

  $$\begin{array}{c}{A}_{32}=\left[\begin{array}{cc}-0.3& 1.2\\ 0.1& -0.08\end{array}\right],B_{32}=\left[\begin{array}{c}1.5\\ 0.8\end{array}\right],C_2=\left[\begin{array}{cc}-0.2& -0.5\\ 0.1& -0.3\end{array}\right],D_2=\left[\begin{array}{c}0.3\\ 0.6\end{array}\right].\end{array}$$

In addition, other parameters are $\Pi =\left[\begin{array}{cc}-1.5& 1.5\\ 2& -2\end{array}\right]$, $\lambda =0.2$, and $\mathcal{X}\left(0\right)={[-11]}^{\prime }$. In Figure 2, the red solid line shows the state trajectory curve of $\Pi {\parallel \mathcal{X}\left(t\right)\parallel }^2$, and the green dashed line shows 10 state trajectory curve of ${\parallel \mathcal{X}\left(t\right)\parallel }^2$. As you can see from Figure 2, the open-loop system (1) has poor transient performance. It is not QMSE-stable for the given ($0.5,4$). Hence, it is essential to design the SFC and the OBC separately to achieve QMSE-stabilization.

Case 1. QMSE-stabilization via SFC

Setting $\lambda =0.2$, the relation curve between $\phi$ and ${\psi }_{min}$ is shown in Figure 3 by using Algorithm 1. From Figure 3, ${\psi }_{min}$ increases with increasing $\phi$, and the maximum attenuation rate is $1.85$ when $\psi \ge 20.99$. According to Figure 3, take $\phi =0.5$ and $\psi =4$ to solve (23) and (24) in Theorem 4; then, we obtain

$$\begin{array}{c}{K}_1=\left[\begin{array}{cc}-0.6811& -0.9584\end{array}\right],K_2=\left[\begin{array}{cc}-0.2607& -0.8331\end{array}\right],{\delta }_1=58.1781>0,{\delta }_2=18.1595>0.\end{array}$$

Thus, the corresponding SFC ${\mathcal{U}}^{*}\left(t\right)=K_i\mathcal{X}\left(t\right)$ can be obtained. Moreover, in Figure 4, the red line represents the state trajectory curve of $\Pi {\parallel \mathcal{X}\left(t\right)\parallel }^2$, the green line represents 10 state trajectory curve of ${\parallel \mathcal{X}\left(t\right)\parallel }^2$, and the blue line represents the curve of $4\parallel {\mathcal{X}}_0{\parallel }^2{e}^{-0.5t}$. As you can see from Figure 4, ${\Pi [\parallel \mathcal{X}\left(t\right)\parallel }^2|{\mathcal{X}}_0,{\eta }_0]<\psi \parallel {\mathcal{X}}_0{\parallel }^2{e}^{-\phi t}=4{\parallel {\mathcal{X}}_0\parallel }^2{e}^{-0.5t}$, i.e., the system (25) is QMSE-stabilizable w.r.t. $(\phi ,\psi )$.

Case 2. QMSE-Stabilization via OBC

We acquire the relation curve between $\phi$ and ${\psi }_{min}$ on the basis of Algorithm 1, which is shown in Figure 5. From Figure 5, $\psi$ increases with increasing $\phi$, and the maximum attenuation rate, which is decay, is $0.94$ when $\psi \ge 2.65$.

According to Figure 5 and SFC case, take $\phi =0.3$ and $\psi =2$ to solve (31) and (32) in Theorem 5; then, we obtain

$$\begin{array}{c}{L}_1=\left[\begin{array}{cc}-17.3853& 17.5821\\ -16.3628& 17.4696\end{array}\right],L_2=\left[\begin{array}{cc}-3.0931& 0.5159\\ -28.6140& 5.5510\end{array}\right],{\theta }_1=59.3293>0,\end{array}$$

${\theta }_2=80.3438>0$, ${\theta }_3=33.8041>0.$

Moreover, in Figure 6, the red line stands for the state trajectory curve of $\Pi {\parallel \mathcal{X}\left(t\right)\parallel }^2$, the green line stands for 10 state trajectory curve of ${\parallel \mathcal{X}\left(t\right)\parallel }^2$, and the blue line stands for the curve of $2\parallel {\mathcal{X}}_0{\parallel }^2{e}^{-0.3t}$ for the OBC case. As you can see from Figure 6, ${\Pi [\parallel \mathcal{X}\left(t\right)\parallel }^2|{\mathcal{X}}_0,{\eta }_0]<\psi \parallel {\mathcal{X}}_0{\parallel }^2{e}^{-\phi t}=2{\parallel {\mathcal{X}}_0\parallel }^2{e}^{-0.3t}$, i.e., the system (29) is QMSE-stabilizable w.r.t. $(\phi ,\psi )$.

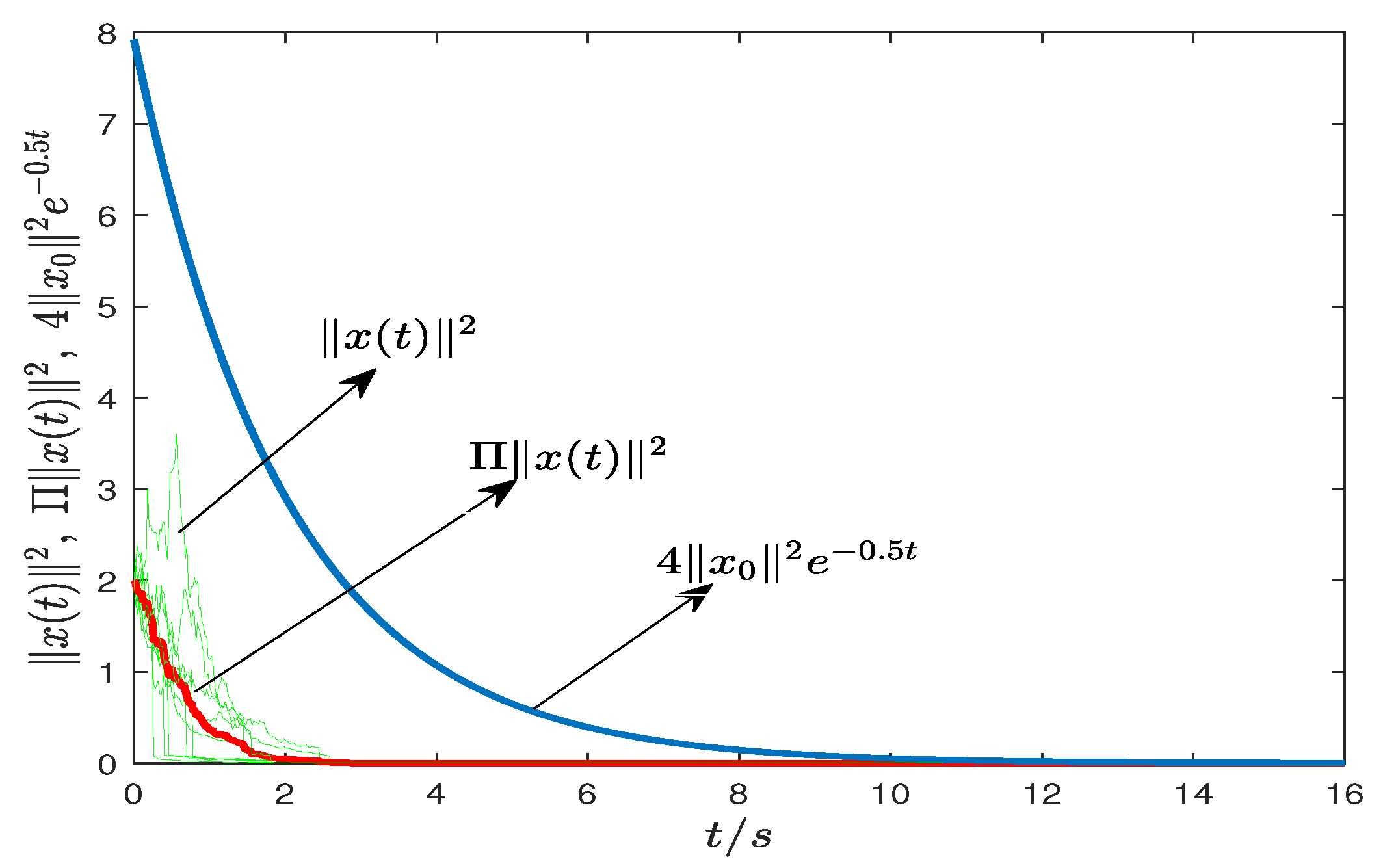
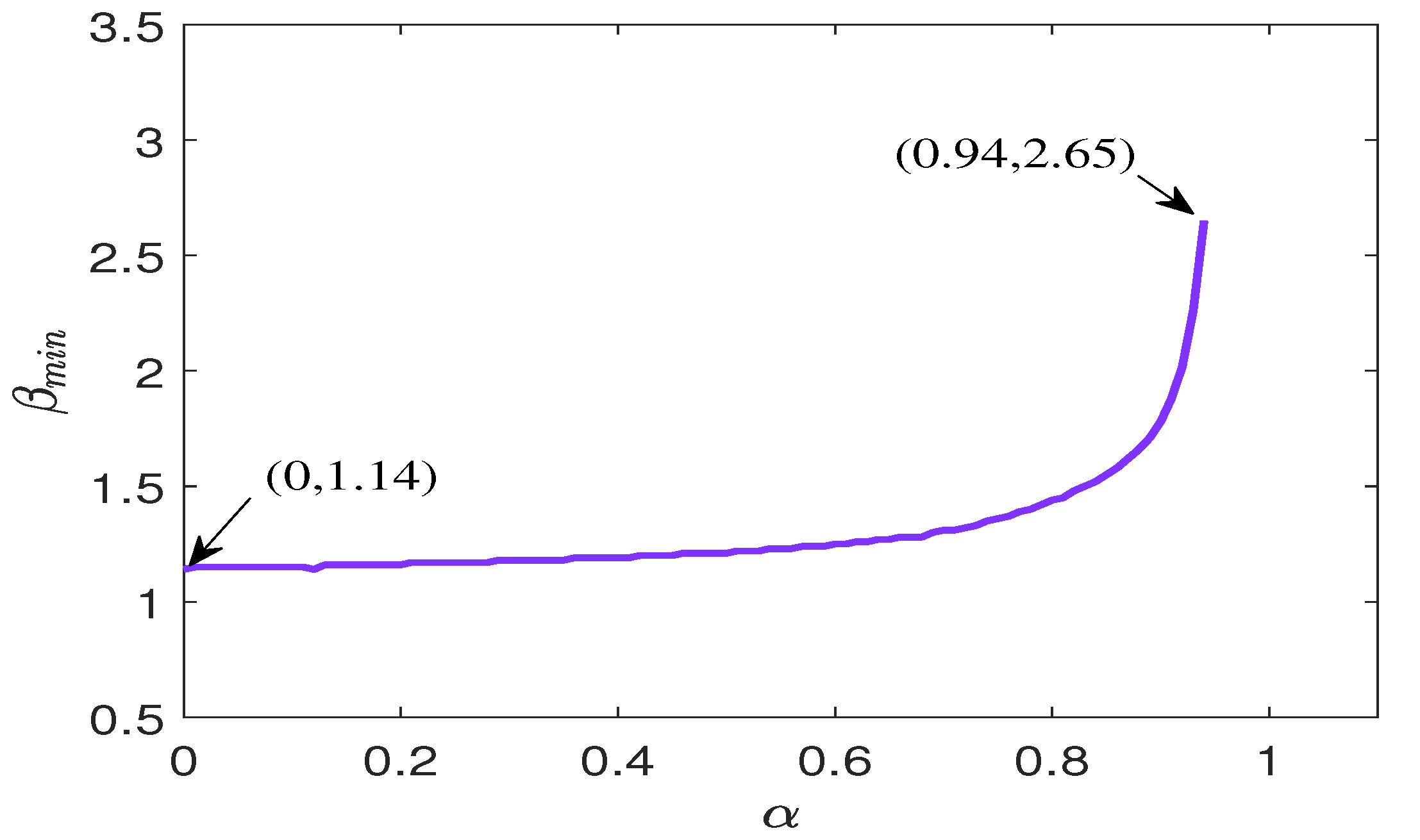
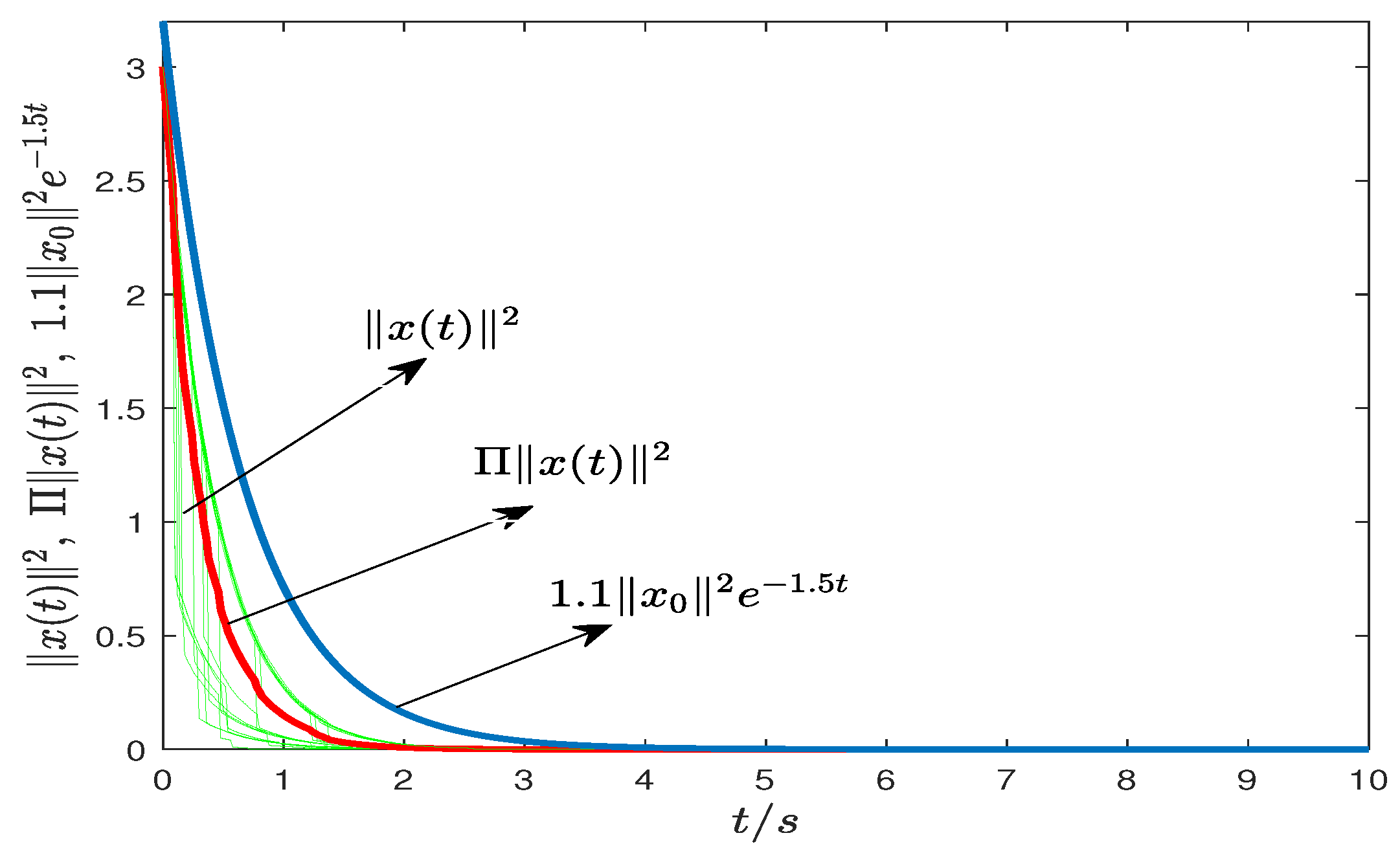
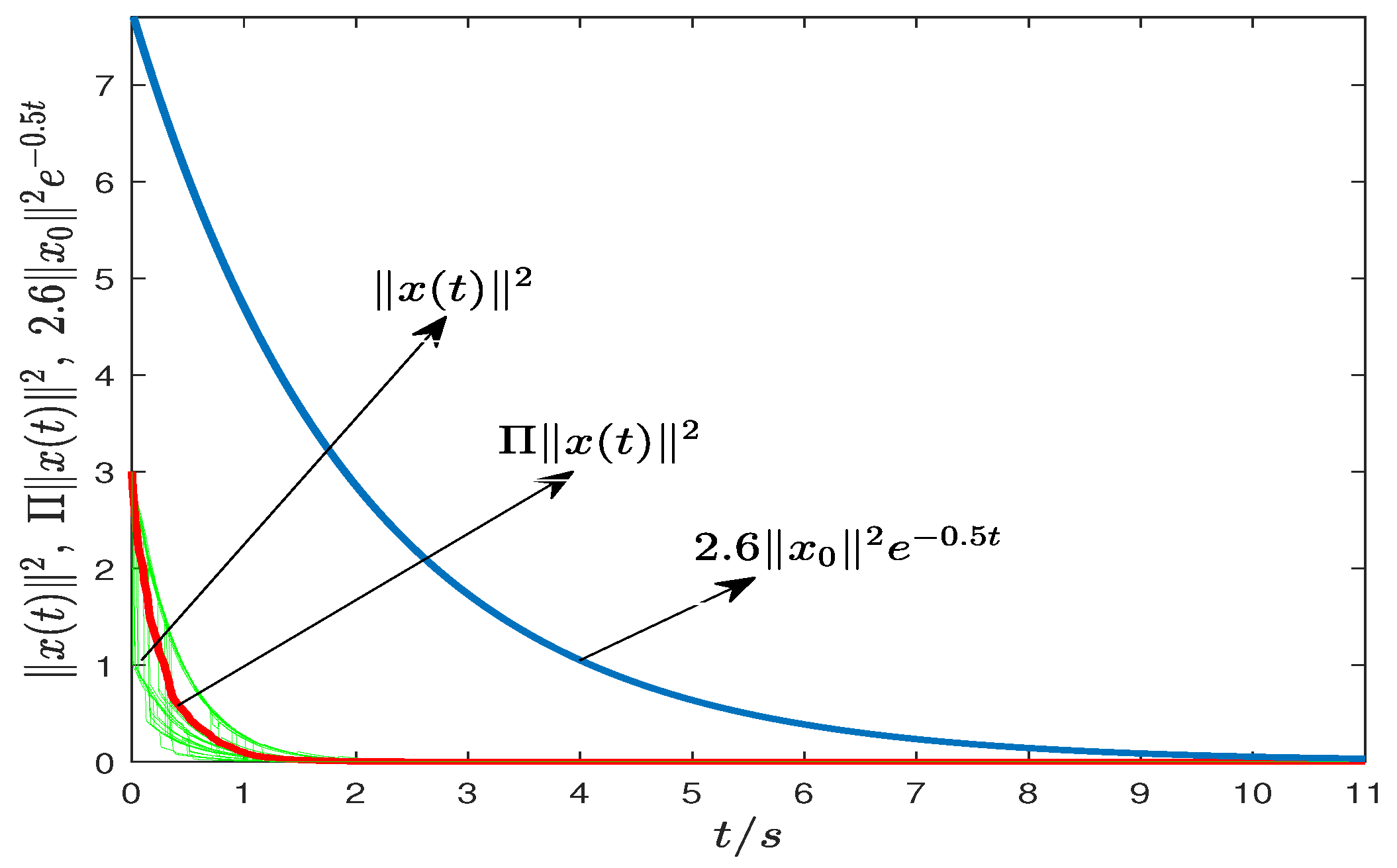
6.2. Example 2

A financial model example is provided to show the usefulness of the proposed approach. In general, financial markets suffer from various factors such as national policies, capital flowing, and investor expectations. Thus, the stochastic financial systems with disturbances are presented as follows in [24]:

$$\begin{array}{c}\left[\begin{array}{c}d\mathbb{X}\left(t\right)\hfill \\ d\mathbb{Y}\left(t\right)\hfill \\ d\mathbb{Z}\left(t\right)\hfill \end{array}\right]=\left(\left[\begin{array}{ccc}\overline{\mathbb{Y}}-\mu & \overline{\mathbb{X}}& 1\\ -2\overline{\mathbb{X}}& -\nu & 0\\ -1& 0& -\tau \end{array}\right]\left[\begin{array}{c}\mathbb{X}\left(t\right)\hfill \\ \mathbb{Y}\left(t\right)\hfill \\ \mathbb{Z}\left(t\right)\hfill \end{array}\right]+I_3\left[\begin{array}{c}{\mathbb{U}}_1\left(t\right)\hfill \\ {\mathbb{U}}_2\left(t\right)\hfill \\ {\mathbb{U}}_3\left(t\right)\hfill \end{array}\right]\right)dt\hfill \\ +\left(\left[\begin{array}{ccc}0.01(\overline{\mathbb{Y}}-\mu )& 0.01\overline{\mathbb{X}}& 0.01\\ -0.02\overline{\mathbb{X}}& -0.01\nu & 0\\ -0.02& 0& -0.02\tau \end{array}\right]\left[\begin{array}{c}\mathbb{X}\left(t\right)\hfill \\ \mathbb{Y}\left(t\right)\hfill \\ \mathbb{Z}\left(t\right)\hfill \end{array}\right]+\left[\begin{array}{ccc}0.01& 0& 0\\ 0& 0.01& 0\\ 0& 0& 0.02\end{array}\right]\right.\hfill \\ \left.\times \left[\begin{array}{c}{\mathbb{U}}_1\left(t\right)\hfill \\ {\mathbb{U}}_2\left(t\right)\hfill \\ {\mathbb{U}}_3\left(t\right)\hfill \end{array}\right]\right)d\mathcal{W}\left(t\right)+\left(A_{3i}\left[\begin{array}{c}\mathbb{X}\left(t\right)\hfill \\ \mathbb{Y}\left(t\right)\hfill \\ \mathbb{Z}\left(t\right)\hfill \end{array}\right]+0.3I_3\left[\begin{array}{c}{\mathbb{U}}_1\left(t\right)\hfill \\ {\mathbb{U}}_2\left(t\right)\hfill \\ {\mathbb{U}}_3\left(t\right)\hfill \end{array}\right]\right)dN\left(t\right),\hfill \end{array}$$

(38)

where $\mathbb{X}\left(t\right)$, $\mathbb{Y}\left(t\right)$, and $\mathbb{Z}\left(t\right)$ are interest rate, investment demand, and price index, respectively. $\mu$, $\nu$, and $\tau$ are amount of savings, unit cost of investment, and elasticity of demand coefficient, respectively.

In addition, $(\overline{\mathcal{X}},\overline{\mathcal{Y}},\overline{\mathcal{Z}})=(0,3,1)$ is the equilibrium point of the system. ${\eta }_t$ is a two-mode Markov chain with generator $\Pi =\left[\begin{array}{cc}-1.5& 1.5\\ 2& -2\end{array}\right]$. System (38) with parameters as follows:

When $i=1$, $a=3.5$, $b=0.2$, $c=0.25$, $B_{11}=I_3$, $B_{31}=0.3I_3$, $D_1=0.2I_3$,

$$\begin{array}{c}{A}_{11}=\left[\begin{array}{ccc}-0.5& 0& 1\\ 0& -0.2& 0\\ -1& 0& -0.25\end{array}\right],A_{21}=\left[\begin{array}{ccc}-0.005& 0& 0.01\\ 0& -0.002& 0\\ -0.02& 0& -0.005\end{array}\right],\\ B_{21}=\left[\begin{array}{ccc}0.01& 0& 0\\ 0& 0.01& 0\\ 0& 0& 0.02\end{array}\right],A_{31}=\left[\begin{array}{ccc}-0.3& 1.2& 0.5\\ 0& -0.05& 0.3\\ 0.5& -0.6& -0.4\end{array}\right],C_1=\left[\begin{array}{ccc}-0.1& -0.3& 0.2\\ 0.2& -0.1& -0.5\\ 0.2& -0.06& -0.3\end{array}\right],\end{array}$$

when $i=2$, $a=2.5$, $b=0.5$, $c=0.35$, $B_{12}=I_3$, $B_{32}=0.3I_3$, $D_2=0.5I_3$,

$$\begin{array}{c}{A}_{12}=\left[\begin{array}{ccc}0.5& 0& 1\\ 0& -0.5& 0\\ -1& 0& -0.35\end{array}\right],A_{22}=\left[\begin{array}{ccc}0.005& 0& 0.01\\ 0& -0.005& 0\\ -0.02& 0& -0.007\end{array}\right],\\ B_{22}=\left[\begin{array}{ccc}0.01& 0& 0\\ 0& 0.01& 0\\ 0& 0& 0.02\end{array}\right],A_{32}=\left[\begin{array}{ccc}-0.1& -0.02& 0.2\\ 0& -0.2& 0.3\\ -0.2& -0.15& 0.2\end{array}\right],C_2=\left[\begin{array}{ccc}-0.1& -0.5& 0.02\\ 0.3& -0.1& -0.2\\ -0.6& -0.3& -0.1\end{array}\right].\end{array}$$

Other parameters are $\lambda =0.2$ and ${\mathcal{X}}_0={[-1,1,-1]}^{\prime }$. In Figure 7, the red solid line shows the state trajectory curve of $\Pi {\parallel \mathcal{X}\left(t\right)\parallel }^2$, and the green dashed line shows 10 state trajectory curve of ${\parallel \mathcal{X}\left(t\right)\parallel }^2$. As you can see from Figure 7, the system (38) has poor transient performance. It is not QMSE-stable for the given ($1.1,1.5$). Hence, it is essential to design the SFC and the OBC separately to achieve QMSE-stabilization.

Case 1. QMSE-stabilization via SFC

The relation curve between $\phi$ and ${\psi }_{min}$ is shown in Figure 8 using Algorithm 1. From Figure 8, ${\psi }_{min}$ remains the same with increasing $\phi$, and the maximum attenuation rate is 10 when $\psi \ge 1.1$.

According to Figure 8, take $\phi =1.5$ and $\psi =1.1$ to solve (23) and (24) in Theorem 4; then, we obtain

$$\begin{array}{c}{K}_1=\left[\begin{array}{ccc}-0.7637& -2.0611& -0.0657\\ 1.8775& -1.0593& -1.4707\\ -0.0470& 1.4722& -0.9681\end{array}\right],K_2=\left[\begin{array}{ccc}-1.6929& 0.0338& -0.6645\\ -0.0430& -0.7178& -0.7579\\ 0.6620& 0.7341& -0.9385\end{array}\right],\\ {\delta }_1=26.4365>0,{\delta }_2=24.2237>0.\end{array}$$

(39)

Thus, the corresponding SFC ${\mathcal{U}}^{*}\left(t\right)=K_i\mathcal{X}\left(t\right)$ can be obtained. Moreover, In Figure 9, the red line represents the state trajectory curve of $\Pi {\parallel \mathcal{X}\left(t\right)\parallel }^2$, the green line represents 10 state trajectory curve of ${\parallel \mathcal{X}\left(t\right)\parallel }^2$, and the blue line represents the curve of $1.1\parallel {\mathcal{X}}_0{\parallel }^2{e}^{-1.5t}$. As you can see from Figure 9, ${\Pi [\parallel \mathcal{X}\left(t\right)\parallel }^2|{\mathcal{X}}_0,{\eta }_0]<\psi \parallel {\mathcal{X}}_0{\parallel }^2{e}^{-\phi t}=1.1{\parallel {\mathcal{X}}_0\parallel }^2{e}^{-1.5t}$, i.e., the system (38) is QMSE-stabilizable w.r.t. $(\phi ,\psi )$.

Case 2. QMSE-Stabilization via OBC

We acquire the relation curve between $\phi$ and ${\psi }_{min}$ on the basis of Algorithm 1, which is shown in Figure 10. From Figure 10, $\psi$ increases with increasing $\phi$, and the maximum attenuation rate is $0.9$ when $\psi \ge 5.6$.

According to Figure 10 and SFC case, take $\phi =0.5$ and $\psi =2.6$ to solve (31) and (32) in Theorem 5; then, we obtain

$$\begin{array}{c}{L}_1=\left[\begin{array}{ccc}1123.5& -432.0& 358.7\\ -681.1& 268.2& -216.4\\ 615.8& -245.5& 188.4\end{array}\right],L_2=\left[\begin{array}{ccc}-622.6& 4225.7& -433.2\\ -376.6& 2552.5& -260.5\\ -235.2& 1593.0& -163.0\end{array}\right],\\ {\theta }_1=192.7086>0,{\theta }_2=273.8596>0,{\theta }_3=226.9786>0.\end{array}$$

(40)

Moreover, in Figure 11, the red line denotes the state trajectory curve of $\Pi {\parallel \mathcal{X}\left(t\right)\parallel }^2$, the green line denotes 10 state trajectory curve of ${\parallel \mathcal{X}\left(t\right)\parallel }^2$, and the blue line denotes the curve of $2.6\parallel {\mathcal{X}}_0{\parallel }^2{e}^{-0.5t}$ for the OBC case. As you can see from Figure 11, ${\Pi [\parallel \mathcal{X}\left(t\right)\parallel }^2|{\mathcal{X}}_0,{\eta }_0]<\psi \parallel {\mathcal{X}}_0{\parallel }^2{e}^{-\phi t}=2.6{\parallel {\mathcal{X}}_0\parallel }^2{e}^{-0.5t}$, i.e., the system (29) is QMSE-stabilizable w.r.t. $(\phi ,\psi )$.

7. Conclusions

An investigation of the QMSES and QMSE-stabilization of linear Itô stochastic MJSs with Brownian and Poisson noises has been presented. The relationships between QMSES, FTSS, and GFTMSS for such system have been established. By using a matrix transformation approach, SFC and OBC have been designed to make the corresponding closed-loop system to achieve QMSE-stabilization, respectively. In addition, the feasible solution curve of ${\psi }_{min}$ vs. $\phi$ has been shown by the linear search algorithm. In conclusion, the techniques used in this paper and some results may be applied in other control problems.