Abstract
This study examines n-balls, n-simplices, and n-orthoplices in real dimensions using novel recurrence relations that remove the indefiniteness present in known formulas. They show that in the negative, integer dimensions, the volumes of n-balls are zero if n is even, positive if n = −4k − 1, and negative if n = −4k − 3, for natural k. The volumes and surfaces of n-cubes inscribed in n-balls in negative dimensions are complex, wherein for negative, integer dimensions they are associated with integral powers of the imaginary unit. The relations are continuous for n ∈ ℝ and show that the constant of π is absent for 0 ≤ n < 2. For n < −1, self-dual n-simplices are undefined in the negative, integer dimensions, and their volumes and surfaces are imaginary in the negative, fractional ones and divergent with decreasing n. In the negative, integer dimensions, n-orthoplices reduce to the empty set, and their real volumes and imaginary surfaces are divergent in negative, fractional ones with decreasing n. Out of three regular, convex polytopes present in all natural dimensions, only n-orthoplices and n-cubes (and n-balls) are defined in the negative, integer dimensions.
MSC:
90C10
1. Introduction
The notion of dimension n of a set has various definitions [1,2]. Natural dimensions define a minimum number of independent parameters (coordinates) needed to specify a point within Euclidean space ℝn, where n = −1 is the dimension of the empty set, the void, having zero volume and undefined surface. Negatively dimensional spaces can be defined by analytic continuations from positive dimensions [3]. A spectrum, a topological generalization of the notion of space, allows for negative dimensions [2,4,5,6] that refer to densities, rather than to sizes as in the natural ones.
Fractional (or fractal) dimensions extend the notion of dimension to real, including negative [7], numbers. Negative dimensions are considered in probabilistic fractal measures [8]. Fractal dimension and lacunarity [9,10] allow for an investigation of the fractal nature of prime sequences [11]. Fractal dimensions have been verified to be consistent with experimental observations and allow for the analysis of the transport properties, such as permeability, thermal dispersion, and conductivities (both thermal and electrical) in multiphase fractal media [12]. The probability models for pore distribution and for permeability of porous media can also be expressed as a function of fractal dimensions [13]. Interestingly, the dimension of the boundary of the Mandelbrot set equals 2 [14], and the generalized Mandelbrot set in higher-dimensional hypercomplex number spaces, when the power α of the iterated complex variable z tends to infinity, is convergent to the unit (α − 1)-sphere [15].
Complex dimensions can also be considered [2]. Furthermore, geometric concepts (such as lengths, volumes, and surfaces) can be related to negative, fractional, and complex numbers. Complex geodesic paths emerge in the presence of black hole singularities [16] and when studying entropic dynamics on curved statistical manifolds [17]. Fractional derivatives of complex functions could be able to describe different physical phenomena [18].
In ℝ2, there is a countably infinite number of regular, convex polygons; in ℝ3, there are five regular, convex Platonic solids; in ℝ4, there are six regular, convex polytopes. For n > 4, there are only three: self-dual n-simplex and n-cube dual to n-orthoplex [19]. Furthermore, ℝn is also equipped with a perfectly regular, convex n-ball. The properties of these three regular, convex polytopes in natural dimensions are well known [20,21,22]. Fractal dimensions of hyperfractals based on these polytopes in natural dimensions were disclosed in [23].
This study examines n-balls, regular n-simplices, and n-orthoplices in real dimensions using novel recurrence relations that remove the indefiniteness present in known formulas.
The paper is structured as follows. Section 2 presents known formulas for volumes and surfaces of n-balls, regular n-simplices, and n-orthoplices in natural dimensions. Section 3 defines novel recurrence relations for these geometric objects in real dimensions and presents their algebraic forms in integer dimensions. Section 4 refers to n-balls circumscribed about and inscribed in n-cubes in real dimensions. Section 5 summarizes the findings of this paper. Their possible applications are discussed in Section 6.
2. Known Formulas
The volume of an n-ball (B) is known to be
where Γ is the Euler’s gamma function and R is the n-ball radius. This becomes
if n is even (n = 2k, k ∈ ℕ0) and
if n is odd (n = 2k − 1, k ∈ ℕ). Expressed in terms of n-ball diameter (1) is the rescaling factor between the n-dimensional Lebesgue measure and Hausdorff measure for n ∈ ℝ+ [2,24].
Another known [21] recurrence relation expresses the volume of an n-ball in terms of the volume of an (n − 2)-ball of the same radius
where V0(R)B = 1 and V1(R)B = 2R. It is also known [21] that the (n − 1)-dimensional surface of an n-ball can be expressed as
Furthermore, it is known [25] that the sequence
satisfies the same recursion formula as (4) for unit radius.
The volume of a regular n-simplex (S) is known [20,26] to be
where A is the edge length. A regular n-simplex has n + 1 (n − 1)-facets [21], so its surface is
The volume of n-orthoplex (O) is known [22] to be
As n-orthoplex has 2n facets [21], being regular (n − 1)-simplices, its surface is
Formulas (1)–(3) and (7)–(10) are undefined in negative dimensions since the factorial is defined only for non-negative integers, while the gamma function is undefined for non-positive integers. Relations (4)–(6) are undefined if n = 0.
3. Novel Recurrence Relations
A radius recurrence relation
for n ∈ ℕ0, where f0 := 1 and f1 := 2, allows for expressing the volumes and, using (5), surfaces of n-balls as
where “⌊x⌋” denotes the floor function giving the greatest integer less than or equal to its argument x.
Proof.
If n = 2k for k ∈ ℕ0, then by equating (2) with (12)
Then, with (11), e.g., for k = 3
For even n ≥ 0, n!! = 2kk!
If n = 2k − 1, k ∈ ℕ, then by equating (3) with (12), we have
Then, with (11), e.g., for k = 4
For odd n ≥ 1, n!! = (2k − 1)!/(2k−1(k − 1)!), which completes the proof. □
The sequence (11) allows for presenting an n-ball’s volume and surface recurrence relations (12), (13) as a product of the rational factor fn or nfn, the irrational factor π^⌊n/2⌋, and the metric (radius) factor Rn or Rn−1. The relation (11) can be extended into negative dimensions as
solving (11) for fn−2 and assigning new n ∈ ℤ as old n − 2. Thus, it is sufficient to define f−1 := 1, f0 := 1 (for the empty set and point dimension) to initiate (11) and (16).
The same assignment of new n ∈ ℤ as old n − 2 can be made in (4) solved for Vn−2(R)B, yielding
which enables us to avoid the indefiniteness of factorial and gamma function in negative dimensions present in Formulas (1)–(3) and removing the singularity present in relation (4).
If n ≤ −3 and odd
Proof.
Set n = −2k − 1, k ∈ ℕ. Then, with (16), e.g., for k = 3
Also
since n is odd. □
The factorial can be expressed by the gamma function. Thus, for n = 2k, k ∈ ℕ, (14) becomes
while for n = 2k − 1, k ∈ ℕ, (15) becomes
the forms which are, similarly to the gamma function, defined for all complex numbers except the non-positive, even integers.
The radius recurrence relation fn (16) is listed in Table 1 for n ∈ ℤ, and shown in Figure 1 along with the even algebraic form of fn (19), odd algebraic form of fn, (20) and the π^⌊n/2⌋ factor for n ∈ ℂ (for complex numbers ⌊a + bi⌋ = ⌊a⌋ + ⌊b⌋i). As shown, (19) and (20) bound the relation (16) for Re(n). Volumes and surfaces of n-balls calculated with (12) and (13) are shown in Figure 2.

Table 1.
Volumes and surfaces of n-balls for −11 ≤ n ≤ 9.
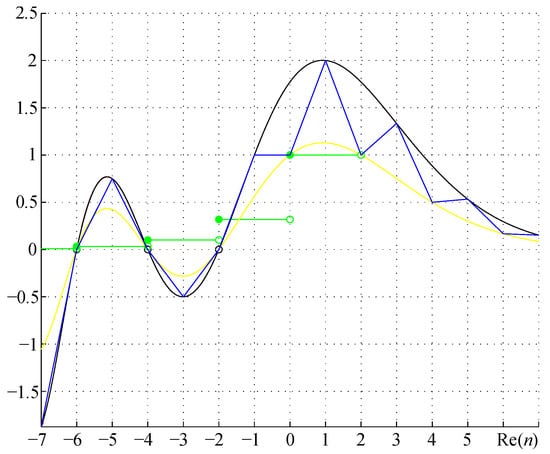
Figure 1.
n-ball radius recurrence relation fn for n ∈ ℤ (blue); even (yellow) and odd (black) algebraic forms of fn, and the π^⌊n/2⌋ factor (green); for −7 ≤ n ≤ 7, n ∈ ℂ.
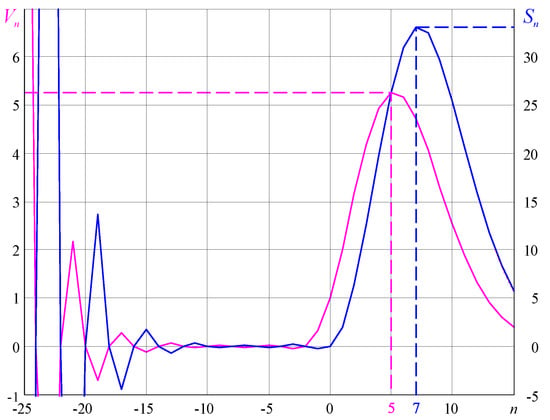
Figure 2.
Graphs of volumes (V) and surface areas (S) of n-balls of unit radius for n = −25, −24, …, 15.
Furthermore, for n ∈ ℤ
where
Proof.
since fn = 0 for negative, even n.
If n = 2k, then
If n = 2k − 1 then, using (15) and (18)
since n is odd. □
Furthermore, for n ∈ ℝ, k ∈ ℤ
Proof.
while for n = 2k − ε
□
If n = 2k, then πkπ−k−1 = π−1. Otherwise, set n = 2k ± ε, where 0 < ε ≤ 1, ε ∈ ℝ. For n = 2k + ε
Furthermore, the following holds for n-balls surfaces (13)
for n ∈ ℤ, where
Proof.
If n = 2k then
for k = {0, 1} and for the remaining k’s, as f−2k = 0 for k ∈ ℕ. Also Re(in−1) = 0 and Im(in−1) = ±1, as n is even.
If n = 2k − 1 then
For k = 1, using (15)
wherein for the remaining k’s, we shall use both (15) and (18) (and f−1 = 1). For instance, for k = {0, 2}
and further, for k ≤ −1 or k ≥ 3
since n is odd and thus, n − 1 is even. □
Furthermore, for n ∈ ℝ, k ∈ ℤ
Proof.
If n = 2k, then πkπ1−k = π. Otherwise, set n = 2k ± ε, where 0 < ε ≤ 1, ε ∈ ℝ. For n = 2k + ε
while for n = 2k − ε
□
Moreover, the following holds for n-ball volumes (12)
for n ∈ ℤ.
Proof.
If n = 2k, k ∈ ℕ, then
If n = 2k − 1, k ∈ ℕ, then
For k = 1, using (15) and f−1 = 1
For the remaining k’s, we shall use both (15) and (18)
since n is odd and, thus n − 1 is even. □
Furthermore, for n ∈ ℝ, k ∈ ℤ
Proof.
□
If n = 2k, then πkπ−k = 1. Otherwise, set n = 2k ± ε, where 0 < ε ≤ 1, ε ∈ ℝ. For n = 2k + ε
while for n = 2k − ε
One can also express the volumes and, using (5), surfaces of n-balls in terms of their diameters D as
defining diameter recurrence relation
having inverse
for n ∈ ℤ, where g−1 := 2 and g0 := 1. The diameter recurrence relation (31), (32) is related to radius recurrence relation (11), (16) by
Proof.
By equating (12) with (29), we have
which completes the proof. □
Furthermore (proof follows from (21) and (33))
The diameter recurrence relation gn (32) is listed in Table 1 for n ∈ ℤ, and shown in Figure 3 along with the even algebraic form of gn ((19) with (33)) the odd algebraic form of gn ((20) with (33)), and the π^⌊n/2⌋ factor for n ∈ ℂ. Volumes and surfaces of n-balls calculated with relations (29) and (30) are shown in Figure 4.
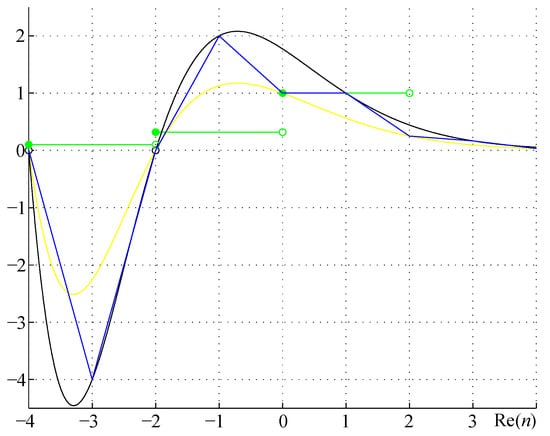
Figure 3.
n-ball diameter recurrence relation gn for n ∈ ℤ (blue); even (yellow) and odd (black) algebraic forms of gn, and the π^⌊n/2⌋ factor (green) for −4 ≤ n ≤ 4, n ∈ ℂ.
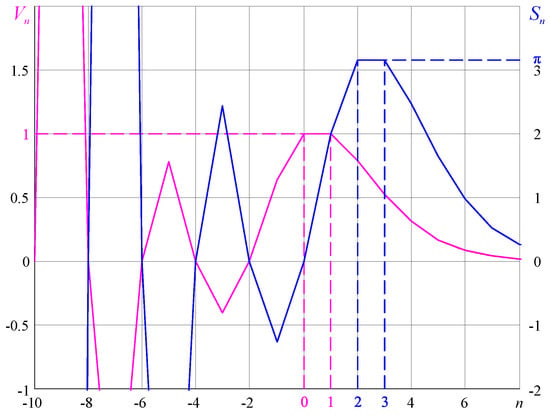
Figure 4.
Graphs of volumes (V) and surface areas (S) of n-balls of unit diameter for n = −10, −9, …, 8.
In the case of regular n-simplices, Equation (7) can be written as a recurrence relation, with V0(A)S := 1
Proof.
By equating (7) with (35), we have
The relation (35) removes the indefiniteness of the factorial for n < 0 and singularity for n = −1 present in (7). Solving (35) for Vn−1 and assigning new n ∈ ℤ as old n − 1, yields
which shows that n-simplices are indefinite only for integer n < −1, as shown in Figure 5. The volume of an empty or void (−1)-simplex is V−1(A)S = 0, while its surface S−1(A)S (8) is undefined, as for the void itself.
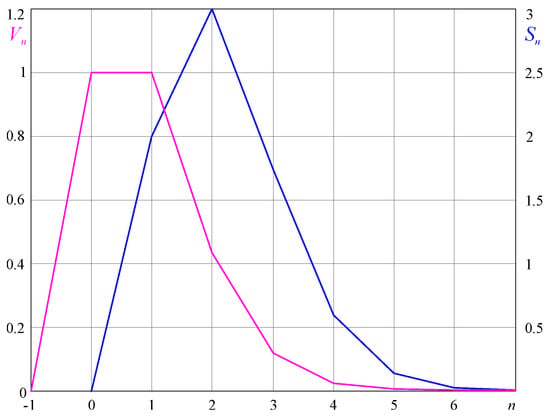
Figure 5.
Graphs of volumes (V) and surface areas (S) of regular n-simplices of unit edge length for n = −1, …, 7.
In the case of n-orthoplices, Equation (9) can be written as a recurrence relation
with V0(A)O := 1.
Proof.
By equating (9) with (37), we have
which recovers (9) and completes the proof. □
The relation (37) removes the indefiniteness of the factorial for n < 0 present in (9). Solving (37) for Vn−1 and assigning new n ∈ ℤ as old n − 1, yields
which removes singularity from (37) and is zero for integer n ≤ −1, showing that for negative, integer dimensions, the volumes of n-orthoplices are zero, while their surfaces (10) are undefined, as shown in Figure 6.
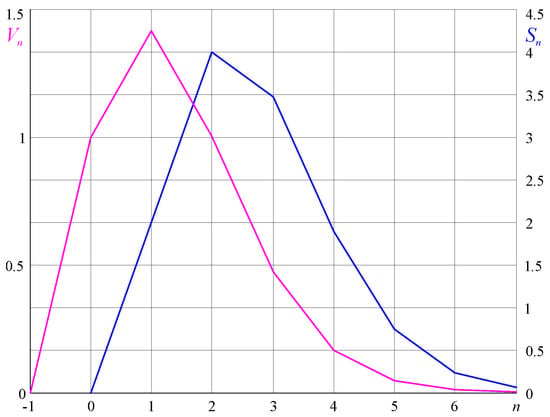
Figure 6.
Graphs of volumes (V) and surface areas (S) of n-orthoplices of unit edge length for n = −1, …, 7.
4. n-Balls Circumscribed about and Inscribed in n-Cubes
The edge length ACC of an n-cube circumscribed (CC) about an n-ball corresponds to the diameter D of this n-ball. Thus, the volume of this cube is simply Vn(D)CC = Dn, and the surface is Sn(D)CC = 2nDn−1.
However, the edge length ACI of an n-cube inscribed (CI) inside an n-ball of diameter D is ACI = D/√n, which is singular for n = 0 and complex for n < 0. Thus, the volume of an n-cube inscribed in an n-ball is
and the surface is
The volumes (39) and surfaces (40) are real if n ≥ 0 (by convention 00 := 1), and complex if n < 0, n ∈ ℝ. To examine reflection relations we set m = −n in (39) and (40). This yields volume
and surface
which are complex for all m ∈ ℝ.
Volume formulas (39) and (41) correspond to each other for n ≤ 0, n ∈ ℝ and for n = 2k, k ∈ ℤ.
Proof.
By equating (39) with (41), we have
Setting n = −m, that is, reflecting (39) around zero, while leaving (41) intact, yields
On the other hand, setting m = −n
□
Thus, the volumes (39), (41) are real if n is negative and even and imaginary if n is negative and odd.
Surface Formulas (40) and (42) correspond to each other for n ≤ 0, n ∈ ℝ, and for n = 2k − 1, k ∈ ℤ.
Proof.
By equating (40) with (42), we have
Setting n = −m yields
On the other hand, setting m = −n, that is, reflecting (42) around zero, while leaving (40) intact, yields
□
Thus, the surfaces (40), (42) are real if n is negative and odd and imaginary if n is negative and even.
Volumes and surfaces of n-cubes given by Formulas (39)–(42) are shown in Figure 7 and listed in Table 2. This peculiar mixture of integer, rational, and irrational coefficients requires further research.
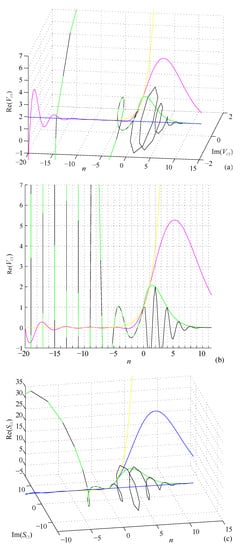
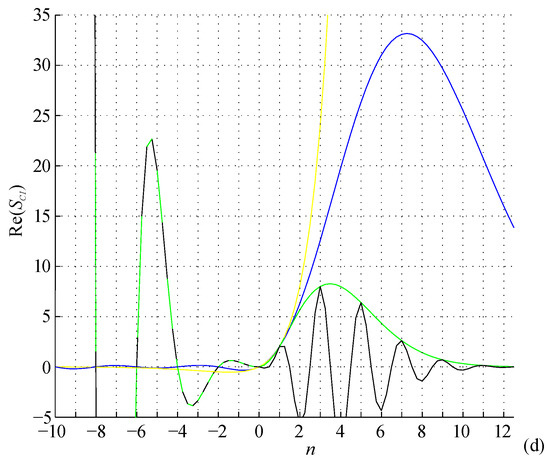
Figure 7.
Graphs of volumes ((a,b), pink) and surfaces ((c,d), blue) of unit radius n-balls, along with volumes and surface areas of n-cubes circumscribed about (yellow) and inscribed in (green, black) these n-balls.

Table 2.
Volumes and surfaces of n-cubes inscribed in n-balls of unit radius and diameter for −8 ≤ n ≤ 3 (rational fraction approximation using Matlab rats function).
The ratio of the volume or surface of an n-ball to the volume or surface of an n-cube circumscribing this n-ball can be expressed using diameter recurrence relations (29), (30) as
and similarly, the ratio of volume and surface of an n-ball to volume (39) and surface (40) of an n-cube inscribed in this n-ball can be expressed as
We conjecture that for 0 < n < 1 volumes of n-cubes inscribed inside n-balls are larger than volumes of those n-balls.
Furthermore, the following holds for (39) and (41) with m = n
5. Summary
The novel radius recurrence relation fn (11) enables us to express the known recurrence relation (4) for n-ball volume and the known relation (5) for n-ball surface as a function of π^⌊n/2⌋, showing that the value of π as n-ball volume and surface irrational factor appears only for n < 0 and n ≥ 2 (π^⌊n/2⌋ = 1 for 0 ≤ n < 2).
Sequence (16), inverse to sequence (11), enables the examination of n-ball volumes and surfaces in the negative dimensions. Since f−2 = 0, in negative, even dimensions, n-balls have zero (void-like) volumes and zero (point-like) surfaces and become divergent with decreasing n. Curiously, the double factorial n‼ can be extended to negative, odd integers by inverting its recurrence relation and is not defined for negative even integers.
For positive dimensions, n = 5 (the largest unit radius n-ball volume) is the largest odd n where fn > fn−1, while n = 7 (the largest unit radius n-ball surface) is the smallest odd n where fn < fn−1. The diameter recurrence relation gn (32) is related with (16) by fn = 2ngn.
Algebraic forms (14), (15), (18)–(20) of the relation (16) were presented for even and odd dimensions. Algebraic forms (19), (20) for n ∈ ℂ, expressed in terms of the gamma function, bound the relation (16) for n ∈ ℤ.
Constant (21) of products of pairs of these sequence values for integer n and −n−2 reveal symmetry that is the additive inverse of the symmetry {n, n−2} or equivalence of an ordinary (n − 2)-dimensional space to the n-dimensional superspace [3]. Furthermore sequence (16) reveals symmetry {n, 2 − n} (24) and {n, −n} (27), respectively, between n-ball surfaces and volumes in integer dimensions.
Sequence (16) comprises rational numbers, while all π^⌊n/2⌋ (for n < 0 and n ≥ 2) are most likely transcendental numbers.
It was shown that the known formula (7) for the volume of a regular n-simplex can be expressed as a recurrence relation (35) to remove the indefiniteness of the factorial, and further expressed as (36) to remove singularity for n = 0. Thus, n-simplices are undefined in the negative, integer dimensions if n < −1. This is congruent with the fact that every simplicial n-manifold inherits a natural topology from Euclidean space ℝn [27], and by researching Euclidean space ℝn as a simplicial n-manifold, topological (metric-independent) and geometrical (metric-dependent) content of the modeled quantities are disentangled [27]. Therefore, the lack of n-simplices in the negative, integer dimensions excludes the notion of negatively dimensional Euclidean space ℝn for n < −1. Volumes and surfaces of regular n-simplices are imaginary in negative, fractional dimensions for n < −1 (surfaces also for n < 0) and are divergent with decreasing n.
It was shown that the known formula (9) for the volume of n-orthoplex can be expressed as a recurrence relation (37) to remove indefiniteness of factorial and further expressed as (38) to remove singularity for n = 0. Thus, the volumes of n-orthoplices are zero in the negative, integer dimensions and divergent in the negative, fractional ones with decreasing n. Moreover, the surfaces of n-orthoplices are undefined for integer n < −1 (n-orthoplex has facets that are regular simplices of the previous dimension (10), and these are undefined for integer n ≤ −1), imaginary for fractional n < 0, and also divergent with decreasing n. Peculiarly, in 1 dimension the volume V1(A)O = A√2 not A, as in the case of 1-simplex and 1-cube.
Relations (4), (5), (8), (10), (12), (13), (17), (19)–(22), (24), (25), (27), (29), (30), (34)–(46) are continuous on their domains of definitions for n ∈ ℝ. The starting points for fractional dimensions can be provided, e.g., using spline interpolation between two (or three in the case of n-balls) subsequent integer dimensions.
In the negative dimensions, n-simplices, n-orthoplices, and n-balls have different properties than their positively dimensional counterparts, with the n-cube being an exception. The volume Vn(A)C = An and surface Sn(A)C = 2nAn−1 = 2dVn(A)C/dA of an n-cube are defined for any n ∈ ℝ, and are real if A ∈ ℝ. Interestingly, in ℝ3, the fractal dimension of the Sierpiński 3-simplex is 2, of the Sierpiński 3-orthoplex is 2.585, while only the Sierpiński 3-cube retains its regular dimension [28].
Out of three regular, convex polytopes (and n-balls) present in all non-negative dimensions [19], only n-cubes, n-orthoplices, and n-balls are defined in the negative, integer dimensions, with n-cubes being dual to the void. This should not be surprising. There are no 0-dimensional points in negative dimensions.
6. Discussion
Once upon a time, there was a (−1)-dimensional void of volume zero and undefined surface. Then, a 0-dimensional point of unit volume and null surface somehow appeared in this void. This first point is now called the primordial Big Bang singularity. The existence of the first point implied a countably infinite number of other labeled points forming various relations among each other. And thus, the void expanded into real and imaginary dimensionalities.
The presented recurrence relations remove indefiniteness and singularities present in known formulas, revealing the properties of the relevant geometric objects in negative and real dimensions.
The results of this study could perhaps be applied in linguistic statistics, where the dimension in the distribution for frequency dictionaries is chosen to be negative [4], and in fog computing, where n-simplex is related to a full mesh pattern, n-orthoplex is linked to a quasi-full mesh structure, and n-cube is referred to as a certain type of partial mesh layout [29].
Another possible application of the results of this study could be molecular physics and crystallography. There are countably infinitely many spherical harmonics, but nature uses only the first four as subshells of s, p, d, and f electron shells that can hold 2, 6, 10, and 14 electrons, respectively. Further subshells are not populated in the ground states of all the observed elements. The first element that would require a g subshell (18 electrons) would have an atomic number of 121, while the heaviest element synthesized is Oganesson, with an atomic number of 118 and a half-life of about 1/1000 of a second. Perhaps this is linked with properties of the unit radius n-balls in negative dimensions, as illustrated in Figure 2. The “flattening” occurring between dimensions −14 and −2 is intriguing. Dimensions −2, −6, −10, and −14 are bounded from both sides, with −14, which would represent the f subshell, already at the onset of divergence. In nature, the f subshell occurs essentially only in lanthanides and actinides. A simple and approximate formula for a spherical nuclear radius that generates very precise results in quantum and nuclear techniques is R = r0A1/3, where A is the atomic number and r0 = 1.25 ± 0.2 fm.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
https://github.com/szluk/balls_simplices_orthoplices (accessed on 20 May 2022).
Acknowledgments
I truly thank my wife and Mirek for their support. I thank Wawrzyniec for hinting derivation of the preliminary forms of Formulas (14) and (15).
Conflicts of Interest
The author declares no conflict of interest.
References
- Schleicher, D. Hausdorff Dimension, Its Properties, and Its Surprises. Am. Math. Mon. 2007, 114, 509–528. [Google Scholar] [CrossRef]
- Manin, Y.I. The notion of dimension in geometry and algebra. Bull. Am. Math. Soc. 2006, 43, 139–162. [Google Scholar] [CrossRef]
- Parisi, G.; Sourlas, N. Random Magnetic Fields, Supersymmetry, and Negative Dimensions. Phys. Rev. Lett. 1979, 43, 744–745. [Google Scholar] [CrossRef]
- Maslov, V.P. Negative dimension in general and asymptotic topology. arXiv 2006, arXiv:math/0612543. [Google Scholar]
- Maslov, V.P. General notion of a topological space of negative dimension and quantization of its density. Math. Notes 2006, 81, 140–144. [Google Scholar] [CrossRef]
- Office Chair Philosophy, Generalised Definition for Negative Dimensional Geometry. Available online: https://tglad.blogspot.com/2017/08/reframing-geometry-to-include-negative.html (accessed on 20 May 2022).
- Mandelbrot, B.B. Negative fractal dimensions and multifractals. Phys. A Stat. Mech. Its Appl. 1990, 163, 306–315. [Google Scholar] [CrossRef]
- Chhabra, A.B.; Sreenivasan, K.R. Negative dimensions: Theory, computation, and experiment. Phys. Rev. A 1991, 43, 1114–1117. [Google Scholar] [CrossRef]
- Allain, C.; Cloitre, M. Characterizing the lacunarity of random and deterministic fractal sets. Phys. Rev. A 1991, 44, 3552–3558. [Google Scholar] [CrossRef]
- Hutchinson, J.E. Fractals and self similarity. Indiana Univ. Math. J. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Guariglia, E. Primality, Fractality, and Image Analysis. Entropy 2019, 21, 304. [Google Scholar] [CrossRef]
- Yu, B. Fractal dimensions for multiphase fractal media. Fractals 2006, 14, 111–118. [Google Scholar] [CrossRef]
- Yu, B.; Zou, M.; Feng, Y. Permeability of fractal porous media by Monte Carlo simulations. Int. J. Heat Mass Transf. 2005, 48, 2787–2794. [Google Scholar] [CrossRef]
- Shishikura, M. The Hausdorff Dimension of the Boundary of the Mandelbrot Set and Julia Sets. Ann. Math. 1998, 147, 225. [Google Scholar] [CrossRef]
- Katunin, A.; Fedio, K. On a visualization of the convergence of the boundary of generalized Mandelbrot set to (n − 1)-sphere. J. Appl. Math. Comput. Mech. 2015, 14, 63–69. [Google Scholar] [CrossRef][Green Version]
- Fidkowski, L.; Hubeny, V.; Kleban, M.; Shenker, S. The Black Hole Singularity in AdS/CFT. J. High Energy Phys. 2004, 2, 14. [Google Scholar] [CrossRef]
- Gassner, S.; Cafaro, C. Information geometric complexity of entropic motion on curved statistical manifolds under different metrizations of probability spaces. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950082. [Google Scholar] [CrossRef]
- Guariglia, E.; Silvestrov, S. Fractional-Wavelet Analysis of Positive definite Distributions and Wavelets on ⅅ (C). Engineering Mathematics II. In Springer Proceedings in Mathematics & Statistics; Springer: Cham, Switzerland, 2016; Volume 179. [Google Scholar] [CrossRef]
- Baez, J. Platonic Solids in All Dimensions. Available online: https://math.ucr.edu/home/baez/platonic.html (accessed on 20 May 2022).
- Wong, B.C.; Sommerville, D.M.Y. An Introduction to the Geometry of n Dimensions; Methuen & Co.: London, UK, 1929; ISBN-10: 1781830312. [Google Scholar] [CrossRef]
- Coxeter, H.S.M. Regular Polytopes, 3rd ed.; Dover Publications: New York, NY, USA, 1973; ISBN-13: 978-0486614809. [Google Scholar]
- Henk, M.; Richter-Gebert, J.; Ziegler, G.M. Basic Properties of Convex Polytopes. In Handbook of Discrete and Computational Geometry; CRC Press, Inc.: Boca Raton, FL, USA, 1997; ISBN 9781315119601. [Google Scholar]
- Katunin, A. Fractals based on regular convex polytopes. Sci. Res. Inst. Math. Comput. Sci. 2012, 11, 53–62. [Google Scholar] [CrossRef][Green Version]
- The Chinese University of Hong Kong. Chapter 3, Lebesgue and Hausdorff Measures. Math 5011. Available online: https://www.math.cuhk.edu.hk/course_builder/1415/math5011/MATH5011_Chapter_3.2014.pdf (accessed on 20 May 2022).
- Gipple, J. The Volume of n-balls. Rose-Hulman Undergrad. Math. J. 2014, 15, 14. [Google Scholar]
- Buchholz, R.H. Perfect pyramids. Bull. Aust. Math. Soc. 1991, 45, 353–368. [Google Scholar] [CrossRef]
- Desbrun, M.; Kanso, E.; Tong, Y. Discrete Differential Forms for Computational Modeling; Birkhäuser: Basel, Switzerland, 2008; pp. 287–324. [Google Scholar] [CrossRef]
- Kunnen, A.; Schlicker, S. Regular Sierpinski polyhedral. Pi Mu Epsil. J. 1998, 10, 607–619. [Google Scholar]
- Roig, P.J.; Alcaraz, S.; Gilly, K.; Juiz, C. Applying Multidimensional Geometry to Basic Data Centre Designs. Int. J. Electr. Comput. Eng. Res. 2021, 1, 1–8. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).