Abstract
Convolutional networks are commonly used in various machine learning tasks, and they are more and more popularly used in the embedded domain with devices such as smart cameras and mobile phones. The operation of convolution can be substituted by point-wise multiplication in the Fourier domain, which can save operation, but usually, it is applied with a Fourier transform before and an inverse Fourier transform after the multiplication, since other operations in neural networks cannot be implemented efficiently in the Fourier domain. In this paper, we will present a method for implementing neural network completely in the Fourier domain, and by this, saving multiplications and the operations of inverse Fourier transformations. Our method can decrease the number of operations by four times the number of pixels in the convolutional kernel with only a minor decrease in accuracy, for example, 4% on the MNIST and 2% on the HADB datasets.
MSC:
68T07
1. Introduction
Neuroscience has inspired artificial intelligence techniques such as Convolutional Neural Networks (CNNs), which were motivated by the visual cortex in the brain. CNNs consist of two main alternating parts: the convolutional and pooling layers, such as simple and complex cells in the visual cortex [1]. Nowadays, CNNs can reach exceptional performance in a wide range of machine learning tasks such as image classification and natural language processing. Convolutional layers are still used in most state-of-the-art architectures [2,3], such as vision transformers [4]. It was also demonstrated in [5] that similar state-of-the-art performance can be reached with highly optimized, purely convolutional architectures. Unfortunately, there are limiting aspects of these architectures as well: updating a large number of parameters and executing myriads of multiplications requires significant computational resources.
There are various approaches aiming to decrease the number of operations and by this the inference time of the networks or to reduce their computational need employing architectural changes. For instance, in the case of SqueezeNet [6], Iandola et al. were able to make a small network architecture with AlexNet-level accuracy on ImageNet by downscaling the number of channels in each layer using 1x1 filters and by this decreasing both the number of operations and trainable parameters simultaneously. Another solution, presented first in MobileNets [7], was described by Howard et al.; their architecture contained two hyperparameters to build small and low-latency models for mobile and embedded vision applications.
The goal of Knowledge Distillation [8] was similar: to make a fast and minimized network. Yim et al. introduced a novel knowledge transfer technique, where the transferred distilled knowledge from a pretrained neural network is determined by computing the inner product of features from two layers and by this decreasing neuron or layer numbers.
The invention of Farhadi et al. [9] is based on weight quantization and in a corner case the binarization of the weights and of the intermediate representations of data in a Convolutional Neural Network. This method includes optimization processes to determine the best approximations of the convolution operations in CNN using binary operations.
A novel approach for compressing deep neural networks was introduced in [10], which took into account the nonlinear responses and the multi-linear low-rank constraint in the kernel tensors. They suggest a convex relaxation strategy that can be solved directly using the alternating direction method of multipliers (ADMM) to address the difficulty of nonconvex optimization. As a result, they can determine the feature matrix of the Tucker decomposition [11] and Tucker-2 rank at the same time. The suggested method is tested on an ImageNet dataset for CNNs such as AlexNet, ResNet-18 and GoogleNet. This method can achieve a significant decrease in model size while sacrificing just a minor amount of accuracy.
In [12], the authors minimized the parameters and saved operations by modifying the DenseNet deep layer block. This technique can reduce the multiple growths of parameter amount for deeper layers by using channel merging procedures while the accuracy remains relatively unchanged. In the case of DenseNet and RetNet-110, the parameters may be lowered by 30–70%. This lightweight network can be used in real time on an embedded device.
In [13], the authors presented a novel minimalist hardware architecture called adder convolutional neural network (AdderNet) to reduce the computational complexity and energy burden. In this architecture, they use adder kernel with hardware accelerators instead of original convolution. They can achieve a 47.85–77.9% reduction in power consumption and a 16% increase in speed.
These previous methods are independent from each other, and they can be combined with each other, but usually, in this case, accuracy drops significantly. They all aim at the simplification of the network structure, merging or completely removing neurons, channels or layers, resulting in different architectures with lower computational need, but since they simplify the network architecture, they are not mathematically equivalent with the original network but approximate it fairly well. Because of this, in most cases, they also decrease the accuracy of the networks. In this paper, we will demonstrate another method which exploits the fact that convolutions can be implemented as point-wise multiplications (Hadamard products) in the Fourier domain, and by this, it can also be combined with all previously mentioned approaches and can be generally used to decrease the computational need of a neural network. Unfortunately, meanwhile, convolutions can be more efficiently executed in the Fourier domain; other elements of a typical neural network such as nonlinearities and pooling operations can only be executed using significantly more operations in this domain and can be more efficiently applied in the time domain. Most approaches of network optimization, also all methods listed earlier, try to substitute and approximate convolution in the time domain. Our approach follows a different path, where we execute all operations in the Fourier domain where convolution can be efficiently applied, and we try to approximate the other operations in the Fourier domain.
There are existing methodologies in the literature which exploit the advantageous property of the Fourier transform or other spectral methods, but all of these substitute only specific computational building blocks in the Fourier domain and return from it with an inverse transformation, which adds extra computation to the system. Some of these go back to the time domain directly after the convolution part to apply the nonlinear activation and the downsampling step (e.g., [14,15], but there exist solutions, which provide an approximation to implement pooling and nonlinear activation functions in the frequency domain as well (e.g., [16,17,18]; thus, even in these architectures, one inverse Fourier transformation is applied at the last layer of the network.
The authors of [19] investigate the implementation of convolution in the Fourier domain using the FFT transform, but for this, the transformation has to be applied at every kernel.
Similarly, discrete cosine transform (DCT) is used in [20], where the authors suggest a faster convolution method for neural networks. They transform the convolutional kernel and the input into the spectral domain with discrete cosine transform and then perform pointwise multiplication between the feature map and kernel. The complexity of DCT is significantly smaller than the FFT method because discrete cosine transform involves only real arithmetic. They use intrinsically extended kernels to suppress repeated domain transformations, and they decrease the kernel symmetry with spectral dropout. This model can accelerate the FFT-based methods without a significant decrease in accuracy.
In [21], the authors proposed a method combining FFT, CNN, and LSTM (long and short-term memory). At first, they convert data to the Fourier domain; then, features are obtained by CNN, and after that, they complete the fault diagnosis of the circuit with the LSTM network. They improved the quality of CSTV analog circuit fault diagnosis with this FFT-CNN-LSTM method.
All these previously introduced spectral approaches use a spectral transformation and an inverse transformation to return to the time domain after convolution, after a layer, or at the end of the network. We will demonstrate in this work that these returns are not necessary and a neural network can be fully trained in the Fourier domain, and their weights, which in our case represent the weights of certain Fourier components, can be directly used in the following layer even in the logit layer for classification. This approach can further decrease the number of required operations, and as we will demonstrate, it also does not decrease the accuracy of the network significantly.
Our paper is structured as follows: In Section 2, we will introduce existing approaches to decrease the number of operations in a network, in Section 3 and we will also explain our approach, which employs all steps in the Fourier domain. In Section 4, we will describe our simulations and results and interpret them in Section 5. Finally, in Section 5, we draw conclusions based on our findings.
2. Acceleration of Networks in the Fourier Domain
The idea that convolutions can be performed as point-wise multiplications in the Fourier domain in case of a convolutional neural network appeared before the appearance of large-scale benchmark datasets emphasized the important need of training acceleration; however, the number of feature maps was too small to apply this method effectively. Nowadays, the speed up caused by Fourier transformations became significant; Mathieu et al. [14] implemented a Fourier based algorithm which requires operations instead of the direct method with operations, where our input image has dimensions of , is the size of the convolution kernel and C is the hidden constant in the notation.
The main additional cost of the frequency-based method is the Fourier transformation especially in [14], because this solution needs inverse transformation before every nonlinear activation part and after that a Fourier transformation again. In [15], two new convolution implementations used together with Fast Fourier transform were introduced and compared. The fbfft outperforms the cuFFT convolution implementation in most deep learning problems (introduced in [14,15]), but both of these outperform the original cuDNN variant.
Nevertheless, these transform methods have limitations as well, such as the problem of the number of instructions issued, for example, the throughput for 32-bit floating-point multiply–add operations is greater than the throughput for shuffles [15]. In [22], a technique was presented to mitigate the bottleneck of transformation cost, and it was shown that the “overlap-and-add” technique can reduce the computational time by a factor of up to 16.3 times compared to the traditional convolution implementation in a special case.
However, not only the operation of convolution can be simplified in the frequency domain, but the subsampling process may also change. In [23], the authors used the spectral pooling method instead of the conventional max-pooling as dimensionality reduction. This method is truncating the representation of the data in the frequency domain; thereby, it preserves more information per parameter and enables flexibility in output dimensionality. This spectral representation-based pooling method was applied in [24], where the training of FCNN architecture was conducted within the frequency domain without the addition of extra nonlinearity.
In [16], the authors introduced a nonlinearity in the frequency domain, which was called Fourier domain exponential linear unit, and they used pyramid pooling layers for downsampling in the frequency domain. Ayat et al. (in [17]) introduced the frequency domain equivalent of the conventional batch normalization, which increases the accuracy of the network. They used a novel nonlinear activation function, the Spectral Rectified Linear Unit (SReLU), after the Spectral pooling. Following the last convolutional layer but before the fully connected layer and softmax layer, they executed an inverse Fast Fourier Transform to obtain real numbers instead of the complex valued representation. Because of this step, this approach used unnecessary computation and cannot be considered a fully, end-to-end spectral training.
In [18], another kind of spectral ReLU operation was proposed (called 2SReLU) that adds low-frequency components with their second harmonics, and this method has two hyperparameters to adjust each frequency contribution to the final result. The equation of 2SReLU is as follows: .
All of these approaches presented implementations of convolution, pooling algorithms or nonlinear activation functions, but all of them applied an inverse transformation after the steps were executed. In the next section, we propose a convolutional neural network architecture, which is entirely in the Fourier domain, and it contains pooling, nonlinear activation function, and batch normalization in the spectral domain, and it calculates the fully connected layer and softmax layer without spectral–spatial domain switching as well. For the sake of reproducibility, the source code of our neural network, which contains the exact network architectures used in training and a detailed list of training parameters for our experiments, can be found in the following GitHub repository: https://github.com/andfulop/TrainingInFourierDomain (accessed on 13 June 2022), as the Supplementary Materials.
3. Methods
3.1. Convolution Theorem
Our method is based on the convolution theorem, which states the following:
where denotes the Fourier transforms of the f and g functions, ★ is the convolution, and · means the point-wise multiplication operators. (The theorem is also true backward: in the time domain, the pointwise multiplication is convolution in the frequency domain.)
3.2. Methods in the Frequency Domain
During the simulations, our datasets were traditional two-dimensional grayscale images (matrices) and one-dimensional time series (vectors). Therefore, at first, a discrete one- or two-dimensional Fourier transform was applied to these datasets accordingly. After the transformation, each one of the values was represented by a complex number, and all operations of the convolutional neural network were executed in the frequency domain.
3.2.1. Convolution Operation
The first and main part of a convolutional neural network is the convolution itself, in which we multiply element-wise the images (or time series) by the appropriate values of the convolutional kernels, which were transformed into the frequency domain before the multiplication as well. If we use smaller kernels than the size of the images or the length of the time series, before the transformation, the kernels had to be padded with zeros for the point-wise multiplication. Due to this padding, after the transformation, we always perform the multiplication operations with matrices of the same size; thus, we can save even more operations if the kernel size is larger. However, since all our network works in the Fourier domain, we applied another technique and generated the kernels directly in the frequency domain instead of transforming them from the time domain using Fourier transform; thus, we can save the cost of kernels’ transformation during training. In this case, the kernel size is the same as the size of the input. We used this approach in our experiments, as we present in the results section. This step has no effect on inference time, which is one of the most important factors in neural network training, but it can reduce training time.
3.2.2. Nonlinear Activation Function
A sufficiently large neural network using nonlinearity can approximate arbitrarily complex functions [17,25]; furthermore, the learning dynamics and the expressive power of the network depend heavily on the applied nonlinearity. The activation function maps the input of a neuron into a specific range, and this value is the output of the cell.
In spectral representation, we can encounter various activation function implementations with the aim of operating similarly to nonlinearities of the time domain and achieving a similar result in terms of accuracy. One of these solutions is the Fourier domain exponential linear unit (FELU, [16]), which is the spectral equivalent of the exponential linear unit (ELU) of the spatial domain. The ELU can be defined as the following:
Another spectral activation function is the Spectral ReLU (SReLU, [17]). This method uses the following polynomial to approximate the traditional ReLU function: . Of course, considering that the multiplication of two signals in the spatial domain is equivalent to the convolution of two signals in the Fourier domain, thus, the previous equation can be modified as follows: , where the ★ denotes the convolution operator.
3.3. Our Implementation
We took the simplicity of the ReLUs (such as , or , where ) methods as a basis, more precisely, the simple and efficient computation (multiplication, addition, and comparison) of it.
During the Fourier transform, we transfer the original input signal from the set of real numbers to the complex plane; thus, the domain of our activation function will also be the set of complex numbers.
Our nonlinear function called FReLU is a nonlinear function, which can be written as follows:
where is equal to complex number, the , is the point in the complex plane and is a tuneable parameter of this method. This solution can be considered as a high-pass filter with the cut-off point or as an equivalent of the traditional ReLU funciton for complex numbers. Figure 1 illustrates how this function maps the complex plane in case of . During our training on the different datasets, the parameter was 0.1.
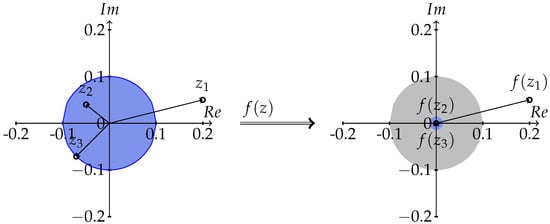
Figure 1.
The nonlinear activation function f (with ) maps to and , to zero, where , and . The position of points outside the blue circle does not change, but all points in the circle will be zero.
3.3.1. Subsampling Operation
We used the spectral pooling method introduced in [23] as a subsampling procedure. In this case, the dimensionality reduction is in the Fourier domain, where the matrix input is truncated and only the central submatrix of frequencies remains. This approach is different from other pooling strategies in the time domain, such as max pooling, which reduces dimensionality by at least a factor of 4 in a two-dimensional cases, and the maximum value in each window sometimes does not represent well enough the contents of the window. In contrast, spectral pooling can tune the output dimensionality, and besides, it can be considered as a filter as well, because the removed higher frequencies encode noise in the two-dimensional case [23].
3.3.2. Classifier
Before we flatten the feature map of the last convolution layer, we calculate the magnitude of the complex values applying a function, which can be written as follows:
This formula is similar to the previously introduced activation function, but the output is the square of the absolute value, which is a real number. The computational complexity of this calculation is instead of inverse FFT’s . (Previous solutions introduced by others used an inverse Fast Fourier Transform). After the flattening step, we used a traditional fully connected neural network with only one layer to predict the classes.
4. Results and Discussions
We started from a simple convolutional neural network, and our goal was to implement all operations in the frequency domain after the initial Fourier transform and replace each element of the network with a suitable spectral solution, then examine how our architecture works on one- and two-dimensional datasets. For demonstration, in the time domain, we also implemented a CNN, which has the same computational complexity as our neural network in the frequency domain (Figure 2) (we used max pooling and ReLU in the time domain); the accuracy results obtained by these CNNs on various datasets can be found in the Table 1.
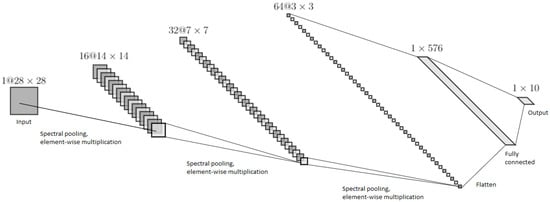
Figure 2.
The schema of the proposed CNN architecture. The input is in the frequency domain, the spectral pooling can be done before the element-wise multiplication, and the nonlinear activation function can be applied after each multiplication.

Table 1.
The table contains the average and maximum of the accuracy achieved on the independent test sets of the examined datasets in case of three different network architectures. One is the reference network in time domain, the other contains the inverse FFT, which was also used in previous articles, and the neural network implemented with the sum of squares solution proposed by us.
4.1. One-Dimensional Datasets
In this case, in the frequency domain and in the time domain, our network contained three convolutional layers and one FC (fully connected) layer. We performed one-dimensional convolution in the time domain with kernels.
A one-dimensional dataset selected for detailed investigation was the Smartphone-Based Recognition of Human Activities and Postural Transitions Data Set Version 2.1 (HADB, [26]). This consists of a smartphone’s accelerometer and gyroscope signals during twelve different activities (such as standing, walking, walking downstairs and upstairs, laying, etc.) of 30 subjects. The training set contains more than 7700 samples, while the test set contains 3100 samples. The accuracy results for the spatial and spectral domain trainings are shown in Figure 3.
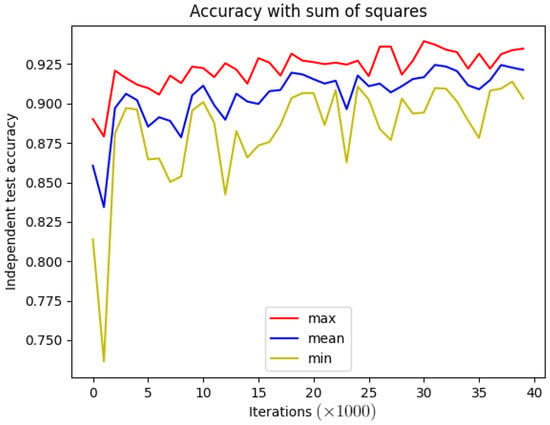
Figure 3.
Five training results of HADB classification in frequency domain with the proposed nonlinear activation function, with square sum. The red color means the maximum accuracy, the yellow color is the minimum accuracy and the blue line shows the mean accuracy.
Another one-dimensional dataset was the Ozone Level Detection Data Set [27]; we used the one hour peak set from that. The samples contain wind speed values at various time and temperature values measured at different times as well. These samples can be categorized into two classes: the first one is the normal day and the second one is the ozone day. The dataset has 2536 instances, and we selected the last 500 as an independent test set. The results of this dataset are presented in Table 1.
4.2. Two-Dimensional Datasets
For two-dimensional datasets, in the frequency domain and in the time domain as well, we used a network with three convolutional layers and one FC (fully connected) layer. We performed two-dimensional convolution in the time domain with kernels.
We used the well-known MNIST dataset, which is a database of handwritten digits, and it has a training set of 60,000 examples and a test set of 10,000 examples. The size of the images is 28 × 28 [28].
Another two-dimensional dataset was the Fashion-MNIST, which is an MNIST-like fashion product database with 10 classes, and it consists of 28 × 28 sized grayscale images, where the number of elements of the training set is 60,000 and the test set has 10,000 examples [29].
Figure 4 and Figure 5 show the accuracy results of the independent test sets in the case of these datasets.
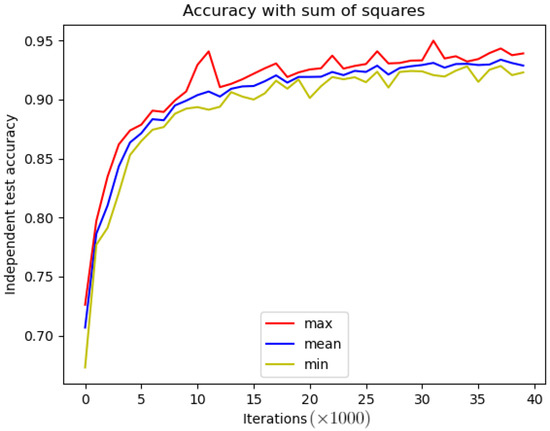
Figure 4.
Five training results of MNIST classification in frequency domain with the proposed nonlinear activation function, with square sum instead of inverse FFT. The red color means the maximum accuracy, the blue line shows the mean accuracy and the yellow color is the minimum accuracy.
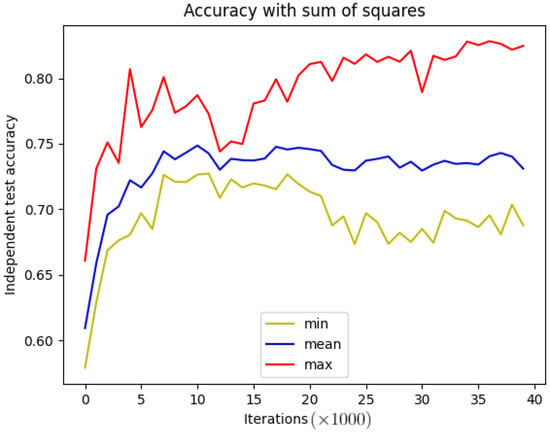
Figure 5.
Five training results of Fashion-MNIST classification in frequency domain with the proposed nonlinear activation function, with square sum. The red color means the maximum accuracy, the yellow color is the minimum accuracy and the blue line shows the mean accuracy.
In every case, we made five different trainings and we determined the maxima, the minima, and the average values of these. After that, we compared the results of inverse FFT version with the method we proposed and in the MNIST, Fashion-MNIST and OZONE cases, we found (see Table 1) that the maximum value was higher (or the same in case of the maximum of OZONE) in the case we proposed than the inverse FFT method, and only the accuracy of HADB was worse. However, the number of calculations decreased in each case, as instead of , only operation had to be performed after the convolutional layers (where n is the size of a sample).
Although the neural network in the time domain outperformed the accuracies of the two frequency-based implementations, in this case, much more multiplication is required (Table 2), as in the time domain, the computational complexity of convolution is , where is the size of the kernel, but in the frequency domain, we have only complexity, since, in the frequency domain, the spectral pooling can be executed before the element-wise multiplication. In the frequency domain, the FFT also requires computation (), but this can be done (and stored) before the training.

Table 2.
The table contains the number of multiplication in case of frequency-based implementation and in case of the time-domain implementation. For example, a typical input 224 × 224 × 3 × 3 number of multiplications is 12,544 in Fourier domain and 451,584 in the time domain.
4.3. Dependence on Hyperparameters
On one hand, our method is theoretical, and it is easy to see that an end-to-end training in the Fourier can decrease the number of operations applied. These decrease is general and are constantly present, since it comes from the reformulation of the convolutions operation and the substitution of the inverse Fourier transform. Because of this, it can be applied and is advantageous for arbitrary network architectures and training processes. On the other hand, the other important property, the accuracy of the investigated neural networks can not be determined theoretically and is typically measured empirically on commonly investigated datasets.
We have measured the performance of six different neural networks variants trained both in the time and Fourier domains and compared their performances. The results can be seen in Table 3. As it can be seen in the results, the overall performance of a network depends on the selected hyperparameters, but the networks trained in the Fourier domain have always performed similarly to the time domain counterparts. The drop of the mean accuracy was 2% on average over the six investigated hyperparameter sets.

Table 3.
The table contains the results of different hyperparameters both in the time and Fourier domains (without inverse FFT) on the HADB dataset. L denotes the number of channels in the consecutive layers from the first to last layer; opt denotes the optimizer, which could be either Adam or Stochastic Gradient Descent (SGD).
5. Discussion
As it can be seen from the results presented in the previous section, our approach can provide an efficient implementation for convolutional neural networks with a minor drop in accuracy.
According to our knowledge, this is the first approach where the whole training process is implemented in the Fourier domain. Other methods used certain operations or selected layers which were implemented in the Fourier domain, but they all contained an inverse Fourier transform, which requires a fairly high number of operations, which are typically comparable with the number of operations in a layer. Our results also demonstrate that convolutions can be more efficiently used in the Fourier domain, which is a well-known fact in the community. We substitute the traditional maximum pooling with spectral pooling, which utilizes a different tpye of dimension reduction which suits ideally for the Fourier domain. The novelty of our method is threefold: (1) We have demonstrated that instead of complicated polynomial approximation of the standard time domain ReLU, one can use a similar approach in the frequency domain and just cut off certain frequencies in the network. (2) We applied the training of the convolutional kernels directly in the frequency domain, which means that the kernels are not initialized and later transformed to the Fourier domain for computation, but in our approach, the Fourier version of the kernels are initialized directly. (3) We substitute the final inverse Fourier transformation of all previously published methods in the literature with a simple magnitude calculation, which can reduce the number of operations from to n, where n is the number of neurons in the logit layer.
We have demonstrated that our method is general. We have demonstrated its validity on four different datasets, and we have investigated six different network architectures. The results were consistent in all cases. The accuracy of the end-to-end Fourier domain networks dropped slightly, typically with 4%, but one can save three-quarters of the multiplications compared to the traditional time-series implementations of the networks.
This mean that this approach might not be a viable optimization strategy in applications where accuracy is utmost important, for example in medical image processing or navigation with self-driving cars, but in case of various other methods where power consumption is more critical such as recommendation systems or photo enhancement or classification in personal photo libraries, our method could provide a viable and significant decrease in computation for possible applications of edge computing.
6. Conclusions
In this paper, a convolutional neural network in the frequency domain was presented without using any inverse Fourier transformation (including the classification part as well). We have introduced an alternative realization of the spatial activation functions in the frequency domain, and we have presented a possible solution to eliminate the inverse Fourier transformation before the fully connected classification layer. Our neural network architecture was tested on one- and two-dimensional datasets and was compared with similar network implementation containing inverse Fourier transformation. The proposed framework could achieve similar or better accuracy without the computational cost of inverse Fourier transformation. For instance, in the case of MNIST, which is a commonly used and often cited dataset, the maximum accuracy of architecture with inverse FFT decreased by about 6% from the time-domain reference (where the maximum was 98.75%), while the maximum accuracy of our solution (sum of squares) dropped just approximately 4%.
Supplementary Materials
Our implementation and experiments can be downloaded from the Github repository at https://github.com/andfulop/TrainingInFourierDomain (accessed on 13 June 2022).
Author Contributions
Conceptualization, A.F. and A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no funding from grants 2018-1.2.1-NKP-00008: Exploring the Mathematical Foundations of Artificial Intelligence TKP2021_02-NVA-27—Thematic Excellence Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Our methods were evaluated on publicly available datasets.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rawat, W.; Wang, Z. Deep convolutional neural networks for image classification: A comprehensive review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Xiao, B.; Codella, N.; Liu, M.; Dai, X.; Yuan, L.; Zhang, L. Cvt: Introducing convolutions to vision transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 22–31. [Google Scholar]
- Raghu, M.; Unterthiner, T.; Kornblith, S.; Zhang, C.; Dosovitskiy, A. Do vision transformers see like convolutional neural networks? Adv. Neural Inf. Process. Syst. 2021, 34, 12116–12128. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Ding, X.; Zhang, X.; Ma, N.; Han, J.; Ding, G.; Sun, J. Repvgg: Making vgg-style convnets great again. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 13733–13742. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50× fewer parameters and <0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Yim, J.; Joo, D.; Bae, J.; Kim, J. A gift from knowledge distillation: Fast optimization, network minimization and transfer learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4133–4141. [Google Scholar]
- Farhadi, A.; Rastegari, M. System and Methods for Efficiently Implementing a Convolutional Neural Network Incorporating Binarized Filter and Convolution Operation for Performing Image Classification. U.S. Patent App. 16/430,123, 4 June 2019. [Google Scholar]
- Liu, Y.; Ng, M.K. Deep neural network compression by Tucker decomposition with nonlinear response. Knowl.-Based Syst. 2022, 241, 108171. [Google Scholar] [CrossRef]
- Kim, Y.D.; Choi, S. Nonnegative tucker decomposition. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Hsia, S.C.; Wang, S.H.; Chang, C.Y. Convolution neural network with low operation FLOPS and high accuracy for image recognition. J. Real-Time Image Process. 2021, 18, 1309–1319. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, M.; Han, K.; Chen, H.; Zhang, W.; Xu, C.; Tao, D. AdderNet and its minimalist hardware design for energy-efficient artificial intelligence. arXiv 2021, arXiv:2101.10015. [Google Scholar]
- Mathieu, M.; Henaff, M.; LeCun, Y. Fast training of convolutional networks through ffts. arXiv 2013, arXiv:1312.5851. [Google Scholar]
- Vasilache, N.; Johnson, J.; Mathieu, M.; Chintala, S.; Piantino, S.; LeCun, Y. Fast convolutional nets with fbfft: A GPU performance evaluation. arXiv 2014, arXiv:1412.7580. [Google Scholar]
- Lin, J.; Ma, L.; Yao, Y. A Fourier Domain Training Framework for Convolutional Neural Networks Based on the Fourier Domain Pyramid Pooling Method and Fourier Domain Exponential Linear Unit. IEEE Access 2019, 7, 116612–116631. [Google Scholar] [CrossRef]
- Ayat, S.O.; Khalil-Hani, M.; Ab Rahman, A.A.H.; Abdellatef, H. Spectral-based convolutional neural network without multiple spatial-frequency domain switchings. Neurocomputing 2019, 364, 152–167. [Google Scholar] [CrossRef]
- Watanabe, T.; Wolf, D.F. Image classification in frequency domain with 2SReLU: A second harmonics superposition activation function. arXiv 2020, arXiv:2006.10853. [Google Scholar] [CrossRef]
- Kushchenko, A.S.; Ternovoy, N.E.; Popov, M.G.; Yakunin, A.N. Implementation of Convolution Function Through Fast Fourier Transform in Convolution Neural Networks Computation. In Proceedings of the 2022 Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), Saint Petersburg, Russia, 25–28 January 2022; pp. 368–370. [Google Scholar]
- Xu, Y.; Nakayama, H. DCT-based Fast Spectral Convolution for Deep Convolutional Neural Networks. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar]
- Sun, B.; Xu, W.; Yang, Q. Analog Circuit Fault Diagnosis Based on FFT-CNN-LSTM. In Proceedings of the 2021 7th Annual International Conference on Network and Information Systems for Computers (ICNISC), Guiyang, China, 23–25 July 2021; pp. 305–310. [Google Scholar]
- Highlander, T.; Rodriguez, A. Very efficient training of convolutional neural networks using fast fourier transform and overlap-and-add. arXiv 2016, arXiv:1601.06815. [Google Scholar]
- Rippel, O.; Snoek, J.; Adams, R.P. Spectral representations for convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2449–2457. [Google Scholar]
- Pratt, H.; Williams, B.; Coenen, F.; Zheng, Y. Fcnn: Fourier convolutional neural networks. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Bilbao, Spain, 13–17 September 2017; pp. 786–798. [Google Scholar]
- Agostinelli, F.; Hoffman, M.; Sadowski, P.; Baldi, P. Learning activation functions to improve deep neural networks. arXiv 2014, arXiv:1412.6830. [Google Scholar]
- Reyes-Ortiz, J.L.; Oneto, L.; Samà, A.; Parra, X.; Anguita, D. Transition-aware human activity recognition using smartphones. Neurocomputing 2016, 171, 754–767. [Google Scholar] [CrossRef] [Green Version]
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2017. Available online: https://archive.ics.uci.edu/ml/index.php (accessed on 13 June 2022).
- LeCun, Y.; Cortes, C.; Burges, C. MNIST Handwritten Digit Database; ATT Labs: Atlanta, GA, USA, 2010; Volume 2. Available online: http://yann.lecun.com/exdb/mnist (accessed on 13 June 2022).
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. Available online: http://xxx.lanl.gov/abs/1708.07747 (accessed on 13 June 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).