Safety Margin Prediction Algorithms Based on Linear Regression Analysis Estimates

Abstract

In this paper, we consider the problem of approximating the safety margin of a single instance of a technical system based on inaccurate observations at specified time points. The solution to this problem is based on the selection of a certain set of reference points in time, in a small neighbourhood of which a sufficiently large number of inaccurate measurements are carried out. Analogously with the failure rate, it is assumed that the rate of decrease in the safety margin over time is represented by a polynomial of the fourth degree, and the safety margin itself is a polynomial of the fifth degree. A system of linear algebraic equations is constructed that determine the coefficients of this polynomial through its values and the values of its derivative at reference points in time. These values themselves are estimated by the method of linear regression analysis based on numerous observations in a small neighbourhood of reference points in time. A detailed computational experiment is carried out to verify the accuracy of the approximation of a fifth-degree polynomial and alternative ways of estimating it are constructed in the vicinity of points where the quality of approximation is insufficient.

1. Introduction

In the theory of reliability, it is known that one of the most popular curves, which has already become classical, is the behaviour of the failure rate depending on time (operating time). An idealized view of the curve is shown in Figure 1.

Such curves were obtained as a result of statistical processing of data on failures during testing and operation of many technical systems. As a rule, three sections can be distinguished on such a curve.

The section I shown in Figure 1 is called the run in stage, it is characterized by an increased failure rate, which decreases over time. This is due to the presence of hidden defects in the new facility, as well as all kinds of design and production errors, the elimination of which reduces the failure rate. The section $II$ is called the normal operation stage. Here, the failure rate is usually approximately (practically) constant. This stage essentially determines the actual resource of the object, its margin of safety. The section $III$ is called the ageing stage. At this site, the failure rate increases as a result of irreversible processes that lead to deterioration of the quality of the elements and the object as a whole.

In accordance with the decreasing or increasing failure rate, reliability theory considers “younger” or “ageing” objects and their corresponding distributions describing the distribution of uptime of objects. This classification of failure rate distributions was given in [1,2] and was further developed in the works of [3,4], including the most recent publications [5,6]. To analyse the failure rate, a sufficiently large statistics of observations of a large number of identical systems is required. It is worth mentioning that the middle stage of the life of the system is very important. Furthermore, some authors have recently considered such curves with the long flat regions [6,7,8,9,10]. Nevertheless in this paper, such systems are not considered. It should be noted that the assumption made in the paper about a system in a single instance does not apply to systems in a large series and vice versa.

However, the high level of technogenic emergencies observed in recent years makes it relevant to solve a number of new problems of the risk theory [11,12,13]. The problem of reducing technogenic risks is becoming particularly relevant in relation to technical facilities whose failures are associated with large losses and negative consequences. As a rule, these are complex systems manufactured in a small number of copies or even in a single copy. Such a statement of the problem can be attributed to the section of technical gerontology [14].

Under these conditions, the use of the ideas of the functional-parametric approach of the theory of technogenic risks [15] may become promising in solving the problem of technogenic risk management. Functional-parametric approach may be used to solve the considered problem, since it does not imply the presence of a statistics of large series of similar systems and with the help of the concept of safety margin allows us to investigate the decrease in the reliability of the system in a single exemplar.

The functional-parametric approach is based on the concept of the safety margin of the system and on a deterministic (mainly linear) model of its decrease. There are some stochastic modifications of this model based on a random initial value or on random measurements of the safety margin.

The description of the failure rate of technical systems in terms of younger and ageing distributions is more qualitative than quantitative. Therefore, it is also advisable to use the analogy between the failure rate and the rate of reduction in the safety margin on a qualitative rather than quantitative level. Indeed, during the lapping period, the uncomplicated mode of operation, it is natural to believe that the intensity of the decrease in the margin of safety decreases over time with the gradual debugging of the system. In contrast with the ageing of the system, the intensity of the decrease in the margin of safety increases, since all its parts begin to work insufficiently accurately. If we move from a complex system to its elements, which can be produced in series, then this pattern fully corresponds to the behaviour of these components. These features of the behaviour of a complex system are sufficiently fully reflected in [16,17].

To analyse a system in a single instance, it is assumed that its unit properties are close to the properties of the average for the ensemble of systems. This assumption arose from observations of changes in the ensemble of systems. The effectiveness of such an assumption may be justified in practice. Let us consider a simple illustrative example of a system that has a pronounced weak link. As such a link, we may take, for example, two rubbing surfaces with a coating of a certain thickness. At the initial stage, various irregularities are erased and therefore the rate of reduction in the coating thickness decreases. Over time, when the coating thickness becomes small, the ageing of the coating material, fractures and run-outs occurring in the system increase the rate of coating erasure.

Within the framework of this approach, the decrease in the safety margin of a technical system over time is investigated in accordance with a certain deterministic model. The simplest model of this type is a linear model of decreasing safety margin. It leads to the use of linear regression analysis to predict the safety margin of a technical product [18,19].

However, such a model is incomplete, since for systems presented in a single instance, the rate of decrease in the safety margin also decreases at the initial stage and increases at the last stage of the system functioning. Therefore, to solve the problem of predicting the safety margin within the framework of the regression method of estimating the parameters of the system, the use of a more complex regression function in the form of a fifth degree polynomial is required. As an example, we point to the function $x\left(t\right),$ for which the graph of the function

$$-x^{\prime }\left(t\right)={(t-5)}^4+1,$$

(1)

characterizing the rate of decrease in the safety margin (see Figure 2), is identical to the typical schedule of decreasing failure rate (see Figure 1). Here $x^{\prime }\left(t\right)$ is the first derivative of $x\left(t\right).$

It should be emphasized that the function $x\left(t\right)$ is taken only as an example by analogy with Figure 1. In fact, it is possible to represent the function $x\left(t\right)$ as a polynomial of the third degree. However, then the area of constancy of its derivative will be small. We can choose the function $x\left(t\right)$ in the form of a polynomial of the seventh degree, which, however, will significantly complicate all calculations. Therefore, the choice of the function $x^{\prime }\left(t\right)$ in accordance with the formula (1) allows for various modifications, common among which is the presence of a small coefficient in comparison with others with the highest degree of the argument.

The choice of polynomials of the fifth or higher degree for this purpose is determined by the complexity of the study, the amount of necessary calculations. However, even with such a simplified analysis, it is possible during the computational experiment to see the presence of a small parameter in the model that affects the quality of the forecast.

In this paper, by analogy with [20,21,22], it is proposed to estimate the coefficients of the polynomial $x\left(t\right)$ from multiple observations in small neighbourhoods of a set of points $t=t_0,t_1,t_2$ (let us call these points reference points). Technically, such multiple observations require the use of non-destructive testing devices.

This task is solved in two stages. First, a system of linear algebraic equations connecting the coefficients is solved $a_0,\dots ,a_5$ of function $x\left(t\right)$ with meanings $x\left(t\right),x^{\prime }\left(t\right),$$t=t_0,t_1,t_2.$ As a result, the coefficients $a_0,\dots ,a_5$ are found as some linear combinations of values $x\left(t\right),x^{\prime }\left(t\right),t=t_0,t_1,t_2.$

Then, based on multiple observations in small neighbourhoods of the points of the experimental plan, estimates $\widehat{x}\left(t\right),{\widehat{x}}^{\prime }\left(t\right)$ are built using linear regression analysis of meanings $x\left(t\right),x^{\prime }\left(t\right),t=t_0,t_1,t_2.$ Estimates $\widehat{x}\left(t\right),{\widehat{x}}^{\prime }\left(t\right)$ are constructed using linear regression analysis, but applied to the non-linear function $x\left(t\right)$ in small neighbourhoods of points $t=t_0,t_1,t_2.$ However, the difference between this function and its linear approximation is quite small [22]. Therefore, it is possible to construct an estimate of the error of linear regression coefficients and prove the validity of these estimates when striving to infinity the number of observations in the vicinity of the points of the experimental plan.

At the last stage, in the relations expressing the coefficients of the polynomial $x\left(t\right)$ in terms of the values $x\left(t\right),x^{\prime }\left(t\right)$, instead of these values, their consistent estimates are substituted by $\widehat{x}\left(t\right),{\widehat{x}}^{\prime }\left(t\right),t=t_0,t_1,t_2.$ Thus, consistent estimates of ${\widehat{a}}_0,\dots ,{\widehat{a}}_5$ coefficients of the polynomial $x\left(t\right)$ are constructed.

2. Calculation of Coefficients of a Polynomial $\mathit{x}\left(\mathit{t}\right)$

Let us now proceed to calculating the coefficients of the polynomial ${\displaystyle x\left(t\right)=\sum _{i=0}^5{a}_i{t}^i}$ from the system of equations defined when we assume for simplicity of calculations, that $t=0,\pm 1,$

$$\left\{\begin{array}{c}x\left(0\right)=a_0,\hfill \\ x^{\prime }\left(0\right)=a_1,\hfill \\ x\left(1\right)=a_5+a_4+a_3+a_2+a_1+a_0,\hfill \\ x^{\prime }\left(1\right)=5a_5+4a_4+3a_3+2a_2+a_1,\hfill \\ x(-1)=-a_5+a_4-a_3+a_2-a_1+a_0,\hfill \\ x^{\prime }(-1)=5a_5-4a_4+3a_3-2a_2+a_1.\hfill \end{array}\right.$$

(2)

The system of Equations (2) can be represented as the equation $A\overrightarrow{a}=\overrightarrow{x},$ where

$$A=\left(\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 1& 1& 1& 1& 1& 1\\ 0& 1& 2& 3& 4& 5\\ 1& -1& 1& -1& 1& -1\\ 0& 1& -2& 3& -4& 5\end{array}\right),\overrightarrow{a}=\left(\begin{array}{c}{a}_0\\ a_1\\ a_2\\ a_3\\ a_4\\ a_5\end{array}\right),\overrightarrow{x}=\left(\begin{array}{c}x\left(0\right)\\ x^{\prime }\left(0\right)\\ x\left(1\right)\\ x^{\prime }\left(1\right)\\ x(-1)\\ x^{\prime }(-1)\end{array}\right).$$

The solution of this equation can be represented in vector form $\overrightarrow{a}=A^{-1}\overrightarrow{x}$ or in a coordinate form

$$\left\{\begin{array}{c}{a}_0=x\left(0\right),\hfill \\ a_1=x^{\prime }\left(0\right),\hfill \\ a_2=-2x\left(0\right)+x\left(1\right)+x(-1)-x^{\prime }\left(1\right)/4+x^{\prime }(-1)/4,\hfill \\ a_3=-2x^{\prime }\left(0\right)+5x\left(1\right)/4-5x(-1)/4-x^{\prime }\left(1\right)/4-x^{\prime }(-1)/4,\hfill \\ a_4=x\left(0\right)-x\left(1\right)/2-x(-1)/2+x^{\prime }\left(1\right)/4-x^{\prime }(-1)/4,\hfill \\ a_5=x^{\prime }\left(0\right)-3x\left(1\right)/4+3x(-1)/4+x^{\prime }\left(1\right)/4+x^{\prime }(-1)/4.\hfill \end{array}\right.$$

(3)

Remark 1.

The formula (3) considers a special case when the moments $t=0,\pm 1.$ In the general case, when the moments t take the values $t_0,t_1,t_2$ matrix $A=\left|\right|a_{i,j}{\left|\right|}_{i,j=0}^5$ is defined by the equalities $a_{2p,j}=t_p^j,a_{2p+1,j}=j{t}_p^{j-1},p=0,1,2,j=0,1,\dots ,5.$ Using well-known algorithms and programs for calculating the inverse matrix $A^{-1},$ it is possible to construct estimates of the coefficients of a polynomial of arbitrary degree for given moments $t.$ Algorithms of matrix inversion are: Gaussian elimination [23], Newton’s method [24], Eigen decomposition of a matrix [25], Cholesky decomposition [26], and Blockwise inversion [27].

Remark 2.

If the function ${\displaystyle x\left(t\right)=\sum _{i=0}^{2r+1}{a}_i{t}^i}$ is a polynomial of odd degree $2r+1,$ then by choosing the points $t_0,t_1,\dots ,t_r,$ it is not difficult to construct the matrix A in the same way, calculate the inverse matrix $A^{-1}$ and by the values $x\left(t_i\right),x^{\prime }\left(t_i\right),i=0,\dots ,r,$ determine the vector $\overrightarrow{a}$ of the coefficients of this polynomial. This technique is transferred to a polynomial of even degree and by slightly more complex constructions to polynomials of general type.

For example, for the function $x\left(t\right)={\sum }_{i=0}^3$ choosing $t_0=0,t_1=1,$ it is easy to obtain the equalities

$$\left\{\begin{array}{c}{a}_0=x\left(0\right),a_1=x^{\prime }\left(0\right),a_2=3x\left(1\right)-3x\left(0\right)-2x^{\prime }\left(0\right)-x^{\prime }\left(1\right),\hfill \\ a_3=x^{\prime }\left(1\right)+x^{\prime }\left(0\right)-2x\left(1\right)+2x\left(0\right).\hfill \end{array}\right.$$

(4)

3. Estimation of the Values of the Polynomial $\mathit{x}\left(\mathit{t}\right)$ and Its Derivatives from Inaccurate Observations

Let us now proceed to the construction of estimates $\widehat{x}\left(k\right),{\widehat{x}}^{\prime }\left(k\right)$ of the quantities $x\left(k\right),x^{\prime }\left(k\right),k=0,\pm 1$ according to inaccurate observations $y(k+ih)=x(k+ih)+\epsilon (k+ih),i=0,\pm 1,\pm 2,\dots ,\pm n,$ where h is a time interval between neighbouring observations and $\epsilon (k+ih)$ are errors of observations. Here, the independent random variables $\epsilon (k+ih)$ have zero mean and finite variance ${\sigma }^2.$ Let us use the following modification of the linear regression analysis method proposed in [22], assuming

$$\widehat{x}\left(k\right)=\frac{{\sum }_{i=-n}^{n}y(k+ih)}{2n+1},{\widehat{x}}^{\prime }\left(k\right)=\frac{{\sum }_{i=-n}^{n}y(k+ih)ih}{{\sum }_{i=-n}^n{\left(ih\right)}^2}.$$

If $hn$ is much smaller than one, the polynomial $x(k+ih)$ deviates slightly from its linear approximation $\tilde{x}(k+ih)=x\left(k\right)+x^{\prime }\left(k\right)ih,i=0,\pm 1,\pm 2,\dots ,\pm n$ (see the formula (5) obtained by Taylor formula with the residual term in the form of Lagrange). Indeed, $\exists C=C(k,nh)$ such that

$$\underset{k-hn\le t\le k+hn}{sup}{x}^{″}\left(t\right)\le C<\infty \Rightarrow |x(k+ih)-\tilde{x}(k+ih)|\le \frac{C{i}^2{h}^2}{2}.$$

(5)

Hence we obtain the inequality (where $E\widehat{x}\left(k\right)$ is an expectation of random variable $\widehat{x}\left(k\right)$),

$$\begin{array}{c}|x\left(k\right)-E\widehat{x}\left(k\right)|=\left|x\left(k\right)-\frac{{\sum }_{i=-n}^{n}x(k+ih)}{2n+1}\right|\le \frac{{\sum }_{i=-n}^n|x(k+ih)-\tilde{x}(k+ih)|}{2n+1}\\ \le \sum _{i=-n}^n\frac{C{h}^2{i}^2}{2n+1}⪯n^2{h}^2.\end{array}$$

(6)

Here, for non-negative sequences $a_n,b_n,n=0,1,\dots$, the icon $a_n⪯b_n$ corresponds to the relation ${\displaystyle lim\; sup\frac{a_n}{b_n}<\infty .}$

In turn, the variance

$$Var\widehat{x}\left(k\right)=\frac{1}{{(2n+1)}^2}\sum _{i=-n}^{n}Var(x(k+ih)+\epsilon (k+ih))=\frac{2n{\sigma }^2}{{(2n+1)}^2}\le \frac{{\sigma }^2}{n}.$$

Let us evaluate now

$$|x^{\prime }\left(k\right)-E{\widehat{x}}^{\prime }\left(k\right)|=\left|x^{\prime }\left(k\right)-\frac{{\sum }_{i=-n}^{n}x(k+ih)ih}{{\sum }_{i=-n}^n{\left(ih\right)}^2}\right|=\left|\frac{{\sum }_{i=-n}^n(\tilde{x}(k+ih)-x(k+ih))ih}{{\sum }_{i=-n}^n{\left(ih\right)}^2}\right|$$

$$\le \frac{C{\sum }_{i=-n}^n{h}^2{i}^2\left|ih\right|}{{\sum }_{i=-n}^n{\left(ih\right)}^2}\le \frac{2C{\sum }_{i=-n}^n{h}^3{i}^3}{{\sum }_{i=-n}^n{\left(ih\right)}^2}⪯hn.$$

In turn,

$$Var{\widehat{x}}^{\prime }\left(k\right)=\frac{{\sigma }^2{\sum }_{i=-n}^n{\left(ih\right)}^2}{{\left({\sum }_{i=-n}^n{\left(ih\right)}^2\right)}^2}=\frac{{\sigma }^2}{{\sum }_{i=-n}^n{\left(ih\right)}^2}⪯\frac{{\sigma }^2}{h^2{n}^3}.$$

Assume that $h=h\left(n\right)=n^{-\alpha }$ then for ${\displaystyle 1<\alpha <\frac{3}{2}}$ we have

$$|x\left(k\right)-E\widehat{x}\left(k\right)|\to 0,|x^{\prime }\left(k\right)-E{\widehat{x}}^{\prime }\left(k\right)|\to 0,Var\widehat{x}\left(k\right)\to 0,Var{\widehat{x}}^{\prime }\left(k\right)\to 0,n\to \infty .$$

(7)

Hence follow (for $n\to \infty$) the convergence in probability estimates of $\widehat{x}\left(k\right)$ to $x\left(k\right)$ and estimates of ${\widehat{x}}^{\prime }\left(k\right)$ to $x^{\prime }\left(k\right).$

The obtained relations for the estimates of ${\widehat{a}}_j$ also imply their convergence to the coefficients $a_j,j=0,\dots ,5,$ of the polynomial $x\left(t\right).$ Now in order to construct estimates from inaccurate observations of the process $x\left(t\right)$ ${\widehat{a}}_j$ of parameters $a_j,j=0,\dots ,5$ it is enough to build estimates $\widehat{x}\left(k\right),{\widehat{x}}^{\prime }\left(k\right),k=0,\pm 1$ and use them to determine the estimates of ${\widehat{a}}_i$ using the equalities

$$\left\{\begin{array}{c}{\widehat{a}}_0=\widehat{x}\left(0\right),\hfill \\ {\widehat{a}}_1={\widehat{x}}^{\prime }\left(0\right),\hfill \\ {\widehat{a}}_2=-2\widehat{x}\left(0\right)+\widehat{x}\left(1\right)+\widehat{x}(-1)-{\widehat{x}}^{\prime }\left(1\right)/4+{\widehat{x}}^{\prime }(-1)/4,\hfill \\ {\widehat{a}}_3=-2{\widehat{x}}^{\prime }\left(0\right)+5\widehat{x}\left(1\right)/4-5\widehat{x}(-1)/4-{\widehat{x}}^{\prime }\left(1\right)/4-{\widehat{x}}^{\prime }(-1)/4,\hfill \\ {\widehat{a}}_4=\widehat{x}\left(0\right)-\widehat{x}\left(1\right)/2-\widehat{x}(-1)/2+{\widehat{x}}^{\prime }\left(1\right)/4-{\widehat{x}}^{\prime }(-1)/4,\hfill \\ {\widehat{a}}_5={\widehat{x}}^{\prime }\left(0\right)-3\widehat{x}\left(1\right)/4+3\widehat{x}(-1)/4+{\widehat{x}}^{\prime }\left(1\right)/4+{\widehat{x}}^{\prime }(-1)/4.\hfill \end{array}\right.$$

(8)

4. Computational Experiments

Experiment 1. Construct estimates of the coefficients of the polynomial

$$x\left(t\right)=-\frac{t^3}{3}+5t^2-26t+2626,$$

satisfying the equality $-x^{\prime }\left(t\right)={(t-5)}^2+1.$ To do this, we will choose random errors $\epsilon (k+ih),$ $k=0,\pm 1,i=0,\pm 1,\dots ,\pm n,$ evenly distributed on the segment $[-1/4,1/4],$ let us put $n={10}^4,h=n^{-5/4}$ and make $N={10}^3$ independent estimates of the coefficients ${\displaystyle a_0=2626,a_1=-26,a_2=5,a_3=-\frac{1}{3}.}$ In

Table 1. $a_0=2626,a_1=-26,a_2=5,a_3=-1/3$.

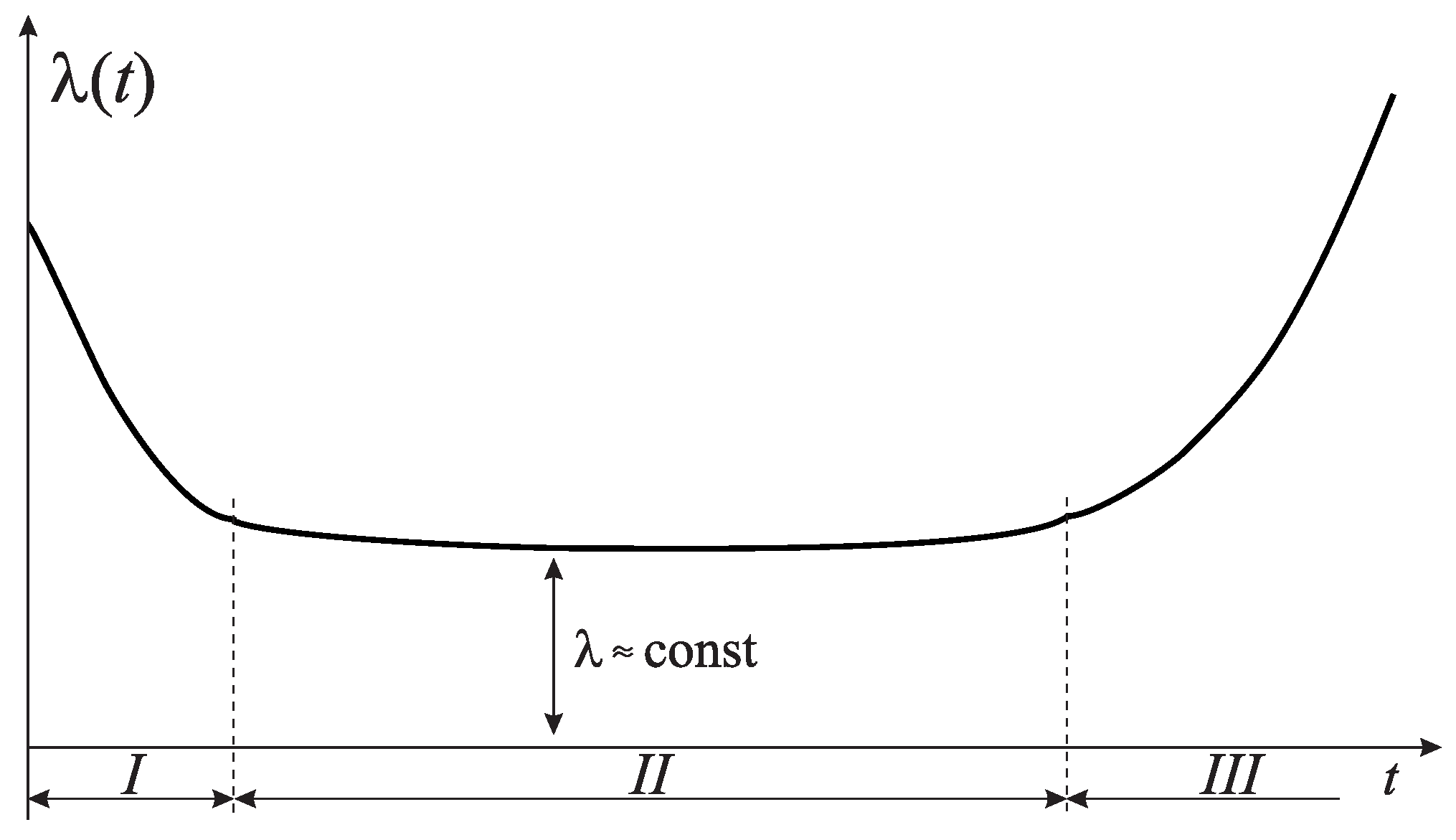
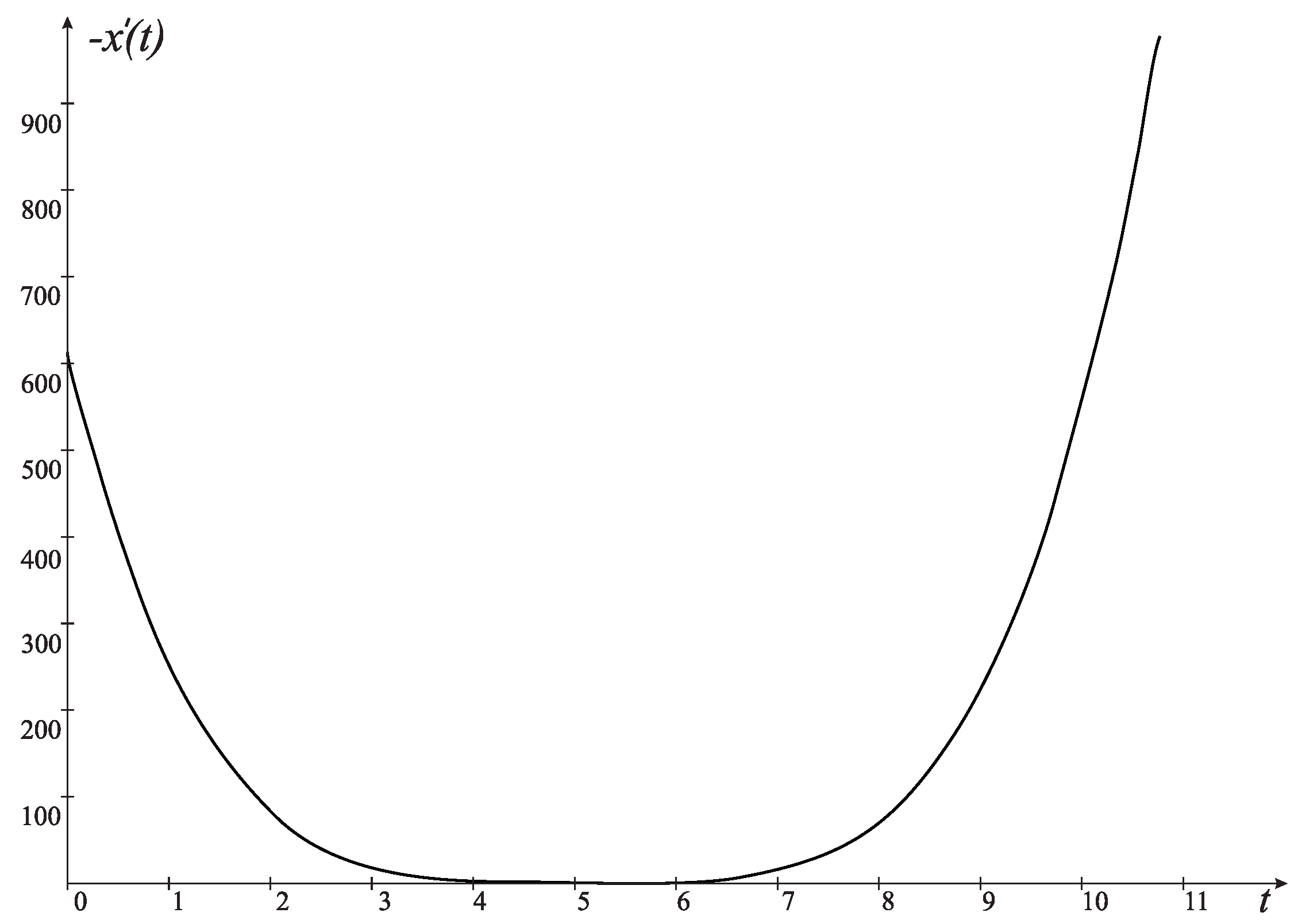
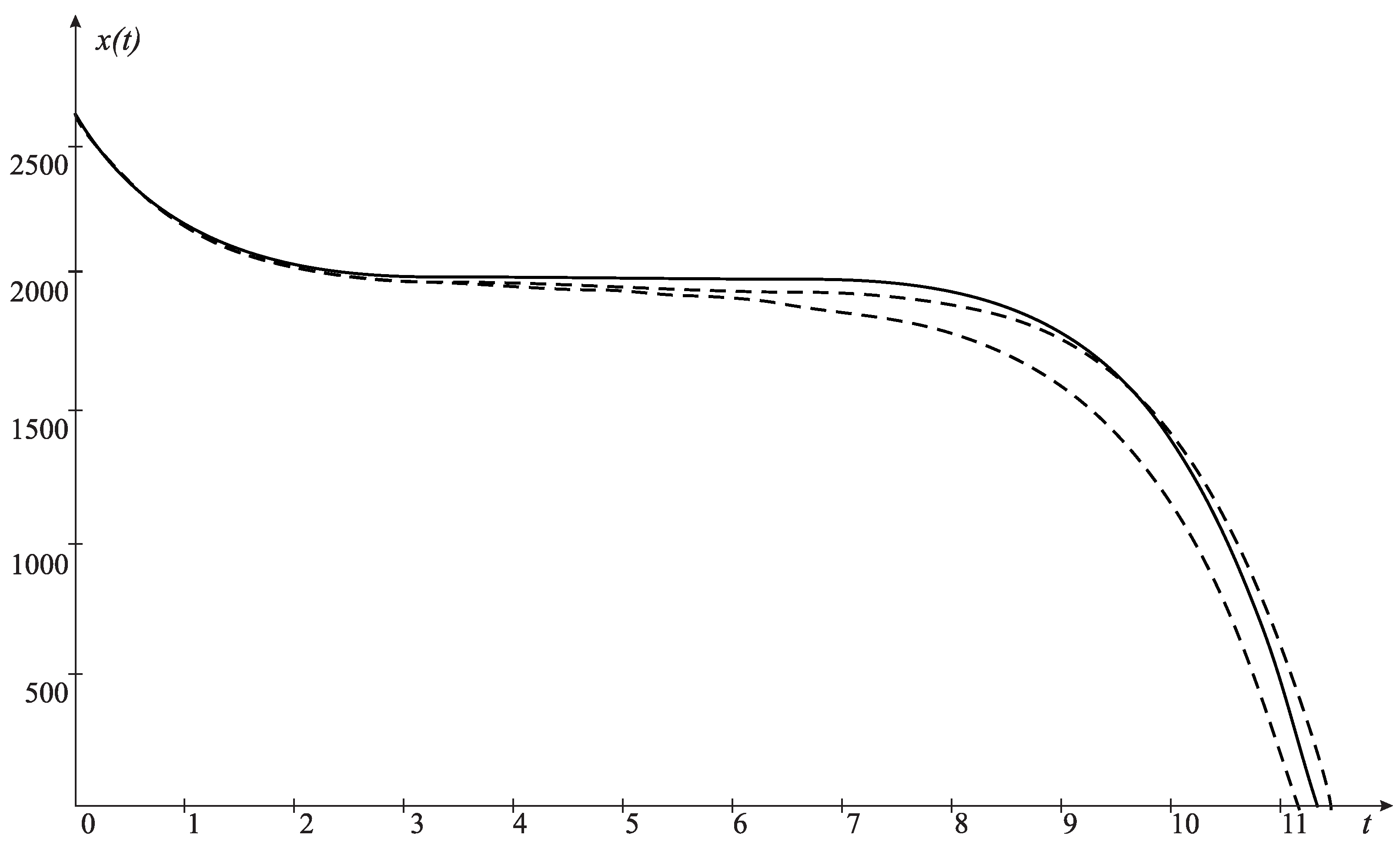
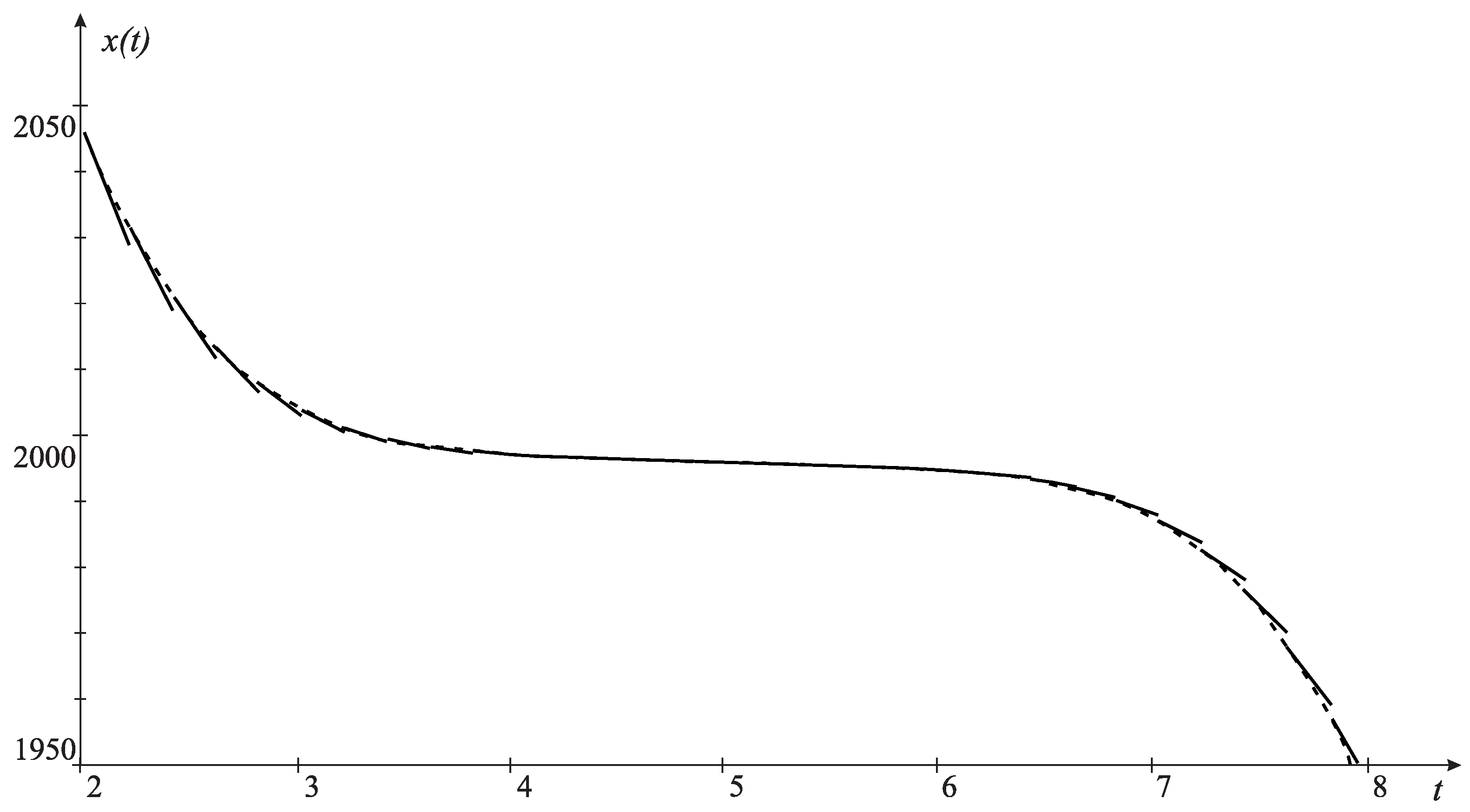
Distribution${\mathit{a}}_0$	Relative	Distribution${\mathit{a}}_1$	Relative
Intervals	Frequencies	Intervals	Frequencies
(2626.02318; 2626.02326)	0.076	(−26.00609; −26.00434)	0.040
(2626.02326; 2626.02334)	0.440	(−26.00434; −26.00259)	0.280
(2626.02334; 2626.02341)	0.376	(−26.00259; −26.00085)	0.484
(2626.02341; 2626.02349)	0.102	(−26.00085; −25.99910)	0.174
(2626.02349; 2626.02357)	0.006	(−25.99910; −25.99736)	0.022
Distribution${\mathit{a}}_2$	Relative	Distribution${\mathit{a}}_3$	Relative
Intervals	Frequencies	Intervals	Frequencies
(4.93801; 4.96285)	0.030	(−0.39637; −0.37248)	0.022
(4.96285; 4.98770)	0.280	(−0.37248; −0.34810)	0.156
(4.98770; 5.01254)	0.492	(−0.34810; −0.32472)	0.474
(5.01254; 5.03739)	0.176	(−0.32472; −0.30083)	0.298
(5.03739; 5.06223)	0.022	(−0.30083; −0.27695)	0.050

, the set of values of the estimates of each of the coefficients is divided into five intervals of the same length and the number of hits of each of the coefficients in the corresponding interval is calculated. The results of the computational experiment (Table 1) show that the drop in accuracy is due to the presence of a small parameter $|a_5|=0.2$ is much smaller than $min\left(\right|a_0|,|a_1|,|a_2\left|\right)=5.$

Experiment 2. Now we construct estimates of the coefficients of the polynomial

$$x\left(t\right)=-0.2t^5+5t^4-50t^3+250t^2-626t+2626,$$

satisfying the equality $-x^{\prime }\left(t\right)={(t-5)}^4+1$ (see (1)). To do this, we will choose random errors $\epsilon (k+ih),$ $k=0,\pm 1,i=0,\pm 1,\dots ,\pm n,$ evenly distributed on the segment $[-1/4,1/4],$ let ’s put $n={10}^4,h=n^{-5/4}$ and make $N={10}^3$ independent estimates of the coefficients $a_0=2626,a_1=-626,a_2=250,a_3=-50,a_4=5,a_5=-0.2.$ In

Table 2. $a_0=2626,a_1=-626,a_2=250,a_3=-50,a_4=5,a_5=-0.2$.

Distribution${\mathit{a}}_0$	Relative	Distribution${\mathit{a}}_1$	Relative
Intervals	Frequencies	Intervals	Frequencies
(2626.26350; 2626.26352)	0.027	(−626.09609; −626.09557)	0.043
(2626.26352; 2626.26353)	0.221	(−626.09557; −626.09506)	0.270
(2626.26353; 2626.26354)	0.483	(−626.09506; −626.09455)	0.455
(2626.26354; 2626.26356)	0.243	(−626.09455; −626.09403)	0.201
(2626.26356; 2626.26357)	0.026	(−626.09403; −626.09352)	0.031
Distribution${\mathit{a}}_2$	Relative	Distribution${\mathit{a}}_3$	Relative
Intervals	Frequencies	Intervals	Frequencies
(250.03414; 250.03838)	0.041	(−50.17271; −50.16861)	0.031
(250.03838; 250.04262)	0.271	(−50.16861; −50.16451)	0.169
(250.04262; 250.04686)	0.458	(−50.16451; −50.16041)	0.441
(250.04686; 250.05110)	0.203	(−50.16041; −50.15631)	0.289
(250.05110; 250.05534)	0.027	(−50.15631; −50.15221)	0.070
Distribution${\mathit{a}}_4$	Relative	Distribution${\mathit{a}}_5$	Relative
Intervals	Frequencies	Intervals	Frequencies
(4.94005; 4.94861)	0.034	(−0.19552; −0.19550)	0.031
(4.94861; 4.95717)	0.287	(−0.19550; −0.19548)	0.333
(4.95717; 4.96572)	0.495	(−0.19548; −0.19547)	0.521
(4.96572; 4.97428)	0.175	(−0.19547; −0.19545)	0.112
(4.97428; 4.98284)	0.009	(−0.19545; −0.19543)	0.003

, the set of values of the estimates of each of the coefficients is divided into five intervals of the same length and the number of hits of each of the coefficients in the corresponding interval is calculated. The minimum $a_i^{-}$ and maximum $a_i^{+},i=0,\dots ,5,$ values of all coefficients are separately found in $N={10}^3$ simulations. The confidence level is determined in Table 1 using Distribution intervals. According to these estimates, the smallest $x^{-}\left(t\right)$ and the largest $x^{+}\left(t\right)$ on the semi axis of the $t\ge 0$ function are constructed $x^{\pm }\left(t\right)=a_5^{\pm }{t}^5+a_4^{\pm }{t}^4+a_3^{\pm }{t}^3+a_2^{\pm }{t}^2+a_1^{\pm }t+a_0^{\pm }.$

In Figure 3, based on the results of the computational experiment, graphs of the functions $x\left(t\right),x^{-}\left(t\right),x^{+}\left(t\right)$ on the segment $[0,12]$ are constructed with solid and dotted lines. These graphs show how much the lower estimate of $x^{-}\left(t\right)$ and the upper estimate of $x^{+}\left(t\right)$ deviate from its exact value.

In Figure 2, shows the curve of the dynamics of the rate of decrease in the safety margin. However, for the purposes of forecasting, it is important to know the dynamics of changes in the safety margin itself, shown in Figure 3. Figure 3 shows that the accuracy of the approximation of the function $x\left(t\right)$ by the functions $x^{-}\left(t\right),x^{+}\left(t\right)$ decreases with an increase in the absolute value of $|x^{″}\left(t\right)|$ is its second derivative. The results of the computational experiment (Table 1) show that the drop in accuracy is due to the presence of a small parameter $|a_5|=0.2\ll min(|a_0|,\dots ,|a_4\left|\right)=5.$

Experiment 3. Therefore, there is a need to choose a more accurate forecast of the function $x\left(t\right),$ even if it is more complex. To do this, by analogy with Section 3, estimates of the functions $x\left(k\delta \right),x^{\prime }\left(k\delta \right),k=0,\dots ,m,$ were constructed for $n={10}^4,h=n^{-11/8},$$\delta =0.2,m=60$ and for them, the forecast estimates $\widehat{x}\left(k\delta \right)+\tau {\widehat{x}}^{\prime }\left(k\delta \right)$ on segments $k\delta +nh\le \tau \le (k+1)\delta +nh,k=0,\dots ,m.$ The results of these assessments are presented in Figure 4. From this figure it can be seen that due to more frequent measurement of the values of $x\left(k\delta \right),x^{\prime }\left(k\delta \right),k=0,\dots ,m$, the accuracy of estimates increases. However, even in this case, estimates in the region of large values of $|x^{″}\left(t\right)|$ is lower than in the region of small values of $|x^{″}\left(t\right)|.$

5. Conclusions

Thus, algorithms have been developed for constructing estimates of the function $x\left(t\right),$ which determines the dynamics of the safety margin of a technical system existing in a single instance. It is found that the solution of this problem requires the development of at least two alternative approaches. The reason for such complexity of the problem is established, due to the fact that the coefficient at the highest degree of the polynomial $x\left(t\right)$ is small with respect to all other coefficients. Therefore, the suppression of errors in the evaluation of the function $x\left(t\right)$ requires the inclusion of a small parameter $\delta$ in an alternative evaluation algorithm. At the same time, additional experiments show that in the area of relative stability of the function $x\left(t\right)$, an increase in the parameter $\delta$ is possible and therefore a decrease in the volume of observations.

6. Discussion

The solution of the considered problem is based on the analogy between the statistics of systems with a large number of instances and systems in a single instance. This analogy turned out to be quite complicated, since it contained a hidden small parameter. It is possible that this problem may require consideration of polynomials of higher degree. In any case, this task does not have a single solution, and short-term forecasts will be required along with forecasting the safety margin for a long time interval.

In our opinion, this problem requires the use of various approaches for its solution. This is clearly seen from computational experiments when the higher coefficient of the polynomial becomes a small parameter. Apparently, along with the polynomial approximation of the function $x\left(t\right),$ other approximations are also possible, for example in the form of B-splines. However, this requires a separate study, since the experiment plan will have to be adapted to B-splines. This circumstance was already identified during Experiment 3, in which the ageing period was clearly associated with an increase in the rate of decrease in the safety margin. Thus, the polynomial approximation becomes a preliminary stage in solving the problem of predicting the safety margin.