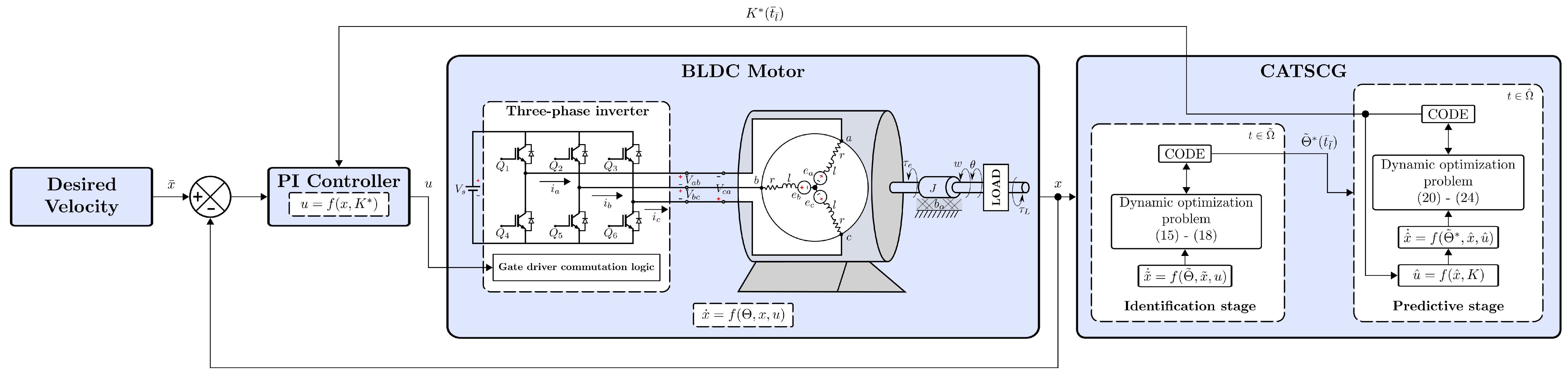
In this section, the proposed adaptive strategy for the brushless motor based on the chaotic online differential evolution (CODE) is tested. The details of the experiments are explained below.
4.1. Details of the Experiment
For the experiments in the simulation, the considered brushless DC motor has the nominal parameters presented in
Table 3. The differential equation associated with the motor is solved by the numerical integration method ode1 using a fixed integration step of
to simulate its dynamics. This integration step also coincides with the sampling interval and refers to it in the same way. The motor must complete the task of speed regulation with the highest possible accuracy for
, utilizing the proposed control strategy. For this, the reference speed is defined as (
32) to test different operating cases.
On the other hand, two experimental conditions are selected to validate the adaptability of the control strategy—the normal operating condition(s) (NOC) and the disturbed operating condition(s) (DOC). In the NOC, the nominal parameters in
Table 3 remain fixed. On the other hand, the DOC consider a scenario closer to reality, where the load torque
is added suddenly when the time is in the interval
; random noise signals up to
,
, and
are included in the angular position (
), angular speed (
), and motor currents (
and
) states, respectively; the motor parameters change continuously according to (
33).
Concerning the re-optimization process in the identification and predictive stages of the CATSCG for the PI controller, it is performed by CODE every .
The dynamic optimization problem for identification is set up using the past brushless states acquired in a backward time window of
from the current time instant. The upper and lower bounds of the model parameters for this problem are set as
and
. As can be noticed, these bounds are based on the nominal values of the system parameters as suggested in [
73] to prevent the model over-fitting. In this way, the lower bounds correspond to half the value of the nominal parameters, while the upper ones correspond to double. The above rule is simple and allows to set the limits considering approximate values of the motor parameters and not necessarily the actual ones.
In the case of the predictive stage, a future horizon of is selected to predict the motor behavior for different sets of controller gains. For this last problem, the input voltage limits are and . For the same problem, the selected upper and lower bounds of the PI controller gains are and . These limits were obtained by a non-exhaustive trial-and-error approach using a fixed-gain PI controller. In this, the PI gains are adjusted to observe limiting behaviors that can be considered acceptable, but not necessarily good..
In addition, the effectiveness of the CODE optimizer in the proposed adaptive tuning strategy is verified through comparisons with other alternatives provided with the same elitist online adaptation (the inclusion of an individual with the best previous knowledge). These are: the genetic algorithm (GA) described in [
50], a particular case of the well-known non-dominated sorting genetic algorithm II (NSGA-II) [
74] where the objective function space considers a single objective; the particle swarm optimization (PSO) with a full-connected topology and a linear-decreasing inertia weight in [
75], and the variant DE/rand/1/bin of differential evolution (DE). These new variants are referred to as OGA, OPSO, and ODE.
Regarding the hyperparameters of the above optimizers, there are many approaches to set them up. For instance, in the algorithms from the works in
Table 1, these parameters were tuned by hand (i.e., the best hyperparameters were selected after a series of trials with different combinations) or chosen as the most promising alternative reported in the literature. In this work, the latter approach is preferred because, in practical applications, it is important to provide the parameter setting in an easy way by using a guideline, and it can be more attractive to engineers for implementation purposes. So, the algorithm parameter settings are set based on the suggestions found in the specialized literature, as follows—crossover rate
and scaling factor
for ODE and CODE [
76]; crossover probability
, mutation probability
with
d as the number of design variables, distribution index
in the simulated binary crossover (SBX), and distribution index
in the polynomial mutation (PM) for OGA [
74]; personal and global knowledge constants
and
, and minimum and maximum value of inertia weight
and
for OPSO [
77]. To produce fair comparisons, the number of objective function evaluations is the same for all optimizers, determined by the number of candidate vectors
and the maximum number of iterations
.
4.2. Discussion of the Results
The proposal was tested for the two operating conditions (NOC and DOC) through thirty independent runs for each of the previously described optimizers. For simplicity, the prefix ATCB (adaptive tuning for the controller in BLDC motors) refers to the adaptive tuning strategy based on any other optimizer than CODE. In this way, the alternatives compared with the proposed CATSCG are ATCB/ODE, ATCB/OGA, and ATCB/OPSO.
Each independent run was evaluated using the integral square error (ISE), a helpful performance metric to assess the transient controller response since it (more) weights the large errors [
78].
Table 4 outlines the descriptive statistics over the ISE results of all runs grouped by the operating conditions. This table includes the mean, standard deviation, minimum, and maximum values of ISE for each adaptive tuning strategy, and the best results are highlighted in boldface. Based on the above values, the proposed CATSCG is the best performing alternative for NOC and DOC, and is followed by ATCB/ODE, which also utilizes DE as the optimizer. On the other hand, ATCB/OGA is not far from these two controllers, and ATCB/OPSO develops the worst results. It is important to note that all strategies have a small increase in error under DOC compared to NOC. This highlights the ability of the online optimization-based strategies to handle perturbations, uncertainties, noise, and abrupt changes in the reference.
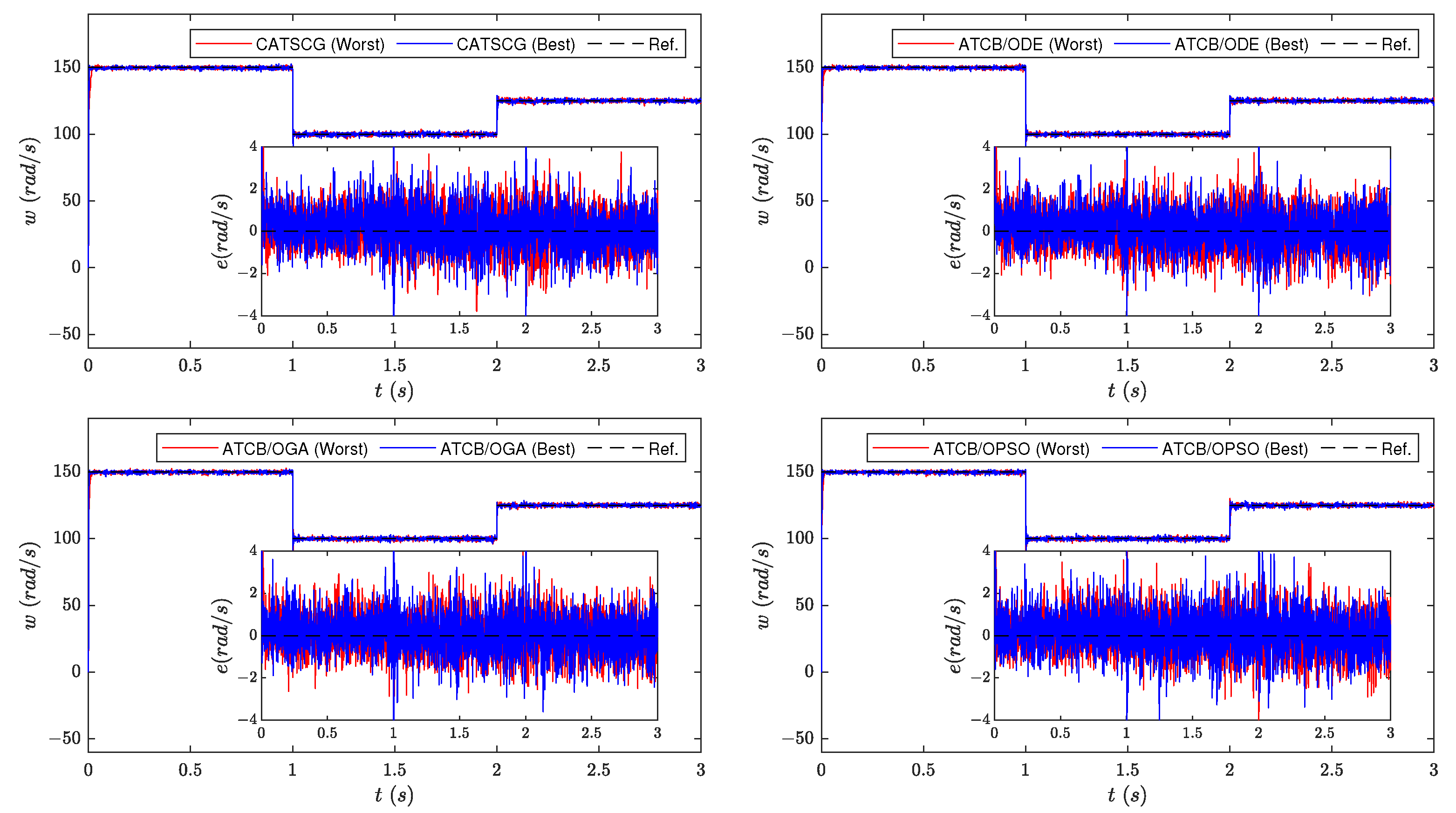
The motor output behaviors of the best and worst runs of each controller are observed in
Figure 6 and
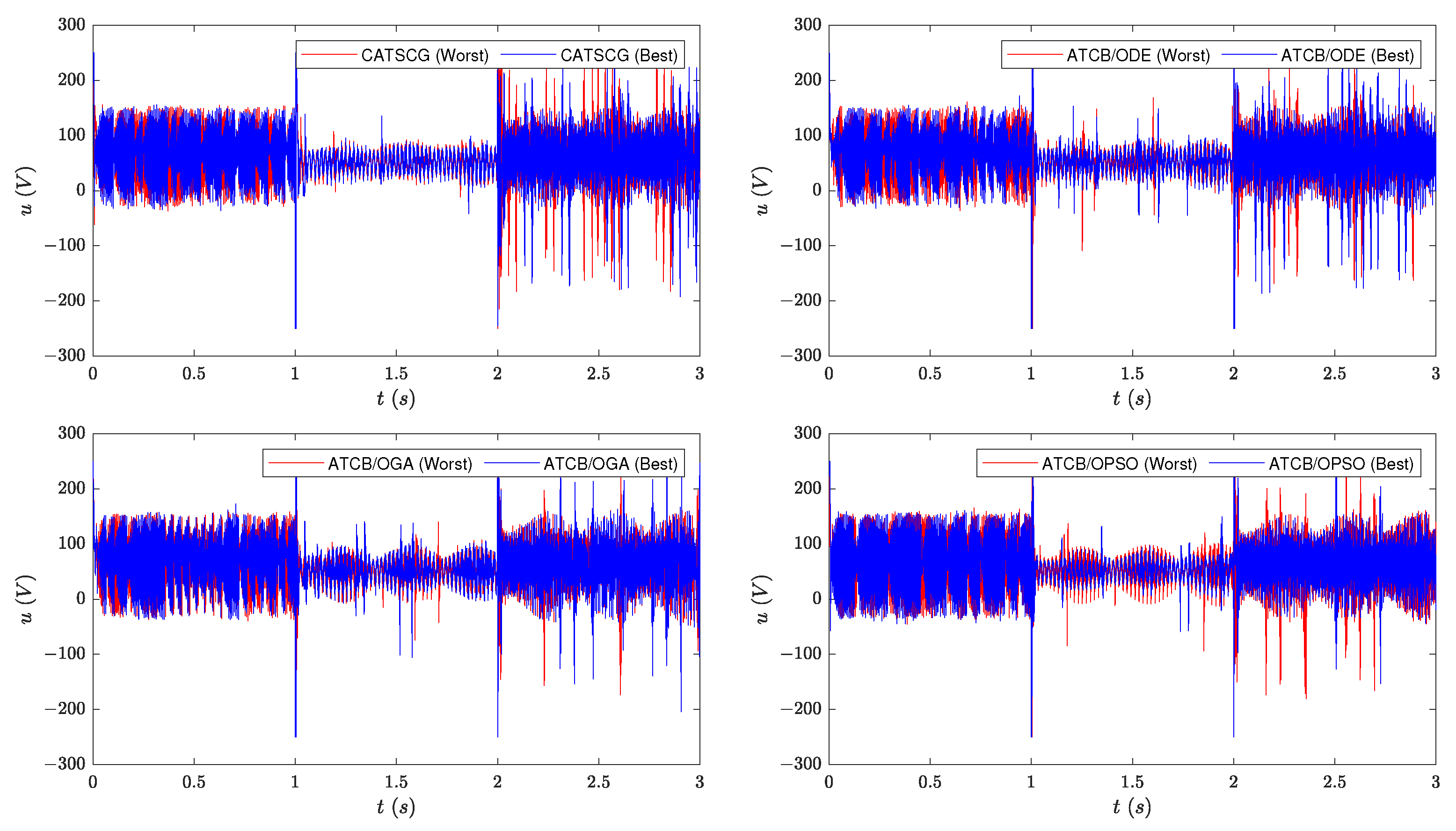
Figure 7 considering NOC and DOC, respectively, while their corresponding control actions are depicted in
Figure 8 and
Figure 9. The inner plots of the speed figures display the evolution of the error in time.
In the speed graphs of all controller alternatives, there is no visible difference between the best and worst outputs for both NOC and DOC conditions. In the case of ATCB/OGA and ATCB/OGA, some error peaks stand out from the inner plots in comparison with the error signals of CATSCG and ATCB/ODE under DOC. In the case of ATCB/OPSO, the peak-to-peak error seems more attenuated than in the rest of the alternatives. Still, it has very high peaks and is always above the reference for both operating conditions.
On the other hand, the control action figures reveal that control strategies require much more energy to compensate for the difficulties of DOC compared to NOC. Concerning the control action,
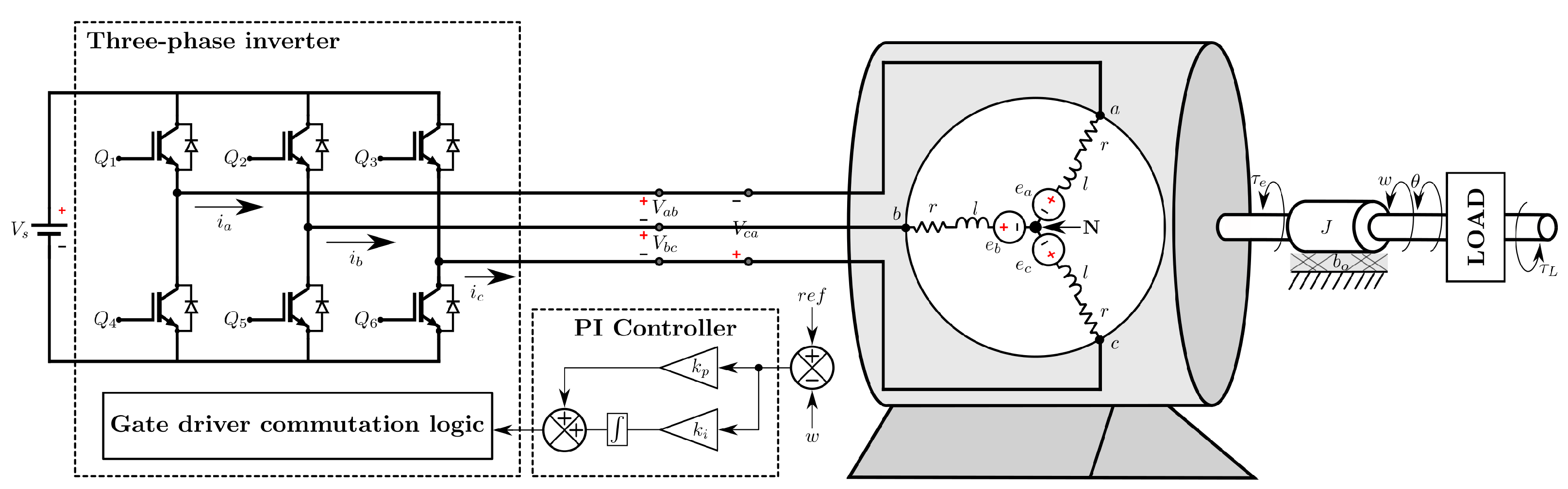
Figure 10 and
Figure 11 give examples of the operation of the coil commutation used in the brushless motor simulation. These figures show the behaviors of the phase voltages
,
, and
for NOC and DOC, respectively. Each figure shows a small time interval of
from the
,
, and
instants.
Returning to the error in the speed regulation task, the remarkable performances of the controllers based on DE are attributed to the suitable balance between the capacities of exploration and exploitation. In the case of ODE, the use of the elitist online adaptation only increases the exploitation ability of DE/rand/1/bin, while exploration may be compromised. In CODE, these two abilities are better balanced by using the chaotic initialization based on the Lozi map, which explains the outstanding performance of CATSCG.
In the case of OGA, the elitism improves the exploitation and is induced by sorting solutions based on fitness. However, the elitism in OGA is tougher than in ODE and CODE, as all poor-performing solutions are removed from the population at the end of each generation, i.e., only the overall fittest ones survive. In contrast, in the DE-based alternatives, selecting the elite solution is performed pairwise between an original solution and its offspring vector, which provides a gap to explore other interesting search space regions. Because of the above, there is a noticeable change in the performance of ATCB/OGA when it passes from NOC to DOC in
Table 4.
On the other side, the opposite happens with OPSO, as the lack of an elitist selection mechanism favors exploration. Therefore, solutions cannot converge to a suitable solution using the available budget of objective function evaluations (this is given by for each optimization process). The above implies a low control performance with ATCB/OPSO when considering NOC, which worsens under DOC.
At this point, it is essential to remember that the approximate optimizers used in this work are stochastic methods. This means that the distribution of their results does not belong to a particular shape (e.g., the normal one). So, the descriptive statistical information in
Table 4 does not provide enough evidence to draw strong conclusions, although it gives a preliminary look at the behaviors of all the controllers. Therefore, the results of the experiments are evaluated in this work through two well-known non-parametric statistical tests: the pairwise Wilcoxon signed-rank test and the multi-comparative Friedman test [
52].
The pairwise Wilcoxon signed-rank test compares the location of two different sets of samples. For this, a null hypothesis indicates no significant differences between the samples of the two sets or they share a similar location. Moreover, an alternative hypothesis suggests that there are noticeable differences between the samples of the two sets in three ways: the samples in the first set are to the left of those in the second (left-sided hypothesis); the samples in the first set are to the right of those in the second (right-sided hypothesis); or the samples in the first set are in a different location than those in the second (two-sided hypothesis). Then, the test outputs a p-value with the probability of accepting the and rejecting the . A statistical significance establishes a threshold of the p-value for which the can be accepted (typically ).
In this study, each sets contains the ISE values of the thirty independent runs of one of the ATCB alternatives and the CATSCG for particular operating conditions. Moreover, the
two-sided hypothesis is selected as the
and the statistical significance is set as
. The results of all possible Wilcoxon tests are presented in
Table 5 and are grouped by the type of operating conditions. In this table, the columns
and
are the sums of ranks calculated for the test. In this way,
indicates the times that a sample of the first set outperforms a sample of the second, while
indicates the contrary. These two columns are displayed to determine the location of the samples of each set and, therefore, decide the winner in boldface when
p-value
.
Table 6 summarizes the results of the Wilcoxon tests, where it is observed that the alternative in boldface, i.e., CATSCG, is the best choice since it obtained a greater number of wins, followed by ATCB/ODE and ATCB/OGA, which performed equally well, and finally by ATCB/OPSO.
Pairwise non-parametric statistical tests, such as the Wilcoxon test, are helpful to compare the samples of two different sets. However, when one wants to compare the samples of several sets as a group, multi-comparative non-parametric statistical tests are necessary [
52].
The multi-comparative Friedman test compares the location of the samples of two or more sets. As in the Wilcoxon case, the Friedman test includes a null hypothesis to indicate no significant differences among the compared sets but adopts a unique alternative hypothesis that suggests the opposite. The p-value obtained with this test also refers to the probability of accepting the . So, a statistical significance (often ) is required to determine when is valid.
In this work, the multi-comparative Friedman test, with
, was applied to the sets of ISE samples for the adaptive controller tuning and the particular operating conditions. The results of this test are displayed in
Table 7 and, according to the
p-value, there are significant differences among the behaviors of all controllers for NOC and DOC (
p-value
in both cases). The magnitude of those differences is observed in the statistic column, which includes the chi-squared (
) statistic value of the test. In this sense, the differences in the performance of the controllers are greater in NOC than in DOC. Additionally,
Table 7 shows the ranks computed with the Friedman test, indicating a particular order of the studied alternatives concerning control performance. In this way, the order from best to worst is the same for both operating conditions: (1) CATSCG, (2) ATCB/ODE, (3) ATCB/OGA, and (4) ATCB/OPSO.
Based on the multi-comparative Friedman test results, all control choices have significantly different performances from each other no matter the operating conditions. Now, it is possible to perform post hoc Friedman tests to analyze particular pairwise cases and determine which ISE sets perform better. For this, the
and
hypotheses are the same as in the multi-comparative Friedman test, and the statistical significance is also established as
.
Table 8 shows the results of all possible post hoc Friedman tests over the sets of ISE samples for adaptive controller tuning and NOC and DOC conditions. In addition to the operating conditions and the information on the test performed, this table includes the unadjusted
p-value and its Holm, Shaffer, and Bergmann corrections [
52], which are highlighted in boldface when they are
(i.e., when
is accepted). The above corrected values help to compensate for errors included in the
p-value calculation for post hoc tests [
52]. Moreover, the test statistic, denoted by
z, is shown in the same table to determine the location of each result set. In this way, a negative value of
z indicates that the first alternative overcomes the second, while a positive one indicates the opposite.
Table 9 summarizes the results of the above post hoc Friedman tests. According to the number of wins in this table, the choice in boldface, i.e., CATSCG, has the best performance and is followed by ATCB/OGA, ATCB/ODE, and ATCB/OPSO.
The results of the non-parametric statistical tests presented previously confirm that CATSCG is the best alternative for the speed regulation of the brushless DC motor under normal operating condition(s) (NOC) and disturbed operating condition(s) (DOC).
In addition to the performance of the CATSCG, it is important to know what are the behaviors of the solutions that it could obtain through online optimization. In this regard,
Figure 12 and
Figure 13 show the brushless motor parameters identified through CODE for the best and worst performances under NOC and DOC, respectively. These results are contrasted with the actual values of the motor parameters, which are also included in the graphs. As can be seen in these figures, the parameters identified by CATSCG are far from the actual ones. This is because the optimization problem for identification does not consider the differences between the real and identified parameters, but the difference between the acquired motor outputs and those obtained through the model simulation. In this way, there can be different combinations of parameters that, used in the model, can generalize the real behavior of the brushless motor.
An additional point to consider is the execution time of each optimization process. Currently, the average time for a run of is with the CATSCG. The above involved using a computer with Intel(R) Core(TM) i5-10400F CPU @ 2.90 GHz and 64.0 GB of RAM, and implementing the control strategy in C++ language through Visual Studio 2019 Community Edition. This indicates that the proposal can be tested in a future experimental stage with a laboratory prototype, but other aspects must be considered, such as the characteristics of the sensors and data acquisition devices, which also consume computational time.