An Image Encryption Scheme Synchronizing Optimized Chaotic Systems Implemented on Raspberry Pis
Abstract
:1. Introduction
2. Chaotic Systems and Random Binary Strings
3. Synchronization of Optimized Chaotic Systems
3.1. Hamiltonian Forms and Observer Approach
3.2. OPCL Synchronization Method
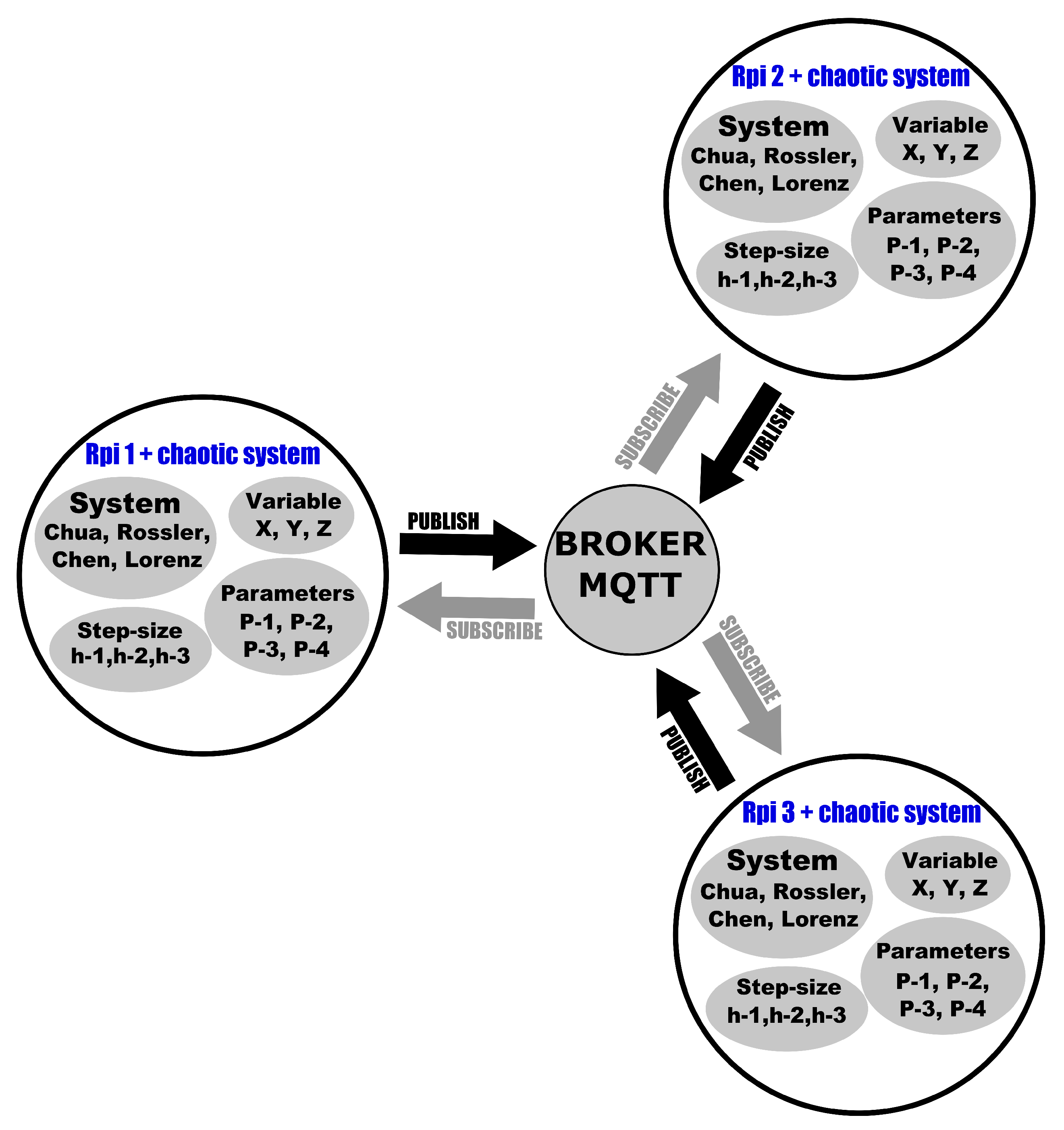
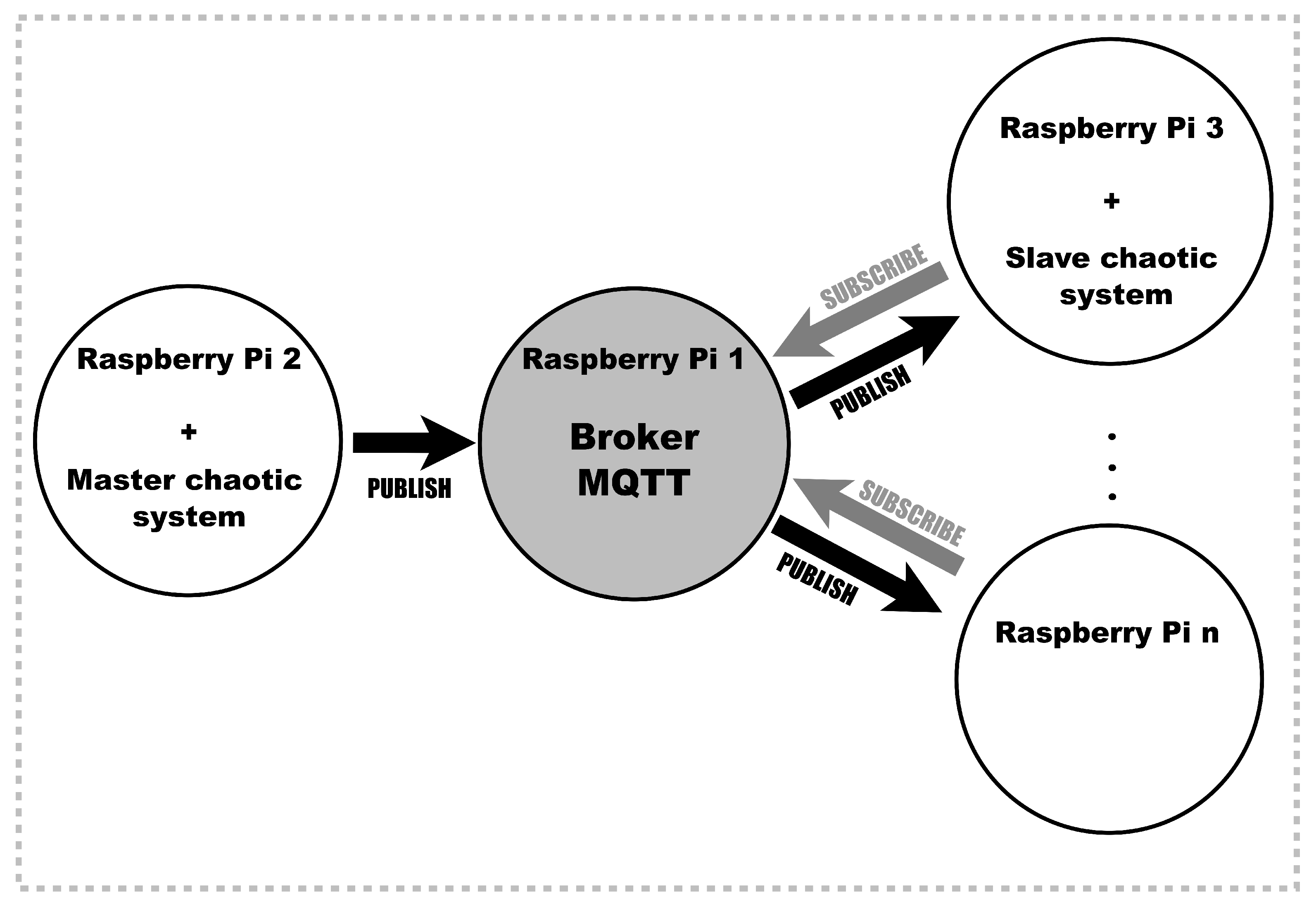
4. Hardware Implementation of an Image Encryption System on MQTT Based on Chaos
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Sira-Ramirez, H.; Cruz-Hernández, C. Synchronization of chaotic systems: A generalized Hamiltonian systems approach. Int. J. Bifurc. Chaos 2001, 11, 1381–1395. [Google Scholar] [CrossRef]
- Li, X.; Zhou, L.; Tan, F. An image encryption scheme based on finite-time cluster synchronization of two-layer complex dynamic networks. Soft Comput. 2022, 26, 511–525. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Zhang, Z.; Huang, Y.; Cai, S.; Du, S. A new multi-scroll Chua?s circuit with composite hyperbolic tangent-cubic nonlinearity: Complex dynamics, Hardware implementation and Image encryption application. Integration 2021, 81, 71–83. [Google Scholar] [CrossRef]
- Deng, J.; Zhou, M.; Wang, C.; Wang, S.; Xu, C. Image segmentation encryption algorithm with chaotic sequence generation participated by cipher and multi-feedback loops. Multimed. Tools Appl. 2021, 80, 13821–13840. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Xiong, L.; Sha, Y.; Yan, H.; Cao, Y. A fast and efficient multiple images encryption based on single-channel encryption and chaotic system. Nonlinear Dyn. 2022, 108, 613–636. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillén-Fernández, O.; Silva-Juárez, A. Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Azizi, M.; Aickelin, U.; Khorshidi, H.A.; Shishehgarkhaneh, M.B. Shape and size optimization of truss structures by Chaos game optimization considering frequency constraints. J. Adv. Res. 2022. [Google Scholar] [CrossRef]
- Hue, A.; Sharma, G.; Dricot, J.M. Privacy-Enhanced MQTT Protocol for Massive IoT. Electronics 2022, 11, 70. [Google Scholar] [CrossRef]
- Liu, S.; Li, C.; Hu, Q. Cryptanalyzing Two Image Encryption Algorithms Based on a First-Order Time-Delay System. IEEE Multimed. 2022, 29, 74–84. [Google Scholar] [CrossRef]
- Meshram, C.; Ibrahim, R.W.; Obaid, A.J.; Meshram, S.G.; Meshram, A.; El-Latif, A.M.A. Fractional chaotic maps based short signature scheme under human-centered IoT environments. J. Adv. Res. 2021, 32, 139–148. [Google Scholar] [CrossRef]
- Radwan, A.; Moaddy, K.; Salama, K.; Momani, S.; Hashim, I. Control and switching synchronization of fractional order chaotic systems using active control technique. J. Adv. Res. 2014, 5, 125–132. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, I.; Ouannas, A.; Shafiq, M.; Pham, V.T.; Baleanu, D. Finite-time stabilization of a perturbed chaotic finance model. J. Adv. Res. 2021, 32, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Bertsias, P.; Psychalinos, C.; Maundy, B.J.; Elwakil, A.S.; Radwan, A.G. Partial fraction expansion-based realizations of fractional-order differentiators and integrators using active filters. Int. J. Circuit Theory Appl. 2019, 47, 513–531. [Google Scholar] [CrossRef]
- Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Minimization of Spread of Time-Constants and Scaling Factors in Fractional-Order Differentiator and Integrator Realizations. Circuits Syst. Signal Process. 2018, 37, 5647–5663. [Google Scholar] [CrossRef]
- Khanday, F.A.; Kant, N.A.; Dar, M.R.; Zulldfli, T.Z.A.; Psychalinos, C. Low-Voltage Low-Power Integrable CMOS Circuit Implementation of Integer- and Fractional-Order FitzHugh-Nagumo Neuron Model. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2108–2122. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Sinencio, E.; Geiger, R.L.; Nevarez-Lozano, H. Generation of continuous-time two integrator loop OTA filter structures. IEEE Trans. Circuits Syst. 1988, 35, 936–946. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef] [PubMed]
- Schuster, H.G.; Just, W. Deterministic Chaos: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Parker, T.S.; Chua, L. Practical Numerical Algorithms for Chaotic Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Hegger, R.; Kantz, H.; Schreiber, T. Practical implementation of nonlinear time series methods: The TISEAN package. Chaos Interdiscip. J. Nonlinear Sci. 1999, 9, 413–435. [Google Scholar] [CrossRef] [Green Version]
- Tlelo-Cuautle, E.; De La Fraga, L.G.; Guillén-Fernández, O.; Silva-Juárez, A. Optimization of Integer/Fractional Order Chaotic Systems by Metaheuristics and Their Electronic Realization; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Hooker, J.N. Testing heuristics: We have it all wrong. J. Heuristics 1995, 1, 33–42. [Google Scholar] [CrossRef]
- Coello, C.A.C. A comprehensive survey of evolutionary-based multiobjective optimization techniques. Knowl. Inf. Syst. 1999, 1, 269–308. [Google Scholar] [CrossRef]
- Rosenberg, R.S. Stimulation of genetic populations with biochemical properties: I. the model. Math. Biosci. 1970, 7, 223–257. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000; pp. 849–858. [Google Scholar]
- Abarbanel, H.D.; Brown, R.; Sidorowich, J.J.; Tsimring, L.S. The analysis of observed chaotic data in physical systems. Rev. Mod. Phys. 1993, 65, 1331. [Google Scholar] [CrossRef] [Green Version]
- Yalçin, M.E. Increasing the entropy of a random number generator using n-scroll chaotic attractors. Int. J. Bifurc. Chaos 2007, 17, 4471–4479. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Technical Report; Booz-Allen and Hamilton Inc.: Mclean, VA, USA, 2001. [Google Scholar]
- L’ecuyer, P.; Simard, R. TestU01: AC library for empirical testing of random number generators. ACM Trans. Math. Softw. (TOMS) 2007, 33, 1–40. [Google Scholar] [CrossRef]
- Pareschi, F.; Rovatti, R.; Setti, G. Simple and effective post-processing stage for random stream generated by a chaos-based RNG. In Proceedings of the NOLTA, Bologna, Italy, 11–14 September 2006; pp. 383–386. [Google Scholar]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.; Zhou, C. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Carroll, T.L.; Pecora, L.M. Synchronizing chaotic circuits. IEEE Trans. Circuits Syst. 1991, 38, 453–456. [Google Scholar] [CrossRef] [Green Version]
- Lerescu, A.; Constandache, N.; Oancea, S.; Grosu, I. Collection of master—Slave synchronized chaotic systems. Chaos Solitons Fractals 2004, 22, 599–604. [Google Scholar] [CrossRef] [Green Version]
- Melendez-Cano, A.; Rodriguez, J.S.; Sandoval-Ibarra, Y.; Cardenas-Valdez, J.R.; Garcia-Ortega, M.J.; Tlelo-Cuautle, E.; Nuñez-Perez, J.C. Chaotic Synchronization of Sprott Collection and RGB Image Transmission. In Proceedings of the Mechatronics, Electronics and Automotive Engineering (ICMEAE), 2017 International Conference, Cuernavaca, Mexico, 21–24 November 2017; pp. 49–54. [Google Scholar]
- Vaidyanathan, S.; Sampath, S.; Azar, A.T. Global chaos synchronisation of identical chaotic systems via novel sliding mode control method and its application to Zhu system. Int. J. Model. Identif. Control. 2015, 23, 92–100. [Google Scholar] [CrossRef]
- Chen, X.; Park, J.H.; Cao, J.; Qiu, J. Sliding mode synchronization of multiple chaotic systems with uncertainties and disturbances. Appl. Math. Comput. 2017, 308, 161–173. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A.; Srinivasan, A.K. FPGA implementation of novel fractional-order chaotic systems with two equilibriums and no equilibrium and its adaptive sliding mode synchronization. Nonlinear Dyn. 2017, 87, 2281–2304. [Google Scholar] [CrossRef]
- Nosrati, K.; Volos, C.; Azemi, A. Cubature Kalman filter-based chaotic synchronization and image encryption. Signal Process. Image Commun. 2017, 58, 35–48. [Google Scholar] [CrossRef]
- Abd, M.H.; Tahir, F.R.; Al-Suhail, G.A.; Pham, V.T. An adaptive observer synchronization using chaotic time-delay system for secure communication. Nonlinear Dyn. 2017, 90, 2583–2598. [Google Scholar] [CrossRef]
- Wang, Y.; Karimi, H.R.; Yan, H. An adaptive event-triggered synchronization approach for chaotic Lur?e systems subject to aperiodic sampled data. IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 442–446. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C.; Pham, V.T.; Madhavan, K. Analysis, adaptive control and synchronization of a novel 4-D hyperchaotic hyperjerk system and its SPICE implementation. Arch. Control. Sci. 2015, 25, 135–158. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Akgul, A.; Kaçar, S.; Çavuşoğlu, U. A new 4-D chaotic hyperjerk system, its synchronization, circuit design and applications in RNG, image encryption and chaos-based steganography. Eur. Phys. J. Plus 2018, 133, 46. [Google Scholar] [CrossRef]
- Pham, V.T.; Kingni, S.T.; Volos, C.; Jafari, S.; Kapitaniak, T. A simple three-dimensional fractional-order chaotic system without equilibrium: Dynamics, circuitry implementation, chaos control and synchronization. AEU-Int. J. Electron. Commun. 2017, 78, 220–227. [Google Scholar] [CrossRef]
- Daltzis, P.A.; Volos, C.K.; Nistazakis, H.E.; Tsigopoulos, A.D.; Tombras, G.S. Analysis, Synchronization and Circuit Design of a 4D Hyperchaotic Hyperjerk System. Computation 2018, 6, 14. [Google Scholar] [CrossRef] [Green Version]
- Ye, G.; Pan, C.; Huang, X.; Zhao, Z.; He, J. A Chaotic Image Encryption Algorithm Based on Information Entropy. Int. J. Bifurc. Chaos 2018, 28, 1850010. [Google Scholar] [CrossRef]
- Jackson, E.A.; Grosu, I. An open-plus-closed-loop (OPCL) control of complex dynamic systems. Phys. D Nonlinear Phenom. 1995, 85, 1–9. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, X.; Wang, M.; Zhang, Y. Simple colour image cryptosystem with very high level of security. Chaos Solitons Fractals 2020, 141, 110225. [Google Scholar] [CrossRef]
- Yousif, S.F.; Abboud, A.J.; Radhi, H.Y. Robust image encryption with scanning technology, the El-Gamal algorithm and chaos theory. IEEE Access 2020, 8, 155184–155209. [Google Scholar] [CrossRef]
- Flores-Vergara, A.; García-Guerrero, E.; Inzunza-González, E.; López-Bonilla, O.; Rodríguez-Orozco, E.; Cárdenas-Valdez, J.; Tlelo-Cuautle, E. Implementing a chaotic cryptosystem in a 64-bit embedded system by using multiple-precision arithmetic. Nonlinear Dyn. 2019, 96, 497–516. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. Cyber J. Multidiscip. J. Sci. Technol. J. Sel. Areas Telecommun. (JSAT) 2011, 1, 31–38. [Google Scholar]


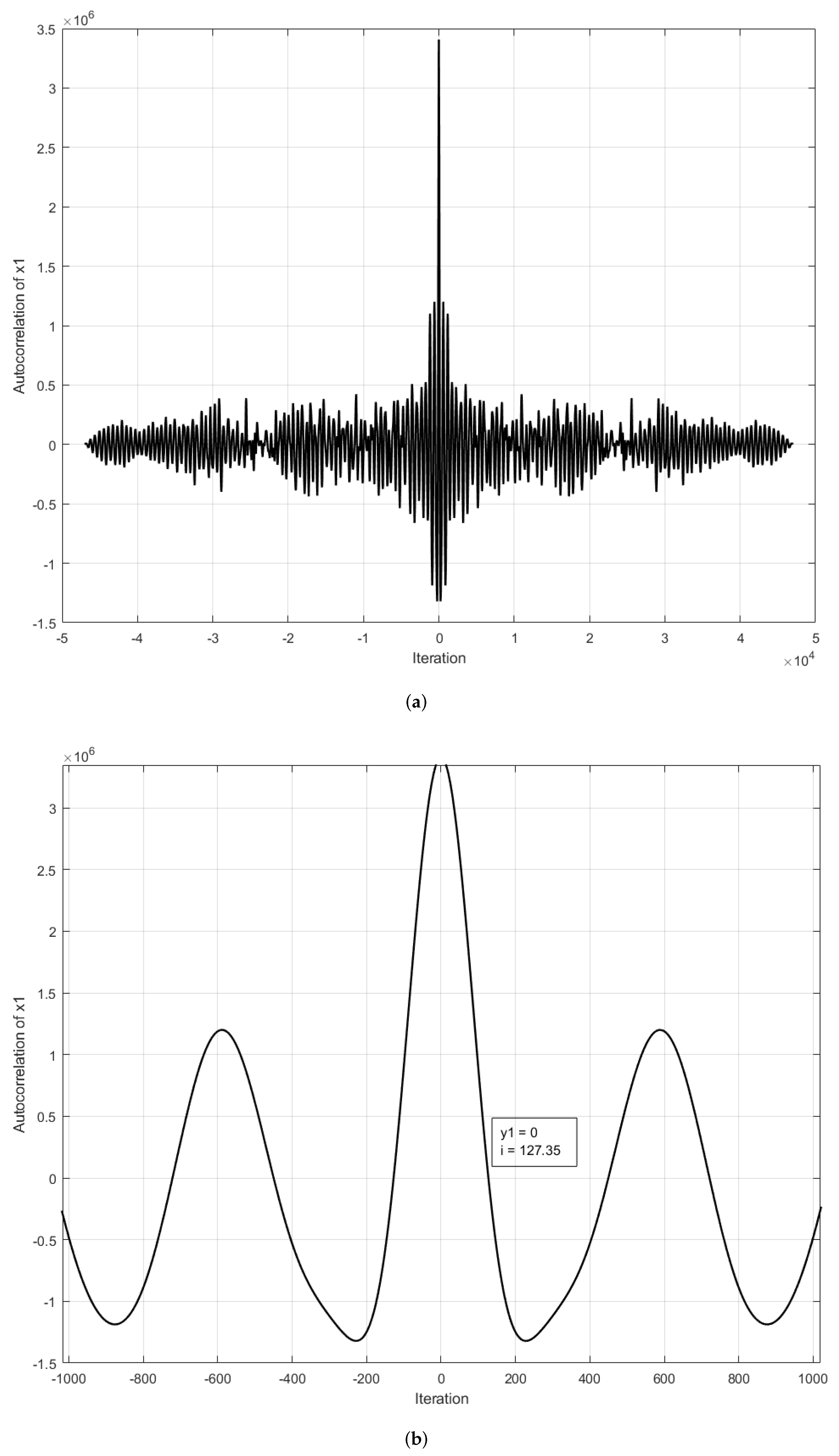
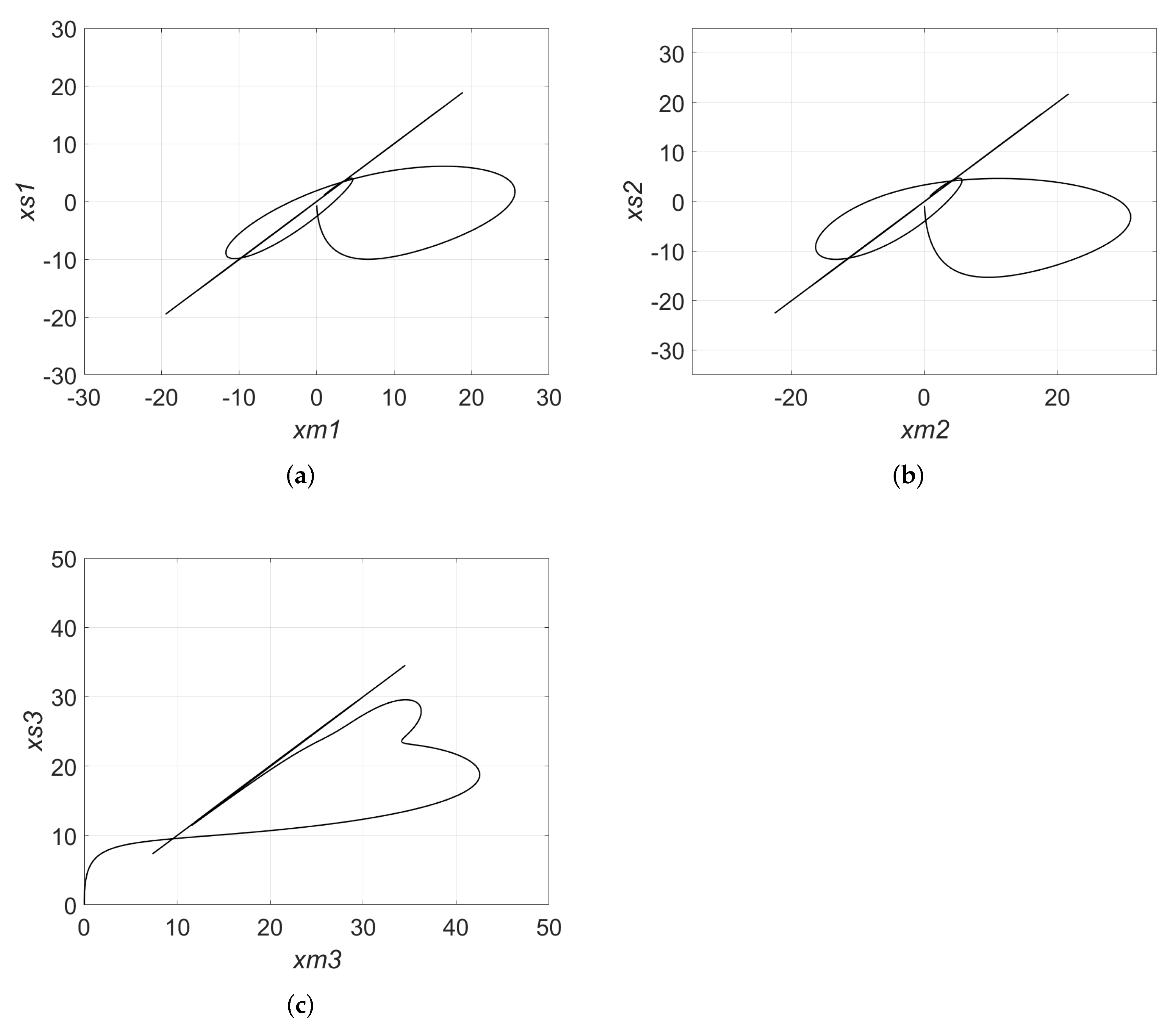
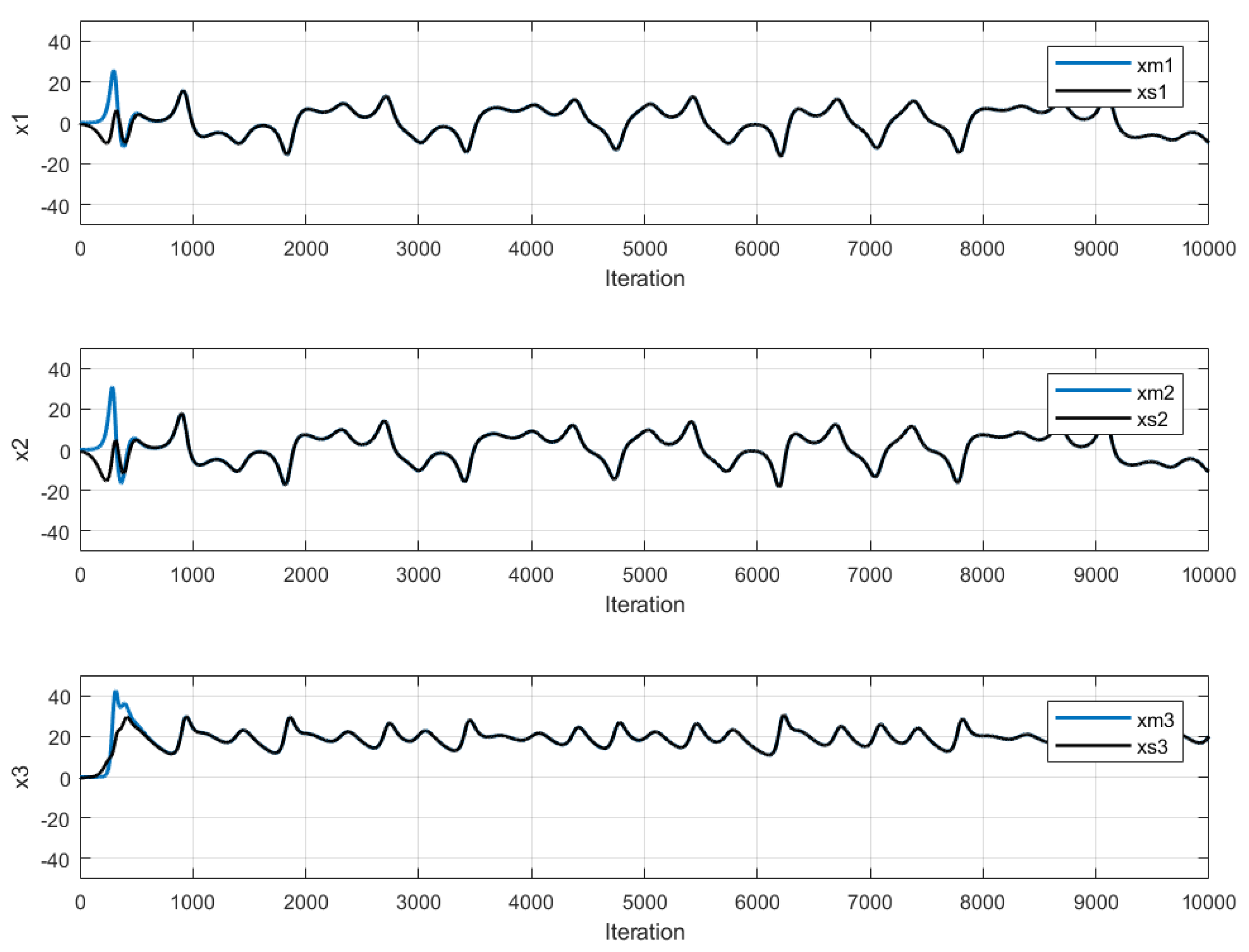
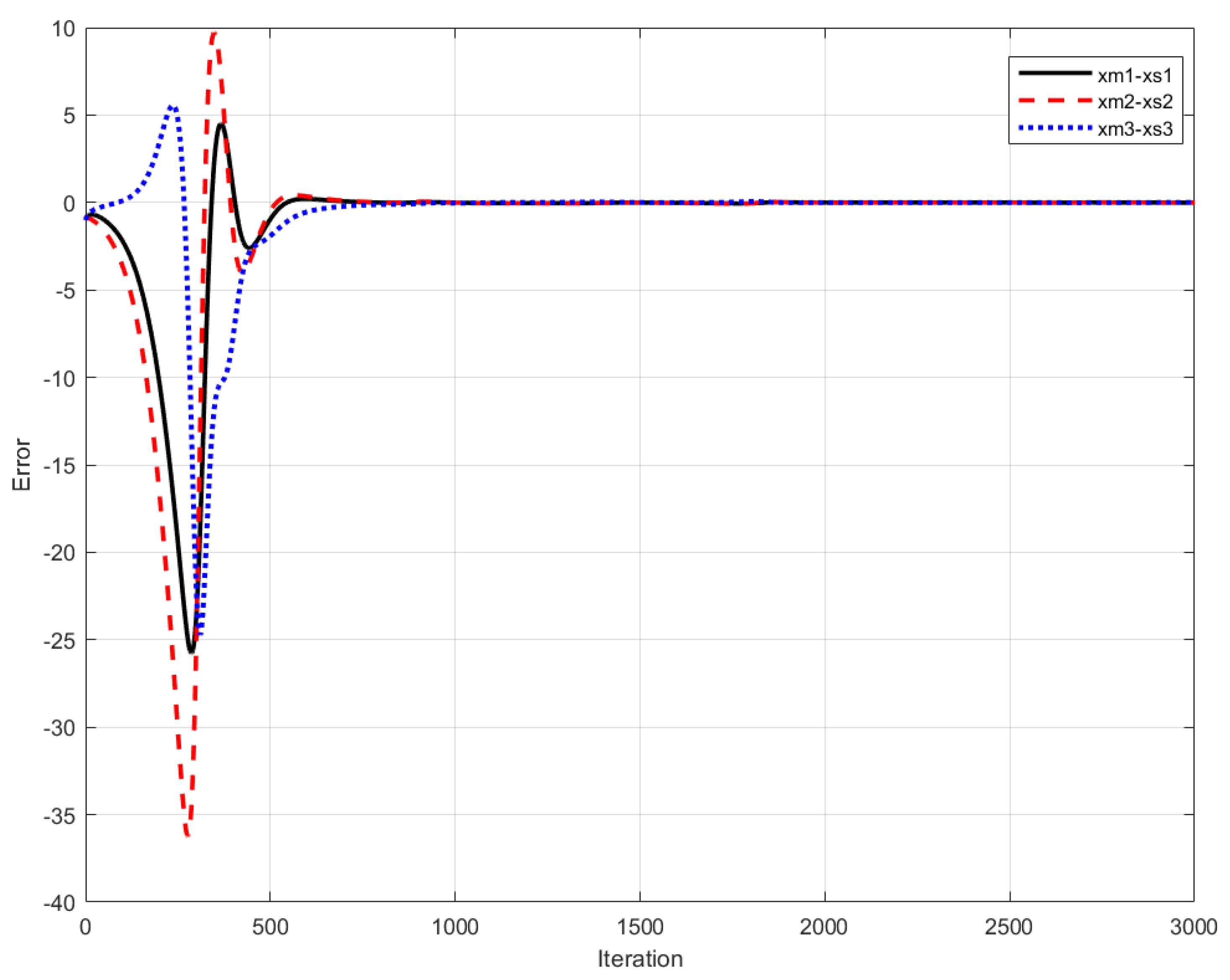






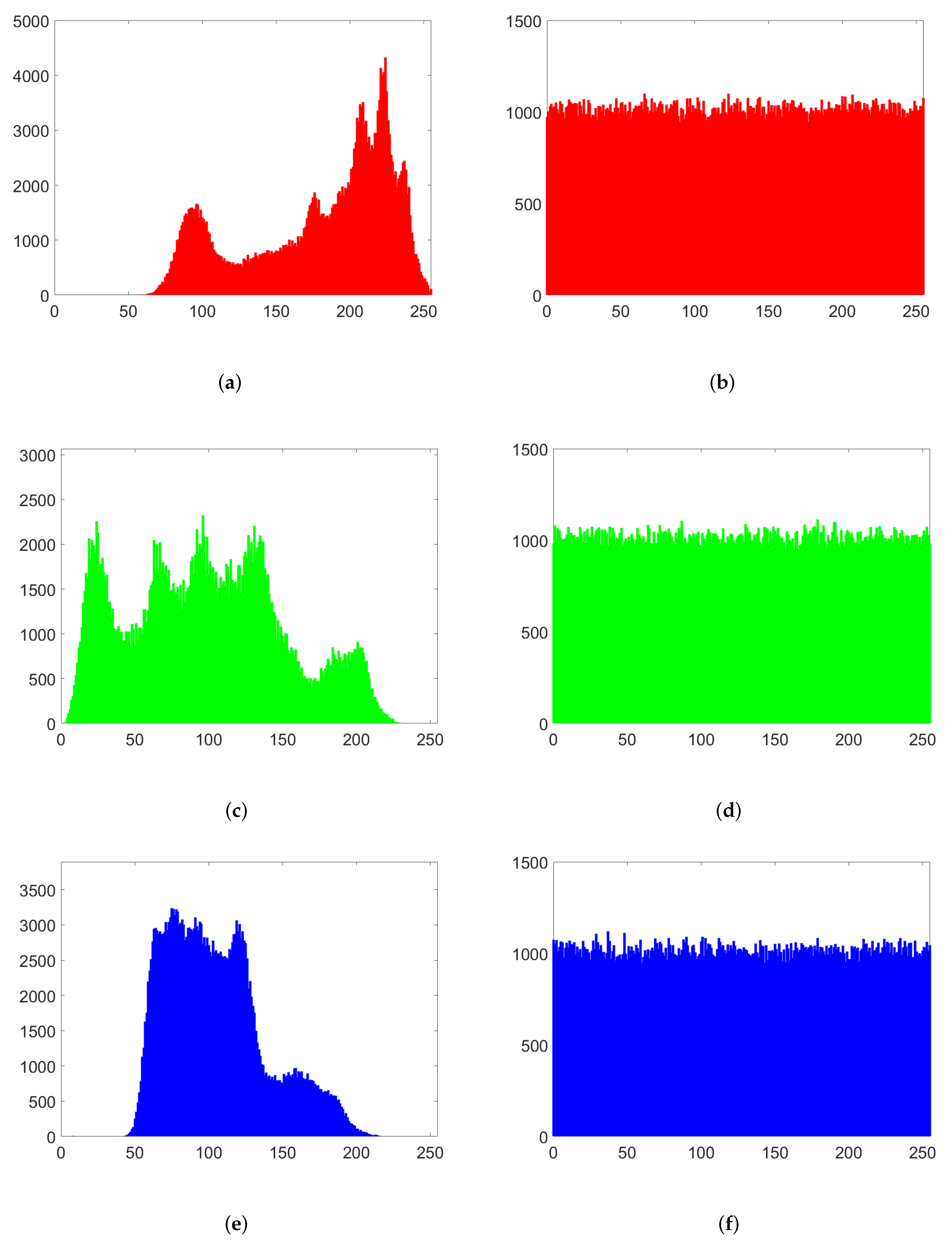

| a | b | c | LE+ | |
|---|---|---|---|---|
| 35.0 | 3.0 | 28.0 | 2.0440 | 2.1698 |
| 35.514979 | 2.6385232 | 27.582793 | 2.6800429 | 2.2042597 |
| 35.488084 | 2.6193955 | 27.584261 | 2.6794532 | 2.2050013 |
| 33.532833 | 1.4708819 | 27.400097 | 2.4047606 | 2.2425449 |
| 33.0 | 1.2355012 | 27.714443 | 2.2429468 | 2.2592703 |
| 33.0 | 1.0910769 | 27.836426 | 2.2172809 | 2.2663249 |
| Statistical Test | p-Value without XOR | Proportion without XOR | p-Value with XOR | Proportion with XOR |
|---|---|---|---|---|
| Frequency | 0.021932 | 96/100 | 0.657933 | 99/100 |
| BlockFrequency | 0.494136 | 98/100 | 0.319084 | 98/100 |
| CumulativeSums | 0.002230 | 87/100 * | 0.236810 | 99/100 |
| CumulativeSums | 0.002357 | 95/100 * | 0.455937 | 99/100 |
| Runs | 0.797481 | 99/100 | 0.137282 | 99/100 |
| LongestRun | 0.887251 | 100/100 | 0.657933 | 99/100 |
| FFT | 0.192597 | 99/100 | 0.616305 | 99/100 |
| ApproximateEntropy | 0.977971 | 100/100 | 0.000555 | 98/100 |
| Serial | 0.076439 | 100/100 | 0.115387 | 100/100 |
| Serial | 0.042955 | 100/100 | 0.000513 | 100/100 |
| LinearComplexity | 0.256352 | 94/100 * | 0.759756 | 98/100 |
| Statistical Set | Number of Bits | Total Time Test | Total Tests | Not Passed Tests | Eps Value |
|---|---|---|---|---|---|
| Rabbit | 100,000,000 | 00:01:04.78 | 40 | 1 MultinomialBitsOver | < |
| 8 Fourier3 | < | ||||
| alphabit1 | 100,000,000 | 00:00:02.14 | 17 | 3 MultinomialBitsOver | < |
| 4 MultinomialBitsOver | < | ||||
| alphabit2 | 100,000,000 | 00:00:02.50 | 17 | 3 MultinomialBitsOver | < |
| 4 MultinomialBitsOver | < |
| Image | Correlation OEI | Correlation ORI |
|---|---|---|
| Lena 512 × 512 pixels | 0.0066 | 1.0 |
| Baboon 512 × 512 pixels | 0.0109 | 1.0 |
| Correlation | Original Image | Encrypted Image |
|---|---|---|
| Vertical | 0.9895 | −0.0013 |
| Horizontal | 0.9796 | 0.0080 |
| Diagonal | 0.9689 | −0.0113 |
| Analysis | Color | Value (%) | Test with Critical Values [53] |
|---|---|---|---|
| NPCR | R | successful | |
| G | successful | ||
| B | successful | ||
| RGB | successful | ||
| UACI | R | successful | |
| G | successful | ||
| B | successful | ||
| RGB | successful |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guillén-Fernández, O.; Tlelo-Cuautle, E.; de la Fraga, L.G.; Sandoval-Ibarra, Y.; Nuñez-Perez, J.-C. An Image Encryption Scheme Synchronizing Optimized Chaotic Systems Implemented on Raspberry Pis. Mathematics 2022, 10, 1907. https://doi.org/10.3390/math10111907
Guillén-Fernández O, Tlelo-Cuautle E, de la Fraga LG, Sandoval-Ibarra Y, Nuñez-Perez J-C. An Image Encryption Scheme Synchronizing Optimized Chaotic Systems Implemented on Raspberry Pis. Mathematics. 2022; 10(11):1907. https://doi.org/10.3390/math10111907
Chicago/Turabian StyleGuillén-Fernández, Omar, Esteban Tlelo-Cuautle, Luis Gerardo de la Fraga, Yuma Sandoval-Ibarra, and Jose-Cruz Nuñez-Perez. 2022. "An Image Encryption Scheme Synchronizing Optimized Chaotic Systems Implemented on Raspberry Pis" Mathematics 10, no. 11: 1907. https://doi.org/10.3390/math10111907
APA StyleGuillén-Fernández, O., Tlelo-Cuautle, E., de la Fraga, L. G., Sandoval-Ibarra, Y., & Nuñez-Perez, J.-C. (2022). An Image Encryption Scheme Synchronizing Optimized Chaotic Systems Implemented on Raspberry Pis. Mathematics, 10(11), 1907. https://doi.org/10.3390/math10111907










